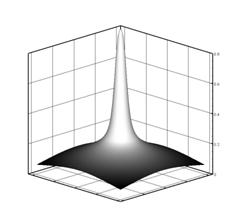
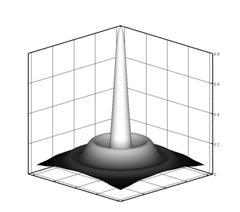
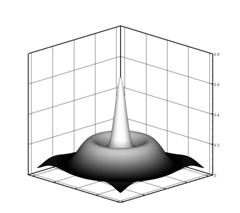
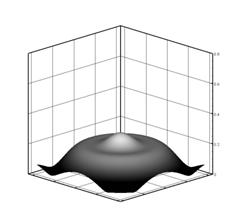
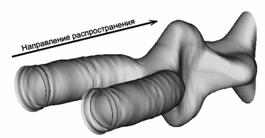
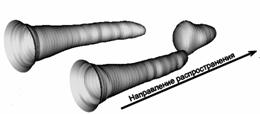
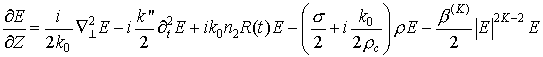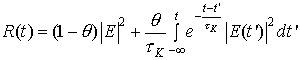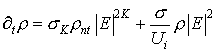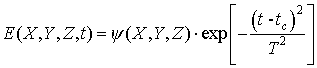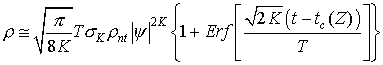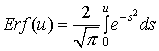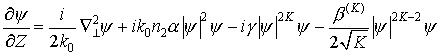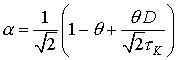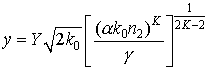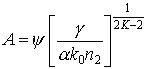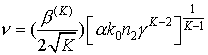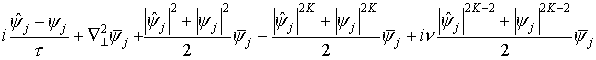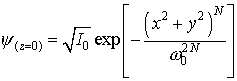Характер образования множественной филаментации фемтосекундного импульса
|
|
|
|
|
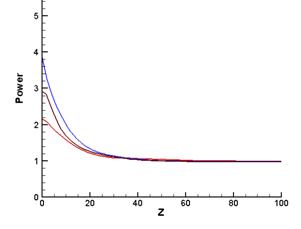
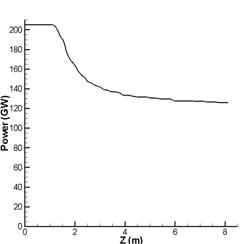
Рис.2–а. Динамика мощности |
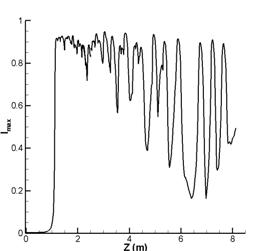
Рис.2–б. Динамика пиковой
интенсивности |
Рост интенсивности в
рассматриваемой задаче ограничен плазменными эффектами и, как видно из рисунка,
максимальное значение интенсивности не превышает 1. В физических величинах
максимальная величина интенсивности составляет ![]() , что согласуется с экспериментальными данными. При возрастании
интенсивности все большую роль начинает играть последний член в уравнении (4),
ответственный за многофотонное поглощение, таким образом, как видно на рис.2-а,
наблюдается резкое уменьшение мощности импульса. В то же время усиливается
влияние другого члена уравнения, ответственного за многофотонную ионизацию,
благодаря которому уменьшается действие эффекта Керра. В результате поглощения
излучения в процессе многофотонной ионизации и дефокусировки падает пиковая
интенсивность импульса, что приводит к прекращению многофотонной ионизации и
постоянству интеграла мощности вплоть до следующего момента возрастания
интенсивности.
, что согласуется с экспериментальными данными. При возрастании
интенсивности все большую роль начинает играть последний член в уравнении (4),
ответственный за многофотонное поглощение, таким образом, как видно на рис.2-а,
наблюдается резкое уменьшение мощности импульса. В то же время усиливается
влияние другого члена уравнения, ответственного за многофотонную ионизацию,
благодаря которому уменьшается действие эффекта Керра. В результате поглощения
излучения в процессе многофотонной ионизации и дефокусировки падает пиковая
интенсивность импульса, что приводит к прекращению многофотонной ионизации и
постоянству интеграла мощности вплоть до следующего момента возрастания
интенсивности.
Значение гамильтониана ![]() к моменту установления
постоянного уровня мощности (рис.2–а) меняет знак на положительный, что, как
известно [13], является необходимым условием расходимости пучка в среднем.
Однако факт расходимости пучка в среднем не противоречит тому, что некоторая
его внутренняя часть может сфокусироваться. Проанализировать дальнейшее
развитие профиля можно с помощью теории Беспалова-Таланова. Для этого рассмотрим
спектральный состав распределения
к моменту установления
постоянного уровня мощности (рис.2–а) меняет знак на положительный, что, как
известно [13], является необходимым условием расходимости пучка в среднем.
Однако факт расходимости пучка в среднем не противоречит тому, что некоторая
его внутренняя часть может сфокусироваться. Проанализировать дальнейшее
развитие профиля можно с помощью теории Беспалова-Таланова. Для этого рассмотрим
спектральный состав распределения ![]() на достаточно большом
расстоянии
на достаточно большом
расстоянии ![]() (рис. 3).
(рис. 3).
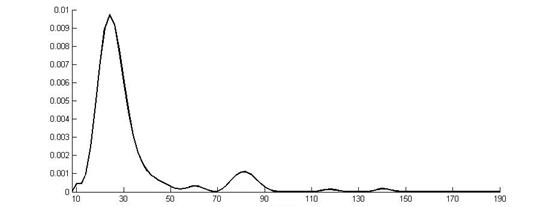
Рис. 3. Спектральный состав
распределения ![]()
Напомним [6], что инкремент неустойчивости играет
роль, только если в спектре импульса присутствуют гармоники, меньшие по
величине среднего значения распределения ![]() , которое для рассматриваемого
, которое для рассматриваемого ![]() почти равно нулю.
Поэтому с точки зрения неустойчивости Беспалова-Таланова дальнейшее развитие
неустойчивых возмущений не возможно.
почти равно нулю.
Поэтому с точки зрения неустойчивости Беспалова-Таланова дальнейшее развитие
неустойчивых возмущений не возможно.
Чтобы объяснить ступенчатый характер падения
мощности, рассмотрим подробнее этапы самофокусировки Гауссова импульса,
описанные в [9]. Как было сказано ранее, для самофокусировки Гауссова импульса
необходима концентрация малых частот спектра. Если ширина пучка велика, то
также велика доля низкочастотных компонент и происходит самофокусировка без
начального уширения импульса в отличие от того, как это бывает с менее широкими
импульсами. В итоге образуется довольно крутой «столб» интенсивности с наличием
вокруг фона из дефокусирующейся части начального импульса (рис.4-а). Но при
достижении пиковым значением интенсивности порогового значения начинается
падение интенсивности как за счет потери энергии на ионизацию, так и
дефокусирующего воздействия электронной плазмы, возникшей в результате
многофотонной ионизации. Первые участки, на которые оказывается воздействие,
являются зонами больших градиентов. В рассматриваемом случае интенсивность
падает быстрее на краю «столба» (рис.4-б).
|
|
|
|
Рис. 4-а.
Распределение |
Рис. 4-б.
Распределение |
|
|
|
|
Рис. 4-в.
Распределение |
Рис. 4-г.
Распределение |
При дальнейшем падении интенсивности отток
мощности от центра встречается с областями подпитки и образуется квазистационарная
кольцевая структура (рис.4-в). На рис.5 (который соответствует рис.4-б)
показаны потоки мощности, определяемые градиентом фазы ![]() . На рисунке можно
выделить 3 структуры: центральный приосевой профиль и 2 кольцевых структуры.
Внутри этих колец поток мощности направлен к центру. Эти структуры можно
отделить друг от друга областями с минимальной интенсивностью, где поток
мощности направлен «от центра» (заштрихованы на рисунке).
. На рисунке можно
выделить 3 структуры: центральный приосевой профиль и 2 кольцевых структуры.
Внутри этих колец поток мощности направлен к центру. Эти структуры можно
отделить друг от друга областями с минимальной интенсивностью, где поток
мощности направлен «от центра» (заштрихованы на рисунке).

Рис. 5 Градиент
фазы распределения комплекснозначной величины ![]() .
.
При концентрации определенной мощности в кольцевой
структуре после падения всего «столба» создаются условия для повторного роста
интенсивности (рис.4-г). Такими условиями в рассмотренном случае являются форма
распределения (рис.4-г) - Гауссов профиль с мощностью, большей критической, и
достаточной для развития самофокусировки полушириной. Таким образом, происходит
первоначальный рост интенсивности, образование кольцевой структуры и после
падения интенсивности формирование такого профиля, который вновь
самофокусируется. В итоге получается ступенчатое падение мощности импульса
(рис.2-а).
Характер изменения мощности на рис.1 можно
объяснить отсутствием вокруг импульса «фона» низкочастотных компонент спектра.
Поэтому моделирование распространения импульсов необходимо начинать с момента
входа лазерного импульса в нелинейную среду, а не со стадии развитой
самофокусировки. Также стоит отметить, что под установлением постоянного уровня
мощности (рис.2–а) понимается лишь
сохранение ее до какого то ![]() , потому что, как
обсуждалось ранее, и в случае устойчивых возмущений возможен процесс
филаментации на дальних расстояниях.
, потому что, как
обсуждалось ранее, и в случае устойчивых возмущений возможен процесс
филаментации на дальних расстояниях.
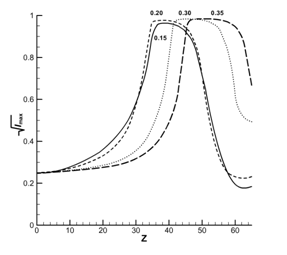
На рис.6 одновременно представлены зависимости
падения мощности импульса (Power) и возрастания
его пиковой интенсивности (Intensity) на
протяжении распространения импульса (z). Можно заметить,
что уровень, при котором начинается поглощение, равен ![]() . Известна оценка
[17], что ионизация воздуха становится существенной при интенсивности
4.5·1013Ватт/см2
, что и
соответствует найденному безразмерному
пороговому значению. По мере уменьшения мощности импульса уменьшается величина
теряемой мощности и длина, на которой наблюдается поглощение.
. Известна оценка
[17], что ионизация воздуха становится существенной при интенсивности
4.5·1013Ватт/см2
, что и
соответствует найденному безразмерному
пороговому значению. По мере уменьшения мощности импульса уменьшается величина
теряемой мощности и длина, на которой наблюдается поглощение.
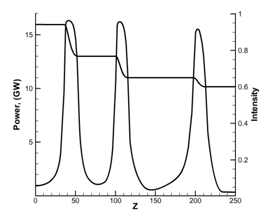
Рис.6
Сопоставление интенсивности и мощности
Напишем уравнение для изменения мощности по ![]() . Для этого умножим
уравнение (4) на
. Для этого умножим
уравнение (4) на ![]() и сложим с комплексно-сопряженным уравнением
для (4), умноженным на
и сложим с комплексно-сопряженным уравнением
для (4), умноженным на ![]() . Проинтегрировав
по всей поперечной плоскости
. Проинтегрировав
по всей поперечной плоскости ![]() , получим
, получим
![]() ;
; ![]() ;
;
![]() .
.
Для получения равенства по порядку величины было
использовано выражение для формы начального профиля импульса. Таким образом,
можно оценить длину диссипативного участка
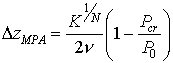 ,
,
которая при ![]() и при
и при ![]() стремится к максимальной величине
стремится к максимальной величине ![]() , что и
подтверждается приведенными выше результатами вычислений. В физических
величинах
, что и
подтверждается приведенными выше результатами вычислений. В физических
величинах ![]() .
.
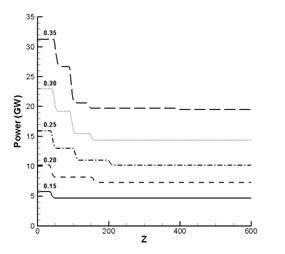
Характер ступенчатого развития мощности импульса
также зависит от его первоначальной ширины. На рис. 7 приведены графики
изменения мощности для импульсов одинаковой мощности.
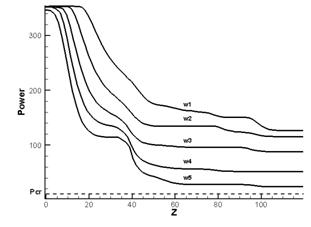
Рис.7. Изменение мощности при
различных начальных ширинах импульсов (![]() )
)
5.
Результаты
вычислений для двух Гауссовых импульсов
В работе [9] нами уже
было рассмотрено взаимное влияние друг на друга двух Гауссовых импульсов. При
наличии многофотонной ионизации влияние становится более заметным. Работы по
моделированию влияния двух импульсов проводились группой исследователей под
руководством В.П. Кандидова и описаны в [10], где приведены условия на мощность
импульсов и расстояние между ними, при которых взаимодействие возможно. Но, как
и во многих работах, не уделено должное внимание к зависимости соотношения
между ширинами импульсов и их интенсивностями – при одинаковых значениях мощности
эти соотношения могут широко варьироваться. Кроме того, наглядно не показан
характер взаимодействия областей высокой интенсивности импульсов и не
рассмотрен вопрос о точке (![]() ) начала взаимодействия.
) начала взаимодействия.
Приведем два
показательных примера расчета двух Гауссовых профилей, демонстрирующих, как
наличие диссипации влияет на характер развития областей высокой интенсивности.
Были рассмотрены два равных Гауссовых возмущений с полушириной ![]() и амплитудой интенсивности
и амплитудой интенсивности ![]() на расстоянии
на расстоянии ![]() . Распространение импульса моделировалось на расстояние
. Распространение импульса моделировалось на расстояние ![]() .
.
|
|
|
|
Рис.8-а. Области высокой
интенсивности для двух равных Гауссовых возмущений с |
Рис.8-б. Области высокой
интенсивности для двух равных Гауссовых возмущений с |
Как видно из рисунков, в
консервативном случае (рис.8-а), т.е. при ![]() в формуле (3), мощность импульса
концентрируется в середине между двух возмущений и сохраняется в области,
подвергаясь колебаниям. При наличии диссипации (
в формуле (3), мощность импульса
концентрируется в середине между двух возмущений и сохраняется в области,
подвергаясь колебаниям. При наличии диссипации (![]() , рис.8-б), каждый из двух импульсов начинает терять мощность, сужаясь при
этом, а момент слияния находится намного дальше по
, рис.8-б), каждый из двух импульсов начинает терять мощность, сужаясь при
этом, а момент слияния находится намного дальше по ![]() , чем в консервативном случае.
, чем в консервативном случае.
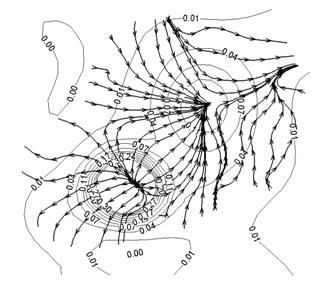
Рис.9 Переток
мощности в широком пучке.
Взаимодействие между филаментами в широком
импульсе с мощностью, на много превышающей критическую более сложно. Пример
перетока мощности из развитой филаменты с максимальной интенсивностью в
область, где зарождается новая филамента, представлен на рис. 9.
6.
Результаты
расчета мощного лазерного импульса
Развитие параллельных вычислительных методов, как
правило, ведет к возможности расчета реальных физических систем. В случае
рассмотрения распространения на дальние дистанции лазерного импульса применение
параллельных технологий также обосновано. Целью данной работы является доказать
возможность такого расчета.
Мощность реального лазерного импульса достигает
нескольких терраватт, ширина импульса может достигать нескольких сантиметров.
Профиль импульса реальных лазерных систем обычно задают в форме функции
супер-гаусса, т.е. показатель степени ![]() в формуле (5).
Особенностью реального лазерного пучка также является наличие шума во входном
профиле. Для воспроизведения случайного поля флуктуаций амплитуды использовался
спектральный метод [15]. Этот метод основывается на суммировании Фурье-гармоник
пространственного спектра. Алгоритм задания спектральным методом случайной
реализации комплексного поля флуктуаций входного сигнала состоит в следующем.
Сначала получаем комплексную случайную величину для каждой точки спектрального
пространства
в формуле (5).
Особенностью реального лазерного пучка также является наличие шума во входном
профиле. Для воспроизведения случайного поля флуктуаций амплитуды использовался
спектральный метод [15]. Этот метод основывается на суммировании Фурье-гармоник
пространственного спектра. Алгоритм задания спектральным методом случайной
реализации комплексного поля флуктуаций входного сигнала состоит в следующем.
Сначала получаем комплексную случайную величину для каждой точки спектрального
пространства ![]() , где
, где ![]() и
и ![]() - независимые равномерно распределенные на отрезке [-1,1]
случайные величины. Затем строится функция
- независимые равномерно распределенные на отрезке [-1,1]
случайные величины. Затем строится функция
![]() , где
, где
![]() - амплитуда шума
(например, 0.1),
- амплитуда шума
(например, 0.1), ![]() - радиус корреляции (например, 1/0.1мм). Для получения амплитудного шума
выполняется преобразование Фурье:
- радиус корреляции (например, 1/0.1мм). Для получения амплитудного шума
выполняется преобразование Фурье:
![]()
Окончательно, накладываем функцию шума на входной профиль по следующему
закону
![]() .
.
Развитие мелкомасштабной самофокусировки [6],
приводящей к распаду симметрии профиля, классически объясняется наличием
амплитудных флуктуаций начального распределения. Вследствие процесса
мелкомасштабной самофокусировки и достижения амплитудами отдельных флуктуаций
порога многофотонной ионизации в мощном лазерном импульсе начинает развиваться
множественная филаментация. При наблюдении этого процесса вырисовывается
картина множественных связей отдельных филамент между собой, вследствие чего
происходят поглощение и зарождение новых филамент. В процессе такого
хаотического развития в лазерных импульсах можно выделить области, где процесс
филаментации продолжается непрерывно за счет поглощения энергии соседних
участков. Такие области называют кластерами [1] и именно их наличие объясняет
характер экспериментальных данных (рис.10).
Чтобы
оценить необходимые размеры расчетной сетки, воспользуемся следующими условиями
и результатами экспериментов (проект Teramobile [8]):
·
для изучения
процесса филаментации используется мощный (от 100GW до 3TW) лазерный импульс, начальная ширина которого
может достигать
·
ширина
образующейся филаменты, как мелкомасштабного эффекта, постоянна и достигает
100-150 мкм, а интенсивность в фокусе
филаменты может превышать интенсивность фона в десятки раз;
·
наблюдаемая длина
распространения импульса составляет от десятков до сотен метров.
Таким образом, длина ребра квадрата расчетной
сетки может достигать ![]() может достигать
может достигать ![]() . Шаг по
. Шаг по ![]() выбирается ~
выбирается ~![]() , и уменьшается
обратно пропорционально максимальной интенсивности
, и уменьшается
обратно пропорционально максимальной интенсивности ![]() . Тем самым
обеспечена не только устойчивость, но и точность. Ввиду большой размерности
решаемой системы линейных уравнений и необходимости численного моделирования
процесса распространения фемтосекундного импульса на длинные дистанции
использовался параллельный вычислительный комплекс.
. Тем самым
обеспечена не только устойчивость, но и точность. Ввиду большой размерности
решаемой системы линейных уравнений и необходимости численного моделирования
процесса распространения фемтосекундного импульса на длинные дистанции
использовался параллельный вычислительный комплекс.

Рис.10 Эксперимент по распространению лазерного
луча
В качестве примера расчета приводим расчет для
среднего по мощности (![]() ) импульса с
полушириной
˜ω0=
3мм
. Расчетная область
представляет собой квадрат с длиной стороны
2см
. На начальном
профиле задан Гауссов шум по описанному выше алгоритму. Расчет проводился на сетке
) импульса с
полушириной
˜ω0=
3мм
. Расчетная область
представляет собой квадрат с длиной стороны
2см
. На начальном
профиле задан Гауссов шум по описанному выше алгоритму. Расчет проводился на сетке ![]() ячеек.
ячеек.
|
|
|
|
Рис.11–а.
Распределение интенсивности при z=1м
|
Рис.11–б.
Распределение интенсивности при z=3м |
|
|
|
|
Рис.11–в.
Распределение интенсивности при z=4м |
Рис.11–г.
Распределение интенсивности при z=6м |

Рис.12 Линии уровня ![]() распространения
импульса
распространения
импульса
с мощностью ![]() на расстояние около
9м
.
на расстояние около
9м
.
Результаты развития мощности (рис. 13-а) и
интенсивности (рис. 11,12,13-б) импульса совпадают с полученными результатами
проекта Teramobile [8], более того сравнение временных характеристик
по скорости счета созданного для данной работы параллельного комплекса также
дает хорошие результаты, не смотря на коренное различие с [8] в подходах к
численному решению задачи. Подробное обсуждение используемых методов
аппроксимации и характеристик параллельного алгоритма приводится в [20]. Как
правило, для большей кучности филамент, на практике применяется эллиптическое
распределение начального профиля.
Заключение
Целью
настоящей работы было описание свойств процесса филаментации и разработка
эффективных алгоритмов для расчета этого явления в реальных экспериментальных
лазерных системах. Были использованы симметричные разностные схемы, обладающие
свойством консервативности, созданы распараллеленные программы для расчета
таких задач.
При использовании начального Гауссова профиля с
высокой, близкой к пороговой (или максимальной) интенсивностью и мощностью не
намного превышающей ![]() , не
наблюдается ступенчатый характер изменения интенсивности при распространении
импульса.
, не
наблюдается ступенчатый характер изменения интенсивности при распространении
импульса.
Литература
1. Kasparian J., Rodrigues
M., Mejean
G., Yu J.,
Salmon E.,
Wille H.,
Bourayou R.,
Frey S.,
Andre Y.-B.,
Mysyrowicz A.,
Souerbrey R.,
Wolf J.-P.,
Woste L.
Science,
61, 301 (2003)
2. Braun A. et al. Opt. Lett. 20, 73 (1995); Nibbering
E.T.J. et al. Opt.
Lett. 21, 62 (1996).
3. Brodeur A. et al. Opt. Lett. 22, 304 (1997)
4. LaFontaine B. et al. Phys. Plasmas, 6, 1615
(1999)
5. Chiao
R.Y. Phys.Rev.Lett, 13, 5 (1964)
6. Беспалов
В.И., Таланов В.И., Письма в ЖЭТФ, 3, 471 (1966)
7.
Fibich G., Ilan B. Phisica D, 157,
113 (2001)
8. Skupin S., Berge L. et al., Phys. Rev.
E, 70, 046602 (2004)
9. Балашов
А.Д., Пергамент А.Х. Математическое моделирование процессов
филаментации в средах с кубической нелинейностью (М.: ИПМ им.
М.В.Келдыша РАН, 2004, препринт №40)
10. Кандидов
В.П., Косарева О.Г., Шленов С.А. и др. Квантовая электроника, 35, 1
(2005)
11. Aztec. A
Massively Parallel Iterative Solver Library for Solving Sparse Linear Systems (Инетернет-ресурс:
http://www.cs.sandia.gov/CRF/aztec1.html)
12. Дацюк
В.Н., Букатов А.А., Жегуло А.И.. Многопроцессорные системы и параллельное
программирование (Ростов: Ростовский государственный университет, http://rsusu1.rnd.runnet.ru/koi8/index.html)
13. Ландау
Л.Д., Лившиц Е.М. Электродинамика сплошных сред (М.: Наука, 1959).
14. Карамзин
Ю.Н., Сухоруков А.П., Трофимов В.А. Математическое моделирование в
нелинейной оптике (М.: Издательство Московского университета, 1989).
15. Миркин
Л.И., Рабинович М.А., Ярославский Л.П. ЖВМ и МФ, 5, 1353 (1972)
16. Волков
В.М. Дифференциальные уравнения, 29, 7 (1993)
17. Kasparian
J., Sauerbrey R., Chin S.L. Appl. Phys. B, 71, 877 (2000)
18. Nibbering
E.T.J., Grillon G., Franco M.A. at al. J.Opt.SocAm.B, 14, 650 (1997)
19. Feit
M.D., Fleck J.A. Appl. Phys. Lett., 24, 169 (1974)
20. Балашов
А.Д., Пергамент А.Х. Математическое моделирование, 18, 4, (2006)