Аннотация
Рассмотрено кинетическое уравнение для электронов в нейтральной среде и самосогласованном
электромагнитном поле. Построен интеграл столкновений в приближении малых передач энергии.
Предложено приближенное решение кинетического уравнения, позволяющее использовать метод
частиц для численного моделирования плотности электрического тока. Использован факт малых
изменений импульса электронов при столкновениях и возрастание сечений столкновений при
движении электронов в среде.
Abstract
The kinetic equation for electrons in the neutral medium and self-consistent electro-magnetic
field is considered. The integral of collisions in the approximation of small energy transfers
is constructed. The approximate decision of the kinetic equation, which allows using particles
method for numerical simulation of the electric current density, is suggested. The smallness
of the pulse transfer in collisions and cross-section increasing during electron movement
in medium are used.
Введение
Математическое
моделирование распространения потоков электронов в исходно нейтральной газовой
среде заданной плотности является актуальной проблемой при исследовании свойств
вещества [1]. Один из эффектов, сопровождающих электронный поток в газе, состоит
в генерации самосогласованного электромагнитного поля, влияющего как на процесс
распространения потока, так и на электронную измерительную аппаратуру любого
назначения.
Достаточно
полная математическая модель самосогласованного электромагнитного поля в потоке
электронов должна использовать уравнение переноса [2] электронов в нейтральной
среде с учетом ее ионизации в совокупности с уравнениями Максвелла. Алгоритмы
численного решения задач для таких уравнений строятся методом дискретных
ординат [3] или Монте-Карло [4]. Однако объемы вычислительных ресурсов,
необходимые для трехмерного моделирования на основе данных методов, могут
оказаться недопустимыми. Кроме того, количественное описание элементарных
процессов взаимодействия электронов с молекулами газа может потребовать
недоступных данных о сечениях.
Предлагается
подход к моделированию электронных потоков, основанный на методе крупных частиц
[5]. Основной проблемой при этом является описание столкновений электронов с
молекулами среды, поскольку исходно метод частиц формулируется для бесстолкновительной
плазмы [6], то есть для систем заряженных частиц, в которых частота
столкновений пренебрежимо мала по сравнению с частотой плазменных колебаний.
Тем не менее, некоторые приближения относительно пространственно-временных и
спектральных характеристик потока электронов и свойств рассеивающей среды дают
возможность построить функцию распределения в виде, допускающем метод частиц,
причем с использованием при расчетах только тех функционалов сечений рассеяния,
которые хорошо известны и экспериментально проверены.
1 Постановка
задачи
Рассмотрим поток электронов с энергиями
1 КэВ – 1 МэВ, распространяющийся в нейтральном газе.
Степень ионизации газа будем считать малой. Пусть также все ионы описываются
изотропной функцией распределения и не создают ненулевой плотности электрического
тока.
Электроны движутся в самосогласованном
электромагнитном поле. Электрическое поле 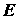 и магнитное поле и магнитное поле  являются функциями времени являются функциями времени
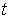 и координат и координат . Импульс электрона . Импульс электрона 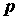 изменяется под
действием силы Лоренца изменяется под
действием силы Лоренца 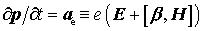 , где , где – заряд электрона, – заряд электрона, 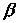 – отношение скорости электрона – отношение скорости электрона 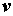 к скорости света к скорости света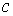 . Для описания импульса электрона будут использоваться
декартовы . Для описания импульса электрона будут использоваться
декартовы 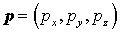 и сферические и сферические  координаты, причем координаты, причем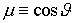 , а , а 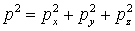 . .
Рассмотрим кинетическое уравнение для функции
распределения электронов : :
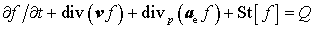 ,
(1) ,
(1)
где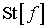 – интеграл столкновений электронов с молекулами
газовой среды, – интеграл столкновений электронов с молекулами
газовой среды,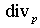 – дивергенция векторной функции в пространстве импульсов.
Правая часть уравнения – дивергенция векторной функции в пространстве импульсов.
Правая часть уравнения 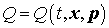 представляет собой источник, в качестве которого может
рассматриваться интенсивность эмиссии электронов. представляет собой источник, в качестве которого может
рассматриваться интенсивность эмиссии электронов.
Отнесение уравнения (1) к тому или иному типу
классических кинетических уравнений в данной работе обсуждаться не будет.
Отметим лишь следующее. Первые два члена левой части уравнения (1) описывают
перенос электронов и являются общими для всех кинетических уравнений. Третий
член описывает взаимодействие электронов в приближении среднего поля и
соответствует уравнению Власова [7]. Четвертый член уравнения есть линейный по
функции распределения интеграл столкновений, соответствующий уравнению переноса.
В целом уравнение (1) выражает баланс числа электронов в элементе фазового
пространства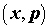 . Для уравнения (1) рассматривается задача Коши с однородными
начальными данными при . Для уравнения (1) рассматривается задача Коши с однородными
начальными данными при 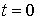 . .
Целью данной работы является построение приближенного
решения уравнения (1) в виде, допускающем применение метода частиц для
вычисления плотности электрического тока электронов. Для иллюстрации цели
рассмотрим уравнение (1) без интеграла столкновений:
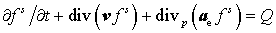 .
(2) .
(2)
Уравнение (4) в совокупности с уравнениями Максвелла
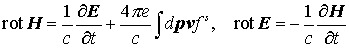 (3) (3)
составляет
неоднородное уравнение Власова. Известно [8], что конечная сумма
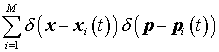
есть
решение однородного уравнению (2) при любом М,
если 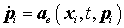 , , 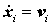 . Точка означает дифференцирование по времени. Решением
однородного уравнения (2) является также интеграл вида . Точка означает дифференцирование по времени. Решением
однородного уравнения (2) является также интеграл вида 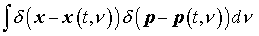 . Аналогом такого решения для неоднородного уравнения
является: . Аналогом такого решения для неоднородного уравнения
является:
 , (4) , (4)
где
 – внутренние векторные
переменные интегрирования, соответствующие по физическому смыслу начальной
координате и импульсу частицы, движение которой описывается функциями – внутренние векторные
переменные интегрирования, соответствующие по физическому смыслу начальной
координате и импульсу частицы, движение которой описывается функциями 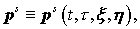 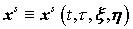 , причем , причем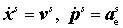 . .
Обозначим  , подставим (4) в уравнение (2), умножим на гладкую финитную
пробную функцию , подставим (4) в уравнение (2), умножим на гладкую финитную
пробную функцию 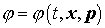 и проинтегрируем по всем переменным. Приведем промежуточные
выкладки. и проинтегрируем по всем переменным. Приведем промежуточные
выкладки.
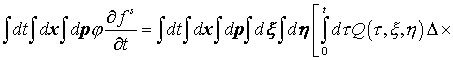
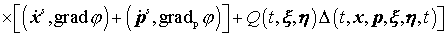 , ,
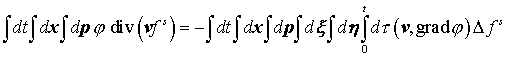 , ,
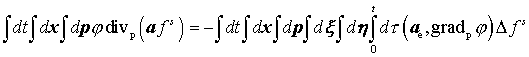 . .
Учтем, что 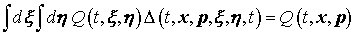 , ,  , , 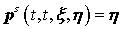 и подставим
промежуточные выкладки в уравнение (2). Получим: и подставим
промежуточные выкладки в уравнение (2). Получим:
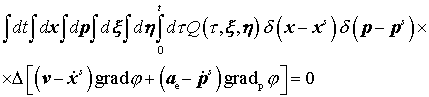 .
(5) .
(5)
Данный результат получен в [9]. Функция 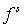 , представленная формулой (4), может вычисляться методом
частиц. Приближенно в аналогичном виде можно представить и решение уравнения
(1). , представленная формулой (4), может вычисляться методом
частиц. Приближенно в аналогичном виде можно представить и решение уравнения
(1).
2
Интеграл столкновений
Для свободных электронов с энергиями более 1 КэВ
основными эффектами взаимодействия с молекулами нейтрального водородоподобного
газа являются упругие и ионизационные столкновения [1]. Представим интеграл
столкновений уравнения (1) в виде суммы:
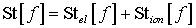
Первый член суммы представляет собой интеграл упругих
столкновений [2,10] 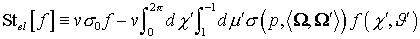 , где , где 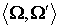 – косинус угла между – косинус угла между 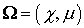 и и 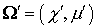 , , 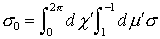 – полное
макроскопическое сечение рассеяния, – полное
макроскопическое сечение рассеяния, 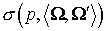 – дифференциальное сечение упругого рассеяния. – дифференциальное сечение упругого рассеяния.
Заметим следующее. Считается, что упругие столкновения
не изменяют энергию электрона, а лишь отклоняют его от первоначального
направления движения. Механизм упругих столкновений состоит в рассеянии
электронов в кулоновском поле ядра, экранированного атомарными электронами.
Изменение модуля импульса при этом пропорционально отношению масс электрона и
ядра и действительно мало в каждом акте столкновений. Если рассматривается все
время жизни электрона, в течение которого происходит много взаимодействий,
суммарное изменение энергии может оказаться существенным.
Ионизационное взаимодействие свободных электронов с
молекулами среды, описываемое интегралом столкновений 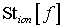 , состоит не только в рассеянии падающего электрона, но и в
образовании в непрерывном спектре одного или нескольких вторичных электронов
при, возможно, одновременном возбуждении молекулы. Наиболее вероятным [11]
ионизационным эффектом для электронов с энергиями, существенно превышающими потенциал
ионизации среды, является процесс однократной ионизации оболочек атомов. За
счет кинетической энергии , состоит не только в рассеянии падающего электрона, но и в
образовании в непрерывном спектре одного или нескольких вторичных электронов
при, возможно, одновременном возбуждении молекулы. Наиболее вероятным [11]
ионизационным эффектом для электронов с энергиями, существенно превышающими потенциал
ионизации среды, является процесс однократной ионизации оболочек атомов. За
счет кинетической энергии 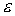 падающего электрона
атомарный электрон переходит в непрерывный спектр и обретает кинетическую
энергию падающего электрона
атомарный электрон переходит в непрерывный спектр и обретает кинетическую
энергию 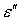 . Падающий электрон рассеивается и теряет энергию. Если . Падающий электрон рассеивается и теряет энергию. Если 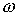 – потеря энергии, то конечная энергия электрона после
рассеяния составляет величину – потеря энергии, то конечная энергия электрона после
рассеяния составляет величину 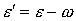 . .
Деление электронов после взаимодействия на падающие и
рассеянные условно. Имеет место тождественная неразличимость частиц.
Исследователи процессов ионизации нейтральных молекул
электронным ударом [12,13] для количественного описания используют дважды
дифференциальное по переданной энергии и углу рассеяния  , дифференциальное по переданной энергии , дифференциальное по переданной энергии 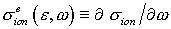 и полное сечение
ионизации и полное сечение
ионизации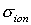 . .
Построение интеграла ионизационных столкновений
рассмотрим на примере модельного атомарного газа с единым для всех оболочек
потенциалом ионизации. Наглядное теоретическое описание более сложных сред
громоздко, поскольку необходимо описывать парциальные вклады каждой оболочки.
Единый потенциал ионизации 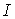 можно рассматривать
как средний по всем оболочкам и сортам атомов, что в ряде задач обеспечивает достаточную
точность. можно рассматривать
как средний по всем оболочкам и сортам атомов, что в ряде задач обеспечивает достаточную
точность.
Возьмем за основу 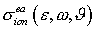 . Пусть при рассеянии электрона с энергией . Пусть при рассеянии электрона с энергией 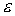 и направлением
импульса и направлением
импульса  образуются электроны с
параметрами образуются электроны с
параметрами 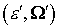 и и  . Последние два электрона тождественно неразличимы. Положим . Последние два электрона тождественно неразличимы. Положим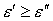 . Это предположение не вносит ограничений, а лишь позволяет
условно рассматривать «штрихованный» электрон в качестве рассеянного, а дважды
штрихованный считать вторичным. Тогда . Это предположение не вносит ограничений, а лишь позволяет
условно рассматривать «штрихованный» электрон в качестве рассеянного, а дважды
штрихованный считать вторичным. Тогда 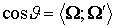 , ,  . В соответствии с законом сохранения энергии . В соответствии с законом сохранения энергии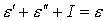 . В импульсном представлении ионизационное взаимодействие
описывается следующей схемой . В импульсном представлении ионизационное взаимодействие
описывается следующей схемой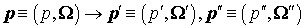 . Модули импульсов однозначно связаны с энергией
соотношениями . Модули импульсов однозначно связаны с энергией
соотношениями 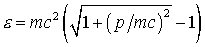 , , 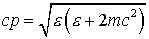 . Заметим, что для произвольной функции . Заметим, что для произвольной функции 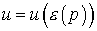 имеет место соотношение имеет место соотношение . .
В соответствии с законом сохранения импульса 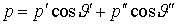 , , 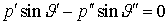 . .
Четырежды дифференциальное сечение,
представляющее собой вероятность того, что падающий электрон с импульсом 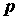 в результате
ионизационного рассеяния образует пару электронов с импульсами в результате
ионизационного рассеяния образует пару электронов с импульсами 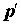 и и 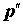 , имеет вид: , имеет вид:
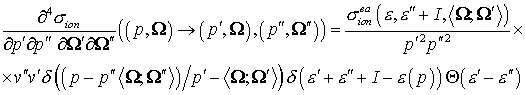 (6) (6)
Интегрируя (6), построим два дважды
дифференциальных сечения
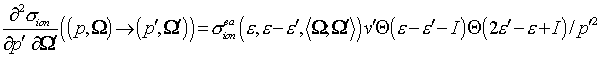 (7) (7)
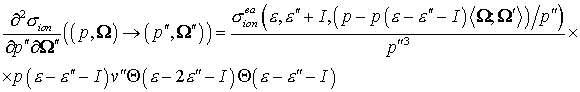 (8) (8)
Дважды дифференциальное сечение (7) описывает
распределение в пространстве импульсов рассеянных электронов, образуемое
падающим электроном с импульсом . Дважды дифференциальное сечение (8) описывает распределение
вторичных электронов. Обе эти конструкции при интегрировании по . Дважды дифференциальное сечение (8) описывает распределение
вторичных электронов. Обе эти конструкции при интегрировании по 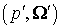 и и 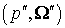 образуют полное
сечение ионизационного рассеяния: образуют полное
сечение ионизационного рассеяния:
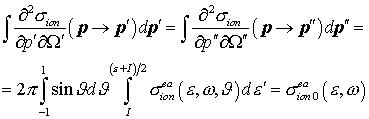 (9) (9)
Коэффициент 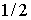 в верхнем пределе
интегрирования исключает одновременный учет тождественных ситуаций. Например,
случай в верхнем пределе
интегрирования исключает одновременный учет тождественных ситуаций. Например,
случай 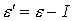 , , 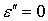 тождественен случаю тождественен случаю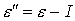 , , 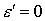 . Если один из электронов, образовавшихся в результате
ионизационного рассеяния, имеет энергию . Если один из электронов, образовавшихся в результате
ионизационного рассеяния, имеет энергию 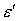 , то второй электрон достоверно имеет энергию , то второй электрон достоверно имеет энергию 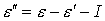 . .
Рассмотрим интенсивность прихода рассеянных
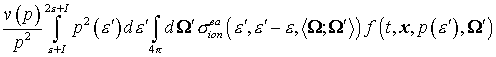 (10)
(10)
и
вторичных
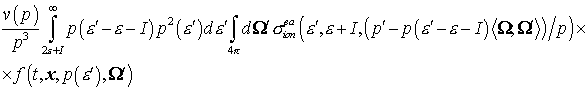 (11) (11)
электронов
в элемент фазового объема 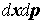 из всех возможных
элементов фазового объема из всех возможных
элементов фазового объема 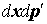 за счет ионизационного
рассеяния. Формулы (10) и (11) получены из формул (7) и (8) соответственно
путем взаимной замены штрихованных и не штрихованных переменных и сверткой с
функцией распределения по штрихованным импульсным переменным и относительной
скоростью. за счет ионизационного
рассеяния. Формулы (10) и (11) получены из формул (7) и (8) соответственно
путем взаимной замены штрихованных и не штрихованных переменных и сверткой с
функцией распределения по штрихованным импульсным переменным и относительной
скоростью.
Интеграл столкновений, описывающий изменение числа
частиц в элементе фазового объема, построим следующим образом. В рамках
уравнения (1) будем рассматривать падающие и рассеянные электроны, исключив
вторичные в отдельное рассмотрение. Это возможно, поскольку взаимодействие электронов
обусловлено только общим самосогласованным электромагнитным полем. Это
целесообразно, поскольку вторичные электроны имеют малые энергии и для них
существенен другой набор столкновительных эффектов. Таким образом, интеграл
ионизационных столкновений, учитывающий уход падающих электронов и приход
рассеянных, можно рассматривать в следующем виде:
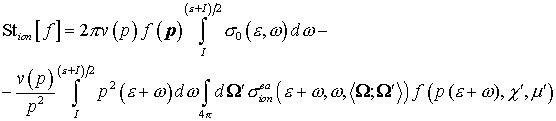 (12) (12)
По сравнению с формулой (10), в (12) выполнена замена
переменной интегрирования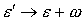 . Заметим, что определить новые пределы интегрирование
необходимо с помощью формулы (6). Разложим интеграл столкновений (12) по
сферическим функциям . Заметим, что определить новые пределы интегрирование
необходимо с помощью формулы (6). Разложим интеграл столкновений (12) по
сферическим функциям  : :
 (13) (13)
Рассмотрим свойства сечений ионизационного рассеяния,
которые можно выявить из доступных источников. Дважды дифференциальное по
энергии и углу сечение ионизационного рассеяния приведено в [12] и повторено в
[13]. В обозначениях, принятых в [12], оно имеет вид:
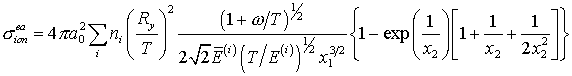
где 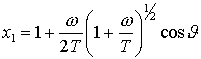 , , 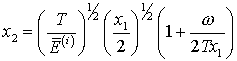 , , 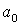 – боровский радиус, – боровский радиус, 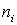 – число электронов на соответствующей оболочке; – число электронов на соответствующей оболочке; 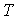 – энергия падающего электрона. Среднюю энергию электрона
на – энергия падающего электрона. Среднюю энергию электрона
на 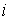 -ой оболочке -ой оболочке  вычисляют по
приближенным формулам Слеттера. Приближенно вычисляют по
приближенным формулам Слеттера. Приближенно 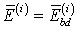 , где , где – энергия связи соответствующей оболочки. – энергия связи соответствующей оболочки.
Такое сечение не применимо для расчетов, поскольку
принимает отрицательное значение при любом разумном сочетании аргументов.
Воспользуемся доступным из [14] дифференциальным по энергии классическим
сечением рассеяния электрона с энергией 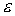 на свободном
электроне, имеющем среднюю энергию U и
изотропное распределение скорости: на свободном
электроне, имеющем среднюю энергию U и
изотропное распределение скорости:
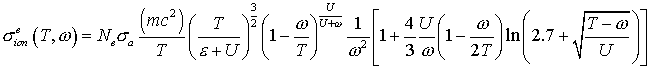
где
 – концентрация атомарных электронов. – концентрация атомарных электронов.
Если подставить вместо U значение средней энергии атомарного электрона, то при
 этой формулой можно
пользоваться для приближенного вычисления дифференциального по переданной
энергии сечения ионизации. Вычисленное по данному дифференциальному сечению
полное сечение удовлетворительно согласуется с экспериментальными данными. этой формулой можно
пользоваться для приближенного вычисления дифференциального по переданной
энергии сечения ионизации. Вычисленное по данному дифференциальному сечению
полное сечение удовлетворительно согласуется с экспериментальными данными.
Достоверным представляется сечение ионизационного
рассеяния на свободных электронах [15]:
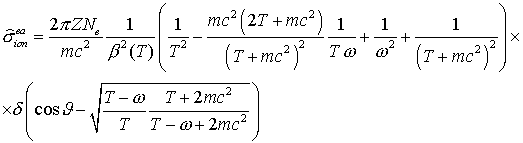 . .
Для молекул это сечение справедливо только при  и и  , то есть энергия всех электронов (падающего, рассеянного и
вторичного) существенно превосходят потенциал ионизации. Поскольку при заданном , то есть энергия всех электронов (падающего, рассеянного и
вторичного) существенно превосходят потенциал ионизации. Поскольку при заданном
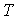 сечение резко
возрастает при сечение резко
возрастает при 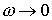 , очевидно, что наиболее вероятны столкновения с малой
передачей энергии. Сечение рассеяния на свободном электроне не может
использоваться для количественного описания ионизационного взаимодействия
электронов с молекулами. Однако оно, как и все представленные сечения, при
малых , очевидно, что наиболее вероятны столкновения с малой
передачей энергии. Сечение рассеяния на свободном электроне не может
использоваться для количественного описания ионизационного взаимодействия
электронов с молекулами. Однако оно, как и все представленные сечения, при
малых 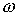 ведет себя как ведет себя как  . .
Разложим функцию 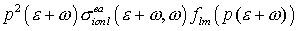 переменной переменной 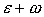 в формуле (13) в ряд
Тейлора с центром в точке в формуле (13) в ряд
Тейлора с центром в точке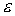 , сохраняя нулевой и первый члены: , сохраняя нулевой и первый члены:
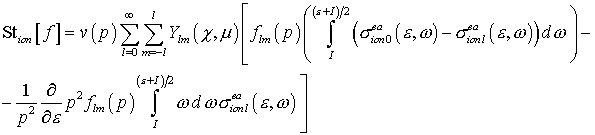 (14) (14)
Рассмотрим величины  . Для анализа применим главное слагаемое дифференциального
сечения рассеяния на свободном электроне. . Для анализа применим главное слагаемое дифференциального
сечения рассеяния на свободном электроне.
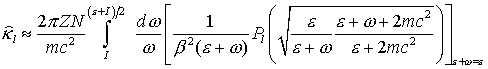
Поскольку 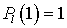 для всех для всех  , ,
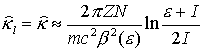 (15)
(15)
Для реального сечения направления движения рассеянного
и падающего электронов при 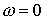 также должны совпадать.
Поэтому также должны совпадать.
Поэтому 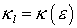 . .
Величина 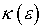 представляет собой
тормозную способность газа относительно электрона с энергией представляет собой
тормозную способность газа относительно электрона с энергией 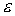 [16]. Тормозные
способности хорошо исследованы для различных веществ и проверены экспериментально.
Если [16]. Тормозные
способности хорошо исследованы для различных веществ и проверены экспериментально.
Если 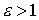 КэВ, то тормозная способность достаточно точно
описывается формулой [17]: КэВ, то тормозная способность достаточно точно
описывается формулой [17]:
 , (16) , (16)
где 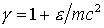 , ,  – масса электрона, – масса электрона, 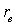 – классический радиус электрона. – классический радиус электрона.
Более точной является формула Рерлиха-Карлсона [1],
позволяющая учесть эффект плотности 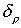 : :
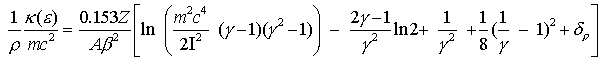 (17) (17)
где
А – атомная масса атомов
среды, а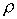 – ее плотность. – ее плотность.
Тормозная способность вещества учитывает суммарную
потерю энергии электроном за счет всех процессов. К ним относятся и возбуждение
молекул электронным ударом и потери импульса при упругих столкновениях.
Формулы (16) и (17) содержат натуральный логарифм
отношения текущей энергии электрона к потенциалу ионизации. Это же отношение
содержит и оценочная формула (15). Происхождение этих логарифмов общее –
поведение реального сечения рассеяния при 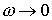 . .
Учитывая выводы относительно тормозной способности, и
раскладывая в ряд по сферическим функциям интеграл упругих столкновений,
получим:
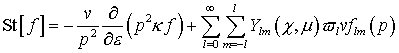 (18) (18)
где
 . .
Данная конструкция есть приближение малых передач
энергии для интеграла столкновений с точностью до члена, содержащего первую
производную по энергии. Классическое приближение Фоккера-Планка подразумевает
наличие второй производной по энергии. Первым членом в разложении функции 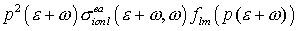 переменной переменной 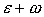 в ряд Тейлора центром
в точке в ряд Тейлора центром
в точке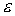 можно ограничиться, если можно ограничиться, если  . Действительно, логарифмическая особенность возникает из-за
того, что при малых передачах энергии сечение пропорционально . Действительно, логарифмическая особенность возникает из-за
того, что при малых передачах энергии сечение пропорционально  . При интегрировании с весом . При интегрировании с весом 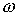 и нижним пределом и нижним пределом 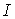 образуется
логарифмическая особенность. Интегрирование с весом образуется
логарифмическая особенность. Интегрирование с весом 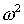 особенности не даст. особенности не даст.
Интеграл столкновений (18) исключает из рассмотрения
вторичные электроны. Действительно, интегрирование (18) по импульсу даст ноль,
то есть общее число электронов за счет столкновений не изменяется. Появление
вторичных электронов описывается формулой (11). Рассмотрение вторичных электронов
в данной кинетической модели, не представляется ни возможным, ни целесообразным
по следующим причинам. Вероятность образования вторичного электрона с малой
энергией резко превосходит вероятность образования электрона с энергией,
сопоставимой с энергией падающего электрона. Вторичные электроны низкой
энергии, кроме ионизационных и упругих столкновений с молекулами среды,
интенсивно участвуют в рекомбинационных процессах [18]. Если в среде
присутствует кислород, существенна вероятность прилипания вторичных электронов
к его молекулам с образованием отрицательных ионов. Отрицательные ионы и
вторичные электроны рекомбинируют с положительными ионами, образовавшимися при
ионизационном рассеянии. Вероятности всех этих процессов резко убывают с ростом
энергии, поэтому брать их в расчет при моделировании потока первичных
электронов высокой энергии не целесообразно. Рассмотрение вторичных электронов
выходит за рамки данной работы. Адекватная модель плотности их тока представлена
в [19].
Обратимся к рассмотрению углового рассеяния.
Аналогично тому, как тормозная способность вещества учитывает потери энергии за
счет всех процессов, коэффициенты  описывают суммарное
угловое рассеяние. описывают суммарное
угловое рассеяние.
Рассмотрим сечение упругого рассеяния [13,20,21]:
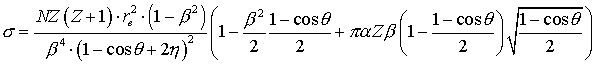 (19) (19)
где
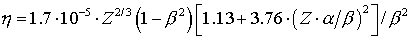 – параметр экранирования, – параметр экранирования,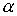 – постоянная тонкой структуры, – постоянная тонкой структуры, – средний заряд ядер атомов газа, – средний заряд ядер атомов газа,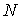 – концентрация атомов газа. – концентрация атомов газа.
При построении параметра экранирования для
дифференциального сечения (19) используется понятие угла экранирования, который
не дает знаменателю обращаться в ноль. Параметр экранирования является малой
величиной, в результате чего дифференциальное сечение крайне чувствительно к
способу его задания. Величины 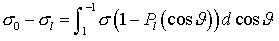 зависят от параметра
экранирования только логарифмически, что существенно повышает их точность и
позволяет использовать теорию многократного рассеяния. зависят от параметра
экранирования только логарифмически, что существенно повышает их точность и
позволяет использовать теорию многократного рассеяния.
Наиболее точным распределением, используемым для
моделирования многократного рассеяния электронов [1], является угловое
распределение Гоудсмита-Саундерсона [22]:
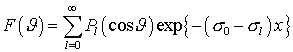 , (20) , (20)
где
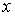 – толщина слоя вещества, в котором исследуется
рассеяние. В [1] приведены формулы для вычисления величин – толщина слоя вещества, в котором исследуется
рассеяние. В [1] приведены формулы для вычисления величин 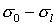 , которые проверены в экспериментах и могут быть использованы
в расчетах. , которые проверены в экспериментах и могут быть использованы
в расчетах.
Заметим следующее. В знаменателе (19) присутствует
величина 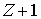 . Она заменяет собой величину . Она заменяет собой величину  для того, чтобы
сечение (19) автоматически учитывало угловые отклонения электронов за счет
ионизационного рассеяния. Таким образом, приведенные в [1] величины для того, чтобы
сечение (19) автоматически учитывало угловые отклонения электронов за счет
ионизационного рассеяния. Таким образом, приведенные в [1] величины 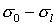 соответствуют
величинам соответствуют
величинам  в интеграле
столкновений (18). в интеграле
столкновений (18).
3 Приближенное
решение кинетического уравнения
Представим уравнение (1) с интегралом столкновений
(18) в следующем виде:
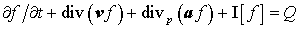 ,
(21) ,
(21)
Здесь учтено, что  , и введены два новых обозначения , и введены два новых обозначения 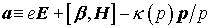 , , 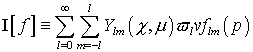 . .
Представим решение (21) в виде разности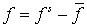 , где , где
 , (22) , (22)
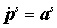 , удовлетворяет уравнению , удовлетворяет уравнению
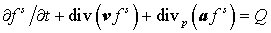 , (23) , (23)
Процедура решения этого уравнения может рассматриваться
следующим образом. Лагранжевы переменные 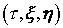 с помощью соотношений с помощью соотношений 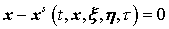 , , 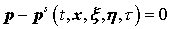 выражаются через
эйлеровы переменные выражаются через
эйлеровы переменные 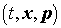 и подставляются вместо
них в уравнение. Уравнение интегрируется по и подставляются вместо
них в уравнение. Уравнение интегрируется по  , результатом чего является функция , результатом чего является функция 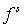 , выраженная формулой (22). Формально можно сказать, что
оператор , выраженная формулой (22). Формально можно сказать, что
оператор  , действующий на функцию , действующий на функцию 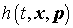 по правилу по правилу
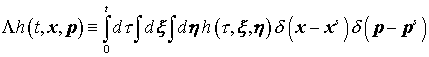 , ,
является обратным к оператору 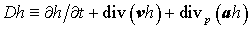 . Действительно, нетрудно показать, что . Действительно, нетрудно показать, что 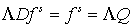 . Заметим, что это просто формальная запись решения гиперболического
уравнения в частных производных первого порядка методом характеристик [23]. В
то же время это решение может, аналогично [24], рассматриваться как континуальный
предел конечной суммы . Заметим, что это просто формальная запись решения гиперболического
уравнения в частных производных первого порядка методом характеристик [23]. В
то же время это решение может, аналогично [24], рассматриваться как континуальный
предел конечной суммы
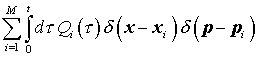 , ,
где 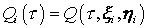 – вес, а – вес, а 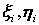 – начальные координаты и импульсы – начальные координаты и импульсы 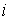 -ой частицы, появившейся в момент времени -ой частицы, появившейся в момент времени 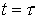 . Если функции . Если функции  и и 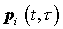 являются решениями
уравнений движения являются решениями
уравнений движения  с начальными условиями с начальными условиями
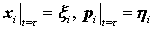 , то такая сумма является решением уравнения , то такая сумма является решением уравнения  для правой части,
представимой в виде для правой части,
представимой в виде  . .
Оператор  обладает свойством: обладает свойством:
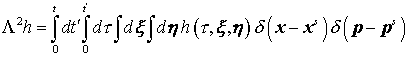
Заметим, что для оператора в левой части уравнения
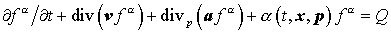
можно
рассматривать обладающий аналогичным свойством обратный оператор
 , ,
где
 . Такая запись позволяет применять метод частиц не только для
уравнений типа (23), но и для неоднородного уравнения Власова с поглощением.
Конечная сумма в этом случае имеет вид: . Такая запись позволяет применять метод частиц не только для
уравнений типа (23), но и для неоднородного уравнения Власова с поглощением.
Конечная сумма в этом случае имеет вид:

Такой ряд является решением уравнения (24)
неоднородного уравнения Власова с поглощением с правой частью, представимой в
виде  при любом М. при любом М.
Для  справедливо следующее
уравнение: справедливо следующее
уравнение:
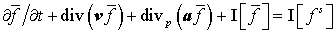 .
(24) .
(24)
Рассмотрим характерные размеры задачи: длительность
импульса  источника источника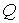 и размер области генерации электронов и размер области генерации электронов 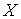 , плазменную частоту электронов , плазменную частоту электронов 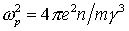 , где , где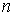 – концентрация электронов, и дебаевский радиус – концентрация электронов, и дебаевский радиус 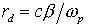 , также длины пробега электрона до полной потери энергии , также длины пробега электрона до полной потери энергии  , до первого упругого столкновения , до первого упругого столкновения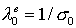 , транспортную длина пробега относительно углового рассеяния , транспортную длина пробега относительно углового рассеяния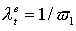 . .
Источник 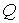 за время за время 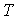 генерирует электроны
некоторого спектра в пространственной области с характерным размером генерирует электроны
некоторого спектра в пространственной области с характерным размером 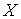 . Электроны под действием силы ионизационного торможения и
самосогласованного электромагнитного поля двигаются по траекториям,
определяемым уравнениями движения. На расстоянии порядка . Электроны под действием силы ионизационного торможения и
самосогласованного электромагнитного поля двигаются по траекториям,
определяемым уравнениями движения. На расстоянии порядка 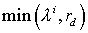 от точки рождения от точки рождения  абсолютная величина импульса
электрона существенно изменяется по сравнению с начальным значением. Начальное
направление движения на траектории может измениться только за счет
самосогласованного поля за время порядка плазменного периода. Плазменная
частота зависит от концентрации электронов и изменяется от нулевого значения. Одновременно
с движением по траекториям электроны испытывают угловое рассеяние, причем его
частота столкновений не зависит от концентрации электронов, а определяется
только свойствами среды и энергией электрона. Поэтому столкновения, в отличие
от самосогласованного поля, начинают сказываться сразу. Столкновения происходят
часто, величина абсолютная величина импульса
электрона существенно изменяется по сравнению с начальным значением. Начальное
направление движения на траектории может измениться только за счет
самосогласованного поля за время порядка плазменного периода. Плазменная
частота зависит от концентрации электронов и изменяется от нулевого значения. Одновременно
с движением по траекториям электроны испытывают угловое рассеяние, причем его
частота столкновений не зависит от концентрации электронов, а определяется
только свойствами среды и энергией электрона. Поэтому столкновения, в отличие
от самосогласованного поля, начинают сказываться сразу. Столкновения происходят
часто, величина  ничтожно мала по
сравнению с ничтожно мала по
сравнению с  , однако, в каждом акте упругих столкновений наиболее
вероятно малое изменение направления движения электрона. Существенное отклонение
электронов от направления, определенного уравнениями движения, происходит на расстояниях
порядка , однако, в каждом акте упругих столкновений наиболее
вероятно малое изменение направления движения электрона. Существенное отклонение
электронов от направления, определенного уравнениями движения, происходит на расстояниях
порядка 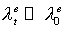 от точки рождения. Функция от точки рождения. Функция
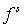 описывает движение
электронов по траекториям без углового рассеяния. Источником для функции описывает движение
электронов по траекториям без углового рассеяния. Источником для функции  является является 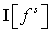 . Существенным по сравнению с . Существенным по сравнению с 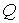 такой источник
становится только на расстояниях порядка такой источник
становится только на расстояниях порядка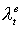 , то есть при , то есть при 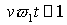 . Характерный размер области, занятой электронами, при этом
не превышает . Характерный размер области, занятой электронами, при этом
не превышает  . Таким образом, функция . Таким образом, функция  становится сопоставимой
по величине с функцией становится сопоставимой
по величине с функцией 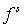 только на временах
порядка только на временах
порядка 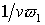 . .
Поскольку для газовых сред 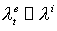 , электроны, описываемые поправкой, успевают существенно
сбросить энергию за счет ионизационного рассеяния по сравнению с начальной.
Сечения рассеяний при этом резко возрастают и столкновения начинают превалировать
над взаимодействием с самосогласованным электромагнитным полем. Столкновения
начинают превалировать и над свободным переносом электронов в пространстве,
поскольку размер занятой ими области определяется длиной пробега, вычисленной
по начальной энергии. , электроны, описываемые поправкой, успевают существенно
сбросить энергию за счет ионизационного рассеяния по сравнению с начальной.
Сечения рассеяний при этом резко возрастают и столкновения начинают превалировать
над взаимодействием с самосогласованным электромагнитным полем. Столкновения
начинают превалировать и над свободным переносом электронов в пространстве,
поскольку размер занятой ими области определяется длиной пробега, вычисленной
по начальной энергии.
Рассмотрим для функции  приближенное уравнение: приближенное уравнение:
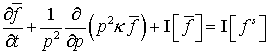 .
(25) .
(25)
Заметим, что возмущение, вносимое исключенными из
рассмотрения членами уравнения, представляется регулярным. Это существенно
упрощает построение приближенного решения по сравнению с методом
Чепмена-Энскога [25].
Разложим уравнение (25) по введенным выше сферическим
функциям. Для коэффициентов разложения 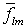 функции функции  получим уравнения получим уравнения
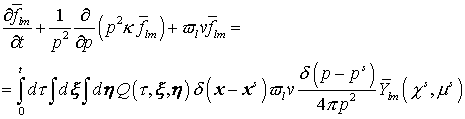 .
(26) .
(26)
Данное уравнение может быть решено применением
оператора типа 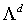 : :

Здесь
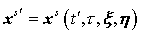 . Величины . Величины 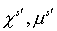 , ,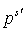 определяются аналогично. Функция определяются аналогично. Функция 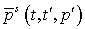 является решение
уравнения является решение
уравнения 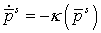 с начальным условием с начальным условием 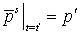 . .
Вычислим интеграл по переменной 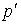 и заменим и заменим 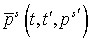 приближенно на приближенно на  . Это оправдано, поскольку для электронов, порожденных источником . Это оправдано, поскольку для электронов, порожденных источником
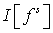 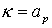 в соответствии с
выбранным приближением. Заметим, что делать это в уравнении (25) нельзя,
поскольку в соответствии с
выбранным приближением. Заметим, что делать это в уравнении (25) нельзя,
поскольку 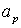 , вообще говоря, зависит от углов , вообще говоря, зависит от углов 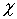 и и  , что приведет к недопустимому для данного рассмотрения
усложнению разложения по сферическим функциям. , что приведет к недопустимому для данного рассмотрения
усложнению разложения по сферическим функциям.
С учетом этого коэффициенты разложения примут вид:
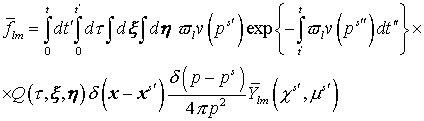
В соответствии с выбранным приближением 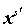 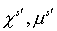 необходимо считать функциями
переменной необходимо считать функциями
переменной 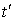 , медленно меняющимися по сравнению с , медленно меняющимися по сравнению с  . Тогда можно вычислить интеграл по . Тогда можно вычислить интеграл по 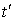 и получить окончательный
ответ для функции распределения и получить окончательный
ответ для функции распределения 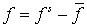 в виде: в виде:
 (27) (27)
Плотность электрического тока, соответствующая такой
функции распределения электронов
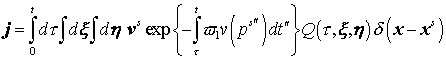 (28)
(28)
можно
вычислять методом частиц.
Таким образом, функция
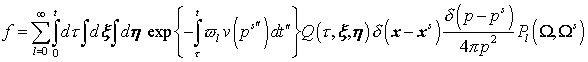 (29) (29)
рассматривается
как приближенное решение уравнения (21). В работе [9] заявлено, что (30)
является точным решением (21). Приходится признать, что это не верно. Допущена
грубая ошибка при вычислении невязки уравнения. Подставим функцию (29) в
уравнение (21) и вычислим невязку:
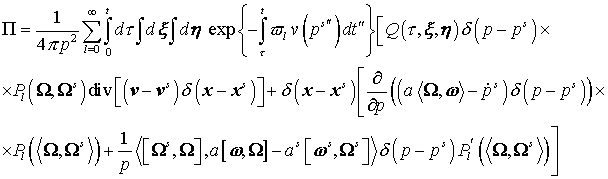 (30) (30)
Данная невязка не обращается в ноль. В момент времени 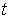 в элементе фазового пространства в элементе фазового пространства
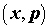 присутствуют электроны
с лагранжевыми координатами присутствуют электроны
с лагранжевыми координатами 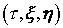 , слабо отклонившиеся от траектории, определяемой уравнениями
движения. Присутствуют также электроны, существенно отклонившиеся от траектории
за счет углового рассеяния. Если разность , слабо отклонившиеся от траектории, определяемой уравнениями
движения. Присутствуют также электроны, существенно отклонившиеся от траектории
за счет углового рассеяния. Если разность 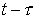 мала по сравнению с мала по сравнению с 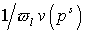 , то превалируют электроны, слабо отклонившиеся от
траектории, определяемой уравнениями движения. Для них , то превалируют электроны, слабо отклонившиеся от
траектории, определяемой уравнениями движения. Для них 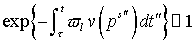 . Сумма . Сумма 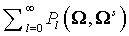 переходит в переходит в 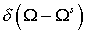 , сумма , сумма  переходит в переходит в 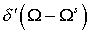 , а невязка (30) обращается в ноль. Если разность , а невязка (30) обращается в ноль. Если разность 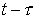 сопоставима с сопоставима с 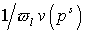 , то величина , то величина  сопоставима с сопоставима с 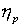 , что приводит к возрастанию сечения упругого рассеяния.
Тогда функция , что приводит к возрастанию сечения упругого рассеяния.
Тогда функция 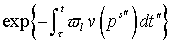 становится быстро меняющейся
по сравнению с становится быстро меняющейся
по сравнению с 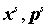 . Невязку можно оценить как отношение времени жизни электрона
с импульсом . Невязку можно оценить как отношение времени жизни электрона
с импульсом 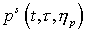 относительно углового
рассеяния к текущему периоду плазменных колебаний или времени жизни электрона
относительно ионизационного торможения. относительно углового
рассеяния к текущему периоду плазменных колебаний или времени жизни электрона
относительно ионизационного торможения.
Приближение накладывает
существенное ограничение на класс решаемых задач. Оно не применимо для узких
пучков электронов. Если источник описывает генерацию мононаправленного потока
электронов в области, размер которой сопоставим или мал по сравнению с
транспортной длиной пробега, то функция 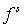 может сохранить малый
пространственный размер. В слагаемом может сохранить малый
пространственный размер. В слагаемом 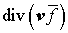 уравнения (24) будет
составляющая, которую нельзя считать малой по сравнению с интегралом углового
рассеяния. уравнения (24) будет
составляющая, которую нельзя считать малой по сравнению с интегралом углового
рассеяния.
Несмотря на то, что функция (29)
является приближенным решением с допустимой для ряда задач погрешностью,
уравнение непрерывности заряда для нее должно выполняться точно. В противном
случае использовать нулевой момент этой функции в расчетах нельзя, поскольку
нарушится калибровка уравнений Максвелла. Уравнение 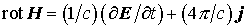 не будет эквивалентно
уравнению не будет эквивалентно
уравнению 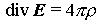 , где , где 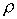 – плотность заряда, в результате чего
электростатическое поле будет вычисляться не правильно. Действительно, из
уравнения (26) при – плотность заряда, в результате чего
электростатическое поле будет вычисляться не правильно. Действительно, из
уравнения (26) при 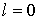 следует, что следует, что 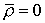 . В уравнении (26) сделано приближение, которое недопустимо с
точки зрения уравнений Максвелла. . В уравнении (26) сделано приближение, которое недопустимо с
точки зрения уравнений Максвелла.
Если величина 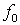 необходима при
вычислениях, например для определения интенсивности ионизации рассеивающей
среды, необходимо вычислять ее непосредственно из уравнения непрерывности: необходима при
вычислениях, например для определения интенсивности ионизации рассеивающей
среды, необходимо вычислять ее непосредственно из уравнения непрерывности:
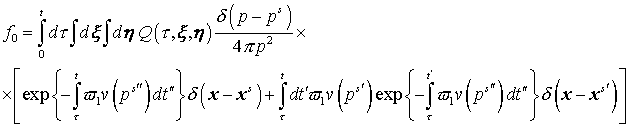 , ,
не допуская в общем случае приближения при
вычислении интеграла по переменной  . .
Заключение
Кинетическое уравнение (21)
с приближенным интегралом столкновений (18) описывает распространение
электронов в нейтральной среде, если энергия отдельного электрона существенно
превосходит характерный потенциал ионизации среды. Описание использует только
данные многократного рассеяния и тормозную способность вещества.
Плотность электрического
тока (30), вычисленная по приближенному решению (29) кинетического уравнения
(21), может быть использована для численного моделирования методом частиц
самосогласованного электромагнитного поля, создаваемого широким потоком
электронов в исходно нейтральной среде при некоторых актуальных наборах исходных
данных. Для этого дополнительно необходима модель плотности тока вторичных
электронов. Метод построения решения основывается как на физических
особенностях электронного рассеяния, так и на использовании существенного
приближения. Особенности состоят в наибольшей вероятности рассеяния на малые
углы в каждом акте столкновений и возрастании сечений с уменьшением энергии
падающих электронов. Для электронов, существенно отклонившихся от траекторий,
определяемых уравнениями движения, считается, что столкновения превалируют над
переносом в фазовом пространстве.
Литература
1. В.И.Бойко, В.А.Скворцов, В.Е.Фортов,
И.В.Шаманин. Взаимодействие импульсных пучков заряженных частиц с
веществом. – М.: Физматлит, 2003.
2. Кейс К., Цвайфель Р. Линейная теория переноса.
– М.:МИР, 1967.
3. Т.А. Гермогенова, Л.П. Басс,
А.М. Волощенко. Методы дискретных ординат в задачах о переносе
излучения. – М.: ИПМ им. М.В. Келдыша АН СССР, 1986.
4. К. Черчиньяни.
Теория и приложения уравнения Больцмана. – М.: МИР, 1978
5. Hockney R.W., Eastwood
J.W. Computer Simulation Using
Particles.– McGraw-Hill, New York, 1981.
6.
Г. Эккер. Теория полностью ионизованной плазмы. – М.: МИР, 1984.
7. А.А. Власов. Теория многих частиц. – М.:
ГИТТЛ, 1952.
8. А.А. Власов. Статистические функции
распределения. – М.: ГИТТЛ, 1952.
9. А.В. Березин, Н.С.
Келлин, М.Б. Марков, С.В. Паротькин О столкновениях электронов в задачах
генерации электромагнитного поля потоком электронов. – Препринт ИПМ
им. М.В. Келдыша РАН, 2003, №61.
10. Л.Д. Ландау, Е.М. Лифшиц. Физическая
кинетика. -М.:Наука, 1979.
11. Г. Мэсси,
Е. Бархоп. Электронные и ионные столкновения.
М.: МИР, 1958.
12. А.Ф.Аккерман. Моделирование траекторий
заряженных частиц в веществе. – М.: Энергоиздат, 1991.
13. А.К. Савинский. Взаимодействие
электронов с ткане-эквивалентными средами. – М.: Энергоатомиздат,
1984.
14. Gryzinski, Phys.
Rev., 115, 374,1959.
15. Экспериментальная
ядерная физика. / под ред. Э. Сегре, т.1, М.: ИЛ, 1958.
16. Тормозная способность электронов и
позитронов: Доклад 37МКРЭ: М.: Энергоатомиздат,1987.
17. В.Б.Берестецкий, Е.М.Лифшиц, Л.П.Питаевский.
Квантовая электродинамика. – М.: Наука, 1980.
18. И. Мак-Даниель. Процессы столкновений в
ионизованных газах. – М.: МИР, 1967.
19. А.В.Березин, Н.С.Келлин, М.Б.Марков, С.В.Паротькин, А.В.Сысенко. О
математических моделях вторичной ионизации. – Препринт
ИПМ им. М.В. Келдыша РАН, 2002, №29.
20. Н.Мотт, Г.Мэсси. Теория атомных
столкновений. – М.: МИР, 1969.
21. G.Moliere.
Theorie der Steuung Schneller Geladener Teilchen. II. Mehrfachung
22. S. Goudsmit,
J.L. Saunderson, Phys. Rev., 57, 24,1940.
23. В.В. Степанов.
Курс дифференциальных уравнений. – М.:ГИТТЛ, 1957.
24. W. Braun, K. Hepp. The Vlasov
Dynamics and Its Fluctuations in the 1/N Limit of Interacting Classical
Particles. – Commun. math. Phys. 56, 1977.
25. С. Чепмен,
Т. Каулинг. Математическая теория неоднородных
газов. – М.: ИЛ, 1960.
|