Аннотация
Представлен программный комплекс, предназначенный для решения задачи теории упругости
композиционных материалов в пространственно трехмерном случае. В качестве расчетного метода
использован метод конечных суперэлементов Р.П. Федоренко. Приведены результаты численного
решения для различных упругих и геометрических параметров материалов, составляющих
композиционный материал.
Abstract
The program complex intended for solving linear 3D elasticity problems in case of composite
materials is presented. As a main computational method the Fedorenko Finite Superelements
Method (FSEM) is used. Numerical results for composite materials with various elastic and
geometrical parameters are presented.
Содержание
1 Введение. 3
2 Метод
конечных суперэлементов. 5
4 Дискретизация
сложной области прямыми методами.. 11
5 Программный
комплекс. 16
6 Результаты
численного моделирования. 19
6.1 Тестовые расчеты.. 20
6.2 Варианты расчетов. 20
6.3 Анализ результатов расчетов. 21
7 Заключение. 29
8 Список
литературы.. 30
1
Введение
Метод конечных
суперэлементов (МКСЭ) предложен в работах [1 - 3] для задач, решения которых имеют локальные
особенности геометрического или физического типа. При этом особенности
геометрического типа порождаются резкими изменениями границы области и наличием
в ней пустот, а физического типа – присутствием подобластей с резко отличными
параметрами материала. Размер особенностей предполагается существенно меньшим
как размера исходной расчетной области, так и приемлемого шага расчетной сетки.
Метод применялся для решения ряда сложных задач диффузии, теории упругости,
кинетики ядерных реакторов и ряда других.
В работах [4 - 9] предложен вариант теоретического исследования МКСЭ,
который позволил, в частности, формально строить аппроксимации метода для
достаточно широкого класса эллиптических задач, в частности, для линейных задач
теории упругости.
Одной из таких задач, для которых возможно ожидать эффективного использования
МКСЭ, является задача расчета напряженно - деформированного состояния
композиционных материалов. Отметим, что использование МКСЭ для подобных задач
проводилось и раньше, в оригинальных работах [1 - 3]. Схема МКСЭ для решения указанной задачи приведена в
[10]. Там же представлены результаты первых расчетов,
указывающих на эффективность метода, проведено сравнение численных результатов
с экспериментальными и известными теоретическими оценками. Получено хорошее совпадение расчетных
значений как с данными эксперимента, так и с теоретическими оценками.
Рассматриваемая работа продолжает работу [10] и посвящена описанию программного комплекса,
предназначенного для проведения массовых практических расчетов на основе МКСЭ и
анализа их результатов.
В качестве объекта исследования выбраны
композиционные материалы с включениями в виде коротких волокон, для которых
рассмотрена задача расчета напряженно - деформированного состояния композитного
тела с помощью МКСЭ. Для решения указанной задачи разработан
программно-вычислительный комплекс (ПК), построенный на модульном принципе,
позволяющий в автоматизированном режиме подготавливать и запускать расчет, а
также анализировать его результаты. В работе описаны архитектура и принципы
работы указанного комплекса, использованные при его реализации вычислительные и
прикладные алгоритмы, а также приведены результаты его применения для решения
некоторых задач.
Остановимся подробнее на рассматриваемой
задаче. В дальнейшем будем считать, что некоторый материал – матрица –
армирован включениями в виде коротких волокон, форма которых близка к
сферической. Поведение материала считаем упругим.
В общем случае представляет интерес
информация о детальном напряженно-деформированном состоянии композита и его
приведенных (усредненных) свойствах в зависимости от упругих и геометрических
параметров матрицы и включения таких, как, например, объемная доля включений в
материале, их геометрия и ориентация и так далее.
Отметим, что в настоящее время существует
несколько различных способов описания и анализа свойств композитов. Такими
подходами являются, например, метод асимптотического осреднения [11], различные микромеханические [12 - 16] и смесевые модели [17 - 20], широко применяемые в инженерной практике. Эти
модели позволяют определять приведенные упругие свойства композита в
зависимости от свойств его структурных элементов. Краткий обзор этих моделей
приведен в [10]. Там же подробно описаны метод и некоторые
результаты применения МКСЭ для определения приведенных упругих свойств
композитов.
Актуальность МКСЭ для решения описанной
задачи связана с тем, что он позволяет проводить прямое численное моделирование
напряженно - деформированного состояния композиционного материала с
непосредственным учетом большого числа включений. Решение такой задачи обычными
конечно - разностными или конечно - элементными методами представляет большую
трудность, связанную с большой размерностью конечномерной задачи. Так, даже в
области с одним включением необходимо использовать очень подробные сетки,
позволяющие хорошо разрешить решение в окрестности контакта матрицы и
включения. Число узлов в такой сетке может доходить до 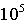 и более. Понятно, что
решить задачу в области с несколькими включениями на сетке с таким шагом очень
сложно. и более. Понятно, что
решить задачу в области с несколькими включениями на сетке с таким шагом очень
сложно.
Помимо этого, в работе [10] приведен алгоритм оценки приведенных характеристик
изучаемого композиционного материала. Он основан на сравнении численного
решения задачи в области с неоднородными упругими свойствами, полученного с
помощью МКСЭ, с аналитическим решением задачи в однородной изотропной области с
неизвестными приведенными упругими свойствами, подлежащими определению. Этот
алгоритм использовался и в данной работе.
Работа выполнена при частичной финансовой поддержке
Российского фонда фундаментальных исследований (проект РФФИ № 06-01-00421).
2
Метод конечных суперэлементов
Не останавливаясь детально на теоретических особенностях
исследования МКСЭ, укажем коротко некоторые его отличительные свойства.
Подробное теоретическое описание метода для ряда задач приведено в работах [4 - 9].
В соответствии с МКСЭ расчетная область
разбивается на некоторое количество подобластей – суперэлементов (СЭ). Далее
каждый СЭ оснащается системой базисных функций, которые являются точными
решениями рассматриваемого уравнения с некоторыми граничными условиями,
заданными на границе СЭ. Приближенное решение исходной задачи ищется в виде
линейной комбинации таких базисных функций из условий, формально совпадающих с
уравнениями метода Галеркина - Бубнова или Галеркина - Петрова.
Использование базисных функций, полученных
точным решением рассматриваемой системы уравнений, является главным отличием
МКСЭ от обычного метода конечных элементов с точки зрения его программной
реализации и применения. С алгоритмической точки зрения в остальном МКСЭ сходен
с обычным методом конечных элементов (МКЭ). А именно, приближенное решение в
обоих случаях ищется как линейная оболочка некоторой системы базисных функций.
Конечномерная задача (система линейных алгебраических уравнений для узловых
значений конечных элементов (КЭ)/СЭ) во всех случаях формально получается из
условия ортогональности невязки приближенного решения некоторому конечномерному
подпространству.
Несмотря на сходства, методы существенно
отличаются с точки зрения теоретического описания. Это связано с тем, что в
общем случае используемые в МКСЭ базисные функции не обладают аппроксимирующими
свойствами в том пространстве, в котором ищется решение исходной задачи. В МКСЭ
базисные функции рассчитываются как решения вспомогательных задач для
рассматриваемого уравнения в каждом СЭ по отдельности, а не задаются
непосредственно, как в случае МКЭ. Однако указанная особенность МКСЭ не
представляет проблемы с точки зрения теории, так как оказывается, что
аппроксимирующими свойствами должны обладать граничные функции, которые
определены на границах СЭ и задают граничные условия при расчете базисных
функций. При этом для построения граничных функций могут использоваться
известные и хорошо разработанные методы интерполяции (см. в качестве примера
[31]) одномерных или двумерных функций (если исходная задача рассматривается в
двумерной или трехмерной постановке соответственно).
Если записать задачу
относительно граничных функций, исключив из рассмотрения «внутренности» СЭ, то
к ней можно применить теоретический аппарат, необходимый для обоснования
метода. При этом ошибка приближенного решения будет определяться ошибкой
интерполяции функции, заданной на границах СЭ, элементами соответствующего
конечномерного пространства функций, также заданных на границе.
Таким образом, исходная
краевая задача может быть заменена эквивалентной ей задачей для определения
следов неизвестного решения на границах СЭ. Такой переход может быть
осуществлен с помощью граничных операторов Пуанкаре – Стеклова, предложенных в
работах В.И. Лебедева и В.И. Агошкова [21 - 24] как средство теоретического исследования методов
декомпозиции области. При этом указанные методы рассматриваются как
итерационные методы решения соответствующих уравнений для следов. Это позволяет
использовать при их исследовании теорию итерационных методов решения
абстрактных операторных уравнений. В соответствии с описанным подходом МКСЭ
может рассматриваться как проекционный метод решения этих же уравнений, что
позволяет использовать при их исследовании известную теорию проекционных
методов.
В результате с точки зрения
теории схема построения аппроксимаций МКСЭ имеет следующий вид. Сначала
расчетная область разбивается на некоторое количество плотно покрывающих ее
непересекающихся подобластей - СЭ. Обобщенная постановка для определения следов
решения исходной задачи на границах СЭ строится на основе операторов
Пуанкаре-Стеклова и формулы Грина, соответствующих оператору задачи. Для
построения аппроксимаций вариационного уравнения для следов могут применяться
стандартные методы теории абстрактных вариационных уравнений и проекционных
методов [25 - 28]. Это позволяет формально и единообразно
рассматривать различные варианты МКСЭ, соответствующие тем или иным
проекционно-сеточным методам, получать оценки ошибок и так далее. Таким образом
МКСЭ вписывается в известную и хорошо разработанную теорию.
Отметим также, что возможен
комбинированный подход, в котором для аппроксимации задачи используется как
МКСЭ, так и МКЭ. Более подробно комбинированные аппроксимации МКЭ/МКСЭ
рассмотрены в [4 - 9].
Сведение задачи к задаче
для следов в МКСЭ или комбинированном подходе необходимо лишь для построения
расчетной схемы и теоретического исследования метода, что позволяет
использовать при обосновании готовую теорию. С точки зрения алгоритма
построения конечномерной задачи эти методы сходны с обычным МКЭ.
Отметим еще одну
особенность. При построении аппроксимаций МКСЭ задача записывается относительно
следов решения на границах СЭ. При этом СЭ сетка не является разностной в
привычном смысле этого слова. Это разбиение области на меньшие подобласти
происходит на этапе построения уравнения для следов до построения конечномерных
аппроксимаций. На границах СЭ задаются некоторая разностная сетка и уже на ней
те или иные граничные функции. Эти функции должны обладать аппроксимирующими
свойствами в подходящем пространстве следов. Шаг граничной сетки h
является параметром дискретизации, то есть приближенное решение задачи сходится
к точному, когда h стремится к нулю. Диаметр СЭ при этом не зависит
от h и не меняется при его стремлении к нулю.
Не рассматривая более общей теории, перейдем к
описанию математической постановки задачи и аппроксимаций МКСЭ.
Применим МКСЭ к решению линейной задачи теории упругости
в трехмерной постановке. В качестве основного приложения взята задача расчета
напряженно-деформированного состояния композиционных материалов для случая
композитов с короткими волокнами. Для каждого полученного решения вычислены
усредненные по расчетной области упругие параметры композиционного материала.
Рассмотрим
постановку задачи. Требуется определить поле перемещений 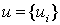 , , 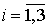 сплошной среды в
ограниченной трехмерной области сплошной среды в
ограниченной трехмерной области  , на границе , на границе  которой заданы
кинематические и динамические граничные условия. Будем считать, что в области которой заданы
кинематические и динамические граничные условия. Будем считать, что в области  задана ортогональная
декартова система координат задана ортогональная
декартова система координат 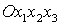 . В дальнейшем будем использовать правило суммирования по
повторяющимся индексам. Производную некоторой величины . В дальнейшем будем использовать правило суммирования по
повторяющимся индексам. Производную некоторой величины  по переменной по переменной 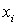 будем обозначать через будем обозначать через
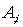 , ,
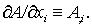
Система
соотношений, описывающих напряженно-деформированное состояние упругого тела,
состоит из уравнения равновесия
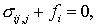
материальных
соотношений, выражающих обобщенный закон Гука
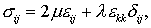
и
кинематических соотношений
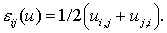
Будет
использоваться также операторная форма уравнения равновесия
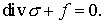
Здесь  – тензор упругих
напряжений, – тензор упругих
напряжений, 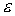 – тензор деформаций, – тензор деформаций, 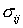 , , 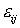 – их компоненты в
выбранной системе координат, – их компоненты в
выбранной системе координат, 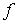 – объемная плотность
внешних сил, – объемная плотность
внешних сил, 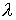 , , 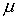 – коэффициенты Ламе, являющиеся
заданными функциями точки пространства, – коэффициенты Ламе, являющиеся
заданными функциями точки пространства, 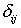 – компоненты
единичного тензора. – компоненты
единичного тензора.
Будем считать, что
граница 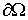 области области  состоит из двух
частей, состоит из двух
частей, 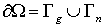 . На части . На части 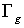 заданы кинематические
граничные условия заданы кинематические
граничные условия
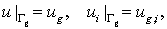
а на части 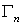 границы заданы
естественные граничные условия границы заданы
естественные граничные условия
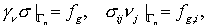
где
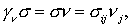
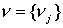 – внешняя нормаль к
границе области. – внешняя нормаль к
границе области.
Рассмотрим также слабую постановку задачи. Она имеет следующий вид:
необходимо определить
вектор - функцию 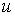 , удовлетворяющую кинематическим
граничным условиям на , удовлетворяющую кинематическим
граничным условиям на 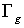 и уравнению и уравнению
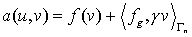
для всех достаточно гладких функций 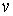 , обращающихся в ноль на той части границы, где заданы
граничные условия первого рода, то есть на , обращающихся в ноль на той части границы, где заданы
граничные условия первого рода, то есть на 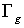 . .
Для ее построения использована следующая формула
Грина:
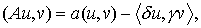
где
для рассматриваемой задачи
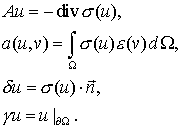
Здесь
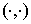 – скалярное
произведение в пространстве – скалярное
произведение в пространстве 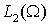 , ,  – скалярное
произведение в пространстве – скалярное
произведение в пространстве 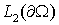 , , 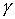 – оператор вычисления
следа функции на границе, – оператор вычисления
следа функции на границе, 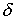 – оператор «нормальной
производной», – оператор «нормальной
производной», 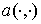 – билинейная форма,
порожденная оператором – билинейная форма,
порожденная оператором 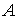 . Отметим, что вид операторов . Отметим, что вид операторов 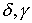 и билинейной формы и билинейной формы 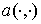 определяется
оператором определяется
оператором 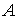 . .
Приведенная формула
Грина верна для достаточно гладких векторных полей 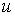 , линейной зависимости , линейной зависимости 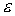 от от 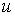 и произвольной
зависимости и произвольной
зависимости  от от 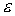 . .
Как указано выше,
МКСЭ может рассматриваться как обычный метод Галеркина - Бубнова с
использованием специальных базисных функций. Поэтому конечномерная задача может
быть получена следующим образом. Необходимо: 1. задать разбиение расчетной
области на СЭ; 2. задать на границах СЭ граничные функции, аппроксимирующие
следы решения на границах СЭ; 3. для каждой такой граничной функции продолжить
ее во внутренность СЭ решением исходного уравнения с указанной функцией как
граничным условием первого рода, для чего внутри каждого СЭ независимо ввести
расчетную сетку и использовать обычный МКЭ; 4. систему линейных алгебраических
уравнений для определения узловых значений СЭ получить из условий, формально
совпадающих с условиями метода Галеркина - Бубнова с рассчитанными функциями в
качестве базисных.
Отметим, что, так
как СЭ базисные функции рассчитываются численно, то, вообще говоря,
суперэлементы могут иметь произвольную форму. Тем не менее, в дальнейшем будем
рассматривать СЭ в виде параллелепипедов, а узловые значения СЭ решения отнесем
к их вершинам.
При этом
естественным требованием при разбиении области на СЭ в случае конкретной
рассматриваемой задачи является расположение каждого включения композита
целиком внутри одного СЭ. Это означает, что на границах СЭ упругие свойства
среды не меняются, и, значит, на границе СЭ решение является относительно
гладким. Это позволяет использовать для аппроксимации перемещений на границах
СЭ простейшие билинейные базисные граничные функции. Для расчета решения внутри
СЭ далее используется достаточно мелкая сетка для того, чтобы описать
особенности решения, в частности, на контактной границе между матрицей и
включением.
В общем случае все
СЭ могут быть разными, каждый СЭ и соответствующее ему включение могут иметь
разную форму и значения упругих параметров. В представленных далее расчетах все
СЭ имеют форму кубов, включения могут иметь разную форму, значения упругих
коэффициентов матрицы и включения не меняются от СЭ к СЭ.
4
Дискретизация сложной области прямыми методами
Рассмотрим ряд вопросов, возникающих при реализации
МКСЭ.
Важную роль при реализации численного метода решения задачи играет
способ построения КЭ сеток, используемых для расчёта СЭ.
Рассмотрим метод дискретизации занимаемой СЭ области на конкретном
примере. Получаемая при этом тетраэдральная сетка используется для расчета
базисных функций СЭ. Пусть имеется неоднородная трехмерная область,
представляющая собой куб (или близкий к нему параллелепипед) с расположенным в
центре куба включением эллипсоидальной формы. Необходимо построить сетку
триангуляции так, чтобы ее ребра не пересекали границу между включением и
матрицей, то есть чтобы каждый элемент построенной сетки принадлежал строго
либо матрице, либо включению.
Оценка типичных для
рассматриваемого в работе класса задач размеров включения (исходя из заданной
объемной доли) показывает, что радиус условного "шара" составляет
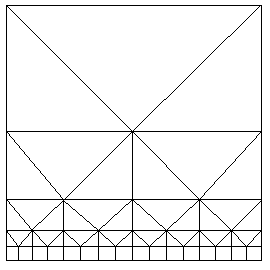
около 1/3 длины ребра "куба". Разбив заданную область на 7
шестигранников, отобразим на каждый из этих шестигранников триангуляцию параллелепипеда.
Разбиение на шестигранники осуществляется следующим образом. Поместим внутрь
включения некоторый параллелепипед, а затем соединим отрезками вершины этого
параллелепипеда с соответствующими вершинами параллелепипеда ячейки. В
результате получатся один параллелепипед и 6 трапециевидных шестигранников
(см. рис.
1).
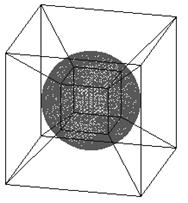
Рис. 1. Разбиение
исходной области на 7 подобластей
На первом этапе
построим в указанных подобластях согласованные кубические сетки, то есть сетки,
элементами которых являются близкие к кубам параллелепипеды (далее по тексту –
«кубы»). Если разбиение центрального параллелепипеда при этом не представляет
сложности, то в трапециевидных шестигранниках есть особенность, связанная с
наличием поверхности раздела, которую не должны пересекать ребра триангуляции.
Пусть поверхность
включения задана в виде функции 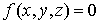 . Рассмотрим одну из трапециевидных областей, заданную в
локальных координатах. Зададим набор из четырех чисел: . Рассмотрим одну из трапециевидных областей, заданную в
локальных координатах. Зададим набор из четырех чисел: 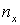 , , 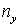 , , 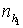 и и 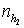 . Пусть . Пусть 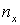 и и 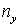 – число сторон
«кубов», укладывающихся, соответственно, вдоль сторон, параллельных координатным
осям – число сторон
«кубов», укладывающихся, соответственно, вдоль сторон, параллельных координатным
осям 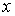 и и 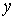 , , 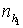 – число сторон
«кубов», укладывающихся вдоль координаты – число сторон
«кубов», укладывающихся вдоль координаты 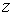 , лежащих ниже поверхности ограничения, а , лежащих ниже поверхности ограничения, а 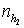 – число сторон
«кубов», лежащих выше поверхности ограничения (см. рис. 2). – число сторон
«кубов», лежащих выше поверхности ограничения (см. рис. 2).
Прямыми отрезками
разобьем верхнюю и нижнюю грани области на 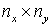 четырехугольников
("квадратов"), получая тем самым четырехугольников
("квадратов"), получая тем самым 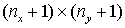 узлов будущей
триангуляции. Проведем отрезки, соединяющие узлы одной грани с соответствующими
узлами на противоположной грани. Рассматривая далее каждый из отрезков, найдем
точку пересечения отрезка с поверхностью ограничения, поместим в нее узел
триангуляции и разобьём каждую из полученных частей на узлов будущей
триангуляции. Проведем отрезки, соединяющие узлы одной грани с соответствующими
узлами на противоположной грани. Рассматривая далее каждый из отрезков, найдем
точку пересечения отрезка с поверхностью ограничения, поместим в нее узел
триангуляции и разобьём каждую из полученных частей на 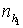 и и 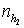 равных частей
соответственно. Соединяя ребрами узлы на отрезках, получим искомое разбиение
области на «кубы». равных частей
соответственно. Соединяя ребрами узлы на отрезках, получим искомое разбиение
области на «кубы».
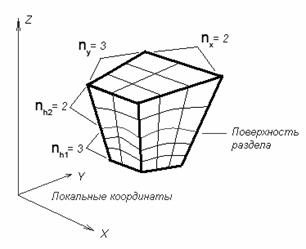
Рис. 2. Разбиение
трапециевидной области, состоящей
из двух материалов
Аналогично разобьем
на «кубы» и остальные пять трапециевидных областей. Заметим, что в силу способа
построения граничные узлы двух любых смежных областей будут автоматически совпадать
(см. рис. 3).
Как
видно из рис.
3, «кубы» в трапециевидных шестигранниках могут быть
сильно искажены, что неминуемо скажется на качестве триангуляции. Ситуацию можно
подправить подбором параметров (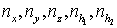 ) и размещением узлов на отрезках, пересекающих ) и размещением узлов на отрезках, пересекающих 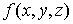 , так, чтобы их длина увеличивалась по мере удаления от
внутреннего параллелепипеда (см. рис.
4). Это позволяет получить ячейки формы, близкой
кубической. При наличии априорной информации можно подобрать параметры
увеличения так, чтобы полученная сетка была адаптирована под решение задачи. , так, чтобы их длина увеличивалась по мере удаления от
внутреннего параллелепипеда (см. рис.
4). Это позволяет получить ячейки формы, близкой
кубической. При наличии априорной информации можно подобрать параметры
увеличения так, чтобы полученная сетка была адаптирована под решение задачи.
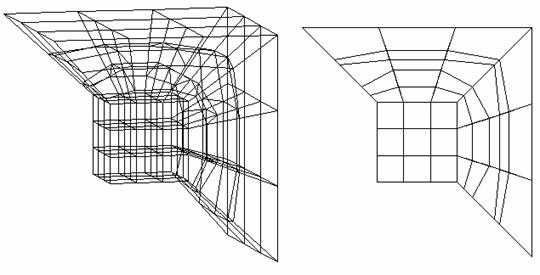
Рис. 3. Построение
согласованной кубической сетки в подобластях (показаны внутренний куб и две
смежные трапециевидные области; 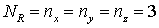 , ,  ) )
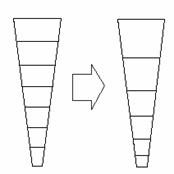
Рис. 4. Улучшение
качества сетки за счет неравномерности разбиения
После того, как
кубическая сетка построена, производится разбиение на тетраэдры. При
"классическом" подходе каждый куб внутренними ребрами разбивается на
5 или 6 тетраэдров (см. рис.
5).
"Классические"
шаблоны имеют ряд недостатков (см. [29, 30]), поэтому вместо них используется
другой шаблон, основанный на вставке в центр каждого куба дополнительного узла.
Каждый из этих дополнительных узлов соединяется ребрами с вершинами своего
«куба», в результате чего исходный параллелепипед разбивается на два типа
элементов (см. рис.
6):
1. граничные – в виде
четырехугольной пирамиды (то есть пирамиды, основанием которой является
квадрат);
2. внутренние – в виде объемного ромба, составленного из двух
четырехугольных пирамид, соединенных основаниями.
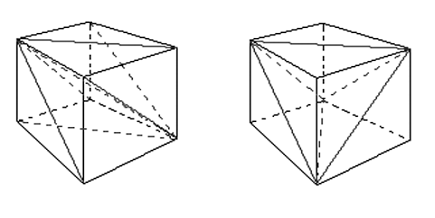
Рис. 5. Разбиение
куба на шесть (слева) и пять (справа) тетраэдров
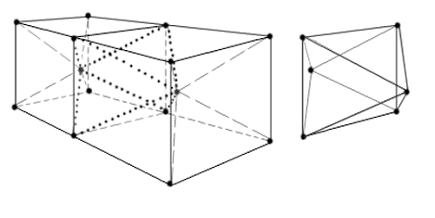
Рис. 6. Вставка
внутрь кубической сетки дополнительных вершин; справа отдельно изображен
получающийся в результате ромбовидный элемент
Чтобы разбить
граничные пирамидальные элементы, достаточно добавить произвольно
ориентированное диагональное ребро, при этом получаются два тетраэдра,
обеспечивающие сетку удовлетворительного качества (о качестве см. [29, 30]). Разбить внутренние ромбовидные элементы
можно путем вставки ребра между дополнительными узлами (то есть центрами
кубов). При этом получаются четыре тетраэдра.
Заметим, что данный
шаблон позволяет получить однородные сетки высокого качества, которые обладают
и рядом других преимуществ – например, простотой согласования элементов в
составной области, подобной заданной (это согласование получается
автоматически). Также этот шаблон позволяет легко добиваться локального сгущения сетки. Для этого
возможно использовать своеобразный «переходный слой», который позволяет перейти
от сетки с шагом 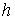 к сетке с шагом к сетке с шагом 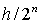 за половину шага за половину шага 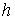 (см. рис.
7.а). Двумерная аналогия этой процедуры представлена на
рис.
7.б. Тетраэдры такого переходного шаблона обладают
«средним» качеством. (см. рис.
7.а). Двумерная аналогия этой процедуры представлена на
рис.
7.б. Тетраэдры такого переходного шаблона обладают
«средним» качеством.
Представленное на рис. 7.б локальное сгущение осуществляется вблизи границы
раздела между матрицей и включением, что существенно улучшает гладкость
получаемого численного решения.
Описанная процедура
триангуляции области СЭ с эллипсоидальным включением используется в
разработанном ПК.
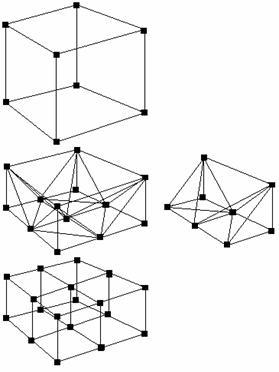 
а) б)
Рис. 7. Построение
переходного слоя и его двумерная аналогия
5
Программный комплекс
Для решения задачи,
поставленной в §3, разработан программно-вычислительный комплекс (ПК).
Отдельный расчет, проводимый с его помощью, состоит из следующих этапов:
1. подготовка входных
данных с помощью пользовательского интерфейса препроцессора (задание размеров
области, размерных и упругих параметров СЭ, подготовка КЭ сеток СЭ и СЭ сетки
области);
2. запуск основной
программы расчета;
3. запуск программы
расчета приведенных параметров материала после завершения расчета;
4. отображение
результатов в окне пользовательского интерфейса.
Как видно из
описания, все этапы работы комплекса делятся на два вида. Первый вид – первый и
четвертый этапы, требующие непосредственного участия пользователя и максимально
удобного и универсального способа ввода входных параметров расчета и анализа
полученных результатов. Другой вид – расчетные этапы (этапы 2 и 3), на ход
которых пользователь не влияет и на которые должно быть выделено максимальное
количество вычислительных ресурсов и, следовательно, в целях оптимизации в них
должны быть минимизированы накладные расходы в виде необязательных операций
ввода-вывода, к которым относится и графический интерфейс.
Соответственно
разбивке на этапы комплекс выполнен в виде нескольких отдельных программ
(модулей), обмен данными между которыми организован с помощью файлов
ввода-вывода:
1. препроцессор,
основанный на пользовательском графическом интерфейсе (GUI);
2. основная расчетная
программа – консольное приложение, запускаемое из программы пользовательского
интерфейса;
3. постпроцессор –
отвечает за обработку результатов и их текстовое или графическое представление.
Следует отметить,
что на всех этапах расчета все входные, промежуточные и результирующие данные
сохраняются в виде текстовых файлов. Поэтому, а также благодаря модульному
исполнению комплекса, любая из перечисленных выше программ может быть
независимо заменена или доработана при условии сохранения форматов файлов
ввода-вывода.
Остановимся
отдельно на функциональных возможностях препроцессора. Он поддерживает
следующие функции:
1. Организация расчета в
виде проекта: для расчета автоматически создается папка, где содержатся файл
проекта со всеми параметрами расчета, файлами с КЭ сетками СЭ, файлами данных
расчетных программ.
2. Сохранение и загрузка
всех параметров расчета в файле проекта.
3. Возможность генерации
и сохранения файлов для расчетной программы, содержащих сведения о КЭ сетках
СЭ, СЭ сетке и граничных условиях в зависимости от введенных параметров, а
также возможность изменения параметров расчета и перегенерации соответствующих
файлов.
4. Графическое
представление и статистический анализ построенных КЭ и СЭ сеток.
5. Автоматизированная
генерация параметров СЭ и распределение СЭ по расчетной области в соответствии
с заданным вероятностным законом распределения некоторых параметров.
6. Автоматизированный
подбор конфигурации расчетной области по параметрам СЭ и заданной объемной
плотности включений.
В ПК интегрирована
возможность генерации СЭ с эллипсоидальными включениями. При этом углы наклона
осей эллипсоида и величины полуосей могут варьироваться в автоматизированном
или ручном режиме. После сохранения изменений происходит автоматическая
перегенерация всех связанных объектов таких, как размеры области СЭ и КЭ сетки
СЭ (см. §4).
На первом этапе при
генерации КЭ сеток СЭ пользователь может выбрать параметры разбиения: число
разбиений ребра СЭ 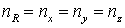 и шаг разбиения КЭ
сетки СЭ и шаг разбиения КЭ
сетки СЭ 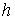 . Одинаковый размер СЭ и единые параметры дискретизации
позволяют состыковывать СЭ без пересчета граничных узлов. При формировании
расчетной области существует возможность добавления в нее СЭ без включений. . Одинаковый размер СЭ и единые параметры дискретизации
позволяют состыковывать СЭ без пересчета граничных узлов. При формировании
расчетной области существует возможность добавления в нее СЭ без включений.
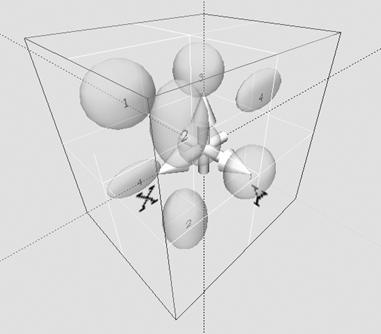
Рис. 8. Расчетная
область композитного тела (снимок экрана препроцессора)
Примерный вид
области размера 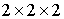 , сгенерированной в препроцессоре и содержащей СЭ четырех
типов, представлен на рис.
8. , сгенерированной в препроцессоре и содержащей СЭ четырех
типов, представлен на рис.
8.
Отметим, что схема
расчета базисных функций СЭ идеально пригодна для параллельных вычислений, так
как в большинстве случаев это самая ресурсоемкая операция, а расчеты отдельных
типов СЭ не зависят друг от друга. Поэтому поддержка распараллеливания этой
процедуры позволит многократно сократить время всего расчета.
6
Результаты численного моделирования
Результатом работы основной расчетной программы является
файл, содержащий решения в узлах СЭ сетки. На его основе проводится расчет
приведенных параметров композита, сохраняющий в файле минимальные (на графиках
– min), максимальные
(на графиках – max) и
средние (на графиках – avg)
значения модуля Юнга 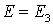 и коэффициентов
Пуассона и коэффициентов
Пуассона 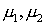 . .
Это набор упругих
параметров, которые можно определить для композиционного материала с помощью
решения задачи об одноосном растяжении упругого стержня в направлении 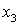 (подробнее см. [10]). Мы ограничиваемся исследованием свойства
растяжения в одном направлении (подробнее см. [10]). Мы ограничиваемся исследованием свойства
растяжения в одном направлении 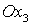 , так как используемые СЭ позволяют анизотропный в общем
случае композит считать в среднем изотропным. Следовательно, можем принять , так как используемые СЭ позволяют анизотропный в общем
случае композит считать в среднем изотропным. Следовательно, можем принять
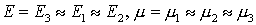 . .
Отметим, что расчеты подтвердили
это предположение и далее приведены результаты только для компонент 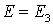 и и 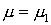 . .
6.1
Тестовые расчеты
Предварительно
проведен ряд расчетов для различных областей и включений при условии, что
материал включений идентичен материалу матрицы СЭ, т.е. проверена степень
соответствия численного решения аналитическому. В результате во всех тестовых
расчетах оно было получено с незначительной погрешностью, величина которой
зависела от количества узлов КЭ сетки СЭ.
6.2 Варианты
расчетов
Проведен ряд расчетов, результаты которых позволяют
проанализировать поведение композитного тела в зависимости от составляющих его
материалов, размеров включений и распределения включений по области, а также
выяснить зависимость решения от параметров дискретизации СЭ и размера расчетной
области  . Расчеты группируются следующим образом. . Расчеты группируются следующим образом.
1. Анализ зависимости
значений приведенных упругих параметров композиционного материала:
а) от значений упругих
параметров включений СЭ;
б) от размеров включения
при неизменных значениях упругих параметров включений СЭ;
в) от значений параметров
разбиения КЭ сетки СЭ при неизменных значениях размеров включения и упругих
параметров включений СЭ;
г) от размера расчетной
области (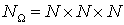 ) при неизменных параметрах материалов и заданном СЭ
(размеры, сетка). ) при неизменных параметрах материалов и заданном СЭ
(размеры, сетка).
2. Анализ изменения
результатов расчетов в зависимости от варианта распределения нескольких типов
СЭ по области при неизменных значениях размеров включения, упругих параметров и
расчетных сетках СЭ.
Область 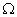 является прямоугольным
параллелепипедом, содержащим является прямоугольным
параллелепипедом, содержащим 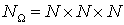 СЭ. При генерации КЭ
сеток СЭ задаются ориентировочный шаг сетки СЭ. При генерации КЭ
сеток СЭ задаются ориентировочный шаг сетки 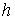 и число и число 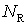 разбиений ребра ячейки
СЭ. Чем больше разбиений ребра ячейки
СЭ. Чем больше 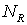 , тем больше узлов у КЭ сетки СЭ. Например, для отдельного СЭ
зависимость количества узлов и ребер тетраэдральной сетки от , тем больше узлов у КЭ сетки СЭ. Например, для отдельного СЭ
зависимость количества узлов и ребер тетраэдральной сетки от 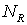 представлена в табл. 1. представлена в табл. 1.
Во
всех расчетах используются ячейки композита со сферическим включением различной
величины, центр которого совпадает с центром СЭ. Все СЭ имеют кубическую форму.
Для удобства модуль Юнга включения 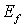 нормирован на модуль
Юнга матрицы, то есть во всех расчетах нормирован на модуль
Юнга матрицы, то есть во всех расчетах 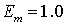 . .
Табл. 1. Базовые
параметры расчетов
|
Число разбиений ребра СЭ
|
Число узлов
|
Число ребер
|
|
4
|
1159
|
7194
|
|
6
|
3597
|
23096
|
|
8
|
8171
|
53470
|
|
10
|
15553
|
103020
|
При проведении
расчетов варьировались следующие параметры задачи: размер расчетной области;
параметры материалов включения и матрицы, 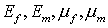 ; параметры разбиения КЭ сетки СЭ, ; параметры разбиения КЭ сетки СЭ, 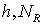 ; распределение фиксированного набора СЭ по области;
количество различных СЭ, составляющих область. ; распределение фиксированного набора СЭ по области;
количество различных СЭ, составляющих область.
В
табл. 2 приведены базовые параметры для расчетов, в которых
изменялись один или несколько из представленных параметров.
Приведем
результаты различных расчетов, выполненных в соответствии с приведенной выше группировкой.
6.3
Анализ результатов расчетов
Разные значения модуля Юнга материала включения
Как указывалось, модуль Юнга включения 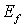 нормирован на модуль
Юнга матрицы нормирован на модуль
Юнга матрицы 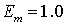 . Использован один тип СЭ с заданными параметрами КЭ разбиения
(шаг и число разбиений ребра СЭ), коэффициенты Пуассона матрицы . Использован один тип СЭ с заданными параметрами КЭ разбиения
(шаг и число разбиений ребра СЭ), коэффициенты Пуассона матрицы 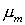 и включения и включения 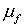 остаются неизменными, остаются неизменными, 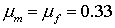 . Модуль Юнга включения . Модуль Юнга включения 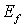 варьировался в
диапазоне [1.0; 15.0]. варьировался в
диапазоне [1.0; 15.0].
Табл. 2. Базовые
параметры расчетов
|
Параметр
|
Обозначение
|
Значение
|
|
Модуль Юнга матрицы
|
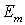
|
1.0
|
|
Модуль Юнга включения
|
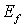
|
6.5
|
|
Коэффициент Пуассона матрицы
|
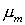
|
0.25
|
|
Коэффициент Пуассона включения
|
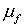
|
0.33
|
|
Длина ребра СЭ
|
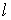
|
1.0
|
|
Радиус включения
|
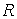
|
0.3
|
|
Число разбиений ребра СЭ
|
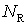
|
10
|
|
Количество типов СЭ в области
|
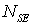
|
1
|
|
Длина ребра расчетной области в СЭ
|
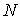 (в скобках (в скобках 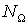 ) )
|
4 (64)
|
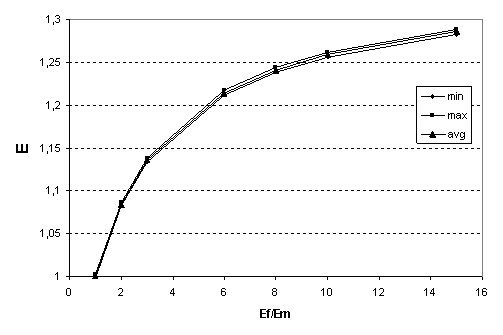
Рис. 9. Зависимость
модуля Юнга 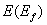
На рис. 9-10 представлены графики зависимости минимальных,
максимальных и средних значений приведенных параметров. Как видно, армирование
включениями с большим 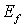 позволяет увеличить общий
средний модуль Юнга композитного тела на 30%. Данная зависимость является
нелинейной. Например, чтобы получить 15% прирост, модуль Юнга включения должен
быть в 4 раза больше, чем модуль Юнга материала матрицы ( позволяет увеличить общий
средний модуль Юнга композитного тела на 30%. Данная зависимость является
нелинейной. Например, чтобы получить 15% прирост, модуль Юнга включения должен
быть в 4 раза больше, чем модуль Юнга материала матрицы (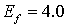 ), а для 28% прироста ), а для 28% прироста 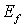 должен быть равным
15.0. должен быть равным
15.0.
На рис. 10 показана зависимость коэффициента Пуассона 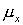 от от 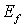 . Коэффициент Пуассона монотонно убывает с ростом параметра,
то есть чем больше модуль упругости армирующих волокон, тем меньше изменение
размера области в поперечном направлении, вдоль . Коэффициент Пуассона монотонно убывает с ростом параметра,
то есть чем больше модуль упругости армирующих волокон, тем меньше изменение
размера области в поперечном направлении, вдоль 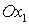 и и  . .
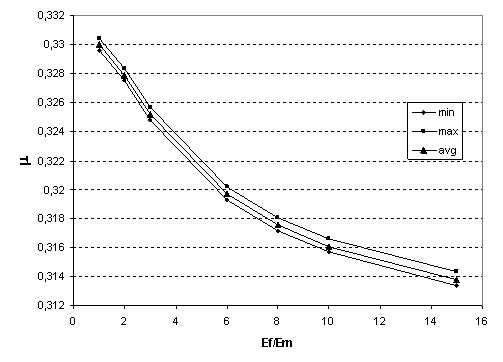
Рис. 10. Зависимость
коэффициента Пуассона 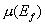
Зависимость упругих параметров
композитов от размеров включений
В каждом расчете
используется один тип СЭ со сферическим включением, радиус которого изменяется
в диапазоне [0.1; 0.45], параметры материалов и разбиения сетки остаются
неизменными, 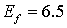 , , 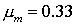 , , 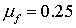 . Предельным значением радиуса включения является . Предельным значением радиуса включения является 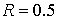 . .
Графики
полученных зависимостей представлены на рис.
11-12. В отличие от предыдущей группы тестов (см. рис.
9-10) график зависимости 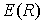 вогнутый, а график,
описывающий зависимость коэффициента Пуассона от радиуса включения вогнутый, а график,
описывающий зависимость коэффициента Пуассона от радиуса включения 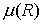 , выпуклый. , выпуклый.
При
этом можно видеть, что изменение радиуса включения сильно влияет на изменение
приведенных параметров композита для 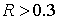 . В частности, при . В частности, при 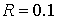 за счет малой объемной
плотности включений за счет малой объемной
плотности включений 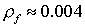 влияние армирующего
материала на композит ничтожно мало; при влияние армирующего
материала на композит ничтожно мало; при 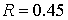 модуль Юнга модуль Юнга 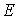 увеличивается более
чем в два раза ( увеличивается более
чем в два раза (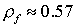 ), а коэффициент Пуассона ), а коэффициент Пуассона 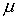 приближается к
значению коэффициента Пуассона включения приближается к
значению коэффициента Пуассона включения 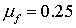 (см. рис. 12). (см. рис. 12).
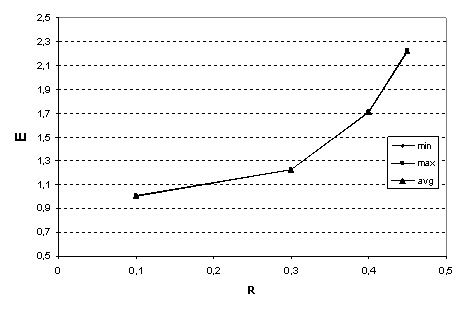
Рис. 11. Зависимость
модуля Юнга от радиуса включения R, 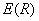
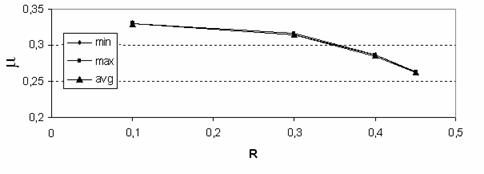
Рис. 12. Зависимость
коэффициента Пуассона от радиуса включения R, 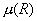
Разные параметры дискретизация
области суперэлемента
В данной группе расчетов изменяется число разбиений
ребра области  , ограничивающей СЭ. От этого параметра зависит число узлов и
тетраэдров сетки СЭ. Результаты расчетов приведены в табл. 3. , ограничивающей СЭ. От этого параметра зависит число узлов и
тетраэдров сетки СЭ. Результаты расчетов приведены в табл. 3.
Для определения
относительной величины отрезка 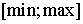 введем оценку «разброс
параметра P»: введем оценку «разброс
параметра P»:
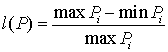 , ,
где 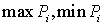 – максимальное
(неравное нулю) и минимальное значения вычисляемого упругого параметра – максимальное
(неравное нулю) и минимальное значения вычисляемого упругого параметра 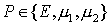 для расчёта с номером для расчёта с номером 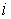 . .
Табл. 3. Результаты
расчетов
|
N
|
min
|
max
|
avg
|
L
|
|
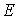
|
|
3
|
1,2350
|
1,2810
|
1,2576
|
0,036
|
|
5
|
1,2328
|
1,2498
|
1,2414
|
0,014
|
|
7
|
1,2246
|
1,2331
|
1,2289
|
0,007
|
|
8
|
1,2190
|
1,2255
|
1,2222
|
0,005
|
|
10
|
1,2234
|
1,2276
|
1,2255
|
0,003
|
|
12
|
1,2209
|
1,2238
|
1,2223
|
0,0024
|
|
14
|
1,2195
|
1,2216
|
1,2205
|
0,0018
|
|
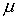
|
|
3
|
0,3086
|
0,3162
|
0,3124
|
0,0242
|
|
5
|
0,3117
|
0,3145
|
0,3129
|
0,0090
|
|
7
|
0,3143
|
0,3156
|
0,3149
|
0,0044
|
|
8
|
0,3154
|
0,3165
|
0,3159
|
0,0035
|
|
10
|
0,3152
|
0,3159
|
0,3156
|
0,0021
|
|
12
|
0,3158
|
0,3163
|
0,3161
|
0,0015
|
|
14
|
0,3162
|
0,3165
|
0,3163
|
0,0011
|
С увеличением числа
узлов сетки происходит уменьшение величин разброса упругих параметров 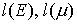 . Графики полученных зависимостей упругих параметров
материала представлены на рис.
13-14. . Графики полученных зависимостей упругих параметров
материала представлены на рис.
13-14.
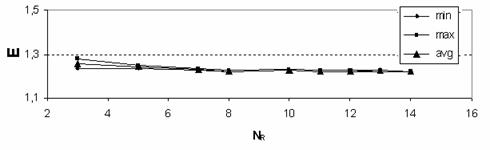
Рис. 13. Зависимость модуля Юнга от числа разбиений
ребра СЭ, 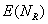
Картину уменьшения
разброса 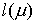 с ростом параметра
можно наблюдать на рис.
14. с ростом параметра
можно наблюдать на рис.
14.
Разный размер расчетной области
Пусть расчетная область состоит из 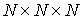 СЭ, где СЭ, где 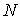 изменяется в
диапазоне изменяется в
диапазоне 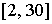 , а общее количество СЭ в области изменяется в диапазоне , а общее количество СЭ в области изменяется в диапазоне 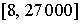 соответственно. Радиус
включения соответственно. Радиус
включения 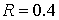 . Как и в других расчетах, параметры материалов матрицы и
включений имеют следующие значения: . Как и в других расчетах, параметры материалов матрицы и
включений имеют следующие значения: 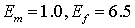 , , 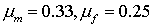 ; число разбиений ребра ячейки СЭ ; число разбиений ребра ячейки СЭ 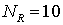 . Чтобы избежать влияния распределения СЭ, все расчеты
проводились для одного фиксированного типа СЭ. . Чтобы избежать влияния распределения СЭ, все расчеты
проводились для одного фиксированного типа СЭ.
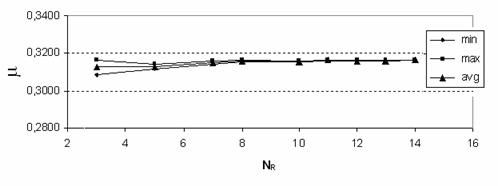
Рис. 14. Зависимость коэффициента Пуассона от числа
разбиений ребра СЭ, 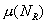
На
рис. 15-16 представлены графики зависимостей приведенных
упругих параметров композитного тела от параметра 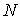 . .
На рис. 16 изображена зависимость коэффициента Пуассона от
параметра 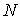 . Как видно, с увеличением . Как видно, с увеличением 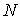 происходит сужение
интервала [min; max], что следует из
увеличения размеров области и большего числа СЭ, по которым происходит усреднение,
и плавное незначительное изменение средних значений avg – увеличение происходит сужение
интервала [min; max], что следует из
увеличения размеров области и большего числа СЭ, по которым происходит усреднение,
и плавное незначительное изменение средних значений avg – увеличение 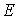 и падение и падение 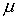 . .
Для анализа
зависимости решения от размера области введем оценку:
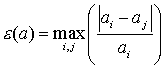 , ,
где
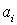 – вычисленное
значение, а – вычисленное
значение, а 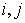 принимают те же
значения, что и принимают те же
значения, что и  . .
Для графиков avg, изображенных на рис. 15-16, величина  составила,
соответственно, составила,
соответственно,  и и 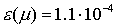 , то есть в целом поведение графиков средних значений не
зависит от значения , то есть в целом поведение графиков средних значений не
зависит от значения 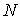 , а для оценки упругих параметров допустимо использовать
значения , а для оценки упругих параметров допустимо использовать
значения 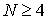 . .
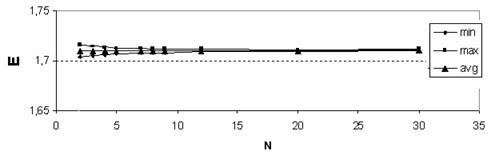
Рис. 15. Зависимость
модуля Юнга от N, 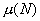
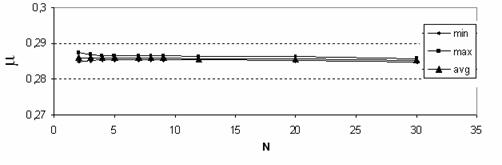
Рис. 16. Зависимость коэффициента Пуассона от N
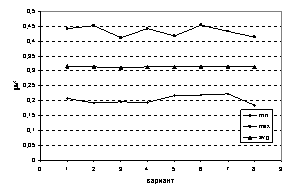
Несколько вариантов распределения
различных СЭ по области
Расчеты проведены для области фиксированного размера 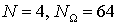 и разных распределений
заданных типов СЭ ( и разных распределений
заданных типов СЭ (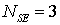 ) по области. ) по области.
СЭ при этом
«разбрасываются» псевдослучайным образом по области. Проведен расчет для 8-ми
случаев распределения, при котором сохранялась объемная плотность включений,
рассчитанная для всей области. Как видно из представленных на рис.
17-18 графиков, распределение СЭ по области
незначительно влияет на средние значения упругих параметров композита.
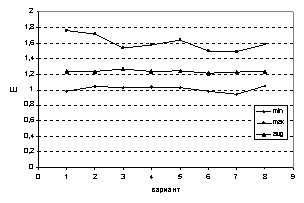
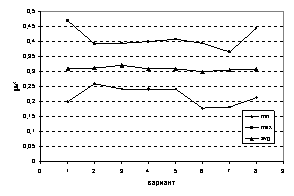
Рис. 17. Зависимость
модуля Юнга 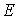 от варианта
распределения, от варианта
распределения, 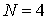
Аналогичные выводы
можно сделать и для коэффициентов Пуассона (см. рис. 18).
Сравнивая графики
на рис.
17-18 с соответствующими графиками на рис. 9-16, где использовался единственный тип СЭ, можно с
уверенностью говорить, что большой разброс размеров СЭ, как в случае данной
группы расчетов, приводит к большому разбросу минимальных и максимальных
приведенных параметров СЭ относительно среднего значения.
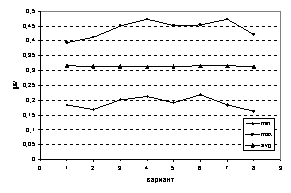
Можно ожидать, что для
больших областей и большего количества типов СЭ зависимость результатов
расчетов от распределения СЭ по области будет еще меньше. Поэтому приведем
результаты аналогичных расчётов для варианта 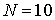 (см. рис. 19-20). (см. рис. 19-20).
a) б)
Рис. 18. Зависимость
коэффициентов Пуассона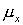 (а), (а), 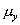 (б) (б)
от варианта распределения, 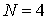
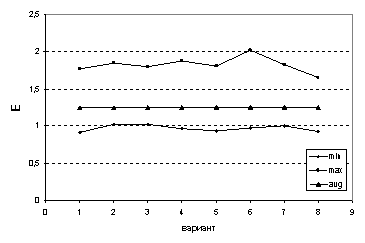
Рис. 19. Зависимость
модуля Юнга 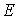 от варианта
распределения, от варианта
распределения, 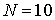
Графики
зависимостей коэффициентов Пуассона от варианта распределения для случая 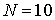 изображены на рис.
20. изображены на рис.
20.
Для
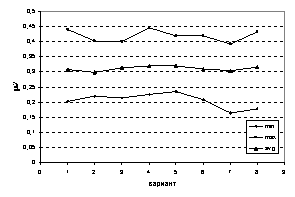
графиков 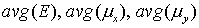 , изображенных на рис. 17-18, получаем: , изображенных на рис. 17-18, получаем:
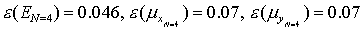 , ,
а
для соответствующих графиков в случае 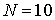 имеем (см. рис. 19-20): имеем (см. рис. 19-20):
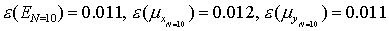 . .
Таким образом, для
области, состоящей из 1000 СЭ, влияние различных вариантов распределений СЭ по
области на среднее значение упругого параметра минимально.
a) б)
Рис. 20. Зависимость
коэффициентов Пуассона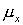 (а), (а), 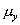 (б) (б)
от варианта распределения, 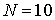
7
Заключение
Разработанный алгоритм МКСЭ применен для решения задачи
теории упругости композиционных материалов в пространственно трехмерном случае.
Для решения задачи разработан программно-вычислительный комплекс, позволяющий в
автоматизированном режиме проводить расчеты упругих параметров композитных
материалов. Программы, входящие в его состав, могут быть легко модифицированы
или дополнены новыми функциональными возможностями, обеспечив поддержку
дальнейшим исследованиям в этой области.
С помощью комплекса
проведены численные исследования свойств композиционных материалов, построены
оценки упругих параметров в зависимости от условий расчета.
Дальнейшее
развитие МКСЭ и программного комплекса обусловлено большой потребностью в
методах разделения областей, эффективных алгоритмах решения краевых задач в
областях простой формы и возможностью эффективной реализации этих алгоритмов на
многопроцессорных и параллельных ЭВМ.
8
Список литературы
1.
Страховская Л.Г., Федоренко Р.П. Об одном
варианте метода конечных элементов // ЖВМиМФ. 1979. Т. 19, 4.
С. 950-960.
2.
Страховская Л.Г., Федоренко Р.П. Расчет диффузии
в многосвязной области методом конечных суперэлементов. // Препринт ИПМ им.
М.В. Келдыша АН СССР. 1987. № 171. 26 с.
3.
Страховская Л.Г., Федоренко Р.П. Расчет
напряжений в композитном теле методом конечных суперэлементов. // Препринт ИПМ
им. М.В. Келдыша АН СССР. 1994. № 97. 26 с.
4.
Галанин М.П., Савенков Е.Б. Совместное
использование метода конечных элементов и метода конечных суперэлементов. //
Препринт ИПМ им. М.В. Келдыша РАН. 2004. № 13. 34 с.
5.
Галанин М.П., Савенков Е.Б. О
связи метода конечных суперэлементов Федоренко и проекционно-сеточных методов.
// Препринт ИПМ им. М.В. Келдыша РАН. 2001. № 67. 35 с.
6.
Galanin M., Savenkov E., Fedorenko finite superelement method as
special Galerkin approximation // Mathematical Modelling and Analysis. 2002.
V. 7, № 1. P.р. 41-50.
7.
Галанин М.П., Савенков Е.Б. К
обоснованию метода конечных суперэлементов Федоренко // ЖВМиМФ. 2003.
Т. 43, № 5. С. 713-729.
8.
Галанин М., Савенков Е. Метод конечных
суперэлементов для задачи о скоростном скин-слое // Труды международной
конференции по вычислительной математике МКВМ-2004. 21-25 июня, 2004 г.,
Новосибирск, Академгородок, Россия. С. 455-460.
9.
Галанин М.П., Савенков Е.Б. Метод
конечных суперэлементов для задачи о скоростном скин-слое. // Препринт ИПМ им.
М.В. Келдыша РАН. 2004. № 3. 32 с.
10.
Галанин М.П., Савенков Е.Б.,
Темис Ю.М. Метод конечных суперэлементов для задач теории упругости.
// Препринт ИПМ им. М.В. Келдыша РАН. 2004. № 38. 38 с.
11.
Бахвалов Н.С., Панасенко Г.П. Осреднение
процессов в периодических средах. М.: Наука, 1984. 352 с.
12.
Кристенсен Р. Введение в механику композитов.
М.: Мир, 1982. 334 с.
13.
Скворцов В.Р. Основы механики композитов.
СПб.: Изд. центр СПбГМТУ, 1995. 111 с.
14.
Aboudi J.
Micromechanical analysis of composites by the method of cells // Appl. Mech.
Rev. 1989. V. 42, № 7. P.р. 193-221.
15.
Aboudi J. A
continium theory for fiber-reinforced elastic-viscoplastic composites // Int.
J. Engng. Sci. 1982. V. 20, № 5. P.р. 605-621.
16. Fleming W.J., Dowson A.L. Prediction of the Fatigue Life of an Aluminium Metal Matrix Composite
Using the Theory of Cells // Science and Engineering of Composite Materials.
1999. V. 8, № 4. P.р. 181-189.
17.
Ефименко А.В., Зарубин В.С., Кувыркин Г.Н. О
двусторонних оценках термомеханических и теплофизических свойств неоднородных
материалов // Динамика, прочность и износостойкость машин. Международный журнал
на электронных носителях. 1996. № 2. С. 3-7.
18.
Зарубин В.С., Кувыркин Г.Н.
Прогнозирование теплофизических и термоупругих характеристик композитов //
Вестник МГТУ. Сер. Машиностроение. 1994. 2. С. 78-83.
19.
Efimenko A.V., Kuvyrkin G.N. New estimates of the effective elastic moduli
of two-component composites // Izv. RAN. Mekhanika Tverdogo Tela. 1994.
V. 29, № 1. P.р. 18-26.
20.
Бураго Н.Г., Галанин М.П., Кувыркин Г.Н.
Основные вариационные принципы механики сплошной среды. М.: Изд-во МГТУ им.
Н.Э. Баумана, 2004. 79 с.
21.
Агошков В.И., Лебедев В.И. Операторы
Пуанкаре-Стеклова и методы разделения области в вариационных задачах //
Вычислительные процессы и системы. Т. 2. М.: Наука, 1985.
22. Агошков
В.И. Методы разделения области в задачах математической физики //
Сопряженные уравнения и алгоритмы возмущений в задачах математической физики.
М.: ОВМ АН СССР, 1989.
23. Лебедев
В.И., Агошков В.И. Операторы Пуанкаре-Стеклова и их приложения в анализе.
М.: ОВМ АН СССР, 1983.
24.
Лебедев В.И. Функциональный анализ и
вычислительная математика. М.: Физматлит, 2000. 296 с.
25.
Марчук Г.И., Агошков В.И. Введение в
проекционно-сеточные методы. М.: Наука, 1981. 416 с.
26. Сьярле
Ф. Метод конечных элементов для эллиптических задач. М.: Мир, 1980.
512 с.
27. Обэн
Ж.-П. Приближенное решение эллиптических краевых задач. М.: Мир, 1977.
384 с.
28.
Красносельский М.А., Вайникко Г.М.,
Забрейко П.П., Рутицкий Я.Б., Стеценко В.Я. Приближенное решение
операторных уравнений. М.: Наука, 1969. 456 с.
29.
Галанин М.П., Щеглов И.А. Разработка и
реализация алгоритмов трехмерной триангуляции сложных пространственных
областей: прямые методы. // Препринт ИПМ им. М.В. Келдыша РАН. 2006. № 10. 32
с.
30.
Галанин М.П., Щеглов И.А. Разработка и
реализация алгоритмов трехмерной триангуляции сложных пространственных
областей: итерационные методы. // Препринт ИПМ им. М.В. Келдыша РАН. 2006. №
10. 32 с.
31. Галанин М.П.,
Лазарева С.А., Савенков Е.Б. Численное исследование метода
конечных суперэлементов на примере решения задачи о скважине для уравнения Лапласа.
// Препринт ИПМ им. М.В. Келдыша РАН. 2005. № 79. 30 с.
|
![]() ; параметры разбиения КЭ сетки СЭ,
; параметры разбиения КЭ сетки СЭ, ![]() ; распределение фиксированного набора СЭ по области;
количество различных СЭ, составляющих область.
; распределение фиксированного набора СЭ по области;
количество различных СЭ, составляющих область.![]() нормирован на модуль
Юнга матрицы
нормирован на модуль
Юнга матрицы ![]() . Использован один тип СЭ с заданными параметрами КЭ разбиения
(шаг и число разбиений ребра СЭ), коэффициенты Пуассона матрицы
. Использован один тип СЭ с заданными параметрами КЭ разбиения
(шаг и число разбиений ребра СЭ), коэффициенты Пуассона матрицы ![]() и включения
и включения ![]() остаются неизменными,
остаются неизменными, ![]() . Модуль Юнга включения
. Модуль Юнга включения ![]() варьировался в
диапазоне [1.0; 15.0].
варьировался в
диапазоне [1.0; 15.0].
![]()
![]() позволяет увеличить общий
средний модуль Юнга композитного тела на 30%. Данная зависимость является
нелинейной. Например, чтобы получить 15% прирост, модуль Юнга включения должен
быть в 4 раза больше, чем модуль Юнга материала матрицы (
позволяет увеличить общий
средний модуль Юнга композитного тела на 30%. Данная зависимость является
нелинейной. Например, чтобы получить 15% прирост, модуль Юнга включения должен
быть в 4 раза больше, чем модуль Юнга материала матрицы (![]() ), а для 28% прироста
), а для 28% прироста ![]() должен быть равным
15.0.
должен быть равным
15.0.![]() от
от ![]() . Коэффициент Пуассона монотонно убывает с ростом параметра,
то есть чем больше модуль упругости армирующих волокон, тем меньше изменение
размера области в поперечном направлении, вдоль
. Коэффициент Пуассона монотонно убывает с ростом параметра,
то есть чем больше модуль упругости армирующих волокон, тем меньше изменение
размера области в поперечном направлении, вдоль ![]() и
и ![]() .
.
![]()
![]() ,
, ![]() ,
, ![]() . Предельным значением радиуса включения является
. Предельным значением радиуса включения является ![]() .
.![]() вогнутый, а график,
описывающий зависимость коэффициента Пуассона от радиуса включения
вогнутый, а график,
описывающий зависимость коэффициента Пуассона от радиуса включения ![]() , выпуклый.
, выпуклый.![]() . В частности, при
. В частности, при ![]() за счет малой объемной
плотности включений
за счет малой объемной
плотности включений ![]() влияние армирующего
материала на композит ничтожно мало; при
влияние армирующего
материала на композит ничтожно мало; при ![]() модуль Юнга
модуль Юнга ![]() увеличивается более
чем в два раза (
увеличивается более
чем в два раза (![]() ), а коэффициент Пуассона
), а коэффициент Пуассона ![]() приближается к
значению коэффициента Пуассона включения
приближается к
значению коэффициента Пуассона включения ![]() (см. рис. 12).
(см. рис. 12).
![]()

![]()
![]() , ограничивающей СЭ. От этого параметра зависит число узлов и
тетраэдров сетки СЭ. Результаты расчетов приведены в табл. 3.
, ограничивающей СЭ. От этого параметра зависит число узлов и
тетраэдров сетки СЭ. Результаты расчетов приведены в табл. 3.![]() введем оценку «разброс
параметра P»:
введем оценку «разброс
параметра P»: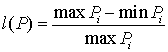 ,
, ![]() – максимальное
(неравное нулю) и минимальное значения вычисляемого упругого параметра
– максимальное
(неравное нулю) и минимальное значения вычисляемого упругого параметра ![]() для расчёта с номером
для расчёта с номером ![]() .
.![]() . Графики полученных зависимостей упругих параметров
материала представлены на рис.
13-14.
. Графики полученных зависимостей упругих параметров
материала представлены на рис.
13-14.![]()
![]() с ростом параметра
можно наблюдать на рис.
14.
с ростом параметра
можно наблюдать на рис.
14.![]() СЭ, где
СЭ, где ![]() изменяется в
диапазоне
изменяется в
диапазоне ![]() , а общее количество СЭ в области изменяется в диапазоне
, а общее количество СЭ в области изменяется в диапазоне ![]() соответственно. Радиус
включения
соответственно. Радиус
включения ![]() . Как и в других расчетах, параметры материалов матрицы и
включений имеют следующие значения:
. Как и в других расчетах, параметры материалов матрицы и
включений имеют следующие значения: ![]() ,
, ![]() ; число разбиений ребра ячейки СЭ
; число разбиений ребра ячейки СЭ ![]() . Чтобы избежать влияния распределения СЭ, все расчеты
проводились для одного фиксированного типа СЭ.
. Чтобы избежать влияния распределения СЭ, все расчеты
проводились для одного фиксированного типа СЭ.![]()
![]() .
.![]() . Как видно, с увеличением
. Как видно, с увеличением ![]() происходит сужение
интервала [min; max], что следует из
увеличения размеров области и большего числа СЭ, по которым происходит усреднение,
и плавное незначительное изменение средних значений avg – увеличение
происходит сужение
интервала [min; max], что следует из
увеличения размеров области и большего числа СЭ, по которым происходит усреднение,
и плавное незначительное изменение средних значений avg – увеличение ![]() и падение
и падение ![]() .
.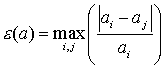 ,
, ![]() – вычисленное
значение, а
– вычисленное
значение, а ![]() принимают те же
значения, что и
принимают те же
значения, что и ![]() .
.![]() составила,
соответственно,
составила,
соответственно, ![]() и
и ![]() , то есть в целом поведение графиков средних значений не
зависит от значения
, то есть в целом поведение графиков средних значений не
зависит от значения ![]() , а для оценки упругих параметров допустимо использовать
значения
, а для оценки упругих параметров допустимо использовать
значения ![]() .
.
![]()
![]() и разных распределений
заданных типов СЭ (
и разных распределений
заданных типов СЭ (![]() ) по области.
) по области.
![]() от варианта
распределения,
от варианта
распределения, ![]()
![]() (см. рис. 19-20).
(см. рис. 19-20).

![]() (а),
(а), ![]() (б)
(б)![]()

![]() от варианта
распределения,
от варианта
распределения, ![]()
![]() изображены на рис.
20.
изображены на рис.
20.![]() , изображенных на рис. 17-18, получаем:
, изображенных на рис. 17-18, получаем:![]() ,
,![]() имеем (см. рис. 19-20):
имеем (см. рис. 19-20):![]() .
.

![]() (а),
(а), ![]() (б)
(б)![]()