Аннотация
Найдены гомогенные (однородные) течения цилиндрически симметричного плазменного шнура в
электромагнитной гидродинамике, в которой масса электронов считается отличной от нуля.
Полученные решения охватывают широкий спектр возможных движений шнура от коллапса и
периодических пульсаций до сложных нелинейных резонансов и автоколебаний. Характер движения
определяется законом изменения полного тока в шнуре, который, в отличие от МГД, может быть
произвольным. Получено электротехническое уравнение простейшей цепи с включенным в неё
плазменным шнуром, движение которого происходит согласно гомогенным решениям. Приведены
результаты численных исследований.
Abstract
Homogeneous flows of cylindrical symmetric plasma cord in Electromagnetic Hydrodynamics.
(EMHD) are obtained. In EMHD it is assumed that electronic mass do not equal to zero.
The solutions obtained include wide range of cord’s motions from collapses and periodic
oscillations to nonlinear resonances and self-sustained oscillations. The type of cord’s
motion, as is shown, is dictated by total current function in cord, which as distinct
from MHD may be arbitrary. The electrotechnical equation for simple circuit involving
plasma cord is obtained. Some numerical results are presented.
Интерес к динамике плазменного шнура возник в 50-е годы прошлого века в связи с работами по управляемому термоядерному синтезу.
Особенно важны режимы динамики шнура, обеспечивающие сильное сжатие и разогрев
плазмы. В этой работе, в частности, показано, что подобные коллапсирующие
режимы возникают при гомогенных (однородных) движениях плазменного шнура,
когда радиальная скорость в каждый момент времени линейна по радиусу.
Поскольку радиальная скорость нечетна по радиусу, то в
первом приближении любое цилиндрически симметричное течение плазмы можно
считать гомогенным.
В газовой среде гомогенные течения были впервые
исследованы Л. И. Седовым [1], а в плазме, в приближении классической магнитной
гидродинамики (МГД), - А.Г. Куликовским [2] (библиографию см. в [3]). Согласно
[2], [3], гомогенные движения МГД – плазменного шнура сводятся либо к
периодическим пульсациям, либо к разлёту плазмы шнура, либо к его коллапсу на
свою ось. При этом для любого типа движений полный ток 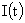 в шнуре остается постоянным. в шнуре остается постоянным.
В этой работе указан значительно более богатый запас
гомогенных течений плазменного шнура с произвольным законом изменения полного
тока 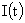 . Более точно, найдены все гомогенные, без особенностей на
оси, движения цилиндрически симметричного плазменного шнура, динамика которого
подчиняется уравнениям электромагнитной гидродинамики (ЭМГД) [4]. В ЭМГД –
теории, в отличие от МГД, электронная масса считается не равной нулю, но
сохраняются, как и в МГД, допущения о квазинейтральности плазмы и
квазистационарного электромагнитного поля. . Более точно, найдены все гомогенные, без особенностей на
оси, движения цилиндрически симметричного плазменного шнура, динамика которого
подчиняется уравнениям электромагнитной гидродинамики (ЭМГД) [4]. В ЭМГД –
теории, в отличие от МГД, электронная масса считается не равной нулю, но
сохраняются, как и в МГД, допущения о квазинейтральности плазмы и
квазистационарного электромагнитного поля.
В работе для гомогенных течений установлена следующая
связь безразмерного радиуса шнура 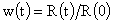 с полным током с полным током 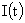 : :
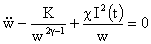 , , 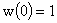 , (*) , (*)
где
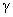 - показатель адиабаты, - показатель адиабаты,
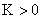 , , 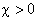 - константы,
определяемые начальным состоянием шнура. Из соотношения (*) видно насколько
ЭМГД содержательнее МГД: почти любой закон движения границы шнура - константы,
определяемые начальным состоянием шнура. Из соотношения (*) видно насколько
ЭМГД содержательнее МГД: почти любой закон движения границы шнура 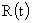 может быть реализован
при подходящем полном токе может быть реализован
при подходящем полном токе 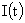 - надо лишь чтобы - надо лишь чтобы 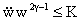 . Практически, однако, интереснее обратная задача: для
заданного закона изменения полного тока . Практически, однако, интереснее обратная задача: для
заданного закона изменения полного тока 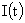 найти характер
движения границы шнура найти характер
движения границы шнура 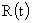 . Для этого необходимо решить уравнение (*). Аналитически это
возможно лишь в редких случаях, в случае . Для этого необходимо решить уравнение (*). Аналитически это
возможно лишь в редких случаях, в случае 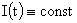 (соответствующего МГД
– теории, [5]) уравнение (*) имеет первый интеграл энергии, позволяющий
полностью проанализировать картину решений. В общем случае пока не удалось дать
качественный анализ решений (*). Численные же исследования приводят к
интересным выводам. При (соответствующего МГД
– теории, [5]) уравнение (*) имеет первый интеграл энергии, позволяющий
полностью проанализировать картину решений. В общем случае пока не удалось дать
качественный анализ решений (*). Численные же исследования приводят к
интересным выводам. При 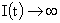 (когда (когда 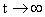 ) имеет место коллапс шнура на свою ось, который, в отличие
от МГД, происходит за бесконечное время, сопровождаясь затухающими
осцилляциями. Похожая картина коллапса в своё время была предсказана М.
Розенблютом [6]. При ) имеет место коллапс шнура на свою ось, который, в отличие
от МГД, происходит за бесконечное время, сопровождаясь затухающими
осцилляциями. Похожая картина коллапса в своё время была предсказана М.
Розенблютом [6]. При 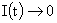 (когда (когда 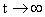 ) происходит разлет плазмы шнура, а когда ) происходит разлет плазмы шнура, а когда 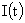 - ограниченная
функция, возможны сложные резонансные и автоколебательные режимы динамики
шнура. Здесь остаются нерешенными ряд физических и математических проблем. - ограниченная
функция, возможны сложные резонансные и автоколебательные режимы динамики
шнура. Здесь остаются нерешенными ряд физических и математических проблем.
Поскольку в ЭМГД для гомогенных течений полный ток в
шнуре 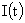 произволен, то
открывается заманчивая возможность, включив плазменный шнур во внешнюю
электрическую цепь, исследовать на основе гомогенных движений влияние
параметров и конфигурации цепи на режимы сжатия плазменного шнура. В работе
выведено электротехническое уравнение для простейшей цепи из последовательно включенных
емкости, индуктивности, сопротивления и плазменного шнура и приведены некоторые
результаты расчетов. произволен, то
открывается заманчивая возможность, включив плазменный шнур во внешнюю
электрическую цепь, исследовать на основе гомогенных движений влияние
параметров и конфигурации цепи на режимы сжатия плазменного шнура. В работе
выведено электротехническое уравнение для простейшей цепи из последовательно включенных
емкости, индуктивности, сопротивления и плазменного шнура и приведены некоторые
результаты расчетов.
Работа выполнена при финансовой поддержке РФФИ, грант
№06-01-00312.
§1. Основные уравнения.
1. Рассмотрим течение бездиссипативной нерелятивисткой
плазмы. В гидродинамическом приближении параметры течения удовлетворяют
уравнениям электромагнитной гидродинамики (ЭМГД – уравнения) [4]:
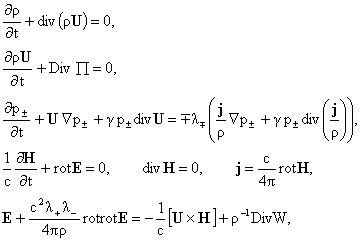 (1) (1)
где
тензоры 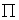 и и 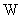 вычисляются по
формулам: вычисляются по
формулам:
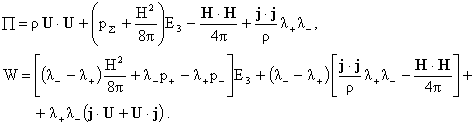 (2) (2)
Выше
предполагалось, что электроны и ионы – идеальные политропные газы с общим
показателем адиабаты 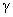 , ,  , а параметры электронов и ионов после решения системы (1-2)
находятся по формулам: , а параметры электронов и ионов после решения системы (1-2)
находятся по формулам:
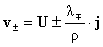 , , 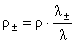 , , 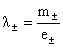 , ,  . (3) . (3)
Система
(1-2) отличается от уравнений классической [3] или холловской МГД [7] полным
учетом инерции электронной компоненты. Это приводит к чрезвычайному богатству
решений, в частности, большому разнообразию движений плазменного шнура.
2. Рассмотрим систему (1-2) в цилиндрически симметричном
случае, дополнительно предполагая 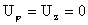 , , 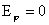 , ,  : :
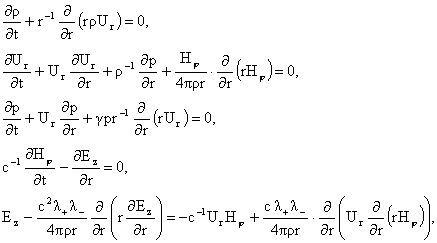 (4) (4)
где
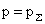 , а производные параметры плазмы равны: , а производные параметры плазмы равны:
 (5) (5)
При
этом считается 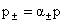 , где , где 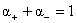 , , 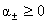 - заданные числа,
определяющие распределение полного давления между компонентами. Система (4)
отличается от уравнений классической МГД только двумя слагаемыми - заданные числа,
определяющие распределение полного давления между компонентами. Система (4)
отличается от уравнений классической МГД только двумя слагаемыми
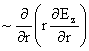 , , 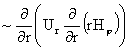
в
последнем уравнении системы. Если указанные слагаемые выкинуть, оставив все
остальные члены последнего уравнения (равно как и другие уравнения) системы (4)
без изменений, то получатся уравнения классической МГД для цилиндрически
симметрического случая.
Наша цель – найти все гомогенные решения системы (4), т.е. такие, для которых:
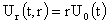 , (6) , (6)
где
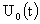 - функция подлежащая
нахождению. Если подставить выражение (6) в систему (4), то для нахождения
функций - функция подлежащая
нахождению. Если подставить выражение (6) в систему (4), то для нахождения
функций
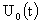 , ,  , , 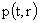 , , 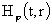 , , 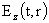
получим
уравнения:
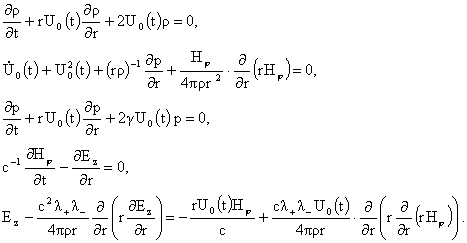 (7) (7)
Ниже
будут найдены все решения системы (7), не имеющие особенности на оси 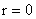 . .
§2. Гомогенные решения в ЭМГД.
Мы укажем точные решения системы (7) двух типов. Потом
окажется, что любое другое решение (7) принадлежит к одному из указанных типов.
3. Прямая подстановка в систему (7) показывает, что она допускает решения вида:
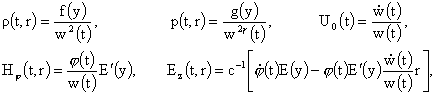 (8) (8)
где 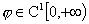 – произвольная, – произвольная, 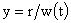 , ,
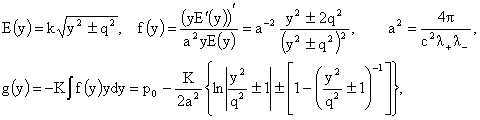 (9) (9)
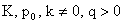 - произвольные константы.
При этом - произвольные константы.
При этом 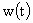 – положительное решение обыкновенного дифференциального уравнения второго
порядка: – положительное решение обыкновенного дифференциального уравнения второго
порядка:
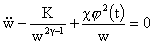 , , 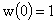 , , 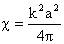 , (10) , (10)
где точка означает дифференцирование по 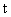 , а штрих –
дифференцирование по , а штрих –
дифференцирование по 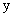 . .
В случае знака «+» решение (8-10) определено для всех 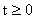 , , 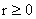 , а в случае знака «–» – для всех , а в случае знака «–» – для всех 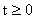 , , 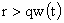 . Однако физические ограничения . Однако физические ограничения 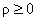 , , 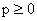 могут дополнительно
сузить область определения решения (8-10). Таким образом, система (8-10) помимо
константного произвола могут дополнительно
сузить область определения решения (8-10). Таким образом, система (8-10) помимо
константного произвола 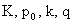 обладает
функциональным произволом обладает
функциональным произволом 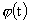 . Производные параметры плазмы для решения (8-10), согласно
(5), вычисляются по формулам: . Производные параметры плазмы для решения (8-10), согласно
(5), вычисляются по формулам:
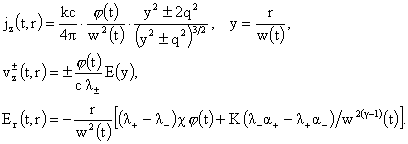 (11) (11)
4. В работах [2, 3, 5] были указаны более простые
решения системы (7). А именно непосредственной подстановкой проверяется, что эта система имеет решения вида:
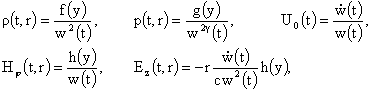 (12) (12)
где 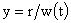 , , 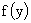 , ,  - произвольная кусочно-гладкая и кусочно-непрерывная неотрицательная
функция, - произвольная кусочно-гладкая и кусочно-непрерывная неотрицательная
функция,
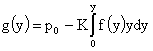 , , 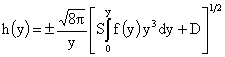 , (13) , (13)
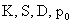 - произвольные константы, а - произвольные константы, а 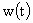 - положительное решение обыкновенного дифференциального уравнения 2-го
порядка - положительное решение обыкновенного дифференциального уравнения 2-го
порядка
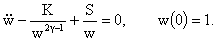 (14) (14)
Выше считалось, что для решения (12-14) функция 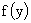 имеет на имеет на 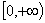 конечное число точек
разрыва 1-го рода, причем конечное число точек
разрыва 1-го рода, причем 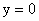 не является точкой
разрыва не является точкой
разрыва 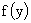 , и на любом сегменте, лежащим в , и на любом сегменте, лежащим в 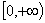 и не содержащим внутри
себя точек разрыва, и не содержащим внутри
себя точек разрыва, 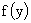 непрерывно
дифференцируема. Тем самым допускаются и разрывные решения системы (4), линиями
разрыва которых являются кривые непрерывно
дифференцируема. Тем самым допускаются и разрывные решения системы (4), линиями
разрыва которых являются кривые 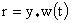 , где , где 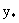 – любая точка разрыва – любая точка разрыва 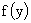 . Полученные разрывы относятся к контактным: они двигаются
вместе с веществом плазмы и не перемещаются по массе. В частности, на линии
разрыва все характеристики плазмы, кроме плотности тока, плотности,
температуры, энтропии и внутренней энергии плазмы, непрерывны и могут иметь
самое большее слабые разрывы, перечисленные же параметры плазмы на линии
разрыва претерпевают скачок. Решение (12-14) удовлетворяет и МГД – уравнениям:
на этом решении указанные в п.2 два “лишних” слагаемых в последнем уравнении
системы (4), которыми ЭМГД отличается от МГД, взаимно уничтожаются. Производные
параметры течения для решения (12-14) вычисляются по формулам: . Полученные разрывы относятся к контактным: они двигаются
вместе с веществом плазмы и не перемещаются по массе. В частности, на линии
разрыва все характеристики плазмы, кроме плотности тока, плотности,
температуры, энтропии и внутренней энергии плазмы, непрерывны и могут иметь
самое большее слабые разрывы, перечисленные же параметры плазмы на линии
разрыва претерпевают скачок. Решение (12-14) удовлетворяет и МГД – уравнениям:
на этом решении указанные в п.2 два “лишних” слагаемых в последнем уравнении
системы (4), которыми ЭМГД отличается от МГД, взаимно уничтожаются. Производные
параметры течения для решения (12-14) вычисляются по формулам:
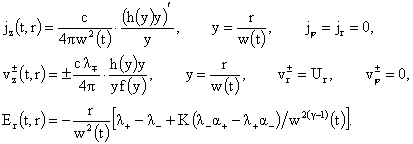 (15) (15)
Решение (12-14) легко проанализировать, поскольку уравнение
(14) имеет первый интеграл:
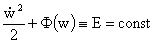 , ,
где
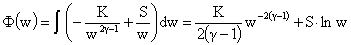 , ,
откуда:
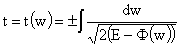 . .
Таким образом, 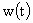 лежит в потенциальной
яме лежит в потенциальной
яме 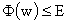 . В частности, для физически наиболее интересного случая . В частности, для физически наиболее интересного случая 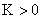 , , 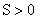 функция функция 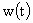 - периодическая, с
периодом - периодическая, с
периодом
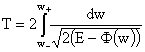 , ,
где
 - корни уравнения - корни уравнения 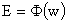 (при (при 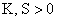 и и 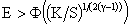 это уравнение имеет
ровно два корня). это уравнение имеет
ровно два корня).
В итоге приходим к периодическим пульсациям
плазменного шнура. В других логически возможных случаях получаем либо разлет
плазменного шнура (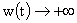 ), либо коллапс его на свою ось [3]. ), либо коллапс его на свою ось [3].
Полученное решение также, как и решение п.3, обладает
функциональным произволом, однако этот произвол ведет к большому разнообразию
пространственных профилей параметров течения, временная же динамика при этом
остается достаточно бедной – это в основном периодические колебания
характеристик плазмы. Для решения п.3 всё наоборот: функциональный произвол
приводит к большому разнообразию временной динамики течения, в чём мы убедимся
ниже, а пространственные распределения параметров плазмы табулируются
несколькими характерными типами.
Если параметры плазмы не имеют особенностей на оси 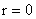 , то любое гомогенное решение, как показано в §5, совпадает с решениями пп. 3, 4. , то любое гомогенное решение, как показано в §5, совпадает с решениями пп. 3, 4.
§3. Гомогенные движения плазменного шнура.
Рассмотрим цилиндрически симметричный плазменный шнур
радиуса 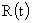 в момент времени в момент времени 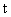 . Допустим, течение плазмы в шнуре подчинено ЭМГД –
уравнениям (4), а вне шнура эволюция вакуумного электромагнитного поля
удовлетворяет квазистационарным уравнениям Максвелла. На границе шнура . Допустим, течение плазмы в шнуре подчинено ЭМГД –
уравнениям (4), а вне шнура эволюция вакуумного электромагнитного поля
удовлетворяет квазистационарным уравнениям Максвелла. На границе шнура 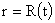 электромагнитное поле
считается непрерывным (отсутствуют поверхностные токи и заряды). Полный ток электромагнитное поле
считается непрерывным (отсутствуют поверхностные токи и заряды). Полный ток 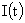 в шнуре удовлетворяет
электротехническому уравнению внешней цепи, которое позже будет рассмотрено.
Пока же будем считать в шнуре удовлетворяет
электротехническому уравнению внешней цепи, которое позже будет рассмотрено.
Пока же будем считать 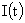 произвольной функцией
времени. Наконец, на границе шнура произвольной функцией
времени. Наконец, на границе шнура 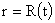 , очевидно, , очевидно, 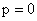 . .
Выражение для вакуумного электромагнитного поля имеет
вид:
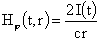 , , 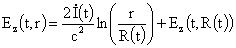 , , 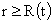 , (16) , (16)
где
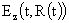 находится из решения
ЭМГД – уравнений в шнуре. находится из решения
ЭМГД – уравнений в шнуре.
5. Ограничимся ниже изучением только такой динамики
шнура, при которой параметры плазмы в шнуре являются гомогенными. Рассмотрим
сначала решение п.3. Поскольку плазма в шнуре расположена вплоть до оси 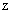 , то в формулах (9) из п.3 надо взять знак «+». Тогда
константа , то в формулах (9) из п.3 надо взять знак «+». Тогда
константа 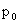 вычисляется по
константе вычисляется по
константе 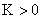 из условия из условия 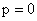 при при 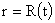 : :
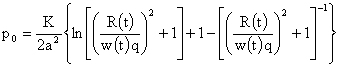 . .
Отсюда
следует, что величина 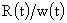 постоянна и равна
начальному (при постоянна и равна
начальному (при 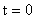 ) радиусу шнура ) радиусу шнура 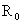 , в частности, , в частности,
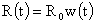 , ,  . .
Очевидно,
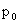 это давление плазмы на
оси это давление плазмы на
оси 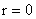 в момент времени в момент времени 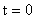 . Константа . Константа 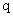 имеет размеренность
длины и равна: имеет размеренность
длины и равна:

где
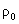 – плотность плазмы на
оси – плотность плазмы на
оси 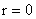 в момент времени в момент времени 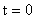 . Наконец, константа . Наконец, константа 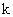 при при  связана с
электрическим полем связана с
электрическим полем 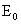 на оси в момент
времени на оси в момент
времени 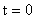 формулой: формулой:
 . .
Функция
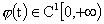 выбирается
произвольно. В зависимости от её выбора получается большое разнообразие
эволюции безразмерного радиуса выбирается
произвольно. В зависимости от её выбора получается большое разнообразие
эволюции безразмерного радиуса 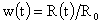 шнура в соответствии с
дифференциальным уравнением (10). Уравнение (10) можно рассматривать как
уравнение движения материальной точки единичной массы на полуоси шнура в соответствии с
дифференциальным уравнением (10). Уравнение (10) можно рассматривать как
уравнение движения материальной точки единичной массы на полуоси 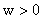 под действием двух
сил: притягивающей к центру под действием двух
сил: притягивающей к центру 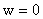 силы силы 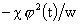 и отталкивающей силы и отталкивающей силы 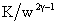 . .
Итоговое движение точки существенно зависит от вида
функции 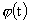 . Из механической аналогии следует, что при . Из механической аналогии следует, что при 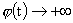 (когда (когда 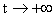 ) радиус шнура ) радиус шнура 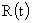 должен стремится к 0.
т.е. происходит коллапс шнура за бесконечное время на свою ось, при должен стремится к 0.
т.е. происходит коллапс шнура за бесконечное время на свою ось, при 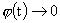 (когда (когда 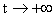 ) радиус шнура ) радиус шнура 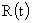 должен неограниченно
увеличивается, т.е. происходит неограниченное расширение шнура. Детальное
выяснение характера этих процессов для заданной функции должен неограниченно
увеличивается, т.е. происходит неограниченное расширение шнура. Детальное
выяснение характера этих процессов для заданной функции 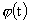 – предмет особого
исследования. Особенно интересно выяснить характер движения шнура, когда – предмет особого
исследования. Особенно интересно выяснить характер движения шнура, когда 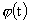 ограниченная (например,
периодическая) функция. Этот интерес подогревается тем обстоятельством, что ограниченная (например,
периодическая) функция. Этот интерес подогревается тем обстоятельством, что 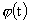 с точностью до
числового множителя совпадает с полным током с точностью до
числового множителя совпадает с полным током 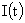 в шнуре в момент
времени в шнуре в момент
времени 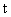 : :
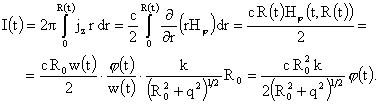 (17) (17)
Проиллюстрируем сказанное следующим примером. Закон
движения границы шнура
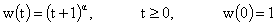
реализуется,
как это следует из (10), для
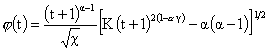 . .
При
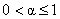 функция функция 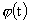 заведомо определена на заведомо определена на 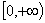 и убывает при и убывает при 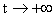 до нуля, в то время
как до нуля, в то время
как 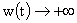 , т.е. происходит неограниченное расширение шнура. , т.е. происходит неограниченное расширение шнура.
Если
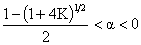 , ,
то
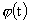 определена на определена на 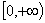 , неограниченно увеличивается при , неограниченно увеличивается при 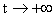 , , 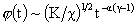 , а , а 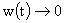 при при 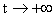 , т.е. происходит коллапс шнура на свою ось за бесконечное
время. , т.е. происходит коллапс шнура на свою ось за бесконечное
время.
В предыдущем примере радиус шнура уменьшается до нуля
или увеличивается до бесконечности за бесконечное время монотонно. В общем
случае это не так. Рассмотрим типичный пример. На Рис.1 изображен график 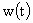 для для 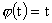 , , 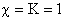 , , 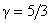 и начальных условий и начальных условий 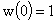 , ,  , полученный численно. , полученный численно.
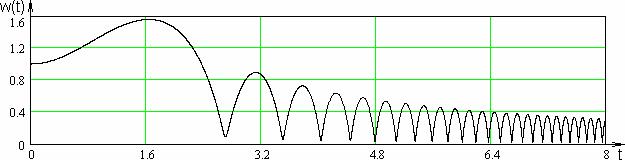
Рис.
1 Радиус шнура 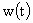 . .
Из него следует, что при линейном нарастании полного
тока за бесконечное время шнур, осциллируя, коллапсирует (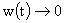 при при 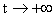 ) на ось ) на ось 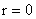 . При этом амплитуда колебаний при . При этом амплитуда колебаний при 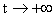 стремится к 0, а
частота колебаний – к бесконечности. Любопытно, что похожий характер коллапса плазменного
шнура был в своё время предсказан Розенблютом [6]. стремится к 0, а
частота колебаний – к бесконечности. Любопытно, что похожий характер коллапса плазменного
шнура был в своё время предсказан Розенблютом [6].
В случае ограниченной  (синусоидальньный
полный ток в шнуре) характер движения границы шнура зависит от (синусоидальньный
полный ток в шнуре) характер движения границы шнура зависит от  и и 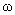 , в частности, от соотношения , в частности, от соотношения 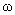 и собственной частоты
колебаний шнура и собственной частоты
колебаний шнура 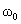 , которая равна частоте малых гомогенных колебаний границы
шнура при , которая равна частоте малых гомогенных колебаний границы
шнура при 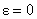 : :
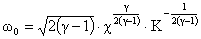 . .
При 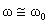 наблюдается явление
нелинейного резонанса: возникают сложные колебания границы, которые в
зависимости от наблюдается явление
нелинейного резонанса: возникают сложные колебания границы, которые в
зависимости от  приводят либо к
автоколебаниям для приводят либо к
автоколебаниям для  (Рис. 2а, 2б), либо к
катастрофическому нарастанию амплитуды (Рис.3) для (Рис. 2а, 2б), либо к
катастрофическому нарастанию амплитуды (Рис.3) для 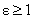 . При промежуточных . При промежуточных  возникают сложные
переходные колебательные процессы (Рис. 4). Теоретический анализ этого явления
ещё предстоит дать. возникают сложные
переходные колебательные процессы (Рис. 4). Теоретический анализ этого явления
ещё предстоит дать.
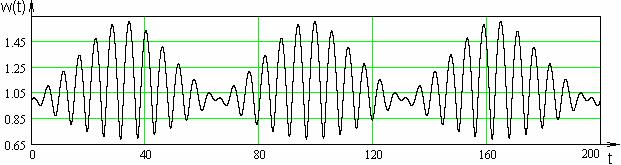
Рис. 2а. Радиус шнура (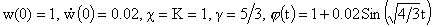 ). ).
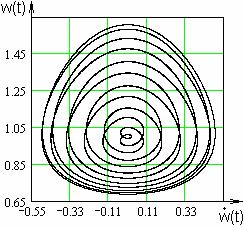
Рис. 2б. Радиус шнура (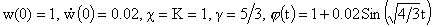 ). ).

Рис. 3. Радиус шнура (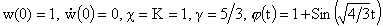 ). ).
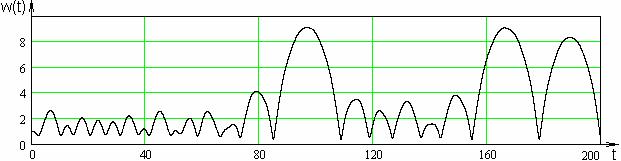
Рис. 4. Радиус шнура
( ). ).
6. Перейдем в решении (8-10) к лагранжевым массовым
переменным. Пусть
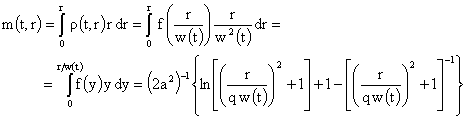
массовая
переменная. Рассмотрим отображение:
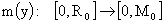 , ,
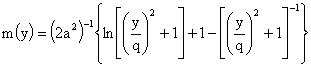 , , 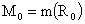 . .
Очевидно,
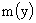 - монотонно
возрастающая гладкая функция, поэтому определена обратная функция - монотонно
возрастающая гладкая функция, поэтому определена обратная функция 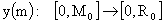 и тогда: и тогда:
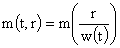 , , 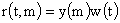 . .
Подставляя
последние выражения в формулы (8), с учетом (9) получим запись решения (8-10) в
лагранжевых переменных в случае выбора знака «+»:
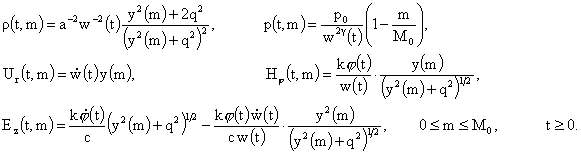
Производные
параметры шнура равны:
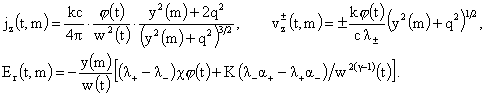
Заметим,
что в полученных выражениях для всех параметров плазмы, за исключением 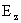 , переменные разделяются. , переменные разделяются.
Аналогично переходят к лагранжевым переменным в
решение (12-14):
 , ,
где
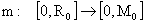 функция: функция:
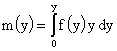 , , 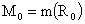 . (18) . (18)
Если
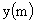 - обратная к ней
функция, то - обратная к ней
функция, то
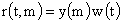
и
формулы (12) дают:
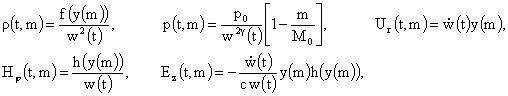 (19) (19)
где
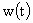 – решение уравнения (14), – решение уравнения (14),  , ,  . .
Производные
параметры плазмы равны:
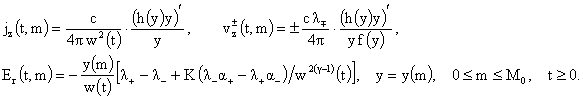
При
этом полный ток в шнуре постоянен:
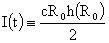 . .
Конкретные
формулы зависят от выбора функции 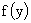 . Например, пусть: . Например, пусть:
 . .
Тогда
из (18) следует:
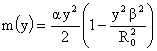 , , 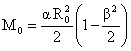 , ,
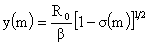 , , 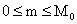 , , 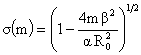 . .
Отсюда,
считая в (13) 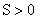 , ,  , получим: , получим:
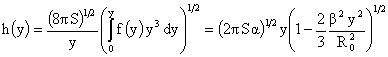 . .
Теперь
из (19) легко получаются нужные формулы:
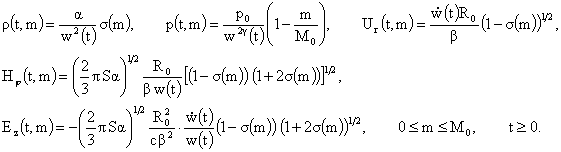
Производные
параметры плазмы равны:
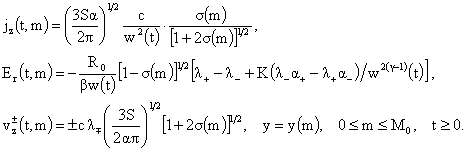
Приведенные
формулы значительно упрощаются для 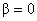 , когда плотность плазмы в шнуре постоянна. При , когда плотность плазмы в шнуре постоянна. При 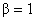 имеем имеем 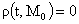 , т.е. на границе шнура плотность равна нулю. , т.е. на границе шнура плотность равна нулю.
7. Рассмотрим более подробно разрывные решения п.4. Если
в формулах (12-13) функция 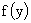 имеет конечное число разрывов 1-го рода, то каждый разрыв имеет конечное число разрывов 1-го рода, то каждый разрыв  функции функции 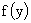 порождает контактный
разрыв в решении, двигающийся по закону порождает контактный
разрыв в решении, двигающийся по закону 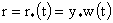 , где , где 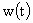 - решение уравнения
(14). В точке - решение уравнения
(14). В точке  терпят произвольный
разрыв плотность, температура, внутренняя энергия, энтропия и плотность тока, а
давление, скорость и компоненты электрического и магнитного полей непрерывны.
При этом разрыв терпят произвольный
разрыв плотность, температура, внутренняя энергия, энтропия и плотность тока, а
давление, скорость и компоненты электрического и магнитного полей непрерывны.
При этом разрыв  не перемещается по
массе. Поскольку, как отмечалось выше, решение (12-14) удовлетворяет МГД –
уравнениям, то на каждом разрыве не перемещается по
массе. Поскольку, как отмечалось выше, решение (12-14) удовлетворяет МГД –
уравнениям, то на каждом разрыве  выполнены известные из
МГД – теории соотношения (типа Гюгонио) [3]. В то же время, как показано в [8],
если ЭМГД – решение претерпевает разрыв 1-го рода вдоль поверхности выполнены известные из
МГД – теории соотношения (типа Гюгонио) [3]. В то же время, как показано в [8],
если ЭМГД – решение претерпевает разрыв 1-го рода вдоль поверхности 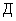 , то 9 скалярных скачков величин , то 9 скалярных скачков величин 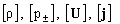 могут быть найдены из
следующих 9 скалярных соотношений на поверхности могут быть найдены из
следующих 9 скалярных соотношений на поверхности 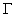 (квадратные скобки
здесь означают скачок величины на разрыве): (квадратные скобки
здесь означают скачок величины на разрыве):
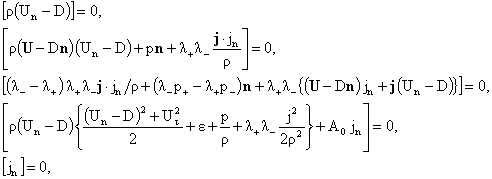 (20) (20)
где
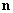 – нормаль к
поверхности – нормаль к
поверхности 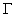 , а , а 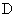 – её нормальная скорость в данной точке, – её нормальная скорость в данной точке, 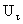 - тангенциальная
компонента скорости. Наконец, - тангенциальная
компонента скорости. Наконец,
 (21) (21)
При
этом  и тангенциальная
компонента электрического поля и тангенциальная
компонента электрического поля 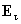 непрерывны на непрерывны на 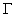 , допускается разрыв только нормальной компоненты , допускается разрыв только нормальной компоненты 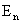 . .
Легко убедиться, что для решения п.4 условия на
разрыве (20-21) выполнены, причем нормальная компонента электрического поля 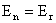 тоже непрерывна. Более
того, это решение является контактным разрывом, поскольку для него тоже непрерывна. Более
того, это решение является контактным разрывом, поскольку для него 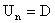 по обе стороны от
разрыва (поверхность разрыва по обе стороны от
разрыва (поверхность разрыва 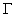 для решения п.4
состоит из боковых поверхностей цилиндров для решения п.4
состоит из боковых поверхностей цилиндров 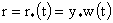 по всем точкам разрыва по всем точкам разрыва
 функции функции 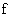 ). ).
Рассмотрим конкретный пример. Пусть 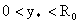 , , 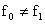 - фиксированные положительные числа. Положим: - фиксированные положительные числа. Положим:

Тогда:
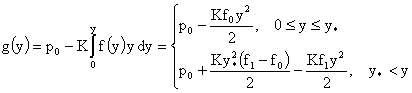
Условие
 связывает величины связывает величины 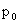 и и 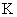 : :
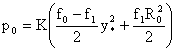 . .
Тогда
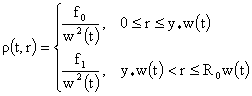
имеет
в каждый момент времени 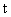 разрыв 1-го рода в
точке разрыв 1-го рода в
точке  функции: функции:
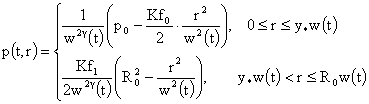
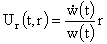 , , 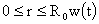
непрерывны,
а  даже непрерывно
дифференцируема. Считая даже непрерывно
дифференцируема. Считая 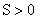 , ,  в формулах (13), получим: в формулах (13), получим:
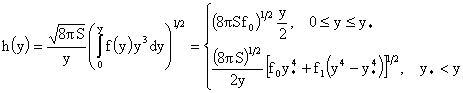
откуда
выводим:
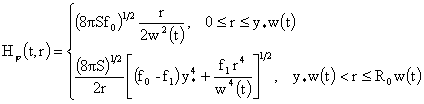
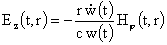 , , 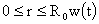 . .
Наконец,
выражение для плотности  тока имеет вид: тока имеет вид:
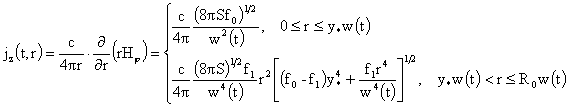
Из
полученных выражений следует, что величины 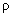 и и  имеют разрыв 1-го рода
на линии имеют разрыв 1-го рода
на линии 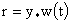 , но при этом величина , но при этом величина 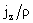 на этой линии
непрерывна. Значит аксиальные компоненты скоростей электронов и ионов на этой линии
непрерывна. Значит аксиальные компоненты скоростей электронов и ионов

тоже
непрерывны на разрыве. Как следует из (15), выражение  не зависит от не зависит от 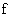 и, очевидно,
непрерывно дифференцируемо по и, очевидно,
непрерывно дифференцируемо по 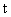 и и 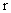 . .
Запишем полученное решение в лагранжевых координатах.
Пусть:

Выражая
отсюда 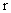 через через 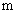 , получим: , получим:
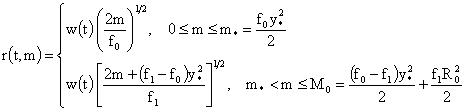
Подставляя
это выражение в полученные выше формулы, имеем:
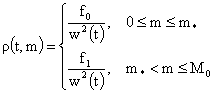
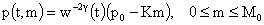
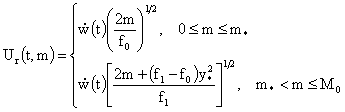
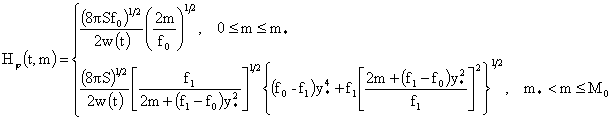
где 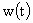 – решение уравнения
(14) с начальным условием – решение уравнения
(14) с начальным условием 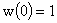 . Итак, . Итак, 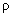 имеет в точке имеет в точке 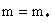 сильный разрыв, сильный разрыв, 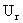 , ,  (и значит (и значит 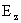 ) – слабые разрывы, а ) – слабые разрывы, а 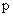 вовсе не имеет разрывов.
Плотность тока вовсе не имеет разрывов.
Плотность тока  тоже имеет в точке тоже имеет в точке 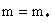 сильный разрыв: сильный разрыв:
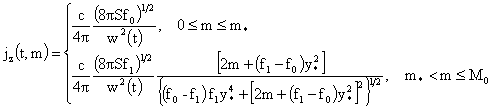
§4. Динамика плазменного шнура с учетом внешней цепи.
8. Как уже говорилось, ток в плазменном шнуре замыкается
на внешнюю цепь, которая в простейшем случае состоит из последовательно
включенных индуктивности (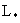 ), емкости ( ), емкости ( ) и сопротивления ( ) и сопротивления (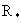 ). ).
Рассмотрим общую ситуацию. Пусть 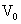 – фиксированный объем,
содержащий плазму и электромагнитное поле, через который проходит ток цепи: – фиксированный объем,
содержащий плазму и электромагнитное поле, через который проходит ток цепи:
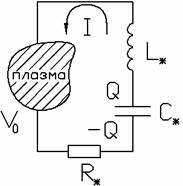
Рис.5.
Схема электрической цепи.
Чтобы получить дифференциальное уравнение для тока 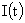 (электротехническое уравнение цепи), рассмотрим баланс энергии в
цепи. Пусть (электротехническое уравнение цепи), рассмотрим баланс энергии в
цепи. Пусть 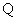 – заряд верхней пластинки конденсатора (см.
Рис.5), где нумерация пластинок определяется направлением тока в контуре, тогда – заряд верхней пластинки конденсатора (см.
Рис.5), где нумерация пластинок определяется направлением тока в контуре, тогда
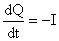 . (22) . (22)
Энергия
электромагнитного поля в объеме 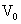 , индуктивности , индуктивности 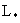 и конденсаторе и конденсаторе  равна соответственно
[9]: равна соответственно
[9]:
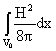 , , 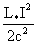 , , 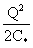 . .
Уменьшение
суммарной энергии за единицу времени равно потерям энергии на тепло (джоулев нагрев) в сопротивлении 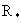 и объеме и объеме 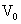 которые соответственно
равны [9]: которые соответственно
равны [9]:
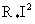 , , 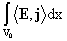 . .
Отсюда
получается основное уравнение баланса энергии:
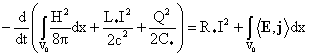 . (23) . (23)
Интегралы в (23) определяются параметрами течения
плазмы в объеме 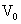 . Эти параметры находятся из решения ЭМГД – уравнения в
области . Эти параметры находятся из решения ЭМГД – уравнения в
области 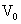 , при этом ток , при этом ток 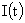 определяет граничные
условия для электромагнитного поля в области определяет граничные
условия для электромагнитного поля в области 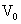 . Поэтому ЭМГД уравнения (1-2) вместе с уравнением (23)
образуют полную систему уравнений для нахождения как параметров течения плазмы
в объеме . Поэтому ЭМГД уравнения (1-2) вместе с уравнением (23)
образуют полную систему уравнений для нахождения как параметров течения плазмы
в объеме 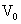 , так и тока , так и тока 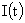 в цепи на Рис.5. В
общем случае эта полная задача весьма нетривиальна и с переменным успехом
решается в частных случаях для более простых моделей плазмы исключительно
численными методами (например, для МГД – плазмы см. [10, 11]). Однако, если
считать что параметры плазмы подчиняются гомогенному решению из п.3, то
возможно получить точное аналитическое решение указанной выше полной системы.
Причина этого в том, что для решений п.3 полный ток в цепи на Рис.5. В
общем случае эта полная задача весьма нетривиальна и с переменным успехом
решается в частных случаях для более простых моделей плазмы исключительно
численными методами (например, для МГД – плазмы см. [10, 11]). Однако, если
считать что параметры плазмы подчиняются гомогенному решению из п.3, то
возможно получить точное аналитическое решение указанной выше полной системы.
Причина этого в том, что для решений п.3 полный ток 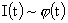 может быть
произвольной гладкой функцией, которую поэтому в принципе можно подобрать так
чтобы она удовлетворяла ещё и уравнению (23), записанному на гомогенном решение
из п.3. В итоге динамика параметров цепи и плазмы выражается по явным формулам
через полный ток может быть
произвольной гладкой функцией, которую поэтому в принципе можно подобрать так
чтобы она удовлетворяла ещё и уравнению (23), записанному на гомогенном решение
из п.3. В итоге динамика параметров цепи и плазмы выражается по явным формулам
через полный ток 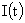 и радиус шнура и радиус шнура 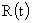 , эволюция которых подчиняется выводимым ниже обыкновенным
дифференциальным уравнениям. Тем самым общая нетривиальная задача сводится в
данном случае к шаблонному численному решению обыкновенных дифференциальных
уравнений, что может быть выполнено с высокой точностью. С другой стороны,
открывается уникальная возможность на гомогенных решениях исследовать влияние
конфигурации и параметров внешней цепи на динамику плазмы. Реализация этой
возможности может привести к весьма важным рекомендациям по режимам нагрева и
удержания плазмы. , эволюция которых подчиняется выводимым ниже обыкновенным
дифференциальным уравнениям. Тем самым общая нетривиальная задача сводится в
данном случае к шаблонному численному решению обыкновенных дифференциальных
уравнений, что может быть выполнено с высокой точностью. С другой стороны,
открывается уникальная возможность на гомогенных решениях исследовать влияние
конфигурации и параметров внешней цепи на динамику плазмы. Реализация этой
возможности может привести к весьма важным рекомендациям по режимам нагрева и
удержания плазмы.
Перейдем к деталям. Рассмотрим конкретную ситуацию,
когда 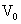 – цилиндр длины – цилиндр длины 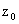 и радиуса и радиуса 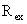 , а ток течет по плазменному шнуру радиуса , а ток течет по плазменному шнуру радиуса 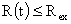 . Предполагается, что торцы цилиндра представляют собой
электроды, преобразующие плазменный ток в ток электрической цепи. При этом
процессом трансформации тока шнура в ток цепи мы, естественно, пренебрегаем.
Считая течение плазмы цилиндрически симметричным, получим: . Предполагается, что торцы цилиндра представляют собой
электроды, преобразующие плазменный ток в ток электрической цепи. При этом
процессом трансформации тока шнура в ток цепи мы, естественно, пренебрегаем.
Считая течение плазмы цилиндрически симметричным, получим:
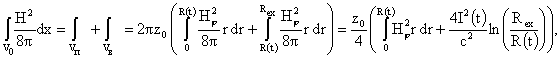 (24) (24)
где
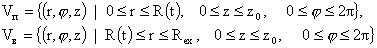
области,
занятые плазмой и вакуумом соответственно, а  в вакууме вычисляется
по формуле: в вакууме вычисляется
по формуле:
 , , 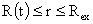 , , 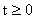 . .
Будем теперь считать, что параметры плазмы в шнуре
подчиняются формулам п.3 для найденного точного аналитического гомогенного
решения ЭМГД – уравнений. Тогда для  в шнуре, учитывая
связь (17) функции в шнуре, учитывая
связь (17) функции 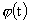 с полным током с полным током 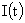 , имеем: , имеем:
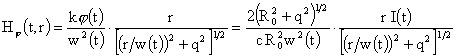 , , 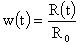 . .
Поэтому
интеграл в правой части равенства (24) легко вычисляется:
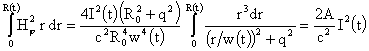 , ,
где
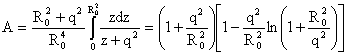 (25) (25)
Поэтому
из (24) получаем окончательное выражение:
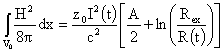 , (26) , (26)
где
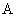 вычисляется по формуле
(25). Итак, мы вычислили один из интегралов в балансе энергии (23) на
гомогенном решении из п.3. Для второго интеграла имеем: вычисляется по формуле
(25). Итак, мы вычислили один из интегралов в балансе энергии (23) на
гомогенном решении из п.3. Для второго интеграла имеем:
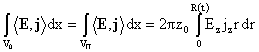 . (27) . (27)
Но
для решения п.3, учитывая формулы (8, 9, 11) и формулу (17), связывающую 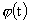 с с 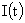 , получим: , получим:
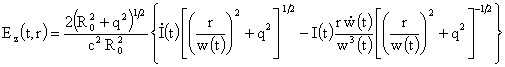 , ,
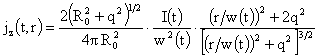 . .
Подставляя
эти выражения в (27), после несложного интегрирования получим:
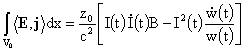 , (28) , (28)
где
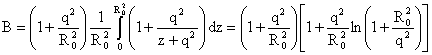 . (29) . (29)
Подставляя (26) и (28) в баланс энергии (23), приходим
к дифференциальному уравнению для полного тока 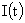 (электротехническое уравнение цепи): (электротехническое уравнение цепи):
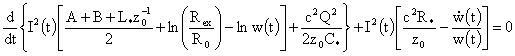 . (30) . (30)
С
учетом связи (22) между 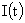 и и 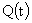 , равенства , равенства 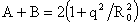 и уравнения (10),
которому удовлетворяет безразмерный радиус шнура и уравнения (10),
которому удовлетворяет безразмерный радиус шнура 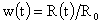 , получим систему уравнений для нахождения функций , получим систему уравнений для нахождения функций 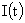 , , 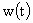 : :
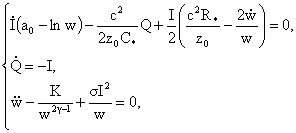 (31) (31)
где
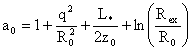 , , 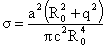 . .
В
безразмерном виде система (31) перепишется так:
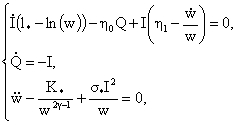 (31’) (31’)
где
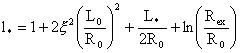 , , 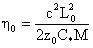 , ,
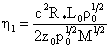 , ,  , , 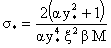
здесь
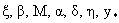 – безразмерные константы: – безразмерные константы:
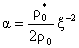 , , 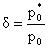 , , 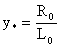 , , 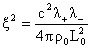 , ,  , , 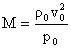 , ,
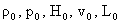 - характерные масштабы плотности, давления и т.д. (при этом - характерные масштабы плотности, давления и т.д. (при этом 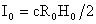 , ,  , , 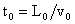 ), ), 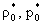 – значения плотности и
давления в момент времени – значения плотности и
давления в момент времени 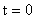 на оси шнура. Наконец, на оси шнура. Наконец,
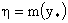 - безразмерная масса
шнура, вычисляемая по формуле: - безразмерная масса
шнура, вычисляемая по формуле:
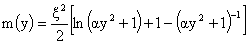 . .
На
Рис. 6, 7, 8 представлены решения системы (31’) для начальных условий:
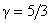 , ,  , , 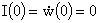 , , 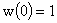 , , 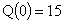 . .
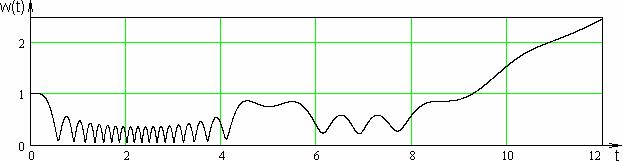
Рис.
6. Радиус шнура 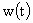 . .
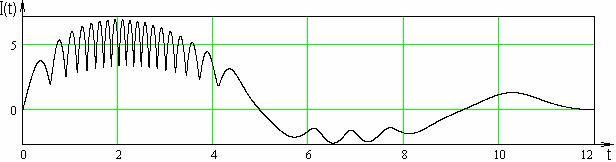
Рис.
7. Ток в цепи 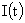 . .
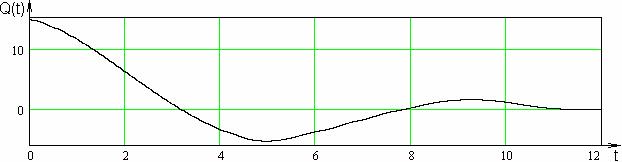
Рис.
8. Заряд конденсатора 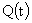 . .
§5. Вывод аналитических решений.
9. Укажем вкратце способ интеграции системы (7). Первое
и третье уравнения системы (7) имеют общие характеристики. Интегрируя уравнения
характеристик 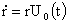 , получим явный вид характеристик: , получим явный вид характеристик:
 , , 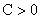 , ,  (32) (32)
интеграция
первого и третьего уравнений (7) вдоль характеристик (32) даёт:
 (33) (33)
где
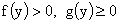 - произвольные
функции, заданные на полуоси - произвольные
функции, заданные на полуоси  . Преобразование четвертого и пятого уравнений системы (7)
основано на следующем ключевом наблюдении [5]: функция . Преобразование четвертого и пятого уравнений системы (7)
основано на следующем ключевом наблюдении [5]: функция  является частным
решением пятого уравнения системы (7). Поскольку это уравнение линейно по является частным
решением пятого уравнения системы (7). Поскольку это уравнение линейно по 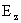 , то его общее решение имеет вид: , то его общее решение имеет вид:
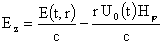 , (34) , (34)
где
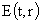 – решение однородного
уравнения – решение однородного
уравнения
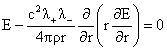 . .
Переходя
в последнем уравнении к переменной 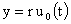 с учетом (33), получим
равносильное уравнение для нахождения с учетом (33), получим
равносильное уравнение для нахождения  : :
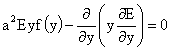 . (35) . (35)
Несложно
установить, что к нетривиальным решениям системы (7) без особенностей на оси
приводят только решения (35) вида 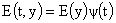 . Для таких решений . Для таких решений  удовлетворяет уравнению: удовлетворяет уравнению:
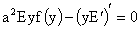 , (36) , (36)
где
штрих означает здесь и ниже дифференцирование по 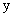 . Подставляя выражение . Подставляя выражение 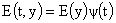 в (34), а (34) – в
четвертое уравнение системы (7), получим уравнение для в (34), а (34) – в
четвертое уравнение системы (7), получим уравнение для  : :
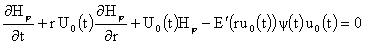 . .
Это
линейное неоднородное уравнение в частных производных 1-го порядка относительно
 , характеристики которого совпадают с (32). Интегрируя его
вдоль характеристик, получим: , характеристики которого совпадают с (32). Интегрируя его
вдоль характеристик, получим:
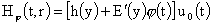 , , 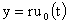 , (37) , (37)
где
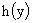 , ,  - произвольная
функция, а - произвольная
функция, а 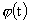 – произвольная
первообразная функции – произвольная
первообразная функции 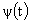 . .
Итак, мы выразили функции 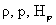 через через 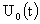 с помощью функций с помощью функций 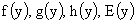 , которые связаны пока единственным соотношением (36).
Подставим выражения (33), (37) во второе уравнение системы (7) , вводя при этом
новую переменную , которые связаны пока единственным соотношением (36).
Подставим выражения (33), (37) во второе уравнение системы (7) , вводя при этом
новую переменную  и учитывая равенства: и учитывая равенства:
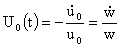 , , 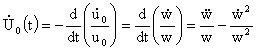 , ,
где
точка над буквой означает дифференцирование по 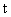 . .
В итоге придем к следующему равенству:
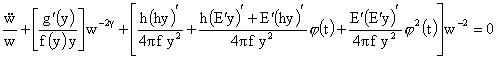 . (38) . (38)
В
уравнении (38) все дроби в квадратных скобках являются функциями от 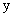 , а , а 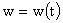 . Поэтому, как несложно проверить, если параметры плазмы не
имеют особенностей на оси . Поэтому, как несложно проверить, если параметры плазмы не
имеют особенностей на оси 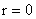 , то указанные дроби должны быть постоянными: , то указанные дроби должны быть постоянными:
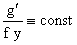 , ,  , , 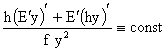 , , 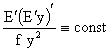 . (39) . (39)
Из четвертого равенства (39) и (36) найдем 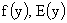 , считая , считая 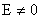 . В самом деле, из (36) находим . В самом деле, из (36) находим  и подставляем это
выражение в четвертое равенство (39): и подставляем это
выражение в четвертое равенство (39):
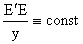 . .
Откуда
элементарным интегрированием получаем:
 , , 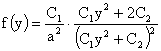 . (40) . (40)
Т.к.
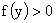 , то , то 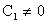 . Если . Если 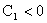 , то , то 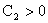 , иначе под корнем в (40) будет всегда отрицательное число, а , иначе под корнем в (40) будет всегда отрицательное число, а
 . Но для таких . Но для таких 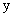 , очевидно, , очевидно,  , что невозможно. Поэтому , что невозможно. Поэтому  . Обозначая . Обозначая 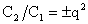 , , 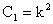 перепишем (40) в виде: перепишем (40) в виде:
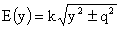 , , 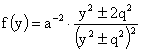 . (41) . (41)
Далее, обозначая 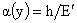 , ,  перепишем второе и
третье соотношение (39) с учетом четвертого в виде: перепишем второе и
третье соотношение (39) с учетом четвертого в виде:
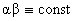 , , 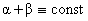 . .
Отсюда,
очевидно, следует  , ,  . Значит . Значит
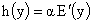 , ,  . (42) . (42)
Из
первого соотношения (39) следует
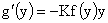 , , 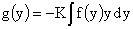 , , 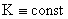 . (43) . (43)
Теперь
из (38) с учетом (42,41,43) получится уравнение для нахождения 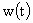 : :
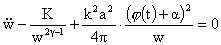 . .
Подставляя
в (34), (37), (43) выражения для  , и заменяя , и заменяя 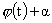 на на 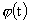 ( (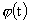 - произвольная первообразная - произвольная первообразная 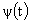 ), получим все заявленные в п.3 формулы. ), получим все заявленные в п.3 формулы.
Что касается формул п.4, то они получаются в случае 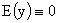 . Тогда (36) выполнено всегда, а выражение (37) для . Тогда (36) выполнено всегда, а выражение (37) для  и уравнение (38)
упрощаются: и уравнение (38)
упрощаются:
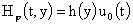 , ,  . .
Дроби
в квадратных скобках являются константами:
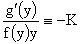 , , 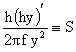 . (44) . (44)
Отсюда
следует, что 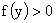 - произвольная
функция, а простая интеграция соотношений (44) приводит к формулам п.4. - произвольная
функция, а простая интеграция соотношений (44) приводит к формулам п.4.
Литература
1. Седов Л.И. Об интегрировании уравнений одномерного
движения газа // ДАН СССР, 1953. Т. 90. №5
2. Куликовский А.Г. К вопросу о пульсации плазменного
шнура // ДАН СССР, 1957. Т. 114. №5
3. Куликовский А.Г., Любимов Г.А. Магнитная
гидродинамика. М.: “Логос”, 2005
4. Гавриков М.Б. Линейные волны в нерелятивистской
магнитной гидродинамике. Препринт ИПМ им. М.В, Келдыша АН СССР, 1988, №199
5. Гавриков М.Б., Соловьев Л.С. Одномерные движения
плазмы в двухжидкостной электромагнитной гидродинамике // Письма в ЖТФ, 1991.
Т. 17. №12
6. Розенблют М. Динамика сжимающегося газа. Магнитная
гидродинамика (материалы симпозиума): Пер. с англ. М.: Атомиздат 1958
7. Морозов А.И., Соловьев Л.С. Стационарные течения
плазмы в магнитном поле. Сб. статей. Вып.8. М.: Атомиздат, 1974
8. Гавриков М.Б. Основные уравнения электромагнитной
гидродинамики, Часть II. Препринт ИПМ
им. М.В. Келдыша РАН, 2006 (в печати).
9. Ландау Л.Д., Лифшиц Е.М, Электродинамика сплошных
сред. М.: Физматлит, 1982
10. Дьяченко В.Ф., Имшенник В.С. В сб. Вопросы теории
плазмы. Вып. 5. М.: Атомиздат, 1967
11. Самарский А.А., Попов Ю.П. Разностные схемы газовой
динамики. М.: “Наука”, 1973
|