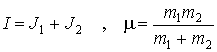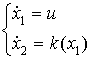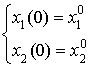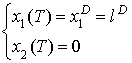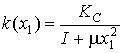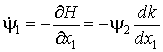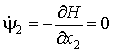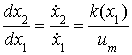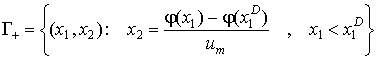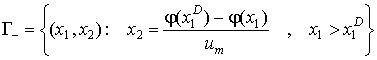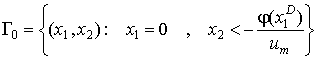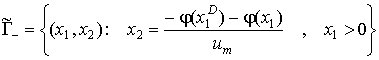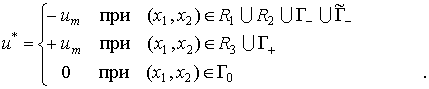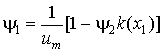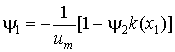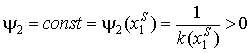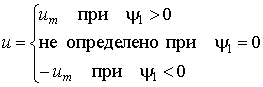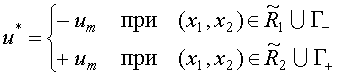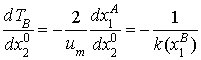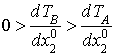Оптимальное управление движением прыгающего аппарата вокруг центра масс
|
|
|
(2.1) |

В безопорной фазе движения имеет место закон сохранения
кинетического момента относительно центра масс (относительно осей Кенига,
перемещающихся поступательно вместе с центром масс) [14]. Кинетический момент ![]() –го тела относительно осей Кенига определим, как сумму
кинетического момента центра масс этого тела, равного
–го тела относительно осей Кенига определим, как сумму
кинетического момента центра масс этого тела, равного ![]() , и кинетического момента вращения относительно собственного
центра масс, равного
, и кинетического момента вращения относительно собственного
центра масс, равного ![]() [14]. Скорость центра
масс
[14]. Скорость центра
масс ![]() –го тела относительно осей Кенига состоит из двух
составляющих: радиальной, направленной вдоль линии
–го тела относительно осей Кенига состоит из двух
составляющих: радиальной, направленной вдоль линии ![]() и равной
и равной ![]() , и трансверсальной, направленной перпендикулярно к
, и трансверсальной, направленной перпендикулярно к ![]() и равной
и равной ![]() . Тогда кинетический момент
. Тогда кинетический момент ![]() –го тела относительно осей Кенига равен
–го тела относительно осей Кенига равен
|
|
|
В силу (2.1) закон сохранения кинетического момента системы относительно центра масс имеет вид
|
|
(2.2) |
где
|
|
(2.3) |
Обозначим ![]() требуемое конечное
положение связки относительно центра масс в конечный момент времени.
требуемое конечное
положение связки относительно центра масс в конечный момент времени.
Для определенности положим
|
|
(2.4) |
За управление примем скорость изменения расстояния между телами
![]() , и положим, что оно ограничено по величине максимальной
скоростью сервопривода
, и положим, что оно ограничено по величине максимальной
скоростью сервопривода ![]() . Обозначим
. Обозначим
|
|
(2.5) |
Задача о минимизации времени разворота в безопорной фазе движения связки двух тел имеет вид
|
|
(2.6) |
|
|
(2.7) |
|
|
(2.8) |
|
|
(2.9) |
где
|
|
(2.10) |
Отметим, что в силу (2.3)–(2.4)
|
|
(2.11) |
при любом значении ![]() . Следовательно, при
. Следовательно, при ![]() система не останется в
программном положении, а продолжит свое вращение относительно центра масс в
положительном направлении отсчета угла
система не останется в
программном положении, а продолжит свое вращение относительно центра масс в
положительном направлении отсчета угла ![]() .
.
3. Решение задачи о минимизации
времени разворота
Для решения задачи быстродействия (2.6)–(2.9) воспользуемся
принципом максимума Понтрягина [15-16]. Гамильтониан ![]() равен
равен
|
|
(3.1) |
Сопряженные переменные являются решениями уравнений
|
|
(3.2) |
|
|
|
Тогда
|
|
(3.3) |
В соответствии с принципом максимума на
оптимальной траектории достигается максимум Гамильтониана по ![]() . Оптимальное управление
. Оптимальное управление ![]()
|
|
(3.4) |
и на оптимальной траектории справедливо условие трансверсальности
|
|
(3.5) |
Если ![]() , то
, то
|
|
(3.6) |
|
|
(3.7) |
где
|
|
(3.8) |
![]() – постоянная
интегрирования.
– постоянная
интегрирования.
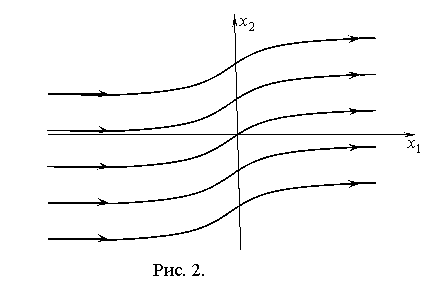
Фазовые траектории при ![]() показаны на рис. 2.
показаны на рис. 2.
Если ![]() , то
, то
|
|
(3.9) |
|
|
(3.10) |
где ![]() – постоянная
интегрирования.
– постоянная
интегрирования.
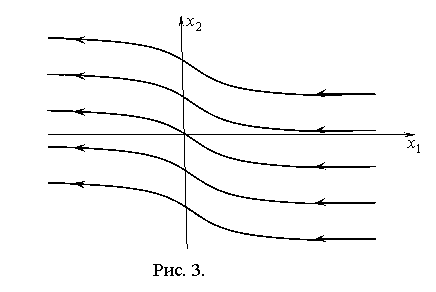
Фазовые траектории при ![]() показаны на рис. 3.
показаны на рис. 3.
В вырожденном случае [16], ![]() в течение
некоторого интервала времени
в течение
некоторого интервала времени ![]() . Из (3.2) следует
. Из (3.2) следует 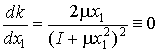 , а тогда
, а тогда ![]() и в силу (2.6)
единственная вырожденная фазовая траектория соответствует управлению
и в силу (2.6)
единственная вырожденная фазовая траектория соответствует управлению ![]() и
и
|
|
(3.11) |
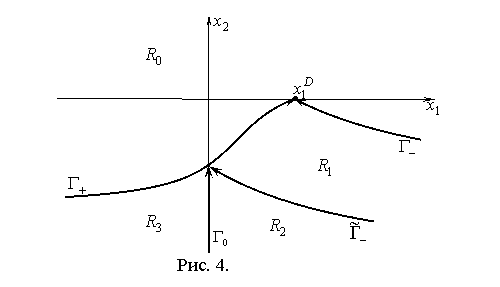
Через программное конечное положение проходят две фазовые
траектории (рис. 4). Одна из них ![]() соответствует
управлению
соответствует
управлению ![]() ,
,
|
|
(3.12) |
а вторая ![]() управлению
управлению ![]()
|
|
(3.13) |
Эти кривые вместе с ![]() , соответствующей вырожденному случаю
, соответствующей вырожденному случаю ![]()
|
|
(3.14) |
и ![]()
|
|
(3.15) |
Делят фазовую плоскость на четыре
области ![]() (рис. 4).
(рис. 4).
Утверждение 3.1. Если
система находится в области ![]() , то ее невозможно перевести в требуемое конечное
положение.
, то ее невозможно перевести в требуемое конечное
положение.
При заданном положительном значении кинетического момента
системы ![]() , невозможно перевести систему из произвольного начального в
заданное конечное положение, т.е. система является неуправляемой.
, невозможно перевести систему из произвольного начального в
заданное конечное положение, т.е. система является неуправляемой.
Доказательство этого утверждения очевидно. Ни одна из фазовых
траекторий (3.6)–(3.11), начинающаяся в области ![]() , не проходит через программное конечное положение.
, не проходит через программное конечное положение.
Не нарушая общности, можно положить, что в конечный момент времени расстояние между телами положительно
|
|
(3.16) |
Утверждение 3.2.
Если ![]() и в начальный момент
времени система не лежит в области
и в начальный момент
времени система не лежит в области ![]() , то оптимальный закон управления имеет вид
, то оптимальный закон управления имеет вид
|
|
(3.17) |
Если система находится в области ![]() , то оптимальная управляющая последовательность
, то оптимальная управляющая последовательность![]() . Если система находится в области
. Если система находится в области ![]() , то оптимальная управляющая последовательность
, то оптимальная управляющая последовательность![]() . Если система находится в области
. Если система находится в области ![]() , то оптимальная управляющая последовательность
, то оптимальная управляющая последовательность![]() .
.
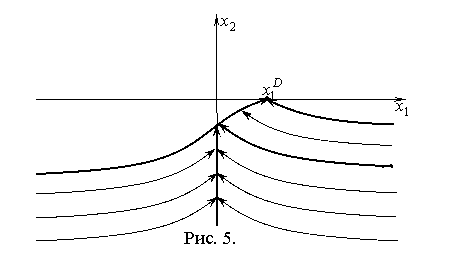
Соответствующие оптимальные фазовые траектории при различных начальных условиях показаны на рис. 5.
Замечание. Механический смысл оптимального решения очевиден. При уменьшении момента инерции связки двух тел относительно их общего центра масс увеличивается угловая скорость вращения в силу закона сохранения кинетического момента. На оптимальной траектории необходимо с максимально возможной скоростью сближать тела и тем самым уменьшать момент инерции связки тел относительно общего центра масс, а затем в конце удалить тела на требуемое конечное расстояние между ними опять же с максимально возможной скоростью. Если при этом удается достичь положения с минимальным моментом инерции (когда совпадают центры масс этих тел), то следует оставаться в этом положении как можно дольше.
Докажем утверждение 3.2. Для этого достаточно доказать, что возможны только перечисленные в этом утверждении оптимальные управляющие последовательности.
Если ![]() , то
, то
|
|
(3.18) |
Отсюда 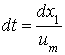 , и в силу (3.2)–(3.3)
, и в силу (3.2)–(3.3)
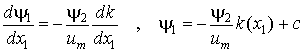 . Подставляя
. Подставляя ![]() в условие
трансверсальности (3.5), получаем, что постоянная интегрирования
в условие
трансверсальности (3.5), получаем, что постоянная интегрирования ![]() . В результате
. В результате
|
|
(3.19) |
Аналогично, если ![]() , то
, то
|
|
(3.20) |
|
|
(3.21) |
В силу непрерывности ![]() кривые (3.19), (3.21)
должны пересекаться в точке переключения
кривые (3.19), (3.21)
должны пересекаться в точке переключения ![]() , причем в силу (3.4)
, причем в силу (3.4)
|
|
(3.22) |
и, если имеется вырожденный участок
оптимальной траектории с управлением ![]() , то в силу (3.11)
, то в силу (3.11)
|
|
(3.23) |
В силу (2.11), (3.3), (3.19), (3.21), (3.22)
|
|
(3.24) |
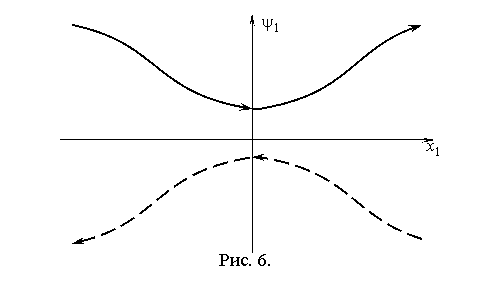
На рис. 6–8 показаны графики кривых (3.19), (3.21), направления
движения по ним при изменении времени и возможное взаиморасположение этих кривых.
Кривая (3.19), соответствующая ![]() , нарисована сплошной линией, а кривая (3.21),
соответствующая
, нарисована сплошной линией, а кривая (3.21),
соответствующая ![]() , пунктирной линией.
, пунктирной линией.
Рис. 6 соответствует тривиальному случаю, когда начальное
положение находится на одной из линий переключения ![]() или
или ![]() . Оптимальное управление в течении всего движения либо равно
. Оптимальное управление в течении всего движения либо равно ![]() , либо
, либо ![]() .
.
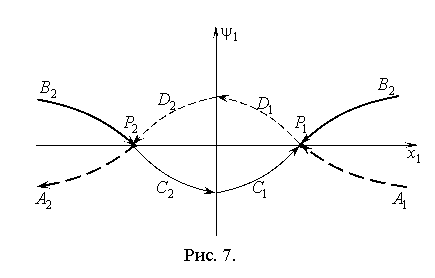
Рис. 7 соответствует движению с одним переключением. Жирной
линией выделена зависимость ![]() на оптимальной
траектории, соответствующая замечанию 3.1.
на оптимальной
траектории, соответствующая замечанию 3.1.
Действительно на оптимальном режиме движения невозможно
движение изображающей точки на плоскости ![]() по участкам
по участкам ![]() и
и ![]() , где
, где ![]() . В соответствии с принципом оптимальности часть оптимальной
траектории должна являться оптимальной для ее краевых значениях. На части
участков
. В соответствии с принципом оптимальности часть оптимальной
траектории должна являться оптимальной для ее краевых значениях. На части
участков ![]() и
и ![]() расстояние между
телами связки увеличивается, а затем возвращается к исходному значению. Такой
участок заведомо не является оптимальным. Если бы расстояние между телами
оставалось неизменным, момент инерции связки тел относительно центра масс на
этом участке был бы меньше, и связка развернулась бы на тот же самый угол за
меньшее время. Подобные траектории на плоскости
расстояние между
телами связки увеличивается, а затем возвращается к исходному значению. Такой
участок заведомо не является оптимальным. Если бы расстояние между телами
оставалось неизменным, момент инерции связки тел относительно центра масс на
этом участке был бы меньше, и связка развернулась бы на тот же самый угол за
меньшее время. Подобные траектории на плоскости ![]() соответствуют решению
задачи о максимизации времени разворота связки тел. Здесь точки
соответствуют решению
задачи о максимизации времени разворота связки тел. Здесь точки ![]() и
и ![]() расположены в местах
возможного переключения управления.
расположены в местах
возможного переключения управления.
Возможные оптимальные управляющие последовательности: а) ![]() на правой ветви
на правой ветви ![]() траектория
траектория ![]() , б)
, б) ![]() на левой ветви
на левой ветви ![]() траектория
траектория ![]() . Отметим, что на оптимальной траектории
. Отметим, что на оптимальной траектории ![]() не меняет знака. В
конечном положении (3.17)
не меняет знака. В
конечном положении (3.17) ![]() . Следовательно, возможна только одна оптимальная управляющая
последовательность с одним переключением, а именно
. Следовательно, возможна только одна оптимальная управляющая
последовательность с одним переключением, а именно ![]() .
.
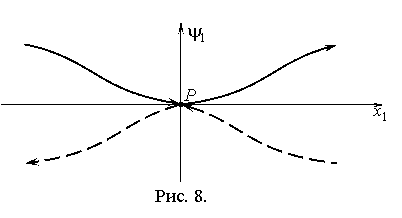
На рис. 8 показан вырожденный случай, когда на оптимальной
траектории имеется вырожденный участок с ![]() (ему на рисунке
соответствует точка
(ему на рисунке
соответствует точка ![]() ). В силу условия (3.17)
). В силу условия (3.17) ![]() имеем, что возможны
две оптимальные управляющие последовательности
имеем, что возможны
две оптимальные управляющие последовательности ![]() и
и ![]() .
.
Тем самым утверждение 3.2 доказано.
4. Задача о максимизации времени
разворота
Для решения задачи (2.6)–(2.8) о максимальном времени разворота или с критерием
|
|
|
осуществляется аналогично предыдущему
разделу. Гамильтониан ![]() равен
равен
|
|
(4.1) |
Оптимальное управление
|
|
(4.2) |
Условие трансверсальности
|
|
(4.3) |
Если ![]() , то
, то ![]() определяются формулами
(3.6)–(3.8)
определяются формулами
(3.6)–(3.8)
|
|
(4.4) |
Если ![]() , то
, то ![]() определяются формулами
(3.9)–(3.10)
определяются формулами
(3.9)–(3.10)
где ![]() – постоянная
интегрирования.
– постоянная
интегрирования.
|
|
(4.5) |
Вырожденный участок ![]() на оптимальной
траектории не возможен, так как ему соответствует максимальная скорость
вращения связки тел (минимальное время разворота).
на оптимальной
траектории не возможен, так как ему соответствует максимальная скорость
вращения связки тел (минимальное время разворота).
В силу непрерывности ![]() кривые (4.4), (4.5) должны
пересекаться в точке переключения
кривые (4.4), (4.5) должны
пересекаться в точке переключения ![]() , причем в силу (4.2)
, причем в силу (4.2)
|
|
(4.6) |
В силу (2.11), (3.3), (4.4) – (4.6)
|
|
(4.7) |
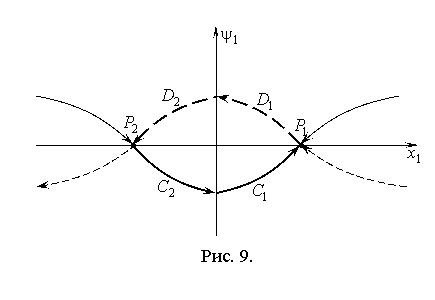
Возможное взаиморасположение кривых (4.4), (4.5) в
нетривиальном случае показано на рис. 9. Кривая (4.4), соответствующая ![]() , нарисована сплошной линией, а кривая (4.5), соответствующая
, нарисована сплошной линией, а кривая (4.5), соответствующая
![]() , пунктирной линией. Зависимость
, пунктирной линией. Зависимость ![]() является частью
участка выделенного жирной линией. Из механических соображений на оптимальной
траектории тела должны удаляться друг от друга с максимальной скоростью, а
затем с максимальной скоростью сближаться, чтобы прийти в требуемое конечное
положение. Возможные оптимальные управляющие последовательности
является частью
участка выделенного жирной линией. Из механических соображений на оптимальной
траектории тела должны удаляться друг от друга с максимальной скоростью, а
затем с максимальной скоростью сближаться, чтобы прийти в требуемое конечное
положение. Возможные оптимальные управляющие последовательности ![]() и
и ![]() . На оптимальном режиме движения возможно движение
изображающей точки на плоскости
. На оптимальном режиме движения возможно движение
изображающей точки на плоскости ![]() только по траекториям
типа
только по траекториям
типа ![]() либо
либо ![]() , где
, где ![]() .
.
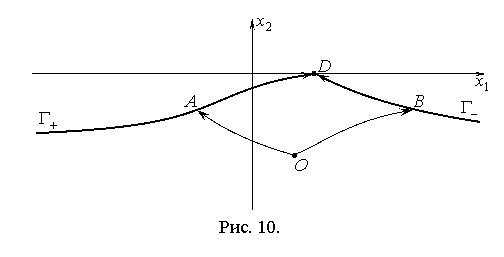
Каждому начальному положению системы на фазовой плоскости ![]() соответствует два типа решений (рис. 10). Решение типа
соответствует два типа решений (рис. 10). Решение типа ![]() – траектория
– траектория ![]() , управляющая последовательность
, управляющая последовательность ![]() ; решения типа
; решения типа ![]() – траектория
– траектория ![]() , управляющая последовательность
, управляющая последовательность ![]() .
.
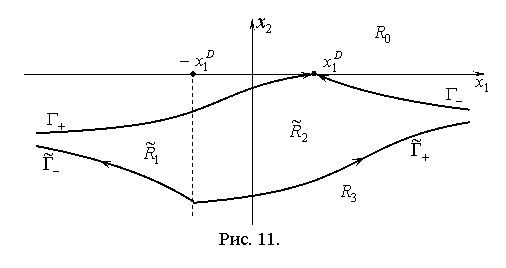
Линии ![]() и
и ![]() (рис. 11) имеют
одинаковые горизонтальные асимптоты, соответственно, с
(рис. 11) имеют
одинаковые горизонтальные асимптоты, соответственно, с ![]() и
и ![]() . Если начальное положение системы находится на
. Если начальное положение системы находится на ![]() или ниже нее, то точка
или ниже нее, то точка
![]() бесконечно удаленная и
время движения по траектории типа
бесконечно удаленная и
время движения по траектории типа ![]() бесконечно большое.
Аналогично, если начальное положение системы находится на
бесконечно большое.
Аналогично, если начальное положение системы находится на ![]() или ниже нее, то время
движения по траектории типа
или ниже нее, то время
движения по траектории типа ![]() бесконечно большое.
бесконечно большое.
Линии ![]() ,
, ![]() ,
, ![]() ,
, ![]() и прямая
и прямая ![]() делят фазовую
плоскость на четыре области
делят фазовую
плоскость на четыре области ![]() (рис. 11).
(рис. 11).
Если в начальный момент времени система находится в области ![]() , ее невозможно перевести в требуемое конечное положение
(утверждение 3.1). Если в начальный момент времени система находится в области
, ее невозможно перевести в требуемое конечное положение
(утверждение 3.1). Если в начальный момент времени система находится в области ![]() (включая границу) то,
ее можно перевести в требуемое конечное положение за сколь угодно большое
время.
(включая границу) то,
ее можно перевести в требуемое конечное положение за сколь угодно большое
время.
Утверждение 4.1.
Если ![]() и в начальный момент
времени система не лежит в области
и в начальный момент
времени система не лежит в области ![]() , то оптимальный закон управления имеет вид
, то оптимальный закон управления имеет вид
|
|
(4.8) |
Если система находится в области ![]() , то оптимальная управляющая последовательность
, то оптимальная управляющая последовательность![]() . Если система находится в области
. Если система находится в области ![]() , то оптимальная управляющая последовательность
, то оптимальная управляющая последовательность![]() .
.
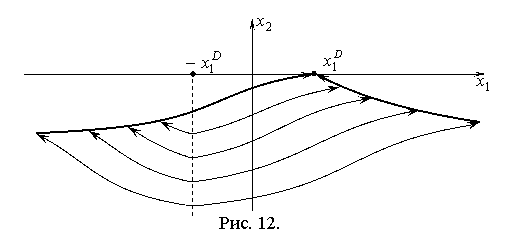
Оптимальные фазовые траектории при различных начальных условиях показаны на рис. 12.
При ![]() время движения по
траекториям типа
время движения по
траекториям типа ![]() и
и ![]() одинаково.
одинаково.
Для доказательства утверждения 4.1 сравним время движения по
траекториям типа ![]() и
и ![]() .
.
Пусть ![]() время движения по
траектории
время движения по
траектории ![]() , а
, а ![]() время движения по
участку
время движения по
участку ![]() (рис. 10).
(рис. 10).
На участке ![]()
![]() справедливы
соотношения (3.9)–(3.10). Постоянную интегрирования
справедливы
соотношения (3.9)–(3.10). Постоянную интегрирования ![]() в (3.10) определим из
условия, что (3.10) справедливо для точки
в (3.10) определим из
условия, что (3.10) справедливо для точки ![]() . Тогда
. Тогда
|
|
|
На участке ![]()
![]() справедливы
соотношения (3.6)–(3.7). Постоянную интегрирования
справедливы
соотношения (3.6)–(3.7). Постоянную интегрирования ![]() в (3.7) определим из
условия, что (3.7) справедливо для точки
в (3.7) определим из
условия, что (3.7) справедливо для точки ![]() . Тогда
. Тогда
|
|
|
Отсюда
|
|
(4.9) |
|
|
(4.10) |
|
|
(4.11) |
Аналогично, для траектории типа ![]()
|
|
(4.12) |
|
|
(4.13) |
|
|
(4.14) |
Лемма 4.2. Если ![]() , то
, то ![]() и
и ![]() , или время движения по траекториям типа
, или время движения по траекториям типа ![]() и
и ![]() одинаково.
одинаково.
Действительно в силу (3.8) ![]() – взаимнооднозначная
нечетная функция, и из условия
– взаимнооднозначная
нечетная функция, и из условия ![]() следует
следует ![]() . Отсюда в силу (4.10), (4.13)
. Отсюда в силу (4.10), (4.13) ![]() . Подставляя эти соотношения в (4.9), (4.12), имеем
. Подставляя эти соотношения в (4.9), (4.12), имеем
|
|
|
Лемма 4.3. Если в
начальный момент времени система находится на линиях переключения в точке ![]() , то время движения по траектории типа
, то время движения по траектории типа ![]() и
и ![]() одинаково
одинаково ![]() .
.
Действительно в этом случае имеет место режим без переключений.
Траектории типа ![]() и
и ![]() совпадают и являются
траекторией
совпадают и являются
траекторией ![]() вдоль линии
переключения. Если
вдоль линии
переключения. Если ![]() , то
, то ![]() и
и ![]() . Если
. Если ![]() , то
, то ![]() и
и ![]() . В силу совпадения этих траекторией одинаково и время
движения по ним.
. В силу совпадения этих траекторией одинаково и время
движения по ним.
Перейдем к доказательству утверждения 4.1.
Пусть точка ![]() лежит в области
лежит в области ![]() , а точка
, а точка ![]() и
и ![]() . Будем изменять положение точки
. Будем изменять положение точки ![]() при фиксированном
положении точки
при фиксированном
положении точки ![]()
Дифференцируя (4.10) и (3.8), имеем 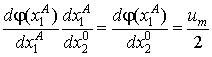 и
и 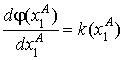 . Отсюда
. Отсюда 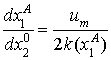 . Дифференцируя (4.9), получаем
. Дифференцируя (4.9), получаем
|
|
(4.15) |
Аналогично, получим
|
|
(4.16) |
Пусть начальное положение ![]() совпадает с точкой
совпадает с точкой ![]() на рис. 13, или
на рис. 13, или ![]() . Точка
. Точка ![]() соответствует
начальному положению
соответствует
начальному положению ![]() . В силу леммы 4.2
. В силу леммы 4.2 ![]() и
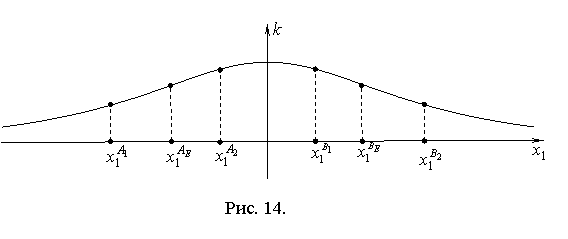
и ![]() . Функция
. Функция ![]() определяется
соотношением (2.10), является четной и монотонно убывающей на множестве
определяется
соотношением (2.10), является четной и монотонно убывающей на множестве ![]() (рис. 14). Отсюда
(рис. 14). Отсюда ![]() ,
, ![]() и в силу (4.15)–(4.16)
и в силу (4.15)–(4.16)
|
|
|
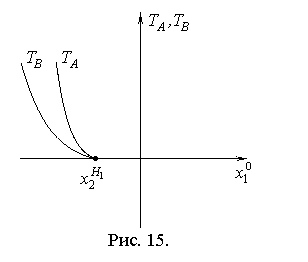
и ![]() . При изменении начального положения вдоль линии
. При изменении начального положения вдоль линии ![]() в области
в области ![]() зависимость
зависимость ![]() и
и ![]() от
от ![]() показана на рис. 15.
показана на рис. 15.
Тогда в области ![]()
![]() и оптимальной
траекторией с максимальным временем движения является траектория типа
и оптимальной
траекторией с максимальным временем движения является траектория типа ![]() .
.

Аналогично, доказывается, что в области ![]()
![]() и оптимальной
траекторией с является траектория типа
и оптимальной
траекторией с является траектория типа ![]() .
.
В заключении отметим, что если при движении аппарата реальное
время полета ![]() (определяемое из
уравнений движения центра масс) удовлетворяет условию
(определяемое из
уравнений движения центра масс) удовлетворяет условию ![]() , то аппарат в движении вокруг центра масс можно перевести из
заданного начального в заданное конечное положение за время
, то аппарат в движении вокруг центра масс можно перевести из
заданного начального в заданное конечное положение за время ![]() . Решение можно искать в виде кусочно-постоянных
управляющих последовательностей
. Решение можно искать в виде кусочно-постоянных
управляющих последовательностей ![]() . При этом возможно любое сочетание знаков управления на
первом и третьем этапе и возможна нулевая продолжительность любого этапа
постоянного значения управления.
. При этом возможно любое сочетание знаков управления на
первом и третьем этапе и возможна нулевая продолжительность любого этапа
постоянного значения управления.
Литература
1. Okhotsimsky D.E., et al. Walking
machines. Advances in mechanics, 1992,
№1–2, p. 39–70.
2. Лапшин В.В. Динамика и управление движением прыгающего аппарата. Известия АН СССР. Механика твердого тела, 1983, № 5, с. 42–51.
3.
Лапшин В.В. Управление движением прыгающего аппарата в фазе полета. Известия АН СССР. Механика твердого тела, 1984, № 1, с. 159–165.
4. Hemami J., Zheng Y. Dynamics and
control of motion on the ground and in the air with application to biped robot.
Journal of robotics systems, 1984,
№ 1, p. 101–116.
5. Hodgins J., Raibert M.H. Biped
gymnastics. Robotics research: The fourth
international symposium.
6. Raibert M.H. Legged robots that
balancemnastics. Robotics research: The
fourth international symposium.
7. Lapshin V.V. Motion control of a
legged machine in the supportless phase of hopping. The international journal of robotics research, 1991, №4, p.
327–337.
8. Кирпичев В.Л. Беседы о
механике. СПб., 1907.
9. Smith P.G., Kane T.R. On the
dynamics of human body in free fall. Journal
of applied mechanics, 1968, № 1.
10. Kane T.R., Scher M.P. A
dynamical explanation of the falling cat phenomenon. International journal of solids and structuresapplied mechanics,
1969, № 7.
11. Степанцов В.О., Еремин А.В. О биомеханике человека в без
опорном положении (невесомости). Космические исследования, 1969, № 6, c. 925–930.
12. Frohlich C. Do springboard
divers violate angular momentum conservation? American journal of physics, 1979, № 47, p. 583–592.
13. Frohlich C. The physics of
somersaulting and twisting. Scientific
American, 1980, № 242, p. 113–120.
14. Аппель П. Теоретическая механика. М., Физматгиз, 1960, т. I –515 c.; т. II – 487 с.
15. Понтрягин Л.С. и др. Математическая теория оптимальных процессов. М., Физматгиз, 1961, 391 с.
16. Атанс М., Фалб П. Оптимальное управление. М., Машиностроение, 1968, 764 с.