E-mail: zabrodin@kiam.ru

                                                      Содержание

                                                                                                                 Стр.

Введение

Известно, что протопланетный диск Солнца играет определяющую роль в образовании солнечной планетной системы.

Образование самого протопланетного диска Солнца непосредственно связано с образованием Солнца как звезды. Гипотезы образования Солнца и солнечной системы можно разделить на две группы. Первая из них восходит к классическим гипотезам Канта и Лапласа о совместном образовании Солнца и его планетной системы из единой протосолнечной туманности. Вторая гипотеза предполагает раздельное образование Солнца и его протопланетного диска, из которого впоследствии сформировались планеты. В данных исследованиях  авторы придерживаются гипотезы о совместном образовании Солнца и его планетной системы из единой протосолнечной туманности.

Настоящие исследования посвящены эволюции уже образовавшегося протопланетного диска Солнца на ее начальной стадии.

Строго говоря, эволюция протопланетного диска Солнца в ее полной и адекватной физическим процессам постановке должна решаться в рамках общей проблемы образования Солнечной системы. В этом случае эволюция протопланетного диска логически следует из определенной фазы эволюции Солнечной системы. В такой постановке задача является чрезвычайно сложной, и в настоящее время только намечаются пути ее решения. Решение этой задачи в полной постановке возможно методами численного моделирования на основе полных физически адекватных многомерных численных моделей образования Солнечной системы с использованием современных вычислительных систем, например, таких, как вычислительная система МВС-1000 Института прикладной математики им. М.В. Келдыша РАН. При отсутствии полных моделей актуальным становится построение упрощенных аналитических и численных моделей для отдельных этапов сценария образования Солнечной системы, способных правильно описать основные физические процессы на соответствующем этапе.

В настоящих исследованиях была использована приближенная аналитическая модель, впервые предложенная в работах [12,13] при исследованиях атмосферы вращающегося коллапсара.

Численные расчеты проводились на основе методик и программных средств двумерного программного комплекса, разработанного в Институте прикладной математики им.М.В.Келдыша РАН [14].

1.     Общая постановка задачи.

Процессы образования протопланетных дисков и соответствующих им планетных систем существенным образом зависят от процессов эволюции космической системы, в которой рассматриваются эти явления. Это относится  и к образованию планетных тел в Солнечной системе. Например, известно, что в межзвездных облаках не образуются изолированные планетные тела, более того, в них не наблюдается рост частиц пыли более 10^-5-10^-4 см [1]. Предполагается, что в облаках межзвездного пространства существуют процессы, препятствующие росту пылевых частиц. В одной из гипотез таким процессом, который «стабилизирует» размер частиц, является столкновение облаков в межзвездном пространстве [1].

Таким образом, образование протопланетного диска Солнца нельзя рассматривать вне зависимости от процессов образования Солнца как звезды, т.е. от модели образования Солнечной системы.

1.1.  Модель образования Солнечной системы.

В общих чертах модель образования Солнечной системы была принята в следующем виде.

1.     Солнце и его протопланетный диск образовались путем единого процесса гравитационного сжатия вращающейся протосолнечной газопылевой туманности (аналогично, как это было предсказано Лапласом) [2], стр. 18; [3], стр. 99.

2.     Формирование Солнца как звезды произошло за промежуток времени, равный примерно 0,1∙10⁶ лет [3], стр. 101. Солнце за этот период аккумулировало около 90 % своей массы. В это же время (одновременно с формированием Солнца) происходило образование протопланетного диска Солнца. На этой стадии Солнце окружено непрозрачной аккреционной оболочкой, которая поглощает интенсивное излучение молодого Солнца и переизлучает его в инфракрасном диапазоне.

3.     Данные последних лет показывают, что коллапс межзвездной газопылевой туманности протекал таким образом, что, по крайней мере, часть этой туманности не была полностью испарена и гомогенизирована [4], стр. 26. На последующих этапах температура протопланетного диска Солнца падала и происходила конденсация первоначально высокотемпературного газа в той части, где ранее протекали процессы испарения.

4.     Вторая стадия формирования Солнечной системы соответствует стадии Т Тельца  до  выхода Солнца  на  главную  последовательность  [3],   стр. 100;

[5, 6], [2]. К началу второй стадии вокруг Солнца может сохраниться лишь незначительная по массе прозрачная часть аккреционной оболочки. Более значительная ее часть может находиться вдали от звезды в виде тора, окружающего звезду и входящего в состав протопланетного диска. На второй стадии идет более медленное формирование протопланетного диска Солнца, и эта стадия по ее продолжительности оценивается примерно в 10⁶ - 10⁷ лет [3], стр. 100; [5]; [2], стр. 207.

5.     Солнечный ветер возникает на второй стадии. По разным источникам информации продолжительность солнечного ветра несколько различается [4, 3, 5], но, вероятно, ее можно оценить равной примерно 10⁶ лет.

6.     Планетная система Земля-Луна образовалась из зоны протопланетного диска Солнца, находящейся на расстоянии около 1 а.е. от Солнца. Средние параметры среды этой зоны диска следующие: плотность  ~10^-9 г/см³, температура  ~400^оК [7], стр. 509.

2.     Состав среды протопланетного диска Солнца.

Для описания эволюции протопланетного диска Солнца весьма важен состав его среды.

По данным работ [2, 3] состав протопланетного диска  Солнца на 98 % состоит из газа, в котором обилия по массе молекулярного водорода, гелия и всех остальных веществ составляет соответственно 0,71; 0,28; 0,01. На пылевые частицы приходится по массе от 0,5 до 1,5 %.

Одним из ключевых вопросов в эволюции протопланетного диска является поведение его пылевой компоненты, а именно: рост размеров частиц и возможность образования достаточно крупных тел, способных далее расти с помощью своего  тяготения. Этот вопрос относится к числу наиболее сложных и не решенных до настоящего времени. По существу от решения этого вопроса зависит путь эволюции планетной системы Солнца. Если реализуется возможность независимого образования достаточно крупных твердых тел, дальнейший рост которых возможен за счет их тяготения, то это путь, который описывается моделью Шмидта-Сафронова [9], в противном случае может быть справедлива, например, капельная модель, предложенная Энеевым Т.М. и Козловым Н.Н. [8, 10, 11].

В межзвездных облаках размер частиц пыли не превышает 10^-4 - 10^-5 см [1], что обусловлено существованием процессов, которые ограничивают рост размеров частиц. Существуют ли такие процессы в протопланетном  диске? Ответ на этот вопрос остается открытым. Ряд авторов утверждает, что в протопланетном диске Солнца может происходить рост размеров частиц при столкновении между собой за счет их слипания [2, 9]. Предлагаемые возможные механизмы слипания частиц пыли: ван-дер-ваальсовые силы;  разные типы «радиационного» спекания [2], стр. 413; эффект холодной сварки [9], стр. 139 и другие. Произойдет ли слипание или дробление частиц при  столкновении зависит от их относительной скорости. По данным работ [3, 7] в протопланетном диске Солнца частицы достигают распределения по размерам, в котором имеются и мелкие частицы размером около 1 мкм, поддерживающие высокую непрозрачность вещества диска, и крупные около 1 см. Средний размер пылевых частиц составляет несколько десятков микрометров.

Так как в данных исследованиях изучалась эволюция протопланетного диска на ее начальном этапе, то было принято, что пылевые частицы однородно распределены по объему протопланетного диска, а их размер не сильно отличался от размера пылевых частиц в протосолнечной туманности.

Для описания поведения протопланетного диска необходимо знать уравнение состояния его среды.

2.1. Уравнение состояния среды протопланетного диска.

Итак, допустим, что начальный состав среды протопланетного диска имеет распределение плотности пылевой компоненты, близкое к однородному,  и содержание пыли по массе не превышает нескольких процентов. При этих условиях можно показать, что усредненные параметры данной среды с доста-точной точностью описываются уравнением состояния идеального газа [15].

Так, по данным работы [3], если на пылевые частицы приходится по массе около 1,5 % вещества солнечного состава, то для такой среды молекулярный вес равен 2,53, а показатель адиабаты - 1,43. Описание протопланетного облака в приближении идеального газа дает достаточно точную картину поведения его некоторых средних характеристик, а именно тех, которые локально определяются газовой компонентой, даже в том случае, когда пылевая компонента конденсируется и превращается в твердое вещество.

3. Упрощенная модель протопланетного газопылевого диска Солнца.

Рассмотрим солнечную систему на стадии, когда уже образовалось Солнце, а аккреционные процессы в протопланетном диске завершились. Будем считать, что в этот момент протопланетный диск однороден по составу и его вещество удовлетворяет уравнению состояния идеального газа. Примем также, что , где  - масса протопланетного диска, в этом случае оправдано использование приближения Роша с центральным источником гравитационного поля [12, 13, 16]. Существенно, что при этом не учитывается излучение.

3.1. Аналитическое решение.

Для принятой модели система уравнений гидростатического равновесия в сферической системе координат примет вид [16]:

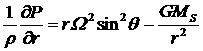,                                        (3.1.1)

,                                            (3.1.2)

где ,  - давление и плотность вещества; ,  - сферические координаты;  - угловая скорость вращения;   - гравитационная постоянная;  - масса протосолнца. Будем считать, что вещество диска подчиняется политропному уравнению состояния:

.                                                 (3.1.3)

В этом случае исходная система уравнений (3.1.1), (3.1.2) преобразуется к виду:

,                                       (3.1.4)

,                                           (3.1.5)

где . Или в эквивалентной записи:

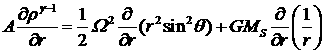,                            (3.1.6)

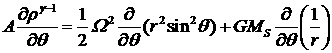.                           (3.1.7)

Рассмотрим законы вращения с угловой скоростью, зависящей только от цилиндрического радиуса  (далее в разделе ,  - цилиндрические координаты,  - сферический радиус), т.е. вида . Введем функцию  такую, что

                   ,                                                (3.1.8)

где . Тогда система уравнений (3.1.6), (3.1.7) сводится к одному уравнению:

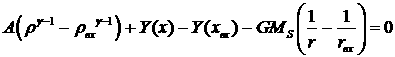,                     (3.1.9)

где  и  - соответственно значения плотности и функции  в некоторой точке с координатами . Удобно принять в качестве  точку на экваторе (), в которой плотность вещества обращается в ноль, т.е. . Вводя обозначения

,           ,

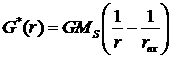получаем из уравнения (3.1.9):

 .                                      (3.1.10)

Выражение (3.1.10) служит основным уравнением как для нахождения распределения плотности вещества  при заданном законе вращения, так и для решения обратной задачи – определения закона вращения , обеспечивающего желаемое распределение плотности вещества на экваторе при .

В работе [16] представленный аналитический подход применялся для описания конфигурации тороидальной атмосферы вращающегося коллапсара с законом вращения вида:

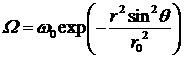                   ,                                      (3.1.11)

где ,   - некоторые константы. Решение уравнения (3.1.10) для выражения (3.1.11) имеет следующие характерные особенности: профиль, вытянутый вдоль оси z; максимум плотности в центральной части диска; большой градиент плотности при приближении к границе диска (см. [16]). Все это делает неприемлемым использование закона вращения вида (3.1.11) в задаче о протопланетном диске, для которого характерна малая толщина  по сравнению с радиальными размерами.

3.2. Модели тонкого протопланетного диска.

Определим параметры рассматриваемой задачи. В соответствии с данными подраздела 2.1 параметр адиабаты имеет значение , тем не менее, во  всех численных результатах, представленных ниже в данном разделе, параметр , что приводит лишь к незначительным количественным отличиям. Внешний размер диска на экваторе , что примерно соответствует радиусу орбиты Нептуна. Радиус внутренней границы протопланетного диска, на котором плотность также обращается в ноль, примем равным расстоянию до Меркурия: . Величину  положим равной . Константа уравнения состояния  определяется оценочно из достаточно грубой предпосылки, что сжатие протосолнечной туманности произошло адиабатически: .

Анализ получаемых решений в рассматриваемой упрощенной модели протопланетного диска показывает, что конфигурация диска существенным образом зависит от вида функции угловой скорости . При изучении протопланетного диска Солнца, как правило, полагают, что дифференциальный закон вращения среды диска подчиняется закону Кеплера, см., например, [17]. В сферической системе координат этот закон имеет вид:

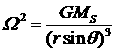.                                              (3.2.1)

В соответствии с уравнением (3.1.9) для закона Кеплера получаем распределение плотности вещества

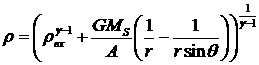,                                (3.2.2)

которое имеет смысл только при , в противном случае . Граничная кривая  () при этом описывается соотношением

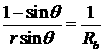                 ,                                               (3.2.3)

где . Из (3.2.3) следует, что граница диска асимптотически приближается к кривой  при стремлении радиуса  к бесконечности:

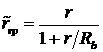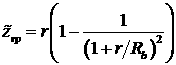,                                     (3.2.4)

Характерное поведение плотности для этого случая представлено на рисунке 3.2.1, параметр  (соответственно ). В экваториальной плоскости диска плотность газа всюду постоянна , т.е. внешняя граница при  отсутствует. В случае  плотность вещества падает с ростом координаты  вплоть до нуля при . Для   согласно (3.2.4) граничного значения  не существует.

Таким образом, полученное для закона вращения Кеплера решение (3.2.2) слабо удовлетворяет требованиям рассматриваемой задачи и при том только в ограниченной области - . Тем не менее, в рамках данной аналитической модели возможны решения в виде «тонких» протопланетных дисков. Рассмотрим поведение уравнения (3.1.10) в экваториальной плоскости. Координата  изменяется в пределах , . Как видно из рисунка 3.2.2, плоские диски будут иметь место в случае, когда  и при этом 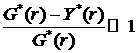. Другими словами, аналитическое решение представляет собой «тонкий» протопланетный диск при условии, что закон вращения лишь незначительно отличается от кеплеровского в области .

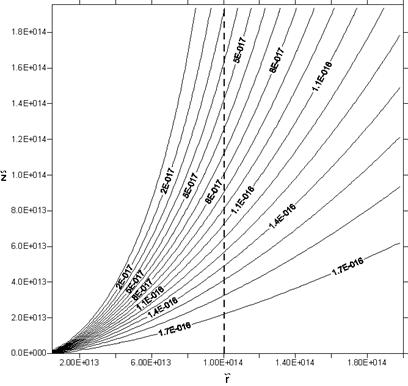
Рис. 3.2.1. Линии постоянной плотности в случае кеплеровского закона вращения (3.2.2) для значения граничной плотности , , . 

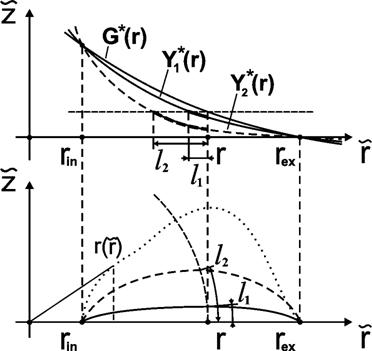
Рис. 3.2.2. Функции ,  и  от расстояния  в экваториальной плоскости. Характер зависимости толщины диска от соотношения между функциями  и .

3.2.1. Модель протопланетного диска для .

Для близкого к кеплеровскому закона вращения

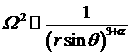,                                            (3.2.5)

при условии обращения в ноль решения в экваториальных точках  и , распределение плотности вещества протопланетного диска принимает вид:

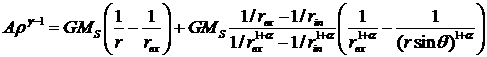.           (3.2.6)

При этом точное выражение для угловой скорости записывается в виде соотношения:

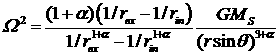.                             (3.2.7)

На рисунке 3.2.3 представлены изолинии плотности вещества протопланетного диска в плоскости пространственных переменных () для двух различных значений параметра .

3.2.2. Модель протопланетного диска для

В модели протопланетного диска с законом вращения  (раздел 3.2.1) максимальная плотность вещества находится вблизи внутреннего радиуса диска -  (см. рисунок 3.2.3). Это приводит к большим градиентам плотности в указанной области, что в ряде случаев создает значительные трудности при численных расчетах. Причина этой особенности заключается в том, что в рассматриваем случае разность   (см. рисунок 3.2.2) имеет максимум в окрестности , который и формирует экстремум в распределении плотности. Простой способ устранить эту особенность – использовать закон вращения вида

,                                 (3.2.8)

который позволяет построить модель «тонкого» диска с нужным профилем плотности на экваторе. Выбор соответствующей функции  однозначно определяет форму зависимости  при значениях  и . По техническим соображениям удобнее решать обратную задачу: 1) задать зависимость , обеспечивающую нужное распределение плотности; 2) по формуле (3.1.8) определить закон вращения, отвечающий заданной функции . Приведем в качестве примера две модели.

•         C квадратичной зависимостью по радиусу  и максимумом плотности при значении  (см. рисунок 3.2.4):

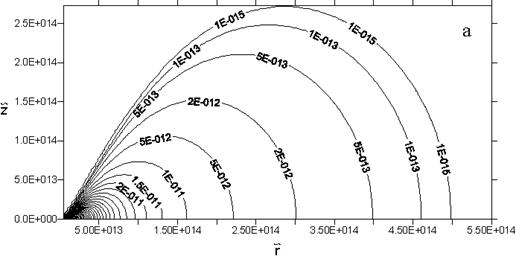
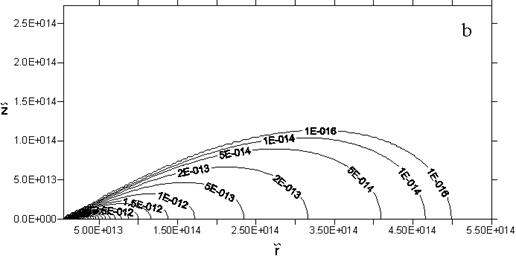
Рис. 3.2.3. Линии постоянной плотности в случае закона вращения (3.2.7) для разных значений . Параметры моделей: (a) , ; (b) , . 

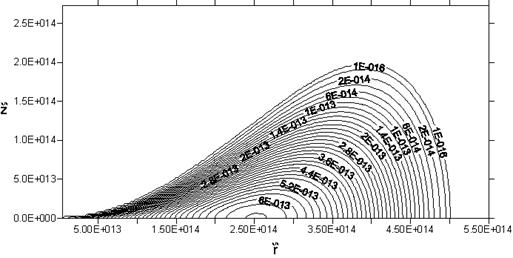
Рис. 3.2.4. Линии постоянной плотности в случае закона вращения (3.2.10). Параметры модели: , .

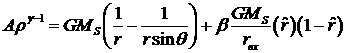                 ,                           (3.2.9)

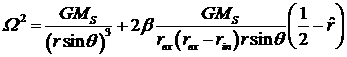                             (3.2.10)

•         C кубической зависимостью по радиусу  и максимумом плотности при значении  (см. рисунок 3.2.5):

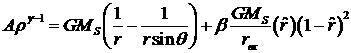                ,                       (3.2.11)

                      .           (3.2.12)

В выражениях (3.2.9) - (3.2.12)  - произвольная константа (в рассматриваемом приближении «тонких» дисков ),  - приведенный цилиндрический радиус. При этом значение  не должно приводить к отрицательным значениям в выражениях для  (3.2.10, 3.2.12). Например, как можно легко показать, из формулы (3.2.10) следует, что  не должно превышать значения .

3.2.3. Модель протопланетного диска с заданной формой границы.

В рамках представленного аналитического решения оказывается возможным построить модель диска с предписанной формой границы. Действительно, из формулы (3.1.10) следует, что на границе диска функция  должна удовлетворять условию

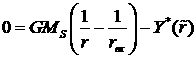,                                     (3.2.13)

из которого непосредственно определяется , если задана форма граничной поверхности диска, иными словами, зависимость  на границе. Так, например, для диска с круглым сечением (плоскостью, проходящей через ось вращения, см. рисунок 3.2.2, пунктирная кривая) функция  имеет вид

,                                      (3.2.14)

и, следовательно, для распределения плотности вещества и закона вращения мы получаем выражения:

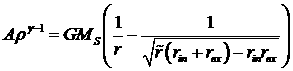,                           (3.2.15)

                                    .                                      (3.2.16)

На рисунке 3.2.6 представлено распределение плотности вещества такого диска в плоскости пространственных переменных .

Рис. 3.2.5. Линии постоянной плотности в случае закона вращения (3.2.12). Параметры модели: , .

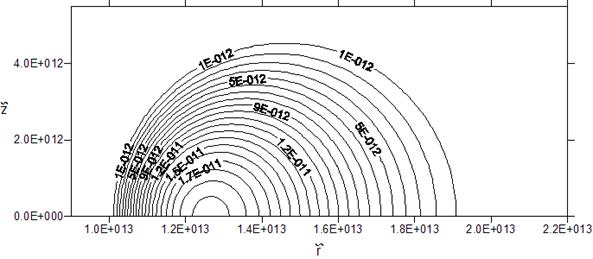
Рис. 3.2.6. Линии постоянной плотности в случае закона вращения (3.2.16). Параметры модели: , ,.

3.3. Устойчивость протопланетных дисков.

Полученные в разделе 3.2 модели дисков представляют собой конфигурации, находящиеся в состоянии стационарного вращения. Однако, следует иметь в виду, что данные модели должны не только подчиняться условиям механического и теплового равновесия, но и быть устойчивыми. При выводе аналитического решения использовалось предположение, что скорость вещества является чисто вращательной. Устойчивость такой конфигурации определяется критерием Хейланда [20], который в предельном случае гомоэнтропического диска, т.е. когда  ( - энтропия вещества), сводится к одному простому неравенству

.                                           (3.3.1)

Следовательно, в устойчивой модели удельный момент количества движения должен увеличиваться наружу. Это критерий Золберга, обобщающий хорошо известный для невязкой несжимаемой жидкости критерий Рэлея [20].

Так, для модели протопланетного диска из раздела 3.2.1 критерий (3.3.1) приводит к условию

 .                                                  (3.3.2)

Для диска, описываемого уравнениями (3.2.9) и (3.2.10), в тех случаях, когда , из требования возрастания удельного момента вращения появляется дополнительное ограничение на параметр  

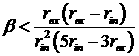 .                                         (3.3.3)

Наконец, в модели протопланетного диска с заданной формой границы зависимость производной удельного момента вращения по радиусу имеет вид

.                              (3.3.4)

Откуда непосредственно следует, что такая модель является заведомо динамически неустойчивой по отношению к осесимметричным движениям при любых  и , кроме случая .

3.4. Модель протопланетных колец.

   В том случае, если происходит фрагментация первоначального протопланетного диска, приводящая к образованию кольцевой структуры, аналитический подход, изложенный выше, также может служить достаточно удобной и простой аппроксимацией для описания отдельных колец новой сформировавшейся структуры. Будем исходить из простого предположения о том, что каждой планете Солнечной системы на указанной стадии соответствует компактное кольцо  с характерным размером сечения, заметно уступающим радиусу орбиты. Определим параметры моделей, необходимые для описания современного набора планет Солнечной системы, т.е. четырех планет земной группы (Меркурий, Венера, Земля и Марс) и четырех планет-гигантов (Юпитер, Сатурн, Уран и Нептун). При этом будем учитывать требование непересечения отдельных колец.

В таблице 3.4.1 приведены данные для трех различных моделей колец, отличающихся выбором закона вращения:  - модель с законом вращения, близким к кеплеровскому (3.2.6);  - модель с заданным профилем плотности (с квадратичной зависимостью по радиусу) в экваториальной плоскости (3.2.9);  - модель с заданной формой граничной поверхности (3.2.15). Конкретные значения параметров модели ( для модели ,  для модели ) для планет-гигантов определялись из условия совпадения полной массы кольца с современным значением массы соответствующей планеты. Для планет земной группы предполагалось, что масса кольца должна превышать современную массу планеты, поскольку масса кольца совпадает с массой газа, заметно превосходящей массу пыли, которую более естественно в этом случае отождествить с массой планеты. Исходя из современного представления об отношении массовых концентраций пылевой и газовой компонент , получаем приблизительное соотношение , где  - масса газа,  - масса соответствующей планеты. Те случаи, когда не удается построить модель кольца с заданной массой газа, в таблице 3.4.1 отмечены символом . Для модели  это ограничение на массу возникает из следующего требования: размер кольца в направлении оси  не должен сильно превышать размера кольца в направлении оси . Для модели  максимально возможная масса определяется предельным значением параметра  (см. раздел 3.2.2), при превышении которого квадрат угловой скорости  (3.2.10) становится отрицательным при некоторых значениях .  Ситуации, когда масса кольца оказывается недостаточной, т.е. , можно избежать, если использовать более мягкое исходное соотношение между массовыми концентрациями газа и пыли, например,  равное .

Таблица 3.4.1. Параметры модели протопланетных колец.  - масса Земли,   - радиус земной орбиты,  - масса планеты,   - радиус орбиты, - внутренний и внешний радиусы диска соответственно,  - параметры моделей  и .

Следует отметить, что в модели  значение параметра , как правило, имеет величину . И, следовательно, соответствующий данному значению  закон вращения уже не совсем корректно называть близким к кеплеровскому. Законы вращения, взятые для отдельных колец, не ложатся на общую для всей совокупности колец кривую. Типичная зависимость угловой скорости от радиуса  приведена на рисунке 3.4.1 (в данном случае использовалась модель ). На рисунке 3.4.1 также показана наилучшая аппроксимация полученной зависимости  прямой (в логарифмических координатах), которая, как видно, довольно точно совпадает с кеплеровским законом вращения. На рисунке 3.4.2 представлено распределение плотности газа для этой же модели.

Рис. 3.4.1. Зависимость угловой скорости  для последовательности про-топланетных колец в модели . Linear fit – наилучшая аппроксимация пря-мой, Kepler law – кеплеровский закон вращения  для .

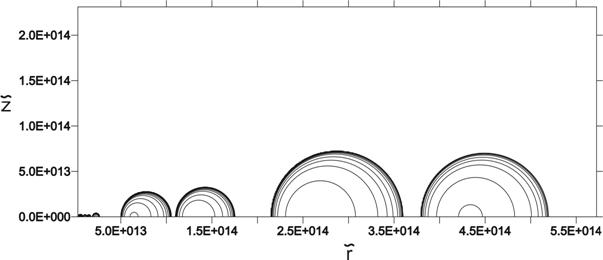
Рис. 3.4.2. Распределение плотности газа группы протопланетных колец в модели  (последний столбец таблицы 3.4.1).

4.         Численная двумерная модель протопланетного газопылевого диска.

Описать с достаточной точностью эволюцию протопланетного диска Солнца можно только с помощью адекватных многомерных численных моделей. Построена численная двумерная газодинамическая модель, которая соответствует осесимметричному движению газовой среды в гравитационном поле. Эта модель может использоваться на начальной стадии эволюции протопланетного диска, когда пылевая компонента распределена относительно равномерно по объему диска.

4.1. Уравнения газовой динамики в форме законов сохранения

                  с учетом собственного гравитационного поля газа.

     Описание газодинамических процессов  в  рассматриваемых  задачах проводится  в  эйлеровом  представлении.  Уравнения газовой динамики в форме законов сохранения в декартовой системе координат записываются в виде:

     уравнение неразрывности

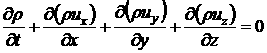                                                                 (4.1.1)

     закон сохранения импульса

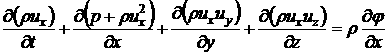                                         (4.1.2)

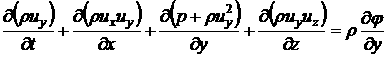                                          (4.1.3)

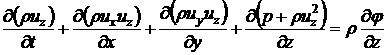                                          (4.1.4)

     закон сохранения энергии

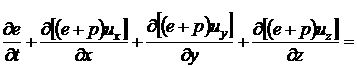
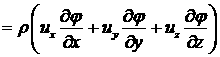                                                                              (4.1.5)

где   x, y, z - декартовы координаты;  t - время; u_x , u_y , u_z  - составляющие вектора скорости  U ;   ;  r= r(x,y,z,t) - плотность газа;        p=p(x,y,z,t) - давление газа;  - энергия единицы объема газа;  e=e(x,y,z,t) - внутренняя энергия единицы массы газа;

         j=j(x,y,z,t) - гравитационный потенциал представлен в виде:

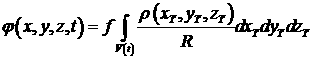                                                        (4.1.6)

где

                                                               (4.1.7)

 x_T ,y_T ,z_T  - текущие декартовы координаты,  по  которым  ведется интегрирование в (4.1.6);  V(t) - объем газового облака;      f - гравитационная постоянная.

       Внутри газового    облака    в   фиксированный   момент   времени гравитационный потенциал удовлетворяет уравнению Пуассона:

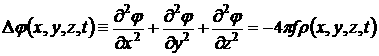                                            (4.1.8)

а вне газового облака - уравнению Лапласа:

                                  Dj (x,y,z,t) = 0                                                                   (4.1.9)

     Для описания газодинамических процессов в случае  учета  вращения более  предпочтительной является цилиндрическая система координат.

4.2. Уравнения  газовой  динамики  при  осевой  симметрии с учетом

собственного гравитационного поля.

     Будем предполагать, что задача об эволюции протопланетного диска Солнца имеет осевую симметрию.     

     В этом случае трехмерная задача сводится к двумерной, которая в цилиндрической системе координат x,r,q описывается следующими уравнениями:

                                                                           4.2.1)

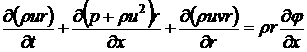                                                       (4.2.2)

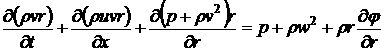                                       (4.2.3)

                                                           (4.2.4)

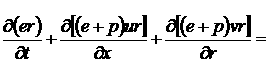
                                                                    (4.2.5)

Ось х направлена по оси вращения газового диска; u, v,  w составляющие вектора скорости U ,соответственно, осевая, радиальная и угловая;

                            |U|² = u²+v²+w²;                                                     (4.2.6)

        r= r(x,r,t) - плотность газа;     p = p(x,r,t) - давление газа;

        e =r[ e+(u² + v² + w² )/2] - энергия единицы объема газа;

        e = e(x,r,t) - внутренняя энергия единицы массы газа;

       j = j(x,r,t) - гравитационный потенциал представлен в виде:

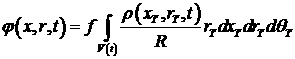                                                        (4.2.7)

где         

                   (4.2.8)

x_Т , r_Т , Q_Т - текущие цилиндрические координаты,  по  которым  ведется                    интегрирование в (4.2.7). В интеграле (4.2.7) в силу симметрии может быть выполнено интегрирование по координате Q_Т.

     Внутри газового    облака    в   фиксированный   момент   времени гравитационный потенциал удовлетворяет уравнению Пуассона:

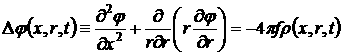                                                 4.2.9)

а вне газового облака - уравнению Лапласа:

                                                Dj(x,r,t) = 0                                                         (4.2.10)

4.3. Уравнения состояния газовой среды протопланетного диска.

       В большинстве случаев газ,  составляющий  протопланетный  диск, можно считать идеальным и использовать на начальной стадии образования планет соответствующее уравнение состояния:

                                              p = RrТ / m ,                                                 (4.3.1)

где   R = 8,31×10  эрг×град^-1× моль^-1 - газовая постоянная;  m - молекулярный вес;   р - давление;  r - плотность.

или                         p = ( g-1) er,                                                                (4.3.2)

где  g - отношение С_р/С_v газовой среды; e - внутренняя энергия единицы массы газа.

     На начальной  стадии  образования  планеты  температура  газового облака составляет ≈ 100⁰К.  При таких температурах основной  вклад  в теплопроводность   газовой  среды  дает  конвекция.  В  этих  условиях газодинамические процессы  в  облаке  можно  с  достаточной  точностью считать  адиабатическими  и  связь  между  давлением и плотностью газа в этом случае может быть описана формулой

                                                                                                     (4.3.3)

где  К - константа;   g - отношение С_p/С_v газовой среды.

     Влияние пылевой компоненты газопылевого диска  можно  приближенно учесть  с помощью   соответствующего   уравнения   состояния.   Для   этой  цели использовалось двучленное уравнение состояния в виде:

                                          p = (g -1) er+( r - r₀)c₀² ,                                            (4.3.4)

где   g, r₀, c₀ - постоянные.

4.4. Уравнения газовой динамики в безразмерных переменных.

     При численных расчетах задач космической газодинамики  в  обычных системах  единиц  измерения,  как  правило,  возникают  проблемы из-за ограниченности диапазона представления чисел  на  ЭВМ.  Эти  трудности могут   быть   преодолены   при  переходе  к  соответствующей  системе безразмерных переменных. В качестве единиц для перехода к безразмерным переменным были выбраны следующие единицы:

  [x]=[r]=r₀ ;        [u]=[v]=[w]=(fm₀/r₀)^1/2 ;  [t]=r₀^3/2/(fm₀)^1/2;

  [r]=m₀/(4pr₀³);  [p]=fm₀²/(4 pr₀⁴);             [e]=fm₀²/(4pr₀⁴);                        (4.4.1)

  [e]=fm₀/r₀;         [w]=(fm₀)^1/2/r₀^3/2;              [T]=(fm₀²/(4pr₀⁴а_r))^1/4,

где   r₀ - начальный радиус облака;  m₀ - масса облака; а_r - постоянная плотности излучения (постоянная Стефана); w = w/r - угловая частота вращения.

     Система уравнений  (4.2.1)-(4.2.5)  в безразмерных переменных сохраняет свой вид. Гравитационный потенциал   сохраняет  свой  вид  с  точностью  до константы:

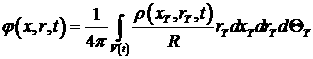                                                      (4.4.2)

и соответственно уравнение Пуассона преобразуется к виду:

                                         Dj(x,r,t) = - r(x,r,t)                                                      (4.4.3)

Уравнение Лапласа остается без изменений. Уравнение Менделеева-Клапейрона принимает вид:

                                        p = А rТ  ,                                                            (4.4.4)

где                                                                    (4.4.5)

есть безразмерная  константа,   значение   которой   зависит   от выбранного масштаба массы.

4.5. Уравнения газовой динамики в форме законов сохранения для

криволинейной системы координат.

Используемая численная методика является вариантом методики для численного решения двумерных газодинамических  течений в областях сложной формы с подвижными границами, разработанной Годуновым С.К.  и Забродиным А.В.  с соавторами [19]. Преимущества данного метода заключаются в том,  что он позволяет выделить границы областей  газа  с разными физическими свойствами (например,  контактные границы, ударные волны,  ввести эйлерову границу и  т.д.) и проследить за сложным движением этих границ.

По положению границ, рассматриваемых как топологический «четырехугольник», строится два семейства координатных линий, разбивающие всю область течения на криволинейные четырехугольники – ячейки счетной сетки. Сетка изменяется во времени, подстраиваясь под характер движения границ. Поэтому ее конфигурация может быть достаточно сложной, а стороны ячеек существенно криволинейными.

Для построения конечно-разностного алгоритма запишем законы сохранения (4.2.1)-(4.2.5) в интегральной форме в локальных криволинейных координатах.

4.5.1. Локальная криволинейная система координат.

          Построим на момент времени t в произвольной точке плоскости (x, r) локальную систему координат

Линии одного семейства координат x-линии задаются уравнением h=const,  линии второго семейства h-линии задаются уравнением  x=const.

     Локальную систему координат можно определить заданием метрических параметров  длины вдоль координатных линий первого и второго семейства и  направляющих   косинусов   касательных   к   координатным   линиям. Метрический параметр и направляющие косинусы с осями x и r для  x-линий обозначим соответственно

                                                                                                            (4.5.1)

     Метрический параметр и направляющие косинусы с осями x  и  r  для h-линий обозначим соответственно

                                                                                                 (4.5.2)

     В этом  случае  a и b, соответственно косинус и синус угла между координатными линиями первого и второго семейства,  через  направляющие косинусы запишутся так:

                                                                             (4.5.3)

          Якобиан перехода к криволинейным координатам  есть 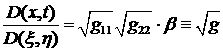. Тогда элемент объема .

     Вдоль каждой   из   координатных   линий   вектор   скорости  U  разлагается  на  касательную  и  ортогональную   к   ней   компоненты. Компоненту  по  касательной вдоль координатных линий h=const обозначим как  m^k,  а ортогональную к ним  как   nⁿ.  При  этом

                                                 (m^k)²+(nⁿ)²= |U|².                                                (4.5.4)

Аналогично, вдоль  координатных  линий  x=const компонентами будут  n^k и mⁿ, где

                                           (n^k)²+(mⁿ)²= |U|²                                              (4.5.5)

     Если выбрать   локальный   базис   из   векторов,   касательных  к координатным линиям в каждой точке, и  разложить  по  ним  произвольный вектор   U ,  то его составляющими будут  m (по касательной к  x-линии) и  n (по   касательной   к    h-линии).    Эти    составляющие    называются контравариантными компонентами. Они связаны с декартовыми компонентами u и v следующим образом:

                  ,                                        (4.5.6)

     Компоненты скорости m^k, nⁿ вдоль x-линий и n^k, mⁿ  вдоль  h-линий выражаются   через  контравариантные  составляющие  в  соответствии  с формулами:

                                     m^k=m+an     ,           nⁿ=nb   ,

                                     n^k=n+am     ,          mⁿ =mb.                                             (4.5.7)

     Через декартовы  компоненты  скорости  (u,v) введенные компоненты выражаются в виде следующих зависимостей:

                           ,      ,

                           ,                                                   (4.5.8)

4.5.2. Интегральная система уравнений газовой динамики

в локальной  системе координат.

     В качестве   исходной   системы   уравнений    выберем    систему дифференциальных  уравнений  газовой динамики в цилиндрических координатах (4.2.1)-(4.2.5).  Для построения интегральной системы уравнений в  локальном базисе  и  выбранных  компонентах  скорости  необходимо выполнить ряд преобразований этой системы. Последовательность таких действий подробно описана в [19], § 29 и 30.

     Приведем окончательный вид системы интегральных уравнений  газовой динамики в локальных криволинейных координатах. Интегрирование было выполнено по некоторому  объёму  V  в  пространстве  x,r,t  с  поверхностью  S. Воспользовавшись   теоремой   Остроградского-Гаусса  о  преобразовании объёмных интегралов в поверхностные и формулами,  задающими переход к локальной криволинейной системе координат, получим следующую интегральную систему уравнений в переменных x, h, t:

,                                (4.5.9)

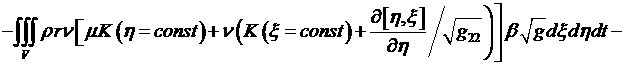
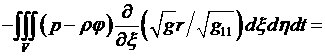
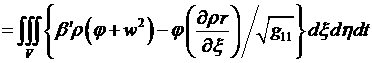,                                                  (4.5.10)

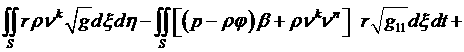
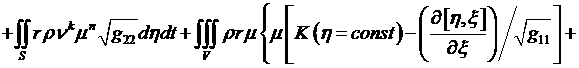
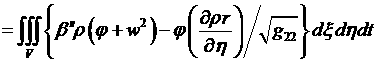                                          (4.5.11)

                                                                                           (4.5.12)

                                    (4.5.13)

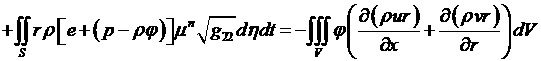
Здесь - кривизны координатных линий.

4.6. Система разностных уравнений  газовой  динамики  с  подвижными сетками в локальной системе координат.

          Разностные уравнения строятся на основе интегральных законов (4.5.9) – (4.5.13), записанных для отдельной ячейки сетки на интервале времени от t₀  до

t₀ + t  с учетом движения сетки (подробный вывод см. [19] § 34).

По  положению  границ  можно  построить  расчетную  сетку и два семейства координатных линий на момент времени  t₀. Координатные  линии разбивают  всю  расчетную  область   на   совокупность   криволинейных четырехугольников – ячейки расчетной сетки, стороны которых будем называть ребрами. Ребра   ячейки   можно  трактовать как координатные линии  локальной  криволинейной системы координат.

Определив  положение границ на момент времени t₀ +t, строим  расчетную  сетку  и два семейства  координатных  линий на  этом временном шаге. Выберем две ячейки сетки с одинаковыми номерами на плоскостях t₀  и t₀ +t. Построим  в  пространстве  x, r, t    поверхность, проходящую через два одноименных ребра этих ячеек.  

Построенный таким образом элементарный объем V представляет собой криволинейный шестигранник в пространстве t, ξ, η.

Нижняя его грань относится к моменту t₀ , верхняя - к моменту t₀ +t. Кроме этих нижней и верхней граней,  существует четыре боковых, каждая из которых есть участок криволинейной поверхности, опирающийся на дуги ζ=const=ζ₀ (или η=const=η₀) плоскости t=t₀ (ребра ячеек сетки нижнего основания) и соответственно дуги    (или   )  на   плоскости

t=t₀+t (ребра одноименной ячейки сетки на t₀+t ). Можно показать, что с точностью до малых более высокого порядка (по сравнению с t) уравнения этих дуг будут (на каждой плоскости t = const) соответственно:

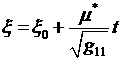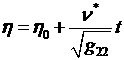          ,        ,       (t₀ ≤ t ≤ t₀ + t)                             (4.6.1)

     Величины μ^*, ν^* по каждой из боковых граней имеют смысл контра-вариантных компонент скорости перемещения соответствующей дуги коорди-натной линии от ее положения на момент t_o  до  положения на момент t₀ + t.

          Для построения конечно-разностных уравнений из интегральной записи (4.5.9)-(4.5.13) следует принять способ усреднения подинтегральных  выражений. Принимается, что по каждой из граней верхнего и нижнего основания значения подинтегральных выражений постоянны и помечаются индексом «0». Аналогично, по каждой из боковых граней значения подингегральных функций также принимаются усредненными и постоянными в течение всего временного шага t. Они отмечаются индексом ребра сетки нижнего основания, на которое опирается боковая грань. Значения самих интегралов (после вынесения из под знака интеграла усредненных подинтегральных функций) имеют следующий геометрический смысл.  Для нижнего S₀ и верхнего S⁰ оснований:

                   ,                                                      (4.6.2)

- объемы фигур, образованных вращением соответственно нижнего S₀ и верхнего S⁰ оснований шестигранника вокруг оси х.

Для боковых граней эти интегралы записываются с использованием (4.6.1) в виде:

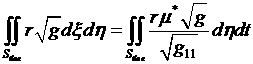
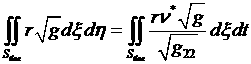       (4.6.3)

    Выражения, содержащие интегрирование по времени, вычисляются по  значениям на момент t = t₀ , т.е.      

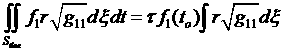           ,                                   (4.6.4)

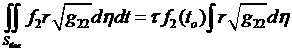                          (4.6.5)

Интегралы, стоящие в правых частях   последних выражений, – это площади поверхности фигур, образованных вращением соответствующих ребер η=const, ζ = const  ячейки вокруг оси х.

          Введем обозначения: - объем, представленный интегралом в (4.6.2) для верхнего основания S⁰ ,  - объем для нижнего основания S₀ ;  - площади поверхности,  образованной  вращением  соответственно ребер 12, 43

(η = const);   - площади   фигур,  полученных  вращением  ребер 14, 23

(ζ = const). Все величины на момент времени t₀ + t помечаются двумя чертами сверху.

          Опустив дополнительные пояснения и промежуточные выкладки, приведем окончательный вид системы разностных уравнений:

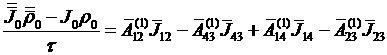,                   (4.6.6)

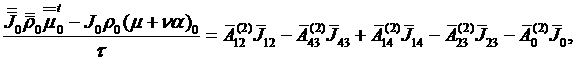(4.6.7)

    (4.6.8)

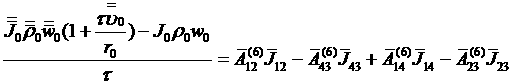      (4.6.9)

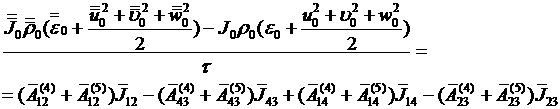 (4.6.10)

Компоненты скорости  пересчитываются в декартовы   по формулам (4.5.6)-(4.5.8).

Величины  (k = 1, 2, 3, 4, 5, 6) рассчитываются следующим образом:

                         (4.6.11)

                                  (4.6.12)

,  (4.6.13)

, (4.6.14)

         (4.6.15)

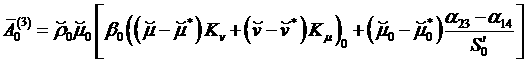                   (4.6.16)

,                    (4.6.17)

,                                                                                            (4.6.18) ,                   (4.6.19)     

 ,                                                                                           (4.6.20)

,                   (4.6.21)

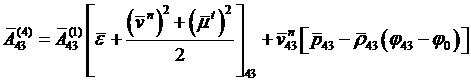,                  (4.6.22)

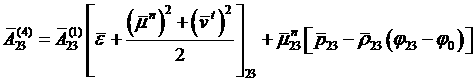,                           (4.6.23)

,                  (4.6.24)

,                            (4.6.25)

,                              (4.6.26)

,                            (4.6.27)

,                              (4.6.28)

,                                     (4.6.29)

,                                      (4.6.30)

,                                     (4.6.31)

.                                      (4.6.32)

В формулах для  ,  используются дополнительные обозначения:

w_0,-1 – значение компоненты скорости из соседней ячейки, прилегающей к ребру 12; w_0,1 – из соседней ячейки, прилегающей к ребру 43; соответственно, w_-1,0 – из ячейки, соседней к ребру 14, w_1,0 – из ячейки, соседней к ребру 23.

          Система разностных уравнений (4.6.6)-(4.6.32) позволяет для каждой пространственной счетной ячейки вычислить по значениям  на нижнем основании шестигранника и известным значениям величин на его боковых гранях значения  на верхнем основании пространственной счетной ячейки, т.е. на последующий момент времени t₀+t. Найти значение гравитационного потенциала  возможно только после выполнения подобной процедуры по всем ячейкам обсчитываемого пространства задачи. После этого придем к исходному состоянию для выполнения следующего шага.

  Таким образом, алгоритм решения задачи складывается из следующих этапов.

     1. Определение положения границ счетной области на момент времени t₀+t.

     2. Построение по положению границ счетной области сетки на момент t₀+t, используя определенный алгоритм расчета.

     3. Определение величин на боковых гранях пространственной счетной ячейки (газодинамических величин и значений потенциала j) по величинам, относящимся к моменту времени t₀.

     4. Решение системы разностных уравнений – определение на момент t₀+t  во всех счетных ячейках. Здесь же определяется допустимый шаг t для выполнения следующего перехода по времени. Шаг t  выбирается из условия устойчивости явной разностной схемы для уравнений газовой динамики.

     5. Расчет гравитационного потенциала j на момент t₀+t. Попутно по всем счетным ячейкам вычисляются и запоминаются значения  - производные по нормали ко всем ребрам каждой счетной ячейки (используются при получении величин на боковых гранях).

          Этим заканчивается расчет одного шага по времени.

4.7. Расчет величин на боковых гранях пространственного

шестигранника.

     В разностных уравнениях системы (4.6.6)-(4.6.32) участвуют величины, относящиеся к боковым граням, отмеченные двойными индексом i,j ребра ячейки:  или .

          Зная значения газодинамических величин в ячейках по обе стороны ребра i,j на момент t₀ , можно рассчитать плоский распад разрыва (см. в [19], §7, §13). Для расчета распада разрыва скорости u,v в соседних ячейках переразлагаются на нормальную и касательную составляющие к ребру.

          Для учета действия гравитации и центробежной силы к нормальной составляющей скорости в каждой из ячеек делается добавка , где 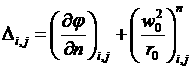 - сумма нормальных к ребру составляющих соответствующих сил (о вычислении  см. ниже).

          Сравнивая скорости разрывов, полученных в расчете распада, и скорость  (или ) отбираем значения (r,p,e)_i,j и (mⁿ,n^t)_i,j для ребра x=const либо (nⁿ,m^t)_i,j для ребра h=const. Полученные величины считаются постоянными на временном интервале (t₀,t₀+t).

          Скорость  ребра i,j вычисляется по разности координат Dx, Dr середины ребра (i,j) соответственно на верхнем (время t=t₀+t) и нижнем (время t=t₀) основаниях счетного шестигранника с использованием формул (4.5.6)-(4.5.8).

          Потенциал j_i,j на боковой грани вычисляется по значениям j₀ в ячейках нижнего основания по обе стороны ребра i,j линейной интерполяцией по расстояниям от центров ячеек до середины ребра i,j.

4.8. Расчет гравитационного потенциала.

          Заметим, что гравитационный потенциал обсчитываемого объекта может складываться из двух частей: . Первое слагаемое обусловлено гравитационным полем, создаваемым внешним источником. Второе слагаемое связано с собственным гравитационным полем обсчитываемого  тела. В этом случае потенциал  удовлетворяет уравнению Пуассона (4.4.3).

4.8.1. Разностный метод расчета гравитационного потенциала.

     Дискретизацию уравнения  (4.4.3) проводим согласованно с дискретизацией уравнений газовой динамики. Переходя к интегральной записи этого уравнения для каждой ячейки S_k,m, верхнего основания счетного шестигранника, ограниченной контуром w, получаем

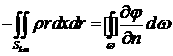                                   ,                                                       (4.8.1)

где  n - внешняя нормаль к w. Для  вычисления двойного интеграла, входящего в соотношение (4.8.1), воспользуемся согласованной с  основными газодинамическими уравнениями  аппроксимацией:

                                     ,

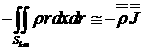где  - объем ячейки S_km на слое t₀+t (см. (4.6.2)). Контурный интеграл 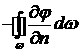 разбиваем на сумму четырех интегралов по числу ребер ячейки: D=D₁₂+D₄₃+D₁₄+D₂₃ и будем аппроксимировать каждый из них отдельно.

     Для аппроксимации криволинейного интеграла

                                                                                                      (4.8.2)

где  - одно из ребер ячейки, воспользуемся методом, являющимся  вариантом  известного интегроинтерполяционного метода. Метод основан на локальном полиномиальном приближении функции j по ее значениям на некоторой совокупности узлов, близких к ребру , с последующим дифференцированием приближающего многочлена и подстановкой нормальной производной в интеграл.

        Свяжем с каждым ребром  регулярный 12-точечный шаблон расчетной сетки, его узлы l=1,…,L₀, L₀=12, j_l - значения функции j в узлах шаблона. Введем специальную локальную криволинейную систему координат (q,s), связанную с ребром.

     Функцию j(q,s) аппроксимируем  в окрестности ребра  многочленом

                                                                               (4.8.3)

 по базисной полиномиальной  системе функций {y_i(q,s), i=1,2,…,i₀}, здесь i₀ - число базисных функций (3, 6 или 12).

     Коэффициенты c_i в (4.8.3) находим из условия наилучшего среднеквадратичного приближения на 12-точечном шаблоне:

                                                                      (4.8.4)

Здесь d_l³0 - весовые множители, они выбираются по некоторым достаточно простым эмпирическим правилам в зависимости от расположения узлов в данном шаблоне.

     Подставляя многочлен (4.8.3) в условие наилучшего приближения и приравнивая нулю производные по коэффициентам с_i, получаем для них систему линейных уравнений с некоторой матрицей A и правой частью f, зависящей от {j_l}.  Вычисляя матрицу A^-1 , обратную к A, получаем для  j(t,q,s) локальное приближение в виде

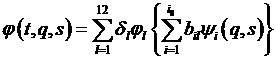                                                            (4.8.5)

где

                                         .

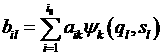     В результате интеграл (4.8.2) для ребра  записывается в виде линейной комбинации значений j_l сеточной функции j в узлах шаблона

                                                                                              (4.8.6)

     Для каждой ячейки (k,m) после суммирования четырех криволинейных интегралов получаем дискретное уравнение

                                                                                                        (4.8.7)

где G_km={(x_l,y_l), l=1,…,21} получен объединением шаблонов четырех ребер ячейки (k,m); здесь l - номер узла шаблона G_km,  - коэффициенты разност-ного уравнения (некоторые разностные коэффициенты  могут быть близки к нулю или нулевые), а сумма берется по всем узлам объединенного шаблона.

Задача свелась к нахождению решения j  разностного уравнения (4.8.7) на момент времени t₀+at, 0.5 £ a £ 1, при известной плотности на слое t₀+t.

     Алгоритм нахождения решения j уравнения (4.8.7) осуществляется за конечное число N явных чебышевских итераций. Пусть n - номер итерации, j⁽ⁿ⁾ - итерационное приближение, a_n - итерационные параметры. Алгоритм схемы ЛИ-М применительно к (4.8.7) имеет вид

              ,

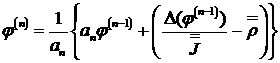n=1,2,..,N. Здесь D(j^(n-1)) - поток через границу ячейки, вычисляемый по значениям    j^(n-1) с помощью формул вида (4.8.6). За начальное приближение  принимается значение j на момент времени t₀. Каждая итерация выполняется одновременно для всех точек расчетной области.

     Результат итераций: . Число итераций и параметры a_n находим по формулам

              ,                   ,

где b_n - корни многочлена Чебышева 1-го рода F_q степени q, наименее уклоняющегося от нуля на отрезке [r_min,r_max], с условием нормировки F_q(0)=1.

     Число r_max - оценку сверху максимального собственного значения разностного аналога оператора Лапласа находим по значениям D-коэффициентов с помощью теоремы Гершгорина:

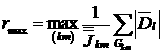
В качестве оценки минимального собственного значения берем r_min=r_max/M, где M - число ячеек в расчетной области. Данный алгоритм можно использовать для решения нестационарного уравнения.

          Решение разностного уравнения (4.8.7) – получение  по известной плотности  завершает расчет шага. Полученные из окончательных значений потока  величины  (см. (4.8.2)) будут использоваться при расчете распада разрыва на следующем счетном шаге.

4.9. Численные расчеты с использованием 2D программного комплекса.

При численном моделировании эволюции протопланетного диска Солнца рассматривается система Солнце-протопланетный диск на той стадии ее эволюции, когда имеет место осевая симметрия. Для рассмотрения данной задачи используется цилиндрическая система координат, начало координат которой помещается в центр Солнца. Гравитационный потенциал системы может быть записан как:

                                ,                                                         (4.9.1)

где потенциал Солнца (j_s) представляется в цилиндрической системе координат в виде:

                                          ,                                              (4.9.2)

где M_s - масса Солнца; G – гравитационная постоянная; φ_d – гравитационный потенциал протопланетного диска.

На первом этапе не будет учитываться излучение, и тогда полностью применим метод расчета, описанный в подразделах 4.1 – 4.8.

4.9.1. Результаты численных расчетов стационарных состояний

протопланетного диска в приближении Роша.

В приближении Роша собственное гравитационное поле протопланетного диска мало по сравнению с гравитационным полем Солнца. Поэтому гравитационный потенциал имеет вид:

                        .                                                             (4.9.3)

Предлагаемый численный метод позволяет проводить расчеты стационарных состояний протопланетного диска, полученных аналитически (раздел 3).

В качестве примера приведем расчет тороидального протопланетного кольца. Для расчета стационарного состояния данного типа кольца, использовались следующие начальные данные. Начальное распределение плотности кольца описывается уравнением:

      .          (4.9.4)

Начальная угловая скорость вращения представлена выражением:

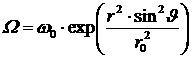                             ,                                               (4.9.5)

где      M_p = Ms = 1,989×10³³ г;            K = 2,4761304847×10¹⁶ .

Определим остальные константы в соотношениях (4.9.4), (4.9.5). В соответствии с данными подраздела 2.1 полагаем γ = 1,43. Константа r_max = 4,52·10¹⁴ см, что примерно соответствует расстоянию до планеты Нептун. Радиус внутренней границы протопланетного кольца примем равным  расстоянию до планеты Меркурий: r_in = 0,449·10¹³ см. Константы ω₀ и r₀ определим из условия равенства соотношения (4.9.5) кеплеровскому закону вращения соответственно в точках r_in и r_max. Тогда ω₀=2×10^-6 1/с, r₀=1,5×10¹⁴ см.

Граничное условие задается в соответствии с равновесным, стационарным состоянием кольца, находящегося в вакууме.

Все результаты приведены в безразмерном виде в соответствии с подразделом 4.4. Приняты следующие константы для приведения уравнений к безразмерному виду: m₀=1,989×10³³ г; r₀ = 4,52×10¹⁴ см; f = 6,67×10^-8 см³/(г×сек²).

Расчетная область и сетка в ней приведены на рис. 4.9.1. На этом и последующих рисунках ось z представляет собой ось вращения, r – цилиндрический радиус.

Для построения расчетной сетки участок границы кольца вдоль оси r разбит на три отрезка точками A(r=0.95), B(r=0.885). Тогда дугу - границу кольца будем считать верхней границей топологического четырехугольника, средний отрезок AB оси r – нижней границей, а два других отрезка вдоль оси  r – левой и правой границами соответственно. Сетку образуют криволинейные лучи, соединяющие точки нижней и верхней границ, и дуги, соединяющие точки левой и правой границ.

Фрагмент сетки вблизи оси  r в увеличенном масштабе приведен на рис. 4.9.2. Верхняя и нижняя границы разделены на 150 счетных интервалов, левая и правая границы – на 100 интервалов.

Начальные распределения плотности, удельной внутренней энергии и линейной скорости вращения среды кольца представлены  изолиниями соответственно на рис. 4.9.3, 4.9.4 и 4.9.5.

Как видно из рис. 4.9.3 - 4.9.5, конфигурация кольца в этой модели резко отличается от обычно рассматриваемых протопланетных дисков, для которых характерна малая толщина диска по сравнению с радиальными размерами, а последние перекрывают размеры солнечной планетной системы. В рассматриваемом же случае радиальный размер составляет по порядку величины расстояние между Нептуном и его ближайшей планетой – Ураном.

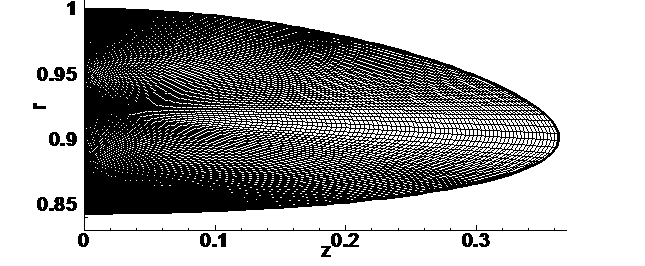
Рис. 4.9.1 Расчетная сетка.

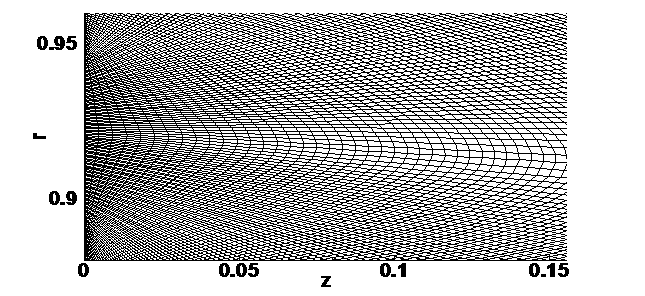
Рис. 4.9.2. Фрагмент расчетной сетки.

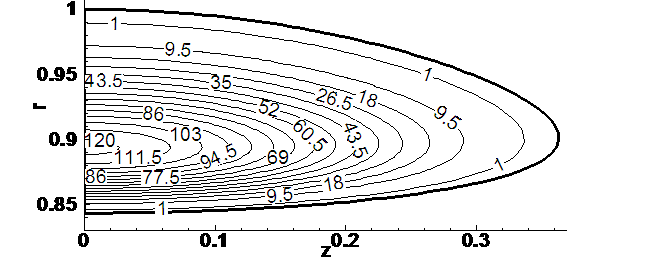Рис. 4.9.3. Начальное распределение плотности.

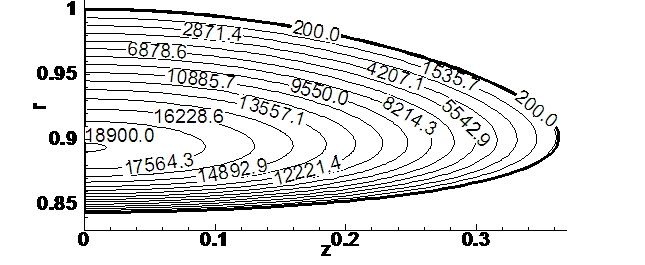
Рис. 4.9.4. Начальное распределение удельной внутренней энергии.

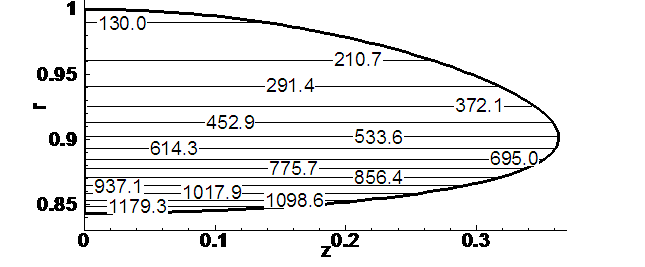
Рис. 4.9.5.  Начальное распределение линейной скорости вращения.

Полученное аналитическое решение, как и решения протопланетных колец (подраздел 3.4), описывает только одну зону протопланетного диска. В данном случае – это зона планеты Нептун, которая задается характерным для него расстоянием  r_max.

Расчеты проводились до времени 0.00146. На рис. 4.9.6 – 4.9.8 показаны соответственно распределения плотности, удельной внутренней энергии и линейной скорости вращения на последний расчетный момент времени.

Сравнительный анализ рис. 4.9.3-4.9.5 и рис. 4.9.6-4.9.8 показывает, что на временах 0.00146 распределения плотности, удельной внутренней энергии и линейной скорости вращения в наиболее значимой области диска, где достига-ется наибольшая плотность (центральная область диска),  изменяются не более, чем на 5% - 10%.

Распределения плотности вдоль оси r на начальный и конечный расчетные моменты времени приведены на рис. 4.9.9. Из этих графиков отчетливо видно, что изменение плотности на расчетных временах, действительно, незначительно.

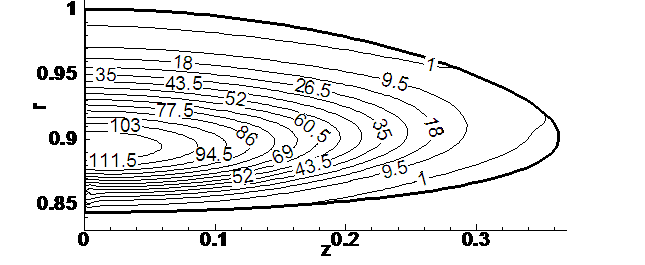
Рис. 4.9.6. Распределение плотности на момент времени t = 0,00146.

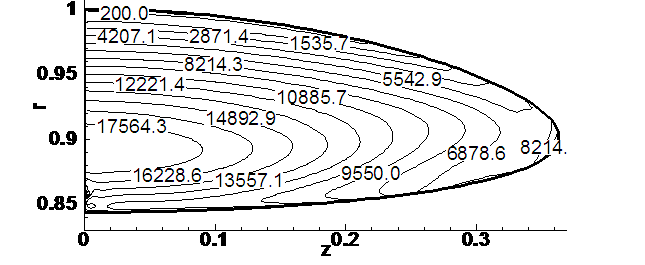
Рис. 4.9.7. Распределение удельной внутренней энергии

на момент времени t = 0,00146.

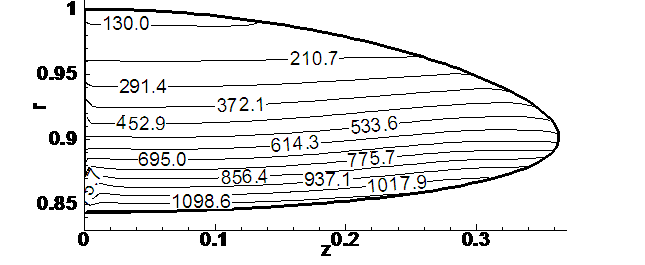
Рис. 4.9.8. Распределение линейной скорости вращения

на момент времени  t = 0,00146.

Рис. 4.9.9. Распределение плотности вдоль оси r.

—— t = 0 – – – t = 0.00146

                                     

4.9.2. Результаты численного расчета нестационарного

        протопланетного кольца в приближении Роша.

Для сравнения со стационарным состоянием были проведены расчеты для протопланетного кольца, распределение плотности которого отличалось от стационарного состояния. С этой целью было взято кольцо, размеры и форма которого совпадали со стационарным диском, а распределение плотности  изменялось по линейному закону от центральной линии тела кольца к его границе. Массы дисков и их начальные угловые скорости в обоих случаях были одинаковы.

На рис. 4.9.10, 4.9.11, 4.9.12 показаны распределения плотности, удельной внутренней энергии и линейной скорости вращения на начальный момент времени, а на рис. 4.9.13, 4.9.14, 4.9.15 – на последний момент расчета t = 0,0005. Сравнительный анализ рис. 4.9.10, 4.9.11, 4.9.12 и рис. 4.9.13, 4.9.14, 4.9.15 показывает, что на временах 0.0005 распределения плотности, удельной внутренней энергии и линейной скорости вращения изменяются значительно во всей области кольца.

Распределения плотности вдоль оси r на начальный и конечный расчетные моменты времени приведены на рис. 4.9.16.

Из этого рисунка отчетливо видно, что плотность на расчетный момент времени даже в центральной части кольца изменилась примерно на 40%. Более детальный анализ эволюции кольца в данной задаче показывает, что начальное неравновесное состояние кольца стремится к равновесному состоянию (рис. 4.9.3, 4.9.4 и 4.9.5), а распределение плотности по координате r – к своему равновесному распределению (рис. 4.9.9). Так как на данном этапе разработки численной модели не учитываются диссипативные эффекты при движении среды, то при движении конфигурации кольца к равновесной конфигурации  происходит колебательный процесс около равновесного состояния кольца.

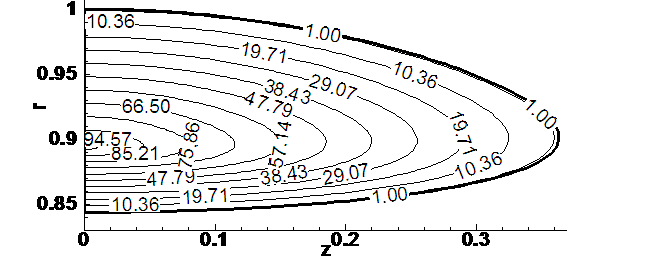
Рис. 4.9.10. Начальное распределение плотности.

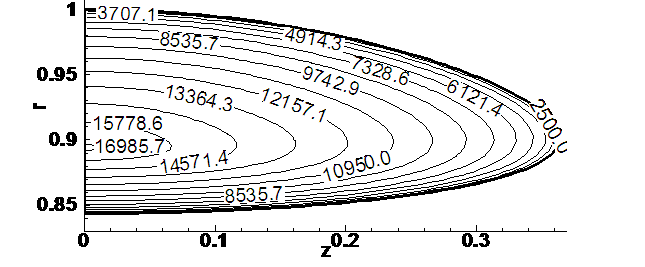
Рис. 4.9.11. Начальное распределение удельной внутренней энергии.

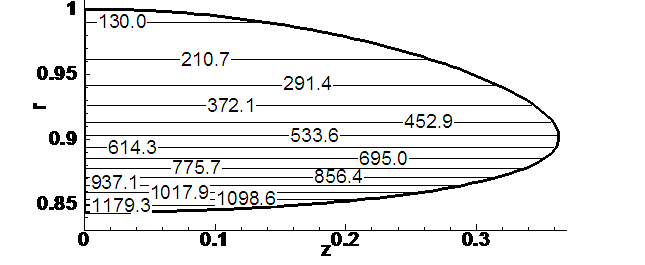
Рис. 4.9.12. Начальное распределение линейной скорости вращения.

Рис. 4.9.13. Распределение плотности на момент времени t = 0,0005.

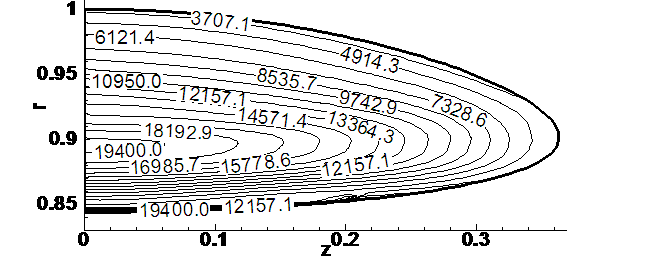
Рис. 4.9.14. Распределение удельной внутренней энергии

на момент времени t = 0,0005.

Рис. 4.9.15. Распределение линейной скорости вращения

на момент времени t = 0,0005.

—— t = 0 – – – t = 0.0005

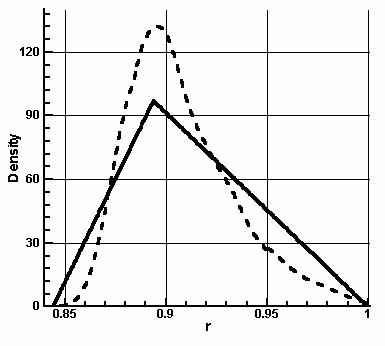
Рис. 4.9.16. Распределение плотности вдоль оси r.

Этот процесс в данной численной модели является затухающим, что на наш взгляд обусловлено схемной вязкостью численного метода.

Время, за которое неравновесное протопланетное кольцо достигает своего состояния равновесия, составляет 0,0005. Максимальное время расчета стационарного протопланетного кольца равно 0,0015, что соответствует 20 годам.

4.9.3. Устойчивость протопланетного кольца.

В принципе численный метод расчета позволяет проследить зарождение и развитие неустойчивости в протопланетном кольце. Однако, эта задача также требует тщательной проверки на устойчивость используемого численного метода при решении данного типа задач. В расчетах стационарного протопланетного (тороидального) кольца на временах больших 0,0015 кольцо постепенно начинает размываться.

Для того чтобы понять причину этого явления, была выполнена оценка устойчивости аналитического решения тороидального кольца, которое заложено в качестве начальных данных при численных расчетах. С этой целью было проверено выполнение критерия Хейланда для закона вращения вида , где ,  - постоянные параметры. Очевидно, что знаки производных  и  совпадают ( j - удельный момент количества движения кольца). Тогда получаем условие

,

которое справедливо в том и только  том случае, когда выполняется неравенство  (при любых значениях  и ). Следовательно, модель диска с параметрами  и  при  будет неустойчива по отношению к осесимметричным возмущениям. Критерий Хейланда не дает возможности оценить время, на протяжении которого развивается неустойчивость, т.е. проследить динамику неустой-чивости. Полученная оценка не исключает возможности неустойчивости используемой численной схемы при решении данной задачи. В данной работе приведена одна из наиболее сложных для численного расчета задач. Трудности расчета связаны с тем, что наблюдается высокий градиент параметров среды, особенно при подходе к внутренней границе кольца. Для того, чтобы строго доказать, насколько устойчива используемая численная схема при решении данного типа задач, необходимы дополнительные исследо-вания. На данном этапе исследований можно утверждать, что протопланетное тороидальное кольцо, параметры которого приведены в этой работе и получены из аналитического решения, устойчиво на протяжении промежутка времени, равного примерно 0.0015, что соответствует 20 годам реального времени.

5.     Анализ результатов исследований.

Используемая аналитическая модель позволила в приближенной постанов-ке (приближение Роша) получить замкнутое решение стационарного состоя-ния протопланетного диска и проследить за распределением всех его харак-теристик: плотности, давления, линейной скорости вращения и температуры.

Как видно из результатов расчетов раздела 3, конфигурация протопланетно-го диска весьма чувствительна к зависимости угловой скорости вращения от цилиндрического радиуса (r). Следует отметить, что задавая массу диска (кольца) и функциональную зависимость Ω(r) могут быть получены как «плос-кие» протопланетные диски, так и тороидальные протопланетные кольца.

В рамках используемого приближения «плоские» протопланетные диски могут быть получены при законе вращения протопланетного диска, близкого к кеплеровскому. Строго кеплеровский закон приводит формально к протопла-нетному диску с бесконечным радиусом. Интересной особенностью диска с вращением, близким к кеплеровскому, является концентрация газа вблизи внутреннего радиуса. При таком распределении газовой среды пылевая компонента при ее движении к экваториальной плоскости одновременно будет смещаться к внутреннему радиусу диска.

В рассматриваемом приближении тороидальные кольца соответствуют независимым решениям, так как собственное гравитационное поле протопла-нетного диска не принимается в расчет. В этом случае протопланетный диск может быть построен из протопланетных (тороидальных) колец, которые соответствуют зонам планет солнечной системы (подраздел 3.4). Обращает на себя внимание тот факт, что планетные кольца земной группы не могут быть построены, если их масса соответствует принятым концентрациям пылевой и газовой компонент протопланетного диска на начальной стадии его эволюции. Одно из возможных объяснений этого факта заключается в том, что на момент образования планетных колец земной группы газовая компонента из этой зоны была частично вынесена солнечным ветром.

Безусловно, полученные аналитические решения доказывают только возможность реализации планетных колец. К сожалению, истинный путь эволюции протопланетного диска нам пока неизвестен. Однако, существуют и другие работы, например, [21, 22], в которых приводятся данные о возможности образования подобного типа колец в протопланетном диске.

Разработанная численная модель позволяет проводить расчеты в осесимметричной постановке как стационарных состояний протопланетного диска, так и его эволюцию. Результаты проведенных численных расчетов в части исследований стационарных решений согласуются с основными результатами аналитических расчетов.

Детальное рассмотрение вопросов устойчивости протопланетного диска Солнца и протопланетных колец не входило в число основных задач на данном этапе исследований. Это, в частности, объясняется тем, что сама природа поставила грандиозный эксперимент - образование солнечной системы, из которого непосредственно следует, что протопланетный диск Солнца, а также протопланетные кольца, если они образуются, неустойчивы. Неустойчивости диска могут иметь различную природу. В данной работе оценивалась только газодинамическая неустойчивость. Следует обратить внимание, что хотя некоторые конфигурации дисков и колец по проведенным оценкам являются устойчивыми, это не значит, что в трехмерной постановке эти конфигурации будут также устойчивы.

5.1.         Модель образования планетной системы Солнца.

В результате проведенных исследований (в том числе и не вошедших в материалы данной публикации) в рамках принятых основных представлений образования Солнечной системы предложена модель образования планетных тел, основные положения которой сводятся к следующим:

1.       При коллапсе протосолнечной туманности образуется протопланетный диск Солнца. На начальной стадии эволюции диска, пока процессы концентрации его пылевой компоненты не привели к существенному изменению среды диска, состояние его газопылевой среды можно описывать уравнением состояния идеального газа.

2.       В период окончания аккреционных процессов и перехода протопланетного

диска в стадию формирования планетных тел в нем образуются крупномасштабные неоднородности в виде протопланетных колец, которые соответствуют зонам планет солнечной системы.

3.       За счет возникновения неустойчивости происходит фрагментация протопланетных колец. В результате этого процесса они распадаются, в общем случае, на несколько газопылевых сгущений.

4.        В процессе гравитационного взаимодействия эти сгущения сближаются, сталкиваются и образуют протопланетное облако или протопланетную систему планета и ее спутники. Эта стадия, по нашему мнению, хорошо описывается капельной моделью Энеева-Козлова.

5.       Процесс образования планетного тела происходит внутри протопланетного облака путем передвижения пылевой компоненты под действием гравитационного поля облака в центральную его часть, где и формируется тело планеты.

6.       Газовая составляющая протопланетных облаков земной группы выносится из них солнечным ветром, когда Солнце находится на стадии Т Тельца. Разрушение газовых оболочек, возможно, связано также с эффектом приливного воздействия Солнца.

7.       В процессе образования планетной солнечной системы часть газопылевого вещества протопланетного диска оказывается вне облаков протопланет и их спутников. В этих сгущениях также происходит концентрация вещества и образование твердых тел. Следует подчеркнуть, что основная масса пылевой компоненты находится в протопланетных облаках планет и их спутников. После того, как произошло образование планетных тел  и твердых тел в сгущениях происходит заключительная стадия формирования планетных тел – твердотельная аккумуляция, которая идет по законам, подробно исследованным Шмидтом О. Ю., Сафроновым В. С. и его учениками.

В настоящее время, по-видимому, общепринятой теорией образования планетной системы Солнца считается модель Шмидта-Сафронова (твердо-тельная аккумуляция). Наиболее труднообъяснимым и до конца не решенным моментом в этой теории является проблема роста размеров частиц пыли и превращение их в твердые тела таких размеров, при которых их дальнейший рост происходит путем гравитационного притяжения других частиц и тел. В рамках предлагаемой модели этой проблемы не возникает, так как формирова-ние планетных тел происходит внутри протопланетного облака под воздейст-вием его гравитационного поля. Другой отличительной чертой предлагаемой модели является то, что классическая твердотельная аккумуляция имеет место на заключительной стадии формирования планетной системы,  и за счет этого процесса происходит незначительный прирост массы планетных тел.

Модель Энеева-Козлова образования планетной солнечной системы является альтернативной моделью по отношению к модели Шмидта-Сафронова. Отличие предлагаемой модели от модели Энеева-Козлова заключается в том, что протопланетные облака образуются не за счет слияния небольших газопылевых сгущений, образовавшихся в результате неустойчивости газопылевой среды протопланетного облака, а за счет фрагментации крупномасштабных неустойчивых образований в виде тороидальных протопланетных колец.

В рамках предлагаемой модели естественным образом может быть объяснено происхождение спутников планет. Основным положением при этом является то, что планеты и их спутники произошли из одного протопланетного кольца. Конкретный сценарий образования спутниковой системы может быть предложен в результате анализа экспериментальных фактов по данной системе -  планета и ее спутники. Например, образование Луны в предлагаемой модели может произойти двумя основными путями. В одном случае на последнем этапе фрагментации протопланетного кольца образуются два протопланетных тела - протоземля и протолуна, находящиеся на близких орбитах. На заключительном этапе образования протосистемы Земля – Луна протоземля захватывает протолуну. В другом случае единое протопланетное облако, образовавшееся из протопланетного кольца, распадается  на две части в резу-льтате его неустойчивости. Привлечение дополнительных экспериментальных фактов, например, таких как - Луна обеднена летучими элементами и другие, может дать возможность выбрать путь, по которому шло  в действительности образование Земли и ее спутника Луны. Как видно, эти сценарии отличаются от столкновительной (giant-impact) модели, выдвинутой американскими учеными (Melosh and Sonet, 1986), по которой Луна образовалась в результате столкновения с Землей космического тела планетарных размеров.

Заключение

Основные результаты работы сводятся к следующим:

1. Получено аналитическое решение в приближении Роша для осесимметричной структуры стационарного протопланетного диска Солнца. Газопылевая среда диска описывается уравнением состояния идеального газа, что соответствует начальной стадии эволюции протопланетного диска. Излучение не учитывается. Показано, что в этой модели конфигурация диска существенным образом зависит от распределения угловой скорости вращения среды диска по цилиндрическому радиусу. При угловой скорости вращения, близкой к кеплеровскому закону, могут быть получены плоские протопланетные диски. Построена модель протопланетных (тороидальных) колец, из которых может состоять протопланетный диск Солнца на одном из начальных этапов своей эволюции. В этом случае кольца соответствуют зонам планет солнечной системы. Исследованы свойства полученных аналитических решений: конфигурации протопланетных дисков, распределения плотности, удельной внутренней энергии и линейной скорости вращения.

2.                 Разработана численная модель протопланетного диска, в основе которой лежит метод численного решения двумерных газодинамических  течений в областях сложной формы с подвижными границами, разработанный Годуновым С.К. и Забродиным А.В. с соавторами. Для сравнения численного моделирования с аналитическим решением были выполнены численные расчеты стационарных состояний протопланетных колец. В качестве начальных данных в этих расчетах были использованы аналитические решения в приближении Роша. Проведен расчет эволюции нестационарного кольца с выходом его в состояние, близкое к стационарному.

3. Предложена модель образования планетной солнечной системы.

Литература

1.    Гринберг М. Межзвездная пыль. М.: Мир, 1979.

2.    Происхождение солнечной системы. //Сборник статей под редакцией Г.Ривса. М.: Мир, 1976.

3.    Макалкин А. Б., Дорофеева В. А. Строение протопланетного аккреционного диска вокруг Солнца на стадии Т Тельца.//Астрономический вестник. Исследования Солнечной системы. 1995. Т.29, № 2. С.99.

4.    Галимов Э.М. Проблема происхождения Луны. //Cб. «Основные направления геохимии», отв. ред. Э.М.Галимов,  М.: Наука, 1995.

5.    Larson R.B. The evolution of spherical protostars with masses 0,25 M_c to M_c. //Mon. Not. Roy. Astron. Soc. 157, 121, (1972).

6.    Larson R.B. The collaps of rotating cloud. //Mon. Not. Roy. Astron. Soc. 156, 437, (1972).

7.    Макалкин А. Б., Дорофеева В. А. Строение протопланетного аккреционного диска вокруг Солнца на стадии Т Тельца. //Астрономический вестник. Исследования Солнечной системы. 1996. Т. 30, № 6. C. 496.

8.    Энеев Т. М., Козлов Н. Н.. Модель аккумуляционного процесса формирова-ния планетных систем. //Астроном. вест. 1981. Т. XV, № 3. С.131-140.

9.    Сафронов В. С. Эволюция допланетного облака и образование Земли и планет. М.: Наука, 1969.

10. Энеев Т. М., Козлов Н. Н.. Модель аккумуляционного процесса формирова-ния планетных систем.//Астроном. вест. 1981. Т. XV, № 2. С. 80-94.

11. Энеев Т. М. Кольцевое сжатие вещества в капельной модели прото-планетного облака. //Астрономический вестник.1993.Т. XXVII,№5. С. 3-25.

12. Имшенник В.С., Мануковский К.В. Двумерная гидростатически равновесная атмосфера нейтронной звезды с заданным дифференциальным вращением .//Письма в Астрон. Журн. 2000. 26, 917.

13. Имшенник В.С., Мануковский К.В.  Гидродинамическая модель асимметричного взрыва коллапсирующих сверхновых с быстрым вращением и в присутствии тороидальной атмосферы.//Письма в Астрон. Журн. 2004. 30, 803.

14. Метод 2D численного расчета газодинамических потоков в подвижных сетках. ИПМ им.М.В.Келдыша РАН, М. 1989.

15. Механизм аккумуляции планетарных тел. Итог. отчет по программе фундамент. исследований № 25, подпрограмма № 1, п. 1.1.2, М., 2004.

16. Мануковский К.В. Гидродинамические процессы в тороидальной атмосфере вращающегося коллапсара.: дис. к. ф.-м. н.//М. 2005.

17. Витязев А.В., Печерникова Г.В., Сафронов В.С. Планеты земной группы: Происхождение и ранняя эволюция. М.: Наука, 1990.

18. Имшенник В.С., Надежин Д.К. Сверхновая 1987А и образование вращающихся нейтронных звезд.// Письма в Астрон. Журн. 1992. 18, 95.

19. Годунов С.К., Забродин А.В., Иванов М.Я., Крайко А.М., Прокопов Г.П. Численное решение многомерных задач газовой динамики. М.: Наука,1976.

20. Тассуль Ж.-Л. (Tassoul J.-L.) Теория вращающихся звезд. М.: Мир, 1982.

21. Снытников В.Н., Пармон В.Н., Вшивков В.А., Дудникова Г.И., Никитин С.А., Снытников А.В. Численное моделирование гравитационных систем многих тел с газом. //Вычислительные технологии. 2002. Т. 7, № 3. С.72.

22. Snytnikov V.N., Dudnikova G.I., Gleaves J.T., Nikitin S.A., Parmon V.N., Stoyanovsky V.O., Vshivkov V.A., Yablonsky G.S., Zakharenko V.S. Space chemical reactor of protoplanetary disk. //Adv. Space Res. Vol. 30, No. 6, pp. 1461- 1467, 2002.