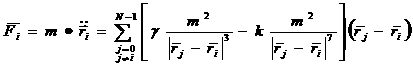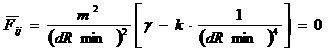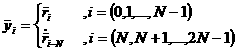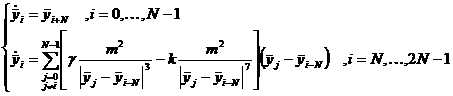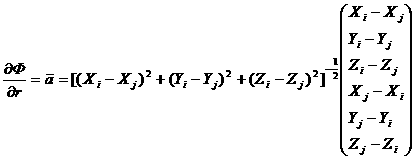Аннотация
В работе формулируется новая гипотеза о возможных механизмах образования естественных
спутниковых систем. Рассматриваются также вопросы подтверждения этой гипотезы при помощи
моделирования на ЭВМ эволюции системы большого числа взаимодействующих тел. Помимо проверки
гипотезы эти вопросы также также тесно связаны такими актуальными проблемами планетной
космогонии, как гравитационное коллапсирование протопланет.
Abstract
In work the new hypothesis about possible mechanisms of formation of natural satellite
systems is formulated. The questions of confirmation of this hypothesis are considered
also through computer simulation of evolution of system of the large number of cooperating
particles. Besides check of a hypothesis these questions also also are closely connected
with such problems of planet cosmogony as gravitational collapse of protoplanets.
Содержание
Введение........................................................................................................ 4
1. Гипотеза о механизмах образования естественных
спутниковых систем.... 7
2. О вычислительной проверке гипотезы.................................................... 7
3. Математическая модель протопланеты................................................... 8
4. Структура программного комплекса.................................................... 11
5. Пробные вычислительные эксперименты.............................................. 17
Заключение.................................................................................................. 19
Литература.................................................................................................. 20
Настоящая работа в основном посвящена моделированию при помощи
ЭВМ эволюции системы большого числа взаимодействующих тел. С другой стороны,
содержанием работы является попытка решения задачи коллапса в одной из ее
постановок.
Наиболее часто задача
коллапса встречается среди астрофизических проблем. Явления коллапса весьма
распространены в этой области. Они встречаются и на начальной стадии
звездообразования, и на конечных стадиях, во время взрывов сверхновых, когда
наблюдается коллапсирование ядра.
В ряде работ, посвященных
коллапсированию протозвездных облаков [13] [14], проводился поиск ответа, каким
будет распределение плотности в экваториальной плоскости облака после
коллапсирования. Четкого ответа так и небыло получено. Решением получался либо
тор, либо диск, в зависимости от типа выбранной разностной схемы.
На конечных стадиях
звездообразования задача коллапса приобретает несколько иной вид – это
астрофизическая задача релятивистского гравитационного коллапса.
Рассматривается взрыв сверхновой с коллапсирующим ядром. В такой постановке
изучается быстрое сжатие космического тела в условиях, когда оно уже достигло
такой плотности, что гравитационный потенциал у поверхности савним по величине
с квадратом скорости света. В таких уловиях для описания явлений необходимо
привлечение общей теории относительности. Эта проблема до конца так и не
решена.
Возникновение предложенной
ниже работы связано с необходимостью решения задачи коллапса в несколько иной
области. Речь идет о таких актуальных проблемах планетной космогонии, как
гравитационное коллапсирование протопланет и образование естественных
спутников. Понимание механизмов происхождения планет Солнечной системы и их
спутников – это фундаментальная проблема космофизики, которая может помочь
развитию представлений об устройстве поверхностных и внутренних слоев Земли,
что очень важно для современной геологии, геохимии, геофизики. Актуальность
этой работы особенно возрастает в настоящее время в связи с открытием более чем
200 планет вне солнечной системы [15].
Известно, что спутниковые
системы можно разбить на два условных класса. Это системы, состоящие из
некоторого количества относительно небольших спутников, такие как Марс, Юпитер,
в которых масса спутников мала по сравнению с массой планеты, и системы, в
которые входят спутники относительно большой массы, такие как Земля-Луна и
Нептун-Тритон. Выдвигаемая гипотеза предлагает к рассмотрению два различных
механизма происхождения этих систем. Также в работе предлагается методика реализации
на ЭВМ этих механизмов.
Приведем небольшую
историческую справку касательно возникновения представлений о формировании
планетных систем, приведшим к появлению гипотезы.
В первой половине ХХ века
О.Ю.Шмидтом была предпринята попытка выхода на новый качественный уровень
гипотез космогонии солнечной системы[1]. Он полагал, что космогоническая теория
происхождения Солнца и планет должна объяснить 4 основных закономерности:
- закономерности орбит (почти круговые, почти в одной плоскости,
вращение в одну сторону);
- закономерности планетных расстояний (по правилу Тициуса-Боде, выраженные
в астрономических единицах расстояния Меркурия, Венеры, Земли, Марса, средней
части кольца малых планет, Юпитера, Сатурна, Урана и Плутона от Солнца (Нептун
выпадает из этой зависимости) получаются следующим образом: к каждому числу
последовательности 0, 3, 6, 12, 24, 48, 96, 192, 384, образующей, начиная с 3,
геометрическую прогрессию, прибавляется число 4, а затем все числа делятся на
10; полученная новая последовательность чисел: 0,4; 0,7; 1,0; 1,6; 2,8; 5,2;
10,0; 19,6; 38,8 с точностью около 3% представляет расстояния от Солнца в
астрономических единицах перечисленных тел Солнечной системы);
- разделение планет на две группы (Земную и группу Юпитера,
существенно отличающиеся как по массам, так и по удаленности от Солнца);
- распределение момента количества движения (основная доля
кинетического момента Солнечной системы приходится на орбитальное вращение
планет (98%), в то время как масса планет составляет всего лишь 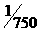 массы системы). массы системы).
О.Ю. Шмидт выдвинул
следующую гипотезу. К началу образования планет Солнце было уже сформировавшейся
звездой. Учавствуя в галактическом вращении, оно захватило часть метеоритной
твердой материи и газа. Первоначальный размер облака захваченной материи
превышал современный размер планетной системы, а его состав соответствовал
тому, который наблюдается в межзвёздных туманностях: 99% газа и 1% пылевых
частиц размерами от долей микрометра до сотен микрометров. Таким образом, около
Солнца образовался рой холодных частиц-планетоземалей, двигавшихся вокруг него
по эллиптическим орбитам. Шмидт полагал, что из этого облака, сталкиваясь,
дробясь и слипаясь, и образовались впоследствии планеты, кометы, метеоры и
метеориты.
С появлением ЭВМ начался
новый этап в развитии представлений о происхождении планет. Появилась
возможность рассчитать эволюцию больших скоплений частиц, и тем самым проверить
модель Шмидта.
В конце 70-х годов
Т.М.Энеевым и Н.Н.Козловым было проведено моделирование на ЭВМ аккумуляционного
процесса формирования планетных систем [2]. В ходе исследований возникли
поправки к гипотезе Шмидта, связанные с механизмом взаимодействия двух
сталкивающихся частиц. Стало понятно, что модель роста протопланет за счет
соударений твердых тел несостоятельна. Энергия удара при падении тела на
поверхность астероида обычно так велика, что разрушается не только само упавшее
тело, но и часть астероида. Поэтому говорить здесь об увеличении размеров не приходится.
В новой модели аккумуляции Т.М.Энеева этот процесс рассматривался близким к
слипанию капель жидкости. Для этой модели с помощью моделирования на ЭВМ была
показана неизбежность появления в протопланетном диске кольцевых зон разряжения
и уплотнения вещества. Дальнейшее развитие зон приводит к образованию протопланет – огромных шаровых
скоплений, движущихся по орбитам вокруг центрального тела. В частности, при
рассмотрении солнечной системы, были найдены параметры, при которых формируются
протопланеты земной группы, а также группы Юпитера, была показана
закономерность образования обратного вращения Венеры [3]. Эволюция любой
отдельно взятой протопланеты представляет собой гравитационный коллапс, в
результате которого и образуются планеты в привычном для нас виде. Исследование
коллапсирования протоземли представляет собой закономерное продолжение работ
Т.М.Энеева и Н.Н.Козлова и является интересной задачей прикладного
моделирования.
А.М.Кривцов провел
моделирование и рассчет на ЭВМ коллапса протоземли сначала в плоской, а потом и
пространственной постановке [4]. В этой работе использовался метод динамики
частиц [Кривцов и Кривцова, 2002], заключающийся в представлении исследуемого
тела ансамблем взаимодействующих частиц. Движение частиц описывается
уравнениями Ньютоновской динамики. Потенциал, помимо гравитационной составляющей,
содержит члены, моделирующие диссипацию энергии и соударения частиц. При этом
физичность такой замены расчета ударов и диссипации на штрафные функции
остается без пояснений. Особое внимание в работе А.М.Кривцова уделяется
скорости коллапса и правильности построения модели протоземли с геохимической
точки зрения. Следует также отметить, что в работе А.М.Кривцова проводилось
интегрирование уравнений динамики алгоритмом Барнса-Хата, который основан на
замене группы взаимодействующих частиц одной частицей.
В предложенной ниже модели
введенные взаимодействия между частицами имеют более строгую физическую
интерпретацию, чем в модели Кривцова. При интегрировании уравнений динамики
используется точный гравитационный потенциал, в отличие от алгоритма
Барнса-Хата. Диссипация энергии и соударения частиц обсчитываются
непосредственно, а не с помощью штрафных функций.
Образование естественных
спутников планет чаще всего рассматривается в рамках следующей модели. В
результате гравитационного сжатия протопланеты значительно возрастает угловая
скорость ее вращения. При этом может произойти отслоение пояса частиц.
Расслаиваясь на кольца и слипаясь, этот пояс может развиться в систему
спутников.
Есть основания полагать, что
относительно протоземли (и протолуны) такое представление ошибочно. На эту
мысль наталкивает тот факт, что соотношение масс Луны и Земли примерно 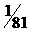 , в то время как для других планет и их спутников эта цифра
гораздо меньше. То есть, обычно спутники гораздо меньше своих планет, нежели
Луна меньше Земли. Аналогичная ситуация наблюдается и в случае системы
Нептун-Тритон. В связи с этим выдвигается предположение о недостаточности
отделяющегося в результате коллапса пояса для образования столь крупного
спутника, как Луна или Тритон. , в то время как для других планет и их спутников эта цифра
гораздо меньше. То есть, обычно спутники гораздо меньше своих планет, нежели
Луна меньше Земли. Аналогичная ситуация наблюдается и в случае системы
Нептун-Тритон. В связи с этим выдвигается предположение о недостаточности
отделяющегося в результате коллапса пояса для образования столь крупного
спутника, как Луна или Тритон.
В 2001г. Т.М.Энеев предложил
гипотезу, согласно которой из отслоившегося пояса частиц могут появиться только
маленькие спутники. А происхождение больших спутников следует объяснять другими
механизмами. Например, захватом небесного тела с близкой орбитой.
Интересной работой в этом
направлении явилась недавняя публикация Агнора и Гамильтона в журнале Nature[7].
Они провели серию экспериментов по моделированию захвата Нептуном своего
спутника Тритона из двойной системы. По их словам, вероятность удержания
спутника из двойной системы гораздо выше, чем захват одиночного тела. К тому
же, вблизи Нептуна имеется огромный резервуар небольших тел, в том числе и
двойных систем, - пояс Койпера. В ходе экспериментов Агнор и Гамильтон получили
соответствие вероятности удержания спутника из двойной системы в зависимости от
параметров орбиты системы, ее скорости, массы.
Мы предполагаем проверить
гипотезу Т.М.Энеева методами математического моделирования с использованием
современных многопроцессорных компьютерных систем, разработанных в ИПМ
им.Келдыша РАН под руководством А.В.Забродина.
Проверка гипотезы будет
проводиться в два этапа:
1. Разработка методики и
программного комплекса для исследования процессов коллапсирования протопланет.
2. Серия экспериментов по
проверке гипотезы.
В настоящей работе
описывается первый этап.
Задачей второго этапа будет
являться, во-первых, проверка реальности образования Луны из отделяющегося
пояса частиц при коллапсировании протоземли. Необходимо будет оценить массу
этого пояса и проверить состоятельность такого механизма происхождения Луны.
Также будет интересна аналогичная оценка для другого типа планет, планет с
маленькими спутниками. То есть проверка образования спутников у протомарса, протоюпитера.
В дальнейшем планируется исследовать на этом же программном комплексе
альтернативный сценарий происхождения крупного спутника, предложенный
Т.М.Энеевым, а именно, захват Землей прототела, послужившего основой Луны.
В качестве модели
протопланеты рассматривается шарообразное скопление большого числа
точек-частиц. Все частицы наделяются равными массами и объемами. Полагается,
что каждая частица по форме – это шар с заданным диаметром dRmin и массой m,
выбранными следующим образом:
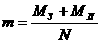 ,
(1) ,
(1)
где 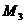 = 5,976е+24кг – масса Земли, = 5,976е+24кг – масса Земли,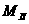 = 7,38е+22кг – масса Луны, N - количество частиц в модели. = 7,38е+22кг – масса Луны, N - количество частиц в модели.
Полагаем, что все частицы в
слипшемся в шар состоянии должны по объему равняться Земле. Для рассчета
диаметра частицы, Земной шар аппроксимируется
N кубиками:
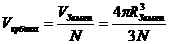
И в каждый кубик вписывается
по шарику-частице:
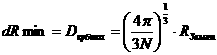 ,
(2) ,
(2)
где 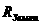 =6,371е+6м – радиус Земли, =6,371е+6м – радиус Земли,  - диаметр кубика. - диаметр кубика.
Частицы двигаются под действием взаимных
гравитационных и Ван-дер-Ваальсовых сил. Сила Ван-дер-Ваальса [6] вводится в
рассмотрение из-за схожести процессов в протопланетном веществе с процессами,
происходящими в реальных газах. Помимо этого, она позволяет ограничить процесс
«проникновения» друг в друга частиц под действием гравитационных сил и улучшает
устойчивость вычислительного процесса.
Начало инерциальной системы
координат поместим в центр масс протопланетного облака. Сила, действующая на
частицу i:
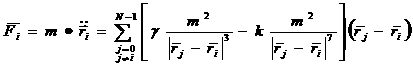 (3) (3)
где m –
масса частицы, 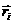 - радиус-вектор i-ой частицы, - радиус-вектор i-ой частицы, 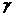 - гравитационная
постоянная, k – коэффициент Ван-дер-Ваальсовой силы. - гравитационная
постоянная, k – коэффициент Ван-дер-Ваальсовой силы.
Коэффициент k выбирается исходя из того
соображения, что суммарная сила гравитационного и ван-дер-ваальсовского взаимодействия
двух касающихся частиц должна равняться нулю:
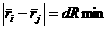 - условие касания двух частиц - условие касания двух частиц
тогда:
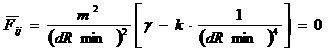 (4)
(4)
откуда:
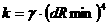 (5)
(5)
Это условие эквивалентно
наличию потенциальной ямы вблизи области касания частиц.
Для перехода от уравнений
вида (1) к уравнениям вида Коши введем новые переменные:
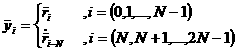 (6) (6)
Таким образом, для i от 0 до N-1 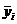 - радиус-вектора частиц, а для i от N до 2N-1 –
это скорости. С помощью новых переменных перепишем уравнения (1) в виде Коши: - радиус-вектора частиц, а для i от N до 2N-1 –
это скорости. С помощью новых переменных перепишем уравнения (1) в виде Коши:
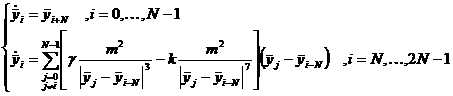 (7) (7)
Численное интегрирование
производится методом Рунге-Кутты второго порядка[7]:
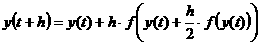 (8)
(8)
где 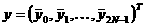 , t –
текущее время, h – шаг
времени, f(y) – правая
часть системы (5). , t –
текущее время, h – шаг
времени, f(y) – правая
часть системы (5).
В процессе интегрирования
при сближении двух частиц на расстояние, меньшее установленного радиуса dRmin, т.е. касании, происходит
диссипативное соударение с потерей энергии. Этот механизм моделирует рассеивание
энергии в газопылевом облаке за счет потерь тепла. При диссипативном
соударении, т.к. массы частиц равны, то нормаль к поверхности удара в кинетической
метрике будет совпадать с нормалью в обычной евклидовой метрике. Изменение
скоростей при ударе запишутся следующими соотношениями:
Условие столкновения частиц i и j:
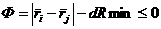 , ,
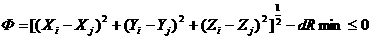  (9) (9)
Введем вектор градиента:
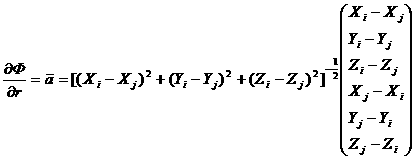 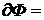 (10) (10)
Тогда нормаль к поверхности удара:
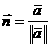 (11) (11)
Нормальная составляющая скорости до удара:
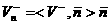 (12)
(12)
Касательная составляющая:
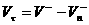 (13) (13)
В соответствии с моделью Ньютона для неупругого
соударения, при ударе касательная составляющая сохраняется, а нормальная
пропорционально изменяетсяменяется:
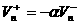 , , 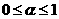 (14) (14)
Скорость после удара
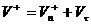 (15) (15)
В момент запуска численного
эксперимента необходимо задать начальные скорости и положения частиц. Начальные
координаты частиц выбираются случайным образом внутри сферы радиуса RCloud. Начальные
условия скоростей берутся исходя из современного состояния системы Луна-Земля.
Они распределяются таким образом, чтобы суммарный кинетический момент частиц
был равен кинетическому моменту Луны и Земли. Для этого все скопление
закручивается вокруг третьей координатной оси как единое тело.
Момент инерции облака:
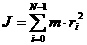 (16)
(16)
Тогда угловая скорость,
которую надо сообщить всему скоплению для задания начальных скоростей:
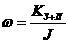 (17)
(17)
где 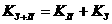 =3,54е+34 =3,54е+34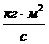 , , 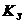 =7,07е+33 =7,07е+33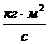 - кинетический момент вращения Земли вокруг своей оси, - кинетический момент вращения Земли вокруг своей оси, 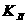 =2,9е+34 =2,9е+34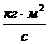 - кинетический момент орбитального вращения Луны вокруг
Земли. - кинетический момент орбитального вращения Луны вокруг
Земли.
Отсюда получаем скорость i-ой частицы:
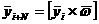 (18)
(18)
где 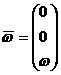 - вектор угловой
скорости. - вектор угловой
скорости.
Для удобства вычислительного
процесса проводится масштабирование величин. За единицу расстояния берется 1
радиус Земли (р.з.), за еденицу времени – 1 год (год), за единицу массы –
суммарная масса Земли и Луны (м.з.).
1 р.з. = 6,371е+6 м., 1 год
= 31,536,000 сек., 1 м.з. = 6,05е+24 кг.
С учетом масштабирования, в (1)-(17)
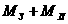 =1 м.з., =1 м.з., 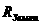 =1 р.з., γ =
1,55е+9 =1 р.з., γ =
1,55е+9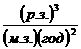 , ,
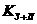 = 4.55e+3 = 4.55e+3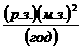
Для реализации данной модели
на ЭВМ разработан программный комплекс.
Прикладной программный
комплекс состоит из двух программ: программы-вычислителя и
программы-визуализатора. На вычислитель ложится вся нагрузка, связанная
непосредственно с процессом вычисления эволюции системы. Визуализатор позволяет
наглядно наблюдать за результатами, полученными вычислителем. Такое разделение
обусловлено большим временем счета эволюционного процесса. Для существенного
увеличения количества участвующих в эксперименте частиц был разработан вариант
вычислителя, предназначенный для работы на многопроцессорных ЭВМ.
Структура однопроцессорного вычислителя. В программе вычислителя
реализованы следующие механизмы:
·
Процедура распределения начальных скоростей и координат между
частицами.
·
Процедура вычисления следующих положений точек по формулам Рунге-Кутты
(6).
·
Процедура вычисления соударений частиц(15).
·
Коррекция центра масс и кинетического момента системы. Необходимость
этих процедур возникает из-за погрешностей вычислений, ведущих к тому, что
величины, которые должны оставаться постоянными, будут «плыть». Таким образом,
введя коррекцию, контролируется сохранение первого интеграла, что является необходимым
показателем для задачи численного интегрирования.
·
Механизм защиты от сбоев в работе программы.
Первые три процедуры
достаточно описаны в пункте, посвященном методике решения. Но механизмы
коррекции и защиты от сбоев относятся только к программной реализации и
нуждаются в пояснении.
Коррекция центра масс
заключается в вычислении текущего центра масс и совмещения его с началом
координат, где он находился изначально, путем сдвига всей системы. Коррекция
кинетического момента заключается в вычислении текущего момента, вычислении
разницы между известным начальным моментом и текущим, и закручивании всего
ансамбля частиц как единого целого для компенсации этой разницы.
Механизм защиты от сбоев
состоит в том, что вывод результатов работы программы происходит не в единый
файл, а в серию однотипных файлов. В начале эксперимента создается файл “output0000.ev”(структуру см. далее). Он
заполняется блоками данных и через FileEndFlag записей блоков завершается.
После этого создается файл “Flag1.txt” и в него записывается «0».
Это означает, что файл с таким номером, т.е. “output0000.ev”, является последним
неповрежденным файлом в серии. Создается файл “output0001.ev” и запись результатов идет
уже в него. После его заполнения и завершения в “Flag1.txt” записывается «1», и
начинается запись в “output0002.ev”. И так далее. Таким
образом, в любой момент времени в “Flag1.txt” содержится номер заведомо
удачно завершенного файла вывода. Поэтому, после сбоя в работе программы, для
продолжения счета достаточно, считав из “Flag1.txt” номер файла, открыть этот
файл, считать из него параметры эксперимента и последнее состояние системы.
Все эти процедуры и
механизмы удобно представить в виде блок-схемы вычислителя:
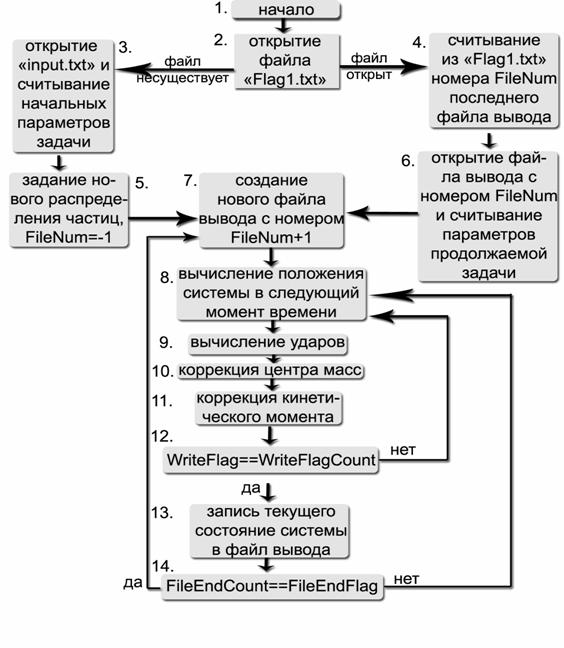
Поясним блок-схему
комментариями к пронумерованым частям.
1.
Начало.
2.
Попытка открыть файл ввода “Flag1.txt”.
3.
Файл не существует. Значит это первый запуск программы. Данные, необходимые для
начала счета, считываются из текстового файла ввода “input.txt”, в котором последовательно
расположены следующие величины:
NExp – номер эксперимента, после
каждого считывания из input.txt увеличивается на еденицу,
N – количество частиц,
WriteFlag – флаг, отражающий
количество шагов интегрирования между двумя записями в файл вывода,
GravConst – гравитационная
постоянная,
h – шаг времени,
tMax – время окончания счета,
dRmin – диаметр частицы,
K – кинетический момент
системы,
dKmax – отклонение кин. момента,
при котором уже надо делать его коррекцию,
RCloud – радиус протопланетного
облака,
alpha – коэффициент диссипации.
4. Файл
“Flag1.txt” существует. Значит это не
первый запуск программы. По всей видимости, ее работа была закончена аварийно.
Тогда файл “Flag1.txt” содержит номер FileNum последнего безаварийно заполненного файла вывода “outputNNNN.ev”(см. ниже).
5.
В соответствии со считанными из “input.txt” данными производится
вычисление:
m – массы отдельно взятой
частицы,
VVCoff – коэффициента Ван-дер-Ваальсовой силы ( k из (3)),
dRmin – диаметра частицы.
Происходит выделение памяти
под массив скоростей и координат и заполнение его начальными значениями (15)-(18).
Переменной FileNum присваивается значение -1.
6.
Например, если считанный FileNum=17, то открывается файл “output0017.ev”. Из него считывается
заголовок, блок [FileEndFlag] и блок скоростей. Таким
образом, мы получаем параметры эксперимента из заголовка и распределение
координат и скоростей из блоков. Помимо этого, необходимо рассчитать m и VVCoff. В таком случае мы обладаем
всем необходимым для продолжения прерванного эксперимента.
7. Записываем
в “Flag1.txt” номер FileNum – номер только что законченного
файла вывода, если он не равен -1. Увеличиваем FileNum на еденицу. Теперь это номер
нового текущего файла вывода. Создаем этот новый файл вывода “outputNNNN.ev” с номером FileNum.
Заполняем заголовок и блок[1]. При этом вместо dR пишем 0, а вместо dK пишем K, т.е. начальный
кинетический момент системы. Фактически, эта первая запись dR и dK является продолжением
заголовка.
8.-12. Основной цикл. WriteFlag введен из тех соображений,
что если записывать каждый шаг интегрирования, то файлы вывода будут занимать
слишком много дискового пространства ЭВМ. Поэтому включается счетчик шагов WriteFlagCount. Он
увеличивается на еденицу на каждой итерации цикла, и запись производится через
каждые WriteFlag итераций.
13.
Счетчик итераций WriteFlagCount сравнялся с WriteFlag, происходит запись в текущий
файл вывода очередного блока[FileEndCount]. WriteFlagCount обнуляется.
14. FileEndCount – счетчик
записей блоков в текущий файл вывода. FileEndFlag – константа. Когда счетчик
записей поровнялся с ней происходит запись в конец файла вывода блока
скоростей. Файл оказывается завершенным. FileEndCount обнуляется.
Структура многопроцессорного вычислителя в целом повторяет структуру
однопроцессорного. Выделяется процесс с номером ноль и наделяется руководящими
функциями. Этот процесс выполняет шаги 1.-7.
Основной цикл (шаги 8.-12.) уже
проходит с участием остальных процессов. Перед каждым шагом процесс номер ноль
сообщает всем остальным текущее состояние системы. Каждый из ведомых процессов
вычисляет свою часть попарных взаимодействий (в шагах 8,9) или характеристик системы (в шагах 10,11) и сообщает результаты процессу номер ноль, который на основании
полученных данных формирует новое состояние системы. Шаги 13 и 14 выполняет опять
же процесс номер ноль и они полностью идентичны однопроцессорному случаю.
Для хранения результатов
интегрирования разработан формат
файлов-контейнеров “outputNNNN.ev”. Они представляют собой
двоичные файлы вывода со следующей структурой:
|
|
Переменная
|
Тип
|
|
Заголовок
|
NExp
|
int
|
|
N
|
int
|
|
WriteFlag
|
int
|
|
GravConst
|
double
|
|
h
|
double
|
|
tMax
|
double
|
|
dRmin
|
double
|
|
dKmax
|
double
|
|
RCloud
|
double
|
|
alpha
|
double
|
|
Тело
|
блок
[1]
|
dR
|
double
|
|
dK
|
double
|
|
GlobalTime
|
double
|
|
Y[0]
|
double
|
|
Y[1]
|
double
|
|
...
|
...
|
|
Y[3*N-1]
|
double
|
|
…
|
…
|
…
|
|
блок [FileEndFlag]
|
dR
|
double
|
|
dK
|
double
|
|
GlobalTime
|
double
|
|
Y[0]
|
double
|
|
Y[1]
|
double
|
|
...
|
...
|
|
Y[3*N-1]
|
double
|
|
блок
скоростей
|
Y[3*N]
|
double
|
|
Y[3*N+1]
|
double
|
|
…
|
…
|
|
…
|
…
|
|
Y[6*N-1]
|
double
|
Структура файлов “outputNNNN.ev” также учитывает
реализованную в вычислителе систему защиты от сбоев в работе программы.
Структуру визуализатора приведем в виде блок-схемы:
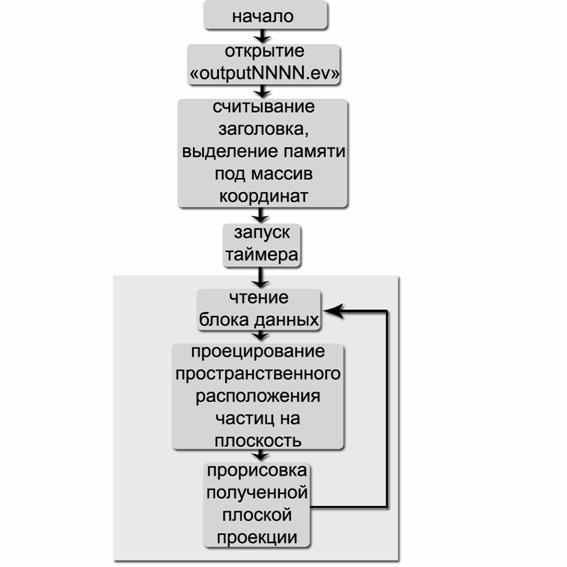
Программа-визуализатор
получает при запуске имя файла “outputNNNN.ev”, содержание которого
необходимо визуализировать на экране монитора. Из заголовка файла программа
узнает о количестве участвующих в эксперименте точек и выделяет память для
массивов, куда их координаты будут считываться. Остальные данные заголовка
просто будут отображаться на экране монитора при прорисовках расположения
точек.
Далее запускается таймер, и
на каждый его такт выполняется цикл:
·
Считывается блок данных из “outputNNNN.ev”.
·
Так как расположение частиц представляет собой трехмерную картинку, то
необходимо выполнить ее проецирование на какую-нибудь плоскость для отображения
на экране. В визуализаторе реализована возможность выбора плоскости
проецирования во время просмотра визуализации. Помимо этого, на этапе проецирования
осуществляется масштабирование картинки, т.е. увеличение ее, или уменьшение.
Также, для удобства экспериментатора, к плоской картинке добавляются записи
параметров эксперимента.
·
Полученное после проекции, масштабирования и добавления параметров
эксперимента изображение прорисовывается на экране монитора.
Следует отметить, так как
структура файлов вывода одинакова как для однопроцессорного, так и для
многопроцессорного вычислителей, то программа-визуализатор является
универсальной и подходит для визуализации результатов в обоих случаях.
Пробные вычислительные
эксперименты проводились с несколькими целями:
1. Убедится в правильности
работы программы, проверить и уточнить модель.
2. Убедиться, что выбранная
схема визуализации позволяет наблюдать за процессами эволюции протопланеты.
3. Попытаться даже на малом
количестве точек получить ожидаемый эффект, а именно недостаточность
отделяющегося пояса частиц для образования столь крупного спутника, как Луна.
Все пробные эксперименты
проводились для начальных параметров аналогичных системе Луна-Земля (см.
методику решения). При этом варьировались лишь количество частиц N, и кинетический момент
системы K. Приведем
результаты некоторых из них.
N=5000; K=4,55e+3 (все параметры в точности
как у Земли-Луны)
Начальное
распределение:
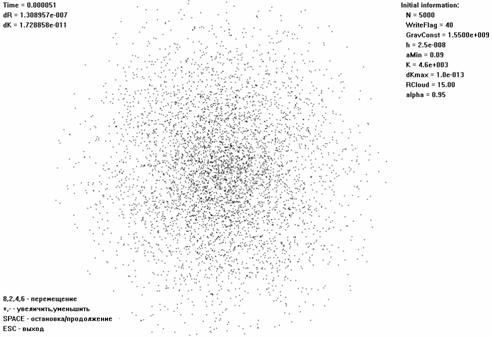
Конечное
распределение (вид сверху, увеличено х10):

Под конечным распределением
имеется ввиду такое, изменения в структуре которого несущественны с течением
времени. Эксперимент показал, что при задании параметров схожих с Землей, в
результате гравитационного коллапса образуется плотное тело шаровидной формы
сплюснутое в районе полюсов. Количество отслоившихся частиц пренебрежимо мало.
Это может быть проявлением не только ожидаемого эффекта, но и недостаточности
количества учавствующих частиц.
N=500; K=2.5e+4
Конечное распределение
(вид сверху):

В этом эксперименте виден сформировавшийся спутник, но чтобы его
получить пришлось существенно увеличить K.
1. Разработана модель эволюции
протопланеты, учитывающая тепловую диссипацию энергии в газопылевом облаке.
2. Разработаны алгоритмы,
реализующие эту методику, и структура вычислительного комплекса.
3. Реализован и полностью
отлажен вычислительный комплекс в однопроцессорном варианте, и проведены
пробные вычислительные эксперименты.
4. На основе проведенных
пробных экспериментов было произведено уточнение модели.
5. Однопроцессорные
эксперименты с небольшим числом точек показали недостаточность отслаиваемого
пояса частиц.
6. На основе уточненной модели
реализован многопроцессорный вариант вычислительного комплекса, который
находится в состоянии отладки.
1. Шмидт О.Ю. 4 лекции
о теории происхождения Земли. М.-Л.: АН СССР, 1949.
2. Энеев Т.М., Козлов Н.Н. О новой модели процесса аккумуляции планетной
системы. Результаты численных экспериментов. Письма в АН, т.5, №9, 1979.
3. Козлов Н.Н. Изучение эволюционных процессов в сложных
дискретных системах методами математического моделирования. Дисс. на соиск.
уч. степ. док. физ.-мат. наук, М.: ИПМ АН СССР, 1981.
4. E.M.Galimov, A.M.Krivtsov, A.V.Zabrodin, M.S.Legkostupov, Yu.I.Sidorov Non-impacts concept of the origin of the
Earth-Moon system. Geochemical constraints and dynamic simulation. В печати.
5.
Krivtsov, A. M., and N. B.
Krivtsova (2002), The particles technique and its use in mechanics of solid
body deformation, Far East Mathematical
Journal, 3(2), 254-276.
6. В.В.Еремин, С.И. Каргов,
Н.Е. Кузьменко "Реальные газы" Москва,1998 (http://www.chemnet.ru/rus/teaching/realgases/chap1(3).html)
7.
Craig B. Agnor & Douglas
P. Hamilton Neptune’s capture of its moon
Triton in a binary-planet gravitational encounter. Nature, vol.441, 11 May
2006, p.192.
8.
A.Morbidelli Interplanetary kidnap. Nature, vol.441,
11 May 2006, p.162.
9. Х.Альвен, Г.Аррениус Эволюция солнечной системы. М.: Мир,
1979.
10.
Корнев, Чижонков Е.В. Упражнения
по численным методам. М.: мех-мат МГУ, 2002.
11.
Богачев К.Ю. Основы параллельных
вычислений. М.: мех-мат МГУ, 2002.
12.
Шилд Г. Программирование на Borland C++. Минск, Попурри, 1997.
13.
Black D.C., Bodenheimer P. Evolution of rotating interstellar
clouds. I-Numerical technicues.
ApJ., 1975, 199.
14.
Boss A.P., Collapseand equilibrium of Rotating,
Adiabting Clouds. ApJ., 1980, 242.
15.
Kailash C. Sahu, Stefano Casertano, Howard
E.Bond at all; Transiting extrasolar
planetary candidates in the Galactic bulge. Nature, vol.443, 5 October 2006, p.534.
|




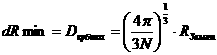 ,
,