Содержание

        

Введение. 4

1. Методологические основы создания систем поддержки научных исследований, ориентированных на технологию трансляции знаний. 7

2. Универсальная спецификация: У – числа. 9

3. Универсальная спецификация: семантический язык SL. 11

3.2. Синтез исходных понятий с использованием У-чисел. 12

3.2.1. Чистое качество (δ) 12

3.2.2. Чистое количество (κ) 14

3.2.3. Мера (μ) 15

3.2.4. Явление, свойство, форма, вещь. 17

3.2.5. Сущность, содержание, функция, закон. 18

3.2.6. Субъекты (Sub) и объекты (Obj) 20

3.2.7. Орудия. 21

3.2.8. Чувства и эмоции. 22

3.2.9. Местоимения и предлоги. 22

4.Лингвистические супероператоры.. 22

5. Морфология семантического языка. 23

6.Запись текста на языке SL. 29

6.1. Спецификация вспомогательных символов. 29

6.2. Пример использования SL для синтеза производных понятий. 30

7. Заключение. 31

Литература. 31

 

Введение

Специализация есть очевидное общественное благо.  В сегодняшнем мире узких специалистов это аксиома, не требующая доказательств. Времена великого Леонардо да Винчи, времена великих ученых-универсалистов, ученых-энциклопедистов, как представляется, ушли в прошлое навсегда. И, тем не менее, крупнейшие открытия делаются именно на стыке различных  дисциплин.  Удивительнейшие изобретения представляют собой следствие соединения, как казалось, несоединимого.  Так ушла ли, действительно, насовсем универсальность мыслителей? Возможна ли сегодня “тотальная” универсализация знаний?

Сама постановка такого вопроса в нашем безумно разнообразном мире, поначалу, кажется не менее “безумной”.  Но, может быть, все-таки, прав Нильс Бор, считавший что идея, чтобы быть верной должна быть “достаточно безумной”? Существуют же, в конце - концов, такие впечатляюще-красивые и бесконечно разнообразные фигуры как фрактали – и при всем этом каждая часть фракталя геометрически подобна любой другой ее части. И ведь нельзя же сказать, что это некие редкие казусы, нет - фрактали чрезвычайно распространены в природе: горы, облака, молнии и деревья лишь некоторые из многочисленных примеров.  Одни и те же геометрические образы характерны для самых, казалось бы, различных явлений: например, спираль появляется и в течении воды у стока домашней ванны и в структуре галактик. Одни и те же уравнения описывают самые различные природные явления, наиболее известный пример - волновые уравнения, описывающие явления от волн морского прибоя до волн возбуждений в мозгу человека и поведения квантов Вселенной.

Иначе говоря, если гипотеза о возможности тотальной универсализации верна, мир должен представлять собой один-единственный фракталь, каждая часть которого, в каком-то смысле, подобна любой другой его части. Или, другими словами, искомое “единое универсальное уравнение” должно описывать мир в любой наперед выбранной его области. Исторически, первым человеком, построившим именно такую единую фрактальную систему мира был великий немецкий мыслитель, творец системы диалектики, Г.Ф.В. Гегель. Основное положение диалектики, ее “универсальное уравнение” или “единый закон” состоит в том, что каждый объект изучения, каким бы он ни был,  выступает в виде противоположностей, причем, именно единство этих противоположностей (противоречие) составляет саму суть объекта. Универсальность этого закона, применимость ко “всему и вся”, естественным образом, приводит к его рекурсивности, применимости к самому же себе.  Утверждаемое единство противоположностей приводит к своей собственной противоположности, к различию-противоположению.  Противоположности не только едины, но и различны, а именно, “противоположны”.  Тем самым возникает универсальное “порождающее правило” для понятий,  знаменитый “метод триад” Гегеля. Продолженный рекурсивно в бесконечность, он порождает саму систему, объемлющую весь мир.  Стоит отметить, что фундаментальной характеристикой и, собственно, математическим определением фракталя, как раз является наличие единого “порождающего правила”, зная которое можно построить весь фракталь целиком.

 Современными, предельно мощными понятиями современной науки, которые можно поставить наравне с диалектическими понятиями единства и различия противоположностей, являются понятия симметрии и инвариантности. Именно, под симметрией какого либо объекта сегодня понимают наличие некоторого преобразования, трансформирующего одну из форм (ипостасей, проекций) объекта в некую другую.  Основным инвариантом преобразования, то есть, сущностью, не изменяемой при преобразовании симметрии, оказывается, таким образом, сам объект. Теперь нетрудно понять, в современной трактовке, саму суть диалектики: она в утверждении наличия некоей “симметрии противоположностей” у каждого объекта и его инвариантности при трансформации одной из противоположностей в другую. Иначе говоря, каждый объект фундаментально имеет две “стороны”, “проекции-ипостаси” которые обычно и выглядят для нас, его “противоположностями”.

Поскольку наличие и повсеместная распространенность противоположных сторон вещей, процессов и явлений, по-видимому, ни у кого не вызывает сомнений, такая “симметрия противоположностей” тех же битов, симметрия нулей и единиц информатики, вполне может претендовать на статус фундаментальной симметрии нашего мира, присутствующей везде и всюду, на всех уровнях познания. Таким образом, гипотеза фрактальности нашего мира находит некоторое подтверждение. Не забудем, однако, что для утверждения истинной фрактальности необходимо еще и наличие универсального рекурсивно порождающего правила, формирующего новые противоположности и, соответственно, новые симметрии – правда, все того же, единого “битового” типа. Нетрудно догадаться, что в данном случае таким порождающим правилом оказывается само преобразование симметрии, превращающее одну из ипостасей объекта в ее “противоположность”.  Это преобразование естественно назвать “противоположением” или, согласно диалектической традиции, “диалектическим отрицанием”. Действуя рекурсивно, такое преобразование и само по себе должно быть симметричным, в смысле противоположения. Противоположным тут будет, как нетрудно догадаться,  отрицание противоположности, то есть, тождество, единство, равенство – или, иными словами, утверждение. Именно так, между прочим, из диалектики отрицания рождается формальная логика. 

Возникающая фрактальная иерархия симметрий описывает объект или процесс, будь он локален или глобален, тем более подробно, чем глубже мы готовы применять наше порождающее правило. При этом в контексте различных использований данного универсального подхода, порожденные симметрии получают, как нетрудно понять, различную интерпретацию. Так в развитой именно таким образом, одним из авторов,  квантовой теории пространства-времени [1] показано, что “памятью” Вселенной, сохраняющей “события времени” является пространство – и диалектический процесс порождения симметрий естественным образом приводит к возникновению уравнений Эйнштейна и Дирака. В более поздней совместной работе авторов [2] подобным же образом развита математическая теория личности. В работах [3,4] тем же способом развито абстрактное исчисление (у-чисел), объединяющее фрактально развивающиеся объекты и, соответственно, усложняющиеся операции над ними. Наиболее же выдающимся примером эффективности данного подхода стал созданный  в 80-е годы прошлого века универсальный фрактальный язык обмена идей и общения Диал [5].  Этот первый в истории истинно “философский” язык, был построен строго согласно порождающему правилу, в котором базой было выбрано “бытие звука” или, иначе, переходы симметрии типа “молчание-звук”, и далее, порождающее ударения, ритмы, интонации, фонемы и полную грамматику вместе со словарным ресурсом языка. Язык, как орудие общения, всегда является средством отображения мира вокруг нас – и сама возможность построения языка подобного уникального типа стала важнейшим доказательством справедливости гипотезы фрактальной Вселенной. В дальнейшем на основе Диала и абстрактного исчисления у-чисел был разработан семантический язык SL [6], предназначенный для формализованной записи смыслов слов и выражений естественного языка для задачи машинного перевода.

         Но вернёмся к проблеме универсализации знаний. В результате крайней специализации специалисты даже близких областей науки перестают понимать друг друга и не имеют достоверной информации о положении дел. Необходимость универсализации знаний и стандартизации терминологии (даже внутри одних и тех же областей) назрела давно. Решение проблем универсализации и стандартизации способно изменить в корне взгляд на науку, на само знание, разработать системы поддержки научных исследований, достичь лучшего взаимопонимания между специалистами узких областей, что, несомненно, приведёт к множеству новых открытий.

         Что же мешает на сегодняшний день осуществить процесс универсализации знаний? Попробуем перечислить проблемы, встающие на этом пути.

1. Терминологический хаос в науке. Омонимия – когда одно и тоже по сути явление в различных предметных областях называется по-разному. Синонимия – когда разным явлениям, процессам, изобретениям из разных предметных областей присваиваются одинаковые имена (термины). Иногда это делается сознательно, но без понимания специфики подобного термина, а лишь по ассоциации. А иногда несознательно, по незнанию, что такой термин уже употребляется, где-то, в ином значении.

2. Различия в структуре наук: в аксиоматике, организации, в методах и инструментах.

3. Отсутствие теории универсализации знаний.

4. Распространённое мнение об узко специальном характере знаний и невозможности их универсализации.

5. Крайне малое количество ученых обладающих энциклопедичными знаниями, необходимыми для проведения соответствующих обобщений.

 

         1. Методологические основы создания систем поддержки научных исследований, ориентированных на технологию трансляции знаний

 

В этом разделе мы попытаемся обосновать необходимость и возможность проверки гипотезы о возможности переноса знаний из одной области науки в другую. Для решения этой фундаментальной задачи необходимо в первую очередь разработать методологию преобразования знаний одной предметной области в универсальные алгебраические структуры и восстановление знаний из этих структур с учетом контекста другой предметной области. Возможность переноса знаний из одной предметной области в другую в философском плане основывается на единстве законов развития природы, общества, языка и мышления. Это положение, многими уже почти забытое с наш век тотальной специализации, не потеряло, тем не менее, своей значимости. Утрата этого тезиса в теоретическом плане означала бы утрату философии как науки. 

Математика в целом уже является таким метаязыком, который позволяет описывать различные на первый взгляд процессы одними и теми же уравнениями. В процессе формализации задачи совокупность процессов сводят к некоторому уравнению (или системе линейных или нелинейных уравнений), в том числе и  дифференциальному уравнению (или системе уравнений) и граничным условиям. В дальнейшем ищется новый или берётся уже известный метод решения уравнений, и получают зависимости. Полученные зависимости или иные результаты подвергаются процедуре обратной формализации - интерпретации, в результате которой получается содержательное решение задачи. Эту схему упрощённо можно представить как преобразование предметной области самой в себя (рис.1).

Передача знаний из одной предметной области в другую схематически можно представить разомкнутой диаграммой (рис.2). Размыкание диаграммы приводит к существенному изменению её содержания. На первой диаграмме метаязык играет роль инструмента анализа и синтеза знаний в одной и той же области. На второй диаграмме метаязык не выполняет никаких аналитических, вычислительных или прогностических задач. Его задача представить знания  в компактной  универсальной форме. После того как знания переданы, они могут быть обработаны математическим методами, как на рис.1.

 

 

 

 

 

 

 

 

 

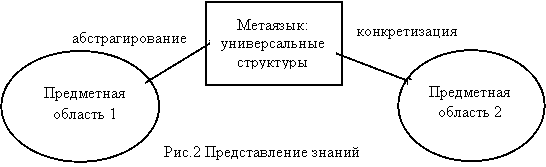На рис. 3 приведена более конкретная диаграмма, учитывающая  некоторые особенности передачи знаний. Между предметной областью и метаязыком появились два модуля: база знаний и модуль анализа.  База знаний должна содержать информацию о данной предметной области в формализованном виде – в виде универсальной спецификации, которая будет описана ниже. Модуль анализа должен выполнять преобразование строки в грамматическую структуру, например, в граф. Модуль синтеза совершает обратное преобразование грамматической структуры  в линейную структуру. База знаний 2 выполняет функцию преобразования универсальной спецификации в понятия предметной области 2. Диаграмма на рис. 3 ещё не описывает весь многосложный процесс трансляции знаний. Отсутствуют многие важные блоки отвечающие, в частности, за обработку естественного языка.

 

2. Универсальная спецификация: У – числа

 

В математическом плане методология опирается на разработанную ранее алгебру У-чисел (игрек) [3,4] и теорию лингвистических супероператоров [2]. Данный математический аппарат описывает процесс синтеза и взаимодействия понятий аналогично тому, как они формировались и взаимодействовали в процессе своего исторического развития. Это позволяет математически формализовать контекст, определяющий предметную область.

      Приведём ниже элементарные сведения по У-числам, которые нам понадобятся для построения открытого семантического языка SL.

Определение 1: элементы  у и ў множества G считаются противоположными, если они связаны операцией  вида:   

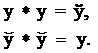                                                                                                                     (1)

Тип операции (_*) будем называть инверсным умножением. Оно определяется как строго упорядоченное.

Свойство: инверсное произведение у или ў операторов не обладает ассоциативностью.

Использование аксиомы упорядоченности приводит к образованию структур из двух исходных элементов. Будем называть числа у и ў числами-операторами первого порядка, а y_*ў и ў_*y числами-операторами второго порядка:

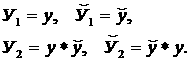                                                                   (2)

У ‑ числа 3-го,  4-го и 5-го, порядков имеют вид:

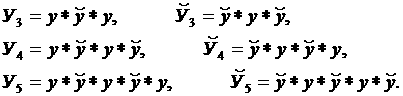                                                    (3)

Определение 2:  операция умножения, названная прямым умножением У-чисел имеет вид:

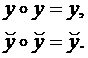                                                                                                         (4)

Как и определённая выше операция инверсного умножения обладает возможностью к образованию новых, более сложных У-чисел. Невозможно сделать утверждение о коммутативности или некоммутативности прямого умножения, однако в противоположность  инверсному умножению это умножение ассоциативно.

В сочетании инверсное и прямое умножение порождают большое разнообразие числовых структур. Логическая связь этих двух операций раскрыта в работе [3].

Определение 3: обособлением составных У-чисел будем называть операцию взятия скобок от произвольного У-числа.

После обособления число вновь может быть умножено инверсно само на себя, например:

                                                                           (5)

Расширим множество - чисел. Во-первых, определим умножение - чисел на вещественное или комплексное число . Будем обозначать новый элемент . Подчиним эту операцию аксиомам коммутативности и ассоциативности, то есть будем полагать:

 ,                                                                                      (6)

 ,                                                                            (7)

где под  подразумевается какое-либо из исходных - чисел. Элементы такого вида будем относить к множеству обобщенных - чисел. Кроме того, после определения операции умножения - числа на вещественное или комплексное число естественно пополнить получающееся множество нулевым элементом , к которому по определению приводит умножение любого - числа на ноль:

 ,     ,     .                                                 (8)

Во-вторых, определим на множестве исходных - чисел, умноженных на вещественное или комплексное число бинарную операцию, которую будем именовать сложением - чисел. Будем считать, что для этой операции выполнены аксиомы коммутативности, ассоциативности и дистрибутивности. Определенная таким образом операция сложения является совершенно аналогичной соответствующей операции сложения для вещественных или комплексных чисел:

 ,                                                                     (9)

 ,                                          (10)

 ,                                                                      (11)

 ,                                                          (12)

 ,                                                                                    (13)

где под обозначениями  ,  ,  ,  подразумеваются исходные - числа, либо исходные - числа, помноженные на вещественное или комплексное число. Получаемые в результате операции сложения элементы будем называть обобщенными - числами. Они являются расширением множества исходных - чисел. В силу аксиом, наложенных на операцию сложения, ее можно определить и для обобщенных - чисел. В результате во множестве обобщенных - чисел справедливы аксиомы (8)-(13).

Если интерпретировать простейшие  У-числа как элементарные семантические единицы – семы, а их комбинации как понятия и категории, то У- алгебра получает следующее толкование.

1.Операция инверсного умножения является алгебраическим аналогом операции перехода к противоположности в диалектической логике.

2.Умножение оператора на самого себя:  у_*у или   ў_*ў     соответствует самоприменимости понятия, а результат умножения интерпретируется как появление противоположного по смыслу понятия.

3.Наличие в составе множества двух противоположных элементов соответствует возникновению внешнего противоречия как отношения (не путать с формально логическим противоречием).

4.Цепочка любых чисел, например,  (ў_*y)_*(y_*ў)_*(ў_*y)_*(y_*ў)_*(ў_*y)_*(y_*ў) …  соответствует структуре и одновременно переходу между понятиями и  может быть сколь угодно длинной. Это отражает тот факт, что противоречие не обязательно разрешается после первого противопоставления. Однако, циклы перехода противоположных понятий друг в друга, в конце концов, завершаются синтезом нового понятия.

5.Операция обособления - аналог процедуры синтеза. Она позволяет любое составное У-число превращать снова в у-число первого порядка. То есть после обособления с У-числом можно обращаться так же как у-числом.  Эта операция, несмотря на внешнюю простоту весьма нетривиальна, ибо одновременно содержит в себе две процедуры: синтез и «снятие понятий».  Она дает возможность строить иерархию понятий, начиная с любого понятия принятого по соглашению за «начало».

6.Операция прямого умножения отвечает за формальное конструирование понятий в семантическом языке, производимое без существенного изменения смысла соединяемых понятий.

7.Операция сложения соответствует следованию слов в предложении (конкатенации).

8.Умножение вещественных и комплексных чисел на У-числа используется в задачах на собственные функции и собственные значения.

3. Универсальная спецификация: семантический язык SL

 

3.1. Принципы семантического языка

Принципы языка SL:

а) абстрактность - каждый знак является абстрактным оператором, преобразованием симметрии;

б) иерархичность - каждый оператор действует над "полем низших операторов";

в) конструктивность - "высшие" операторы составляются из "низших" и являются формулами или словами языка;

г) правила составления формул (или слов) также являются операторами SL;

д) основанием иерархической системы, порождающим оператором; выражающим полное отсутствие всякой информации, является ноль (ничто);

е) развитие - переход от одной симметрии к другой. Оно описывается как воздействие операторов на себя;

ж) с целью устранения омонимии его слова содержат семантические пометы.

Каждый оператор играет в языке двойственную роль:

    а. является однозначным представителем некоторого слова (понятия) в случае если употребляется отдельно от остальных слов в тексте, для него прописаны семантические поля и он имеет ссылку на тему;

    б. является представителем класса слов-понятий, если  используется в составе некоторого слова или не имеет ссылки на тему.

Например. Оператор α⁺ <общ> - рождение (абстрактное рождение чего-либо вообще), но в составе слова (α ⁺г*о<чел>) это будет класс: рождение, появление, возникновение, рост. При этом значение самого слова (α ⁺г*о<чел>) однозначно можно установить, только используя ссылки и семантические поля, которые добавляются  к слову. Без них, в данном случае без семантических полей, это слово является многозначным и имеет целый список значений: молодой, ребёнок, мальчик, беби, дитя, итд.

Таким образом, в SL разрешается противоречие между однозначностью и многозначностью (полисемичностью) слова.

4. Исходный алфавит содержит русские, английские, греческие буквы и некоторый набор спецсимволов.

5. Содержит строгие правила образования понятий и определения их смыслов настолько, насколько это возможно на сегодняшнем уровне развития.  

 

3.2. Синтез исходных понятий с использованием У-чисел

При построении семантического языка невозможно обойти стороной проблему выбора  «модели мира». В естественном языке одновременно уживаются несколько картин мира. К основным можно отнести: архаичную, наивно-бытовую и научную. Для большей полноты, ясности и строгости изложения предпочтительнее строить семантику на основе научной картины мира, однако на этом пути мы сталкиваемся с проблемой отсутствия единой современной картины мира. Высокая динамика развития отраслей знания приводит к семантическим разрывам между картинами мира не только для различных наук, но и внутри различных научных направлений в рамках одной и той же науки. В этих условиях приходится опираться на картину мира, в конструкцию которой положены наиболее общие понятия, хорошо согласующиеся с диалектической философской позицией и современными физическими представлениями. Хорошо известно, что невозможно построить исчерпывающую систему понятий языка посредством одних лишь логических или иных определений.  Поэтому в нашем случае роль «экспериментальных параметров» будут играть ссылки на темы (или контексты), например, <фил>, <физ>, <био>. Полный набор тем должен быть открытым и может быть сконструирован и описан в рамках SL.

 

3.2.1. Чистое качество (δ)

 Для каждого оператора мы будем давать краткое описание, выявлять противоречие и определять SL-представление. Под SL-представлением будем понимать запись - спецификацию или в некотором смысле «кодирование» понятий посредством У-чисел.

За основание языка возьмем то общее, что имеется во всех без исключения явлениях и процессах Вселенной. То, что все они существуют. Философская категория бытия отождествляется с первым оператором и имеет смысл НАЧАЛА.

Бытие выступает как лишенное всяких определенностей, чистое есть. Теперь, чтобы мы ни взяли за “иное”, не тождественное бытию, а значит различное с ним, оно будет противоположно бытию. За такую противоположность бытию возьмём ничто,  т. к. и оно   лишено всяческих определенностей и равно относится ко всему (присутствует во всем).

Такое определение исходных понятий, что называется «по Гегелю», приводит к диалектическому противоречию, рассмотренному в работе [6].

Рассмотрим формализованную модель саморазвития понятий:

1.     у - ничто, ў- бытие;  

2.     А{ў, у, _*}  - взаимодействие  между понятиями;  

3.     у ≠ ў,  - противоположность понятий;

4.     у _* у = ў – самодействие понятия, ничто действует на себя, уничтожает себя, порождая бытие, так как других понятий кроме бытия собственно и нет.

ў _* ў = у – аналогично, бытие действует на себя, порождая ничто, (что соответствует известной шутке «жизнь вредная штука - от неё умирают»). В несколько иной трактовке противоречием будет то, что с одной стороны ничто тоже “есть”, а с другой - что бытие, лишенное само по себе определенности, равно ничто.

        5. Разрешением противоречия (синтезом) между бытием и ничто является категория, содержащая их в “снятом” виде, переход между ними – рождение:                           

                    (у _* ў) = α ⁺ - рождение.

Противоположностью будет обратный переход от бытия к ничто:       

                  (ў _* у) = α ^-   - уничтожение.

Совершенно очевидно, что нельзя уничтожить бытие, не породив ничто, и нельзя родить бытие, не уничтожив ничто. Категории рождения и уничтожения несут в себе “первородный грех” противоречия, доставшийся им от бытия и ничто. Рождение содержит в себе уничтожение, а уничтожение содержит в себе рождение (невозможно рождение чего-либо без уничтожения чего-либо и наоборот):

                  α ⁺ _*  α ⁺ = α ^- ,

                  α ^-  _*  α ^-   = α ⁺ .

Разрешением противоречия (снятием) между α ⁺ и α ^-  является переход между рождением и уничтожением – изменение или «квант времени»:                      

(α ⁺ _* α ^-) = τ   - квант времени,  изменение.

Обратный переход даст нам противоположный оператор:            

                    (α ^- _* α ⁺) = χ  -  квант пространства, сохранение.

Оператор τ будем соотносить с категорией времени. Собственно, это есть определение времени как элементарного изменения. В литературе такое время называют «временем типа А», как лишенное количественных характеристик. Противоположностью времени как того, в чём все изменяется, будет пространство, как то, в чём все сохраняется. И это есть определение пространства как элементарного сохранения. Здесь пространство определяется, отвлекаясь от его геометрических, топологических и иных характеристик.

Таким образом, время есть более развитая форма бытия, а пространство - более развитая форма ничто.

Это не единственная пара понятий, которая возникает при данном синтезе. Надо заметить, что квант времени можно трактовать и как частицу, а квант пространства - как поле.

Кванты времени и пространства также являются противоположностями, а поскольку всякое изменение невозможно и бессмысленно без сохранения, как сохранение возможно только в процессе изменения (например, сохранение энергии в процессах перехода ее из одной формы в другую), то можно зафиксировать новое противоречие:

                   τ  _* τ = χ,

                   χ _* χ = τ.

Разрешается противоречие, как и ранее, переходом между категориями - объединением времени и пространства в единую категорию пространства-времени:

                  (τ _* χ) = γ ⁺   -  одновременно это переход времени в пространство.

Противоположный оператор, описывающий переход пространства во время:

                   (χ _* τ) = γ ^-   .

Если мы не различаем γ ^- и γ ⁺ , то имеем единое динамическое пространство-время, различие же γ ^- и γ ⁺  дает нам смысл двух абстрактных поворотов,  содержащихся друг в друге:

                   γ ⁺ _* γ ⁺ = γ^-,

                   γ ^- _* γ ^- = γ ⁺.

      Переход или соединение поворотов, приводит к понятию скачка:

                  (γ ⁺_* γ ^-) = η  - скачок кванта времени,            

                   (γ ^- _* γ ⁺) = ω - скачок кванта пространства.

      Здесь появляются новые смыслы. Оператор η приобретает дополнительно значение оператора дискретности, а ω – оператора непрерывности. Дискретное содержит в себе непрерывное и без него не существует, и обратно. Что бы мы делили и разделяли, если бы не было непрерывного? Непрерывное же должно быть отделено хотя бы мысленно, иначе его невозможно различить.

                   η  _* η = ω,

                   ω _* ω = η.

 

3.2.2. Чистое количество (κ)

Разрешением противоречия является переход между скачком во времени и скачком в пространстве, между дискретным и непрерывным:

                   (η _* ω ) =  k⁺- рождение количества,

                   (ω_*  η ) = k^- - уничтожение количества.

С появлением количества появляется различение его с чистым качеством, изложенным выше. Это значит, что чистое качество и чистое количество также образуют алгебру: А{K, Q, _*}.

Операторы рождения и уничтожения количества находятся между собой в отношении противоречия, так как являются всего лишь более развитой формой операторов α ⁺ и α ^-. В то же время совершенно очевидно, что рождение одного количества невозможно без уничтожения другого:

                   k⁺_*  k⁺ = k ^-,

                   k^- _*  k^- = k⁺.

Переход между рождением и уничтожением количества дает новый оператор, который можно описать как  ограниченное количество. Противоположностью ограниченного количества будет неограниченное количество или БЕСКОНЕЧНОСТЬ.

(κ⁺ _*  κ ^-) = κ _τ - ограниченное количество (конечное),

(κ ^- _*  κ ⁺) = κ _χ – неограниченное количество (бесконечное).

То, что конечное количество содержит в себе бесконечное, легко понять. Достаточно вспомнить, что любой конечный отрезок числовой оси содержит в себе бесконечное количество точек, и, наоборот,  любая бесконечность состоит из конечных величин.

                   κ _{τ *}  κ _τ = κ _χ,

                   κ _{χ *} κ _χ = κ _τ.

Синтезом конечного и бесконечного количества (или времени и пространства количества) являются, как и положено, операторы поворота – перехода конечного количества в бесконечное и обратно:

(κ _{χ *}  κ _τ)=ρ⁺ - преобразование конечного в бесконечное,

(κ _{τ *}  κ _χ)=ρ^- - преобразование бесконечного в конечное.

Эти операторы поворота или операторы пространства-времени также противоположны друг другу:

                   ρ⁺ _*  ρ⁺ = ρ^-,

                   ρ^- _*  ρ^- = ρ⁺

Рассмотрим их взаимный переход:

(ρ^- _*  ρ⁺)=ρ_∞ - отношение бесконечных,

(ρ⁺ _*  ρ^-) = ρ_κ - отношение конечных.

Видно, что одно конечное количество переходит в другое конечное количество через бесконечность, и, действительно, (например) чтобы попасть на числовой оси из одной точки в другую, нужно пройти через бесконечное количество точек между ними. Переход от одной бесконечности к другой осуществляется через конечное количество, или отношение бесконечных есть конечное. Здесь бесконечные разных порядков не различены. Мы не будем рассматривать переходы между отношением конечных и отношением бесконечных.

Чистое качество, породив чистое количество как свою противоположность,  должно соединиться с ним в МЕРЕ.

         (δ_* κ) = μ – мера.

 

3.2.3. Мера (μ)

1) Философская категория, выражающая диалектическое единство качества и количества объекта; указывает предел, за которым изменение количества влечет за собой изменение качества объекта и наоборот.

2) Мера как соразмерность лежит в основе ритма, гармонии, мелодии в музыке, ансамбля в архитектуре,  метрологии, и т. п.

Синтез категорий качества и количества даёт МЕРУ. Теперь качество не просто наполнено количеством, но и зависит от него. Комбинация понятий меры и вещества дает понятие состояния или фазы вещества. Например, хорошо известно, что фазы и состояния вещества зависят от меры температуры. Термодинамическое состояние физической системы, в случае равновесия определяется равновесными значениями ее параметров: температуры, давления, объема, концентраций, потенциалов и т. п.; неравновесное состояние характеризуется наличием в системе перепадов (градиентов) температуры, концентрации или др. параметров.

 Здесь же появляются и измерения, в том числе измерения пространства. ИЗМЕРЕНИЕ - протяжённость измеряемой величины в каком-нибудь направлении (спец.).

Рассмотрим переход от отсутствия меры к ее наличию – рождение меры:

         (δ*κ) = μ⁺ -  возникновение меры,  и соответственно,

(κ*δ) = μ^- - уничтожение меры.

Возникновение одной меры всегда есть уничтожение другой меры. Мы уже можем воспользоваться понятием множества и определить все возможные меры как произведение множества качеств на множество количеств. Однажды возникнув, мера совершает свой цикл внутри себя (внутри множества мер).

μ⁺_* μ⁺= μ^- ,

μ^- _* μ^- = μ⁺.

Это уже хорошо знакомое противоречие. Его разрешением являются понятия времени и пространства мер:

(μ⁺ _* μ^-) = μ_τ - время меры,

(μ^- _* μ⁺) = μ_χ - пространство меры.

Временной цикл меры может начинаться с одной, а заканчиваться другой мерой, не обязательно совпадающей с первой, и этим они существенно отличаются от первых операторов – бытия и ничто.

μ_{τ *} μ_τ = μ_χ,

μ_{χ *} μ_χ = μ_τ.

Переход порождает пространство - время мер:

(μ_{χ *} μ_τ) =μ_γ+ – поворот в пространстве мер,

(μ_{τ *} μ_χ) = μ_γ- – обратный поворот.

Следующим шагом мы получаем скачок (прорыв) меры.

      Далее можно рассмотреть переходы (отношения) и этих операторов. Но на этом пути нас ждет дурная бесконечность понятий, преодоление которой приводит к возникновению понятий явления и сущности. Итак, бесконечное количество мер, состояний, фаз, взятое в единстве, в одном, есть по определению вещь.

 

3.2.4. Явление, свойство, форма, вещь

Далее мы будем использовать следующие пары противоположных категорий (каждая пара записана в своём столбце):

Явление -	Свойство- А	Вещь – V	Форма – PH	Проявление-	Аргумент-X	Вещество-R
Сущность -G	Отношение-R	Процесс-W	Содержание- S	Закон-	Функция- F	Поле – D

В естественном языке употребление этих понятий достаточно хаотично, часто их используют как синонимы, например, вместо слова сущность употребляют закон или функция и наоборот. Даваемые в словарях определения носят скорее толковательный характер. Негативную роль также играет омонимия, усиливающая языковую неразбериху. Ниже приводятся определения этих категорий заимствованные из энциклопедий и словарей. Нам же для построения семантического языка необходимо выделить главные смыслы этих понятий, а различение оставить для дальнейших исследований.

ЯВЛЕНИЕ.

1.     В философии: проявление, выражение сущности, то, в чём она обнаруживается.

2.     Вообще всякое обнаруживаемое проявление чего-нибудь. Физическое явление. Явление природы. Социальные явления.

ВЕЩЬ, в философии предмет материальной действительности, обладающий относительной независимостью и устойчивостью существования.

«ВЕЩЬ В СЕБЕ» (нем. Ding an sich), философское понятие, означающее вещи, как они существуют сами по себе («в себе»), в отличие от того, как они являются «для нас» в познании; одно из центральных понятий «Критики чистого разума» И. Канта.

СВОЙСТВО, философская категория, выражающая отношение данной вещи к др. вещам, с которыми она вступает во взаимодействие. Свойство нередко рассматривается как внешнее выражение качества.

Будем исходить из того, что вещь является нам посредством своих свойств, через свои свойства. В необъятном мире вещей, каждая вещь обладает бесконечным количеством свойств. Но вещь является нам не всеми свойствами, а лишь некоторыми, другие же остаются до поры до времени скрытыми для нас.  Вещь со свойством мы будем обозначать как V с индексом-гласной.

Выделим в мире вещей два противоположных класса: вещи с главным свойством пассивности,  и вещи с главным свойством активности.

 “о” -свойство пассивности, 

 “а” –свойство активности,

                   V_o * V_o = V_a,

V_a *V_a = V_o.

(а_*о) = а^- – переход от активности к пассивности- успокоение

(о_*а) = а⁺ – переход от пассивности к активности – активизация

(а^-_*а⁺) =а^х– постоянство, неизменность,

(а⁺ _*а^-) =а^t– непостоянство, изменчивость, итд.

      Преодоление дурной бесконечности переходов в дереве противоположностей а и о выделяет новые классы вещей: с главным свойством связи и с главным свойством разделения.

Вещь с главным свойством связи “у”:   V_y,

Вещь с главным свойством разделения “и”: V_и.

V_y*V_y =V_и,

V_и*V_и = V_y.

Переходы между “у” и “и” дают: (у_*и)=у^- - отделение, (и_*у)=у⁺- присоединение, и т.д.. Преодоление дурной бесконечности переходов в дереве противоположностей у и и выделяет новые классы вещей: с главным свойством неустойчивости приводящей к структуризации и с главным свойством неустойчивости приводящей к деструкции. Действительно самопроизвольный переход от связанного, целостного состояния вещи к раздельному, раздробленному её состоянию или наоборот возможно, если вещь неустойчива, нестабильна.

Вещь со свойством неустойчивости “ы”: V_ы,

Вещь со свойством деструктивности “э” : V_э.

V_э*V_э = V_ы,

V_ы*V_ы = V_э.

      Количество возможных классов вещей со свойствами может быть и больше, но мы ограничимся основными шестью. Все остальные можно получить синтезом или конструированием. Вопрос же об оптимальном количестве классов остается открытым. По-видимому, для каждого класса задач оптимальное количество своё.  Цикл противоположностей, начавшись с “пассивности”, пройдя через шесть типов, заканчивается предельным понятием “деструктивной неустойчивости”:

                   (V_ы*V_э)= V_o,

(V_э*V_ы )= V_a.

      Выйдя из “О”, мы в “О” и вернулись. В развернутой противоположности “О” обнаружилось множество оппозиций. Разрешается это противоречие переходом к СУЩНОСТИ. Свойствам вещи, их проявлениям, противопоставляется ЗАКОН вещи.

 

3.2.5. Сущность, содержание, функция, закон

СУЩНОСТЬ в философии: внутреннее содержание предмета, обнаруживающееся во внешних формах его существования.

СОДЕРЖАНИЕ и форма, философские категории, во взаимосвязи которых содержание, будучи определяющей стороной целого, представляет единство всех составных элементов объекта, его свойств, внутренних процессов, связей, противоречий и тенденций, а форма есть внешняя организация содержания. Отношение С. и ф. характеризуется единством, доходящим до их перехода друг в друга, однако это единство является относительным. Во взаимоотношении С. и ф. содержание представляет подвижную, динамичную сторону целого, а форма охватывает систему устойчивых связей предмета. Возникающее в ходе развития несоответствие С. и ф. в конечном счёте разрешается «сбрасыванием» старой и возникновением новой формы, адекватной развившемуся содержанию.

Это определение  из философского словаря является прекрасной иллюстрацией к развиваемой нами динамической  модели понятия.

ЗАКОН, необходимое, существенное, устойчивое, повторяющееся отношение между явлениями в природе и обществе. Понятие закон родственно понятию сущности.

ФУНКЦИЯ

1. В философии: явление, зависящее от другого и изменяющееся по мере изменения этого другого явления.

2. В математике: закон, по которому каждому значению переменной величины (аргумента) ставится в соответствие некоторая определённая величина, а также сама эта величина.

В отличие от тех свойств, посредством которых вещь является перед нами, существуют свойства скрытые от нас: «свойства свойств» или «явления явлений» – сущности.

,

             .

Сущности определяют свойства вещи и выступают как ее внутренний закон. Свойства вещей, выступающие как аргументы, связаны между собой законами – функциями.

Будем далее обозначать сущности буквами алфавита, обозначающими согласные. Сущности также рождаются и умирают, у них есть свое время и пространство, и они могут перемещаться в своём пространстве-времени и т. д.. Все эти операторы можно ввести явно. Но на данном этапе нас интересует типология сущностей. Для сложных понятий, какими являются сущности и явления, их типология зависит от тех эволюционных этапов, которые пройдены ранее. В процессе прохождения  циклов противопоставления и снятия в вещи/понятии накапливается информация о «предыдущем опыте», которая затем и проявляет себя в типологии – снятое вновь становиться актуальным. Однако, этот «опыт» проявляется на новом уровне бытия и в новых контекстных условиях. Так категории рождения и уничтожения актуализируются в виде функций поглощения и выделения, кванты времени и пространства в виде преобразования и тождества (сохранения), а дискретности и непрерывности в виде функций отделения и связи. Понятия скачка и покоя, проходя свой путь развития, поднимаются до абстракции движения.

г⁺ – закон потребления, г^- - закон выделения,

г^t - закон преобразования, г^x- закон тождества (сохранения)

Оппозиция пары «действие закона» и «существование закона» в SL отражает в естественном языке форму противоположности между глаголом и существительным. Например: бег – бежать, еда – есть, потребление – потреблять, выделение – выделять. Переход между «существованием закона» и «действием закона», как между глаголом и существительным, порождает «качество закона» (прилагательное), а обратный переход «качество действия закона» (отглагольную форму - причастие), например: задумчивый – думающий, беглый  - бегущий, употребляющий – употребляемый.

В семантическом языке посреднике нет необходимости вводить отдельные слова для глаголов, прилагательных и т. д. Для их различения достаточно основному понятию приписать параметр части речи: n- существительное, v- глагол, ad – прилагательное, adj- наречие, и т.д.

В результате  многократного использования вещи происходит специализация её функций, например, функция отделения распадается (порождает) на множество узкоспециализированных функций: резания, отрубания, скалывания, отпиливания и т д.. При этом появляются новые потребительские возможности вещи.

х – возможность, новые потребительские возможности вещи. Они распадаются на:

ж – регулярные преобразовательно-потребительские функции,

ш – нерегулярные преобразовательно-потребительские функции,

р – закон движения,

р^о -закон неподвижности,

б – закон связи,

д – закон отделения,

з – закономерность, закономерные функции отделения,

с – случайность, случайные функции отделения.

й, ь – символы ориентированных границ, понадобятся в основном для местоимений и  предлогов. В собственном смысле они обозначают й- границу, ь- предел.

ф --  действительность, и новые возможности объединения,

Сущность имеет набор атрибутов, производя отрицание по которым, можно получить разные результаты.

Переходы между разными сущностями отражают причинно–следственные связи:  Ч =ТШ, Щ =ШЬ, Ц=ТС, ДЗ, ДЖ, ТШ, ПШ, БЖ.

Йотированные гласные Я, Ё, Е, Ю, служат в качестве личных местоимений и служат строительным материалом  для образования других типов местоимений.

 

3.2.6. Субъекты (Sub) и объекты (Obj)

Противоположность между явлением и сущностью снимается в их синтезе. Имеются, как и раньше, два варианта синтеза:

(Явл * Сущ) =Объект, (О),

(Сущ * Явл) = Субъект, (С).

Здесь и далее будем понимать субъект  более расширительно, как нечто, что может действовать на другое. Эта понимание ближе к тому, как функционирует это понятие в языке. Например: «строители строили дом» - субъект строители, но «дом строился строителями» - субъект дом.

На самом деле имеется несколько подходов при определении понятия субъекта. Условно их можно разделит следующим образом:

1.  абсолютный – под субъектом понимается только человек, как существо одушевлённое (то есть обладающее душой), разумное сознательное;

2.  биологический – субъектом считается только живое существо;

3.  относительный – любой объект может быть субъектом, если он в зависимости от ситуации находится в активной позиции.

Диалектически для SL ближе третий вариант определения субъекта. Но при этом возникает проблема - нельзя записать слово одновременно и как субъект и как объект (хотя в процессе синтаксического анализа можно приписать слову параметр субъекта или объекта). Эта проблема снимается введением субъективной системы отсчета связанной с человеком как наблюдателем. Это позволяет фиксировать объекты и субъекты привычным для нас образом.

Далее можно поступать, как и на всех предыдущих ступенях развития – вводить время, пространство, движение, количества субъектов и объектов и т.п. и т.д., но у нас уже  достаточно средств, чтобы отобразить их, не прибегая к неоправданному удлинению слов. Поступим так, как будто этот путь мы уже прошли, свернули смыслы и в процессе очередной трансформации присвоили морфемам смыслы объектов и субъектов.

Тогда в соответствии с принятой выше логикой объект превращается в субъект и наоборот по привычным правилам:

O * O = C,

C * C = O.

На этом уровне можно составить уже около тысячи  морфем – субъектов, объектов, их существительных и  глагольных форм, прилагательных, причастий, модальных слов, местоимений и предлогов. Они составляют базовый словарь языка. Например: (о_*р) – объект обладающий свойством «о»  устойчивости и функцией движения «р».

 

3.2.7. Орудия

Противоречие между субъектом и объектом раскрывает нам относительный, но отнюдь не абсолютный характер отношений между ними. Само же противоречие разрешается с возникновением некоторого посредника между Субъектом и Объектом, несущего в себе их несовместимое – Орудия:

(О*С) = Oрудия, по средством которых объекты “переходят” в субъекты, например: столовые приборы – c их помощью пища переходит в человека.

(C*O) = Орудия, с помощью которых субъекты переходят в объекты, например: сельскохозяйственные орудия – с их помощью объекты сельского хозяйства опосредованно поглощают человека,  в виде его труда.

Знаковой формой орудий являются двусложные конструкции, например: (((а_*р)<общ>)_*((г_*о)<чел>)) – орудие, посредством которого движение (а_*р)<общ> переходит в человека-потребителя (г_*о)<чел>. Таким орудием, очевидно, будет транспорт.

Отношения между объектами осуществляются орудиями особого типа – субъектами:

O * O = C,

а отношения между  субъектами осуществляют орудия – объекты:

C * C = O.

Глагольной формой орудия является метод (или способ), как последовательность действий одного или нескольких орудий.

 

3.2.8. Чувства и эмоции.

Эмоции есть отражение в психической деятельности человека внешних отношений между людьми, отношений к вещам, процессам и явлениям. Например, внешние отношения ПРИТЯЖЕНИЯ и ОТТАЛКИВАНИЯ связаны с внутренними процессами – ЛЮБОВЬЮ и НЕНАВИСТЬЮ. Будем описывать чувства и эмоции следующим образом:

(С * О * С) = Эм, эмоции,

(О * С * О) = Ср, сродство.

“Сродство” или “афинность” (термин из химии) – отражение отношений вещей между собой, их склонность или антипатия друг к другу.

 

3.2.9. Местоимения и предлоги

Местоимения и предлоги представляют два противоположных репера. Местоимения составляют субъективный репер личности, например простейший, Я,ТЫ,ОН, а предлоги  составляют объективный репер личности, например, ВВЕРХ, ВНИЗ, ВПРАВО, ВЛЕВО, ВПЕРЕД, НАЗАД. Для местоимений преимущественно используются гласные вместе с «й», а для предлогов - согласные с «ь».

        

         4.Лингвистические супероператоры

    Дадим трактовку понятию супероператора. Будем называть супероператором объект обладающий самоприменимостью  и входящий в систему супероператоров. При этом один самодействующий элемент составляет тривиальную систему супероператоров. В этом определении нет замкнутого круга, так как круг разрывает самоприменимость. В системе супероператоров все элементы-понятия принадлежат к динамической модели. Динамическая модель системы понятий введена ранее в работе [6]. Входящие в динамическую систему понятия могут изменять объем содержания. Систему супероператоров нельзя считать аксиоматической системой вообще. Но мы будем называть её «условно аксиоматической» по той причине, что с неё можно делать «срезы», получая классические аксиоматические системы. Более подробное описание супероператоров дано в работе [8]

Важно заметить, что условие вхождения супероператоров в систему супероператоров является весьма существенным. Этим супероператоры отличаются от других систем обладающих самоприменимостью, например, от лямбда-исчисления. Таким образом, и У-числа, хотя и относятся к динамической модели и имеют самодействие, но, поскольку не входят в систему супероператоров (а входят в алгебру), то и сами супероператорами не являются.

В динамической модели все формулы имеют различную интерпретацию. Здесь мы встречаемся с понятием «дурной бесконечности» - регулярным и неограниченным повторением одних и тех же конструкций. Примером «дурной бесконечности» является натуральный ряд чисел. Проблема называния каждого числа натурального ряда решается алгоритмом записи любого числа в позиционной системе исчисления, т. е. его имя исчисляется. Необходимость интерпретации всех конструкций динамической модели приводит к следующей проблеме. С одной стороны, процесс бесконечной интерпретации в том виде, в котором он описан выше явление бессодержательное, с другой - переход на следующий уровень интерпретации без него невозможен. Эта проблема разрешается введением бесконечных У-чисел [3].

    Система супероператоров является условно аксиоматической и являясь обобщением аксиоматических систем занимает промежуточное положение между математикой и естественным языком. Введение супероператоров диктуется потребностями построения семантического метаязыка предоставляющего возможность сворачивать смыслы и знания к некой универсальной квазиматематической записи. Выстраиваемый нами язык содержит в себе в частном  случае алгебру, теорию симметрии, теорию операторов, диалектику. Не представляет труда дополнить его формально-логическими теоретико-множественными операциями.

Окончательно можно сказать, что система супероператоров обладает следующими признаками:

самодействием – самоприменимостью, переводящей супероператор в ему противоположный;

 конструктивностью, когда из более абстрактных (и относительно простых) супероператоров можно строить более сложные и более конкретные;

 имеет открытый характер, она принципиально не фиксирована относительно некоторого числа аксиом.

На наш взгляд именно супероператор лучше всего подходит для описания процессов происходящих при смыслообразовании, а самоприменимость является той первичной, фундаментальной операцией, отвечающей за переходы смыслов из одной противоположности в другую. Образование новых смыслов непосредственно связано с синтезом понятий и уже только после этого к «смысловой материи» могут быть применимы формальные теоретико-множественные операции, использование которых может осуществляться уже и без самоприменимости и синтеза.

 

5. Морфология семантического языка

В качестве примера использования семантического языка рассмотрим категоризацию понятий описывающих движение в пространстве-времени. Полная категоризация представляет сложную задачу, поэтому здесь будет рассмотрена частичная категоризация, с единственной целью разобрать на данном примере использование супероператоров. В данном случае мы не будем онтологически выводить исходные подсистемы, а возьмём их готовыми из определения понятия движения.

Под конечным (финитным) движением будем понимать конечное перемещение объекта рассмотрения в пространстве данного объекта за конечное время. Таким образом, по определению конечного движения, имеем следующие подсистемы:

1 – собственно подсистема понятий движения,

2 – подсистема понятий пространства времени,

3 – подсистема понятий движущегося объекта.

         Первоначально рассмотрим подсистему движения в её собственном развитии. За отправные, исходные понятия возьмём понятия «покоя» и «движения». Их синонимы: неподвижность, недвижимость, обездвиженность, остановка, перемещение, передвижение и другие более конкретны и поэтому не подходят на роль исходных понятий. Обозначим:

у – покой,

ў – движение,

формула  у _* у = ў,  имеет следующую интерпретацию: покой покоя есть движение.

Покой – неустойчивое состояние, которое сменяется движением. Здесь нет речи о причинах возникновения движения, а только о различении покоя и движения. С другой стороны, покой имеет место не сам по себе, не абсолютно, а только по отношению к собственной системе отсчёта, и рекурсия здесь может быть рассмотрена как выход в другую систему отсчёта. Из другой системы отсчёта прежняя система отсчёта наблюдается нами как движущаяся – покой по отношению к другому покою есть движение. Однако, понятие системы отсчета ещё не введено, поэтому мы вынуждены принимать интерпретацию в простейшей и как результат в не очень очевидной форме: покой покоя есть движение. При максимальной степени абстракции нельзя осуществлять конкретную интерпретацию, так как это будет сильным забеганием вперёд, именно поэтому абстрактные диалектические выводы часто встречают непонимание.

И наоборот:

ў _* ў = у – движение движения есть покой.

Синтез «покоя» и «движения» даёт новые понятия:

(ў _* у) = а^- –  уничтожение движения (торможение, финиш);

(у _* ў) = а⁺ –  рождение движения (ускорение, старт).

Ускорение и торможение – наилучшие понятия, описывающие процесс перехода от покоя к движению, и обратно, но они обладают тем  недостатком, что тяготеют к понятию скорости, которое ещё не выделилось. Наиболее точными являются «рождение движения» и «уничтожение движения». Хотя сами понятия рождения и уничтожения имеют иные прототипические значения, чем рождение и уничтожение движения, однако в  сочетании с категорией движения их значения уточняются:

(а^-_*а⁺) = t – квант движения или скачок, (прыжок, перескок, этап).

(а⁺_*а^-) = x – квант покоя или остановка (временное прекращение движения, остановка, пауза, перерыв).

Квант движения и квант покоя – абстракции, которые являются строительным материалом, элементарными семами в SL. Эти категории отсутствуют в естественном языке, так как столь абстрактные представления появились сравнительно недавно. В естественном же языке представлены системы понятий, соответствующие наивной картине мира, сформировавшейся стихийно в процессе исторического развития языка, и отвечающие потребностям общественной практики. Каждое слово несёт в себе множество значений и смыслов. Это сильно осложняет процесс постановки слов в соответствие формулам SL, так как из живого слова приходится делать некоторую предельную абстракцию, например, «остановку» назначать «квантом покоя».

 Переход между t и x есть «поворот» от «скачка» к «остановке», содержащий их вместе:

(t _* x) = v^- – «отклонение»,

(x _* t) =v⁺ – «возвращение».

Здесь из абстрактного понятия «движение» выделяется его важнейшая фундаментальная форма:

 (v⁺о v^-) = ν -«колебание»,

 которая сама в дальнейшем порождает новые формы и, в конечном итоге, высшую форму – “равномерное прямолинейное движение”. Здесь и в некоторых формулах ниже употребляется операция прямого умножения (о), которая по смыслу близка к логическому &.  Переходы

(v^- _* v⁺)  = ω ^- – «правое вращение» (спиральность или киральность),

(v⁺ _* v^-)  = ω ⁺ –  «левое вращение»,

(ω ^–о ω ⁺) = ω – «вращение»,

ν  * ν  = λ – «волна»,  и наоборот,

λ _* λ = ν – колебание как вырождение волнового процесса (стоячая волна).

Волны и колебания  - это две противоположности, хотя, на первый взгляд, это может показаться и неочевидным. Одним из атрибутов колебательного процесса является замкнутость (как возвращение в исходное положение) и его конкретной противоположностью именно по этому атрибуту будет процесс «разомкнутый» т. е. волновой.

Колебательное и вращательное движения порождают поступательное, в первую очередь, волновое. Например, движение волны складывается из колебательных движений точек среды. И наоборот, колебательное и вращательное движения можно представить как последовательность бесконечно малых поступательных движений. Однако, поступательное движение среды (перенос массы) нередко осуществляется с участием вращательного движения, например, волны на воде:

(ν  _* λ )  =  δ⁺ – поступательное движение вперёд,

(λ _*  ν)  = δ^- – обратное поступательное движение,

(δ⁺_* δ^-) – поворот, смена направления на обратное.

В подсистеме пространства времени за исходные понятия возьмём «квант пространства» – «место» или «здесь»  – X  и «квант времени» – «время»  – T. Что бы получить «прошедшее» и «будущее» подействуем операторами «рождения движения»  и «уничтожения движения» на Т. Здесь приводится одна из возможных моделей пространства – времени, и в соответствии с ней используется способ объединения супероператоров:

(а⁺Т) = t_p, прошедшее, истекшее время или время, совершившее движение,

(Т а^- ) = t_f, будущее, надвигающееся время,

(а⁺T о Т а^- )= (а⁺T а^- ) = t, настоящее, «остановившееся время», «сейчас», как слившееся прошлое и будущее.

Действие этих же операторов на «здесь» по аналогии с тем, как были получены операторы времени,  даёт возможность получить три измерения пространства:

(а⁺Х) = х,

(Х а^- ) = у,

(а⁺Х о Х а^- ) = (а⁺Х а^- ) = z,

которые можно объединить в понятия трёхмерного пространства и трёхмерного времени:

(x о y о z)_*(x о y о z)  = (t_pо t_f о t ) ,

(t_pо t_f о t )_*(t_p о t_f  о t ) = (x о y о z),

 а затем  синтезировать понятие пространства  времени:

((x о y о z)_*(t_p о t_f  о t )) = Ŧ.

В подсистеме объекта рассмотрения за исходные понятия  возьмём: частицу – m и поле - p. Переход от частицы к полю есть понятие «делокализации» (m _* p), и наоборот переход от поля к частице есть процесс «локализации» (p _* m).  На макроскопическом уровне рассмотрения частицу и поле можно заменить следующими парами: телом - М и средой - Р, вещью - V и процессом -W, объектом -О и субъектом - С. Здесь делокализация необязательно сопровождается исчезновением тела и, соответственно, необязательно полное исчезновение среды в процессе локализации.  Интересно, что явление синонимии наблюдается и в SL. Так, понятие «локализации» можно получить, умножая а⁺ на m,  а^- на p или (p _* m).

Построим простейшую системную (морфологическую) таблицу 1, в которой перемножим в качестве супероператоров понятия из подсистемы движения и понятия из подсистемы объекта, и таблицу 2, составленную из понятий подсистемы пространства-времени и подсистемы объекта.

 

Таблица №1  Морфологическая таблица умножения супероператоров подсистемы движения  и подсистемы объекта

частица - m

поле - p

тело - M

среда - Р

вещь - V

процесс - W

О - объект

С - субъект

у - покой

местонахож-дение

стационар-ность

неподвиж-ность статичность

лежать простираться наполнять

находится

неизменность

недвижимость расположение

неподвиж-ность

ў - движение

перемещение

динамика возмущение

кинематика смещение

сползание течение, сдвиг,

движение перемещение

процесс изменение

передвижение

передвиже-ние

а+- рождение движения

делокали-зация

излучение

ускорение

смещение истечение

разгон ускорение

инициация

ускорение разгон

старт разбег

а- - уничтожение движения

локализация

поглощение

торможение

остановка

остановка торможение

стагнация застой угасание

остановка

Финиш

t - квант движения

скачок тунеллирова-ние

мода

перемещение импульс

сдвиг

импульс

цикл период

пауза, цикл

Прыжок

х - квант покоя

остановка

квазистацио-нарность

остановка

застой

лежать покоиться

пауза

стоять находиться

отдых передышка

v-- отклонение

отклонение

флуктуация

занос

отклонение

наклон отклонение

отклонение флуктуация

накат

уклонение толкание

v+- возвращение

возвращение

релаксация

выправление

отток, откат

выпрямление

восстанов-ление

откат

Отход

v - колебание

колебания

осцилляция

вибрация качание

вибрация

дрожание флаттер

флуктуации

тряска обертон раскачивание

дрожание виляние трепетание

ω - вращение

спин момент (мех.) спиральность ротатор

поляризация вихревое поле ротор

вращательный момент кручение верчение

вихрь торнадо смерч воронка

волчок гироскоп ротор

вращение круговорот

заворот вращение вертеть(ся)

вертеться крутиться выворачи- ваться

λ - волновое движение

солитон

волна

стоячая волна

волна

изгибание

волновой процесс

извиваться

δ+-поступат. движение вперёд

перемещение

фронт

перемещение

течение прилив

перемещение

ход

передвижение

идти, ползти бежать

δ- - обратное поступат. движение

возвращение

обращение фронта

возвращение отражение отскок

отлив отток

отскок

реверс

возврат

пятиться отступать

(δ+*δ-) - поворот

поворот

искривление

сворачивать

обтекание огибание

поворачива-ние

обращение

поворот

поворот разворот

.

Таблица №2  Морфологическая таблица умножения супероператоров подсистем пространства - времени и объекта.

	частица – m	р – поле	тело – M	среда – Р	вещь – V	процесс – W	О – объект	С – субъект
Т – время	время жизни	квант	собственное время	существование	существова-ние	длительность	существование	жизнь
Х – место  здесь	положение координата	область	располо-жение	область объем	местонахож-дение	локализация	находится располагается	пребывание территория
(а+Т) – прошлое	рождение	излучение	появление	возникновение	новая	начало старт	новый	молодость
(а+T а-) –настоящее сейчас	жизнь	существо-вание	пребывание	существование	функциони-рующая современная	протекание осуществление прохождение	современный	зрелость
(Т а- ) – будущее	распад	поглощение	исчезновение	уничтожение	старая	завершение окончание	старый	старость
x,y,z – измерения	нульмерное		трёхмерное	трёхмерное	трёхмерная		трёхмерный	трёхмерный
Ŧ – простр.-время	событие	область	объём	объём область	пребывание	осуществление	история	биография
Кх –расстояние	мат. точка, размер	объём	сечение, диаметр	протяжённость	размер	коридор	длина, ширина, высота	рост

 

Произведению операторов в таблицах ставились в соответствие лексемы русского языка независимо от того, какая это часть речи, так как в метаязыке часть речи задаётся параметром. В данном же случае нас интересовала возможность интроспективного покрытия поля понятий языка SL понятиями естественного (в данном случае русского) языка.

На пересечении строк и столбцов находятся понятия, соответствующие умножению операторов (насколько это возможно точно на данном этапе). Например, в первой ячейке таблицы на пересечении столбца <частица – m> и строки <у – покой> находится понятие, образованное от их произведения уm – (покой частицы) – местонахождение (а также, местоположение, нахождение,…). Так, если частица покоится, то обычно говорят «частица находится в точке А».

Некоторые клеточки таблицы остались незаполненными. Мы затрудняемся окончательно ответить на вопрос, отсутствуют ли эти понятия в языке или они просто не найдены нами. Из таблицы видно, что понятия, расположенные вдоль строк, часто являются синонимами, тем более, если они образованы для близких и синонимичных понятий: частицы, тела, объекты. Понятия же, в столбцах, как правило, попарно противоположны или являются антонимами. Результаты, размещённые в таблице, имеют приближённый характер, что особенно хорошо видно для столбца «Субъект». Эта таблица является всего лишь словарём второго порядка (если считать, что исходные понятия по строкам и столбцам - словари первого порядка). Дальнейшее построение приведёт к словарям третьего, четвертого порядка и так далее. Вопрос, на каком порядке остановиться имеет сугубо практическое значение и зависит от характера решаемых задач и ресурсов, требуемых для их решения. Однако совершенно очевидно, что идеального и полного соответствия не будет ни в каком порядке, так как невозможно точное описание слова в принципе. Те понятия в таблице, которые не достаточно абстрактны, получат свое более точное определение в словарях более высоких порядков, остальные же останутся, как есть, единственно к ним добавятся семантические поля, темы и параметры.

6.Запись текста на языке SL

 

6.1. Спецификация вспомогательных символов

( ) – скобки, обозначающие целостное понятие, понятие в скобках вставляется внутрь основного понятия  как ссылка, например, ((а_*г)_*(о_*р_*а));

[] - скобки обозначающие семантическое поле, например, [(г_*о)<чел>];

< > - скобки, обозначающие тему (тематические пометы);

// -скобки для параметров частей речи, n – существительное, v – глагол, adj – прилагательное, num – числительное, adv – деепричастие, prts – причастие, prep – предлог, part – частица;

|| -скобки для морфологических параметров;

_* - разделитель, операция перехода понятий;

 индексы: 1, 2, 3, 4, .. -номера фазы или состояния (твердое, жидкое, газообразное, плазма..);

+ атрибут появления чего – либо;

- атрибут исчезновения чего – либо;

o - операция объединения понятий ;

, - разделитель перечисления;

É - символ включения;

Î - символ принадлежности;

 

6.2. Пример использования SL для синтеза производных понятий

о, а, у, и, ы, э    – свойства;

б, д, г, в, т, h, к, п, х, ф, з, с ш,  ..  - сущности, например, г - потребление,  использование, б - принадлежность, связь, р- движение;

фазы: о1 - твердое вещество, о2 – жидкость,  о3 – газ;

фазы со ссылкой: о1 <геогр> - грунт, о2<геогр> - воды, о3<геогр> - воздух;

(о1_*б) - твердое вещество с функцией связывания (например, цемент);

 (г_*о)<чел> - человек, без тематической ссылки просто потребитель;

(г_*о1) <фауна> - животное;

(г_*о2) <фауна> - рыба или водоплавающее животное;

(г_*о3)< фауна > - птица или насекомое, (г_*о)<био> - живое;

(о_*р)/n/<дв> – вращение (как процесс) , (о_*р)/v/<общ>  – вращать;

(о_*р_*о)/n/<дв> - цикл, вращение;

(о_*р_*а)/n/<дв>  - движение вращательное переходит в поступательное;

(а_*р)/n/<дв>  – движение прямолинейное, поступательное;

(у_*р)/n/<дв>  - приближение, (и_*р)/n/<дв>  - удаление,

(у_*р_*и)/n/<дв>  - колебание;

((о_*р)_*(а_*р)) - колесо – орудие, преобразующее вращательное движение в поступательное;

((χьоо<гео>)_*(а_*р))/n/<общ> - дорога -ограниченная часть пространства (земли), предназначенная для движения;

 ((а_*р)_*(г_*о)<чел>) - транспорт (орудие при помощи которого человек потребляет движение);

((а_*г)_*(о_*р_*а)) - двигатель, орудие (преобразующее) использующее активное вещество (а_*г) для  движение (о_*р_*а);

((а2_*г_*а3)_*(о_*р_*а)) - двигатель внутреннего сгорания;

Автомобиль - транспортное средство с двигателем внутреннего сгорания на колесах движущееся по грунтовым дорогам – ((а_*р)_*(г_*о))<чел>É((а2_*г_*а3)_*(о_*р_*а))) [(((χьоо<гео>)_*(а_*р))/n/<общ>)]

(а_*р)[(г_*о)<чел>] – бежать;

(а_*р)[(а_*р)_*(г_*о)<чел> ]- ехать.

Пример записи предложения: «Автомобиль ехал по грунтовой дороге»:

((а_*р)_*(г_*о))<чел>É((а2_*г_*а3)_*(о_*р_*а)))[(((χьоо<гео>)_*(а_*р))/n/<общ>)] (а_*р)[((а_*р)_*(г_*о))<чел>] ((χьоо<гео>)_*(а_*р))/n/<общ>.

Запись можно заметно упростить, если скобки «( )» и знак умножения «_*» использовать только там где они действительно необходимы, а семантические поля хранить в отдельной информационной базе. Тогда предложение будет иметь вид:

(ар_*го)<чел>É(а2га3_*ора) (ар)((χьоо<гео>)_*(ар))/n/<общ>.

7. Заключение

         В работе изложены основные положения необходимые для разработки методологии трансляции знаний между различными научными областями. Стержнем методологии являются семантический язык SL  и теория лингвистических супероператоров. Мы предполагаем, что система понятий всякой области знаний структурно представляет собой некий  универсальный фрактал. Важный вклад в его изучение внесла классическая немецкая философия, хотя в те времена понятие фрактала ещё не существовало. Наши чисто теоретические исследования, опирающиеся на анализ исторического  развития философских систем, должны быть подкреплены экспериментальными исследованиями, которые мы намерены осуществить на базе машинного переводчика «Магнус», разработанного в лаборатории АСОЛИ. Адекватность наших представлений об универсальном фрактале можно проверять, пытаясь транслировать знания из одной области науки в другую. Одновременно мы получим инструмент для заполнения белых пятен в той или иной предметной области.

Литература

1.V.V.Koulikov, http://www.pycbi.com/science/UnivInfoSpace.html

2. Куликов В.В., Ёлкин С.В. Супероператоры и теория информационного взаимодействия Материалы 8-го научно-практического семинара "Новые информационные технологии".М.:МГИЭМ,  2005, С. 150-193.

3. Ёлкин С.В. Информационное исчисление Вестник ВИНИТИ НТИ. 2002. сер 2, N11. С17-24.

4. Ёлкин С.В., Игашов С.Ю. Алгебра у-чисел: возможности в области построения функций и множеств  Препринт ИПМ им. М.В.Келдыша РАН   N 60 за 2005г.

5. Куликов В.В., Гаврилов Д.А., Елкин С.В., Универсальный искусственный язык- “hOOM-Диал”. -М.:  Гэлэкси Нэйшн, 1994, -113 с.

6.Ёлкин С.В. Открытый cемантический язык SL. Вестник ВИНИТИ НТИ. 2003. сер 2, N4. С.5-15

7. http://www.ura.mephist.ru/

8. Куликов В.В., Ёлкин С.В. От информационного исчисления к теории супероператоров Материалы 8-го научно-практического семинара "Новые информационные технологии". М.:МГИЭМ,  2005, С. 194-223.