Применение реактивных двигателей для управления поступательным движением КА
одновременно с разгрузкой кинетического момента электромеханических исполнительных органов
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
(2) |

Рассмотрим следующую задачу: сформировать с помощью РД
некоторый заданный вектор корректирующего импульса ![]() , таким образом, чтобы при работе РД одновременно было
сформировано заданное приращение кинмомента КА
, таким образом, чтобы при работе РД одновременно было
сформировано заданное приращение кинмомента КА ![]() . Здесь
. Здесь ![]() - проекция КИ на ось X,
- проекция КИ на ось X, ![]() - проекция КИ на ось Y,
- проекция КИ на ось Y, ![]() - проекция КИ на ось Z,
- проекция КИ на ось Z, ![]() - проекция приращения кинетического момента на ось OX,
- проекция приращения кинетического момента на ось OX, ![]() - проекция приращения кинетического момента на ось OY,
- проекция приращения кинетического момента на ось OY, ![]() - проекция приращения кинетического момента КУДМ на ось OZ.
- проекция приращения кинетического момента КУДМ на ось OZ.
Импульс силы, создаваемый реактивными двигателями: 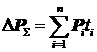 , приращение вектора кинетического момента (импульс момента):
, приращение вектора кинетического момента (импульс момента):
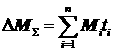 где
где ![]() - время работы РД.
- время работы РД.
Потребуем, чтобы выполнялась система уравнений:
|
|
(3) |
Здесь
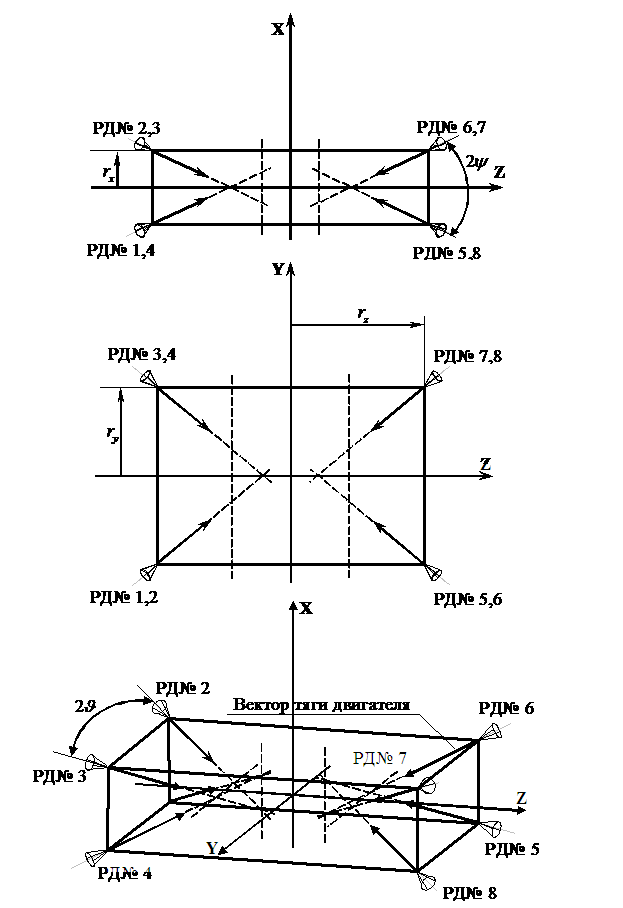
j,k,l,m,q,s – номера РД, установленных на КА (см. рисунок 1) и
определяющих РД, которые необходимо включить на время, определяемое вектором ![]() чтобы обеспечить
выполнение поставленной задачи. Данная система уравнений содержит 6 переменных,
то есть требуется включение 6 реактивных двигателей. Искомой величиной является
вектор
чтобы обеспечить
выполнение поставленной задачи. Данная система уравнений содержит 6 переменных,
то есть требуется включение 6 реактивных двигателей. Искомой величиной является
вектор ![]() . Решение системы в матричном виде:
. Решение системы в матричном виде: ![]() (4)
(4)
Здесь
![]() - вектор, состоящий из
компонент заданных векторов корректирующего импульса и приращения кинетического
момента КА;
- вектор, состоящий из
компонент заданных векторов корректирующего импульса и приращения кинетического
момента КА;
|
|
- матрица, характеризующая силы и
моменты, создаваемые выбранной группой из 6 РД. i –
обозначает сочетание номеров j,k,l,m,q,s двигателей, таких, что: |
Для
n=8
существует 28 сочетаний j,k,l,m,q,s,
удовлетворяющих условиям (5).
Можно утверждать, что задача формирования заданного
импульса силы одновременно с заданным приращением кинетического момента решена,
если для заданного вектора ![]() существует такое сочетание j,k,l,m,q,s, для
которого решение (4) системы (3) даёт вектор
существует такое сочетание j,k,l,m,q,s, для
которого решение (4) системы (3) даёт вектор ![]() , все компоненты которого неотрицательны. То есть сохраняется
физический смысл компонент вектора
, все компоненты которого неотрицательны. То есть сохраняется
физический смысл компонент вектора ![]() , определяющих время работы соответствующих реактивных
двигателей.
, определяющих время работы соответствующих реактивных
двигателей.
Предположим, что схема установки РД на КА симметрична
относительно центра масс КА. То есть модули проекций сил и моментов РД на связанные
оси КА одинаковы для всех РД (что может быть обеспечено конструктивно):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() , i=j,k,l,m,q,s.
, i=j,k,l,m,q,s.
Это обеспечивается равенством с точностью до знака
углов установки и координат точек приложения сил РД. Зададим значения углов
установки и координат точек приложения сил РД для схемы на рис. 1. В таблице 1 ![]() ,
,![]() - углы установки i-го РД,
- углы установки i-го РД, ![]() ,
,![]() ,
,![]() - координаты установки i-го РД.
- координаты установки i-го РД.
Таблица 1.
|
№РД |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
8 |
|
|
|
|
|
В системе (3) разделим обе части уравнения на величину
![]() модуля тяги РД, получим
в матричном виде:
модуля тяги РД, получим
в матричном виде:
|
|
(6) |
Введём обозначения:
|
|
(7) |
где
![]() - модуль тяги РД;
- модуль тяги РД; ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() есть величины,
рассчитанные по соотношениям (1) и (2) с для заданных величин
есть величины,
рассчитанные по соотношениям (1) и (2) с для заданных величин ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Величины
. Величины ![]() не зависят от
характеристик конкретных РД и характеризуются только углами установки и координатами
РД.
не зависят от
характеристик конкретных РД и характеризуются только углами установки и координатами
РД.
Матрицы ![]() для различных
вариантов сочетаний номеров j,k,l,m,q,s можно
представить ввиде произведения диагональной матрицы S на матрицу N, элементами которой являются +1 и -1.
для различных
вариантов сочетаний номеров j,k,l,m,q,s можно
представить ввиде произведения диагональной матрицы S на матрицу N, элементами которой являются +1 и -1.
![]() ,
где
,
где  ,
, 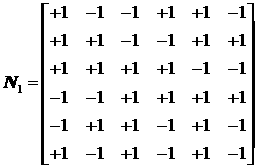 .
.
Матрица S
определяется параметрами установки РД, матрица Ni определяется сочетанием номеров включаемых РД.
Определитель матрицы ![]() :
: ![]() , где
, где ![]() ,
, ![]() в зависимости от
сочетания РД. Таким образом, для 16 вариантов сочетаний
в зависимости от
сочетания РД. Таким образом, для 16 вариантов сочетаний ![]() или
или ![]() ; для 12 вариантов
; для 12 вариантов ![]() , Здесь
, Здесь
![]() . То есть для 16 вариантов сочетаний номеров РД из 28
возможных можно записать аналитическое выражение для матрицы
. То есть для 16 вариантов сочетаний номеров РД из 28
возможных можно записать аналитическое выражение для матрицы ![]() и рассмотреть условия
неотрицательности компонент вектора
и рассмотреть условия
неотрицательности компонент вектора ![]() .
.
Рассмотрим далее матрицу ![]() для группы РД с
номерами 1,2,3,4,5,6 и запишем выражения для решения системы (6), то есть
компонент вектора
для группы РД с
номерами 1,2,3,4,5,6 и запишем выражения для решения системы (6), то есть
компонент вектора ![]() .
.
В этом случае:
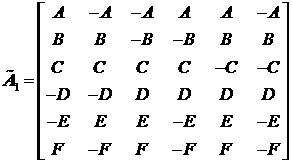 .
.
Найдём
матрицу ![]() . Воспользуемся соотношением:
. Воспользуемся соотношением: ![]() ,
,
где
 ,
,
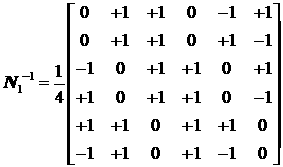 .
.
Для рассматриваемой матрицы:
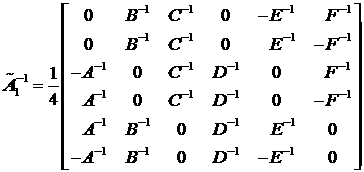 .
.
Выражения
для компонент вектора ![]() :
:
|
|
(8) |
Здесь ![]() - компоненты вектора
- компоненты вектора ![]() (см. выражения 6).
(см. выражения 6).
Из
условия неотрицательности компонент вектора ![]() имеем систему неравенств:
имеем систему неравенств:
 (9)
(9)
Положим ![]() , то есть потребуем, чтобы кинетический момент КА не
изменился в процессе формирования корректирующего импульса. В этом случае неравенства
(9) записывается в виде:
, то есть потребуем, чтобы кинетический момент КА не
изменился в процессе формирования корректирующего импульса. В этом случае неравенства
(9) записывается в виде:  или, учитывая выражения
(1) и (7):
или, учитывая выражения
(1) и (7):
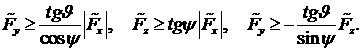 (10)
(10)
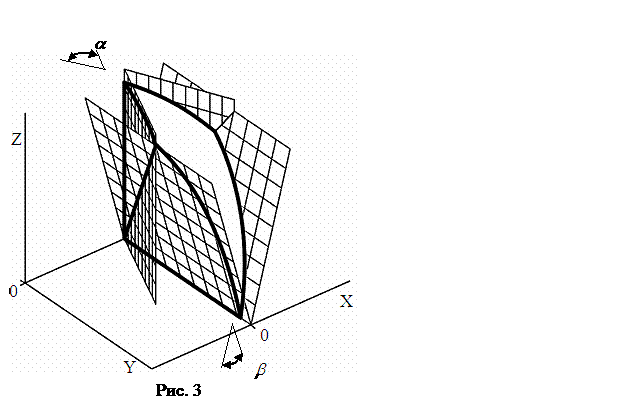
Последнее
неравенство в системе (10), учитывая положительность углов ![]() и
и ![]() , автоматически получается из первых двух неравенств. Таким
образом, в пространстве направлений векторов корректирующего импульса область,
в которой выполняются неравенства (10), ограничена 4 плоскостями (см. рисунок
3), положение которых определяется геометрией схемы установки РД.
, автоматически получается из первых двух неравенств. Таким
образом, в пространстве направлений векторов корректирующего импульса область,
в которой выполняются неравенства (10), ограничена 4 плоскостями (см. рисунок
3), положение которых определяется геометрией схемы установки РД.
Углы
между плоскостями равны: 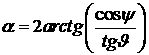 ,
, 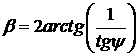 .
.
 Для оценки суммарного огневого времени просуммируем
уравнения (8). Суммарное огневое время равно
Для оценки суммарного огневого времени просуммируем
уравнения (8). Суммарное огневое время равно 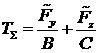 . Данное выражение можно представить, как скалярное
произведение двух векторов
. Данное выражение можно представить, как скалярное
произведение двух векторов ![]() , где
, где ![]() ,
, ![]() . В выражение для величины
. В выражение для величины ![]() не входит составляющая
не входит составляющая
![]() и для заданного вектора
и для заданного вектора
![]() , компоненты которого удовлетворяют условиям (10) огневое
время уменьшается с увеличением составляющей
, компоненты которого удовлетворяют условиям (10) огневое
время уменьшается с увеличением составляющей ![]() за счёт
соответствующего уменьшения
за счёт
соответствующего уменьшения ![]() и
и ![]() . Вектор
. Вектор ![]() определяется первыми
тремя компонентами вектора
определяется первыми
тремя компонентами вектора ![]() - величиной заданного
корректирующего импульса, а вектор
- величиной заданного
корректирующего импульса, а вектор ![]() - геометрическими характеристиками схемы управления.
Скалярное произведение векторов максимально тогда, когда угол между векторами
равен нулю, то есть вектора
- геометрическими характеристиками схемы управления.
Скалярное произведение векторов максимально тогда, когда угол между векторами
равен нулю, то есть вектора ![]() и
и ![]() совпадают по направлению.
Следовательно, данное сочетание РД имеет наименьшую эффективность в направлении
вектора
совпадают по направлению.
Следовательно, данное сочетание РД имеет наименьшую эффективность в направлении
вектора ![]() . Компоненты вектора корректирующего импульса в этом случае:
. Компоненты вектора корректирующего импульса в этом случае:
![]() ,
,  ,
, ![]() .
.
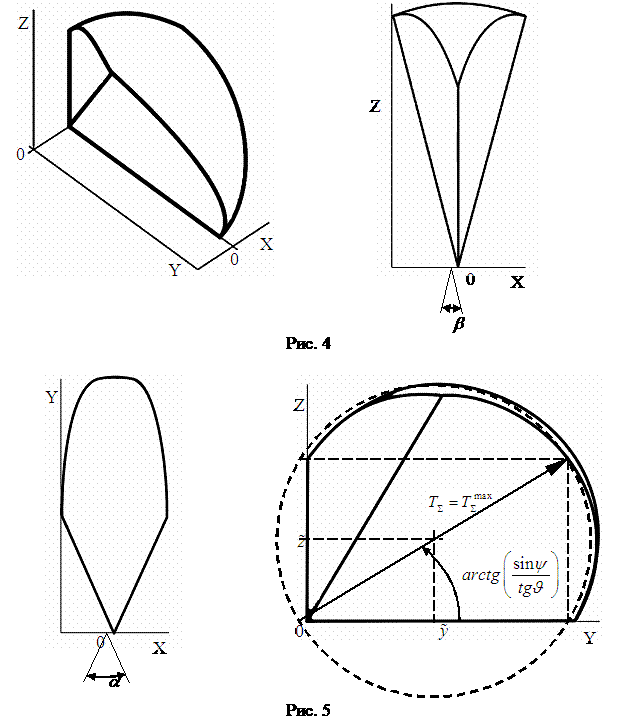
В пространстве направлений вектора корректирующего
импульса, имеющего модуль ![]() можно построить
область значений суммарного огневого времени, образованную векторами,
направление которых совпадает с направлением корректирующего импульса, а модуль
равен суммарному огневому времени РД. Такая область представляет собой часть
сферы (см. рис. 4 и 5) диаметром, равным максимальному огневому времени:
можно построить
область значений суммарного огневого времени, образованную векторами,
направление которых совпадает с направлением корректирующего импульса, а модуль
равен суммарному огневому времени РД. Такая область представляет собой часть
сферы (см. рис. 4 и 5) диаметром, равным максимальному огневому времени: 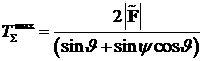 , координаты центра которой равны:
, координаты центра которой равны: 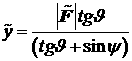 ,
, 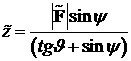 . Часть сферы отсекается плоскостями, изображёнными на рис.
3. Если в неравенствах (9) компонента
. Часть сферы отсекается плоскостями, изображёнными на рис.
3. Если в неравенствах (9) компонента ![]() , то неравенства принимают вид:
, то неравенства принимают вид:
|
|
(11) |
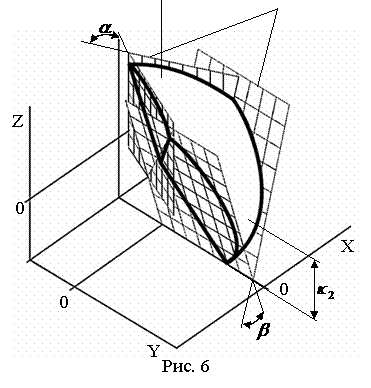
В пространстве единичных векторов корректирующего
импульса область, в которой выполняются условия системы (11), ограничена 4
коническими поверхностями с вершинами в начале координат, высоты которых лежат
в плоскостях XZ и XY, а основания которых параллельны плоскостям, взаимное
угловое положение которых (углы ![]() и
и ![]() ) соответствует рисунку 3, однако плоскости эти сдвинуты по
осям Y и Z на величины
соответственно
) соответствует рисунку 3, однако плоскости эти сдвинуты по
осям Y и Z на величины
соответственно ![]() и
и ![]() (см. рисунок 6). Углы
при вершинах конических поверхностей равны, соответственно
(см. рисунок 6). Углы
при вершинах конических поверхностей равны, соответственно
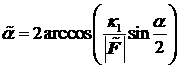 ,
,
 . Суммарное огневое время равно
. Суммарное огневое время равно  . Данное выражение можно представить, как сумму скалярного
произведения двух векторов
. Данное выражение можно представить, как сумму скалярного
произведения двух векторов ![]() и
и ![]() и константы
и константы ![]() :
: ![]() . Аналогично предыдущему
случаю, скалярное произведение векторов максимально тогда, когда угол между
векторами равен нулю, то есть вектора
. Аналогично предыдущему
случаю, скалярное произведение векторов максимально тогда, когда угол между
векторами равен нулю, то есть вектора ![]() и
и ![]() совпадают по направлению.
Добавка огневого времени
совпадают по направлению.
Добавка огневого времени ![]() на создание импульса
момента вокруг оси Х не зависит от направления вектора корректирующего
импульса. Для заданной величины модуля вектора корректирующего импульса
на создание импульса
момента вокруг оси Х не зависит от направления вектора корректирующего
импульса. Для заданной величины модуля вектора корректирующего импульса ![]() и величины
и величины ![]() , область значений суммарного огневого времени, образованная
векторами, направление которых совпадает с направлением корректирующего импульса,
а модуль равен суммарному огневому времени РД представляет собой фигуру,
образованную суммой двух сфер: сферы радиуса
, область значений суммарного огневого времени, образованная
векторами, направление которых совпадает с направлением корректирующего импульса,
а модуль равен суммарному огневому времени РД представляет собой фигуру,
образованную суммой двух сфер: сферы радиуса ![]() (огневое время на создание импульса момента
(огневое время на создание импульса момента ![]() ) с центром в начале координат, и сферы, аналогичной изображённой
на рис. 5, диаметром, равным максимальному огневому времени на корректирующий
импульс:
) с центром в начале координат, и сферы, аналогичной изображённой
на рис. 5, диаметром, равным максимальному огневому времени на корректирующий
импульс: 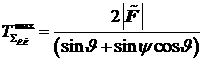 , координаты центра которой равны:
, координаты центра которой равны:
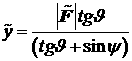 ,
, 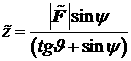 .
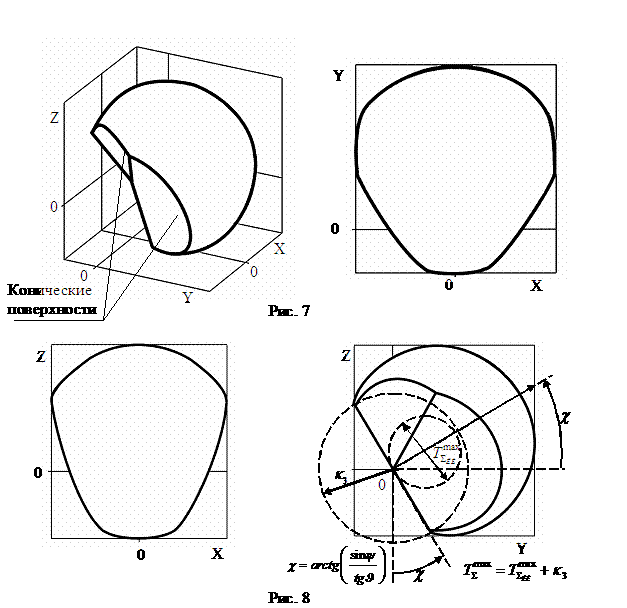
Фигура ограничена четырьмя
описанными выше коническими поверхностями, а также, при некоторых значениях
.
Фигура ограничена четырьмя
описанными выше коническими поверхностями, а также, при некоторых значениях ![]() и
и ![]() , плоскостью, определяемой третьим неравенством выражения
(11) (см. рисунки 7,8). Эта плоскость перпендикулярна направлению, в котором
достигается максимальное значение потребного огневого времени
, плоскостью, определяемой третьим неравенством выражения
(11) (см. рисунки 7,8). Эта плоскость перпендикулярна направлению, в котором
достигается максимальное значение потребного огневого времени ![]() .
.
![]()

![]()
Если в неравенствах (9) положить ![]() , то неравенства принимают вид:
, то неравенства принимают вид:
|
|
(12) |
Здесь 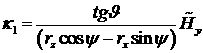 ,
,
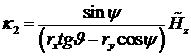 ,
,

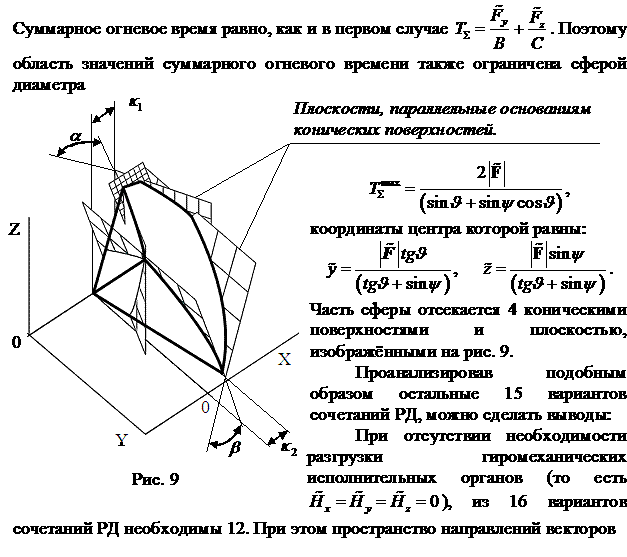
В пространстве единичных векторов корректирующего
импульса область, в которой выполняются неравенства (12), ограничена 4
коническими поверхностями с вершинами в начале координат, высоты которых лежат
в плоскостях XZ и XY, а основания которых параллельны плоскостям, взаимное
угловое положение которых (углы ![]() и
и ![]() ) соответствует рисунку 3, однако плоскости эти сдвинуты по
оси X на величины соответственно
) соответствует рисунку 3, однако плоскости эти сдвинуты по
оси X на величины соответственно ![]() и
и ![]() (см. рисунок 9). Углы
при вершинах конических поверхностей равны, соответственно
(см. рисунок 9). Углы
при вершинах конических поверхностей равны, соответственно 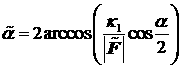 ,
, 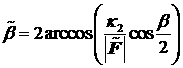 .
.
Данная
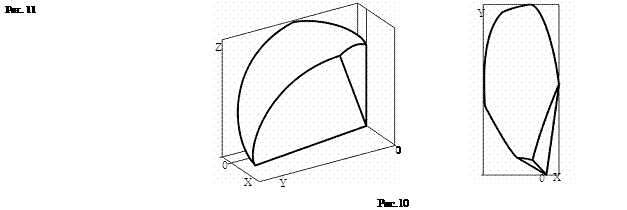
область также, при определённых значениях ![]() , ограничена полуплоскостью, определяемой третьим
неравенством выражения (12). Плоскость, определяющая эту полуплоскость,
перпендикулярна плоскости YZ, наклонена
под углом
, ограничена полуплоскостью, определяемой третьим
неравенством выражения (12). Плоскость, определяющая эту полуплоскость,
перпендикулярна плоскости YZ, наклонена
под углом 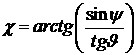 к плоскости XY и смещена от начала координат на величину
к плоскости XY и смещена от начала координат на величину ![]() по оси Y (см. рисунки 10,11).
по оси Y (см. рисунки 10,11).
корректирующего импульса делится 6-ю плоскостями
(см. рисунок 14) на 12 частей. Уравнения плоскостей:
|
|
|
На
рис. 12 цифрами обозначены сочетания РД, которые дают неотрицательные решения
уравнений (4). При этом рабочие области всех 12 групп не пересекаются и между
ними нет пустых областей, в которых система (4) не имеет неотрицательных решений.
Таким образом схема управления, состоящая из 8-ми РД обеспечивает возможность
выдачи корректирующего импульса, произвольно ориентированного в связанной с КА
системе координат, сохраняя при этом исходное (до начала КИ) состояние
комплекса двигателей-маховиков (или гиродинов). При наличии ненулевых ![]() данные 6 плоскостей
подвергаются смещению на величины, пропорциональные
данные 6 плоскостей
подвергаются смещению на величины, пропорциональные ![]() . При этом также рабочие области различных групп РД не
пересекаются и не образуют пустых областей. В зависимости от соотношения
величин корректирующего импульса и импульса момента появляются области значений
КИ, в которых задействуются 4 группы, не используемые в случае отсутствия импульсов
моментов. На рис. 13 приведён пример, когда наряду с КИ обеспечиваются заданные
ненулевые приращения кинмомента КА.
. При этом также рабочие области различных групп РД не
пересекаются и не образуют пустых областей. В зависимости от соотношения
величин корректирующего импульса и импульса момента появляются области значений
КИ, в которых задействуются 4 группы, не используемые в случае отсутствия импульсов
моментов. На рис. 13 приведён пример, когда наряду с КИ обеспечиваются заданные
ненулевые приращения кинмомента КА.
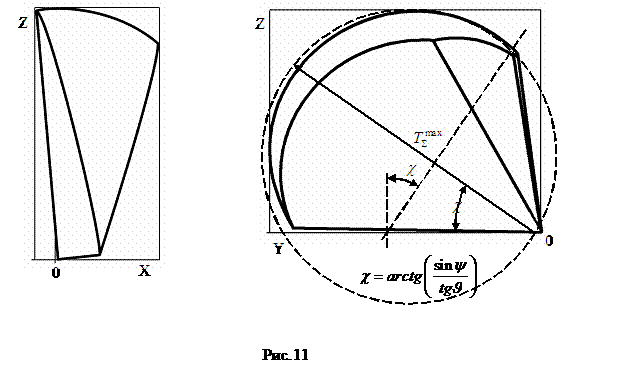
Область, характеризующая суммарное огневое время,
потребное на проведение КИ и возможную разгрузку ДМ или ГД в зависимости от
направления КИ, состоит из набора фигур, описанных выше (см. рис.
4,5,7,8,10,11). Пример такой области приведён на рис. 14. Если в направлении
единичного вектора корректирующего импульса отложить величину, обратную суммарному
огневому времени, получим область характеризующую возможности данной схемы
управления по располагаемому (при данном запасе рабочего тела) суммарному
корректирующему импульсу при наличии того или иного потребного момента импульса
на разгрузку исполнительных органов за время службы КА. Например, если ![]() , то такая область приобретает форму, показанную на рис. 15.
Допустим, в процессе эксплуатации, КА подвергается некоторым внешним возмущающим
моментам и необходима периодическая разгрузка исполнительных органов КА некоторым
характерным значением импульса момента. В этом случае область располагаемых
значений суммарного корректирующего импульса
может выглядеть, например, как показано на рис 16.
, то такая область приобретает форму, показанную на рис. 15.
Допустим, в процессе эксплуатации, КА подвергается некоторым внешним возмущающим
моментам и необходима периодическая разгрузка исполнительных органов КА некоторым
характерным значением импульса момента. В этом случае область располагаемых
значений суммарного корректирующего импульса
может выглядеть, например, как показано на рис 16.
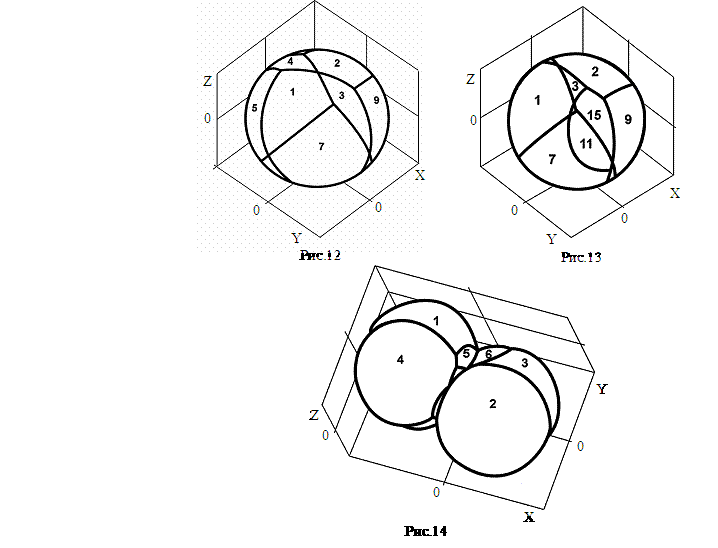
Исследуя и анализируя эту область, можно
скорректировать схему управления КА с учётом характерных особенностей данного
КА по разгрузке исполнительных органов.
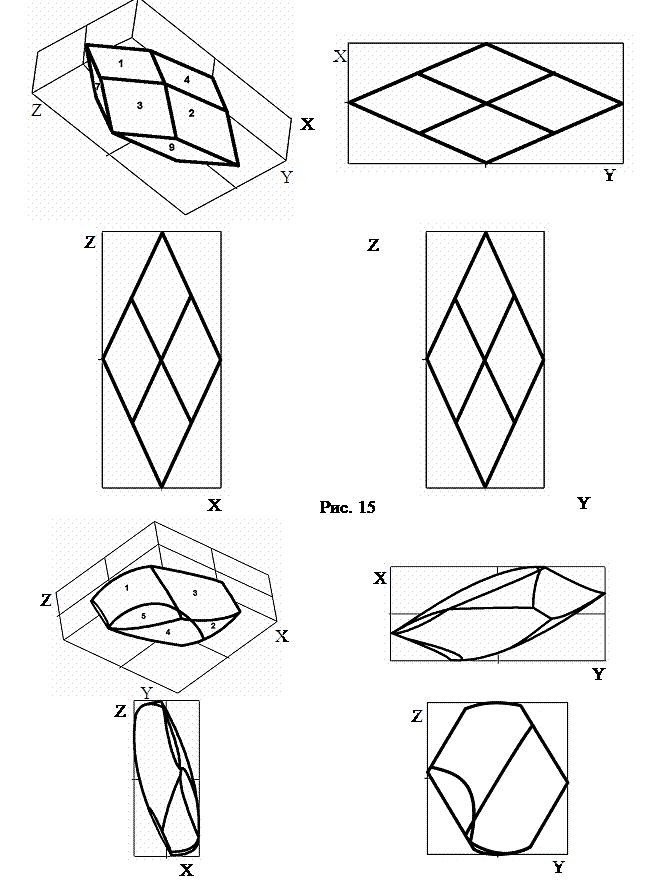
Рис.16
Определим условия, по которым можно найти для
заданного вектора ![]() нужное сочетание РД.
нужное сочетание РД.
Введём обозначения:
|
|
(13) |
Данные величины имеют размерность времени. Определим
так же соотношения:
|
|
|
|
|
(14) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В таблице 2 c учётом
подстановки матриц ![]() в выражение (4) и вышеприведённых
соотношений (13) и (14) приведены выражения для компонент вектора
в выражение (4) и вышеприведённых
соотношений (13) и (14) приведены выражения для компонент вектора ![]() и условия их неотрицательности
для всех 16 вариантов сочетаний РД. В таблице номером обозначены сочетания
включаемых РД.
и условия их неотрицательности
для всех 16 вариантов сочетаний РД. В таблице номером обозначены сочетания
включаемых РД.
Таблица 2.
|
№ |
Условия
неотрицательности |
Компоненты
вектора |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
По этим зависимостям, для заданного вектора ![]() можно выбрать
пригодную группу из 6 РД и определить время работы каждого РД в группе. Соответствие
номеров сочетаний и номеров РД, показанных на рис. 1, приведено в таблице 3.
можно выбрать
пригодную группу из 6 РД и определить время работы каждого РД в группе. Соответствие
номеров сочетаний и номеров РД, показанных на рис. 1, приведено в таблице 3.
Таблица 3.
|
№ |
i |
j |
k |
l |
M |
n |
№ |
i |
j |
k |
l |
m |
n |
|
1 |
1 |
2 |
3 |
4 |
5 |
6 |
9 |
1 |
2 |
5 |
6 |
7 |
8 |
|
2 |
1 |
2 |
3 |
4 |
5 |
8 |
10 |
1 |
3 |
4 |
5 |
6 |
7 |
|
3 |
1 |
2 |
3 |
4 |
6 |
7 |
11 |
1 |
3 |
4 |
5 |
7 |
8 |
|
4 |
1 |
2 |
3 |
4 |
7 |
8 |
12 |
1 |
4 |
5 |
6 |
7 |
8 |
|
5 |
1 |
2 |
3 |
5 |
6 |
7 |
13 |
2 |
3 |
4 |
5 |
6 |
8 |
|
6 |
1 |
2 |
3 |
5 |
7 |
8 |
14 |
2 |
3 |
4 |
6 |
7 |
8 |
|
7 |
1 |
2 |
4 |
5 |
6 |
8 |
15 |
2 |
3 |
5 |
6 |
7 |
8 |
|
8 |
1 |
2 |
4 |
6 |
7 |
8 |
16 |
3 |
4 |
5 |
6 |
7 |
8 |
Литература
1. Гантмахер Ф. Р. Теория матриц. М., Наука, 1966.
2. Белецкий В. В. Движение искусственного спутника
относительно центра масс. М., Наука, 1965.
3. Раушенбах Б.В., Токарь Е.Н. Управление ориентацией
космических аппаратов. М., Наука, 1974.
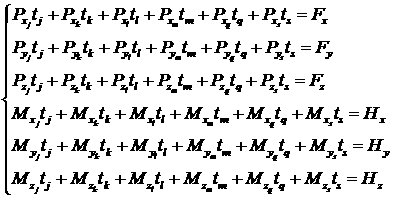
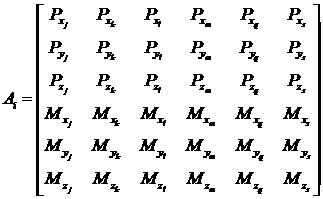

 .
.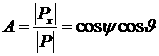 ,
,
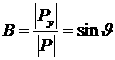 ,
,
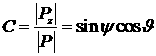 ,
,
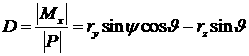 ,
,
 ,
,
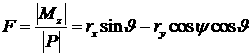 .
.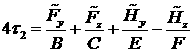
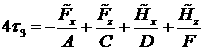
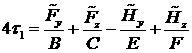


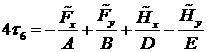
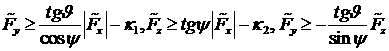 , где
, где 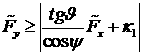 ,
,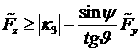 .
.
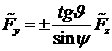
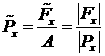 ,
,  ,
, 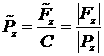 ,
, ,
, 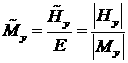 ,
,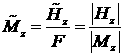 .
.