Методы численного моделирования квазистационарных электромагнитных полей в областях
с негладкими границами проводящих и диэлектрических подобластей
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
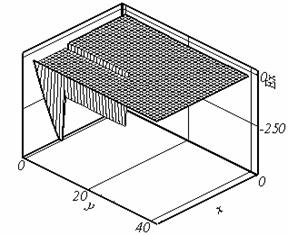
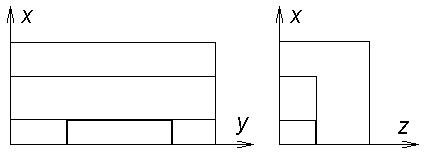
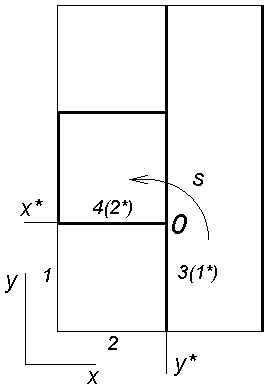
Рис. 0.1. Схема расчетной области. Здесь 1 — рельс, 2 — якорь. |
Целью
настоящей работы является построение эффективных алгоритмов численного
моделирования электромагнитных явлений и процессов в областях с негладкими
границами проводящих и диэлектрических подобластей.
Работа
выполнена при частичной финансовой поддержке Российского фонда фундаментальных
исследований (проект РФФИ № 06 – 01 – 00421) и Фонда содействия отечественной
науке.
§1.
Преобразование математической модели путем изменения калибровочных соотношений.
Для описания электромагнитных полей мы
будем использовать т.н. квазистационарное или МГД - приближение [1] уравнений
Максвелла.
rot H = 4 ps E,
rot E
- rot [u ![]() H] = -
H] = - ![]() , (1.1)
, (1.1)
div Н
= 0,
j = sE.
Здесь
и далее E и H — векторы напряженности электрического и магнитного
полей соответственно, j — вектор плотности тока, s — электропроводность, u — вектор скорости движения
вещества, r = (x, y, z) — радиус-вектор, t — время.
Система уравнений (1.1) записана в безразмерном виде. В ней E —
напряженность электрического поля в системе координат, в которой вещество
покоится. Будем обозначать через E* напряженность электрического поля в
неподвижной (лабораторной) системе координат. Здесь и всюду ниже в формульных
выражениях все величины даются в безразмерном виде (в частности, в (1.1) H
= B, где B — вектор магнитной индукции).
В дальнейшем используется постановка
задачи [1] для определения электромагнитных полей внутри области после введения
векторного потенциала A (H
= rot A).
Согласно
[1, 12] при расчете будем рассматривать не весь трехмерный ускоритель, а лишь
его часть, приходящуюся на область, жестко связанную с якорем и движущуюся
вместе с ним. Длина этой области (в направлении оси y) составляет
несколько калибров ускорителя в обе стороны от якоря (рис. 0.1). В силу
геометрической симметрии достаточно найти решение задачи в верхней половине
области в двумерном случае или в правой верхней четверти расчетной области в
трехмерном случае. Единственной заданной извне электромагнитной величиной можно
считать полный ток, определяемый в основном источником питания. В
рассматриваемом случае ненулевое граничное значение Ht задается
только на одном торце расчетной области (y = 0).
Обозначим
G = G1 È G2, G — рассматриваемая область, G1
= {r Î G: s > 0} — проводящая подобласть, G2 = {r Î G: s = 0} — диэлектрическая подобласть, ¶G1 и ¶G2 — границы G1 и G2 соответственно, ¶G12 = ¶G1 Ç ¶G2, Г1 — часть общей границы ¶G, на которой задано условие для Et* (то есть
для At), Г2
— часть ¶G, на которой задано условие для Ht, ¶G = Г1 È Г2, Г12 = Г1 Ç ¶G2, g12 = ¶G12 È Г12.
При моделировании будут использоваться смешанные эйлерово–лагранжевы (СЭЛ)
переменные: D/Dt = ¶/¶t + (v,Ñ), где ¶/¶t —
производная при фиксированных эйлеровых переменных, D/Dt — при фиксированных
СЭЛ - переменных (в нашем случае
v — скорость движения якоря как
целого, независящая от координат пространственной точки). Индекс n
указывает на нормальную по отношению к границе составляющую вектора, t — тангенциальную.
В
СЭЛ переменных в соответствии с [1, 11], поскольку v не зависит от координат, справедливо представление
E= - DA/Dt + (v,![]() )A + [u, rot A] + grad f = (1.2)
)A + [u, rot A] + grad f = (1.2)
-
DA/Dt + grad (v, A) +[w, rot A] + grad f .
Здесь w
= u - v — вектор относительной скорости вещества по отношению к
движущейся со скоростью v области.
Для
получения единственного решения в диэлектрической подобласти в [1]
предполагается
f = 0 в G2
,
div
A = 0 в G2 ,
An = 0 на Г22.
В
двумерном случае в рассматриваемых ниже задачах (в декартовых координатах) поля
имеют вид E = (E x, E y, 0), Н = (0, 0, Н z)
[1].
В исследуемых в данной работе задачах
распределение каждой из декартовых составляющих векторного потенциала в
диэлектрических подобластях описывается уравнением Лапласа. Граничные условия
для его решения в G2
определяются значениями тангенциальных составляющих векторного потенциала на
границе раздела проводящей и диэлектрической подобластей и условием равенства
нулю дивергенции решения на границе ( в пределе изнутри G2). Для
эллиптической части квазистационарного приближения системы уравнений Максвелла
граничными условиями второго рода являются значения производной решения по
нормали к границе раздела сред, а для параболической – тангенциальные
компоненты ротора векторного потенциала. Граничными условиями первого рода для
параболической и эллиптической частей являются тангенциальные компоненты A
на границе раздела сред.
При
выборе кулоновской калибровки f = 0 векторный потенциал А
является решением следующей задачи:
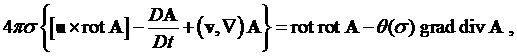
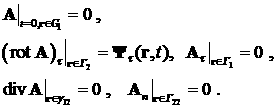 (1.3)
(1.3)
или уравнений
4 ps (- DA/Dt + grad (v,A)
) = rot rot A в якоре;
4 ps (- DA/Dt + (v, ![]() )A ) = rot rot A в рельсе;
)A ) = rot rot A в рельсе;
DA = 0 в
диэлектрике.
Здесь учтена неоднородность задачи по
пространству: q(s) = 0 в G1 и q(s) = 1 в G2 ; Yt —
известная вектор-функция.
Напряженность
магнитного поля не изменится (см., например, [11]), если в (1.2) вместо
нулевого взять любое согласующееся с граничными условиями для Е значение
f. При f = - (v,A) =
-vAy (в данной задаче) конвективные слагаемые будут входить только в
уравнения для Ax в рельсе. Для векторного потенциала поставим
аналогичные (1.3) граничные условия
div A = 0 на g12 ,
An= 0 на Г22.
Тогда
поля описываются уравнениями:
4 ps (- DA/Dt +[w, rot A]) = rot rot A - q (s) grad div A (1.4)
или
4 ps (- DA/Dt ) =
rot rot A в якоре;
4 ps (- DA/Dt - [v,
rot A]) = rot rot A в рельсе
(здесь w = u - v, w = 0 в движущейся части).
Легко видеть, что в этом случае
дивергенция решения (при s = const) с учетом начальных
условий в якоре обнуляется.
§2.
Результаты численного моделирования в двумерном случае и
преобразование разностных соотношений
Рассмотрим
задачу в двумерном приближении. Область состоит из проводников (якорь, рельс) и
диэлектриков (области впереди и позади якоря).
Схема
модельной пространственной области, использованной в расчетах (в простейшем
двумерном случае), представлена на рис. 0.1. Якорь при этом движется в
положительном направлении оси у.
Для
построения разностных схем в области вводится пространственная сетка.
Дискретный аналог векторного потенциала относится к ребрам ячеек сетки (в нашем
случае - к центрам ребер), напряженность магнитного поля – к их граням.
Подробности математической модели и вычислительного алгоритма представлены в
работах [1, 12]. Разностные схемы записываются для безразмерных величин.
Задача
решается на разностных сетках с различным числом ячеек в диэлектрической
подобласти:
1) Nx = 10+10, Ny
= 10+10+10;
2) Nx = 20+10, Ny
= 20+10+10;
3)
Nx = 40+10, Ny = 40+10+10.
Здесь Nx
— сумма количества ячеек
вдоль линии 0x в подобластях
диэлектрика и рельса , Ny — сумма количества ячеек вдоль линии
0y в подобластях диэлектрика перед
якорем, якоря и диэлектрика после якоря..
При
переходе с одного временного слоя на другой используются внешние и внутренние
итерации (подробнее описаны дальше). Для решения системы линейных
алгебраических уравнений на внутренних итерациях используется метод сопряженных
градиентов совместно с неполным разложением Xолесского [13 – 15].
В
[1] отмечалось отсутствие гладкости у y-составляющей векторного потенциала
в диэлектрике при наличии движения в системе. Для исследования влияния на
точность решения особенности, вызванной наличием именно конвективных слагаемых,
будем исследовать процессы с постоянной электропроводностью в проводящей
подобласти. Начальная скорость и другие параметры (входной (полный) ток (I(t) = Imax*(t/t0)exp(1-t/t0)), параметры в критериях
прекращения итераций, сетка и т. д.) для всех расчетов (с различной
калибровкой) берутся одинаковыми.
На
рис. 2.1.a – 2.6.a представлено решение для случая калибровки f = 0. На рис. 2.1.б – 2.6.б представлен вид решения с
измененной калибровкой f = -(v,A) на тот же
момент времени. Вдоль осей для наглядности расположены номера ячеек (координаты
диэлектрической подобласти, в которой исследуется особенности решения, для
сетки 1 по оси x — (0 – 10), по оси y — (0 – 10);
для сетки 2 по оси x — (0 – 20), по оси y — (0 – 20);
для сетки 3 по оси x — (0 – 40), по оси y — (0 – 40)).
|
a |
б |
|
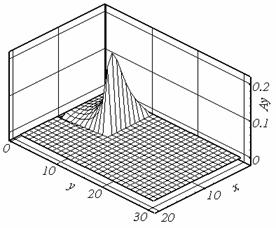
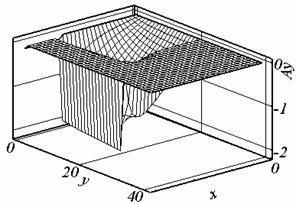
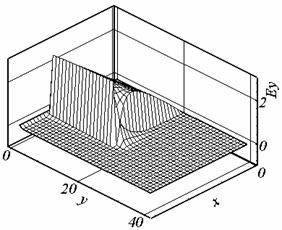
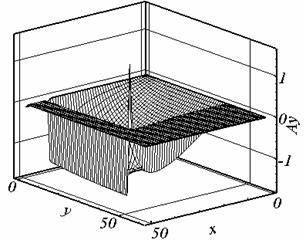
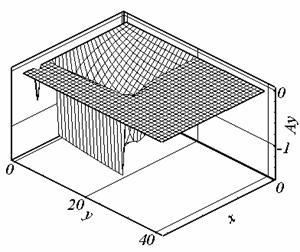
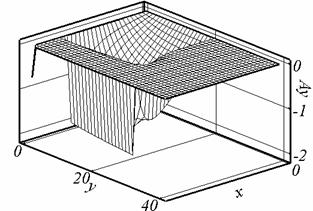
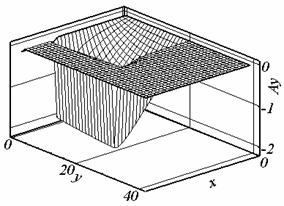
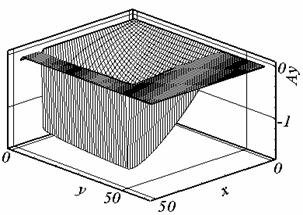
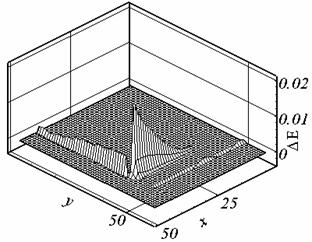
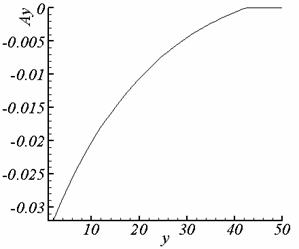
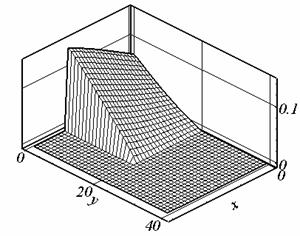
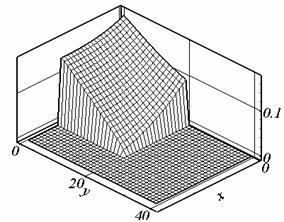
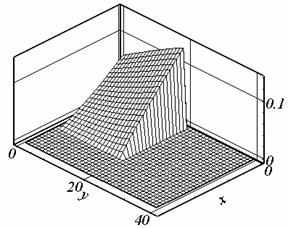
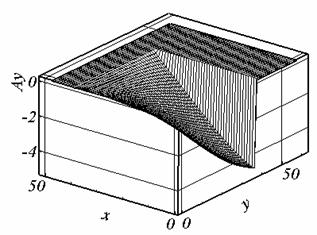
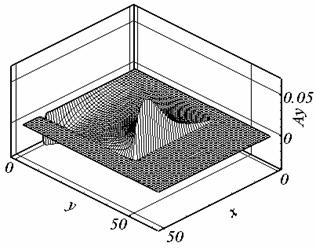
Рис. 2.1. Ay, t = 0.507, сетка 1. |
|
|
a |
б |
|
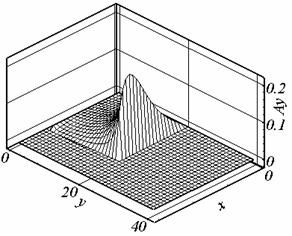
Рис. 2.2. Ay, t = 0.524, сетка 2. |
|
|
а |
б |
|
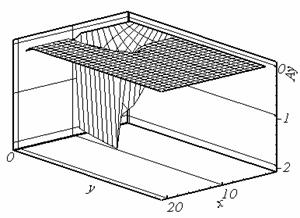
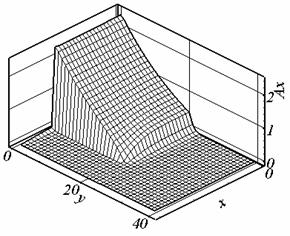
Рис. 2.3. Ax, t = 0.524, сетка 2. |
|
|
а |
б |
|
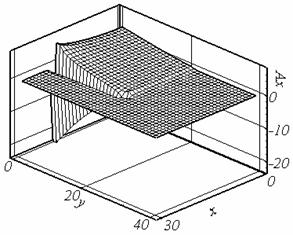
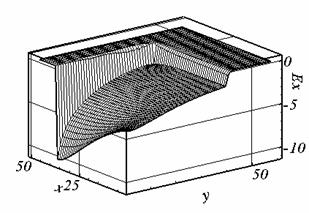
Рис.
2.4. Ex, t
= 0.524, сетка 2. |
|
|
а |
б |
|
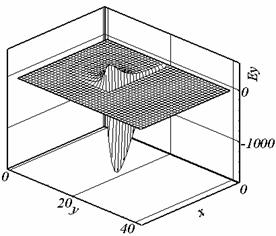
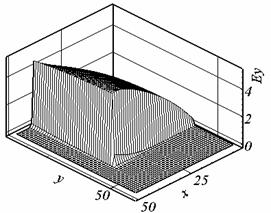
Рис. 2.5. Ey, t = 0.524, сетка 2. |
|
|
а |
б |
|
Рис. 2.6. Ay, t = 0.395, сетка 3. |
|
В
рассматриваемой задаче Ht задается
постоянным на торце диэлектрической подобласти и линейно изменяющимся вдоль
торца рельса. При другом задании Ht , например, если Ht терпит разрыв в некой точке
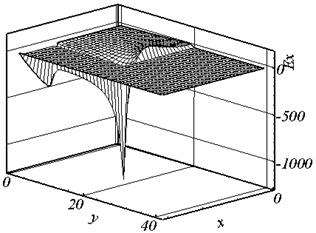
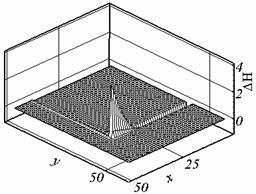
токоподвода, возможно появление экстремума Ay в этой точке (см. рис.
2.7. а — точка токоподвода в центре (по оси x) рельса, б — точка токоподвода в верхней по оси
x части рельса). Появление
экстремума в точке токоподвода не влияет заметно на точность расчета при
различных видах калибровки.
|
|
|
|
|
а, t
= 0.464 |
б, t
= 0.524 |
|
|
Рис. 2.7. Ay , сетка 2, калибровка f = -(v,A). |
||
При
изменении калибровки и сгущении сетки в угловой точке появляется экстремум
решения (см. рис. 2.1.б, 2.2.б, 2.6.б). Причиной появления экстремума в
рассматриваемом случае может являться выбранный способ разностной аппроксимации
дифференциальных операторов.
Аппроксимация
векторного произведения [w , H] в [1] представляет собой форму,
переводящую векторные сеточные функции, задаваемые своими компонентами на
гранях ячеек, и векторные сеточные функции, относящиеся к вершинам, в векторные
сеточные функции, задаваемые своими компонентами на ребрах ячеек. Для лучшей
аппроксимации такая форма должна включать в себя полусумму составляющих вектора
H по граням, прилегающим к ребру, но это приводит к немонотонности
решения [1].
Для обеспечения монотонности решения
произведение [w , H] в [1] берется в виде
[w ,
H]3,x = 1/hx,i(hx,i+1,i wi+1,j+ hx,i,i
wi,j)Hz,ij (2.1)
(здесь hx,i
— длина ребра сетки, hx,i,i — расстояние от центра ребра до
вершины). В этом случае при калибровке f = -(v,A)
конвективное слагаемое будет входить в уравнение для Ax в якоре
вблизи угловой точки, что нарушает однотипность уравнений вдоль границы раздела
и может служить причиной невозможности выполнения условий сопряжения [2]
граничных условий в углах области (для принадлежности решения уравнения Лапласа
к классу гладких функций Ck,l). Для
обеспечения однотипности векторное произведение возьмем в виде:
[w , H]3,x =
wi,j Hz,ij.
(2.2)
В результате (для сеток 2, 3) получим гладкое
решение (отсутствие экстремума в углу диэлектрической части) для случая
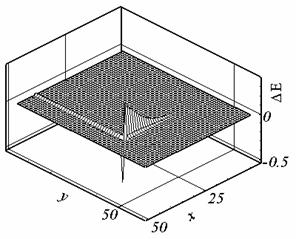
калибровки f = -(v,A) см. рис. 2.8. Для
случая калибровки f = 0 и векторного произведения в
форме (2.2) вид и расположение особенности не изменяется по сравнению с рис.
2.2. а, 2.6. а.
Если векторное произведение взять в форме (2.2), то экстремум решения вблизи угловой точки устраняется (см. рис. 2.8 а, в), но изменение вида векторного произведения (2.2) приводит к некоторому изменению решения вдоль границы проводника с диэлектриком и может отрицательно повлиять на монотонность решения. Компоненты вектора A при различных видах калибровки принимают экстремальные значения на границе раздела проводящей и диэлектрической подобластей.
Экстремум
Еx в диэлектрической
подобласти вдоль границы рельса при использовании формы (2.2) также устраняется
(см. рис. 2.8,б, сравните с рис. 2.4,б).
|
|
|
|
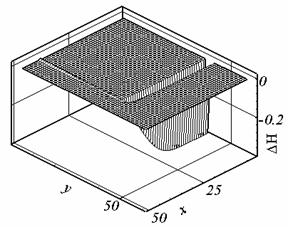
Рис. 2.8. а. Ay , t = 0.507, сетка 2. |
Рис. 2.8. б. Ex , t = 0.507, сетка 2. |
|
|
|
|
Рис. 2.8. в/. Ay , t = 0.395, сетка 3. |
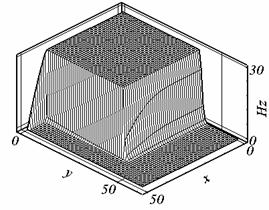
Рис. 2.9. Hz , t = 0.395, сетка 3. |
На
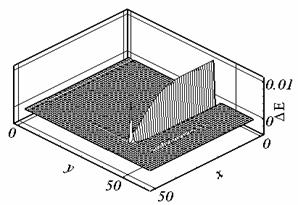
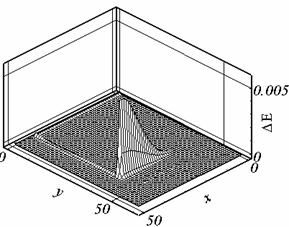
значение напряженности магнитного поля изменение модели не влияет (см. рис.
2.9, 2.10, где DНz означает разность решений Нz
в момент времени t с калибровкой f = 0 и f = -(v,A) ). Векторное произведение для случая
калибровки f = -(v,A) бралось в форме
(2.1) (рис. 2.10.а) и в форме (2.2) (рис. 2.10.б).
Тем,
что в (2.1) Н фигурирует только на правой по направлению движения ячейки
грани, вызвано отличие магнитного поля на границе проводника для калибровки f = 0 по сравнению со случаем калибровки f = -(v,A), когда математическая модель не содержит
векторного произведения в подобласти якоря (см. рис. 2.10.а). Это связано с
резким изменением Н при переходе через границу раздела проводник -
диэлектрик.
|
|
|
|
Рис. 2.10.а. DНz , t = 0.199, сетка 3. |
Рис. 2.10.б. DНz , t = 0.202, сетка 3. |
Составляющая
Ex при
аппроксимации векторного произведения в форме (2.2) принимает наибольшие по
модулю значения на торце области (см. рис. 2.8.б). Поле E строго внутри расчетной области (при аппроксимации
векторного произведения в форме (2.2)) имеет вид, представленный на рис. 2.11 –
2.12.
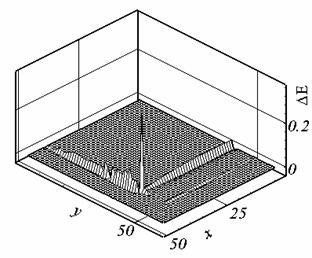
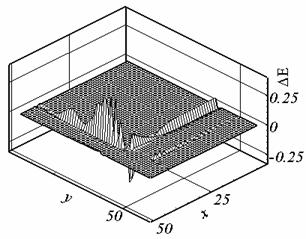
Компоненты
вектора Е принимают экстремальные значения на внутренней границе
диэлектрической подобласти и не должны различаться в проводящей подобласти при
различных видах калибровки (различие может быть вызвано накоплением погрешности
при выполнении шагов по времени и формой
разностных операторов (см. рис. 2.13 - 2.14 — разность решений (DE) в проводнике с калибровкой
f = 0 и f = -(v,A))). Векторное
произведение для случая калибровки f = -(v,A)
взято в форме (2.1) (рис. 2.13.а - 2.14.а) и в форме (2.2) (рис. 2.13.б -
2.14.б).
|
|
|
|
Рис. 2.11. Ex , t=0.202, сетка 3, форма (2.2). |
Рис. 2.12. Ey , t=0.202, сетка 3, форма (2.2). |
|
|
|
|
Рис. 2.13.. DEx , t=0.199, сетка 3, форма (2.1). |
Рис. 2.13.б. DEx , t=0.202, сетка 3, форма (2.2). |
|
|
|
|
Рис. 2.14.a. DEy , t=0.199, сетка 3, форма (2.1). |
Рис. 2.14.б. DEy , t=0.202, сетка 3, форма (2.2). |
§3. Сравнение числа итераций для различных способов моделирования в двумерном случае
Для
решения (1.3) при переходе с одного временного слоя на другой используются
внешние и внутренние итерации [1]. На каждой внешней итерации методом
сопряженных градиентов [13 – 15] решается система линейных алгебраических
уравнений с симметричной матрицей. При этом внедиагональные слагаемые,
связанные с конвективным переносом, берутся с предыдущей внешней итерации и
записываются в правую часть системы.
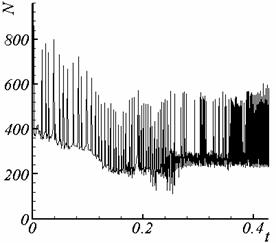
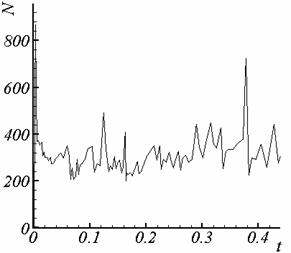
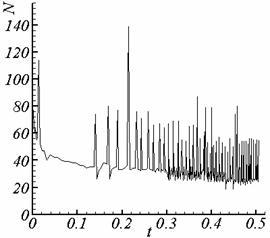
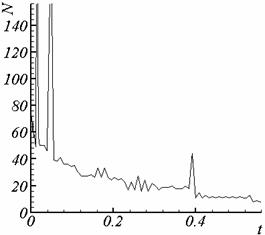
На
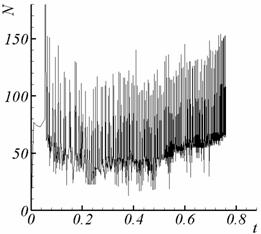
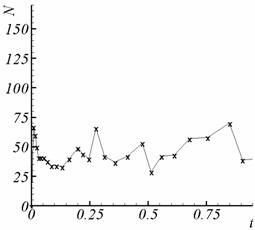
рис. 3.1 – 3.2 приведена зависимость суммарного количества итераций (внешних и
внутренних) от времени для двух расчетов с
f = 0 и с f = -(v,A)
для сетки 1, соответственно.
|
|
|
|
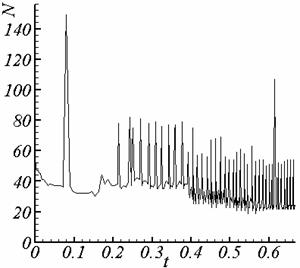
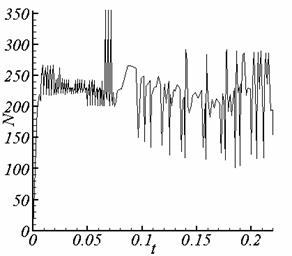
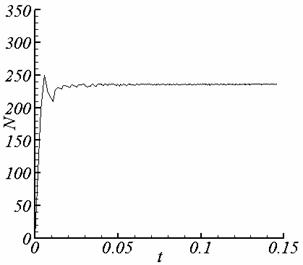
Рис. 3.1. Суммарное количество итераций, калибровка f = 0. |
Рис. 3.2. Суммарное количество итераций, калибровка f = -(v,A). |
При
увеличении точности расчета различие между решениями с различной калибровкой
уменьшается. Уменьшим на порядок параметры в критериях прекращения итераций для
внешних и внутренних итераций. На рис. 3.3 приведена разность решений для E в проводнике с калибровкой f = 0 и f = -(v,A) (и векторным
произведением в форме (2.1)) на момент времени t=0.200 (ср. с рис.2.13.а
, 2.14.а).
При
увеличении точности в критериях прекращения итераций вклад в разность решений
накопленной (при выполнении шагов по времени) погрешности уменьшается, наличие
ненулевой разности решений на рис. 3.3 вызвано несимметричностью конвективных
слагаемых относительно ребра сетки в разностной схеме для модели с калибровкой f = 0. В связи с резким изменением магнитного поля при
переходе через границу проводника и диэлектрика разностная схема для модели с
калибровкой f = -(v,A) лучше
аппроксимирует решение на границе якоря (по сравнением с моделью с калибровкой f = 0).
|
а |
б |
|
Рис. 3.3. DEx, t=0.200, сетка 3, форма (1.5). |
Рис. 3.3. DEy, t=0.200, сетка 3, форма (1.5). |
Сопоставим
также суммарное количество итераций (внешних и внутренних) от времени для
вариантов с f = 0 (рис. 3.4) и с f = -(v,A) (рис.
3.5) для сетки 3 с увеличенной точностью.
|
|
|
|
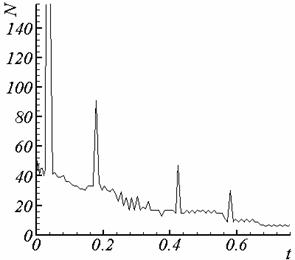
Рис 3.4. Суммарное количество итераций, калибровка f = 0. |
Рис 3.5. Суммарное количество итераций, калибровка f = -(v,A). |
При недостижимости заданной
точности за определенное число итераций шаг по времени приходится уменьшать
[1]. Условия прекращения итераций, как правило, выполняются при малом шаге.
Преобразование математической модели делает возможным достижение необходимой
точности с большим шагом по времени. Проведем сравнение количества шагов по
времени, сделанных к моменту времени t, для различных способов моделирования (см. таб. 1).
Таблица 1.
|
№ сетки |
Момент времени |
Число шагов по времени с
калибровкой φ = 0 |
Число шагов по времени с
калибровкой φ = -(v,A) |
|
1 |
t=0.755 |
705 |
25 |
|
2 |
t=0.524 |
570 |
22 |
|
3 |
t=0.432 |
415 |
35, 18 (с векторным произведением
в форме (1.6)) |
|
3 (повышенная точность) |
t=0.428 |
681 |
97 |
§ 4. Сравнение числа итераций для различных способов моделирования
в трехмерном случае.
Рассмотрим
два простейших варианта конфигурации (упрощение конфигурации [12]) в трехмерном
случае (вариант 1 — рис. 4.1 и вариант 2 — рис. 4.2).
|
|
|
Рис. 4.1. Вариант конфигурации 1. |
|
|
|
Рис. 4.2. Вариант конфигурации 2. |
Задача
решалась на разностных сетках
1:
(Nx = 5+5+5, Ny = 5+5+5, Nz = 5+5) и
2:
(Nx = 5+5+5, Ny = 5+5+4, Nz = 5+5+4),
соответственно.
Сравнение количества шагов
по времени, сделанных к моменту времени t, для различных способов моделирования приведено в
таб. 2.
Таблица 2.
|
№ сетки |
Момент времени |
Число шагов по времени с
калибровкой φ = 0 |
Число шагов по времени с
калибровкой φ = -(v,A) |
|
1 |
t=0.500 |
243 |
77 |
|
2 |
t=0.650 |
236 |
89 |
На
рис. 4.3 – 4.4 приведена зависимость суммарного количества итераций (внешних и
внутренних) от времени для вариантов с f = 0 (а) и с f = -(v,A) (б).
В двух- и трехмерном случаях суммарное количество итераций, необходимых для получения решения, существенно сокращается при изменении модели – это позволяет вести расчет с большим шагом по времени и получать разностное решение на каждом временном слое за меньшее число итераций.
|
a |
б |
|
Рис.
4.3. Суммарное количество итераций. Конфигурация 1. |
|
|
а |
б |
|
Рис. 4.4. Суммарное количество итераций. Конфигурация 2. |
|
§ 5. Явное
выделение особенности.
Рассмотрим
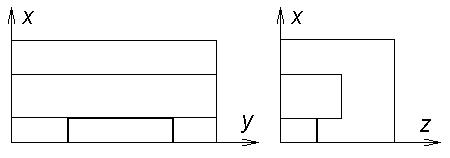
задачу в двумерном приближении. Схема модельной пространственной области,
использованной в расчетах (в простейшем двумерном случае), представлена на рис.
5.1. Якорь при этом движется в положительном направлении оси у. За нуль
отсчета принят левый нижний угол области. Нас интересует поведение решения в
диэлектрической подобласти перед якорем (которая представляет собой
прямоугольник).
В [2] исследованы условия,
при выполнении которых решение уравнения Лапласа в области с угловой точкой и
граничными условиями различных типов принадлежит к классу функций с непрерывной
k-й производной Сk,l, показана
возможность выделения сингулярной части решения в явном виде. Рассмотрим
условия принадлежности решения к классу С2,l (k = 2).
Для
удобства за нуль отсчета в системе, которая понадобится нам для записи
слагаемых, явно выделяющих особенность решения, примем угловую точку границы
проводника (сместим оси и в новой системе координат обозначим: y* = y0
- y, x* = x0 – x, (x0 , y0)
— координаты точки O в несмещенной системе координат).
|
|
|
|
Рис. 5.1. Схема расчетной области. |
|
В
[2] нумерация вершин и сторон прямоугольника ведется против часовой стрелки, за
начало направления обхода s берется левый верхний угол прямоугольника
(на рис.5.1 обозначены стороны прямоугольника в разных системах координат).
Решение
представим в виде суммы негладкой (выделяющей особенность и обозначенной через A0)
и гладкой (A*) частей A=A0 + A*.
Составляющие
A0 имеют вид:
A0x
= 2/p k Im (z ln z)=2/p k (y* ln r + x*arctg (y*/x*)),
(5.1)
A0y = 2/p k Re (z ln z)=2/p k (x* ln r - y*arctg (y*/x*)),
здесь r2 = (x*2+y*2), k = 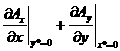 — разность значений
производной в точке O по внутренней нормали к грани y* = 0 и производной
по дуге s — тангенциального условия на x* = 0 (с учетом равенства нулю
дивергенции решения при стремлении изнутри к границе диэлектрика).
— разность значений
производной в точке O по внутренней нормали к грани y* = 0 и производной
по дуге s — тангенциального условия на x* = 0 (с учетом равенства нулю
дивергенции решения при стремлении изнутри к границе диэлектрика).
При приближенном вычислении k используем полиномиальную интерполяцию. Значения k берутся с прошлой внешней итерации (см. § 1).
При
таком задании A0 выполняются требования: div A0 =
0 и rot A0 = 0 в диэлектрической подобласти. Воспользовавшись
равенством arctg (y*/x*)
= p/2-arctg (x*/y*)
и тем, что добавление к A0x слагаемых (a x*+ b y*) и к
A0y слагаемых (b x*- a y*) не влияет на гладкость решения,
вектор A0 можно представить в виде :
A0x = 2/p k (y* ln r - x*arctg (x*/y*)) , (5.2)
A0y = 2/p k (x* ln r + y*arctg (x*/y*)),
это
обеспечивает равенство нулю A0у при x* = 0.
Модуль
A0 можно уменьшить добавлением слагаемых (b y*) к A0x
и слагаемых (b x*) к A0y.
Параметр b можно
выбрать, например, из условия равенства нулю A0y в левом нижнем углу
области (рис. 5.1). Предположим, что в рассматриваемой задаче At вдоль границ x* = 0 и y* = 0
изменяется достаточно гладко.
|
a |
б |
|
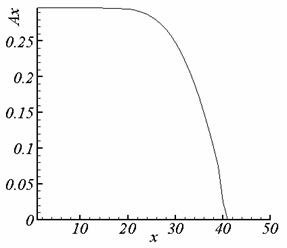
Рис. 5.3. At , сетка 3 (§ 1), t=0.200, Координаты
угловой точки (40,40) |
|
На
рис. 5.3. представлены значения At (a) – вдоль границы y* = 0, (б) – вдоль границы x* = 0. Вдоль осей 0x и 0y вблизи угловой точки At изменяется
по-разному. Этим и обусловлено неравенство нулю коэффициента k и появление особенности вблизи угловой точки. На графике
вдоль осей расположены номера ячеек сетки (не учтено сгущение сетки в
направлении к угловой точке). В разностной модели компоненты вектора A0
задаются в средних точках ребер сетки (далее символом A обозначаются
разностные величины). Разностное решение представляется в виде: A = A*
+ A0, A* — разностный аналог гладкой части решения.
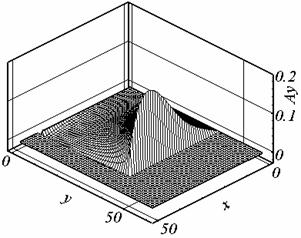
При k = 1 (для примера) проекция слагаемых (5.1), (5.2) на сетку 2 имеет вид,
представленный на рис.5.4, a – г.
|
а |
б |
|
Рис. 5.4. а – A0x в виде (5.1), б – A0y в виде (5.1). |
|
|
в |
г |
|
Рис.
5.4. в – A0x в виде (5.2), г – A0y в виде (5.2). |
|
На
внешних итерациях для вычисления A* строится система M A* = f - M A0.
Здесь М — матрица, аппроксимирующая на разностной сетке симметричную
часть оператора системы уравнений Максвелла, f — правая
часть системы, к которой на внутренних итерациях относятся конвективные
слагаемые. После получения A* вычисляется A = A* + A0.
Такое изменение правой части системы помогает стабилизировать среднее число
итераций, необходимых для решения системы методом сопряженных градиентов. После
добавления к правой части системы слагаемых (- M A0) и
добавления к A* слагаемых A0 суммарная погрешность в
вычислении вектора A увеличивается. Для улучшения сходимости внешних
итераций достаточно повысить точность в критериях прекращения внутренних
итераций. Среднее число итераций, необходимых для решения системы методом
сопряженных градиентов для сетки 3 с повышенной точностью в критериях
прекращения внутренних итераций, представлено на рис. 5.4. (а — без явного
выделения особенности, б — с явным выделением особенности). На рис. 5.5
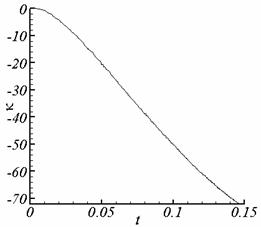
представлена зависимость параметра k от времени.
На рис. 5.6.a.
представлен вид решения A*, а на рис. 5.6.б. — A (после
добавления слагаемых A0) для сетки 3.
|
а |
б |
|
Рис. 5.4. Среднее число внутренних итераций при различных способах выделения особенности решения, сетка 3. |
|
|
|
|
|
Рис. 5.5.Зависимость параметра k от времени, сетка 3. |
|
|
|
|
|
Рис. 5.6. Ay* (a) и Ay (б), t = 0.150, сетка 3. |
|
Заключение
Исследовано
влияние калибровки математической модели и разностных эффектов (формы
разностных операторов) на появление экстремумов, отражающих особенность
решения. Модель с измененной калибровкой позволяет увеличить шаг по времени,
необходимый для выполнения условий сходимости итераций с учетом конвективных
слагаемых. При изменении формы разностных операторов устраняются экстремумы,
обусловленные особенностью решения вблизи угловой точки. После проведения
преобразований модель остается однородной по пространству. Явное выделение
особенности решения позволяет стабилизировать число внутренних итераций, но не
изменяет способа учета конвективных слагаемых при решении системы линейных
алгебраических уравнений и вследствие этого не может существенно увеличить шаг
по времени, необходимый для сходимости внешних итераций.
Литература
1. М. П. Галанин, Ю. П. Попов. Квазистационарные электромагнитные поля в неоднородных средах: Математическое моделирование. М.: Наука. Физматлит, 1995, 320 с.
2. Е. А. Волков. О дифференциальных свойствах решений краевых задач для уравнений Лапласа и Пуассона в прямоугольнике. // Тр. МИАН СССР.—1965.— Т.77.— С. 89 - 112.
3. Волков Е. А. Об устранении особенностей при решении краевых задач для уравнения Лапласа в областях с гладкой границей // ЖВМ и МФ. —1963.—Т.3, №.1.—С. 109–119.
4. Кондратьев В. А. Краевые задачи для эллиптических уравнений в областях с коническими или угловыми точками// Тр. Моск. мат. о-ва.—1967.— Т.16.—С. 209–292.
5. Кондратьев В. А., Копачек И., Олейник О. А. О поведении обобщенных решений эллиптических уравнений второго порядка и системы теории упругости в окрестности граничной точки// Тр. сем. им. И. Г. Петровского.—1982.— Т.8.—С. 135–152.
6. Фрязинов И. В. Разностные схемы для уравнений Лапласа в ступенчатых областях.// ЖВМ и МФ. —1978.— Т.18, №.5.—С. 1170–1185.
7. Фикера Г. Асимптотическое поведение электрического поля и плотности электрического заряд в окрестности сингулярных точек проводящей поверхности // Успехи мат. наук—1975.— Т.30, вып.3(183).—С. 105–24.
8. М. Борсук. Вырождающиеся эллиптические краевые задачи второго порядка в негладких областях // Современная математика. Фундаментальные направления. —2005.—Т. 13 . С. 3–137
9. Волков Е. А. Метод составных сеток для конечных и бесконечных областей с кусочно-гладкой границей// Тр. МИАН СССР.—1968.— Т.96.—С. 117–148.
10. Волков Е. А. О методе регулярных составных сеток для уравнения Лапласа на многоугольниках// Тр. МИАН СССР.—1976.—Т.140.—С. 68–102.
11. Тамм И.Е. Основы теории электричества — М. Наука. 1976. — 616 с.
12. М.П. Галанин, А.П. Лотоцкий, С.С. Уразов. Моделирование эрозии металлического контакта в ускорителе типа рельсотрон // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки, 2004, № 4(15), с. 81-97.
13. А.А. Самарский, Е.С. Николаев. Методы решения сеточных уравнений. М.: Наука, 1978, 592 с.
14. D.S. Kershaw. The incomplete
Cholessky - Conjugate Gradient Method for the iterative solution of system of a
linear equations // J. Comput. Phys, 1978, Vol. 26, p.p. 43 - 65.
15. А. Джордж, Дж. Лю. Численное решение больших разреженных систем уравнений. М.: Мир, 1984, 333 с.