Аннотация
Представлена замкнутая формулировка трехмерной нестационарной задачи в ограниченной области
о взаимодействии электромагнитного импульса, падающего под произвольным углом,
с диспергирующим материалом, пространственное распределение свойств которого является
периодическим по двум направлениям. Для исключения оператора свертки из системы уравнений
Максвелла для среды с дисперсией диэлектрической проницаемости по частоте предлагается
аппроксимировать зависимость диэлектрической восприимчивости от времени суммой экспонент
и добавить дополнительные вспомогательные неизвестные функции с соответствующими уравнениями
для них. Для периодизации задачи предлагается перейти к новым искомым функциям специального
вида. Для открытых границ предложены точные прозрачные граничные условия (ПГУ), т.е. такие,
которые обеспечивают совпадение решения задачи в области с этими ПГУ с решением задачи
во всем пространстве. Такая задача является актуальной, в частности, для разработки
нанотехнологий.
Abstract
A closed formulation for 3D diffraction problem in a bounded domain, when an oblique incident
electromagnetic pulse interacts with a double periodic grating of dispersive materials,
is presented. In order to eliminate the convolution operator from the Maxwell equations
for dispersive materials it is suggested to approximate with respect to time the susceptibility
function by a sum of exponentials and to extend the set of unknown functions and the
governing equation system accordingly. The field transformation technique is used to
periodize the problem. The exact transparent boundary conditions for open boundaries
are proposed. Problems of such type arise, for an example, while developing nanotechnologies.
Введение
В настоящей работе рассматривается задача о
распространении электромагнитного поля в средах с дисперсией, т.е. в таких
средах, в которых скорость света зависит от частоты (цвета). На самом деле все
среды обладают такой зависимостью. Все дело в том, с каким диапазоном частот
приходится иметь дело. Для некоторых приложений дисперсией можно пренебречь, но
во многих случаях такое упрощение является неприемлемым. Зависимость
диэлектрической проницаемости от частоты необходимо учитывать в таких
актуальных задачах как взаимодействие электромагнитного поля с биологическими
тканями (томография, влияние сотовых телефонов на мозг и другие органы,
электростимуляторы и т.п.), при радиолокации подземных слоев и др. Так,
например, экспериментальные данные показывают, что эффективная диэлектрическая
проницаемость может изменяться более, чем на 20%, а эффективная проводимость
более, чем в 2 раза при изменении частоты от 30 до 500 Мгц. Поэтому при расчете
распространения сверх коротких импульсов, содержащих в себе очень широкую
полосу частот, необходимо учитывать это свойство среды в ее математической
модели.
Кроме того, интегрирование уравнений Максвелла по
времени позволяет за один расчет решить задачу сразу для большого количества
частот путем применения преобразования Фурье к найденному нестационарному
решению. Примером актуального приложения является расчет взаимодействия
электромагнитных волн с диэлектриками (лоренцевские среды, например, кремний) в
задачах контроля изделий в электронной промышленности, где конечной целью
является решение обратной задачи. Именно эта задача и будет иметься в виду
всякий раз, когда потребуется конкретизация постановки задачи.
При решении нестационарных уравнений Максвелла в
средах с зависящей от частоты диэлектрической проницаемостью возникают
дополнительные трудности связанные с появлением нелокальной по времени
зависимости между электрической индукцией и напряженностью электрического поля.
В простейшем случае эта связь является линейной и выражается сверткой по
времени напряженности электрического поля с диэлектрической восприимчивостью.
Целью настоящей работы является формулировка замкнутой
задачи для расчета взаимодействия электромагнитного импульса с дисперсивной средой.
В §1 для максимально широкого класса дисперсивных сред уравнения Максвелла со
сверткой переформулируются в расширенную систему гиперболических уравнений.
Затем в §2 уточняется та физическая задача, для которой формулируется
математическая модель в последующих параграфах. В §3 вводится преобразование
искомых функций, позволяющее сделать задачу периодической по двум
пространственным направлениям. В §4 обсуждаются граничные условия на открытых
концах расчетной области и в §5 формулируются для них прозрачные граничные
условия.
§1.
Уравнения Максвелла для дисперсивных сред
Уравнения Максвелла для дисперсивных сред можно
записать в следующем виде:
 , ,
 , ,
где
 , ,
 , ,
 , ,
 и и  – индукция и
напряженность электрического поля, – индукция и
напряженность электрического поля,  и и  – индукция и
напряженность магнитного поля, – индукция и
напряженность магнитного поля,  – магнитная
проницаемость, – магнитная
проницаемость,  – электрическая
постоянная, – электрическая
постоянная,  – относительная
диэлектрическая проницаемость для бесконечной частоты, – относительная
диэлектрическая проницаемость для бесконечной частоты,  – диэлектрическая
восприимчивость в пространстве – диэлектрическая
восприимчивость в пространстве  , ,  – вектор поляризации
диэлектрика (см. [1] и [2]). – вектор поляризации
диэлектрика (см. [1] и [2]).
Если рассматриваемая задача такова (именно такие
задачи мы и будем рассматривать), что  при при  , то соотношение
может быть записано в следующем виде: , то соотношение
может быть записано в следующем виде:
 . .
Безразмерная форма уравнений
Перейдем
к безразмерным переменным, используя следующие соотношения:

Здесь
безразмерные величины помечены сверху чертой (за исключением относительной
магнитной проницаемости  ), ),  , ,  и и  — характерная
амплитуда электрического поля, характерное время и характерная длина
соответственно, — характерная
амплитуда электрического поля, характерное время и характерная длина
соответственно,  – магнитная
проницаемость в вакууме, – магнитная
проницаемость в вакууме,  . .
Уравнения
–
в безразмерной форме имеют вид следующей системы
(черточки над безразмерными величинами здесь и далее опущены):
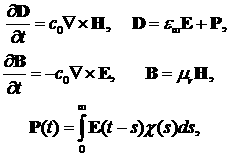
где
 — безразмерная
скорость света: — безразмерная
скорость света:
 . .
Расширенная система
дифференциальных уравнений для «экспоненциальных» сред
После
исключения  и и 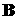 из
получим из
получим

Далее мы будем предполагать, что функция
диэлектрической восприимчивости  может быть приближена
суммой экспонент следующего вида: может быть приближена
суммой экспонент следующего вида:

Именно такие среды, у которых функция
диэлектрической восприимчивости имеет вид суммы экспонент
мы будем для краткости называть «экспоненциальными».
В частности, такой вид имеет диэлектрическая восприимчивость в модели среды
Лоренца (см., например, [3]):

В
этом случае

где  — функция Хевисайда.
После преобразования Фурье
дает комплекснозначную восприимчивость как функцию
частоты: — функция Хевисайда.
После преобразования Фурье
дает комплекснозначную восприимчивость как функцию
частоты:
 . .
Функция Хевисайда присутствует в
для того, чтобы существовало преобразование Фурье.
Это можно сделать, потому что отрицательные значения  соответствуют будущим по отношению к
актуальному моментам времени (см.
). соответствуют будущим по отношению к
актуальному моментам времени (см.
).
Для перехода от
к
мы использовали следующий вид преобразования Фурье:
 . .
Соответствующее
обратное преобразование выглядит следующим образом:
 . .
Для того, чтобы получить
систему уравнений без оператора свертки, введем комплекснозначную функцию
восприимчивости

и
соответствующий комплекснозначный вектор поляризации
 , ,
где

и  . .
Дифференцируя
по  , получим , получим

При условии, что  , справедливо следующее: , справедливо следующее:  , ,  , ,  , ,

и

После подстановки
в
получим систему дифференциальных уравнений, не
содержащую оператора свертки:



–
— искомая гиперболическая
система уравнений, описывающая эволюцию электромагнитного поля в
«экспоненциальных» средах.
Для решения конкретных задач необходимо еще
сформулировать соответствующие начальные и граничные условия.
§2. Постановка задачи о
взаимодействии наклонно падающей плоской электромагнитной волны с периодическим
по двум направлениям образцом
Мы
будем рассматривать взаимодействие плоской электромагнитной волны с дважды
периодической структурой. Пример такой структуры приведен на рисунке 1.

Рисунок 1. Пример фотографии дважды
периодической структуры, полученной с помощью электронного микроскопа.
Будем предполагать, что
падающая волна движется из бесконечности, и что подстилающая структура состоит
из периодически повторяющихся вдоль двух координат элементов. Каждый элемент
состоит из одного или более материалов, которые в общем случае являются
«экспоненциальными», т.е. их функция восприимчивости имеет вид
.
Идеальная модель такой дважды периодической структуры
изображена на рисунке 2 (цилиндрические выступы взяты для примера).

Рисунок 2
. Идеализированная схема
трехмерной рассеивающей периодической структуры.
Без ограничения общности
будем считать, что функции зависимости физических свойств материалов, по
которым распространяется электромагнитная волна, от координат являются
периодическими вдоль координаты  с периодом с периодом  и вдоль координаты и вдоль координаты  с периодом с периодом  , а ось , а ось  перпендикулярна
средней поверхности раздела между воздухом и периодической структурой. Направление распространения
плоской волны определяется волновым вектором перпендикулярна
средней поверхности раздела между воздухом и периодической структурой. Направление распространения
плоской волны определяется волновым вектором  . Для определенности будем считать, что волновой вектор и ось . Для определенности будем считать, что волновой вектор и ось
 направлены в одно и то же полупространство
относительно плоскости направлены в одно и то же полупространство
относительно плоскости  (см. рисунок 3).
Волновой вектор и ось (см. рисунок 3).
Волновой вектор и ось  образуют угол образуют угол  (угол падения). В
случае нормального падения волны угол (угол падения). В
случае нормального падения волны угол  . Плоскость, проходящая через волновой вектор и ось . Плоскость, проходящая через волновой вектор и ось  — плоскость падения.
Ось — плоскость падения.
Ось  и плоскость падения
образуют угол и плоскость падения
образуют угол  (азимутальный угол).
Если (азимутальный угол).
Если  , то плоскость падения совпадает с плоскостью , то плоскость падения совпадает с плоскостью  . Угол между вектором напряженности электрического поля . Угол между вектором напряженности электрического поля  и плоскостью падения
обозначим буквой и плоскостью падения
обозначим буквой  . .

Рисунок 3
. Системы координат и определяющие
задачу углы.
Для описания падающей волны
введем связанную с ней вспомогательную систему координат  такую, что ось такую, что ось  сонаправлена с
волновым вектором, ось сонаправлена с
волновым вектором, ось  перпендикулярна оси перпендикулярна оси  и лежит в плоскости
падения, ось и лежит в плоскости
падения, ось  направлена таким образом, чтобы система координат направлена таким образом, чтобы система координат  была правой.
Электромагнитное поле в падающей волне не зависит от координат была правой.
Электромагнитное поле в падающей волне не зависит от координат  и и  . .
Будем предполагать, что
падающая из бесконечности волна имеет линейную поляризацию, т.е. что угол
поляризации  постоянен. Тогда
удобно ввести еще одну вспомогательную систему координат постоянен. Тогда
удобно ввести еще одну вспомогательную систему координат  такую, что ось такую, что ось  совпадает с осью совпадает с осью  , ось , ось  параллельна вектору
поляризации параллельна вектору
поляризации  , а ось , а ось  направлена таким образом, чтобы система координат направлена таким образом, чтобы система координат  была правой. В этой системе координат была правой. В этой системе координат  а остальные компоненты
электромагнитного поля имеют вид а остальные компоненты
электромагнитного поля имеют вид
 , ,
т.к. в вакууме  . Константа . Константа  определяет положение
падающей волны в начальный момент времени определяет положение
падающей волны в начальный момент времени  . .
Компоненты произвольного
вектора

в основной и вспомогательной системах координат
связаны между собой следующими соотношениями

Следовательно, в системе координат  компоненты поля
падающего электромагнитного импульса имеют вид компоненты поля
падающего электромагнитного импульса имеют вид


Нам
еще нужно перейти от  в
к координатам в
к координатам  . Компоненты
единичного волнового вектора . Компоненты
единичного волнового вектора

в
системе координат  имеют вид имеют вид
 . .
Следовательно,
для произвольной точки 
 . .
Задание падающего электромагнитного импульса
полностью определяет задачу с физической точки зрения (нужно только чтобы в
начальный момент времени вне вакуума электромагнитное поле было равно нулю или
пренебрежимо мало). Но для проведения расчетов необходимо поставить
соответствующие граничные условия на границах расчетной области. Мы будем
использовать минимально возможную расчетную область: прямоугольный
параллелепипед с гранями, ортогональными координатным осям, у которого
расстояния между гранями  и и  равны равны  и и  — пространственным
периодам свойств облучаемого образца. Грани — пространственным
периодам свойств облучаемого образца. Грани  должны быть выбраны
таким образом, чтобы границы раздела сред проходили целиком внутри
параллелепипеда. Для постановки граничных условий на границах должны быть выбраны
таким образом, чтобы границы раздела сред проходили целиком внутри
параллелепипеда. Для постановки граничных условий на границах  и и  мы сделаем такую
замену зависимых переменных, чтобы задача в целом стала периодической по мы сделаем такую
замену зависимых переменных, чтобы задача в целом стала периодической по  и по и по  (см. §3). Тогда на этих границах можно будет использовать условия
периодичности для любой функции поля (см. §3). Тогда на этих границах можно будет использовать условия
периодичности для любой функции поля  : :

На открытых границах  задание падающего
электромагнитного импульса задает входящее в область излучение. Для отраженного
и преломленного излучения на этих границах должны быть поставлены условия
прозрачности (см. §5). При этом
существенно используется, что в начальный момент времени падающий
электромагнитный импульс локализован вне расчетной области. Из этого следуют
нулевые начальные данные в расчетной области для всех величин, включая задание падающего
электромагнитного импульса задает входящее в область излучение. Для отраженного
и преломленного излучения на этих границах должны быть поставлены условия
прозрачности (см. §5). При этом
существенно используется, что в начальный момент времени падающий
электромагнитный импульс локализован вне расчетной области. Из этого следуют
нулевые начальные данные в расчетной области для всех величин, включая  (см.
). (см.
).
§3. Периодизация задачи
(переход к новым зависимым переменным)
Описание замены переменных
Пусть электромагнитный
импульс, набегающий на облучаемый образец из бесконечности, является плоской
волной, распространяющейся вдоль единичного вектора  . Это означает, что вдали от облучаемого образца, в области
невозмущенной падающей плоской волны, для любой компоненты электромагнитного
поля . Это означает, что вдали от облучаемого образца, в области
невозмущенной падающей плоской волны, для любой компоненты электромагнитного
поля 

(см.
и
) справедливы соотношения

и
 , ,
где
 . .
Несмотря на то, что после взаимодействия с
облучаемым образцом электромагнитное поле уже не имеет формы плоской волны,
соотношения
–
справедливы во всем пространстве, потому что с физической
точки зрения невозможно различить процессы, начавшиеся в точках  и и  . .
Преобразование
Фурье обеих частей
дает
 , ,
где
 . .
Аналогично,
преобразование Фурье обеих частей
дает
 , ,
где
 . .
Введем
новую, модифицированную функцию
 . .
Используя
, получим:

т.е.
функция  является периодической
по переменной является периодической
по переменной  с периодом с периодом  . Аналогично можно показать, что функция . Аналогично можно показать, что функция  является также
периодической по переменной является также
периодической по переменной  с периодом с периодом  . .
Для
каждой электромагнитной функции (компоненты электромагнитного поля)  мы определим
модифицированную функцию мы определим
модифицированную функцию  как обратное
преобразование Фурье по времени функции как обратное
преобразование Фурье по времени функции  : :

где  — оператор
преобразования Фурье по времени. Применяя преобразование
к каждой компоненте, получим модифицированное
электромагнитное поле: — оператор
преобразования Фурье по времени. Применяя преобразование
к каждой компоненте, получим модифицированное
электромагнитное поле:

Аналогичное
преобразование применим и к поляризации
.
Система дифференциальных уравнений для
модифицированных полей
Вводя вещественнозначные
функции  и и  такие, что такие, что

( есть физический вектор поляризации диэлектрика), мы можем
переписать
–
, используя только вещественнозначные функции: есть физический вектор поляризации диэлектрика), мы можем
переписать
–
, используя только вещественнозначные функции:




где

В
координатной форме уравнения
–
имеют вид:












Делая
преобразование обратное к
и исключая
производные по времени из правой части уравнений, несложно из
–
получить систему
уравнений для модифицированного электромагнитного поля (уравнения
–
для
модифицированных функций сохраняют тот же вид):






Выражение падающего электромагнитного
импульса в терминах модифицированных функций
Плоская волна
после замены
принимает вид:
 , ,
что означает, что наклонно падающая исходная плоская
волна становится в терминах модифицированных функций нормально падающей плоской
волной, двигающейся со скоростью
 . .
Следовательно, падающий электромагнитный импульс в
терминах модифицированных функций имеет вид:


§4. Граничные условия
После замены зависимых
переменных соответствующими модифицированными аналогами, задача стала дважды
периодической по переменным  и и  . Поэтому мы используем условие периодичности на границах . Поэтому мы используем условие периодичности на границах  и и  . .
Квазиодномерная
задача на открытых границах
Мы также должны поставить
граничные условия на верхней и нижней границах. Для того, чтобы понять какие
граничные условия допустимы, а какие нет, рассмотрим квазиодномерную систему,
которая получается из
–
после переноса всех членов, не содержащих производные по  и по и по  в правую часть: в правую часть:
 (4.1а) (4.1а)
 (4.1б) (4.1б)
 (4.1в) (4.1в)
 (4.1г) (4.1г)
 (4.1д) (4.1д)

где выражения для правых частей  , ,  , ,  , ,  , ,  и и  не содержат
производные по не содержат
производные по  и по и по  . .
Матричная форма записи квазиодномерной задачи
Запишем
систему уравнений (4.1) в матричной
форме:

где
 . .
Собственные числа системы
являются корнями характеристического уравнения
 . .
 является диагональной
матрицей: является диагональной
матрицей:

где  — единичная матрица.
Матрица — единичная матрица.
Матрица  имеет вид: имеет вид:

Собственные числа и
соответствующие собственные векторы системы
имеют вид:


Таким образом, на левой (верхней,  ) границе две характеристики, ) границе две характеристики,  , являются выходящими, две — входящими ( , являются выходящими, две — входящими ( ) и две, ) и две,  , — нулевыми (мы считаем, что ось , — нулевыми (мы считаем, что ось направлена вниз). направлена вниз).
Это означает, что мы должны поставить два граничных
условия на левой (верхней) границе. Функции, на которые ставятся эти граничные
условия, должны не принадлежать линейной оболочке векторов  , и граничные условия должны быть независимыми. , и граничные условия должны быть независимыми.
Остальные уравнения, которыми должны быть дополнены
граничные условия, должны являться следствием системы уравнений
и размерность линейной оболочки проекции этой
подсистемы на подпространство  должна равняться 4.
Одним из вариантов системы уравнений на границе, удовлетворяющим
сформулированным требованиям, является комбинация пары граничных условий,
поставленных на функции должна равняться 4.
Одним из вариантов системы уравнений на границе, удовлетворяющим
сформулированным требованиям, является комбинация пары граничных условий,
поставленных на функции  и и  , и четырех проекций системы
на векторы , и четырех проекций системы
на векторы  . Однако, другие варианты системы уравнений на границе могут
оказаться предпочтительнее, например, из соображений удобства. . Однако, другие варианты системы уравнений на границе могут
оказаться предпочтительнее, например, из соображений удобства.
Аналогично,
на правой (нижней,  ) границе две
характеристики, ) границе две
характеристики,  , являются выходящими, две — входящими ( , являются выходящими, две — входящими ( ) и две, ) и две,  , — нулевыми. Следовательно, соответствующие граничные
условия должны содержать функции , — нулевыми. Следовательно, соответствующие граничные
условия должны содержать функции  и и  . .
Мы будем использовать на открытых границах прозрачные
граничные условия (ПГУ), которые будут сформулированы в следующем параграфе.
§5.
Прозрачные граничные условия
Под
прозрачными граничными условиями мы понимаем такие граничные условия, которые
обеспечивают совпадение решения, полученного как решение задачи в ограниченной
области с этими граничными условиями, с решением, полученным во всем
пространстве. Понятие условий полной прозрачности и сами условия для
трехмерного волнового уравнения были предложены И. Л. Софроновым в [4].
Электромагнитное поле в расчетной области состоит из
поля падающей волны и отраженного/преломленного поля. Падающая волна известна
из постановки задачи. Сформулируем прозрачные граничные условия для
отраженного/преломленного поля.
Система уравнений
с оператором свертки и система
–
без оператора свертки эквивалентны при выполнении
условия
. Поэтому мы можем использовать любую из них для
получения ПГУ. Удобнее для этой цели использовать
. Перепишем эту систему для модифицированных функций:









При выводе этих уравнений мы использовали то
обстоятельство, что электромагнитное поле было равно нулю при  . .
После преобразования
Лапласа, с учетом соответствия

и
начального условия

для
всех компонент электромагнитного поля, уравнения
–
перейдут в следующие:







Или,
после исключения  из
–
: из
–
:


 . .
Мы предполагаем, что  , ,  и и  не зависят от
пространственных координат вне открытых границ, включая некоторую их
окрестность. Тогда из уравнений
–
и
–
следует, что не зависят от
пространственных координат вне открытых границ, включая некоторую их
окрестность. Тогда из уравнений
–
и
–
следует, что

где
 — любая из компонент — любая из компонент  или или  . И, следовательно, . И, следовательно,

Итак, каждая компонента модифицированного
электромагнитного поля удовлетворяет полученному выше уравнению в тех областях,
где электромагнитные свойства среды постоянны по пространству. Как известно, в
вакууме, например, каждая из компонент немодифицированного электромагнитного
поля удовлетворяет волновому уравнению.
Для получения ПГУ вернемся к
уравнению
, снова сделав преобразование Лапласа. Поскольку  является периодической
функцией по является периодической
функцией по  с периодом с периодом  и периодической по и периодической по  с периодом с периодом  , мы можем представить , мы можем представить  в виде двойного ряда
Фурье: в виде двойного ряда
Фурье:
 , ,
где

Для каждого  и и  коэффициент Фурье коэффициент Фурье  должен удовлетворять
уравнению должен удовлетворять
уравнению

Уравнение
является обыкновенным дифференциальным уравнением
вида
 , ,
где

Общее
решение
есть
 . .
Мы будем выбирать ту ветвь  , у которой , у которой  . Тогда общее решение, убывающее при . Тогда общее решение, убывающее при  , имеет вид , имеет вид

и
убывающее при  : :

Следовательно, для любого убывающего при  решения справедливо
соотношение решения справедливо
соотношение
 . .
Аналогично, для любого убывающего при  решения справедливо
соотношение решения справедливо
соотношение
 . .
Соотношения
и
являются ПГУ в пространстве Фурье-Лапласа:

на
верхней границе и

на
нижней.
Пусть  — единичный вектор
внешней нормали на верхней и нижней границах. На верхней границе — единичный вектор
внешней нормали на верхней и нижней границах. На верхней границе  , на нижней , на нижней  . Тогда уравнения
и
можно переписать в универсальном виде: . Тогда уравнения
и
можно переписать в универсальном виде:

Уравнение
можно переписать, выделив слагаемые с  и и  : :

где

При
условии, что  убывает по крайней
мере как убывает по крайней
мере как  при при  , ,  убывает как убывает как 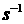 . .
Обратное преобразование
Лапласа
дает

где
символ  обозначает оператор
свертки, а обозначает оператор
свертки, а
 . .
Делая
затем обратное преобразование Фурье, получаем ПГУ для  : :

где
 . .
Заметим, что  . Следовательно, . Следовательно,  . Кроме того, . Кроме того,  . Следовательно, и . Следовательно, и  . В самом деле, . В самом деле,

Это
должно быть равно

Следовательно,

Для нулевой гармоники это
означает, что  и и 
Замечание. В дискретном случае четыре
коэффициента Фурье должны быть вещественными:  , ,  , ,  и и  , где , где  и и  — количество расчетных
точек по осям — количество расчетных
точек по осям  и и  . .
ПГУ
содержит оператор свертки,
что делает его неудобным для использования. Модифицируем его так, чтобы
избавиться от свертки.
С этой целью аппроксимируем
с требуемой точностью ядро свертки суммой эксрронент:

Пусть
мы имеем такую аппроксимацию. Тогда ПГУ
можно переписать в следующем виде:

Для того, чтобы исключить
оператор свертки из
, введем такие вспомогательные функции  , чтобы уравнение
было эквивалентно уравнению , чтобы уравнение
было эквивалентно уравнению

Чтобы получить уравнения,
которым должны удовлетворять  , сделаем преобразование Фурье
: , сделаем преобразование Фурье
:

где
 , а , а  является является  тым коэффициентом Фурье функции тым коэффициентом Фурье функции  : :
 . .
Из сравнения
и
следует, что
 . .
Верхний
предел равен  , потому что все электромагнитные функции равны нулю для всех , потому что все электромагнитные функции равны нулю для всех
 . .
Очевидно, что  удовлетворяют
следующему уравнению: удовлетворяют
следующему уравнению:

Делая обратное преобразование Фурье, получаем
замыкающие уравнения для ПГУ
, которые не содержат оператора свертки:

Эти уравнения должны быть добавлены к
, чтобы полученная система была эквивалентна
.
Теперь у нас есть все
необходимое, чтобы сформулировать систему уравнений на открытых границах и
замкнуть таким образом постановку задачи в целом.
Для удобства перейдем от
к системе уравнений в следующем виде:

где

Система
имеет те же собственные числа
и те же собственные векторы
, что и система
.
Пусть  — матрица, состоящая
из левых собственных векторов
. Умножая
слева на — матрица, состоящая
из левых собственных векторов
. Умножая
слева на  , получим систему уравнений с диагональной матрицей: , получим систему уравнений с диагональной матрицей:

где
 — диагональная
матрица, состоящая из собственных чисел
. — диагональная
матрица, состоящая из собственных чисел
.  -тая строчка системы
имеет вид: -тая строчка системы
имеет вид:

Очевидный путь получения
корректной системы уравнений на границе — замена строчек в уравнении
, которые соответствуют приходящим характеристикам, на
ПГУ
, примененные к соответствующим комбинациям
неизвестных функций.
Система
уравнений на нижней границе 
На
нижней границе  (ось (ось  направлена вниз) мы
можем вместо 5-го и 6-го уравнений использовать следующие два уравнения: направлена вниз) мы
можем вместо 5-го и 6-го уравнений использовать следующие два уравнения:


В этом случае система уравнений на границе может
быть записана в следующем виде:

где первые четыре собственных числа диагональной
матрицы  совпадают с первыми
четырьмя собственными числами матрицы совпадают с первыми
четырьмя собственными числами матрицы  , первые четыре элемента вектора , первые четыре элемента вектора  совпадают с первыми четырьмя элементами
вектора совпадают с первыми четырьмя элементами
вектора  и и

Система
должна быть дополнена следующими уравнениями:

Умножая
слева на  , получим окончательный вид системы уравнений на нижней
границе: , получим окончательный вид системы уравнений на нижней
границе:

или

где

Система
уравнений на верхней границе 
На
верхней границе  (ось (ось  направлена вниз) мы
можем вместо 3-го и 4-го уравнений
использовать следующие два уравнения: направлена вниз) мы
можем вместо 3-го и 4-го уравнений
использовать следующие два уравнения:


В этом случае система
уравнений на границе может быть записана в следующем виде:

где два первые и два последние собственных числа
диагональной матрицы  совпадают с двумя
первыми и двумя последними собственными числами матрицы совпадают с двумя
первыми и двумя последними собственными числами матрицы  , два первые и два последние элемента вектора , два первые и два последние элемента вектора  совпадают с двумя
первыми и двумя последними элементами вектора совпадают с двумя
первыми и двумя последними элементами вектора  и и

Система
должна быть дополнена следующими уравнениями:

Умножая
слева на  , получим окончательный вид системы уравнений на нижней
границе: , получим окончательный вид системы уравнений на нижней
границе:

или

где

Более простой
вариант системы уравнений на открытых границах
Пожалуй,
простейший вариант системы уравнений на открытых границах, не противоречащий
характеристическим свойствам системы уравнений в области, получается заменой
первых двух уравнений прозрачными граничными условиями
, примененными к  и и  . В этом случае система уравнений на верхней
границе . В этом случае система уравнений на верхней
границе  имеет вид имеет вид

а
на нижней границе  — —

где

 , ,




а  и и  являются решениями
следующих уравнений: являются решениями
следующих уравнений:

Таким образом, мы сформулировали замкнутую корректную
постановку задачи для решения нестационарных уравнений Максвелла в случае
падения на периодическую по направлениям  и и  решетку, состоящую из
диспергирующего материала, электромагнитного импульса, который «на
бесконечности» (до взаимодействия с решеткой) является плоской волной. Угол
падения может быть произвольным. Соберем вместе детали этой постановки. решетку, состоящую из
диспергирующего материала, электромагнитного импульса, который «на
бесконечности» (до взаимодействия с решеткой) является плоской волной. Угол
падения может быть произвольным. Соберем вместе детали этой постановки.
Предполагается, что
1) облучаемая решетка обладает периодической структурой
вдоль осей  и и  ; ;
2) диэлектрическая
восприимчивость вещества решетки  может быть приближена
суммой экспонент вида
; может быть приближена
суммой экспонент вида
;
3) в начальный момент времени в
области, где ищется решение, электромагнитное поле отсутствует;
4) падающий на решетку
электромагнитный импульс имеет форму плоской волны.
Тогда
эволюция электромагнитного поля в области описывается гиперболической системой
уравнений
–
совместно с
–
. На границах  и и  ставятся условия
периодичности (не смотря на то, что исходная физическая задача не обладает
такой периодичностью). На границах ставятся условия
периодичности (не смотря на то, что исходная физическая задача не обладает
такой периодичностью). На границах  для отраженного/преломленного поля ставятся ПГУ
(прозрачные граничные условия)
и
или
и
, позволяющие выйти электромагнитному полю из области
без отражения. для отраженного/преломленного поля ставятся ПГУ
(прозрачные граничные условия)
и
или
и
, позволяющие выйти электромагнитному полю из области
без отражения.
Выбор между граничными условиями
,
и
,
зависит от применяемого численного метода и должен
быть приведен экспериментально.
References
|
[1]
|
Ландау
Л.Д., Лифшиц Е.М. Теоретическая физика, Т. VIII. Электродинамика сплошных сред
|
|
[2]
|
A. Taflove, S. Hagness,
Computational Electrodynamics, The finite-difference time-domain methed,
Second Edition, Artech House, pp. 253, 2000.
|
|
[3]
|
R. J. Luebbers and F. Hunsberger, “FDTD for Nth-Order Dispersive
Media”, IEEE Transactions on Antennas
and Propagation, vol. 40, No.
11, November 1992.
|
|
[4]
|
Софронов
И. Л. Условия полной прозрачности на сфере для трехмерного волнового
уравнения. Доклады РАН. Т. 326, № 6, с. 453 – 457
(1992)
|
|
 ,
, .
.
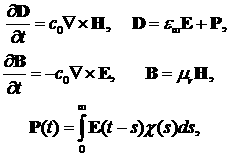
 .
.


 .
. .
. .
.
 ,
,













 .
. .
. .
.

 есть физический вектор поляризации диэлектрика), мы можем
переписать
есть физический вектор поляризации диэлектрика), мы можем
переписать 




















































 .
.

 ,
,









 .
.





 .
.




















 ,
,



