Аннотация
Двумерная компьютерная модель взаимодействия плотной плазмы с электромагнитным полем
в рамках уравнений Максвелла – Власова применена для расчета коэффициента поглощения
плазмой энергии падающего потока при различных конфигурациях границы вакуум-плазма.
Abstract
Two-dimensional computer code is considered plasma-field interaction in the frame of the
equations of Maxwell - Vlasov. The absorption by electrons of the incident wave energy is
calculated for the tips different vacuum-plasma boundary.
Содержание
Введение............................................................................................ 3
§1 Постановка задачи....................................................................... 3
§2 Результаты расчета...................................................................... 4
§3
Заключение……………………………………………………. 9
Литература.................................................................................. …10
Введение
В
экспериментах с мощным лазерным излучением наблюдается интенсивное поглощение плазмой энергии
электромагнитной волны, падающей на её поверхность, даже если концентрация
электронов плазмы превосходит критическую, для данной частоты
волны w значение nкр= mω2/4πe2. Хорошо
известно, что вещество в мишенях имеет концентрацию электронов 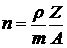 , как правило,
превосходящую критическую концентрацию nкр. В предположении полной ионизации вещества с
плотностью , как правило,
превосходящую критическую концентрацию nкр. В предположении полной ионизации вещества с
плотностью 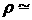 1г/см3
превосходство величины 1г/см3
превосходство величины 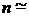 3.1023см-3
над nкр можно оценить для характерной частоты w=5.37×1015сек-1 (в случае длины волны l = 0.351mм третьей гармоники неодимового лазера) как, грубо говоря, десятикратное, т.к. 3.1023см-3
над nкр можно оценить для характерной частоты w=5.37×1015сек-1 (в случае длины волны l = 0.351mм третьей гармоники неодимового лазера) как, грубо говоря, десятикратное, т.к. 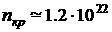 см-3 (Z=6, A=12 в случае углерода). см-3 (Z=6, A=12 в случае углерода).
Одним из основных параметров расчета,
помимо массы электрона m, служит масса ионов с зарядом Z и с атомной массой A. Во всех расчетах
предполагается, что эти параметры A
= Z= 1, т.е. в качестве ионов
рассматриваются протоны.
В работе [1] показано, что одной из причин
поглощения может быть неоднородность плазмы. Настоящая работа посвящена
описанию результатов численного решения задачи о проникновении излучения в
плазму и является продолжением работы [1].
Рассматриваются некоторые простые случаи,
когда неоднородность плазмы порождается гофрированностью ее поверхности.
§1 Постановка задачи
Взаимодействие излучения с плазмой
описывается системой уравнений Максвелла-Власова:
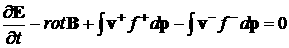 , ,
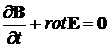 , ,
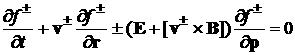 , ,
где
Е - напряженность электрического поля, B -
магнитная индукция, f+ и 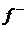 - функции распределения ионов и электронов,
соответственно. - функции распределения ионов и электронов,
соответственно.
Здесь
и далее в качестве единиц измерения [*] используются следующие:
время
[t] = 1/ω, ω - частота
падающего излучения,
расстояние
[r] = c/ω, c - скорость
света,
поле
[E] = [B] = mcω/e, m и
e - масса
покоя и заряд электрона,
концентрация
[n = ∫fdp] = mω2/4πe2,
импульс
[p] = mc,
энергия
[H = -μ+(μ2 +p2)1/2]
= mc2, μ = m±/m,
скорость
[v =
∂H/∂p] = c.
Падающее излучение – линейно-поляризованная монохроматическая волна с постоянной амплитудой, распространяющаяся
вдоль оси х, с электрическим
полем в направлении у и
магнитным - z.
Начальное распределение плазмы не зависит
от z и задача двумерна (∂/∂z ≡ 0). Отличны от нуля лишь три компоненты поля Ex, Ey, Bz. В падающей волне Ex = 0, Ey = Bz = aSin(x-t).
Полагая,
что мощное электрическое поле волны ионизует поверхностный слой практически
мгновенно, будем считать плазму в начальный момент полностью
ионизованной. В то же время пренебрежем
имеющимся в ней тепловым
движением, и будем считать
ее холодной и неподвижной
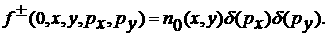
Поверхность плазмы образована плоскостями,
образующими с направлением падающей волны угол
±θ, и имеет периодическую
по у структуру ( рис.1).
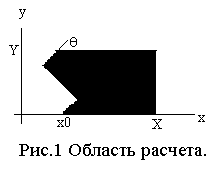
Параметрами задачи являются амплитуда волны а, начальная концентрация ионов и
электронов n0, характеристики области плазмы - (x0,X), период Y, угол θ.
Область расчета 0<x<X,
0<y<Y. Граничные
условия: периодичность по у и
Ey + Bz= -2aSint при x = 0,
Ey - Bz= 0
при x = X.
Основные принципы расчетного алгоритма, т.е. разностная схема
для уравнений Максвелла и метод макрочастиц
для уравнения Власова, изложены в
[2,3].
§2 Результаты
расчета
В
описываемых вариантах начальная концентрация ионов и электронов плазмы
постоянна n0 =10. Масса иона 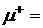 1837. Амплитуда
волны a = 0.01. Границы плазмы
x0 = 2, X = 10.
Варианты отличаются значениями периода Y = 2, 4, 6 и угла
θ = 26. 50 , 450 ,
63. 50. На рис.2 показана форма
границы области расчета для q= 26. 50
, 450 , 63. 50. 1837. Амплитуда
волны a = 0.01. Границы плазмы
x0 = 2, X = 10.
Варианты отличаются значениями периода Y = 2, 4, 6 и угла
θ = 26. 50 , 450 ,
63. 50. На рис.2 показана форма
границы области расчета для q= 26. 50
, 450 , 63. 50.
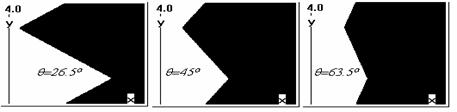
Рис.2 Форма
границы (Y=4, θ =
26. 50 , 450 , 63. 50).
Основным результатом каждого варианта
расчета является, очевидно, набранная частицами кинетическая энергия
 , ,
для удобства сравнения
нормированная на плотность потока
энергии в падающей волне. Варианты характеризуются значением доли поглощаемой электронами энергии – средней по времени величиной
κ = dW/dt.
На
рис.3 показана зависимость W(t) электронов для трех вариантов,
отличающихся только периодом Y = 2, 4, 6 при одном и том же угле θ = 45о. Максимальная
интенсивность поглощения энергии, κ = 0.4, достигается при Y = 4.
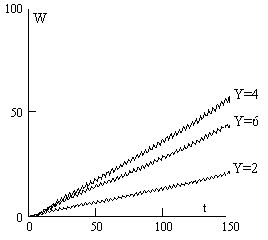
Рис.3 Энергия электронов при q = 45о.
На рис.4 показана зависимость W(t) электронов для трех вариантов, отличающихся только углом θ = 26.5о, 45о , 63.5о при
одном и том же периоде Y = 4. Интенсивность поглощения
энергии убывает с ростом угла
θ, т.е. с выпрямлением поверхности. При θ = 26.5о
- к = 0.6 , при θ = 63.5о - к= 0.1.
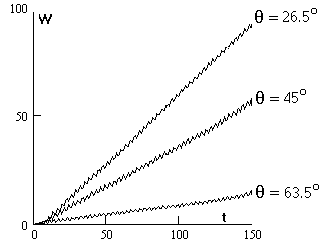
Рис.4 Энергия
электронов при Y = 4.
При θ = 90о, т.е. при падении волны на
плоскую поверхность, задача одномерна (∂/∂y≡0), к= 0 - имеет место полное отражение, W(t) колеблется с периодом
π.
Энергия электронной компоненты W растет, в основном, за счет вовлечения в
процесс новых электронов. На рис.5 показаны их фазовые портреты Px(x) и Py(x) на три момента времени (вариант Y =
4,
θ = 45о).
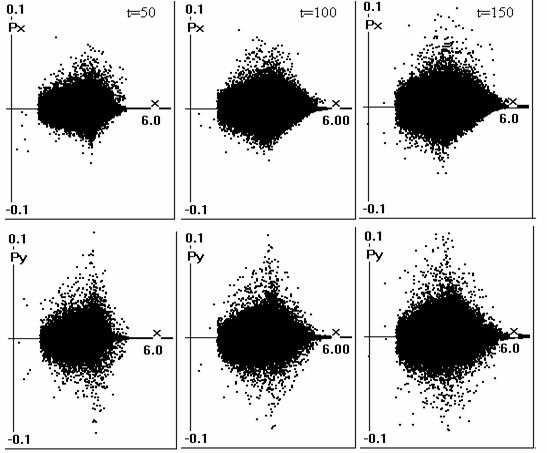
Рис.5 Проекции фазовых
портретов Px(x) и Py(x) электронов, t=50, 100,
150.
Область движения заметно
расширяется, а величина импульса остается в пределах |P| £ 0.1. На фазовых портретах направления x и y
практически не отличаются.
На рис.6 показана энергия ионной компоненты (вариант Y = 4, θ
= 45о). Она на полтора
порядка меньше электронной и появляется позже. Импульс ионов монотонно
растет и к моменту t=100 достигает единицы.
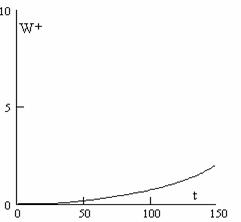
Рис.6 Энергия ионов
На рис.7 изображены проекции фазовых
портретов ионов в момент t=100, для того же варианта Y = 4, θ = 45о.
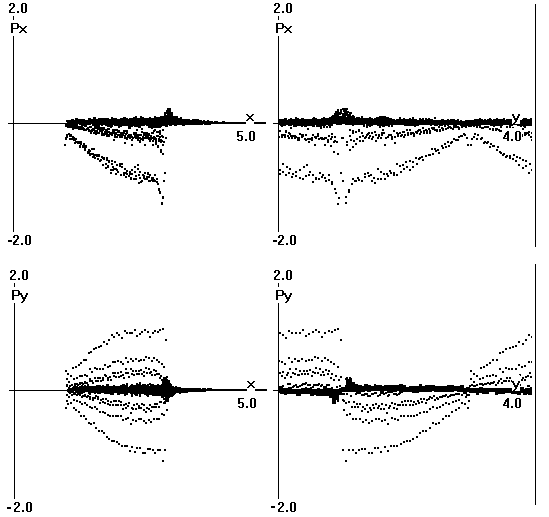
Рис.7 Проекции фазовых
портретов ионов на момент t=100.
Форма поверхности плазмы практически не
меняется. Лишь незначительное число электронов отрывается от малоподвижной
ионной массы, хорошо сохраняющей гофрированную структуру. Распределение
концентрации частиц меняется несущественно.
Все предыдущее относилось к случаю а =
0.01, n0 = 10.
Изменение амплитуды волны а (при прочих равных условиях, т.е. X=10, Y = 4,
θ = 45о, n0 =
10) ощутимо сказывается на процессе
при переходе через критическое значение а = 0.001. Рис.8 демонстрирует
это.

Рис.8 Энергия
электронов.
При а < 0.001 поглощение
незначительно - доля поглощаемой энергии к
< 0.1, начиная с а = 0.001
и выше к = 0.4~0.5. Интенсивность
процесса, величина импульса растут вместе с
амплитудой. При а = 0.0001 импульс электронов порядка 10-3,
при а = 0.001 на порядок больше, при а= 0.1 порядка единицы, т.е.
скорости становятся релятивистскими, v~0.7.
Таким образом, данный расчет
продемонстрировал уже указанное во
введении аномальное поглощение лазерного излучения в характерных условиях
разрабатываемого ЛТС на будущей установке ИСКРА-6 [4] (стр. 507). Для основного
варианта расчета с безразмерной амплитудой волны a=0.01 можно выписать физические характеристики этой
волны: амплитуда
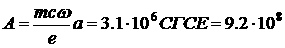 В/см, В/см,
а модуль вектора Пойнтинга
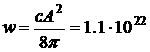 эрг/(сек×см2)=1.1×1015Вт/см2.
Тогда, согласно [4] осуществляется трансформация энергии электромагнитного
поля в тепловую энергию электронов плазмы без нелинейного вредного эффекта генерации «горячих»
электронов, поскольку произведение эрг/(сек×см2)=1.1×1015Вт/см2.
Тогда, согласно [4] осуществляется трансформация энергии электромагнитного
поля в тепловую энергию электронов плазмы без нелинейного вредного эффекта генерации «горячих»
электронов, поскольку произведение 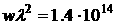 Вт×(mм)2/см2,
а его критическая величина из [4]
равна 1014 Вт×(mм)2/см2. Строго говоря, в данной оценке есть небольшое
превышение величины Вт×(mм)2/см2,
а его критическая величина из [4]
равна 1014 Вт×(mм)2/см2. Строго говоря, в данной оценке есть небольшое
превышение величины 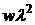 над её критическим
значением, но оно несущественно, ибо эффект численных расчетов сохраняется
вплоть до амплитуды a=0.001.
Отсутствие генерации «горячих» электронов качественно видно на рис.5 (в виде
относительно небольшого числа макрочастиц над их плотными облаками). Тем самым
сделанные расчеты согласуются с критерием из [4]. над её критическим
значением, но оно несущественно, ибо эффект численных расчетов сохраняется
вплоть до амплитуды a=0.001.
Отсутствие генерации «горячих» электронов качественно видно на рис.5 (в виде
относительно небольшого числа макрочастиц над их плотными облаками). Тем самым
сделанные расчеты согласуются с критерием из [4].
Заметим, наконец, что увеличение начальной
концентрации до n0 = 1000 приводит к
повышению критического значения
амплитуды до а ~ 1, когда
доля поглощаемой энергии к ~ 0.5.
Заключение
Установленный в [1] эффект аномального поглощения энергии
поля плазмой с плотностью выше критической (n0>1, в используемых единицах) для случая неоднородной
поверхности подтверждается при широкой вариации параметров неоднородности и
амплитуды волны. Рассмотрены простейшие случаи неоднородности, определяемые
периодом и величиной гофра. Как показали расчеты, важную роль в этом эффекте
играет угол θ, определяющий величину нормальной к поверхности
компоненты электрического поля падающей волны.
Тем не менее, роль рассматриваемого эффекта аномального
поглощения для реальных условий, в частности, для будущей установки ИСКРА-6
[4], может быть интересной, если требуемая для аномального поглощения
неоднородность не повлияет отрицательно на сам термоядерный эффект путем
развития неустойчивости Рэлея-Тэйлора (в
качестве начальных возмущений этой неустойчивости).
В обзоре [5], отражающем современную
мировую ситуацию в лазерном термоядерном синтезе, сделан вывод (стр. 39), что в
связи с указанной неустойчивостью допустимы неоднородности с характерным
масштабом 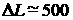 нм = 5×10-7м
= 0.5mм. Такие
неоднородности, (ограниченные сверху указанной величиной), однако, превышают
период неоднородности Y, заданный
в расчетах. Максимум аномального поглощения
получается с периодом Y=4, что соответствует
в размерных единицах величине нм = 5×10-7м
= 0.5mм. Такие
неоднородности, (ограниченные сверху указанной величиной), однако, превышают
период неоднородности Y, заданный
в расчетах. Максимум аномального поглощения
получается с периодом Y=4, что соответствует
в размерных единицах величине 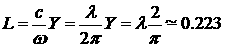 , где l длина электромагнитной
волны. Таким образом, выполнено требуемое неравенство L < DL. , где l длина электромагнитной
волны. Таким образом, выполнено требуемое неравенство L < DL.
Эффект аномального поглощения еще имеет
место при уменьшении периода неоднородности вдвое (Y=2), а это
только усиливает приведенное неравенство. Наоборот, увеличение периода при
сохранении эффекта (Y=6), несколько ослабляет его, но не нарушает. Нужно
особо подчеркнуть, что в целом эффект аномального поглощения попадает в
область допустимой с точки зрения работы [5] неоднородности поверхности.
Возможна, конечно, в расчетах вариация формы неоднородности еще и за
счет угла q, но и она не может изменить сделанный выше вывод.
В данной работе предполагалась, напомним,
линейная поляризация лазерного
излучения (вектор поляризации был строго параллелен невозмущенной поверхности
плазмы), в то время как лазерное излучение может быть неполяризованным, а
принудительная неоднородность поверхности
хаотической. По всей вероятности, полученный эффект аномального
поглощения все же сохранится, если поверхность плазмы будет покрыта
осесимметричными бугорками с характерным масштабом порядка длины волны
излучения.
Литература
1. В.Ф.Дьяченко, В.С. Имшенник. Об аномальном
взаимодействии мощных световых потоков с плотной плазмой. // Физика плазмы.
1979, Т. 5, Вып. 4.
2. В.Ф.Дьяченко. О расчетах задач бесстолкновительной
плазмы. // ЖВМ и МФ. 1985, № 4.
3. В.Ф.Дьяченко. Десять лекций по физической математике.
// Издательство «Факториал», г. Москва, 1997.
4. Р.И.
Илькаев, С.Г. Гаранин. // Вестник РАН. 2006, Т. 76, № 6.
5. M.M.
Basko. // Nuclear Fusion. 2005, V. 45.
|