Аннотация
Рассматривается задача об испарении твердого тела в вакуум. Эволюция функции распределения
описывается кинетическим уравнением, правая часть которого принимается равной интегралу
столкновений Бхатнагара-Гросса-Крука и реальному интегралу столкновений Больцмана.
Численно продемонстрирована неадекватность первой модели столкновений реальному физическому
процессу столкновений, что происходит из-за того, что частота столкновений в данной модели
не зависит от скоростей сталкивающихся частиц. С помощью уравнения Больцмана исследована
структура приповерхностного слоя, для которого численно установлено существование трех
зон для распределения макропараметров: область интенсивных столкновений, где устанавливается
локальное термодинамическое равновесие и справедливы уравнения газовой динамики, переходная
область и зона, где течение остается свободномолекулярным.
Abstract
The problem of solid body vaporization into vacuum is considered. Evolution of distribution
function is governed by kinetic equation, whose right hand-side is equal to the
Bhatnagar-Gross-Krook integral of collisions and the real integral of collisions of Boltzmann.
Inadequacy to real physical process of collisions is numerically demonstrated, which occurs
due to the fact that frequency of collisions does not depend on the velocities of collided
particles. Due to the use of the Boltzmann equation the structure of the surface layer
is investigated for which three zones for macroparameters are numerically established,
these are: the zone of intense collisions, where local thermodynamic equilibrium is setting
in, the transitional area and the zone where the flow is collisionless.
Содержание.
1) Введение…………………………………………………………………….3
2) Постановка
задачи для уравнения БГК…………………………………...4
3) Метод
решения……………………………………………………………..6
4) Алгоритм
расчета уравнения……………………………………………...7
5) Предполагаемая
структура решения……………………………………...9
6) Постановка
задачи для уравнения Больцмана…………………………..12
7) Метод
решения уравнения Больцмана…………………………………..13
8) “Весовой”
алгоритм ……………………………………………………...18
9) Заключение……………………………………………………………….20
Введение.
Скорость испарения конденсированного тела,
имеющего температуру значительно
меньшую, чем энергия связи атомов, определяется 2-мя процессами: уходом атомов
с поверхности и возвращением их
обратно на поверхность в результате столкновений в газовой фазе. При достаточно медленном
испарении в вакуум плотность пара у поверхности мала и вторым процессом
можно пренебречь. Фактически в работах
[1-3], посвященных испарению рассматривался только этот наиболее простой
случай.
При интенсивном (равно как и при
длительном) испарении пренебрежение обратным потоком становится некорректным. В
условиях, характерных для лазерных экспериментов при мощности излучения ~ [16,17], движение основной массы пара подчиняется уравнениям
газодинамики. При этом возникают следующие вопросы:1) какова скорость испарения твердого тела в системе
координат, в которой координата раздела фаз тело-газ покоится 2) каким
граничным условиям должны удовлетворять уравнения газодинамики? Второй вопрос
связан с тем, что газодинамическое приближение заведомо неприменимо
в тонком кнудсеновском слое вблизи границы фаз, где функция
распределения сильно отличается от локально равновесной. С газодинамической точки
зрения кнудсеновский слой
является поверхностью разрыва. Для получения газодинамических граничных условий
надо найти функцию распределения атомов по скоростям внутри кнудсеновского слоя.
Эта задача была решена в работах [5,6]. Было установлено, что на внешней
границе кнудсеновского слоя температура пара равна примерно [16,17], движение основной массы пара подчиняется уравнениям
газодинамики. При этом возникают следующие вопросы:1) какова скорость испарения твердого тела в системе
координат, в которой координата раздела фаз тело-газ покоится 2) каким
граничным условиям должны удовлетворять уравнения газодинамики? Второй вопрос
связан с тем, что газодинамическое приближение заведомо неприменимо
в тонком кнудсеновском слое вблизи границы фаз, где функция
распределения сильно отличается от локально равновесной. С газодинамической точки
зрения кнудсеновский слой
является поверхностью разрыва. Для получения газодинамических граничных условий
надо найти функцию распределения атомов по скоростям внутри кнудсеновского слоя.
Эта задача была решена в работах [5,6]. Было установлено, что на внешней
границе кнудсеновского слоя температура пара равна примерно 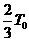 ( (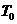 - температура конденсированной фазы), а плотность близка к
1/3 - температура конденсированной фазы), а плотность близка к
1/3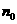 ( (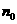 - равновесная плотность пара при температуре - равновесная плотность пара при температуре 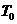 ). В [7] проведено детальное исследование испарения в вакуум
при постоянной температуре испаряющей поверхности в приближении
Бхатнагара-Гросса-Крука, и было установлено время установления
газодинамического режима. Задача о неравновесном испарении в приближении
Больцмана при изменяющейся температуре поверхности была решена в [15], где было
показано, что при временах больших по сравнению с временем интенсивного
испарения функция распределения достаточно быстро приближается к функции
распределения атомов, испаряющихся при постоянной температуре ). В [7] проведено детальное исследование испарения в вакуум
при постоянной температуре испаряющей поверхности в приближении
Бхатнагара-Гросса-Крука, и было установлено время установления
газодинамического режима. Задача о неравновесном испарении в приближении
Больцмана при изменяющейся температуре поверхности была решена в [15], где было
показано, что при временах больших по сравнению с временем интенсивного
испарения функция распределения достаточно быстро приближается к функции
распределения атомов, испаряющихся при постоянной температуре  , т.е. при средней по времени температуре испаряющей
поверхности [14]. В [14] показано, что при слабом испарении функция
распределения сильно отличается от максвелловского распределения во всей
области, занятой испаренными частицами, в отличие от интенсивного испарения,
когда поток частиц частично распределен равновесно, на что указывалось в [7].
Задача об испарении в пространство,
занятое газом, была рассмотрена в [17] в
газодинамическом приближении. , т.е. при средней по времени температуре испаряющей
поверхности [14]. В [14] показано, что при слабом испарении функция
распределения сильно отличается от максвелловского распределения во всей
области, занятой испаренными частицами, в отличие от интенсивного испарения,
когда поток частиц частично распределен равновесно, на что указывалось в [7].
Задача об испарении в пространство,
занятое газом, была рассмотрена в [17] в
газодинамическом приближении.
Таким образом, правильный подход к
задаче об испарении в вакуум предполагает решение кинетического уравнения для расширяющегося
пара на достаточно большом интервале времени. Такое решение позволяет
проследить переход от свободномолекулярного разлета пара к газодинамическому и определить характер
течения в области малой плотности, где неприменимы законы газодинамики.
Постановка задачи для уравнения БГК.
Будем рассматривать испарение полу бесконечного
твердого тела с постоянной температурой 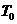 в первоначально пустое
полупространство. Выберем систему координат, в которой
граница раздела фаз покоится. Твердая фаза занимает полупространство в первоначально пустое
полупространство. Выберем систему координат, в которой
граница раздела фаз покоится. Твердая фаза занимает полупространство  . .
Движение
газа описывается уравнением Больцмана:
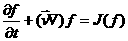 (1).
(1).
Для
интеграла столкновений примем модельное выражение
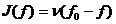 , (2) , (2)
, где
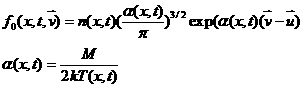
Входящие
в (2) функции 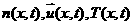 определяются
интегральными соотношениями определяются
интегральными соотношениями
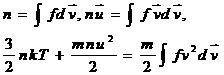 (3) (3)
Определение
n, u
, T по
соотношениям (3) обеспечивает сохранение сумматорных инвариантов для уравнения (1). Входящая в (2) частота
столкновений 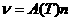 определяется законом взаимодействия
атомов. В дальнейшем будет рассматриваться модель твердых сфер, для которой определяется законом взаимодействия
атомов. В дальнейшем будет рассматриваться модель твердых сфер, для которой  . В качестве граничного условия для (1)-(3) нужно задать
функцию распределения атомов, входящих в полупространство . В качестве граничного условия для (1)-(3) нужно задать
функцию распределения атомов, входящих в полупространство  . Согласно [2] будем считать ее максвелловской для частиц с . Согласно [2] будем считать ее максвелловской для частиц с 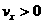 : :
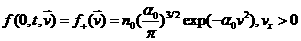 (4) (4)
, где 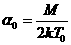 , M –масса
атома, , M –масса
атома, 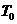 -температура
поверхности, -температура
поверхности, 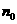 -равновесная
плотность пара,
соответствующая этой температуре. Поскольку наибольший
практический интерес представляет
испарение металла, примем коэффициент прилипания частиц
к поверхности равным единице.
Кроме (4), имеют место
очевидные условия, налагаемые на функцию -равновесная
плотность пара,
соответствующая этой температуре. Поскольку наибольший
практический интерес представляет
испарение металла, примем коэффициент прилипания частиц
к поверхности равным единице.
Кроме (4), имеют место
очевидные условия, налагаемые на функцию 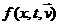 : :
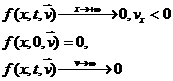
Для дальнейшего удобно перейти к безразмерным
переменным. Введем их следующим образом. За единицу длины выберем длину
свободного пробега атомов при плотности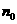 , за единицу скорости – величину , за единицу скорости – величину 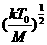 ; температуру и
плотность будем измерять в единицах ; температуру и
плотность будем измерять в единицах 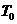 и и 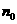 соответственно. Поскольку в дальнейшем будут использоваться безразмерные величины, сохраним для них те же
обозначения , что и для размерных. соответственно. Поскольку в дальнейшем будут использоваться безразмерные величины, сохраним для них те же
обозначения , что и для размерных.
В формулах (3) интегрирование производится
по всему пространству скоростей,
т.е. с учетом симметрии задачи интегралы
в (3) – двукратные . Имея в виду
численное решение задачи, удобно перейти от
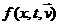 к новым неизвестным функциям, зависящим от к новым неизвестным функциям, зависящим от 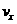 . В терминах этих функций удается с формулировать замкнутую
систему уравнений и вычислить все
гидродинамические переменные
, характеризующие поток пара. При таком подходе теряется часть информации о
функции распределения, которая сама по себе является бесполезной , а
нужна лишь для расчета гидродинамических средних. . В терминах этих функций удается с формулировать замкнутую
систему уравнений и вычислить все
гидродинамические переменные
, характеризующие поток пара. При таком подходе теряется часть информации о
функции распределения, которая сама по себе является бесполезной , а
нужна лишь для расчета гидродинамических средних.
Введем новые искомые функции 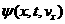 и и 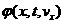 по соотношениям: по соотношениям:
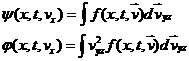
,
где 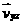 имеет компоненты имеет компоненты  . Тогда уравнения для . Тогда уравнения для 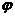 и и 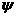 имеют вид: имеют вид:
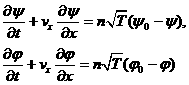 (5)
(5)
Здесь
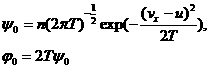
а функция
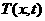 определяется
соотношением: определяется
соотношением:
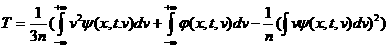 (6) (6)
Соотношения
для 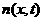 и и 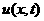 выглядят следующим
образом выглядят следующим
образом
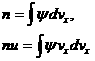
Граничные
условия для 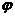 и и 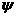 имеют следующий вид: имеют следующий вид:
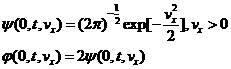
Условия
на бесконечности получаются аналогично.
Метод решения.
Для
решения (5) фиксируем 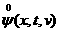 и и  во всей счетной
области во всей счетной
области 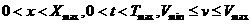 . Вводим сетку по . Вводим сетку по 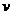 с постоянным шагом с постоянным шагом 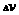 . .
Подставляя
в правую часть (5) наше нулевое приближение при фиксированной скорости получаем
линейное уравнение адвекции с источником, разрешая которое для всех скоростей
из нашей сетки получаем 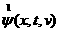 и и 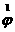 . Пусть мы уже получили . Пусть мы уже получили  и и 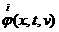 , тогда по формуле
трапеций подсчитываем , тогда по формуле
трапеций подсчитываем 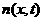 , , 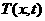 и и 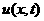 , затем подставляя в правую часть вместо , затем подставляя в правую часть вместо 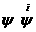 и соответственно
вместо и соответственно
вместо 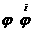 , получаем , получаем 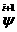 и и 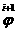 . То есть: . То есть:
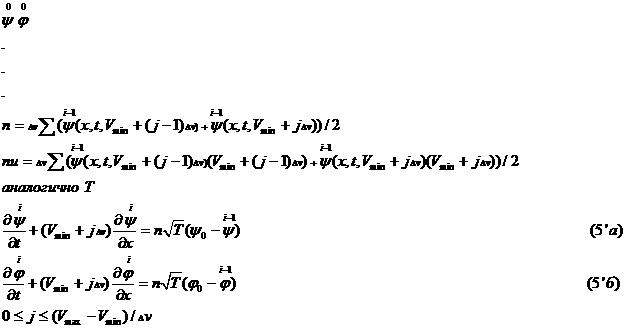
Для решения (5’) вводим сетку в
плоскости (x,t) c постоянными
шагами по времени и пространственной переменной
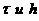 и получаем и получаем  в узлах расчетной сетки. В качестве
нулевого приближения используем свободномолекулярное течение,
получаемое из (5’) при условии равенства источника нулю. Первоначально использовалась явная двухслойная схема TVD c ограничителем
потоков minmod. Однако за счет наличия схемной вязкости происходит
изменение структуры фронтов, так что
вычисление по этой схеме представлялось возможным проводить только на
подробной сетке (число узлов по X порядка 500). в узлах расчетной сетки. В качестве
нулевого приближения используем свободномолекулярное течение,
получаемое из (5’) при условии равенства источника нулю. Первоначально использовалась явная двухслойная схема TVD c ограничителем
потоков minmod. Однако за счет наличия схемной вязкости происходит
изменение структуры фронтов, так что
вычисление по этой схеме представлялось возможным проводить только на
подробной сетке (число узлов по X порядка 500).
Поэтому был предложен другой алгоритм
решения уравнения адвекции, достаточно
точно передающий структуру фронтов. Таким алгоритмом является, как известно, интегрирование по характеристикам.
Алгоритм
расчета уравнения 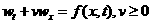 . .
Пусть 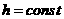 шаг по пространству и шаг по пространству и 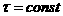 шаг по времени и шаг по времени и  . .
Принимается, что начальное
распределение кусочно-постояннно и непрерывно слева, с точками разрыва,
расположенных в расчетных узлах.
Рассмотрим работу алгоритма на первых
двух шагах, при условии f(x,t)=0, v>0.
Рассмотрим узел расчетной сетки 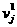 . Выпуская из него вниз характеристику до пересечения с
нулевым слоем по времени, замечаем, что . Выпуская из него вниз характеристику до пересечения с
нулевым слоем по времени, замечаем, что 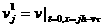 . Но при условии . Но при условии 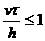 , и, отбрасывая тривиальные случаи v=0 и , и, отбрасывая тривиальные случаи v=0 и 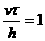 , получаем, что точка A=(0,jh-v , получаем, что точка A=(0,jh-v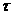 ) лежит между узлами
расчетной сетки. Обычный подход разрешает эту проблему при помощи интерполяции
в точку A значения из прилежащих
расчетных узлов, что, в случае разрывных начальных данных порождает
сглаживание. Мы же, отказавшись от интерполяции, требуем, чтобы ) лежит между узлами
расчетной сетки. Обычный подход разрешает эту проблему при помощи интерполяции
в точку A значения из прилежащих
расчетных узлов, что, в случае разрывных начальных данных порождает
сглаживание. Мы же, отказавшись от интерполяции, требуем, чтобы 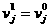 . .
Далее, выпуская характеристику вниз из
узла (2,j) до пересечения с осью t=0 в
точке A с координатами А=(0,
jh-2v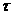 ) видим, что при условии 2v ) видим, что при условии 2v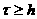 , необходим снос по характеристике значения , необходим снос по характеристике значения 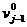 , т.е. значения сеточной функции из ближайшего справа от А расчетного узла. , т.е. значения сеточной функции из ближайшего справа от А расчетного узла.
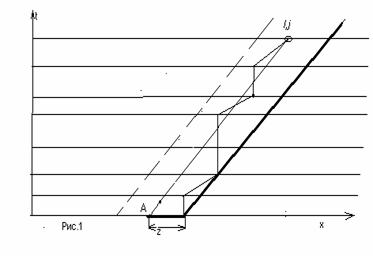
Продолжая
аналогичным образом интегрировать уравнение переноса вдоль характеристик,
приходим к следующему алгоритму: вводим новую сеточную переменную 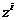 и и 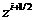 , , 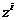 имеет смысл
расстояния по имеет смысл
расстояния по 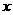 от характеристики ,
выпущенной из узла (i, j) вниз до
пересечения с линией t=0 (точку пересечения назовем А), до ближайшего справа к А
узла расчетной сетки (0,j’) (Рис.1).
А от характеристики ,
выпущенной из узла (i, j) вниз до
пересечения с линией t=0 (точку пересечения назовем А), до ближайшего справа к А
узла расчетной сетки (0,j’) (Рис.1).
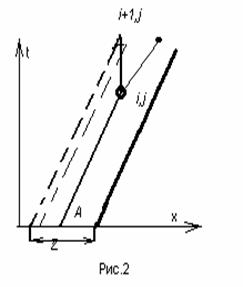
А 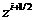 , в свою очередь,
имеет смысл аналогичного расстояния по x от характеристики, выпущенной из узла (i+1, j)
вниз до пересечения с линией t=0, до точки А
(рис.2). , в свою очередь,
имеет смысл аналогичного расстояния по x от характеристики, выпущенной из узла (i+1, j)
вниз до пересечения с линией t=0, до точки А
(рис.2).
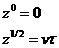
если 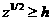 то то
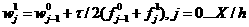 , ,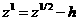
иначе
 и и 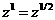 , ,
предположим , что мы вычислили 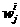 и и 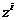 , тогда , тогда 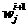 и и  считаем так: считаем так:
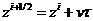
если  то то
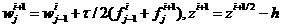
иначе
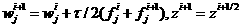
.
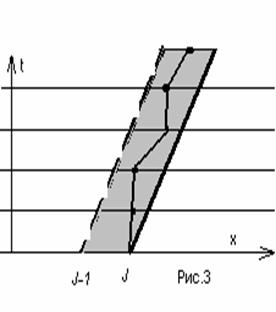
Таким образом, для только что
рассчитанного узла получаем область зависимости выделенную на рис. 3 черной
ломаной, а серым обозначена область влияния начального полуинтервала.
Это означает, что алгоритм дает
минимально возможную, т.е. наиболее приближенную область зависимости
разностного решения к области зависимости исходного дифференциального
уравнения, область зависимости. Алгоритм имеет 1-й порядок сходимости по
времени и пространству (ср. [18]).
Пример тестовых расчетов.
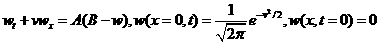 . Такое уравнение решаем итерациями, т.е. сначала решаем
уравнение чистого переноса, подставляем в источник , применяем алгоритм и т.д.
Точное решение имеет вид: . Такое уравнение решаем итерациями, т.е. сначала решаем
уравнение чистого переноса, подставляем в источник , применяем алгоритм и т.д.
Точное решение имеет вид: 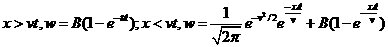 . .
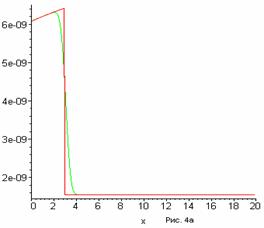
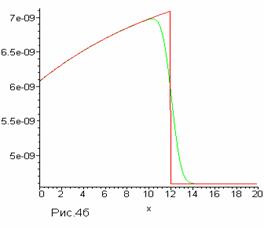
На Рис.4 приведена 5 итерация алгоритма
при v=6, совпадающая с точным решением, и 5-я итерация
схемы TVD.
Предполагаемая структура решения.
Пусть
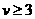 (Рис.5) и начинаем
итерировать, отступя по времени на некоторое (Рис.5) и начинаем
итерировать, отступя по времени на некоторое 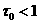 . Тогда можно ввести для . Тогда можно ввести для 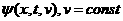 и и 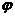 пространственные зоны,
характеризующие интенсивность столкновений, а именно зона частых столкновений,
зона, где столкновения сравнительно редки и зона, где столкновений нет. Для
этих зон можно построить приближение 1-й итерации, которым можно пользоваться
и при последующих
итерациях. Его можно получить
следующим образом. Ввиду того, что источник на 1-й итерации автомодельный ,
т.е. пространственные зоны,
характеризующие интенсивность столкновений, а именно зона частых столкновений,
зона, где столкновения сравнительно редки и зона, где столкновений нет. Для
этих зон можно построить приближение 1-й итерации, которым можно пользоваться
и при последующих
итерациях. Его можно получить
следующим образом. Ввиду того, что источник на 1-й итерации автомодельный ,
т.е. 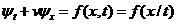 , достаточно найти
точку (назовем ее , достаточно найти
точку (назовем ее 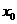 ) первую правую точку
удовлетворяющую условию ) первую правую точку
удовлетворяющую условию 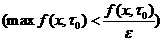 , где , где 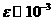 (точку в которой источник по сравнению с максимумом равен
нулю). Тогда в области слева от прямой (точку в которой источник по сравнению с максимумом равен
нулю). Тогда в области слева от прямой 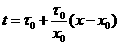 получаем область
интенсивных столкновений, справа от прямой получаем область
интенсивных столкновений, справа от прямой
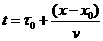 получаем чисто
свободномолекулярное течение, а между этими прямыми расположена переходная область, где
столкновения сравнительно малы. получаем чисто
свободномолекулярное течение, а между этими прямыми расположена переходная область, где
столкновения сравнительно малы.
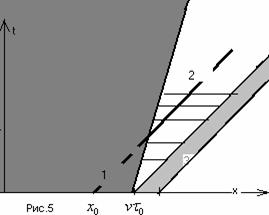
В 1 область интенсивных столкновений, в 2 те
частицы, которые вылетели из 1 и
больше не сталкиваются, в 3– чисто (в отличие от 2) свободномолекулярное
течение, т.е.  длина свободномолекулярного “хвоста” для длина свободномолекулярного “хвоста” для 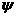 при данном при данном 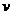 . .
Для
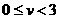 (Рис. 6) качественно
иная ситуация, если выше перед фронтом, идущим с границы, ничего не возникало,
то для
этих возникает, что объясняется тем, что (Рис. 6) качественно
иная ситуация, если выше перед фронтом, идущим с границы, ничего не возникало,
то для
этих возникает, что объясняется тем, что  . .
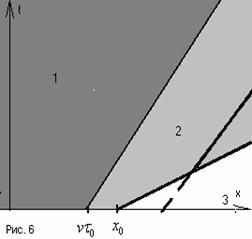
Если фиксировано 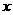 , то с течением времени , то с течением времени  в этой точке меняется следующим образом: вначале они
свободномолекулярные, затем возникает поток частиц назад и спустя еще какое-то
время устанавливается локально-равновесное распределение Максвелла. в этой точке меняется следующим образом: вначале они
свободномолекулярные, затем возникает поток частиц назад и спустя еще какое-то
время устанавливается локально-равновесное распределение Максвелла.
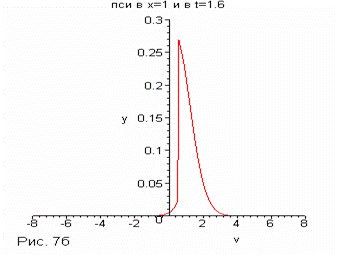
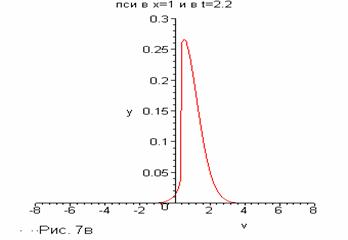
Например, в 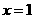 получаем с течением
времени следующие результаты(Рис.7): получаем с течением
времени следующие результаты(Рис.7):

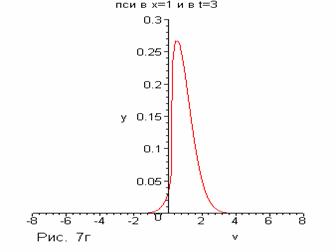
В то же время, для макропараметра температуры (напоминаем, что счет
ведется с некоторого 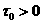 ) существует зона, где частицы интенсивно сталкиваясь,
образуют область, в которой с течением времени
устанавливается газодинамическое течение; достаточно далеко возникает
область свободномолекулярного течения, между ними образуется переходная зона
(Рис.9). ) существует зона, где частицы интенсивно сталкиваясь,
образуют область, в которой с течением времени
устанавливается газодинамическое течение; достаточно далеко возникает
область свободномолекулярного течения, между ними образуется переходная зона
(Рис.9).

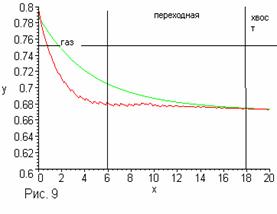
Очевидно, что последнюю формируют частицы, находящиеся на хвосте
соответствующих 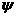 , но ведь эти зоны зависят от того, на сколько мы отступили
по времени, а именно- чем меньше мы отступаем , тем меньше получается
протяженность этой зоны. В области
свободномолекулярного течения аналогом температуры является средняя энергия
теплового движения, ее асимптотическое значение равно , но ведь эти зоны зависят от того, на сколько мы отступили
по времени, а именно- чем меньше мы отступаем , тем меньше получается
протяженность этой зоны. В области
свободномолекулярного течения аналогом температуры является средняя энергия
теплового движения, ее асимптотическое значение равно  . .
Если считать с нуля, то получим для температуры следующее.
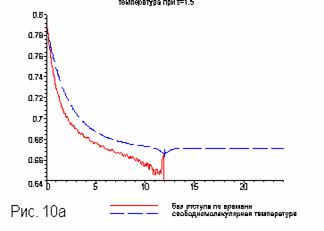
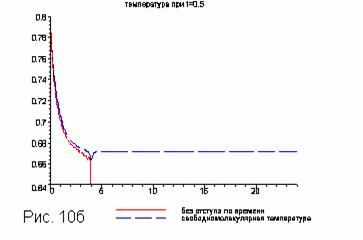
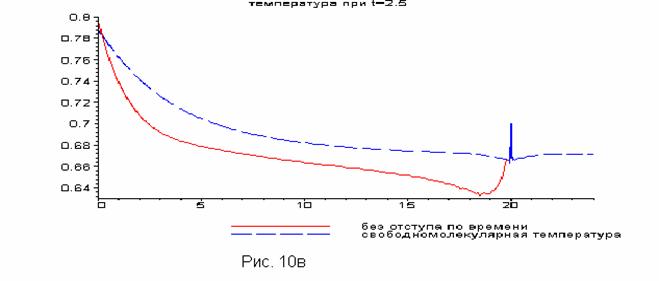
Хорошо
видно, что свободномолекулярного хвоста нет (Рис.10). Действительно, очевидно,
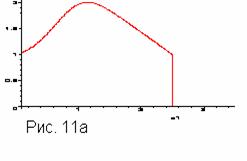
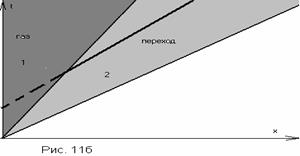
что “хвост” должны формировать быстрые частицы, однако при расчете 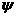 и и 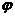 обнаруживается его отсутствие(рис.11а), что объясняется
следующей картинкой(рис.11б). В зоне 1
источник никак не 0. обнаруживается его отсутствие(рис.11а), что объясняется
следующей картинкой(рис.11б). В зоне 1
источник никак не 0.
Действительно,
при расчете ф-ии распределения при высоких
скоростях частота столкновений  такая же как при
расчете ф-ии распределения на низких скоростях, что приводит к чрезмерной и
нефизичной релаксации ф-ии распределения на высоких скоростях, т.е. модель БГК
не применима при такая же как при
расчете ф-ии распределения на низких скоростях, что приводит к чрезмерной и
нефизичной релаксации ф-ии распределения на высоких скоростях, т.е. модель БГК
не применима при 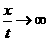 . .
Таким
образом не остается другого выхода как рассчитывать решение уравнение с
реальным интегралом столкновений.
Постановка задачи для уравнения Больцмана.
Рассматривается процесс испарения с
поверхности полубесконечного твердого тела в первоначально пустое
пространство. Граница тела расположена в
точке  . Пар расширяется
в полупространство . Пар расширяется
в полупространство 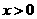 . Искомой является
функция распределения . Искомой является
функция распределения 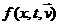 (поскольку она в силу
симметрии задачи не зависит от продольных координат) : произведение (поскольку она в силу
симметрии задачи не зависит от продольных координат) : произведение 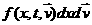 есть масса
частиц, содержащихся в окрестности есть масса
частиц, содержащихся в окрестности 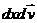 точки точки 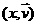 4-х мерного фазового
пространства в момент времени 4-х мерного фазового
пространства в момент времени 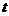 . .
Динамика
функции распределения определяется уравнением Больцмана:
 (1’), (1’),
где
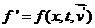  ( (  скорости частиц после
столкновения, первоночально имевших скорости скорости частиц после
столкновения, первоночально имевших скорости 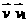 ), ), 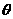 - угол рассеяния, - угол рассеяния,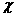 -азимут столкновения, -азимут столкновения, 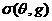 - дифференциальное
сечение рассеяния, - дифференциальное
сечение рассеяния,  - модуль относительной скорости, равный - модуль относительной скорости, равный 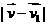 [1]. Граничные условия
имеют следующий вид: [1]. Граничные условия
имеют следующий вид:
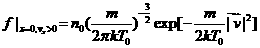 и и  (2’), (2’),
где  - масса атома , - масса атома , 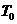 -температура испаряющего тела, -температура испаряющего тела, 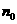 - равновесная плотность пара, соответствующая этой
температуре. - равновесная плотность пара, соответствующая этой
температуре.
В настоящей работе используется модель твердых сфер, для
которой 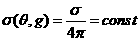 , где , где  -полное сечение рассеяния. -полное сечение рассеяния.
Перейдем к безразмерным переменным.
 (2’’) (2’’)
Переходя к старым обозначениям для
безразмерных переменных получим следующее уравнение
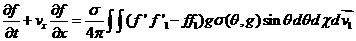 (6а) (6а)
с граничными условиями
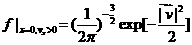 , ,  (при (при 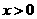 ) ) 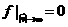 (6б) (6б)
Интересующие нас
макропараметры определяются выражениями :
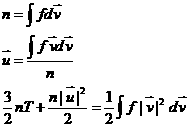 (7) (7)
Метод решения уравнения Больцмана.
Предполагалось использовать алгоритм прямого статистического
моделирования, предложенный в [8,9].
Моделируемая среда разбивается на
ячейки, которые заполняются частицами, равномерно размазанными по ячейке, распределенные по
скоростям в соответствии с начальной функцией распределения. Далее,
используется метод расщепления по физическим процессам, а именно моделируемое
уравнение Больцмана расщепляется на свободномолекулярный перенос и процесс
столкновений.
Для свободномолекулярного
переноса, используется алгоритм, предложенный в [10]. А именно, перебираются все ячейки , в которых
перебираются все частицы и с вероятностью 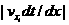 i-я частица в зависимости от знака x-вой
компоненты скорости перемещается в соседнюю ячейку. Пусть для определенности i-я частица в зависимости от знака x-вой
компоненты скорости перемещается в соседнюю ячейку. Пусть для определенности 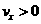 и и 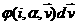 - вероятность обнаружить частицу в i -ой ячейке в момент времени - вероятность обнаружить частицу в i -ой ячейке в момент времени 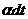 со скоростью ,
заключенной в элементе со скоростью ,
заключенной в элементе 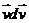 . Тогда вероятность того, что частица покинет ячейку равна . Тогда вероятность того, что частица покинет ячейку равна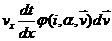 , вероятность того , что частица переместится из i-1 –ой
ячейки равна , вероятность того , что частица переместится из i-1 –ой
ячейки равна  , следовательно вероятность найти эту частицу на следующем
слое по времени равна , следовательно вероятность найти эту частицу на следующем
слое по времени равна 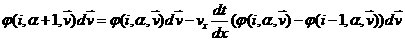 . .
Если
устремить параметры сетки к 0 , то получим аппроксимацию оператора
свободномолекулярного переноса первого порядка по времени и пространству.
Для моделирования решения уравнения 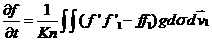 использовалась схема
Бернулли, состоящая в выполнении для частиц каждой ячейки следующих действий
[10]: использовалась схема
Бернулли, состоящая в выполнении для частиц каждой ячейки следующих действий
[10]:
поочередно перебираем все пары частиц 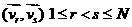 в ячейке для каждой из
них разыгрывается столкновение с вероятностью в ячейке для каждой из
них разыгрывается столкновение с вероятностью
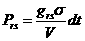 , ,
если столкновение состоялось
, то разыгрываем скорости  из распределений из распределений
 , ,
где 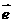 - единичный вектор, направленный вдоль вектора относительной
скорости после столкновения, его сферические координаты разыгрываются исходя из распределений - единичный вектор, направленный вдоль вектора относительной
скорости после столкновения, его сферические координаты разыгрываются исходя из распределений
для азимута столкновения -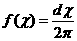 , ,
для угла рассеяния - 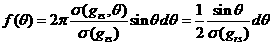 ; ;
если столкновение не
состоялось, то частицы своих скоростей не меняют.
Пусть 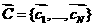 - вектор скоростей частиц , находящихся в ячейке, тогда
плотность функции распределения частиц при применении вышеописанного алгоритма
столкновений удовлетворяет уравнению - вектор скоростей частиц , находящихся в ячейке, тогда
плотность функции распределения частиц при применении вышеописанного алгоритма
столкновений удовлетворяет уравнению
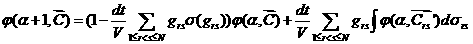 , ,
которое является
аппроксимацией прямого уравнения Колмогорова процесса Каца [11],
 . .
В
[11] показано, что если в начальный момент скорости частиц статистически
независимы, то для распределений
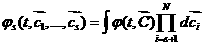
скоростей первых s-частиц при всех t>0, 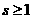 почти всюду почти всюду
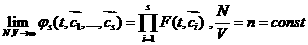 , ,
причем 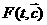 является уравнением
Больцмана является уравнением
Больцмана
 , что нам и требовалось. , что нам и требовалось.
Феноменологически
процесс Каца можно ввести при помощи следующих определений ([9]).
Определение
1: Столкновением называется случайное
событие , в результате которого точка 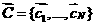 мгновенно
изменяет свое положение
в пространстве мгновенно
изменяет свое положение
в пространстве 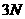 измерений и принимает
новое значение измерений и принимает
новое значение  , удовлетворяющее следующим постулатам. , удовлетворяющее следующим постулатам.
1)результатом столкновения может быть
изменение значений лишь какой-то одной
пары векторов 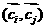 ; будем говорить , что эта пара испытала столкновение; ; будем говорить , что эта пара испытала столкновение;
2) новые значения векторов 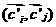 пары, испытавшей
столкновение, являются случайными величинам, но такими , что пары, испытавшей
столкновение, являются случайными величинам, но такими , что  и и 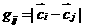 своих значений не
меняют. своих значений не
меняют.
3)вероятность того, что после столкновения пары 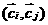 новый вектор
относительной скорости новый вектор
относительной скорости 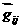 попадает в телесный
угол попадает в телесный
угол 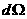 , есть , есть
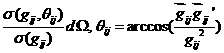 . .
Определение
2: Система N векторов 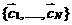 называется пространственно однородной марковской
моделью идеального одноатомного газа из называется пространственно однородной марковской
моделью идеального одноатомного газа из 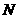 частиц, если эволюция
точки частиц, если эволюция
точки 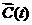 определяется
последовательностью столкновений, разделенных случайными интервалами времени T, причем: определяется
последовательностью столкновений, разделенных случайными интервалами времени T, причем:
1) вероятность того, что в момент 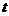 столкнулась пара
частиц столкнулась пара
частиц 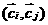 (при условии, что
столкновение какой-то одной пары состоялось) равна (при условии, что
столкновение какой-то одной пары состоялось) равна
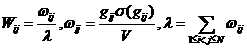
2) время ожидания очередного столкновения имеет
распределение
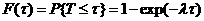 , ,
не зависящее от выбора начала
отсчета времени и от пары , реализующее это столкновение, и определяемое
состоянием всей системы в целом ([9]).
Таким образом возможно моделирование релаксации в
газе, точно передающее, в отличие от распространенного метода Берда, статистику столкновений. Но, к сожалению,
реализация этой модели имеет большую трудоемкость 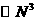 , поэтому и был предложен ([8]) упрощенный алгоритм
столкновений с трудоемкостью порядка , поэтому и был предложен ([8]) упрощенный алгоритм
столкновений с трудоемкостью порядка 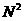 . .
Методика расчета.
Для
численного решения (6) разбиваем полупространство 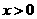 на ячейки объема на ячейки объема 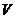 и длины и длины 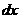 . Проводим . Проводим 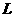 реализаций
( реализаций
(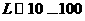 ) описанного выше марковского процесса. Для каждой реализации выполняем следующие
действия. В нулевой ячейке число частиц , обладающих положительной скоростью
принималось равным ) описанного выше марковского процесса. Для каждой реализации выполняем следующие
действия. В нулевой ячейке число частиц , обладающих положительной скоростью
принималось равным 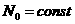 , скорости этих частиц
,в соответствии с граничными условиями, разыгрываем по (6б) с учетом того
факта, что , скорости этих частиц
,в соответствии с граничными условиями, разыгрываем по (6б) с учетом того
факта, что 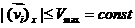 , также должно быть выполнено условие Куранта , также должно быть выполнено условие Куранта 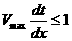 . В начальный момент в
соответствии с начальными условиями (6) все ячейки , кроме граничной , пусты. А далее применяем описанный выше алгоритм. С учетом, однако, того факта, что
интересующая нас особенность решения, хвост, образована частицами с высокими
скоростями, требуется огромное число
модельных частиц. Ввиду квадратичной по
числу частиц трудоемкости алгоритма, применение в чистом виде этого алгоритма
крайне затруднительно, поэтому для уменьшения времени счета применялся алгоритм сталкивания в группах. А
именно, пусть в ячейке находится . В начальный момент в
соответствии с начальными условиями (6) все ячейки , кроме граничной , пусты. А далее применяем описанный выше алгоритм. С учетом, однако, того факта, что
интересующая нас особенность решения, хвост, образована частицами с высокими
скоростями, требуется огромное число
модельных частиц. Ввиду квадратичной по
числу частиц трудоемкости алгоритма, применение в чистом виде этого алгоритма
крайне затруднительно, поэтому для уменьшения времени счета применялся алгоритм сталкивания в группах. А
именно, пусть в ячейке находится 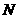 частиц, тогда разбиваем нашу ячейку объема частиц, тогда разбиваем нашу ячейку объема 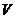 на 10 на 10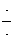 100 маленьких однородных ячеек, далее локализуем наши 100 маленьких однородных ячеек, далее локализуем наши 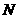 частиц по этим объемам и там разыгрываем столкновения между
ними. Как показали проведенные тесты результирующее распределение по скоростям,
при достаточно большом числе частиц, будет
таким же, как если бы мы считали без разбивания по группам. частиц по этим объемам и там разыгрываем столкновения между
ними. Как показали проведенные тесты результирующее распределение по скоростям,
при достаточно большом числе частиц, будет
таким же, как если бы мы считали без разбивания по группам.
Для
вычисления макропараметров, определенных следующим образом
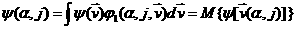 , где , где 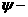 интересующий нас макропараметр, интересующий нас макропараметр,  соответственно момент времени, и номер ячейки, используем
формулу соответственно момент времени, и номер ячейки, используем
формулу 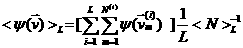 , которая дает состоятельную оценку (см. [9]). , которая дает состоятельную оценку (см. [9]).
Результаты работы программы прямого стат.
моделирования.
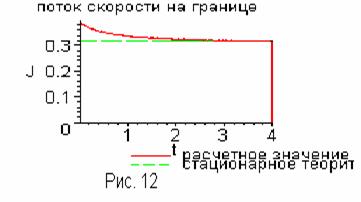
На следующих рисунках
(Рис.12,
13, 14) представлены результаты работы программы
при
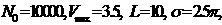

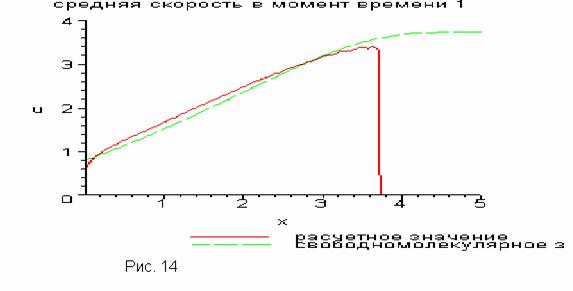
На представленных графиках
отчетливо видна структура ранее качественно описанного решения (см.
Предполагаемая структура решения), а
именно : при малых 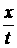 устанавливается
газодинамический режим , при больших же значениях устанавливается
газодинамический режим , при больших же значениях 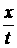 значения
макропараметров близки к свободномолекулярным. значения
макропараметров близки к свободномолекулярным.
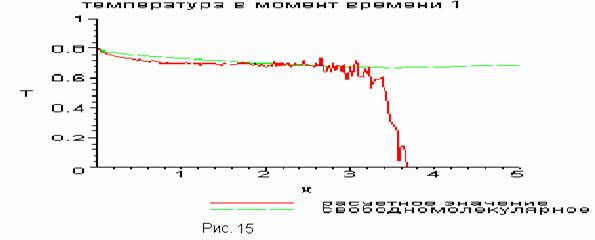
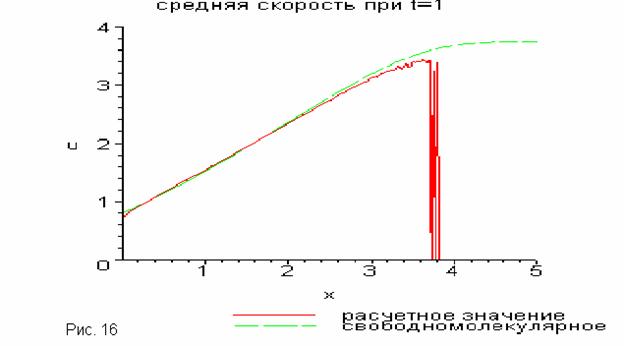
Ввиду того, что наибольшим для нас интересом является область “хвоста”,
были проведены расчеты с уменьшенным полным сечением столкновений, а именно
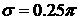 , графики приведены ниже (Рис.15,16).
, графики приведены ниже (Рис.15,16).
«Весовой» алгоритм
К сожалению,
описанный выше алгоритм,
затруднительно применять к случаю, когда 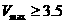 из-за ограничения на
объем используемой оперативной памяти. Поэтому было решено применить весовой
алгоритм моделирования столкновений, разработанный из-за ограничения на
объем используемой оперативной памяти. Поэтому было решено применить весовой
алгоритм моделирования столкновений, разработанный
для расчета макропараметров релаксирующих смесей
газов([9],[12],[13]).
Для 2-х
компонентной смеси схема Бернулли
выглядит следующим образом ([13]):
в ячейке производится перебор всех пар частиц вида  , так что , так что 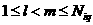 , если , если
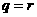 , и , и 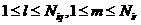 , если , если 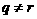 . Для каждой пары частиц разыгрывается столкновение , приводящее к изменению
скорости хотя бы одной из этих частиц с вероятностью . Для каждой пары частиц разыгрывается столкновение , приводящее к изменению
скорости хотя бы одной из этих частиц с вероятностью
 , ,
где  , ,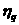 -вес -вес  -ой компоненты. Если
столкновение принято, то -ой компоненты. Если
столкновение принято, то 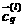 и и 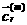
заменяются на послестолкновительные значения с
вероятностями 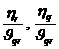 соответственно. соответственно.
В [13]
доказано, что этот алгоритм аппроксимирует уравнение Больцмана с тем же
порядком что и схема прямого статистического алгоритма. Отметим, что функция распределения реальных частиц сортов
1 и 2 по скоростям 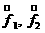 , входящие в уравнение Больцмана, связаны с функциями
распределения модельных частиц , входящие в уравнение Больцмана, связаны с функциями
распределения модельных частиц 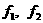 следующими соотношениями следующими соотношениями
 . .
Вес частицы показывает, сколько реальных частиц
заменяет одна модельная.
Таким
образом, описанный алгоритм позволяет “выпрямить” граничное распределение.
Действительно, можно разыгрывать x-овую компоненту скорости частиц исходя из
равномерного распределения, а в вес частицы записывать значение граничной функции распределения для x-овой
компоненты скорости. Полученный алгоритм позволил повторить приведенные выше
результаты при числе частиц с положительной x-вой компонентой скорости равным 1000 при 100
реализациях.
Результаты расчетов.
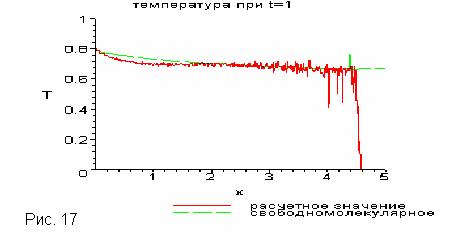
Нижеприведенные графики (Рис.17) – результат работы
“весовой программы” при следующих параметрах

Наложение на график температуры, рассчитанной при помощи
весового алгоритма с 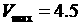 , графика температуры , вычисленной при помощи программы
прямого стат. моделирования для , графика температуры , вычисленной при помощи программы
прямого стат. моделирования для 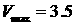 , дает в области их перекрытия идентичные результаты (Рис.18). , дает в области их перекрытия идентичные результаты (Рис.18).

Однако, если увеличивать  , т.е. увеличивать
скорость релаксации, происходит значительный “провал” хвоста (Рис.19). , т.е. увеличивать
скорость релаксации, происходит значительный “провал” хвоста (Рис.19).
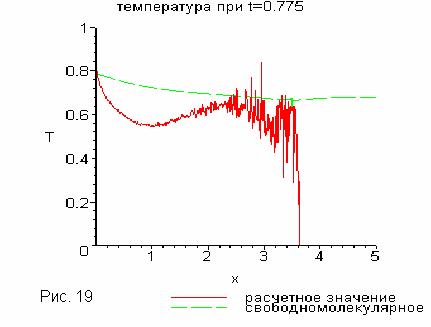
Происходит это, на наш взгляд, из-за огромного разброса в значениях весов (напомним, что
 ),тогда как работоспособность весового алгоритма проверена
лишь для отношения весов компонент равного 1000 ([13]). Таким образом, затруднительно
использовать весовой алгоритм при больших значениях ),тогда как работоспособность весового алгоритма проверена
лишь для отношения весов компонент равного 1000 ([13]). Таким образом, затруднительно
использовать весовой алгоритм при больших значениях
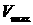 и и  . .
Заключение.
В настоящей работе исследованы
различные модели описания динамики функции распределения применительно к
испарению твердого тела: уравнение БГК и полная модель Больцмана. Численно
доказана неприменимость модели БГК вдали
от границы. Разработан алгоритм решения линейного уравнения адвекции, с помощью
которого удалось с большой точностью проинтегрировать уравнение БГК, что, в
свою очередь, сняло ограничения на густоту сетки по скоростям и позволило применить
простейший метод расчета уравнения БГК.
Но, ввиду того, что частота столкновений в модельном интеграле
столкновений не зависит от скоростей сталкивающихся частиц, решение уравнения
БГК вдали от границы не соответствует решению уравнения Больцмана, для которого
в настоящей работе опробованы численные методы Монте-Карло, метод прямого
статистического моделирования (для которого произведена некоторая адаптация к
большому числу частиц в ячейках), и «весовой» метод статистического
моделирования.
Автор признателен А.Х.
Пергамент и С.И. Анисимову за ценное обсуждение данной работы.
Список литературы:
1)
Я.И.Френкель
“Статистическая физика”
2)
Д.Хирс,
Г.Паунд “Испарение и конденсация ”
3)
С.Кнаке, И.Н.
Странский , УФН, 68, 261, 1959
4)
С.И. Анисимов,
Я.А. Имас, Г.С. Романов, Ю.В. Ходыко
“Действие излучения большой мощности на металл”
5)
С.И.Анисимов ,
ЖЭТФ, т.54, №1, 339, 1968
6)
Коган «Динамика
разреженного газа».
7)
С.И. Анисимов,
А.Х. Рахматулина «Динамика расширения пара при испарении в вакуум» препринт ИПМ
РАН 1972.
8)
Белоцерковский
О.М., Яницкий В.Е. «Статистический метод частиц в ячейках для
решения
задач динамики разреженного газа»
ЖВМиМФ-1975-Т15 №5(I),
ЖВМиМФ-1975-Т15 №6(II).
9)Белоцерковский
О.М. «Численное моделирование в механике сплошных сред»
10)Яницкий
В.Е. «Применение процессов случайных блужданий для моделирования
свободномолекулярного движения газа»
ЖВМиМФ 1974 Т.14 №1.
11)Кац
«Вероятность и смежные вопросы в физике»
12)
Королев А.Е., Яницкий В.Е. «Прямое статистическое моделирование
столкновительной релаксации в смесях газов с большим различием в концентрациях»
ЖВМиМФ
1983 Т.23, №3.
13)Генич
А.П., Куликов С.В., Манелис Г.Б., Сериков В.В., Яницкий В.Е. «Применение
весовых схем статистического моделирования течений многокомпонентного газа к
расчету структуры ударной волны» ЖВМиМФ 1986 Т.26 №12.
14) D. Sibold, H.M. Urbassek
“Kinetic study of pulsed desorption flows into vacuum” Phys.Rev. A. 1991, 43
6722.
15) O.Ellegard, J. Schou, H.M.
Urbassek “ Monte Carlo description of gas flow from laser-evaporated silver”
Appl.Phys. A 1999 69, S577-S581.
16) S.I. Anisimov, B.S.
Luk’yanchuk, A. Luches “An analytical model for three-dimensional laser plume
expansion into vacuum in hydrodynamic regime” Applied Surface Science 1996
96-98, pp. 24-32.
17) M. Aden, E. Beyer, G.
Herziger, H. Kunze “Laser-induced vaporization of a metal surface” J. Phys. D: Appl.Phys. 1992 25, pp. 57-65
18)
Головизнин В.М., Карабасов С.А. «Метод прыжкового переноса для численного
решения гиперболических уравнений. Точный алгоритм для моделирования конвекции
на эйлеровых сетках» препринт ИБРАЭ-2000-04.
|