ConDat 1.0 – программа преобразования исходных данных из комбинаторной геометрии в растровую с использованием алгоритма трейсинга (tracing)
Инструкция для пользователя

( ConDat 1.0 – code for converting by the tracing algorithm the combinatorial geometry presentation to the bit-mapped one. Users guide
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Содержание

Введение. 3

1. Постановка задачи. 4

2. Метод решения. 5

3. Особенности программы.. 6

4. Диагностическая информация. 7

5. Структура файла начальных данных для программы ConDat 8

6. Пакет начальных данных для двумерного варианта программы ConDat 9

7. Пакет начальных данных для трёхмерного варианта программы ConDat 12

8. Визуализация данных о геометрии задачи. 16

9. Использование метода трэйсинга для конвертации источника деления. 17

Заключение. 19

Литература. 19

Приложение 1. Описание бинарного формата mixmap для 2D геометрий. 20

Приложение 2. Описание бинарного формата mixmap для 3D геометрий. 22

Приложение 3. Формат текстового файла 1D геометрического описания. 23

Приложение 4. Пример пускового пакета для 2D версии программы ConDat. 24

Приложение 5. Пример пускового пакета для 3D версии программы ConDat. 26

Введение

Для задания реальной 3D геометрии ЯЭУ могут быть успешно использованы методы комбинаторной геометрии. Этот подход достаточно хорошо развит и с необходимой для практических приложений полнотой реализован в программах решения уравнения переноса методом Монте-Карло, таких как MCNP (LANL) или MCU (РНЦ «Курчатовский институт») [1], а также в генераторе сеток BOT3P 5.1 (ENEA) [2, 3].

Выбор геометрического модуля NCG программы MCU представляется наиболее приемлемым и доступным. Ввод данных для геометрического модуля NCG программы MCU осуществляется на языке задания комбинаторной геометрии NCGSIM. Существенно, что геометрический модуль программы MCU снабжен визуализатором геометрии MCU Viewer, что значительно упрощает задание геометрии.

         Аппроксимация комбинаторной геометрии на сетке требует, вообще говоря, использования нерегулярной разностной сетки, что влечёт за собой существенную переделку расчётных программ и алгоритмов, ориентированных на использование регулярных ортогональных разностных сеток. Однако, даже использование нерегулярных сеток приводит к нарушению баланса масс в сеточной модели расчётной области, который приходится корректировать, например, путем изменения плотности входящих в расчётную область тел.

Вместе с тем, при наличии вычислительного алгоритма, позволяющего достаточно быстро определить с необходимой степенью точности доли объёма ячейки, занятые различными материалами, для поддержания баланса масс в каждой ячейке сетки можно осуществить локальную коррекцию состава исходных материалов путем образования, при необходимости, дополнительных смесей для ячеек, в которых имеется несколько исходных материалов. Процентное содержание исходных материалов в дополнительных смесях определяется в соответствии с их объёмными долями в ячейке сетки. В данном подходе, известном как Volume Fraction (VF) метод [4, 5, 6], гомогенизация задачи производится на уровне разностной ячейки сетки и её  эффект может быть сделан сколь угодно малым при сгущении пространственной сетки.

Ясно, что такой алгоритм сеточной гомогенизации задачи может быть применен к сеткам любого типа, покрывающим расчётную область, в том числе, и к более простым и широко используемым регулярным ортогональным пространственным сеткам.

Для определения объёмных долей исходных материалов, попадающих в каждую пространственную ячейку сетки, может быть использован метод трэйсинга (tracing), который применяется, в частности, в методе Монте-Карло для расчёта объёмов тел, входящих в расчётную область, и в методе характеристик для решения уравнения переноса.

Метод трэйсинга реализован в созданном на базе геометрического модуля программы MCU конвертере ConDat [7, 8, 9], который предназначен для преобразования комбинаторного задания трёхмерной геометрии задачи в двумерное (для заданного сечения расчётной области) или трёхмерное сеточное (или растровое) с сохранением баланса масс в каждой пространственной ячейке сетки путем расчёта методом трэйсинга долей материалов, присутствующих в каждой ячейке сетки, и введения дополнительных смесей для ячеек, в которых имеется несколько исходных материалов.

Разработанная программа конвертации комбинаторного задания геометрии в растровое позволяет проводить расчёты задачи как методом Монте-Карло, так и  методом на основе единого комбинаторного описания геометрии задачи на языке NCGSIM. Данный документ содержит постановку задачи, описание алгоритма и инструкцию для пользователя программы ConDat (включая описание подготовки начальных данных, примеры пусковых пакетов и т.д.).

Сходимость VF метода в зависимости от выбора разностной сетки задачи исследовалась в работах [4, 5, 6, 7, 8, 9].

1. Постановка задачи

Исходные данные трёхмерного комбинаторного представления геометрии задачи записываются на языке NCGSIM, который используется в программе MCU [1], проводящей расчёты переноса излучения методом Монте-Карло. Исходные данные двумерной и трёхмерной растровой геометрии записываются в бинарном формате mixmap, который определен в описании генератора сеток BOT3P 5.1 [2] как один из возможных выходных форматов задания геометрии задачи на сетке. Возможность ввода данных о геометрии задачи в этом формате реализована, в частности, в 2D и 3D  программах КАСКАД-С-2.5 [11] и КАТРИН-2.0 [12].

Исходные данные комбинаторной геометрии задаются в глобальной системе координат . Единица измерения длины – сантиметр, согласно принятому в MCU соглашению. Данные трёхмерной растровой геометрии генерируются в локальной системе координат ; данные двумерной растровой геометрии – в плоскости  локальной системы координат. Для задания локальной системы координат  необходимо не менее 6 независимых переменных (в частности, задание начала координат на плоскости требует 3 переменные, к тому же ориентация локальной системы координат требует 3 переменные, которыми могут являться, к примеру, углы Эйлера). Далее в локальной системе координат задаётся сеть, в которой будет производиться расчёт методом дискретных ординат. Если параметры растровой геометрии задаются в декартовой системе, то осями служат оси локальной системы координат; если же в полярной или цилиндрической, то правила перехода описываются естественным образом: , , . При этом, как видно, угол  отсчитывается от  в направлении от  к . В двумерном случае цилиндрической системы расчёт производится в плоскости , при этом принцип работы совпадает с принципом расчёта в случае задания растровой геометрии в двумерной декартовой системе, за исключением введения соответствующего весового множителя при подсчёте содержания материалов.

2. Метод решения

Существующая версия конвертера ConDat ориентирована на использование по каждой из пространственных переменных сквозных ортогональных пространственных сеток с кусочно-постоянным шагом. В отличие от генератора сеток, в конвертере параметры пространственных сеток: границы пространственных интервалов (или геометрических зон) с постоянным шагом по каждой из пространственных переменных («грубая» пространственная сетка), число интервалов сетки в каждом из пространственных интервалов «грубой» сетки по каждой из пространственных переменных задаются пользователем. Для уменьшения числа создаваемых дополнительных смесей рекомендуется границы «грубой» пространственной сетки совмещать с границами материальных зон.

Чтобы наглядно пояснить принцип работы, например, двумерного варианта программы рассмотрим, вкратце, содержание формата mixmap [2]. В этом формате, при заданной сети, производится описание материалов, соответствующих каждой ячейке сети. Материал каждой ячейки может быть двух видов: простой и составной. В первом случае считается, что ячейка целиком состоит из одного материала, описанного в исходных данных комбинаторной геометрии, во втором – ячейка состоит из нескольких материалов, при этом описание составного материала эквивалентно описанию процентного содержания всех материалов, входящих в ячейку. Для определения составных материалов применяется модуль NCG программы MCU. Целесообразность его применения обусловлена возможностью моделировать прямолинейные участки траектории. Исходя из прямолинейных участков траектории, лежащих в пределах области с одним материалом, подсчитывается вклад от каждого отрезка (см. Рис. 1). Сходимость метода трейсинга при его использовании в задаче о конвертации геометрии задачи из комбинаторной формы в растровую исследовалась в работах [7, 8].

Рис. 1.

3. Особенности программы

Из особенностей программы необходимо отметить то, что производится автоматическое локальное сохранение материалов с погрешностью численного интегрирования по формуле прямоугольников, а также возможность использования геометрического модуля NCG, изначально разрабатывавшегося для иных задач.

Для определения содержания простых материалов в двумерном случае каждый отрезок по второй координате ( или ) разбивается на равное число частей, причём это число соответствует параметру точности, содержащемуся в файле вспомогательных исходных данных. После этого через середину каждой части проводится луч при фиксированной второй координате. Далее производится подсчёт вклада отрезков луча, каждый из которых лежит в пределах зоны с одним материалом. В трёхмерном случае принцип определения аналогичен с естественным дополнением параметра, который численно равен числу частей, на которые разбивается отрезок по третьей координате. Следует отметить, что все вычисления в программе ConDat производятся с использованием арифметики двойной точности.

В программу добавлены некоторые улучшения для оптимизации алгоритма подсчёта содержания материалов. Первое улучшение состоит в возможности коррекции концов отрезков луча в случае совпадения их длин с длинами отрезков сети с точностью до малого параметра, содержащегося в файле вспомогательных исходных данных (см. Рис. 2).

Рис. 2.

Второе улучшение состоит в выдаче диагностической информации, облегчающей пользователю контроль корректности задания исходных данных.

4. Диагностическая информация

Для контроля работы программы предусмотрена выдача диагностической информации в файл контроля вводимой информации и на стандартный поток вывода, в случае невозможности открытия последнего.

При вводе вспомогательной информации присутствуют параметры EpsI и EpsO, а также один или два параметра Prec, или Prec1, Prec2, в зависимости от используемого варианта - двумерного или трёхмерного. Детальное описание задания параметров дано в описании файла вспомогательных исходных данных, здесь же представлена суть параметров. После проведения луча производится сравнение сумм длин отрезков луча и отрезков сети разбиения по первой координате. Если разница по абсолютной величине превосходит параметр EpsI, то выдаётся диагностическая информация "!!! Attention, bad ray", при этом вклад от данного луча игнорируется.

В случае невозможности проведения луча средствами MCU (например, когда луч точно лежит на поверхности раздела зон с различными материалами), производится корректировка положения начала луча для декартовой системы по оси O`Y` и корректировка направления луча для полярной и цилиндрической систем, при этом выдаётся диагностическая информация "!!! Warning, can''t draw the line with one effort, correction". Величина корректировки положения равна EpsO×Δ2/Prec (Prec1), где Δ2 – отрезок сети по второй координате, в котором производится определение содержания материалов в данный момент, Prec (Prec1) – параметр точности по второй координате, задаваемый в файле вспомогательных исходных данных. При повторении невозможности проведения луча производится корректировка положения по оси Z`, при этом величина опять же равна EpsO×Δ/Prec (Prec2), где значения величин Δ и Prec (Prec2) различаются для разных случаев задания растровой геометрии (декартовой, полярной). Грубо говоря, Δ – характерная длина отрезка сети по первой координате, Prec (Prec1, Prec2) – параметр точности. Принцип корректировки для 2D и 3D геометрий нагляднее представляется в Табл. 1 и 2.

Таблица 1.

Таблица 2.

При невозможности проведения хотя бы одного луча при определении содержания материалов для конкретного отрезка по второй координате для двумерного случая и для конкретных отрезков по второй и третьей координатам для трёхмерного выдаётся диагностическая информация: "!!! Attention !!! Can''t process cells with next number (second)" и программа прекращает свою работу.

Диагностическая информация "!!! Attention !!! Massiv is too small for one ray." выдаётся в случае, когда число отрезков при проведении одного луча превышает 20000, программа в этом случае также прекращает свою работу

5. Структура файла начальных данных для программы ConDat

Файл начальных данных программы ConDat предназначен для задания параметров, определяющих режим конвертации комбинаторного описания геометрии, представленного в файле начальных данных программы MCU, формат которого определен в [1], в сеточную или растровую форму. Он состоит из следующих частей:

<Описание вводимых/выводимых файлов>

<Описание плоскости и локальной системы координат>

<Описание типа системы координат, в которой задаётся сеть>

<Описание параметров сети>

<Описание параметров точности определения процентного содержания материалов>

<Описание параметров луча для формирования 1D файла геометрического описания[4]>

Cтроки в файле, имеющие в первой позиции знак “!”, не учитываются, после этого знака можно писать комментарии. Длина каждой строки должна быть не более 80 символов. Символы, начиная с 81, игнорируются. Действительные и целые числа записываются в свободном формате. Целые числа обозначаются буквой I, действительные – E. Формат строк соответствует стандартным обозначениям языка Fortran.

6. Пакет начальных данных для двумерного варианта программы ConDat

Задание файлов для ввода и вывода информации.

Включает признаки ввода/вывода используемых файлов, их имена и название варианта.

Описание плоскости и локальной системы координат

Состоит из задания начала локальной системы координат на плоскости, а также координат двух базисных векторов.

Описание типа системы координат, в которой задаётся сеть

Содержит информацию о типе 2D системы координат, которая может быть декартова ( или ), полярная () либо цилиндрическая ().

Описание параметров сети

Включает параметры разбиения по первой и второй пространственным координатам.

Описание параметров точности определения процентного содержания материалов

Содержит следующие переменные: переменную целого типа Prec, которая равна числу равных частей, на которые делится отрезок по второй координате, служащих для определения содержания простых материалов; действительные переменные EpsO и EpsI, которые влияют на подсчёт процентного содержания материалов в ячейках. Переменные EpsO и EpsI не обязательны, в случае игнорирования их задания они принимаются равными значениям по умолчанию.

Описание параметров луча для формирования 1D файла геометрического описания. Эта информация вводится только при M5>0.

Замечание. Файл 1D геометрического описания, формируемый в канале M5, не содержит дополнительных смесей. Заданные границы зон с постоянным шагом вдоль выбранного луча дополняются, при необходимости, границами материалов вдоль луча, не вошедшими в исходные границы зон.

Для запуска программы необходимо в командной строке набрать следующую строку:

vmn < inp_file

где vmn – имя исполняемого файла программы ConDat, inp_file – имя файла начальных данных. При вводе программа производит выдачу в файл листинга информации о введенных начальных данных. В этот файл также записывается диагностическая информация, суммарные площади, занимаемые каждым материалом (что позволяет контролировать необходимую плотность лучей метода трейсинга, задаваемую параметром Prec), а также время работы программы. Пример пускового пакета для 2D версии программы ConDat приведен в Приложении 1.

7. Пакет начальных данных для трёхмерного варианта программы ConDat

Задание файлов для ввода и вывода информации.

Включает признаки ввода/вывода используемых файлов, их имена и название варианта.

Описание плоскости и локальной системы координат

Состоит из задания начала локальной системы координат на плоскости, а также координат двух базисных векторов.

Описание типа системы координат, в которой задаётся сеть

Содержит информацию о типе 3D системы координат, которая может быть декартова () либо цилиндрическая ().

Описание параметров сети

Включает параметры разбиения по первой, второй и третьей пространственным координатам.

Описание параметров точности определения процентного содержания материалов

Содержит следующие переменные: переменные целого типа Prec1 и Prec2, задающие число равных частей, на которые делятся пространственные интервалы сетки по второй и третьей координатам, служащих для определения содержания простых материалов; действительные переменные EpsO и EpsI, которые влияют на подсчёт процентного содержания материалов в ячейках. Переменные EpsO и EpsI не обязательны, в случае игнорирования их задания они принимаются равными значениям по умолчанию.

Для запуска программы необходимо в командной строке набрать следующую строку:

vmn < inp_file

где vmn – имя исполняемого файла программы ConDat, inp_file – имя файла начальных данных программы. При вводе программа производит выдачу в файл листинга с названием, определяемым четвёртой записью в файле начальных данных, информации о введенных начальных данных. В этот файл также записывается диагностическая информация, суммарные объёмы, занимаемые каждым материалом (что позволяет контролировать необходимую плотность лучей метода трейсинга, задаваемую параметром Prec1 и Prec2), а также время работы программы.

Конвертация комбинаторной 3D геометрии задачи в растровое представление производится программой ConDat последовательно по шагам аксиальной сетки задачи. При этом, для удобства пользователя, на монитор выдается информация о текущем шаге конвертации и времени решения задачи. Пример пускового пакета для 3D версии программы ConDat приведен в Приложении 2.

8. Визуализация данных о геометрии задачи

Как уже отмечалось выше, тестирование и визуализация комбинаторного задания геометрии в файле начальных данных программы MCU производится посредством программы MCU Viewer [1]. Формат mixmap двумерной растровой геометрии по своей сути подобен растровым графическим форматам. Следовательно, файл может быть визуализирован естественным образом. Для построения изображения, например, в формате bmp[8], нужно знать, какой цвет сопоставлять данной точке. Цвет логичнее определять, исходя из информации о материале, который содержится в ячейке сети, содержащей данную точку. В результате, требуется лишь реализовать функцию сопоставления данной точке ячейки сети. После получения растрового изображения в формате bmp, его можно конвертировать в любой формат по желанию пользователя. Из свободных средств обработки изображений хочется отметить ImageMagick [13], которое предоставляет разнообразные утилиты командной строки.

Однако необходимости в реализации описанного алгоритма не возникло, поскольку имелось средство визуализации файла геометрического описания в формате mixmap – специально разработанный скрипт Maplook, позволяющий воспользоваться средствами графической программы SURFER, которому в качестве исходных данных задаются *.bna файлы в формате Atlas boundary, содержащих карты физических зон задачи (т. е. зон, заполненных одинаковым материалом) в заданном сечении расчётной области. Указанные файлы создаются на этапе ввода данных о геометрии задачи программами КАСКАД-С и КАТРИН, либо постпроцессорами этих программ KASF [11] и KATRIF [12] на этапе обработки файла решения задачи. Скрипт Maplook объединяет указанные карты материалов в единую цветную картограмму расчётной области, в которой различным материалам соответствуют различные цвета. Ячейки с дополнительными смесями материалов закрашиваются как дополнительный материал.

В качестве примера визуализации геометрии задачи приведем взятые из [7] рисунки поперечного сечения варианта реактора ТОПАЗ при использовании комбинаторного представления задачи (Рис. 3) и в растровом представлении в  геометрии на сетке 276×276 после конвертации геометрии задачи на сетку программой ConDat (Рис. 4).

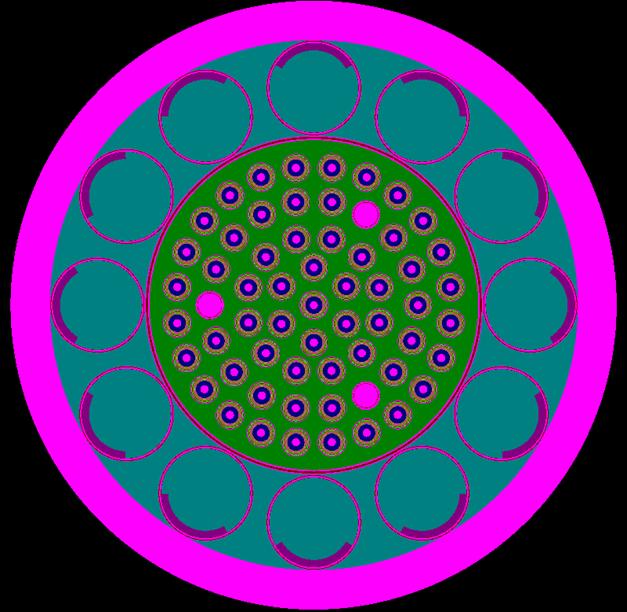
Рис. 3. Радиальное сечение варианта реактора ТОПАЗ. СУЗ (регулирующие трубы с накладками, содержащими поглотитель (бор)), повернуты в положение с максимальным значением . Для визуализации геометрии задачи использована программа MCU Viewer.

9. Использование метода трэйсинга для конвертации источника деления

         Метод трэйсинга может быть использован также и для конвертирования заданного по-твэльно и (или) по-кассетно источника деления на разностную сетку задачи с сохранением числа нейтронов источника в каждой пространственной ячейке сетки. В использованной модели источника предполагается, что в поперечном сечении твэла или кассеты пространственное распределение источника деления постоянно, а аксиальное изменение источника достаточно гладкое и может быть получено линейной интерполяцией по заданным значениям источника в относительно небольшом числе точек по высоте АЗ (порядка 20).

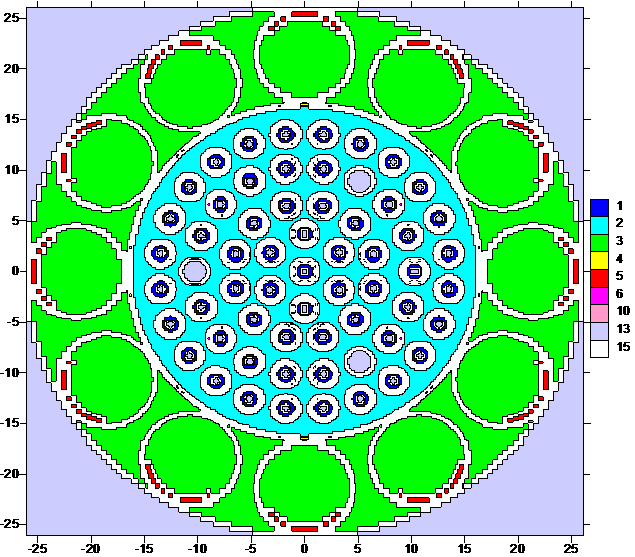
Рис. 4. Аппроксимация радиального сечения варианта реактора ТОПАЗ в  геометрии на сетке 276×276. Белым цветом закрашены ячейки с дополнительными смесями (15-ый материал). Регулирующие трубы с накладками, содержащими поглотитель (бор), закрашенные красным цветом, повернуты в положение с максимальным значением . Для визуализации геометрии задачи использован скрипт Maplook.

Следует отметить, что в программе MCU нет готовых средств для реализации метода трейсинга для конвертации по-твэльно и (или) по-кассетно заданного источника, кроме базы данных о введённых источниках. Поэтому, для конвертации заданного источника деления программы MCU в источник для  программ КАСКАД-С и КАТРИН был разработан специальный модуль, осуществляющий методом трейсинга расчёт вклада по-твэльно и (или) по-кассетно заданных источников в каждую пространственную ячейку сетки, покрывающую область источника, с использованием вышеуказанной базы данных о введенных источниках. Учитывая ранее разработанный интерфейс, позволяющий преобразовать по-твэльные и по-кассетные данных о выгорании (пропорциональные интегральному по времени распределению плотности нейтронов деления), рассчитанные программами ПЕРМАК и БИПР, в начальные данные об источнике деления для программы MCU, разработанная утилита позволила конвертировать указанные данные также и в источник деления для  программ КАСКАД-С и КАТРИН. Примеры использования этой утилиты для конвертации по-твэльно и (или) по-кассетно заданного источника деления для реакторов ВВЭР-440 и ВВЭР-1000 в растровую форму приведены в работе [9].

Заключение

         Разработана программа ConDat 1.0 – представляющая собой конвертер для преобразования исходных данных о геометрии задачи, заданной с использованием методов комбинаторной геометрии, в растровое представление с поддержанием баланса масс в каждой пространственной ячейке сетки, покрывающей расчётную область задачи. ConDat позволяет за короткое время, с необходимой, контролируемой точностью преобразовывать 3D комбинаторное задание геометрии задачи в трёхмерное или двумерное (для заданного сечения расчётной области) растровое представление. В дополнение к программе написан скрипт Maplook, позволяющий воспользоваться средствами графической системы SURFER для визуализации полученного растрового описания геометрии задачи с использованием файлов формата Atlas boundary, создаваемых программами КАСКАД-С и КАТРИН при вводе данных о геометрии задачи, а также их постпроцессорами KASF и KATRIF в процессе обработки файла решения задачи. Комплекс программных средств обеспечивает как сравнительно быстрое преобразование исходных данных, так и контроль за преобразованием, что важно для расчёта нейтронно-физических характеристик реальных сложных систем, которыми, как правило, являются современные ЯЭУ.

Литература

1.      “Программа MCU-REA/2 с библиотекой констант DLC/MCUDAT-2.2. Описание применения и инструкция для пользователя,” Отчет ИЯР РНЦ “Курчатовский институт”, инв. № 36/2004, М., 2004.

2.      R. Orsi, “BOT3P Version 5.1: A Pre/Post-Processor System for Transport Analysis,” ENEA report FIS-P9H6-014, Italy, 2006.

3.      R. Orsi, “A General Method of Conserving Mass in Complex Geometry Simulations on Mesh Grids and Its Implementation in BOT3P5.0,” Nucl. Sci. and Eng., 154, 247–259 (2006).

4.      Jon A. Dahl and Raymond E. Alcouffe, “PARTISN Results for the C5G7 MOX Benchmark Problems,” TANS, 89, 274, 2003.

5.      J. A. Dahl, “3-D Extension C5G7 MOX Benchmark Results Using PARTISN,” Proc. of International Conference on Mathematics and Computation, Supercomputing, Reactor Physics and Nuclear and Biological Applications, Avignon, France, September 12-15, 2005, on CD-ROM.

6.      P. Humbert, “Results for the C5G7 3-D Extension Benchmark Using the Discrete Ordinates Code PANDA,” Proc. of International Conference on Mathematics and Computation, Supercomputing, Reactor Physics and Nuclear and Biological Applications, Avignon, France, September 12-15, 2005, on CD-ROM.

7.      А. М. Волощенко, М. И. Гуревич, А. А. Руссков, “Об аппроксимации геометрии задачи посредством генератора сеток, сохраняющего баланс масс в ячейке сетки,” доклад на 16-ом семинаре Нейтроника 2005, Обнинск, 2005, http://www.neutronica.ru.

8.      M. I. Gurevich, D. S. Oleynik, A. A. Russkov and A. M. Voloschenko, “About the Use of the Monte-Carlo Code Based Tracing Algorithm and the Volume Fraction Method for S_n Full Core Calculations,” Proc. of International Conference Advances in Nuclear Analysis and Simulation – PHYSOR 2006, Vancouver, Canada, September 10-14, 2006, on CD-ROM.

9.      А. М. Волощенко, А. А. Руссков, М. И. Гуревич, Д. С. Олейник, Д. А. Шкаровский, В. И. Цофин, А. Д. Джаландинов, “Опыт использования генератора сеток, поддерживающего баланс масс в разностной ячейке сетки, для расчётов радиационных полей в активной зоне и радиационной защите ЯЭУ,” доклад на 17-ом семинаре Нейтроника 2006, Обнинск, 2006, http://www.neutronica.ru.

10.  А. М. Волощенко, А. А. Дубинин, “РОЗ-6.6 – программа для решения уравнения переноса нейтронов, фотонов и заряженного излучения методом дискретных ординат в одномерных геометриях,” Инструкция для пользователя, Отчет ИПМ им. М. В. Келдыша РАН, инв. № 7-25-2004, M., 2004.

11.  А. М. Волощенко и А. В. Швецов. “КАСКАД-С-2.5 - программа для решения уравнения переноса нейтронов, фотонов и заряженного излучения методом дискретных ординат в двумерных геометриях,” Инструкция для пользователя, Отчет ИПМ им. М. В. Келдыша РАН, инв. № 7-26-2004, M., 2004.

12.  А. М. Волощенко, В. П. Крючков, “КАТРИН-2.0 – программа для решения уравнения переноса нейтронов, фотонов и заряженного излучения методом дискретных ординат в трёхмерной геометрии,” Инструкция для пользователя, Отчет ИПМ им. М. В. Келдыша РАН, инв. № 7-27-2004, M., 2004.

13.  ImageMagick, http://www.imagemagick.org/

14.  DOORS3.2 – One, Two- and Three Dimensional Discrete Ordinates Neutron/Photon Transport Code System, RSICC Computer Code Collection, CCC-650, ORNL, 1998.

Приложение 1. Описание бинарного формата mixmap для 2D геометрий.

Опишем последовательность записей в формате mixmap (см. [2], Tab. 1-E) для случая 2D ,  и  геометрий. Размеры массивов указаны в квадратных скобках.

Запись 1

title (character *72)

Запись 2

im, jm, ntc, nmix, lmix, izm (6 integer*4 переменных)

где:

im – число пространственных интервалов по переменным  или .

jm - число пространственных интервалов по переменным ,  или .

ntc – идентификатор геометрии (1 для , 2 для , 3 для ).

nmix – число пространственных ячеек, содержащих более 1 материальной

            зоны.

lmix – длина записей 5 и 6.

izm – число материальных зон.

Запись 3

(x1(i), i=1,im+1), (x2(j), j=1,jm+1) ((im+jm+2) real*4 переменных)

где:

x1[im+1] – границы пространственных интервалов по переменным  или , см.

x2[jm+1] - границы пространственных интервалов по переменным (в см),

                  (в оборотах) или , см.

Запись 4

((matz(i,j),i=1,im),j=1,jm) (im*jm integer*4 переменных)

где:

matz(i,j) > 0 – номер материальной зоны в (i,j)-ой пространственной ячейке;

matz(i,j) < 0 - |matz(i,j)|= числу материальных зон в (i,j)-ой пространственной

                      ячейке; полное число пространственных ячеек с matz(i,j)<0 = nmix.

Запись 5

(mixlaw(i),i=1,lmix) (lmix integer*4 переменных)

где:

mixlaw[lmix] – информационный массив, задающий последовательно для

                          каждой ячейки (полным числом nmix), содержащей более 1

                          материальной зоны, информацию о номерах материальных зон,

                          присутствующих в ячейке:

mixlaw[lmix]=(mix₁[|matz(i₁,j₁)|], mix₂[|matz(i₂,j₂)|],…mix_nmix[|matz(i_nmix,j_nmix)|]),

где:

mix₁(i) -> последовательность |matz(i₁,j₁)| номеров материальных зон в первой

                 ячейке с matz(i,j)<0,

mix₂(i) -> последовательность |matz(i₂,j₂)| номеров материальных зон во второй

                 ячейке с matz(i,j)<0,

…..

mix_nmix(i) -> последовательность |matz(i_nmix,j_nmix)| номеров материальных зон в

                 nmix-ой ячейке с matz(i,j)<0,

Запись 6

(denmix(i),i=1,lmix) (lmix real*4 переменных)

где:

denmix[lmix] - denmix(i) это доля площади ячейки, занимаемая материальной

                         зоной с номером, указанном в массиве mixlaw(i).

Запись 7

(mater(i),i=1,izm) (izm integer*4 переменных)

где:

mater[izm] – номера материалов по материальным зонам (9$$ DORT массив

                      [14])[9].

Запись 8

(density(i),i=1,izm) (izm real*4 переменных)

где:

density[izm] – плотностной фактор по материальным зонам (=1. в данной

                        версии ConDat).

Приложение 2. Описание бинарного формата mixmap для 3D геометрий.

Опишем последовательность записей в формате mixmap (см. [2], Tab. 2-F) для случая 3D  и  геометрий. Размеры массивов указаны в квадратных скобках.

Запись 1

title (character *72)

Запись 2

im, jm, km, ntc, izm, jmcnp (6 integer*4 переменных)

где:

im – число пространственных интервалов по переменным  или .

jm - число пространственных интервалов по переменным  или .

km - число пространственных интервалов по переменной .

ntc – идентификатор геометрии (1 для , 2 для ).

izm - число материальных зон.

jmcnp = 0 если запись 7 отсутствует (jmcnp = 0 в данной версии ConDat);

           ≥ 1 если запись 7 присутствует.

Запись 3

(x1(i), i=1, im+1), (x2(j), j=1, jm+1), (x3(k), k=1, km+1) ((im+jm+km+3) real*4

переменных) где:

x1[im+1] – границы пространственных интервалов по переменным  или , см.

x2[jm+1] - границы пространственных интервалов по переменным (в см) или

                  (в оборотах).

x3[km+1] – границы пространственных интервалов по переменной , см.

do k=1, km

Запись 4.1 nmixk, lmixk (2 integer*4 переменных)

Запись 4.2 ((matzk(i,j), i=1,im), j=1,jm) (im*jm integer*4 переменных для

                    каждой записи)

Запись 4.3 (mixlawk(n), n=1,lmixk) (lmixk integer*4 переменных)

Запись 4.4 (denmixk(n), n=1,lmixk) (lmixk real*4 переменных)

enddo

где:

nmixk - число пространственных ячеек, содержащих более 1 материальной

              зоны для k-ого пространственного слоя.

lmixk – длина Записей 4.3 и 4.4. Если lmixk = 0, Записи 4.3 и 4.4 отсутствуют.

matzk(i,j) > 0 – номер материальной зоны в (i,j,k)-ой пространственной ячейке;

                < 0 - |matzk(i,j)|= число материальных зон в (i,j,k)-ой

                  пространственной ячейке; полное число ячеек с matzk(i,j)<0 = nmixk.

mixlawk[lmixk] – информационный массив, задающий последовательно для

       каждой ячейки (полным числом nmixk), содержащей более 1 материальной

      зоны, информацию о номерах материальных зон, присутствующих в ячейке:

mixlawk[lmixk]=(mix1[|matzk(i1,j1)|] mix2[|matzk(i2,j2)|] mixnmixk[|matzk(inmix,jnmix)|]),

где:

mix1(n) -> последовательность |matzk(i1,j1)| номеров материальных зон в

                   первой ячейке с matzk(i,j)<0,

mix2(n) -> последовательность |matzk(i2,j2)| номеров материальных зон во

                   второй ячейке с matzk(i,j)<0,

…..

mixnmixk(n) -> последовательность |matzk(inmix,jnmix)| номеров материалных

                            зон для nmixk-ой ячейки с matzk(i,j)<0.

denmixk[lmixk] - denmixk(n) - доля объема ячейки, занимаемая материальной

                              зоной с номером, указанном в массиве mixlawk(n)

Запись 5

(mater(i),i=1,izm) (izm integer*4 переменных)

где:

mater[izm] - номера материалов по материальным зонам (9$$ массив TORT [14])[10].

Запись 6

(density(i),i=1,izm) (izm real*4 переменных)

где:

density[izm] – плотностной фактор по материальным зонам (=1. в данной

                        версии ConDat).

Запись 7

(den_mc(i), i=1,izm) (izm real*4 переменных) (Note 2)

где:

den_mc[izm] - плотностной фактор по зонам для MCNP [2] (в данной версии

                         ConDat эта запись отсутствует).

Приложение 3. Формат текстового файла 1D геометрического описания.

Необходимость файла 1D геометрического описания возникает для обеспечения геометрического интерфейса с 1D  программами. 1D расчет может быть использован для оценки ослабления излучения вдоль заданного направления, для оценки правильности выбора пространстственной сетки, в методе синтеза и т. д. Данный текстовый файл предназначен для вывода данных о геометрическом описании задачи непосредственно в формате входных данных программы РОЗ-6.6 [10] (вводимых в виде образов карт). 2D версия конвертера ConDat программы позволяет формировать этот файл для случая 1D  (плоской) и  (цилиндрической) геометрий. Файл содержит 5 записей следующего содержания:

Приложение 4. Пример пускового пакета для 2D версии программы ConDat.

Файл геометрического описания тестовой задачи на языке NCGSIM

HEAD  1  0  0

CONT  B B B

EQU    H=320.0

EQU    H1=165.0

EQU    H2=75.0

C=    ===== M A I N   G E O M E T R Y ========

RCZ   N1   0. 0. 0.   H  320.0

RCZ   N2   0. 0. 0.   H1 162.5

RCZ   N3   0. 0. 0.   H2 162.5

RCZ   N4   0. 0. 0.   H2 148.0

RCZ   N5   0. 0. 0.   H2 82.5

RCZ   N6   0. 0. 0.   H1 32.5

RCZ   N7   0. 0. 0.   H2 32.5

END

CORE  5 -7                            /11:1/1

COR1  4 -5                            /11:2/1

COR2  3 -4                            /11:3/1

OTR   2 -3 -6                         /11:5/1

LEAD  1 -2 U 6                        /10:4/1

END

FINISH

Файл начальных данных для 2D версии программы ConDat. 2D  геометрия.

! M1,M2,M3,M4,M5 keys

   1  2  4  6  0

! binary mixmap format file

mixmap_ads_rz.bin

! ASCI mixmap format file

mixmap_ads_rz.txt

! MCU input file

ads

! listing file

ads_rz.out

! problem title

ads

! origin of coordinates

0. 0. 0.

! frame of reference

Z

! \alpha, degrees

0.

! geometry

3

! number of radial spatial zones

-6

! number of axial spatial zones

-4

! radial variable zone boundaries

0.     10.0     22.5     50.0     65.5     14.5    157.5

! axial variable zone boundaries

0.     25.0     50.0     90.0    155.0

! number of spatial meshes by radial spatial zones

  3  6  9 12  3 18

! number of spatial meshes by axial spatial zones

  7  9 12 18

! Prec

10

!EpsO & EpsI are defaults

0

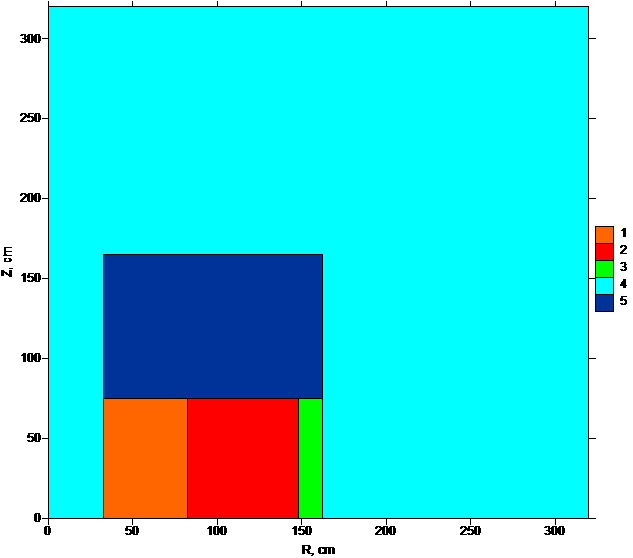
Рис. 5. Тестовой задачи в  геометрии (ADS бенчмарк). Для визуализации геометрии задачи использован скрипт Maplook. В данной задаче дополнительные смеси отсутствуют.

Приложение 5. Пример пускового пакета для 3D версии программы ConDat.

Файл геометрического описания тестовой задачи на языке NCGSIM. 3D  геометрия.

HEAD   1 0 8000

CONT B B B M B B

RPP N1  0.  580.   0. 205.    0.   500.

RPP N2  0.  580.   0. 205.    380.   500.

RPP N3  460.  580.   0. 205.    0.   370.

RPP N4  80.  460.  125. 185.    30.   370.

RPP N5  385.  460.   185. 205.    30.   370.

RPP N6  80.  200.   185. 205.    30.   370.

RPP N7  80.  160.  90. 125.     30.   370.

RPP N8  40.  80.   90. 155.     30.   370.

RPP N9  95.  160.   80.  90.    63.   370

RPP N10  95.  105.   41. 80.    63.   370.

RPP N11  40.  61. 0.   90.      30.   60.

RPP N12  61.  160.   0.  90.      30.   63.

RPP N13  160.  280.   0.  90.    30.   70.

RPP N14  0.  580.   0. 205.    0.   30.

RPP N15  40.  160.   0.  90.    334.   370.

RPP N16  40.  160.   0.  90.   284.   334.

RPP N17  40.  160. 0.   90.    265.  284.

RPP N18  95.  160.   0.  90.    226.  265.

RPP N19  40.  95.   0.  90.    151.   265.

RPP N20  40.  80.   0.  90.    132.75  151.

WED N21  80. 0. 151.  15.  0.  0.  0. 0. -55.  0. 90. 0.

WED N22  80. 0. 132.75 -40. 0. 0. 0. 0. -36. 0. 90. 0.

RPP N23  105.  130.   0.  90.    63.   120.

RPP N24  130.  160.   0.  90.   63.  110. 

WED N25  121.4894 0. 120. -16.4894 0. 0. 0. 0. 31. 0. 80. 0.

RPP N26  121.4894  130.   0.  80.    120.   151.

RPP N27  130.  138.42105 0.  90.    110.  151.

WED N28  138.42105 0. 110. 21.57895 0. 0. 0. 0. 41. 0. 90. 0.

WED N29 130. 0. 151. -8.5106 0. 0. 0. 0. 16. 0. 90. 0.

WED N30 130. 0. 151. 8.42105 0. 0. 0. 0. 16. 0. 90. 0.

BOX N31  56.82 0. 92.68 11.36 0.  17.71 -16.82 0. 10.82 0. 90. 0.  

BOX N32  40. 0. 103.5  11.36  0. 17.66   -19.35  0. 12.44  0. 90. 0. 

BOX N33  20.65 0. 115.94 11.36  0. 17.66 -16.82 0. 10.82  0. 90. 0. 

RPP N34  40.  61.    0.  90.     60.  90.  

WED N35 40. 0. 90.  21.  0.  0.   0. 0. 13.5   0. 90. 0.

RPP N36 25.  40.    0.  90.     55.  103.5

WED N37 25. 0. 103.5  15.  0.  0.  0. 0. 9.6429 0. 90. 0.

RPP N38 15.  25.    0.  90.     55.  113.1429

WED N39 15. 0. 113.1429  10. 0. 0. 0. 0. 6.4286 0. 90. 0.

RPP N40 25.  40.    0.  90.    138.1079 226.

WED N41 40. 0. 138.1079 -15. 0. 0. 0. 0. -9.6429 0. 90. 0.

RPP N42 15.  25.    0.  90.    144.5565 226.

WED N43 25. 0. 144.5565 -10. 0. 0. 0. 0. -6.4486 0. 90.  0.

RPP N44  15.  25.    0.  90.    30.  60.

RPP N45  180.  198.    0.  50.    110.  116.

RPP N46  0.  580.   0. 205.    370.   380.

C=PLEX POSITION 1

RPP N47  160. 161. 0. 80. 110. 226. 

RPP N48  25.  40.    0.  90.     30.  55.

RPP N49  15.  40.    0.  40.     226.  284.       

END

BET     2 U 3 U 4 U 5 U 6 U 7 U 8 U 9 U 10 U 11 U 12 U 13 /1:1/1 

BET1    14 U 15              /1:1/2       

BET2    44  U 48  /2:1/3

CHYG   21 U 22 U 34  U 35 U 19 U 20              /3:9/3

CHYG   23 U 24  U 26 U 27 U 25 U 28              /4:9/4

PB         29 U 30  U 42 U 43 U  38 U 39 U 49     /5:7/5

TF-5     31                    /6:6/6

VODA   32                   /7:10/7

PLEX   33   U 39 U 40 U 41 U 36 U 37 U 47       /8:11/8

TOPL     45                                     /9:8/9

GBET    46 U 17 U 18                         /10:3/10

RUDA   16                                       /11:4/11

VOZD   1 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12 -13 -14 -15 -16 -17 -18 -38 -39 -41 -42 -45

-19 -20 -22 -23 -24  -25 -26 -27 -28 -29 -30 -31 -32 -33 -34 -35 -36 -37 -40 -43 -44 -46 -47 -48 -49  /12:2/2 

END                   

FINISH

Файл начальных данных для 3D версии программы ConDat.

! M1,M2,M3,M4 keys

   1  2  4  6

! binary mixmap format file

mixmap_CAMCON_XYZ.bin

! ASCI mixmap format file

mixmap_CAMCON_XYZ.txt

! MCU input file

CAMCON

! listing file

CAMCON.out

! problem title

var_CAMERA

! origin of coordinates

0. 0. 0.

! frame of reference

Z

! \alpha, degrees

0.

! geometry

1

! number of x-variable spatial zones

20

! number of y-variable spatial zones

7

! number of z-variable spatial zones

23

! x variable zone boundaries

0. 15. 20.65 25. 40. 56.82 61. 80. 95. 105. 121.4894  130. 138.42105

160. 161. 180. 198. 280.

385. 460. 580.

! y variable zone boundaries

 0. 41. 50. 80. 90. 125. 185. 205.

! z variable zone boundaries

 0. 30. 55. 60. 63. 70. 90. 103.5 104. 110. 113.1429 116. 120. 132.75

 138.1079 144.5565 151. 226. 265. 284. 334. 370.

 380. 500.

! number of spatial meshes by x variable spatial zones

5 6 3 15 5 2 4 3 4 6 3 2 4 1 4 6

18 23 20 20

! number of spatial meshes by y variable spatial zones

 20 3 6 3 7 10 3

! number of spatial meshes by z variable spatial zones

 5 5 2 2 3 5 4 1 3 2 1

 3 4 2 2 3 20 10 5 5 7 3 37

! Prec1 Prec2

20 20

!EpsO & EpsI are defaults

0

Рис. 6. Сечение расчётной области (модель камеры для манипуляций с ЯТ) в плоскости y=0.0 см. Для визуализации геометрии задачи использована программа MCU Viewer.

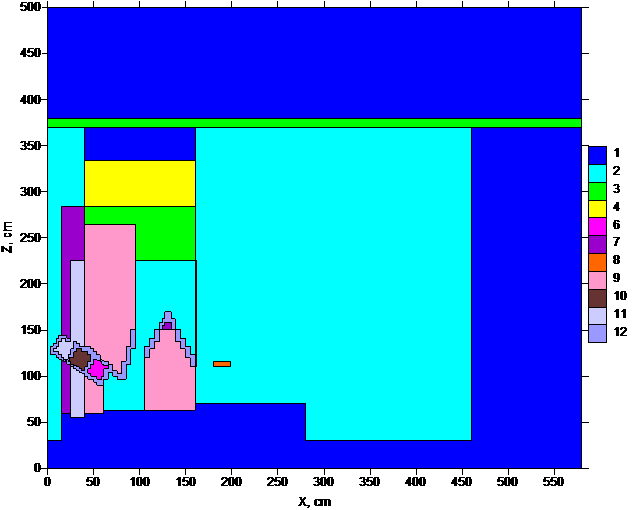
Рис. 7. Сечение расчётной области в плоскости y=0.0 см. Для визуализации геометрии задачи использован скрипт Maplook. Дополнительные смеси обозначены как 12-ый материал.