Математическое моделирование форсунки канала плазматрона в двумерном приближении
|
|
|
|
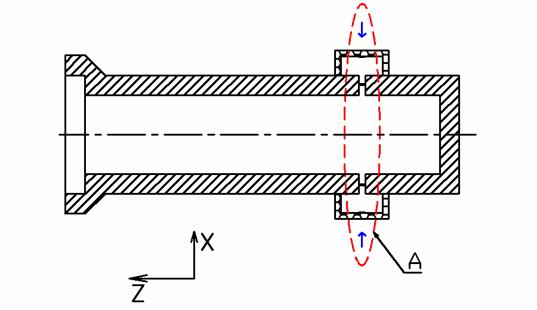
Рис. 1. Сечение (x, z) канала плазматрона, А - форсунка |
1.1
Физическая постановка
|
|
|
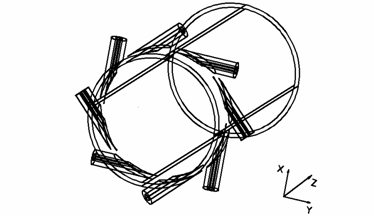
Рис. 2. Схема форсунки канала плазматрона |
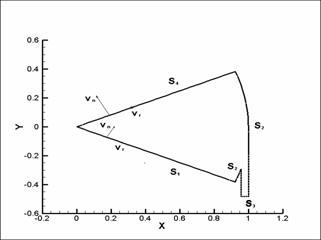
Через
форсунку в канал плазматрона (рис. 1, 2) из нескольких симметричных
относительно оси канала тангенциальных отверстий поступает поток газа.
Трехмерная по пространству задача состоит в нахождении распределения основных параметров
газа в трехмерной области (рис. 1, 2) и анализа влияния геометрии форсунки на
течение в канале. В качестве первого шага к изучению процесса рассмотрим
пространственно двумерную задачу.
В отличие от трехмерной задачи в
двумерной (рис. 3, 4) будут рассматриваться основные параметры газа (поле
скоростей, плотности, давления) только в сечении форсунки. Для того, чтобы
двумерная задача могла передавать качественные характеристики трехмерной
газовой динамики, в правую часть уравнений газовой динамики необходимо добавить
функции типа источников-стоков.
|
|
|
|
Рис. 3. Схема сечения форсунки |
Рис. 4.
Секторная область
|
1.2 Основные предположения модели
1)
зависимость
решения от координаты вдоль оси плазматрона не учитывается; скорость газа вдоль
этой же оси равна нулю;
2)
трехмерная
задача заменяется двумерной путем добавления к правой части определяющих
уравнений газовой динамики функций типа источников - стоков массы, импульса и
энергии;
3)
не
учитывается отличие диаметра канала от диаметра форсунки (рис. 1,2), т.е. при
движении газа будем рассматривать процесс образования вихря только в
зависимости от диаметров отверстий и скорости вдува;
4)
включение
правой части осуществляется, когда в канале форсунки газ дойдет до середины
форсунки, т.е. выбирается некоторое малое число ![]() такое, что при
достижении разностью безразмерных начальной плотности и плотности в текущий
момент времени в центре канала, величины, большей
такое, что при
достижении разностью безразмерных начальной плотности и плотности в текущий
момент времени в центре канала, величины, большей ![]() , включаются функции типа источника - стока;
, включаются функции типа источника - стока;
5)
число
![]() одинаково для всех
рассматриваемых форсунок;
одинаково для всех
рассматриваемых форсунок;
6)
при
включении стоков полная масса, энергия и момент импульса в сечении канала
должны сохраняться;
7)
толщина
стенок канала пренебрежимо мала;
8)
отверстия,
через которые ведется подача газа, располагаются симметрично относительно оси
канала плазматрона;
9)
задача
будет решаться в каналах с форсунками, содержащими шесть или восемь отверстий;
10) в начальный момент времени газ покоится;
11) на границе области задана постоянная температура,
различная для границы вдува и границы, соответствующей твердым стенкам;
12) на границе вдува задано постоянное давление ![]() , одинаковое для всех форсунок;
, одинаковое для всех форсунок;
13) через боковые отверстия газ поступает в основную часть
форсунки с постоянной скоростью;
14) расчеты будут вестись для дозвуковых течений (числа Маха меньше 1);
15) газ берется вязким, но нетеплопроводным;
16) описание будет вестись только в эйлеровых переменных.
1.3
Обозначения
Будем
использовать следующие обозначения: t
– время; ![]()
![]() -
точка пространства;
-
точка пространства; ![]() - плотность газа;
- плотность газа; ![]() - скорость газа в
декартовой системе координат (в рассматриваемом случае
- скорость газа в
декартовой системе координат (в рассматриваемом случае ![]() );
); ![]() - скорость газа в цилиндрических координатах
- скорость газа в цилиндрических координатах ![]() ;
; ![]() - удельная внутренняя
энергия газа;
- удельная внутренняя
энергия газа; ![]() - давление;
- давление; ![]() - полная энергия газа;
- полная энергия газа; ![]() - температура газа;
- температура газа; ![]() - вектор вихря скорости;
- вектор вихря скорости; ![]() - показатель адиабаты;
- показатель адиабаты;
![]() - массовый расход
газа;
- массовый расход
газа; ![]() - секторная область;
- секторная область; ![]() - граница области
- граница области ![]() ;
; ![]() (
(![]() ) – радиус (диаметр) форсунки канала плазматрона;
) – радиус (диаметр) форсунки канала плазматрона; ![]() (
(![]() ) - радиус (диаметр) отверстия, через которое происходит вдув
газа в канал;
) - радиус (диаметр) отверстия, через которое происходит вдув
газа в канал; ![]() – максимальная длина ребра сетки;
– максимальная длина ребра сетки; ![]() - скорость звука на входе; M - число
Маха на входе;
- скорость звука на входе; M - число
Маха на входе; ![]() - единичный тензор;
- единичный тензор; ![]() - тензор напряжений;
- тензор напряжений; ![]() - коэффициент
динамической вязкости;
- коэффициент
динамической вязкости; ![]() - число Рейнольдса;
- число Рейнольдса; ![]() - функции типа
источников или стоков в уравнениях модели, позволяющие описывать интересующее
нас течение путем решения двумерной задачи;
- функции типа
источников или стоков в уравнениях модели, позволяющие описывать интересующее
нас течение путем решения двумерной задачи; ![]() - момент времени,
соответствующий включению функций стока;
- момент времени,
соответствующий включению функций стока; ![]() - начальная плотность;
- начальная плотность; ![]() - температура
на границе вдува;
- температура
на границе вдува; ![]() - граничная скорость
(втекания газа);
- граничная скорость
(втекания газа); ![]() - начальная
температура (она же температура стенок);
- начальная
температура (она же температура стенок); ![]() - давление на входе в форсунку.
- давление на входе в форсунку.
1.4
Критерий выбора оптимальной форсунки
При расчетах
распределения параметров движения газа в форсунке канала плазматрона будем
рассчитывать норму вектора вихря ![]() . Для двумерной задачи вектор вихря
. Для двумерной задачи вектор вихря ![]() направлен вдоль оси Z декартовой системы координат XYZ, так что:
направлен вдоль оси Z декартовой системы координат XYZ, так что:
где ![]() - единичный вектор,
направленный вдоль оси
- единичный вектор,
направленный вдоль оси ![]() .
.
Из форсунок разной
геометрии и разного фиксированного расхода газа оптимальной будем считать ту,
норма вектора вихря в которой минимальна. В связи с тем, что рабочий газ
вязкий, а при подаче газа в канал образовавшийся вихрь проникает в глубь
форсунки, полагаем, что после достижения локального максимума далее величина
во времени не увеличивается.
1.5
Описание математической модели
Рассмотрим
следующую математическую модель, составленную на основе базовых законов
механики жидкости и газа. В основе лежат дифференциальные уравнения газовой
динамики, выражающие баланс массы, энергии и импульса и дополненные уравнениями
состояния идеального газа. Добавление функций стока к правым частям уравнений
газовой динамики призвано обеспечить
передачу качественных характеристик реальной задачи. Исходя из предположения о
симметрии вдува газа в канал, первоначальную двумерную область (рис. 3) заменим
другой (секторной) областью D (рис. 4), в которой и будем искать решение. При такой замене
на боковых границах сектора необходимо поставить граничное условие
периодичности.
Неизвестными величинами
являются ![]() - плотность,
- плотность, ![]() = (u, v) – скорость газа,
= (u, v) – скорость газа, ![]() - давление, T – температура,
- давление, T – температура,![]() -
норма вектора вихря.
-
норма вектора вихря.
Для полной постановки
задачи необходимо задать зависимость функций ![]() типа мощностей
источников - стоков.
типа мощностей
источников - стоков.
Функции ![]() подберем так, чтобы
они обеспечивали возможность существования стационарных решений задачи,
возможно, начиная с некоторого момента времени. Будем выбирать их равными нулю
до момента времени
подберем так, чтобы
они обеспечивали возможность существования стационарных решений задачи,
возможно, начиная с некоторого момента времени. Будем выбирать их равными нулю
до момента времени ![]() , соответствующему достижению разностью безразмерной
плотности и безразмерной начальной плотности в центре форсунки величины
, соответствующему достижению разностью безразмерной
плотности и безразмерной начальной плотности в центре форсунки величины ![]() .
.
§2. Математическая постановка задачи
Ниже представлена система
определяющих уравнений газовой динамики.
Система состоит из
уравнений неразрывности, импульса и энергии.
Она дополнена уравнениями состояния для идеального газа
и начальными и граничными условиями.
Система решается в секторной области (рис. 4). В правых частях дифференциальных
уравнений стоят функции типа источника - стока.
Компоненты
тензора напряжений ![]() возьмем в виде [3, 6]:
возьмем в виде [3, 6]:
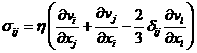 .
.
Будем считать, что в начальный
момент времени в области D выполнены следующие условия:
![]() ,
,
![]() ,
,
![]() .
.
|
|
|
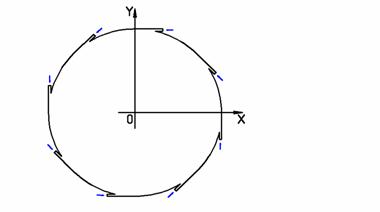
Рис. 5. Область с обозначением границ |
Обозначения границ
соответствуют рис. 5: ![]() - боковые границы
сектора,
- боковые границы
сектора, ![]() - граница,
соответствующая стенкам форсунки,
- граница,
соответствующая стенкам форсунки, ![]() - граница вдува.
- граница вдува.
На границе ![]() (см. рис. 5)
поставлены следующие граничные условия:
(см. рис. 5)
поставлены следующие граничные условия:
условие втекания: ![]() ,
, ![]() ,
, ![]() на
на ![]() ;
;
условие прилипания: ![]() на
на ![]() ;
;
условие периодичности на
боковых границах сектора:
где ![]() - в данном случае угол
сектора (рис. 5),
- в данном случае угол
сектора (рис. 5), ![]() - угол между нижней
гранью сектора и осью OX,
- угол между нижней
гранью сектора и осью OX, ![]() (в данном случае
(в данном случае ![]() ) - нормальная к
) - нормальная к ![]() составляющая скорости,
составляющая скорости,
![]() - радиальная составляющая скорости.
- радиальная составляющая скорости.
§3. Выбор функций типа источников – стоков
В правой часть функции
источников - стоков берутся равными нулю до некоторого момента времени ![]() . Этот момент выбирается равным времени достижения
поступающим газом середины форсунки. Ясно, что при различных правых частях
исходное решение будет иметь разный вид. Возможно, тип функций стока можно
будет уточнить, решая задачу о распределении газа по всему каналу плазматрона.
В данной работе вид функций правой части определяющей системы уравнений газовой
динамики выбирался исходя из физических соображений о движении газа в канале.
. Этот момент выбирается равным времени достижения
поступающим газом середины форсунки. Ясно, что при различных правых частях
исходное решение будет иметь разный вид. Возможно, тип функций стока можно
будет уточнить, решая задачу о распределении газа по всему каналу плазматрона.
В данной работе вид функций правой части определяющей системы уравнений газовой
динамики выбирался исходя из физических соображений о движении газа в канале.
3.1 Уравнение неразрывности (баланс
массы)
Правую часть в уравнении
неразрывности будем выбирать в виде:
![]() .
.
Постоянная ![]() находится из условия
сохранения полной массы газа при стационарном движении. Интегрируя уравнение
в стационарном случае по области
находится из условия
сохранения полной массы газа при стационарном движении. Интегрируя уравнение
в стационарном случае по области ![]() , с учетом граничных условий получим выражение для
, с учетом граничных условий получим выражение для ![]() :
:
3.2 Уравнение импульса (баланс момента
импульса)
Запишем правую часть в уравнении импульса в виде
(считаем что ![]() ):
):
![]() ,
,
где ![]() - компоненты вектора
функции источника-стока в декартовой системе координат,
- компоненты вектора
функции источника-стока в декартовой системе координат, ![]() - компоненты вектора
функции источника-стока в цилиндрической системе координат.
- компоненты вектора
функции источника-стока в цилиндрической системе координат.
Запишем закон эволюции
момента импульса в цилиндрической системе координат в проекции на ось ![]() :
:
По
аналогии с уравнением неразрывности функцию типа источника - стока ![]() в правой части
будем брать в виде:
в правой части
будем брать в виде:
![]() .
.
Интегрируя
по области ![]() с учетом достижения
стационарности, находим значение константы
с учетом достижения
стационарности, находим значение константы ![]() :
:
Предполагая, что ![]() , записываем компоненты функции стока
, записываем компоненты функции стока![]() :
:
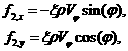
где ![]() - угловая координата
рассматриваемой точки.
- угловая координата
рассматриваемой точки.
3.3 Уравнение энергии (баланс энергии)
Аналогично стоку массы
правую часть в уравнении баланса энергии будем выбирать в виде:
![]()
Постоянная ![]() находится из условия
сохранения полной энергии при стационарном движении. Интегрируя уравнение
по области
находится из условия
сохранения полной энергии при стационарном движении. Интегрируя уравнение
по области ![]() с учетом
стационарности, получим выражение для
с учетом
стационарности, получим выражение для ![]() :
:
§4. Задача в безразмерном
виде
Ниже
представлена система дифференциальных уравнений газовой динамики, записанная в
декартовых координатах в безразмерных переменных. По одинаковым индексам
ведется суммирование.
Введем следующие
безразмерные переменные: ![]() -
безразмерная i–ая координата, отвечающая декартовой
системе координат,
-
безразмерная i–ая координата, отвечающая декартовой
системе координат,![]() -
безразмерная i–ая координата скорости,
-
безразмерная i–ая координата скорости, ![]() - i–ая координата единичной нормали,
- i–ая координата единичной нормали, ![]() ,
, ![]() - безразмерные
плотность, давление, температура, время и внутренняя энергия соответственно,
- безразмерные
плотность, давление, температура, время и внутренняя энергия соответственно, ![]() - число Маха на входе, где
- число Маха на входе, где ![]() - скорость звука на входе,
- скорость звука на входе, ![]() - число Рейнольдса,
- число Рейнольдса, ![]() - функция Хевисайда. Тогда
- функция Хевисайда. Тогда
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
где ![]() - безразмерная полная
энергия,
- безразмерная полная
энергия, 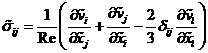 - безразмерный тензор
напряжений.
- безразмерный тензор
напряжений.
Начальные условия: ![]() ,
,![]() ,
, ![]() .
.
Граничные условия:
условие втекания: ![]() ,
, ![]() на
на ![]() ;
;
условие непротекания: ![]() на
на ![]() ;
;
условие периодичности на
боковых границах: на ![]() задано условие
.
задано условие
.
Правые
части: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
Где
![]() ,
,
![]() .
.
Далее обозначение волны «![]() » у
безразмерных величин опустим.
» у
безразмерных величин опустим.
§5. Алгоритм и его численная реализация
5.1.
Программный комплекс
Для численной реализации
на базе программного комплекса plasma.m [4] разработан программный комплекс plasma_f.m, адаптированный под данную
физическую задачу.
В отличие от [4] в данной
работе исследуется неидеальная газовая динамика. Разработанный комплекс
позволяет получать решения, зависящие от безразмерных критериев, и учитывать
влияние вязкости и теплопроводности. В основе алгоритма лежит прием
«расщепления по физическим процессам». Численные решения, отвечающие различным
физическим процессам, реализуются в отдельных программных модулях. В plasma_f.m численное
решение уравнений
идеальной газовой динамики велось методами, основанными на приближенном решении
задачи Римана. Потоки через границы ячеек, отвечающие невязким и
нетеплопроводным слагаемым, вычислялись методом Хартена-Лакса-ван Лира (HLLC) (см.
[5, 6]). Алгоритм аппроксимации слагаемых, отвечающих эффектам вязкости и
теплопроводности газа, взят из [7] и описан подробнее для рассматриваемой
задачи ниже.
5.1.1
Расщепление по физическим процессам
При построении
аппроксимации вязких слагаемых и выделения правой части используется прием
«расщепления по физическим процессам» (см. [9]). Запишем задачу в операторном виде:
![]() ,
,
![]() - вектор консервативных переменных,
- вектор консервативных переменных, ![]() - оператор задачи,
- оператор задачи, ![]() - правая часть.
- правая часть.
Оператор ![]() представим в виде:
представим в виде:
![]() ,
,
где ![]() - оператор,
соответствующий гиперболическим потокам,
- оператор,
соответствующий гиперболическим потокам, ![]() - оператор,
соответствующий диссипативным эффектам (в нашем случае - вязкости).
- оператор,
соответствующий диссипативным эффектам (в нашем случае - вязкости).
Интегрирование исходной
задачи на отрезке ![]() заменяем
интегрированием трех задач, которое состоит из следующих этапов:
заменяем
интегрированием трех задач, которое состоит из следующих этапов:
![]() ,
,
где ![]() соответствуют
промежуточным временным слоям на отрезке
соответствуют
промежуточным временным слоям на отрезке ![]() .
.
На этапе
решается система уравнений идеальной
газовой динамики для декартовой системы координат; на этапе
осуществляется учет правой части; на
этапе
– учет эффектов вязкости.
Все три задачи считаются
в отдельно написанных модулях. О методах решения
подробно написано в [5, 6]. Расчет
потоков в
ведется методом HLLC. Аппроксимации правой части
описана ниже. Для решения задачи
использован алгоритм, основанный на
аппроксимации градиента для конечно-объемных схем [7].
5.1.2
Алгоритм аппроксимации слагаемых,
соответствующих диссипативным эффектам
Решение
подобно решению задачи вида:
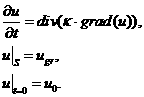
Ниже представлен
используемый алгоритм её решения (см. [7]).
![]() ,
,
![]() ,
,
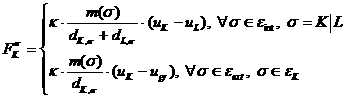 .
.
Здесь ![]() - шаг по времени;
- шаг по времени; ![]() - объем ячейки;
- объем ячейки; ![]() - элемент множества ребер (
- элемент множества ребер (![]() ), соответствующий ячейке K;
), соответствующий ячейке K; ![]() - поток через ребро
- поток через ребро ![]() ,
, ![]() - значение в ячейке K(L);
- значение в ячейке K(L); ![]() - мера Лебега ребра (в
данном случае длина ребра
- мера Лебега ребра (в
данном случае длина ребра ![]() );
); ![]() (
(![]() ) – множество всех внутренних (внешних) ребер, т.е. ребер, не
принадлежащих границе области (ребер, принадлежащих только границе области);
) – множество всех внутренних (внешних) ребер, т.е. ребер, не
принадлежащих границе области (ребер, принадлежащих только границе области); ![]() - расстояние от центра элемента (центра масс треугольника) до
ребра.
- расстояние от центра элемента (центра масс треугольника) до
ребра.
|
|
|
Рис. 6. Вид
используемых элементов и обозначения |
Cходимость
алгоритма доказана в [7]. Недостатком метода является условная устойчивость. К
достоинствам следует отнести свойство консервативности.
5.1.3
Вычисление множителей в правой части
При нахождении констант в
правых частях использовались дискретные аналоги соотношений
,
,
.
Интегралы по контуру
вычислялись при помощи того же метода, которым велся расчет потоков в
программном комплексе (методом HLLC), а интегралы по области ![]() (всему сектору)
заменялись квадратурной формулой:
(всему сектору)
заменялись квадратурной формулой:
где ![]() - координаты центра i-ой ячейки,
- координаты центра i-ой ячейки, ![]() - «объем» i-ой ячейки. В программе величины
- «объем» i-ой ячейки. В программе величины ![]() и
и ![]() вычислялись из
соотношений:
вычислялись из
соотношений:
В числителе
и
суммирование ведется по ребрам границы ![]() .
. ![]() - потоки массы и
энергии через j – ое ребро соответственно,
- потоки массы и
энергии через j – ое ребро соответственно, ![]() - длина j-ого ребра,
- длина j-ого ребра, ![]() - объем (равный в
двумерном случае площади) i - ой ячейки. В знаменателе интеграл по объему заменяется
согласно формуле
, суммирование ведется по всем
ячейкам области.
- объем (равный в
двумерном случае площади) i - ой ячейки. В знаменателе интеграл по объему заменяется
согласно формуле
, суммирование ведется по всем
ячейкам области.
Такая замена необходима
для выполнения дискретных аналогов законов
сохранения полной массы и энергии в области ![]() .
.
Выражение
дает для нахождения параметра ![]() формулу, аналогичную
и
.
формулу, аналогичную
и
.
5.2 Расчет нормы
вектора вихря
Норма
вектора вихря вычисляется по формуле
(см. [11]). Для
аппроксимации частных производных использован алгоритм, аналогичный описанному
в 5.1.2. В каждый сеточный момент времени и в каждой ячейке вычисляется норма
вектора вихря. Целью расчета является нахождение этой величины для различных
типов форсунок.
5.3 Другие параметры
Показатель
адиабаты в вычислениях взят равным ![]() . Шаг по времени
. Шаг по времени ![]() . Начальная температура
. Начальная температура ![]() . Начальное давление
. Начальное давление ![]() = 1 атм, давление при подаче газа
= 1 атм, давление при подаче газа ![]() атм. Число Рейнольдса Re = 548167. Скорость звука
атм. Число Рейнольдса Re = 548167. Скорость звука ![]() ,
, ![]() м/c.
м/c.
Включение
источников - стоков будет осуществляться при выполнении в центре форсунки
неравенства, свидетельствующего, что разность между начальной и текущей
безразмерной плотностью больше заданной величины ![]() :
:
![]() ,
,
![]() - безразмерная
плотность,
- безразмерная
плотность, ![]() - для всех форсунок.
- для всех форсунок.
Расчеты проведены для форсунок с разным числом отверстий (6 или 8),
различных числах Маха (0.2, 0.4, 0.6, 0.8, 1.0), и разных диаметров отверстий
вдува. Для форсунки, содержащей шесть отверстий, брались диаметры 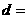 2.0, 2.2, 2.5, 3.1 мм, для восьми отверстий брались диаметры
2.0, 2.2, 2.5, 3.1 мм, для восьми отверстий брались диаметры 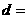 1.0, 1.75 мм при диаметре форсунки
1.0, 1.75 мм при диаметре форсунки 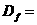 46.0 мм.
46.0 мм.
§ 6. Пространственная сетка
Ниже на рис. 7, 8
представлены пространственные сетки, построенные с помощью пакета программ PDE Toolbox системы Мatlab7.0 [2].
|
|
|
|
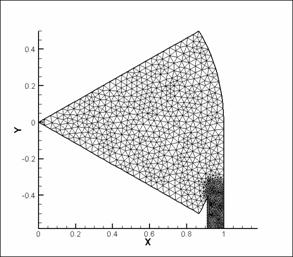
Рис. 7. Триангуляция области D. 6
отверстий, расположенных касательно к каналу. |
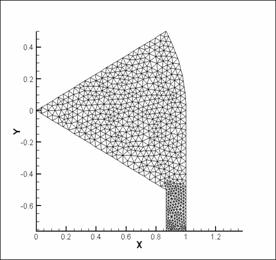
Рис. 8. Триангуляция области D. 6
отверстий, расположенных касательно к каналу. |
|
|
|
|
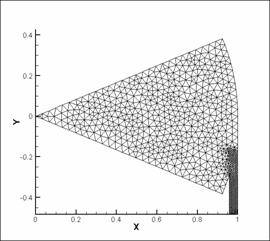
Рис. 9. Триангуляция области D. 8 отверстий, расположенных касательно к каналу. |
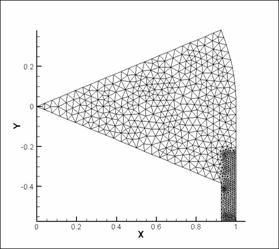
Рис. 10. Триангуляция области D. 8
отверстий, расположенных каса-тельно к каналу. |
Построенные сетки удовлетворяют
следующим свойствам:
- при триангуляции области необходимо
учитывать периодичность на боковых границах сектора. Из - за этого необходимо
проверять равенство чисел ребер треугольников на верхней и нижней границах
сектора;
- в большинстве случаев при
построении сетки генератором сеток Matlab возникает проблема с крайним левым
треугольником. Выполнение условия периодичности требует написания
дополнительной процедуры разбиения этого треугольника;
- так как отношение ![]() мало, то возникает необходимость
дополнительного сгущения сетки в окрестности области вдува;
мало, то возникает необходимость
дополнительного сгущения сетки в окрестности области вдува;
- во всех случаях сеток рис.
7–10 выполнено равенство ![]() .
.
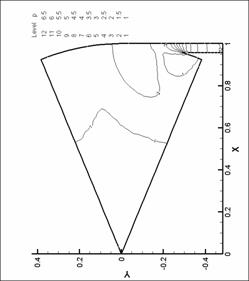
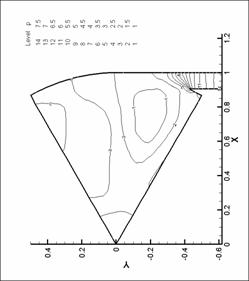
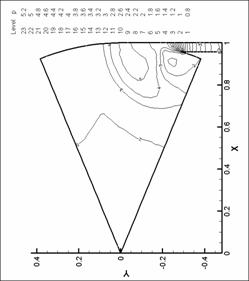
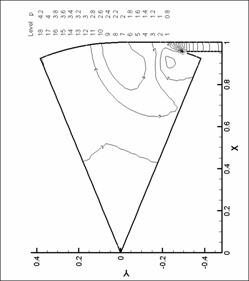
§ 7. Результаты расчетов
7.1 Расчеты нормы вектора вихря
Ниже представлены графики
зависимости нормы вектора вихря для различных форсунок и различных расходов
газа. Точками обозначены результаты численного эксперимента. При рисовании
точки соединены прямыми отрезками. Для сравнения графики для различных форсунок
построены в одной системе координат.
|
|
|
|
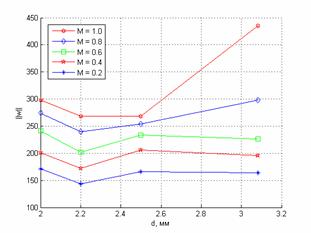
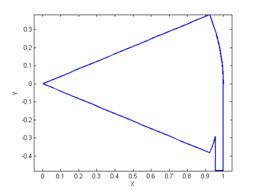
Рис. 11. Зависимость нормы вектора вихря от диаметра отверстий. 6 отверстий |
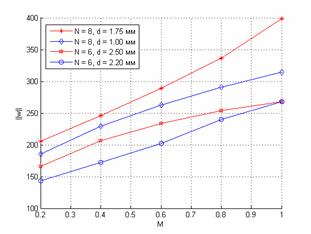
Рис. 12. Зависимость модуля вектора вихря от числа Маха. 6 и 8 отверстий |
На
основании проведенных расчетов можно заключить, что норма вектора вихря для
различных типов форсунок линейно зависит от числа Маха и растет при увеличении
скорости вдува. Для форсунок, содержащих шесть отверстий, при различных числах
Маха на графиках зависимости нормы вектора вихря от диметра отверстий вдува
имеется минимум в точке, соответствующей диаметру отверстий 2.2 мм (рис. 11).
На рис. 12 изображены графики зависимости модуля вектора вихря от числа Маха
для различных геометрий форсунок. Видно, что геометрия форсунок, содержащих
восемь отверстий, хуже, чем геометрии форсунок, содержащих, шесть отверстий.
7.2 Распределения параметров газовой
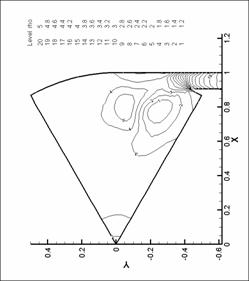
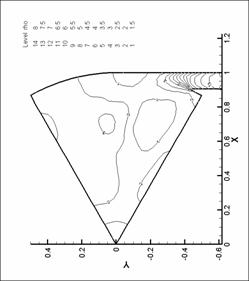
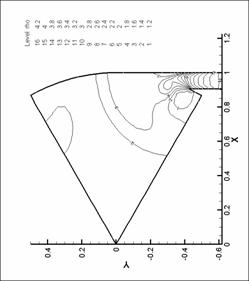
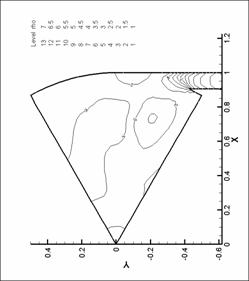
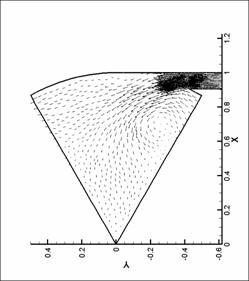
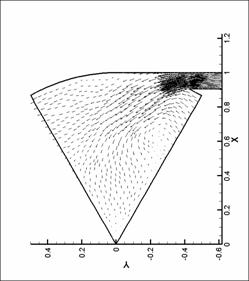
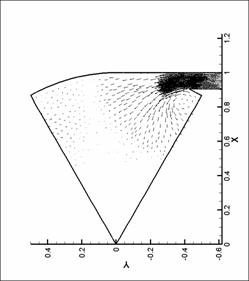
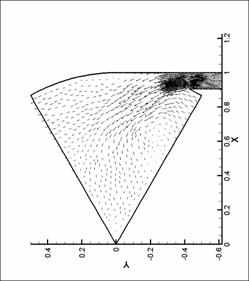
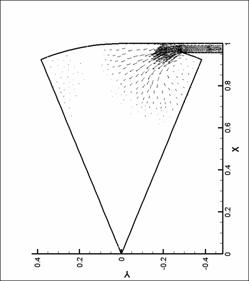
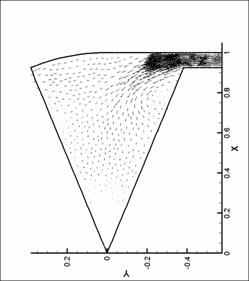
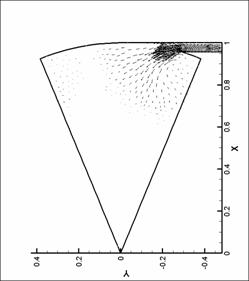
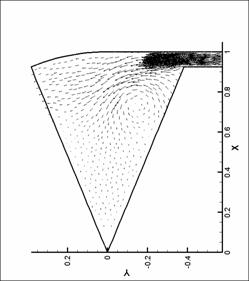
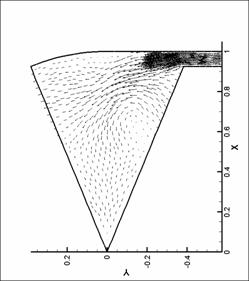
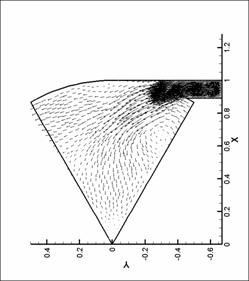
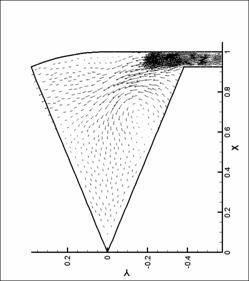
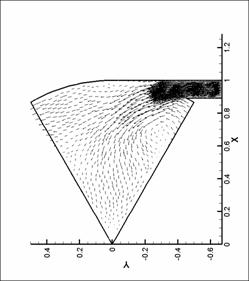
динамики в форсунке канала плазматрона
Для представления
распределений основных параметров течения газа в форсунке ниже представлены
результаты численных экспериментов – линии уровня плотности, давления и поле
скорости для нескольких видов форсунок в моменты времени, соответствующие
максимуму модуля вектора вихря.
Графики линий уровня и
векторных полей выполнены с помощью пакета TecPlot 360.0. Среднее число линий уровня
выбрано равным 20. Различное число линей
уровня соответствует оптимизации TecPlot для наглядного представления изменения параметров в
исходной области. Все величины на
графиках имеют размерность системы СИ (давление – в атм). При рисовании
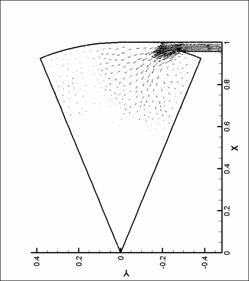
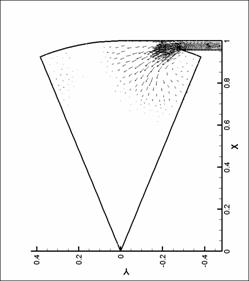
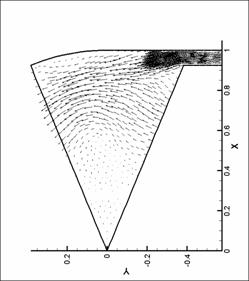
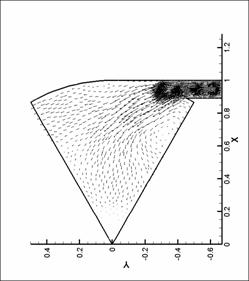
векторных полей показан вектор в каждом узле сетки. Этим вызвано большое число
векторов в области вдува (особенно для N = 8), так как там проводилось
дополнительное сгущение сетки. Чем большее значение принимает модуль физической
величины (в нашем случае - модуль скорости), тем больше длина этого вектора.
Все графики построены для момента времени, соответствующего достижению модулем
вектора вихря наибольшего значения.
7.3 Обсуждение результатов
В п. 7.1 представлены
зависимости нормы вектора вихря от скорости подачи газа в канал и диаметра
входного отверстия.
Из рис. 11 видно, что для
форсунок, содержащих шесть отверстий, для чисел Маха 0.2 - 1.0 и рабочего
давления на входе ![]() атм оптимальным является диаметр отверстий 2.2 мм. При числах
Маха 0.8 - 1.0 возможен выбор диаметра отверстий 2.5 мм.
атм оптимальным является диаметр отверстий 2.2 мм. При числах
Маха 0.8 - 1.0 возможен выбор диаметра отверстий 2.5 мм.
Отметим, что можно
предположить, что норма вектора вихря линейно возрастает с увеличением скорости
подачи газа в канал. Нелинейность зависимости нормы вектора вихря от числа Маха
для форсунки с отверстиями диаметра 3.1 мм вызвана влиянием функций стока.
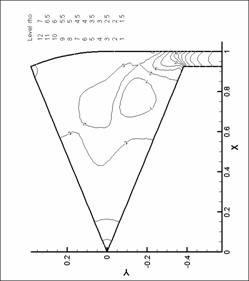
|
|
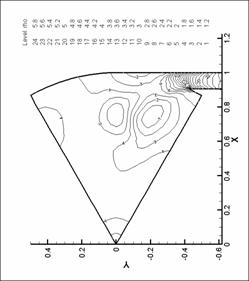
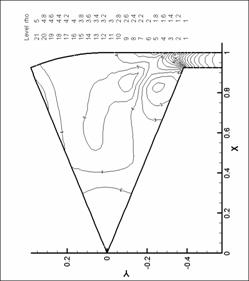
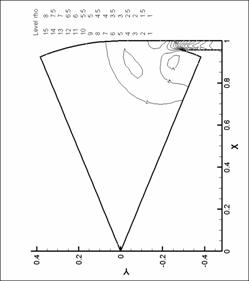
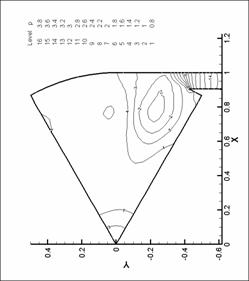
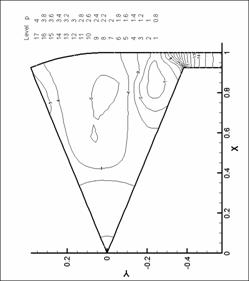
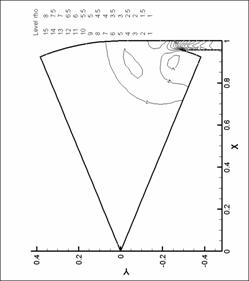
Рис. 15. Линии уровня плотности. N=6. d=2.2 мм.
М=0.6 |
|
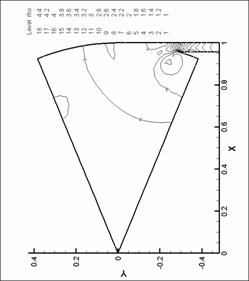
Рис. 18. Линии уровня плотности. N=8. d=1.0 мм.
М=0.2 |
|
|
Рис. 14. Линии уровня плотности. N=6. d=2.2 мм.
М=0.4 |
|
Рис. 17. Линии уровня плотности. N=6 d=2.2 мм.
М=1.0 |
|
|
Рис. 13. Линии уровня плотности. N=6. d=2.2 мм.
М=0.2 d=2.2 мм.
М=0.2 |
|
Рис. 16. Линии уровня плотности. N=6. d=2.2 мм.
М=0.8 |
|
|
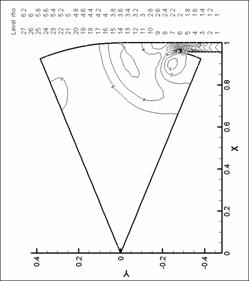
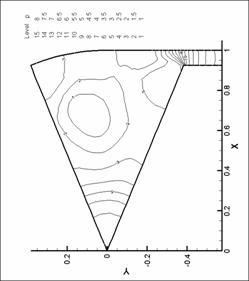
Рис. 21. Линии уровня плотности. N=8. d=1.0 мм.
М=0.8 |
|
Рис. 24. Линии уровня плотности. N=8. d=1.75 мм.
М=0.4 |
|
|
Рис. 20. Линии уровня плотности. N=8. d=1.0 мм.
М=0.6 |
|
Рис. 23. Линии уровня плотности. N=8. d=1.75 мм.
М=0.2 |
|
|
Рис. 19. Линии уровня плотности. N=8. d=1.0 мм.
М=0.4 |
|
Рис. 22. Линии уровня плотности. N=8. d=1.0 мм.
М=1 |
|
|
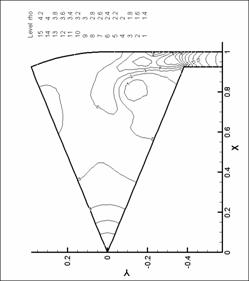
Рис. 27. Линии уровня плотности. N=8. d=1.75 мм.
М=1.0 |
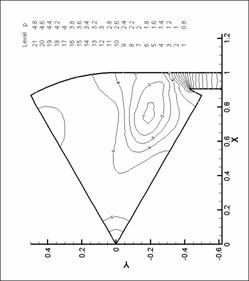
|
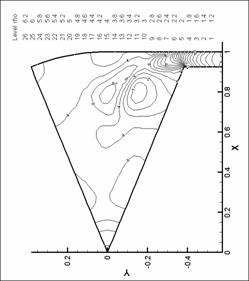
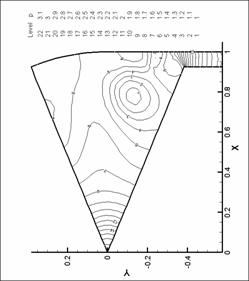
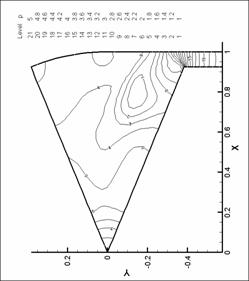
Рис. 30. Линии уровня давления. N=6. d=2.2 мм.
М=0.6 d=2.2 мм. М=0.2 |
|
|
Рис. 26. Линии уровня плотности. N=8. d=1.75 мм.
М=0.8 |
|
Рис. 29. Линии уровня давления. N=6. d=2.2 мм.
М=0.4 |
|
|
Рис. 25. Линии уровня плотности. N=8. d=1.75 мм.
М=0.6 |
|
Рис. 28. Линии уровня давления. N=6. d=2.2 мм.
М=0.2 |
|
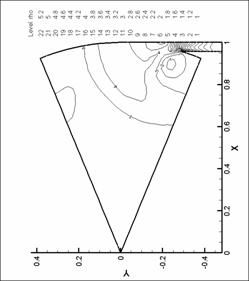
|
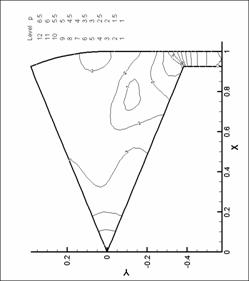
Рис. 33. Линии уровня давления. N=8. d=1.0 мм.
М=0.2 d=2.5 мм.
М=0.2d=2.2 мм. М=0.8 |
|
Рис. 36. Линии уровня давления. N=8. d=1.0 мм.
М=0.8 d=1.0 мм.
М=0.2d=3.0 мм. М=0.2 |
|
|
Рис. 32. Линии уровня давления. N=6. d=2.2 мм.
М=1.0 d=2.2 мм.
М=1.0 |
|
Рис. 35. Линии уровня давления. N=8. d=1.0 мм.
М=0.6 |
|
|
Рис. 31. Линии уровня давления. N=6. d=2.2 мм.
М=0.8 |
|
Рис. 34. Линии уровня давления. N=8. d=1.0 мм.
М=0.4 |
|
|
Рис. 39. Линии уровня давления. N=8. d=1.75 мм.
М=0.4 |
|
Рис. 42. Линии уровня давления. N=8. d=1.75 мм.
М=1.0 |
|
|
Рис. 38. Линии уровня давления. N=8. =1.75 мм. М=0.2 d=1.75 мм.
М=0.2 |
|
Рис. 41. Линии уровня давления. N=8. d=1.75 мм.
М=0.8 |
|
|
Рис. 37. Линии уровня давления. N=8. d=1.0 мм.
М=1.0 |
|
Рис. 40. Линии уровня давления. N=8. d=1.75 мм.
М=0. М=0.6 |
|
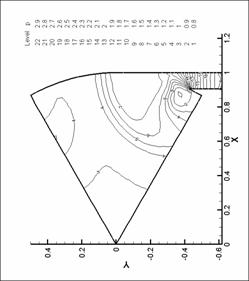
|
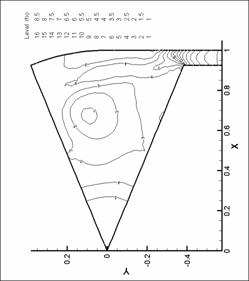
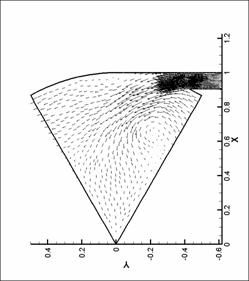
Рис. 45. Поле скоростей. N=6. d=2.2 мм.
М=0.6 |
|
Рис. 48. Поле скоростей. N=8. d=1.0 мм.
М=0.2 |
|
|
Рис. 44. Поле скоростей. N=6. d=2.2 мм.
М=0.4 |
|
Рис. 47. Поле скоростей. N=6. d=2.2 мм.
М=1.0 |
|
|
Рис. 43. Поле скоростей. N=6. d=2.2 мм.
М=0.2 |
|
Рис. 46. Поле скоростей. N=6. d=2.2 мм.
М=0.8 |
|
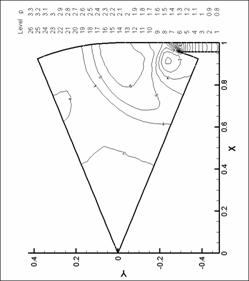
|
Рис. 51. Поле скоростей. N=8. d=1.0 мм.
М=0.8 |
|
Рис. 54. Поле скоростей. N=6. d=1.75 мм.
М=0.4 |
|
|
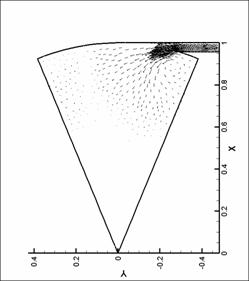
Рис. 50. Поле скоростей. N=8. d=1.0 мм.
М=0.6 |
|
Рис. 53. Поле скоростей. N=8. d=1.75 мм.
М=0.2 |
|
|
Рис. 49. Поле скоростей. N=8. d=1.0 мм.
М=0.4 |
|
Рис. 52. Поле скоростей. N=8. d=1.0 мм.
М=1.0 |
|
|
Рис. 57. Поле скоростей. N=8. d=1.75 мм.
М=1.0 |
|
Рис. 60. Поле скоростей. N=6. d=2.5 мм.
М=1.0 |
|
|
Рис. 56. Поле скоростей. N=8. d=1.75 мм.
М=0.8 |
|
Рис. 59. Поле скоростей. N=6. d=2.5 мм.
М=0.8 |
|
|
Рис. 55. Поле скоростей. N=8. d=1.75 мм.
М=0.6 |
|
Рис. 58. Поле скоростей. N=6. d=2.5 мм.
М=0.6 |
Заключение
Для различных типов
форсунок канала плазматрона исследовано влияние отношения диаметра входного
отверстия к диаметру форсунки на течение в канале плазматрона. При
фиксированном диаметре форсунки и давлении на отверстиях вдува в канал выполнен
цикл численных экспериментов при варьировании скорости вдува газа (числа Маха)
и относительного диаметра отверстий вдува. Для различного числа входных
отверстий (шести и восьми) найдены оптимальные размеры отверстий. Проведено
сравнение форсунок с различными размерами, числом отверстий и при различных
числах Маха поступающего потока. Предложены оптимальные варианты форсунок.
Разработан программный
комплекс, предназначенный для решения задач газовой динамики в сложных областях
с учетом эффектов вязкости и теплопроводности. Программа предназначена для
расчетов форсунок канала плазматрона различной геометрии при различных
начальных и граничных условиях. Программа позволяет находить распределение
основных параметров газа (плотности, давления, поле скоростей, температуры) в
двумерном приближении для широкого класса геометрий форсунок. Найдены функции
типа источников-стоков. Их вид соответствует физике задачи. Полученные
результаты качественно соответствуют проведенным экспериментам.
Список
литературы
1. В.С. Зарубин, Г.Н. Кувыркин.
Математические модели термомеханики. М., Физматлит. 2002. – 168 с.
2.
Website: http://www.matlab.com.
3. Л.Д. Ландау, Е.М. Лифшиц.
Теоретическая физика. Т. 6. Гидродинамика. М., Наука, Физматлит. 1986. – 736 с.
4. Галанин М.П., Грищенко Е.В.,
Савенков Е.Б., Токарева С.А. Применение
RKDG метода для численного решения задач газовой динамики. // Препринт ИПМ им.
М.В. Келдыша РАН. 2006. № 52. 31 с.
5. Куликовский А.Г., Погорелов
Н.Б., Семенов А.Ю. Математические
вопросы численного решения гиперболических систем уравнений. – М., Физматлит,
2001. – 608 с.
6.
Toro E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics. A
Practical Introduction. Springer, Berlin. 1999. 624 p.
7.
R. Eymard, T. Gallouët, R. Herbin
- Finite volume approximation of elliptic problems and convergence of an
approximate gradient. //Appl. Num. Math. 37/1-2. P.p. 31 - 53,
2001
8. В.С. Энгельшт, и др. Математическое моделирование электрической
дуги. Фрунзе 1983., Илим, – 363 с.
9. Марчук Г.И. Методы вычислительной математики М., Наука, 1977. 462
с.
10. А. Пуанкаре. Теория Вихрей. Ижевск.: НИЦ
«Регулярная и хаотическая динамика». 2000. – 162 с.
11. И.И.
Смульский Аэродинамика и процессы в вихревых камерах. – Новосибирск: ВО
«Наука». Сибирская издательская фирма, 1992 г. – 301 с.
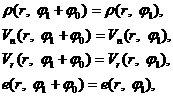
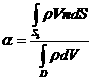 .
.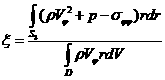 .
.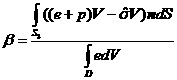 .
.
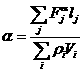 ,
,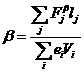 .
.