Аннотация
В данной работе рассматриваются методы оптимизации вычислительных свойств гибридных разностных
схем. Применяется подход численно-визуального исследования, позволяющего модифицировать
и изучить параметрические свойства разностной схемы с помощью визуального представления.
Применяемый подход основан на многократном решении обратных задач с одновременным построением
предельных поверхностей для весовых коэффициентов гибридной разностной схемы. Данный подход
продемонстрирован на примере конкретной задачи моделирования сверхзвуковых ламинарных
и турбулентных течений в дальнем следе.
Abstract
This paper presents the numerical-visual approach to hybrid finite-difference schemes design,
optimization and verification. The proposed approach is based on multiple inverse problems
solution and simultaneous construction of limitation surfaces for weight parameters
of hybrid finite-difference scheme. Further analysis and transformation of these surfaces
allow fast and effective optimization of hybrid finite-difference schemes properties.
The way of practical application for this approach is considered for laminar and turbulent
supersonic wake flow problem.
Версия статьи с цветными
иллюстрациями размещена по адресу
http://www.keldysh.ru/pages/cgraph/publications/cgd_publ.htm
Содержание
1. Введение.......................................................................................................... 4
2. Описание методического подхода для
случая 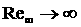 ............................. 7 ............................. 7
3. Применение к ламинарным сверхзвуковым
вязким течениям........................ 10
4. Введение модели турбулентности. Результаты расчетов для
турбулентного течения .................................................................................... 11
5. Обсуждение................................................................................................... 13
6. Заключение................................................................................................... 14
Список литературы.......................................................................................... 15
Данная работа является продолжением цикла
работ по развитию концепций и методов научной визуализации для решения
нестационарных вычислительных задач математической физики и построения и оптимизации применяемых для
решения численных методов [3-10].
Развитие вычислительных средств, усложнение современных
задач математического моделирования приводит к тому, что получить и понять
научный результат становится возможным зачастую только с помощью совокупности
методов и концептуальных подходов визуального представления численных данных. Эту
совокупность методов и концептуальных подходов визуального представления
численных полей, полученных в результате математического моделирования,
называют научной визуализацией.
Проблемы, задачи и пути развития научной визуализации
были подробно представлены в работах
[1-10] на примере такого важного раздела математического моделирования как
вычислительная аэрогазодинамика.
На современном этапе параллельно с развитием средств
вычислительной техники и техническим прогрессом в области создания летательных
аппаратов значительно усложнились задачи вычислительной аэрогазодинамики. Это ,
как правило, двумерные и трехмерные задачи, имеющие существенно нестационарный
характер, обладающие сложной геометрией. Часто подобные задачи кроме численного
решения чисто аэродинамических проблем предполагают моделирование иных
физических процессов, например, горения. Также при современных вычислительных средствах особое значение получают алгоритмы решения
обратных задач аэрогазодинамики, имеющих своей целью обычно оптимизацию тех или
иных конструктивных параметров при рассмотрении задач обтекания летательных
аппаратов или оптимизацию процессов в рабочих камерах и соплах двигательных
установок. Эти задачи предъявляют совершенно новые требования к графическому
представлению результатов расчетов , да и в целом к роли визуализации в задачах
вычислительной аэродинамики. На этом этапе средства и методы визуального
представления могут быть успешно применены не только к решению самих задач
математического моделирования, но и к совершенствованию и оптимизации самих
вычислительных методов, применяемых для численного решения задач.
В работах [8-10]
содержатся описания методических подходв к изучению, конструированию и
оптимизации разностных схем, применяющихся для решения конкретных задач вычислительной аэрогазодинамики, с помощью
визуального представления параметров, определяющих аппроксимирующие и
стабилизирующие свойства разностных схем. Рассматриваемые в [8-10] разностные
схемы относятся к классу гибридных разностных схем.
Согласно [11], в
простейшем случае гибридную схему можно записать как комбинацию GS1 + (1-G)S2, где G – коэффициент
гибридности, S1 и S2 – разностные
схемы, обладающие различными интересующими исследователя свойствами. Например, S1 – схема
первого порядка точности, а S2 – второго порядка и т.п. Большинство применяемых для
решения практических задач аэрогазодинамики являются гибридными. Согласно [11],
к гибридным схемам относятся такие
широко известные алгоритмы как FCT (flux corrected transport), различные
типы TVD (total variation diminishing) разностных
схем, схемы типа ENO (essentially non-oscillatory) и WENO (weighted essentially non-oscillatory) и многие другие. Подробное описание и
классификация различных типов гибридных разностных схем приведена в [11]. Использование
гибридных схем позволяет исследователю использовать наилучшие свойства разных
схем. Одновременно необходимо иметь достаточно четкое представление о свойствах
и ограничениях коэффициентов гибридности (весовых коэффициентов) для того,
чтобы используемое свойство соответствовало физической модели рассматриваемой
задачи.
В работах [8-10] рассматривают пример конкретной
разностной гибридной схемы WW (with weights)
, описанной в работах [8,12,13] и
успешно применявшейся для решения широкого круга модельных и практических задач
вычислительной аэрогазодинамики [14-16].
Данная разностная схема записывается как
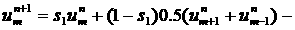 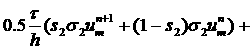
 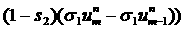 (1.1) (1.1)
в
применении к одномерному аналогу
уравнений Навье-Стокса - уравнению Бюргерса
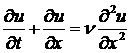 (1.2), (1.2),
где 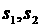 - весовые коэффициенты; - весовые коэффициенты;
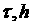 - шаг по времени и
пространственной переменной, а разности обозначены как - шаг по времени и
пространственной переменной, а разности обозначены как 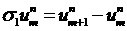 ; ; 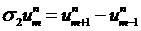 . .
При выборе 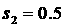 разностная схема
(1.1) является линейной комбинацией схемы Крэнка-Никольсона, обладающей вторым
порядком точности по времени и пространству, и схемы Лакса, обладающей
существенной искусственной вязкостью. Выбирая разностная схема
(1.1) является линейной комбинацией схемы Крэнка-Никольсона, обладающей вторым
порядком точности по времени и пространству, и схемы Лакса, обладающей
существенной искусственной вязкостью. Выбирая 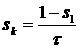 добавочный член с
искусственной вязкостью записывается в явном виде как добавочный член с
искусственной вязкостью записывается в явном виде как 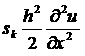 . Разностная схема (1.1) представляет собой
неявную безусловно устойчивую гибридную схему второго порядка по времени и
пространству, обладающую искусственной вязкостью, позволяющей устранять
нефизические осцилляции вблизи разрывов путем выбора весов. Достоинством в
данном случае является то обстоятельство, что искусственной вязкостью можно
управлять непосредственно путем выбора соответствующего значения весового
коэффициента . Разностная схема (1.1) представляет собой
неявную безусловно устойчивую гибридную схему второго порядка по времени и
пространству, обладающую искусственной вязкостью, позволяющей устранять
нефизические осцилляции вблизи разрывов путем выбора весов. Достоинством в
данном случае является то обстоятельство, что искусственной вязкостью можно
управлять непосредственно путем выбора соответствующего значения весового
коэффициента 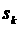 . .
2. Описание
методического подхода для случая 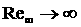 . .
Основные результаты, изложенные в данном разделе,
получены и подробно описаны в предыдущих работах [8-10]. Для разработки и демонстрации методического
подхода выбирается гибридная конечно-разностная схема (1.1) в применении к
задаче математического моделирования участка течения в дальнем следе за телом.
В прямоугольной расчетной области рассматривается течение
вязкого сжимаемого теплопроводного газа, описываемое полной системой нестационарных
уравнений Навье-Стокса. На нижней границе задаются граничные условия симметрии.
На выходных границах задаются «мягкие» граничные условия типа линейной экстраполяции. На входной границе задаются
распределения газодинамических параметров, полученные из расчетов обтекания
осесимметричного тела и участка следа за ним. Эти начальные распределения
давления P и скорости U представлены на
рис.1,2.
Основной целью было тщательное изучение свойств
искусственной вязкости, заложенных в гибридной разностной схеме. Необходимо было на примере данного класса
задач изучить, как управлять схемной вязкостью с помощью выбора весовых
коэффициентов, какие существуют ограничения на значения весовых коэффициентов и
т.д. Это необходимо в конечном итоге для
четкого представления какая
вязкость в конкретном расчете определяет численное решение: физическая
вязкость математической модели или искусственная вязкость разностной схемы.
С этой целью исследовались свойства 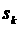 на примере задачи
о течении в дальнем следе и частично определялись существующие для на примере задачи
о течении в дальнем следе и частично определялись существующие для 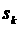 ограничения. ограничения.
Данная задача решалась
для широкого диапазона чисел Рейнольдса 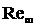 , но в данном разделе рассматривается предельный случай , но в данном разделе рассматривается предельный случай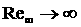 , тогда мы
решаем систему невязких уравнений Эйлера. Подобный переход от решения уравнений
Навье-Стокса к уравнениям Эйлера заложен в используемом для численного решения
программном комплексе. , тогда мы
решаем систему невязких уравнений Эйлера. Подобный переход от решения уравнений
Навье-Стокса к уравнениям Эйлера заложен в используемом для численного решения
программном комплексе.
С целью анализа
численного решения введем понятие «решения без осцилляций» следующим
образом. Выберем решение для
определенного значения 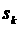 где не возникает нефизических осцилляций, и
проанализируем количество локальных экстремумов в счетной области, обозначив
это количество как где не возникает нефизических осцилляций, и
проанализируем количество локальных экстремумов в счетной области, обозначив
это количество как 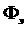 . Пусть . Пусть 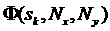  - функционал, характеризующий количество
локальных экстремумов в счетной области в зависимости от выбора веса - функционал, характеризующий количество
локальных экстремумов в счетной области в зависимости от выбора веса 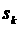 и сеточного разбиения (при условии равномерного разбиения) по соответствующим
направлениям и сеточного разбиения (при условии равномерного разбиения) по соответствующим
направлениям 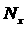 и и 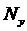 . Тогда задача
формулируется так: определить при каких значениях . Тогда задача
формулируется так: определить при каких значениях 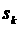 для каждого набора для каждого набора  сеточного разбиения сеточного разбиения
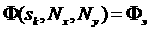 (2.1) (2.1)
Иначе говоря, для каждого набора  нужно решить обратную задачу, варьируя нужно решить обратную задачу, варьируя 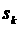 до тех пор, пока не будет выполнено условие
(2.1). до тех пор, пока не будет выполнено условие
(2.1).
Схема расчета
выглядит следующим образом. При 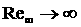 для каждого сеточного разбиения для каждого сеточного разбиения  решается прямая задача моделирования течения в
дальнем следе с помощью WW- схемы при некотором заданном начальном значении решается прямая задача моделирования течения в
дальнем следе с помощью WW- схемы при некотором заданном начальном значении 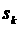 . В счетной
области определяется значение . В счетной
области определяется значение 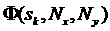 - количество локальных экстремумов. Далее
решается классическая обратная задача путем вариации - количество локальных экстремумов. Далее
решается классическая обратная задача путем вариации 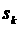 до выполнения условия (2.1). Одновременно
проводится в режиме online визуальное представление до выполнения условия (2.1). Одновременно
проводится в режиме online визуальное представление 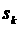 в виде поверхности в виде поверхности 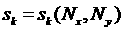 . .
Таким образом, в
результате должна получиться поверхность 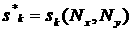 предельных весовых коэффициентов. При выборе
веса предельных весовых коэффициентов. При выборе
веса 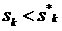 для каждого для каждого  в численном решении возникают нефизические
осцилляции, которые могут приводить к развалу решения. в численном решении возникают нефизические
осцилляции, которые могут приводить к развалу решения.
Полученная в результате расчетов поверхность значений
предельных весовых коэффициентов 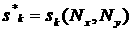 представлена на рис.3.
Эти же данные представлены в виде изолиний на рис.4. представлена на рис.3.
Эти же данные представлены в виде изолиний на рис.4.
Анализируя вид данных, представленных на рис.3,4,
естественно применить преобразование данных и представить их в виде 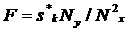 . Вид поверхности после применения преобразования представлен
на рис.5,6 в виде преобразованной предельной поверхности и изолиний
соответственно. . Вид поверхности после применения преобразования представлен
на рис.5,6 в виде преобразованной предельной поверхности и изолиний
соответственно.
Характер данных на рис. 5,6 свидетельствует о том, что
для набора  при условии при условии 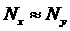 выполняется
соотношение выполняется
соотношение 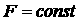 . Следовательно, значения предельного веса . Следовательно, значения предельного веса 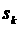 , при котором не возникает нефизических осцилляций, может
определяться как , при котором не возникает нефизических осцилляций, может
определяться как
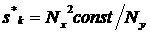 (2.2) (2.2)
Или учитывая что 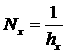 , , 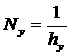 , выражение (2.2)
можно представить как , выражение (2.2)
можно представить как
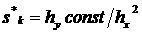 (2.3) (2.3)
Следует заметить, что наиболее сильные отклонения от
полученной зависимости наблюдаются, как показывает рис.6, в тех областях, где
соотношение между размерами вычислительной ячейки наиболее велико, что
определенным образом согласуется с результатами исследования [17]. Согласно
[17] при резкой диспропорции, т.е. при резком возрастании или убывании шага по
пространству в одном направлении, после некоторого предела численное решение
разрушается.
3. Применение к ламинарным сверхзвуковым вязким
течениям
Примененный подход и результаты, полученные с его помощью
и описанные в предыдущем разделе для предельного случая 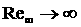 ,естественно расширить и применить к ламинарным
сверхзвуковым вязким течениям, где число ,естественно расширить и применить к ламинарным
сверхзвуковым вязким течениям, где число 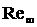 служит одним из
основных определяющих параметров задачи. Учитывая результаты, полученные для
предельного случая, положим служит одним из
основных определяющих параметров задачи. Учитывая результаты, полученные для
предельного случая, положим 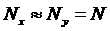 . В данной группе расчетов нас интересует поведение
коэффициента . В данной группе расчетов нас интересует поведение
коэффициента 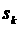 в зависимости от
изменения параметров в зависимости от
изменения параметров 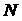 и и 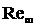 . Тогда, сохраняя введенное в предыдущем разделе понятие
«решения без осцилляций», задача формулируется как определение при каких
значениях . Тогда, сохраняя введенное в предыдущем разделе понятие
«решения без осцилляций», задача формулируется как определение при каких
значениях 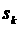 для каждого набора для каждого набора
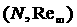 сеточного разбиения выполняется сеточного разбиения выполняется
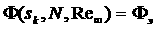 (3.1) (3.1)
Схема расчета выглядит аналогично представленной в
разделе 2. Для каждого набора 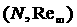 решается прямая задача моделирования
течения в дальнем следе с помощью WW- схемы при некотором заданном начальном значении решается прямая задача моделирования
течения в дальнем следе с помощью WW- схемы при некотором заданном начальном значении 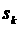 . В счетной области определяется значение . В счетной области определяется значение 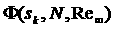 - количество
локальных экстремумов. Далее решается классическая обратная задача путем
вариации - количество
локальных экстремумов. Далее решается классическая обратная задача путем
вариации 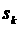 до выполнения
условия (3.1). Одновременно проводится в режиме online визуальное представление до выполнения
условия (3.1). Одновременно проводится в режиме online визуальное представление 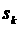 в виде поверхности в виде поверхности
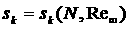 . .
Таким образом, в результате должна получиться поверхность
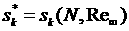 предельных весовых
коэффициентов . Построенная
поверхность обладает тем свойством, что
для каждого набора значений предельных весовых
коэффициентов . Построенная
поверхность обладает тем свойством, что
для каждого набора значений 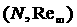 при при 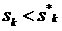 в численном решении возникают
нефизические осцилляции, которые могут приводить к развалу решения. в численном решении возникают
нефизические осцилляции, которые могут приводить к развалу решения.
Полученная в результате расчетов поверхность 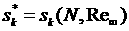 представлена на
рис.7. Эти же данные представлены в виде изолиний на рис.8. Следует заметить,
что по оси Y отмечены
координаты после преобразования Y=lg представлена на
рис.7. Эти же данные представлены в виде изолиний на рис.8. Следует заметить,
что по оси Y отмечены
координаты после преобразования Y=lg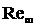 . Данное преобразование применяется ко всем последующим
рисункам. . Данное преобразование применяется ко всем последующим
рисункам.
Аналогично разделу 2, естественно применить
преобразование данных, представленных на рис.7,8, и представить их в виде 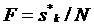 . Вид поверхности после применения преобразования
представлен на рис.9,10 в виде преобразованной предельной поверхности и
изолиний соответственно. . Вид поверхности после применения преобразования
представлен на рис.9,10 в виде преобразованной предельной поверхности и
изолиний соответственно.
Данные на рис. .9,10
свидетельствуют о том, что для каждого набора значений 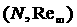 при условии lg при условии lg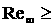 3.5 выполняется
соотношение 3.5 выполняется
соотношение 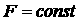 . Следовательно, значения предельного веса . Следовательно, значения предельного веса 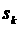 , при котором не возникает нефизических осцилляций, может
определяться как , при котором не возникает нефизических осцилляций, может
определяться как
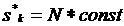 или или 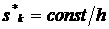 (3.2) (3.2)
4. Введение модели
турбулентности. Результаты расчетов для турбулентного течения
Построение
предельной поверхности весовых коэффициентов для турбулентного течения на
участке дальнего следа за телом проводится полностью аналогично разделу 3. Для
моделирования турбулентного течения применяется полуэмпирическая модель
Бондарева-Лисичко, описанная в [18]. Данная полуэмпирическая модель
турбулентности хорошо зарекомендовала себя в практических приложениях к
течениям подобного типа. В рамках данной модели для описания течения в
турбулентном дальнем следе в системе уравнений Навье-Стокса вместо значения
коэффициента вязкости 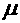 для ламинарных течений
используется полуэмпирическая зависимость для эффективного коэффициента
вязкости для ламинарных течений
используется полуэмпирическая зависимость для эффективного коэффициента
вязкости 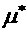 , соответсвующего турбулентному течению типа струи или следа.
В работе приведены соотношения для , соответсвующего турбулентному течению типа струи или следа.
В работе приведены соотношения для 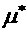 , которые учитывают общие свойства осредненного турбулентного
движения и позволяют решать конкретные задачи: , которые учитывают общие свойства осредненного турбулентного
движения и позволяют решать конкретные задачи:
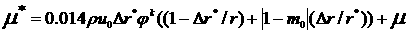 ; (4.1) ; (4.1)
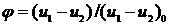 ; ; 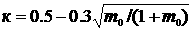
Здесь 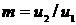 - отношение скорости
во внешнем потоке к скорости на оси; - отношение скорости
во внешнем потоке к скорости на оси;
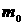 - отношение скоростей
в начальном сечении; - отношение скоростей
в начальном сечении;
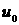 - скорость на оси в
начальном сечении; - скорость на оси в
начальном сечении;
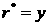 в точке, где в точке, где 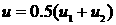 . .
Линейный размер,
характеризующий толщину зоны смешения, 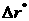 определяется как определяется как 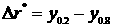 , где , где 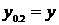 в той точке, в которой в той точке, в которой
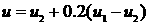 , а , а 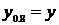 в той точке, в которой в той точке, в которой
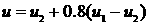 . .
Общая схема расчетов аналогична представленной в
предыдущем разделе для ламинарных вязких течений. В результате расчетов получаем поверхность 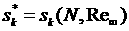 предельных весовых
коэффициентов для турбулентного случая. Полученная в результате расчетов
поверхность предельных весовых
коэффициентов для турбулентного случая. Полученная в результате расчетов
поверхность 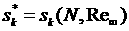 представлена на
рис.11. Эти же данные представлены в виде изолиний на рис.12. Из рис.11,12 следует, что для случая
турбулентного течения значение представлена на
рис.11. Эти же данные представлены в виде изолиний на рис.12. Из рис.11,12 следует, что для случая
турбулентного течения значение 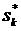 практически не зависит от числа практически не зависит от числа 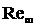 . .
Аналогично предыдущему разделу применяется преобразование
данных, представленных на рис.11,12. Это преобразование выглядит каке 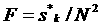 . Вид поверхности после применения преобразования
представлен на рис.13,14 в виде преобразованной предельной поверхности и
изолиний соответственно. . Вид поверхности после применения преобразования
представлен на рис.13,14 в виде преобразованной предельной поверхности и
изолиний соответственно.
Данные на рис. 13,14
свидетельствуют о том, что для каждого набора значений 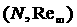 выполняется
соотношение выполняется
соотношение 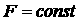 . Следовательно, значения предельного веса . Следовательно, значения предельного веса 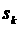 , при котором не возникает нефизических осцилляций, может
определяться как , при котором не возникает нефизических осцилляций, может
определяться как
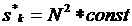 или или 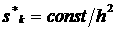 (3.2) (3.2)
5. Обсуждение
Задача оптимизации и управления вычислительными
свойствами гибридных конечно-разностных схем является как весьма актуальной и
интересной с практической точки зрения, так и достаточно трудоемкой. Проводить многократное решение обратных задач
с одновременным визуальным представлением результатов, подобно представленному
в данной работе, достаточно затруднительно. Развитие вычислительных средств и
появление возможности параллельных расчетов позволяют теперь проводить анализ
вычислительных свойств конечно-разностных схем с применением подобного подхода.
Применение изложенного выше вычислительного подхода может
быть полезно для определенных классов практических задач, особенно для
проведения тех расчетов, которые используются в индустриальных проектах. Здесь
можно выделить два основных направления дальнейшего развития применения
подобного подхода.
1. Контроль, оптимизация и управление вычислительными
свойствами применяемых конечно-разностных схем в зависимости от выбранных групп
геометрических и физических параметров задачи.
2. В классах задач, где качественная картина решения
обычно известна, как правило, вычислительные процессы необходимы для того,
чтобы в первую очередь определить ключевые зависимости решения от различных
определяющих параметров задачи: геометрических, физических,
вычислительных. Применение данного
подхода позволяет строить взаимозависимости ключевых параметров, визуально представлять
их , и, таким образом, наиболее эффективно и точно работать с ними.
Следует заметить также, что полученные результаты имеют
определенное отношение к дискуссии, продолжавшейся многие годы. Известно из
экспериментов, что основные параметры турбулентных течений при развитой
турбулентности слабо зависят от числа 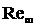 . Это порождало у многих исследователей намерение
попытаться моделировать турбулентные течения в рамках модели Эйлера,
дополненной различными граничными условиями. Подобные попытки зачастую давали
численные результаты, сопоставимые с экспериментальными. Данное совпадение
характерно для разностных схем с большой схемной вязкостью на недостаточно
мелкой сетке. Соотношение необходимой искусственной вязкости для ламинарного и
турбулентного случаев иллюстрирует рис.15, где представлены зависимости . Это порождало у многих исследователей намерение
попытаться моделировать турбулентные течения в рамках модели Эйлера,
дополненной различными граничными условиями. Подобные попытки зачастую давали
численные результаты, сопоставимые с экспериментальными. Данное совпадение
характерно для разностных схем с большой схемной вязкостью на недостаточно
мелкой сетке. Соотношение необходимой искусственной вязкости для ламинарного и
турбулентного случаев иллюстрирует рис.15, где представлены зависимости 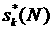 для ламинарного и
турбулентного случая при фиксированном числе Рейнольдса для ламинарного и
турбулентного случая при фиксированном числе Рейнольдса 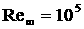 . .
6. Заключение
С помощью вышеизложенного способа можно быстро и
эффективно анализировать аппроксимирующие свойства гибридных разностных схем,
что важно для верификации результатов математического моделирования. В
вышеизложенном конкретном случае он позволяет для любого набора определяющих
параметров задачи (сеточные разбиения, определяющие физические параметры)
определять ограничения для предельного весового коэффициента без дополнительных
вычислений, пользуясь лишь свойствами визуально представленной поверхности и
полученным с помощью ее преобразований аналитическими выражениями.
Концептуальный подход к анализу свойств
разностной схемы заключается в сочетании решения обратной задачи для каждого
набора определяющих параметров с одновременным визуальным построением
предельных весовых поверхностей. Данный подход имеет важное методическое
значение, т.к. позволяет эффективно изучать и представлять свойства гибридных
разностных схем в процессе их конструирования. Визуальное представление online позволяет резко
ускорить процесс анализа численного решения. Реализация данного методического
подхода показана на примере применения конкретной разностной схемы к конкретной
задаче об участке дальнего следа за
телом для невязких, а также вязких ламинарных и турбулентных сверхзвуковых
течений.
Иллюстрации получены при помощи комплекса GeoGraph, разработанного
под руководством В.Н.Кочина, которому автор выражает свою признательность.
Список литературы.
[1] V.Interrante, C. Grosch «Visualizing 3D Flow»
IEEE Computer Graphics and applications, v.18, N 4, 1998, p.70-74.
[2] S.Uselton «ExVis:
Developing A Wind Tunnel Data Visualization Tool» Proc.IEEE Visualization 97,
ACM press, New York, Oct.1997, pp.417-420.
[3] А.Е.Бондарев
«Визуализация в вычислительной аэрогазодинамике: проблемы развития». Тр.
ГРАФИКОН-99, М., МГУ, 1999, с.9-13.
[4] А.Е.Бондарев,
Е.Н.Бондарев «Функции визуализации в вычислительной аэрогазодинамике»
Общероссийский научно-технический журнал «Полет», М., «Машиностроение», N 10, 2000, с.53-60.
[5] А.К.Алексеев,
А.Е.Бондарев, Ю.А.Молотилин «О визуализации сопряженных полей при идентификации
и управлении трехмерным течением вязкой жидкости». Сб. «Применение методов
научной визуализации в прикладных задачах», М., МГУ, 2000, с.8-18.
[6] А.К.Алексеев, А.Е.Бондарев «Визуализация переноса погрешности при расчете
поля течения» Сб. «Научная визуализация в прикладных задачах», М., МГУ, 2003,
с.4-13.
[7] А.Е.Бондарев,
Е.Н.Бондарев «О трассировке вихревых структур» Сб. «Научная визуализация в прикладных задачах», М., МГУ, 2003, с.40-45.
[8] А.Е.
Бондарев «Конструирование и оптимизация разностных схем с применением методов
визуализации» Тр. ГРАФИКОН-2003, М., МГУ, 2003, с.261-264.
[9] А.Е. Бондарев «Применение методов визуализации
для оптимизации конечно-разностных схем» Сб. «Научная визуализация в прикладных
задачах», Москва, МГУ, 2003, с.34-39
[10]А.Е. Бондарев «Применение методов
научной визуализации для оптимизации вычислительных свойств конечно-разностных
схем» Препринт ИПМ им. М.В. Келдыша РАН, № 79, 2006, 17 с.
[11]А.Г.Куликовский, Н.В.Погорелов,
А.Ю.Семенов «Математические вопросы численного решения гиперболических систем
уравнений» М, Физматлит, 2001, 608 с.
[12]А.Е.Бондарев «Численное решение
уравнения Бюргерса в области высоких градиентов» Препринт ИПМ им М.В.Келдыша РАН, М., № 12, 1990, 13 с.
[13]А.Е.Бондарев «Влияние параметров
сверхзвукового потока на характерное время установления течения при обтекании
уступа» Изв.АН СССР, «Механика жидкости и газа», N 4, 1989, с.137-140.
[14]А.K.Alexeev, A.E.Bondarev, Y.A.Molotilin « On Inverse Problems for 3D Time-Dependent
Free Convection Heat Transfer» Proc.
of National Heat Transfer Conference ASME, v.10, 1995, p.113-122.
[15] Alexeev, А.K., Bondarev, A. E., Molotilin, Y.A. «On Boundary Condition
Determination Using Inverse Free Convection Problem.» Proc. of
National Heat Transfer Conference ASME,
Oregon, USA, v.10, 1995.
[16] А.К.Алексеев, А.Е.Бондарев,
Ю.А.Молотилин «Обратные задачи на основе уравнений Навье-Стокса для задач
свободной конвекции» Препринт ИПМ им
М.В.Келдыша РАН, М., № 32, 1995, 15 с.
[17]Н.А. Черанева «Неявная разностная
схема на неравномерной сетке для решения уравнений Навье-Стокса сжимаемого
газа» Сб. «Численные методы в
аэродинамике» Вып.4, НИВЦ МГУ, Изд.МГУ, 1980, сс. 3-19.
[18]Е.Н. Бондарев, И.Д. Лисичко
«Распространение недорасширенной турбулентной струи в спутном сверхзвуковом
потоке» Изв.АН СССР, «Механика жидкости и газа», N4, 1974, сс.36-41.
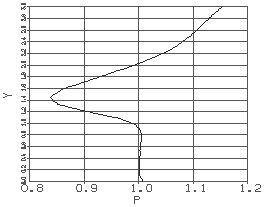 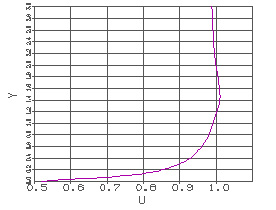
Рис.1
Рис.2
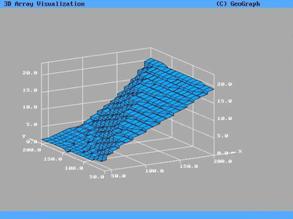 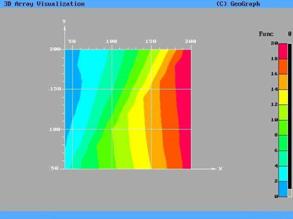
Рис.3
Рис.4
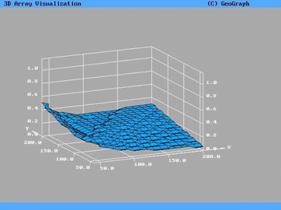 
Рис.5 Рис.6
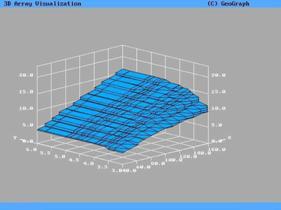 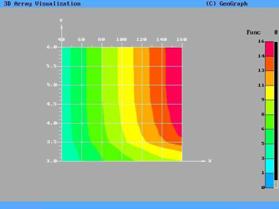
Рис.7 Рис.8
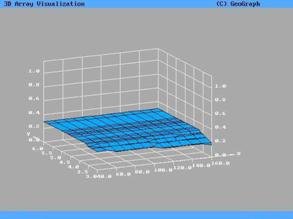 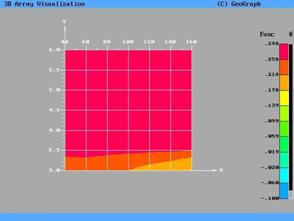
Рис.9
Рис.10
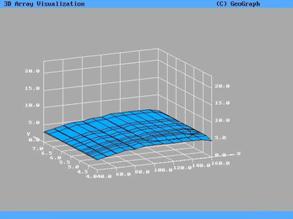 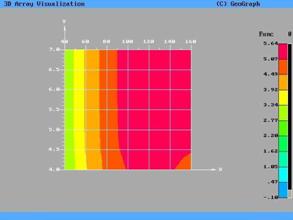
Рис.11
Рис.12
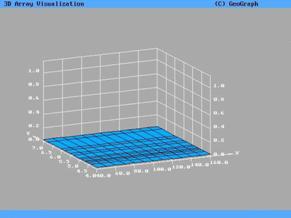 
Рис.13
Рис.14
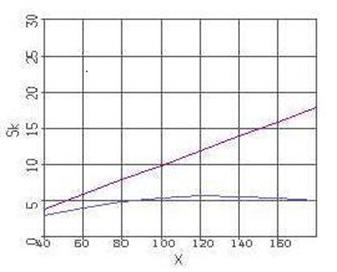
Рис.15
|