Оглавление

1. Точность общемировых энергетических прогнозов ……………………4

2. Динамика мирового потребления энергоресурсов …………………….13

3. Прогнозные системы МЭ США и МЭА ………………………………...22

Источники  …………………………………………………………………...28

Перечень рисунков

Рис. 1. Динамика спроса/потребления энергии в мире и прогнозы

МЭА и МЭ США 1996 г.  …………………………………………………..18

Рис. 2. Динамика спроса/потребления природного газа в мире

и прогнозы МЭА и МЭ США 1996 г.  ……………………………………..20

Перечень таблиц

Табл. 1. Сравнение прогнозов МЭ США

мирового потребления энергии в 1995 и 2000 гг. ………………………….6

Табл. 2. Относительная ошибка прогнозов МЭА

мирового спроса на энергию в период 1993-2002 гг. ………………...……8

Табл. 3. Потребление энергии в мире по данным МЭ США

за разные годы ……………………………………………………………….19

Табл. 4. Мировое потребление природного газа

и энергии в целом ……………………………………………….………..….21

Табл. 5. Данные прогнозов МЭ США мирового

потребления энергии, базовый сценарий  ………………………………….24

Табл. 6. Данные прогнозов МЭА мирового спроса

на энергию, базовый сценарий   …………………………………………….25

         С начала 80-х годов прошлого века достаточно регулярно стали публиковаться прогнозы мирового потребления энергии в целом и отдельных энергоносителей в частности. С течением времени наступали годы, относительно которых как раз и делались прогнозы тех или иных энергетических величин, и, таким образом, накапливался статистический материал из прогнозных и фактических значений. При наличии такого материала возникает естественный вопрос: а как соотносятся между собой прогнозные и фактические значения упомянутых величин? Или, иначе говоря, какова точность выполненных прогнозов? Ответам на эти вопросы как раз и посвящается данная работа.

         Разумеется, подобные вопросы, в силу их очевидности, исследователями уже ставились. В качестве примера можно указать один из последних обзоров Международного энергетического агентства – World Energy Outlook 2004 [1], в котором приводится сопоставление прогнозных и фактических значений спроса на энергию. Особенностью же данного исследования является то, что в нем авторы попытались придать такого рода сравнению более основательный, более системный характер.

         Данное исследование разбито на две части: «Часть I» - постановочно-методологическая) и «Часть II», в которой проводится статистический анализ конкретных прогнозов. Условимся ниже по тексту называть Части I и II, в совокупности, «статьёй». А «данной работой», «данным исследованием» и т.п. будем называть в данном тексте только Часть I или, что то же самое, Часть I статьи.

1. Точность общемировых энергетических прогнозов

Итак, предметом настоящей работы является проведение ретроспективного анализа долгосрочных прогнозов мирового потребления энергии в целом и – как одного из основных мировых топливно-энергетических ресурсов – природного газа, в частности, с целью выяснения точности данных прогнозов. Исследование основывается на сопоставлении прогнозных и фактических значений указанных величин (объемов потребления энергии и природного газа) и строгом статистическом подходе к их описанию. Следует подчеркнуть, что предметом анализа в данной работе являются сами прогнозы, а не объект прогнозирования – мировой рынок энергоресурсов. Исследование такого рода, по мнению авторов, может представлять интерес для специалистов, занимающихся вопросами развития мировой энергетики.

Необходимость достоверных энергетических прогнозов достаточно очевидна. В самом деле, такие прогнозы, во-первых, имеют важный прикладной характер и являются ключевым элементом решения вопросов перспективного обеспечения энергетической безопасности. А энергетика, как известно, представляет собой, без преувеличения, главнейший экономический и даже политический фактор благополучия как отдельных стран, так и мира в целом. Потребность в таких прогнозах привела к формированию рынка услуг по их предоставлению. Широко известны, например, прогнозы Международного энергетического агентства, Министерства энергетики США, Международного института прикладного системного анализа (IIASA), ряда работающих в сфере энергетики исследовательских центров Европейской Комиссии и Организации Объединенных Наций. Кроме того, прогнозы добычи, спроса и цен на энергоресурсы составляются многими крупнейшими нефтегазовыми компаниями, такими как «Ройял Датч / Шелл», «Бритиш Петролеум», «Коноко Филипс», а также различными консалтинговыми организациями («Вуд Макензи», ПИРА «Энерджи Груп», «Глобал Инсайт» и др.)

Во-вторых, имеет место чисто академический интерес. Повышение качества прогнозов и прогнозных систем способствует развитию всего научного прогнозирования, а также, с более широкой точки зрения, – развитию системного анализа, в рамках которого разрабатываются новые модели эволюции сложных систем и расчетные алгоритмы.

Менее очевидным является ответ на вопрос, а что, собственно, следует понимать под качеством или под точностью прогноза? Вообще говоря, понятие «качества» является достаточно широким и может включать в себя помимо точности прогноза такие аспекты, как полноту набора прогнозируемых величин (с точки зрения достаточности для проведения перспективного анализа), регулярность выполнения прогнозов, обоснованность методики расчета (корректность математической модели) и т.д. Как видно из преамбулы, в данной работе рассматривается только «точностный» аспект качества прогнозирования. Иначе говоря, здесь под «качеством» прогнозирования понимается исключительно «точность» прогнозирования.

Одними из наиболее известных ведущих зарубежных организаций, специализирующихся, в том числе, на составлении прогнозов мирового развития, являются Международное энергетическое агентство (International Energy Agency, IEA), далее – МЭА, и Министерство энергетики США (US Department of Energy, DOE), далее – МЭ США. Они публикуют результаты исследований перспектив развития рынков энергоресурсов как отдельных государств, так и совокупностей государств, объединяемых в единое целое по тем или иным принципам: географическим, экономическим, политическим, а также – мира в целом. При этом, МЭ США публикует свои ежегодные обзоры (Международные энергетические обзоры, International Energy Outlook, IEO [2]), начиная с 1985 г. (без учета стран социалистического содружества), а с 1990 г. – по миру в целом. Прогнозы МЭА регулярно издаются с 1993 г. (Мировые энергетические обзоры, World Energy Outlook, WEO [3]) с интервалом в 1-2 года. В данной работе рассматриваются прогнозы именно этих двух широко известных организаций, поскольку они чаще других оказываются востребованными специалистами в области энергетики.

При этом авторами используется определенный инструментарий оценки погрешности прогнозирования, который, не претендуя на завершенность или существенное методологическое значение, тем не менее, позволяет оценивать точность анализируемых прогнозных систем, а затем, на основе такой оценки, и сопоставлять их между собой. Следует отметить, что наряду с указанными двумя прогнозами в оценке точности и в сопоставлении участвует еще один – так называемый «авторский» – прогноз, который выполняется с помощью экстраполяционной модели на основе парного регрессионного анализа. Эта модель не имеет какого-то существенного практического значения в качестве прогнозного инструмента в силу своей идеологической тривиальности и используется здесь лишь для того, чтобы выявить некоторые особенности двух других прогнозных систем. Тем не менее, несмотря на свою простоту, эта «авторская» модель демонстрирует в данной работе вполне конкурентные, по сравнению с анализируемыми здесь прогнозами, результаты. Забегая вперед, можно сказать, что сравнительно высокая прогнозная точность экстраполяционной «авторской» модели является, по-видимому, не свидетельством качества этой прогнозной системы, а, скорее, показателем особенностей или даже недостатков двух других вышеуказанных.

Также в данной работе авторами намечаются некоторые подходы к определению критериев качества прогнозных систем. В частности, делается попытка определить, что такое точность прогноза, какая точность может считаться желательной и проанализировать с этих позиций точность двух прогнозных систем – МЭА и МЭ США.

Насколько известно авторам, детального статистического анализа точности прогнозов, включая сравнительный анализ точности прогнозов, выполненных различными организациями, ранее не проводилось. Этого не делалось, возможно, потому, что попросту не было достаточного набора данных для регулярного, т.е. ежегодного, сравнения прогнозных и фактических величин.

Вместе с тем, следует отметить, что в обзорах МЭ США [2] (IEO-1999 и IEO-2004) было представлено выборочное сопоставление некоторых прогнозов – на 1995 г. и 2000 г., выполненных этой организацией за период с 1985 по 1995 гг., – с фактическими данными. В Табл. 1 представлена часть вышеуказанных прогнозов, выполненных с 1990 по 1993 гг. Качество прогнозов в указанных обзорах прокомментировано не было, т.е. не было проведено анализа как такового.

Табл. 1. Сравнение прогнозов МЭ США мирового потребления энергии в 1995 и 2000 гг. Источник: [2], DOE/EIA-0484(2006), IEO 2006, pp. 185, 187

Напомним, что 1 BTU (британская тепловая единица) – это принятая в мировой практике энергетическая величина, определяемая как количество теплоты, которое необходимо затратить, чтобы нагреть 1 фунт воды, находящейся при нормальном давлении, на 1 градус Фаренгейта, и равная приблизительно 252 калориям; 1 QBTU – это 10¹⁵ BTU (квадриллион BTU).

Как можно видеть, данная таблица содержит весьма ограниченное количество информации, не позволяющее провести приемлемый статистический анализ точности прогнозирования. При этом следует отметить, что вся аналогичная информация из цитированных обзоров МЭ США не является качественно более информативной, чем Табл. 1, а всего лишь превосходит её по количеству лет, в которые выполнялись прогнозы, а именно, с 1985 по 1995 гг., как уже упоминалось.

В обзоре МЭА WEO-2004 проведен более детальный (по сравнению с МЭ США) анализ собственных прогнозов, разработанных этой организацией за период с 1993 г. по 2002 г. Мы приводим соответствующую таблицу (Табл. 2) для последующего сравнения с нашими расчетами. В этой таблице разработчиками приведены также величины средних ошибок их прогнозов, трактуемых в тексте указанного обзора как точность (accuracy) прогноза за рассматриваемый период. Это определение, на наш взгляд, не совсем удачно с точки зрения математической статистики, хотя бы уже потому, что используемое в нем среднее значение модуля ошибки не является моментом распределения случайной величины, а именно моменты дают такие производные величины от рассматриваемых случайных величин, которые имеют практическое значение (как иногда говорят – «физический смысл»). В настоящей работе мы предлагаем иной формальный критерий, с помощью которого различные прогнозы можно корректно сравнивать между собой по точности.

Следует также отметить, что фактически в рассматриваемой таблице специалисты МЭА приводят два различных по содержанию вида средних ошибок. А именно, приведенные в нижней строке Табл. 2 величины являются средними значениями модулей ошибок прогнозов, выполненных в один и тот же год относительно ряда лет. Величины же, приведенные в правом крайнем столбце таблицы, представляют собой средние значения модулей ошибок прогнозов, выполненных в различные годы относительно одного и того же года. Однако в Табл. 2 (воспроизведенной в данной статье тождественно содержанию оригинала) данные строка и столбец озаглавлены одинаково – просто «средняя ошибка» («Average absolute per cent error», что, впрочем, не меняет существа данного замечания).

Помимо этого в рассматриваемой таблице имеет место еще одно несоответствие. Так, указанные строка и столбец со средними значениями в соответствии со структурой Табл. 2 «заканчиваются» одним и тем же полем – правой нижней ячейкой данной таблицы, – в котором, согласно логике таблицы, должно располагаться «среднее из средних» – результат усреднения как по строке, так и по столбцу. Следует отметить, что приведенное в таблице 2 в этой ячейке значение соответствует только усреднению по нижней строке, тогда как усреднение по правому столбцу дает другое значение (1,88), отличающееся, даже с учетом округления, от указанного значения в ячейке (2,2).

Табл. 2. Относительная ошибка (%) прогнозов МЭА мирового спроса на энергию в период 1993-2002 гг. Источник: [1]

Также отметим, что приведенная в Табл. 2 относительная ошибка определена в [1] как разность между прогнозным и фактическим значениями энергопотребления, деленная на прогнозное значение. При таком определении за основу берется прогнозное значение, поскольку отклонение делится именно на прогноз, а фактическое значение приобретает смысл отклонения от «основы» (от прогноза). Таким образом, по своему смыслу эта величина показывает относительное отклонение реальности от прогноза. Подчеркнем, что в настоящей работе используется относительная погрешность с фактическим значением в знаменателе, что имеет смысл отклонения прогноза от реальности. Такая  погрешность в числовом выражении несколько отличается от погрешности, используемой в [1]. Как нетрудно видеть, отношение этих двух видов относительных ошибок равно отношению факта и прогноза, так что, как правило, переход от одного способа определения погрешности к другому не приводит к значительным отличиям. Например, при относительной ошибке в 5% её значение при переходе к другому определению относительной погрешности (из двух рассматриваемых) изменится приблизительно всего лишь на 0,2%. Тем не менее, для строгости изложения считаем необходимым указать на некоторое различие в применяемой методологии по сравнению с [1].

Также следует отметить, что сами анализируемые данные, как правило, известны не точно. И связано это не только с неизбежной погрешностью в измерениях. В разных странах применяются различные системы учета энергоресурсов, калорийность добываемого топлива также определяется не абсолютно точно, а иногда и сознательно искажается. Учет данных внутри каждой страны и их согласование для получения данных по миру в целом является самостоятельной проблемой, здесь не рассматриваемой. В нашем анализе мы считаем величины фактического потребления энергоресурсов, приводимые, в частности, МЭ США, «абсолютно точными», т.е. реально совпадающими с данными, предоставляемыми статистическими организациями по странам мира.

Представляется важным, не слишком углубляясь в существо дела, указать еще на один примечательный аспект настоящего анализа. Дело в том, что в данной работе мы рассматриваем прогнозные величины, характеризующие использование энергии потребителями. При этом исследуемые нами две прогнозные системы – МЭ США и МЭА – работают с различными характеристиками вышеупомянутого «использования». Так, МЭ США прогнозирует потребление («consumption») энергии или отдельных его видов. Тогда как МЭА в своих обзорах оперирует величиной спроса («demand») на энергию. (Строго говоря, в обзорах МЭА с данной характеристикой ситуация несколько сложнее. В изданиях World Energy Outlook (WEO) до 1996 года включительно используется именно величина «спроса» («demand») на энергию. Но, начиная с 1998 года, в WEO вместо спроса на энергию начинает использоваться величина поставок («supply») энергии, а точнее – величина TPES («total primary energy supply»). При этом несколькими годами ранее, в WEO-94, имел место краткий комментарий по данному вопросу, в котором говорилось об «эквивалентности» использования величин «primary energy demand» и «total primary energy supply».) В свою очередь специалисты МЭ США в своих обзорах – International Energy Outlook – регулярно проводят сравнение результатов своих прогнозов с прогнозами МЭА, в том числе, и в отношении вышеупомянутых характеристик использования энергии, тем самым неявно указывая на сопоставимость, а значит и на содержательную близость сравниваемых величин.

Авторы данного исследования также придерживаются той точки зрения, что вышеупомянутые характеристики использования энергии и отдельных ее видов из обзоров МЭА и МЭ США сопоставимы, отмечая при этом, что, строго говоря, проблема их сопоставимости требует более детального анализа.

Как указано выше, в данной работе анализируется только один из аспектов качества прогноза – его точность. Выберем критерий точности для рассматриваемых долгосрочных энергетических прогнозов. В качестве такового предлагается принять величину относительного среднеквадратичного отклонения, определяемого следующим образом.

Прогнозом P(k, l) будем называть сформированный в год k набор из M значений прогнозируемой величины, соответствующих некоторым годам l(1),l(2),…,l(M). Рассматриваемая выборка из M лет представляет собой целочисленный вектор l = ( l(1),l(2),…,l(M) ). Например, запись P(2000, l) означает, что этот прогноз сформирован в 2000-ом году и содержит набор опорных прогнозных точек в соответствии с числом компонент вектора l. Если, в частности, этот прогноз сделан до 2020 года с интервалом в 5 лет, то вектор l имеет вид l = (2005, 2010, 2015, 2020). Таким образом, мы имеем M прогнозных значений (в вышеприведенном примере M = 4) величины Vпрогн(k, l(j)) и, по прошествии соответствующего времени, M фактических её значений Vфакт(l(j)), j=1,…,M. На основе сравнения наборов значений Vпрогн и Vфакт вычисляется вышеупомянутое относительное среднеквадратичное отклонение (или ошибка) s(k, l) данного конкретного прогноза, сделанного в год k, для выборки, определяемой вектором l:

            s(k, l)  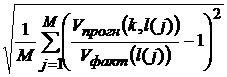=  ,                                (1)

которое и предлагается принять в качестве критерия точности долгосрочного энергетического прогноза.

Почему предложена именно такая величина? Для ответа на этот вопрос нужно, прежде всего, пояснить, чего мы ждем от данного критерия.

Очевидно, что критерием качества (точности) должна быть такая величина, значение которой, вычисляемое в каждом конкретном случае, при его сравнении с некоей априори заданной величиной говорило бы о том, хороша или плоха точность рассматриваемой совокупности прогнозных значений.

Из анализа имеющейся статистики по рассматриваемым в данной работе величинам – мировому потреблению энергии в целом и природного газа – известно, что их изменения («тренды») год от года (особенно это относится к энергии в целом) не подвержены резким скачкам. Такое «нескачкообразное» поведение рассматриваемых величин делает их прогнозирование достаточно «благодарным» занятием. Поэтому при более-менее приличном прогнозировании и при условии, что в мировой энергетике не происходит каких-либо «катастрофических», то есть очень сильных и быстрых изменений, можно ожидать, что практически не будет таких лет, в которые прогнозные значения значительно (в разы) – по сравнению с другими годами – отличались бы от фактических.

Если прогнозируемая величина обладает указанным выше свойством «достаточной гладкости поведения», то для оценки прогнозных значений целесообразно использование «интегральных» критериев, то есть критериев, основанных на совокупном учете «точностей» отдельных прогнозных значений. В то же время, поскольку ошибкой считается отклонение как в большую, так и в меньшую стороны, то обычная алгебраическая сумма отдельных «точностей» не будет адекватна поставленной задаче. Необходимо применять критерии, в которых используются величины одного знака. Предложенная формула (1) как раз и относится к критериям такого рода.

И напротив, если бы за рассматриваемый период времени, в течение которого регулярно стали делаться прогнозы в сфере энергетики (то есть, за последние 20-25 лет), «точности» прогнозов достаточно часто были бы существенно хуже среднего за рассматриваемый период, то использование небольшого числа (одного – двух) «интегральных» критериев вряд ли можно было бы признать удовлетворительным. Дело в том, что такие критерии скрадывали бы отдельные «провалы» по точности, выдавая вполне приличную интегральную величину. Для величин с подобными «выбросами» необходимо использовать критерии других типов (например, модуль максимального по выборке относительного отклонения прогнозного значения от фактического), которые по своей конструкции способны выявлять и показывать такие «выбросы» погрешности, либо работать с большим количеством моментов случайной величины.

Для целей анализа точности совокупности прогнозных значений удобно использовать следующий частный случай вышеуказанного критерия (1), основанный на определенном типе выборки лет прогнозирования. Именно, удобно использовать выборку из M последовательных лет l(i), начинающуюся с года, следующего за годом прогнозирования k:  l(1)=k+1, l(2)=k+2,…, l(M)=k+M. В этом случае получаем относительное среднеквадратичное отклонение, зависящее от двух параметров – года прогнозирования k и горизонта прогноза M:

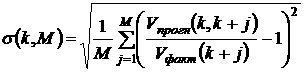              .                                 (2)

Отметим, что, зачастую, в публикуемых прогнозах значения прогнозируемых величин даются с интервалом в пять лет. При этом также приводятся среднегодовые темпы их роста на указанных интервалах. В таком случае значения прогнозных величин в промежуточные годы можно получать линейной интерполяцией. Это дает возможность работать с ежегодными выборками l, состоящими из ряда последовательных лет, что весьма удобно.

Теперь от рассмотрения одного набора из M прогнозных значений, сделанных в некоторый год k, перейдем к серии из N прогнозов P(k(i), l(i)), сделанных в N различных лет k(i), i=1,…,N. Тогда получаем еще один целочисленный вектор, характеризующий набор лет, в которые были сделаны прогнозы: k = ( k(1),k(2),…,k(N) ). В этом случае для каждого года k(i) мы имеем свой набор из  прогнозных значений относительно различных лет l(i) = L(i, j), j=1,…,. Так, например, для двух прогнозов P(2000, l(1)) и P(2005, l(2)) значения аргумента k таковы: k(1) = 2000, k(2) = 2005. Если первый прогноз сделан до 2020 г. с интервалом в 5 лет, а второй – до 2030 г. с двумя интервалами в 10 лет и одним, последним, интервалом в 5 лет, то l(1) = (2005, 2010, 2015, 2020), а l(2) = (2015, 2025, 2030), так что  = 4 прогнозных значения,  = 3. В общем случае объектом нашего рассмотрения окажется набор из M(k(1)) + M(k(2)) + … + M(k(N)) прогнозных значений, которые представляют собой таблицу чисел, обозначаемую как L = ( L(i, j),  i=1,…,N, j=1,…,M(k(i)) ). А, соответственно, в частном случае нашего примера, L(1, 1) = 2005, L(1, 2) = 2010 и т.д., а L(2, 1) = 2015, L(2, 2) = 2025 и т.д. Тогда выражение (1) для относительной ошибки отдельного прогноза, выполненного в год k(i), примет вид:

  s(k(i), l(M(k(i)))) = 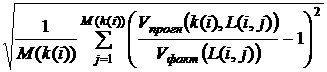,                 (3)

где l(i) = ( L(i,1), L(i,2),…, L(i, M(k(i))) ).

Отдельной проблемой статистического анализа является оценка статистической погрешности, обусловленной варьированием выборки, используемой при анализе прогнозов. С этой точки зрения представляет интерес, например, оценка влияния на величину среднеквадратичного отклонения (1), во-первых, объема M выборки прогнозов и, во-вторых, использования различных выборок прогнозов одного и того же объема M.

         Иногда приходится проводить анализ с использованием данных различных прогнозов P(k(i), l(i)), сделанных в N различных лет k(i), i=1,…,N. В этом случае правомерно поставить вопрос об определении точности прогнозирования для всей этой совокупности прогнозов. Такую величину можно было бы интерпретировать и как меру точности самой прогнозной системы (естественно, применительно к интервалу времени, соответствующему использованным для определения точности прогнозам).

Рассматривая данные прогнозов P(k(i), l(i)) за N лет k(i), i=1,…,N  как единый массив прогнозных значений Vпрогн(k, L), для которого относительное отклонение может быть определено по формуле типа (3), где суммирование под корнем ведется не только по индексу j (годам, относительно которых делается прогноз), но и по i  (т.е. по всем прогнозам от 1 до N), получаем известную формулу (см., напр., [4]) для среднеквадратичного отклонения нескольких совокупностей случайных величин:

           ^{s (k, L)  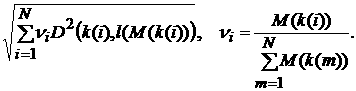=}                   (4)

Определяемая таким образом величина s(k, L), как указано выше, может служить критерием качества (точности) прогнозной системы (с учетом вышеупомянутой оговорки относительно интервала времени).

Изложенный в этом параграфе подход используется в следующих разделах этой работы при анализе прогнозов потребления природного газа в мире и мирового энергопотребления в целом.

2. Динамика мирового потребления энергоресурсов

Для количественной оценки динамики мирового потребления энергоресурсов можно использовать два близких по смыслу понятия, характеризующих среднее значение прироста рассматриваемой величины (в данном случае – прироста мирового потребления энергии).

Пусть в течение некоторого периода времени в n лет, начиная с года k, потребление энергии () за год (k+j) росло с постоянным темпом p % в год. Это означает, что

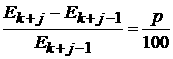                                                                              (5)

для любого j за рассматриваемый период ( j = 1,…, n ). Вводя величину

                                                     ,                                                (6)

получаем из (5)

                                            .                                               (7)

Теперь перейдем к рассмотрению реальной ситуации. Пусть на том же промежутке времени в n лет имеется n произвольных значений величин , j = 1,…,n (и, естественно, само значение  в год k). Тогда выражение (5) трансформируется в следующее:

                                                .                                             (8)

Среднее арифметическое значение величин  на промежутке времени в n лет определяется по формуле:

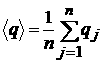                                                  .                                                    (9)

Из (6) и (9) следует соотношение между средними арифметическими значениями величин q и p:

                                             .                                                 (10)

         Вместе с тем, на основании выражения (7) можно ввести среднее геометрическое значение величин  на том же промежутке времени:

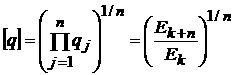                                     .                                   (11)

Этому значению  можно поставить в соответствие по формуле (6) значение среднего годового прироста на промежутке в n лет:

                                                  .                                             (12)

Важно отметить, что  не имеет того же статистического обоснования, что и  в формуле (10), т.к. само значение  не есть среднее геометрическое величин годовых приростов за отдельные годы, в силу нелинейности операции, определяемой формулой (11):

                                      .

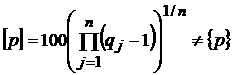В свою очередь, удобная для анализа роста энергопотребления величина  оказывается не связанной простым соотношением типа (12) с величиной , что, таким образом, лишает последнюю существенной  практической значимости. Еще одним недостатком величины  является то, что она определена только для монотонного поведения рассматриваемой величины, поскольку в противном случае операция извлечения корня может быть некорректной.

         В соответствии с определениями, принятыми в статистике, величину , определяемую выражением (10), будем называть математическим ожиданием (МО) прироста энергопотребления за год.

Соответственно, величину  назовем среднегодовым приростом (СГП) энергопотребления.

Подчеркнем, что именно величина  часто используется на практике. Дело в том, что наиболее распространенная и легко воспринимаемая характеристика динамики анализируемой величины (в данном случае – энергопотребления) – средний темп роста – понимается следующим образом: высказывание «в течение n лет средний прирост энергопотребления был равен p % » воспринимается в том смысле, что , как в формуле (7). Однако, как было показано выше, это выражение математически верно только тогда, когда в нем  и, соответственно, q = [q].

Поэтому в обзорах и прогнозах для удобства анализа изменения энергопотребления на промежутках времени в несколько лет используется

именно средняя величина [q] показателя роста энергопотребления. При этом, из соображений математического удобства и удобства восприятия, вместо [q] часто используется величина , определяемая, исходя из формулы (7), следующим образом:

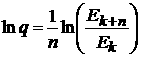                                         .                                        (13)

Как легко видеть из соотношения (6), при , близком к единице, . Если фактические значения ежегодных относительных приростов потребляемой энергии изменяются год от года не очень значительно (а именно такое поведение анализируемых в данной работе величин – мирового потребления энергии в целом и природного газа, в частности, – отмечалось в предыдущем параграфе), то СГП  {p} , определяемый на основании соотношений (11) – (13), может служить величиной, характеризующей процесс в среднем.

Введенные выше МО (10) и СГП (12) определены через величины, выраженные в процентах. В отдельных случаях бывает удобно пользоваться указанными математическими объектами, определяемыми не через проценты, а просто через безразмерные относительные величины. Будем таковые называть – МО или СГП в относительном выражении. А их численные выражения будут получаться делением «процентных» МО и СГП на 100.

Теперь, с учетом данных выше определений и если не оговаривается иное, будем в данной работе попросту отождествлять СГП в относительном выражении и .

Следует отметить, что для величин, рассматриваемых в данном анализе, отличия СГП от МО будут невелики. Так, например, расчет СГП потребления энергии во всех формах в мире за последние 25 лет по имеющимся статистическим данным, предоставляемым МЭ США [2] (Рис. 1, Табл. 3), дает величину 1,86 % в год (т.е. ). Расчет МО за тот же период наблюдения дает величину в 1,89 % в год. Разумеется, если потребление энергии будет меняться менее регулярно или появится частая смена тенденции (рост сменяется падением и наоборот), то СГП уже не будет иметь особого практического смысла, и тогда следует использовать менее удобную величину МО.

В дальнейшем будем пользоваться понятиями «базовый сценарий» и «базовый прогноз», определяемыми следующим образом. Будем называть «базовым» любой сценарий, в рамках которого предполагается, что некоторые показатели, используемые при прогнозировании, будучи вычисленными на дату составления прогноза, принимаются затем при составлении прогноза постоянными. Соответственно, прогноз, выполненный в рамках такого «базового сценария», будем называть «базовым прогнозом». Базовых сценариев подобного рода существует, разумеется, множество. Говоря об энергопотреблении, можно в качестве такого сценария принять, например, постоянство прироста потребления за последний год, СГП за два последних года и т.д., либо считать, как это и делается в рассматриваемых нами прогнозах, что постоянными являются величины годового прироста ВВП и иных экономических показателей.

Используя величину [q], определяемую соотношением (11), рассмотрим зависимость вида (7) на промежуточных годах, начиная с  и заканчивая :

                                    .                                     (14)

Очевидно, что, по определению величины [q], значения E, вычисляемые согласно (14), будут тождественно совпадать с фактическими значениями E за соответствующий год только в год . Продолжая зависимость (14) в будущее, т.е. за пределы рассматриваемого промежутка в n лет, получаем прогноз, который, дает оценку энергопотребления в предположении постоянства величины [q] на рассматриваемом расширенном интервале времени и который, согласно данному выше определению, можно назвать «базовым». Отметим, что на коротком промежутке времени степенная зависимость от j выглядит почти линейной, что связано с незначительным отличием основания [q] от единицы.

Полезно получить оценку СГП на основе линейного регрессионного анализа величины логарифма относительного прироста  (см. формулу (13)) в зависимости от года k. Такого рода оценка представляет интерес потому, что она позволяет показать, насколько результаты, выведенные чисто статистическими методами прогнозирования, отличаются от полученных в рамках экономико-математических моделей. Для построения регрессии по данным таблицы 2 численно определяются такие коэффициенты q и b, что прямая

                                             y(k) = lnq + klnb                                                   (15)

отстоит от значений  на наименьшее среднеквадратичное расстояние. Полагая затем = lnq + klnb и продолжая k за границу статистической выборки, получаем базовый прогноз в предположении постоянства параметров регрессии q и b.

Напомним (см., например, [5]), что если требуется связать случайную величину  и неслучайную величину линейной регрессионной зависимостью вида  по имеющимся N парам значений  методом наименьших квадратов, то      

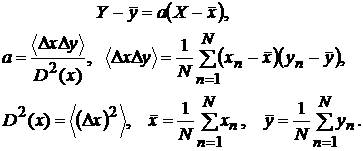                                             (16)

Прямолинейную зависимость для регрессии принято записывать в симметричном виде:

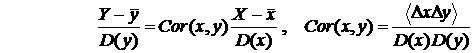     .               (17)

Для данных, приведенных в таблице 3 за период с 1980 по 2004 гг., расчеты приводят к следующей формуле:

            , где  r = 1,01484, b = 1,00028.                  (18)

В частности, если прогноз начинается с некоторого «первого» года, то

                                        .                                            (19)

Для данных, образующих другую статистическую базу (взятых за иной промежуток времени), значения r и b могут, разумеется, отличаться от приведенных в формуле (18).

         Смысл выражения (18) достаточно очевиден и заключается в том, что данное приближение содержит в себе допущение о монотонности изменения относительного прироста величины E. Имеется в виду следующее. Если b > 1, то относительный прирост величины E монотонно увеличивается по мере увеличения года k, а если b < 1, то, соответственно, – монотонно уменьшается. Для соотношения (18) b > 1, т.е. происходит увеличение относительного прироста. При этом, поскольку значение b очень близко к 1, указанное увеличение прироста (т.е. рост темпов роста) крайне незначительно.

         Модель (18), наряду с монотонностью изменения прогнозируемого показателя (СГП), характеризуется монотонностью изменения также и его производной, т.е. темпов изменения СГП. Более тонко настроенная статистическая модель может использовать, например, результаты корреляционного анализа, в случае, если между темпами изменения изучаемой величины за различные годы будет обнаружена статистическая связь (корреляция). Автокорреляционный анализ СГП для мирового потребления энергии будет проведен нами в заключительном разделе продолжения данной работы (Часть II).

Рассмотрим теперь динамику мирового потребления энергоресурсов. На графиках Рис. 1 и Рис. 2, наряду с фактическими значениями мирового потребления энергии в целом и природного газа, соответственно, приведены также прогнозы МЭ США и МЭА за 1996 г. для иллюстрации отличий как одного прогноза от другого, так и каждого из них от фактических данных. Оба прогноза начинаются с фактического значения энергопотребления в 1993 г. Значения в промежуточные годы между 1993 и 2005 получены интерполяцией по указанным в этих прогнозах значениям среднегодовых приростов.

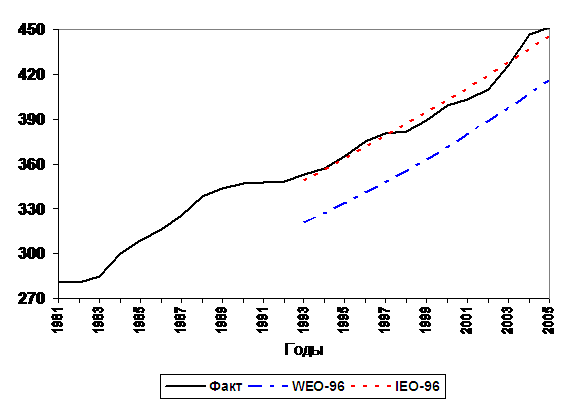
Рис. 1. Динамика спроса/потребления энергии в мире и прогнозы МЭА и МЭ США 1996 г., QBTU. Источники: [2, 3, 6, 11]

Отметим, что, фактические значения энергопотребления по данным МЭА и МЭ США различаются между собой. Это связано с тем, что при подсчете фактического потребления энергоресурсов до 1998 г. МЭА учитывались не все страны «третьего мира» (под «третьим миром» здесь понимается совокупность стран, которые не относятся ни к ОЭСР (Организация экономического сотрудничества и развития; OECD), ни к странам СНГ и Восточной Европы). Указанное различие связано также и с тем, что Агентством не учитывался вклад традиционной биомассы (древесина) по ряду стран, статистика по которым считалась недостоверной. Именно поэтому прогнозные кривые на Рис. 1 начинаются из разных точек (несовпадение исходных данных за 1993 г. составило 28,3 QBTU). Если устранить указанное изначальное расхождение (так сказать, «систематическую ошибку»), то в остальном прогнозы 1996 г. МЭ США и МЭА практически совпадают, т.к. графики идут приблизительно параллельно один другому. Отличие прогноза МЭА от МЭ США в трендах состоит в том, что прогнозная область в нем разбита на два периода – с 1993 г. по 2000 г. с темпом роста 2,08% в год и с 2000 г. по 2010 г. с темпом роста 2,35% в год, – тогда как в прогнозе МЭ США в течение всего периода с 1993 г. по 2010 г. идет линейный рост с одним и тем же темпом –2,02% в год.

Следует также отметить, что в обзорах МЭ США, представляемых в электронном виде на сайте Energy Information Administration [6], данные по потреблению энергии за уже прошедшие годы с течением времени подвергаются некоторой «коррекции» (см. Табл. 3), оставляемой в этих обзорах без комментариев. Поэтому исходные данные, взятые с сайта МЭ США и анализируемые в этой работе, могут с течением времени не совпасть с уже «скорректированными» данными того же самого источника. Это обстоятельство создает дополнительные трудности при оценивании точности прогноза, поскольку сами фактические значения приобретают неприятное свойство постфактум изменяться. Например, приведенный на графике Рис. 1 прогноз IEO-96 начинается с фактического значения за 1993 г., равного 349,1 QBTU [2], тогда как впоследствии в 2006 г. в [6] приводится значение 353,3 QBTU (см. также Табл. 4), вследствие чего первая (т.е. «фактическая») точка прогнозной кривой не лежит на кривой фактического энергопотребления, построенной по последним данным МЭ США. Данное замечание в полной мере уместно и в отношении сравнения прогнозов по газу (Рис. 2.)

Табл. 3. Сравнение данных МЭ США [6] по потреблению энергии в мире за разные годы, QBTU.

Наш статистический анализ будет основываться на данных фактического энергопотребления [6] за 2006 г., приведенных далее в Табл. 4, фрагмент которых представлен в последней строке Табл. 3.

Анализируя кривую фактических значений потребления энергии на Рис. 1, можно заметить, что на определенных временных участках (приблизительно с интервалом 5-7 лет) относительно быстрый рост  мирового потребления энергии сменяется кратковременным режимом насыщения (пологие участки), т.е. график на этих участках имеет вид S-образной линии. Насколько известно авторам, такой колебательный характер энергопотребления не отражен ни в одном долгосрочном прогнозе, выполненном до 2000-го года. Если это действительно так, то до 2000 г. при анализе мировой энергетики не применялись модели, которые давали бы прогнозы, содержащие, в том числе, указанные периодические колебания относительных годовых приростов.

Рассмотрим теперь динамику потребления природного газа в мире (Рис. 2, Табл. 4). На интервале с 1980 по 2005 гг. потребление природного газа росло с показателем СГП (11) 2,72 % в год, что выше соответствующего значения для общемирового потребления всех видов энергии в совокупности. Следует отметить, что если для расчета СГП пользоваться не точным выражением (11), а приближенным (13), то для СГП на данном интервале получается значение 2,68%. МО приростов потребления газа составило за тот же промежуток времени 2,74% в год. В силу близкого к линейному характера роста общемирового потребления газа все три вышеприведенных значения примерно одинаковы, однако следует помнить об их методологическом различии. Так, в случае рассмотрения величин с иным характером поведения во времени расхождение соответствующих значений СГП и МО может быть весьма существенным.

Как и в прогнозе потребления энергии (Рис. 1), прогноз МЭ США по газу дает на интервале с 1993 по 2005 гг. постоянный СГП, который с принятой точностью вычислений совпал с фактическим: 2,72%. В прогнозе МЭА СГП с 1993 по 2000 гг. равен 2,57%, а с 2000 по 2005 гг. – 3,10%.

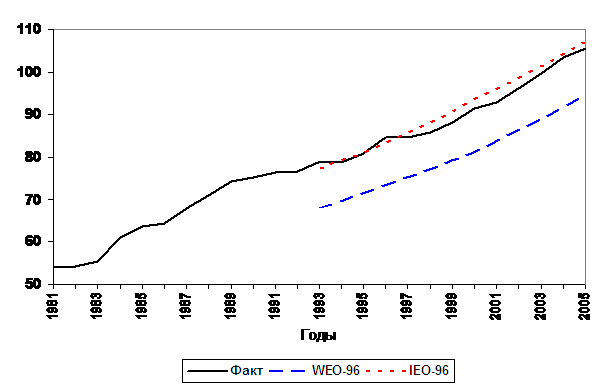
Рис. 2. Динамика спроса/потребления природного газа в мире и прогнозы МЭА и МЭ США 1996 г., QBTU . Источники: [2, 3, 7]

Далее мы сравним фактические данные (Табл. 4) общемирового потребления энергии в совокупности и, отдельно, природного газа, с серией прогнозов, сделанных за 12-летний период (с 1993 г. по 2004 г.) МЭ США и МЭА на годы, соответственно, с 1994 по 2005. Отметим, что прогнозы МЭА [3] выражены в тоннах нефтяного эквивалента (т н.э.). Для единообразия мы переведем их в BTU согласно соотношению, принятому в обзорах МЭА [8]: 1 млн. т н.э. = 0,0397 QBTU. Строго говоря, переводной коэффициент BTU в т н.э. не постоянен, а меняется по годам, что связано с различной калорийностью добываемой в каждый конкретный год нефти, но на данном этапе анализа этим различием считаем возможным пренебречь.

Коэффициент перевода между объемными единицами природного газа и массовыми единицами нефтяного эквивалента устанавливается на основе принципа равенства тепловых эквивалентов (т.е. сравниваются количества вещества, обладающие равным теплосодержанием). В МЭ США принят следующий коэффициент перевода [9]: 1027 BTU/куб. фут газа, что соответствует коэффициенту 0,85 т н.э./тыс. м³ газа.

Необходимо отметить, что в МЭА аналогичный коэффициент (т н.э./тыс. м³; определялся авторами настоящей статьи расчетным путем  по данным соответствующих таблиц обзора МЭА) не выдерживается постоянным внутри одного и того же обзора даже для одной группы стран (см., например, WEO-2004, с.130 и с.430, 434, 470 и 478) и варьируется от 0,793 т н.э./тыс. м³ до 0,866 т н.э./тыс. м³, со средним значением 0,837. Таким образом, отклонение указанного коэффициента перевода от среднего значения достигает 5%. Возможно, что это расхождение связано с различной калорийностью добываемой в разных регионах нефти, но понятие «нефтяной эквивалент» в мировых прогнозах не имеет региональных различий, во всяком случае, в прогнозах [3] такого указания не делается. Поэтому приходится воспринимать непостоянство коэффициента перевода как случайную ошибку данных, и при статистическом анализе прогнозов МЭА следовало бы учитывать, что точность исходных данных в них, в силу вышеуказанных причин, имеет некоторое дополнительное среднеквадратичное отклонение. Однако на данном этапе анализа мы этого для простоты делать не будем.

Табл. 4. Мировое потребление природного газа и энергии в целом, QBTU. Источники: [6, 7, 10, 11]

*Данные за 2005 г. взяты: по газу – из пресс-конференции руководства  ОАО «Газпром» [10] со ссылкой на Cedigaz, а по энергии в целом – из данных МЭА к обзору World Energy Outlook 2006 [11].

Далее мы кратко охарактеризуем прогнозные системы МЭ США и МЭА, а в Части II проведем подробное сравнение прогнозов, выполненных этими организациями.

3. Прогнозные системы МЭ США и МЭА

Кратко опишем методические особенности моделей, которые используются для прогнозирования в МЭ США и МЭА.

Прогнозы МЭ США до 1996 г. осуществлялись на основе так называемой Прогнозной системы мировой энергетики (World Energy Projection System, WEPS) [2], в которой внешними (экзогенными) параметрами являлись показатели экономического и демографического роста по отдельным странам, которые, в свою очередь, также являлись результатом прогнозирования. Эти показатели моделировались независимо от энергетического блока, что, строго говоря, неверно, особенно для целей долгосрочного прогнозирования. При определении трендов регионального, а также и мирового спроса на отдельные виды энергоресурсов полагалась линейной зависимость между относительным приращением соответствующего потребления энергии E и ВВП G с коэффициентом эластичности (пропорциональности) a:

                                          .                                                   (21)

Соотношение (21) можно записать также в форме линейной зависимости между логарифмическими производными (здесь – дифференциалами) энергопотребления и ВВП:

                                     dlnE = a dlnG.                                                   (22)

В указанных соотношениях (21) и (22) коэффициент эластичности a является функцией времени, а точнее – года, поскольку здесь мы имеем дело со среднегодовыми величинами E и G, а значит – и с такими величинами a, которые также можно называть среднегодовыми.

Для определения зависимости коэффициента эластичности a от времени в [2] использовались модели регрессионного анализа (по типу приведенных выше формул (16)). При этом по известным фактическим значениям E и G определялись соответствующие значения a, которые затем с помощью упомянутого регрессионного соотношения экстраполировались в будущее и использовались в соотношении (21).

Например, в прогнозе МЭ США 1995 г. приводятся следующие значения для эластичности в зависимости от года: a(1990) = 0,78 (расчет по фактическим данным); a(1995) = 0,94 (расчет на основе экстраполяции данных, учитываемых до 1993 г.); a(2000) = 0,55 (сценарное значение, принятое авторами прогноза).

Прогнозные цены на энергоносители и объемы их поставок по регионам мира моделировались в этой системе на основе принципа минимизации транспортных расходов для стран-поставщиков. Конкуренция между видами топлив моделировалась в предположении линейной связи между спросом и ценой единицы теплосодержания для каждого топлива на основе принципа минимизации затрат для стран-покупателей.

Отметим некоторые ограничения такого подхода. Во-первых, в модели WEPS не учитывается обратное влияние рынка на сферу добычи, поскольку темпы роста производства первичных ТЭР задаются в ней независимо от темпов потребления. Вместе с тем, именно от потребления зависит объем приобретаемых энергетических ресурсов, а значит и связанный с этим объем финансовых средств, поступающих в сферу энергетики и формирующих инвестиционный ресурс, который, в свою очередь, затем направляется в сферу добычи, в значительной мере определяя ее объем. Во-вторых, не вполне корректным является предположение о том, что как только какой-то ресурс становится дешевле из расчета калорийности, то потребители сразу же переключаются на использование именно его (словно они имеют у себя технические средства сжигания всех топлив в любом количестве). А именно это неявно предполагается в моделях линейной связи в один и тот же момент времени между ценой и спросом на продукт.

В 1996 г. система WEPS была дополнена блоком «Национальной системы моделирования энергетики» (National Energy Modeling System, NEMS) [2], в котором делаются прогнозы мирового потребления нефти и развития мировой ядерной энергетики. В 2003 г. система была еще раз модифицирована в части моделирования цен на энергоносители и стала называться «Система анализа глобальных энергетических рынков» (SAGE). Математическая модель системы SAGE изложена весьма подробно в приложении к обзору [2] за 2005 г., содержащему ряд прогнозов с характеристикой моделей, использовавшихся для их получения. Указанная модель включает в себя описание энергосистемы по секторам деятельности и рынкам энергоресурсов отдельных крупных государств в рамках эконометрических моделей, которые комбинируются с «технологическими» моделями функционирования отдельных отраслей (т.е. моделями, содержащими более детализированное – по сравнению с эконометрикой – описание, учитывающее наличие различных технологий потребления энергоресурсов). При описании отраслей используются различные производственные функции, позволяющие определить энергоемкость производимого отраслями продукта. Использование производственных функций за пределами периода, для которого они были определены, является некоторой прогнозной гипотезой, от справедливости которой зависит и точность самого прогноза. Состояние отрасли в этих моделях изменяется с учетом того, что согласно имеющимся официальным данным (в предположении выполнения принятых официальных решений) запланировано выведение из эксплуатации в рассматриваемом секторе части промышленных объектов, а также ввод ряда объектов в эксплуатацию.

Данные прогнозов приводятся в [2] с интервалами в пять лет, внутри которых тренды (т.е. СГП за каждые пять лет, рассчитываемые по формуле (13)), предполагаются постоянными.

Мы будем анализировать только базовые варианты прогнозов. Отметим, что МЭА и МЭ США в своих обзорах также анализируют точность прогноза именно по базовому варианту.

Повышенный и пониженный варианты отличаются от базового тем, что при заданных коэффициентах эластичности a в формулах вида (21) предполагается больший или, соответственно, меньший экономический рост. Так, например, в прогнозе IEO-2000 средний рост ВВП в мире с 1997 по 2020 г. предполагается равным 2,8% в базовом варианте, 4,0% – в повышенном варианте и 1,5% – в пониженном. При этом энергопотребление в 2020 г. в пониженном сценарии составляет 496 QBTU, а в повышенном – 722×QBTU.

Рассмотрим базовый вариант прогнозов МЭ США (Табл. 5). В этой таблице мы приводим (округленные) прогнозные значения потребления энергии в мире по годам с интервалом в 5 лет, следуя [2]. Как видно из таблицы, соответствующие прогнозы ежегодно делались в течение 12 лет с 1993-го по 2004 годы.

Табл. 5. Данные прогнозов МЭ США мирового потребления энергии, QBTU. Базовый сценарий. Источник: [2]

* Примечание: данные IEO-93 взяты из раздела «Сравнение прогнозов» в обзоре IEO-94, где они приведены в млн баррелей нефтяного эквивалента (б н.э.) в день. При пересчете данных IEO-93 в QBTU здесь, во-первых, используется соотношение 1 б н.э./день = 49,64 т н.э./год. А, во-вторых, учитывается тот факт, что коэффициент перевода в BTU в обзоре IEO-94 отличается от принятого в последующие годы и равняется 0,0411 QBTU/млн т н.э.

Проведем качественный анализ прогнозов, представленных в Табл. 5, сравнивая их с данными Табл. 4 фактического энергопотребления. Детальный количественный анализ будет проведен в следующей работе (Часть II). Для базовых прогнозов МЭ США можно отметить завышение величины энергопотребления по сравнению с фактическими значениями для прогнозов на 2000-й год и, напротив, – занижение для большинства прогнозов на 2005 г. Это может быть связано с ошибкой экстраполяции на основе текущих трендов и с отсутствием учета последующего колебательного характера темпов роста, о чем говорилось выше. Например, причиной резкого снижения в 1999 г. уровня прогнозных значений энергопотребления на ряд лет с 2000 по 2025 послужили, в первую очередь, экономический кризис в Юго-Восточной Азии 1997 года и дефолт банковской системы России в 1998 году.

Обратимся теперь к прогнозам МЭА [3] (Табл. 6), построенным на базе прогнозной системы «Модель мировой энергетики» (World Energy Model, WEM). В скобках мы приводим данные этих прогнозов в исходных единицах – млн т н.э.

Табл. 6. Данные прогнозов МЭА мирового спроса на энергию, QBTU (млн т н.э.). Базовый сценарий. Источник: [3]

Примечание: данные * получены интерполяцией по СГП, рассчитанному для самого короткого временного промежутка, содержащего данный год, конечные точки которого (промежутка) отражены в прогнозе; в прогнозе WEO-2002 даны прогнозные значения на 2010 и 2030 гг.

** Данные WEO-93 взяты из раздела «Сравнение прогнозов» в обзоре IEO-94, где они приведены в млн баррелей нефтяного эквивалента в день.

В прогнозной системе WEM [3] энергопотребление рассчитывается отдельно для каждого из следующих государств и регионов мира (сохранены используемые авторами модели географическое деление и названия регионов): США и Канада; Мексика, Бразилия, остальные страны Латинской Америки; страны Евросоюза (Евросоюз рассматривается в трех вариантах: ЕС-15, ЕС-25 и ЕС-30, причем последний вариант ЕС включает в себя 5 стран, не являющихся членами ЕС в настоящее время), прочие страны Европы с переходной экономикой (эта группа стран, разумеется, также рассматривается в трех вариантах, соответственно тому или иному рассматриваемому варианту ЕС); Россия; Индия, остальные страны Южной Азии, Средний Восток, Япония, Южная Корея, Китай, Индонезия, остальные страны Восточной Азии; Австралия и Новая Зеландия; Африка; остальные страны ОЭСР.

Математическая модель системы WEM содержит пять основных блоков для каждого из рассматриваемых в ней регионов мира: блока энергопотребления, блока производства электроэнергии, блока переработки топлив, блока транспорта углеводородов и блока эмиссии парниковых газов. Экзогенными параметрами для них являются внутренние цены на энергоносители по странам, темпы роста населения, темпы роста ВВП и темпы развития технологий. Первые три блока (энергопотребления, производства электроэнергии и переработки топлив) взаимосвязаны и определяют спрос на топливо, являющийся входной информацией для транспортного блока, в котором, в свою очередь, решается задача определения объемов поставок топлив и цен на них, причем таких, которые бы соответствовали расчетам в первых трех блоках. В блоке эмиссии парниковых газов по рассчитанным величинам энергопотребления определяются выбросы CO2 и других соединений (окислов азота и серы), что позволяет определять затраты на экологические мероприятия.

С экономико-географической точки зрения в модели WEM страны делятся на две группы: страны ОЭСР и остальной мир. Энергетический сектор стран ОЭСР описывается детально, с подразделением на под-сектора (промышленность, энергетика, транспорт, бытовое потребление, коммерческий сектор) и на крупные отрасли в самих под-секторах. В этих странах спрос на энергоносители определяется из решения динамических уравнений относительно цен на различные виды топлива и объемов поставок (потребления). Цены  на топливо и объемы  потребления как функции времени моделируются для каждой отрасли в под-секторе системой уравнений вида

                                             ,                          (23)

где F и f – заданные «модельные» функции, а x – набор прочих экзогенных величин, входящих в систему в качестве параметров. Можно также отметить, что почти все страны этой группы являются крупными импортерами энергоресурсов.

Энергетика остальных стран рассматривается более укрупненно, причем для каждой из них энергопотребление прогнозируется на основе трендового подхода по формулам вида (21) в рамках некоторого сценария экономического роста (повышенного, пониженного или базового).

Прогноз энергопотребления для индустриально развитых стран, рынок энергоресурсов которых образован как внутренним производством, так и импортом, составляется с учетом конкуренции всех видов топлива на внутреннем рынке и с учетом особенностей местного законодательства (эти «особенности» при математическом моделировании находят свое выражение в появлении определенных ограничений на множестве возможных решений системы уравнений (23)).

Моделирование спроса по каждому виду топлива опирается на деление всех вышеуказанных регионов мира на две группы: нетто-импортеры и нетто-экспортеры. Нетто-экспортеры конкурируют между собой за поставки энергоресурса странам-импортерам, с учетом того, что емкость рынка последних уменьшается на величину, покрываемую их собственным производством.

Отметим, что детализация рыночных отношений через посредство моделирования спроса и цен на энергоносители имеет и свои недостатки, обусловленные прежде всего сложностью реальных рыночных процессов, для которых оказывается трудным найти адекватное описание даже с помощью такого более изощренного по сравнению с эконометрическими моделями инструмента, каковым является система эволюционных уравнений вида (23). Другие величины, входящие в эти уравнения как параметры (такие, как эластичность спроса на топливо по его цене для разных видов ресурсов или связь между удельными энергозатратами на доллар ВВП и на человека в год), определяются в модели по различным эконометрическим зависимостям на основе данных за период с 1970 г. Надо сказать, что выбор модельных функций (23) для среднесрочных прогнозов (на 10-15 лет) не сильно сказывается на точности прогнозирования, в отличие от предположений о трендах экзогенных величин, чувствительность прогноза по которым очень велика, что отмечается в [3] и самими авторами этой прогнозной системы.

В следующей Части II мы проведем систематическое сравнение рассмотренных прогнозных систем на основе методологии, описанной в разделе 1 данной работы (Части I). Это, полагаем, позволит математически корректно охарактеризовать точность прогнозных систем двух рассматриваемых организаций на достаточно большом отрезке времени.

В заключение данной работы еще раз отметим выявленные нами в статистических обзорах МЭ США и МЭА искажения неслучайной природы, которые, не будучи объясненными, могут трактоваться как случайный фактор, увеличивающий неточность либо фактических данных, либо прогнозных величин. Для МЭ США – это «флуктуации» с течением времени фактических данных в размещенных на соответствующих сайтах электронных версиях обзоров Министерства, тогда как они по своему смыслу должны быть «намертво заморожены» после того, как год состоялся. Для МЭА – это непостоянство тепловых эквивалентов в соседних графах одной и той же таблицы данных по мировому энергопотреблению, чему авторы данной работы также не смогли найти рационального объяснения. Оценка влияния указанных искажений будет приведена нами в следующей работе.

Источники

1. International Energy Agency. World Energy Outlook 2004, p. 524.

2. International Energy Outlook. DOE/EIA-0484.

/ http://tonto.eia.doe.gov/reports/reportsD.asp?type=International

3. International Energy Agency. World Energy Outlook. / www.iea.org

4. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1972.

5. Кремер Н.Ш., Путко Б.А. Эконометрика. М.: ЮНИТИ-ДАНА, 2002.

6. Energy Information Administration. International Energy Annual, July 2004.

http://www.eia.doe.gov/pub/international/iealf/table18.xls

7. EIA – International Total Primary Energy Consumption and Energy Intensity Data. / http://www.eia.doe.gov/emeu/international/energyconsumption.html

8. Конвертер МЭА. / www.iea.org/Textbase/stats/defs/defs.htm

9. Calculators for Energy Used in the United States. / http://www.eia.doe.gov/kids/energyfacts/science/energy_calculator.html#oilcalc

10. Справочные материалы. / http://www.gazprom.ru/articles/article20350.shtml

11. World Energy Outlook 2006. Key graphics. / http://www.worldenergyoutlook.org/graphics.htm