Аннотация
Рассмотрены разрывные течения в двухжидкостной электромагнитной гидродинамике (ДЖЭМГД) плазмы.
Выведены соотношения, связывающие параметры плазмы по разные стороны от разрыва, получены
уравнения ударной адиабаты и формулы разрешения соотношений на разрыве. Исследованы ограничения,
налагаемые на параметры плазмы перед фронтом ударной волны, условием возрастания энтропии
электронов и ионов на разрыве. Показано наличие в ДЖЭМГД ударных волн как сжатия, так и
разрежения. Для существования последних получено легко проверяемое необходимое и достаточное
условие.
Abstract
Discontinuous currents in two-fluid electromagnetic hydrodynamics (TFEMHD) plasma are considered.
Equations for plasma parameters on different sides of discontinuity surface and shock adiabatic
equations are derived. Restrictions on plasma parameters behind shock wave surface due to law
of entropy growth with discontinuity surface are investigated. The existence of rarefaction
shock waves in TFEMHD is shown and the simple necassary and sufficient conditions for one's are
indicated.
В [1
, 2] была предложена гидродинамическая модель двухкомпонентной нерелятивистской
полностью ионизованной плазмы, которая, являясь формально одножидкостной,
позволяет исследовать двухжидкостные эффекты коллективного течения электронов и
ионов. В ней в полном объеме учтена инерция электронов. Она получается
математически корректной процедурой из уравнений общей теории относительности
(ОТО) и составляет основу теории двухжидкостной электромагнитной
гидродинамики (ДЖЭМГД, или ЭМГД) плазмы. Для бездиссипативной плазмы ДЖЭМГД
– уравнения имеют вид [2]:
(а) 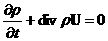 , (б) , (б) 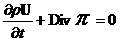 , ,
(в) 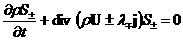 , , 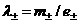 , ,
(1)
(г) 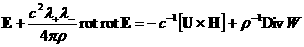 , ,
(д) 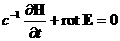 , (е) , (е)
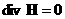 , (ж) , (ж)
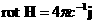 , ,
где 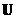 – массовая скорость
плазмы, – массовая скорость
плазмы, 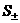 – плотности энтропии
электронов и ионов, а тензоры внутренних напряжений – плотности энтропии
электронов и ионов, а тензоры внутренних напряжений 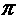 и электродинамического
состояния и электродинамического
состояния 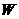 вычисляются по
формулам: вычисляются по
формулам:
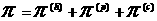 , , 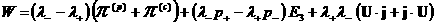
(2)
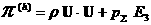 , , 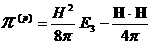 , , 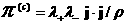 , , 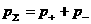
Система (1) и (2) дополняется уравнениями состояния
электронов и ионов, подчиняющихся второму закону термодинамики:
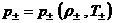 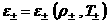
(3)
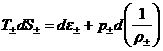
По решению системы
(1) ÷ (3) вычисляются скорости и плотности электронов и ионов:
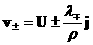 , , 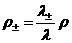 , , 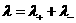 (4) (4)
Уравнения (1) ÷ (3) допускают разрывные
решения. Например, в [3] исследовалось разрывное течение цилиндрического
плазменного шнура. В этой работе
выведены соотношения, связывающие параметры течения по разные стороны от
разрыва. В отличие от МГД – теории, магнитное поле на ЭМГД – разрывах
непрерывно, в частности, отсутствуют поверхностные токи. Это принципиальный момент теории разрывных
течений, приводящий к кардинально различным соотношениям на разрыве в МГД и
ДЖЭМГД. Причина этого в том, что в ДЖЭМГД, в отличие от МГД, плотность
электрического тока 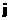 связана с плотностями и скоростями плазменных
компонент, связана с плотностями и скоростями плазменных
компонент, 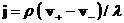 . Поэтому допущение о наличии поверхностных токов в ДЖЭМГД с
неизбежностью приведет, в силу (4), к существованию поверхностных течений
электронов и ионов с конечным импульсом. Однако наличие таких течений, с одной
стороны, противоречит физическим представлениям о сплошных средах, а, с другой,
– ведет к нарушению обычных гидродинамических условий Гюгонио на разрыве
(скажем, наличие поверхностной плотности влечет нарушение закона сохранения
импульса на поверхности разрыва и т. д.). . Поэтому допущение о наличии поверхностных токов в ДЖЭМГД с
неизбежностью приведет, в силу (4), к существованию поверхностных течений
электронов и ионов с конечным импульсом. Однако наличие таких течений, с одной
стороны, противоречит физическим представлениям о сплошных средах, а, с другой,
– ведет к нарушению обычных гидродинамических условий Гюгонио на разрыве
(скажем, наличие поверхностной плотности влечет нарушение закона сохранения
импульса на поверхности разрыва и т. д.).
На
поверхности разрыва нормальная компонента плотности тока 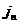 непрерывна, иначе на
ней будет накапливаться заряд. В работе выведены четыре соотношения,
связывающие значения непрерывна, иначе на
ней будет накапливаться заряд. В работе выведены четыре соотношения,
связывающие значения 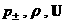 по разные стороны от
поверхности разрыва, а также по разные стороны от
поверхности разрыва, а также 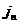 и нормальную скорость движения поверхности
разрыва и нормальную скорость движения поверхности
разрыва 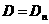 . В итоге десять величин будут связаны четырьмя уравнениями.
Поэтому фиксация любых шести из них позволяет в принципе найти четыре
оставшиеся. Из возникающих . В итоге десять величин будут связаны четырьмя уравнениями.
Поэтому фиксация любых шести из них позволяет в принципе найти четыре
оставшиеся. Из возникающих 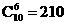 возможных задач в
работе решена лишь одна: зная возможных задач в
работе решена лишь одна: зная 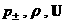 по одну сторону от
поверхности разрыва, а также по одну сторону от
поверхности разрыва, а также 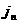 и и 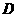 , найти , найти 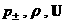 по другую сторону разрыва.
Явные формулы в этой задаче получены для случая, когда электроны и ионы
являются идеальными политропными газами (или газами с двучленным уравнением
состояния [4]) с общим показателем адиабаты, а также для изотермического газа. по другую сторону разрыва.
Явные формулы в этой задаче получены для случая, когда электроны и ионы
являются идеальными политропными газами (или газами с двучленным уравнением
состояния [4]) с общим показателем адиабаты, а также для изотермического газа.
В работе
получено уравнение ударной адиабаты, связывающей термодинамические параметры
плазмы по разные стороны от разрыва. Поскольку в ДЖЭМГД независимых
термодинамических параметров на 1 больше чем в газовой или магнитной
гидродинамике (например 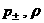 ) , то ударная адиабата состоит из пары уравнений,
позволяющих по известным термодинамическим параметрам по одну сторону от
разрыва и какому – нибудь термодинамическому параметру по другую сторону
восстановить оставшиеся термодинамические параметры. ) , то ударная адиабата состоит из пары уравнений,
позволяющих по известным термодинамическим параметрам по одну сторону от
разрыва и какому – нибудь термодинамическому параметру по другую сторону
восстановить оставшиеся термодинамические параметры.
Наконец, в
работе рассмотрено условие устойчивости разрыва, состоящее в возрастании
энтропии электронов и ионов при пересечении ими фронта ударной волны. Это
условие нарушает симметрию сторон разрыва и приводит к дополнительным
ограничениям на параметры плазмы перед фронтом ударной волны, которые выделяют
на плоскость 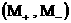 , где , где 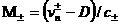 – числа Маха, – числа Маха, 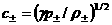 – звуковые скорости
компонент плазмы, некоторую найденную в работе область. Анализ этой области
показывает, что в двухжидкостной плазме, в отличие от одножидкостной (МГД),
возможны ударные волны как сжатия, так и
разрежения. В последнем случае плотность плазмы и давления компонент за фронтом
ударной волны меньше, чем перед фронтом. Такие ударные волны возможны, если
электроны и ионы пересекают фронт ударной волны в противоположных направлениях
и определяются отношением температур – звуковые скорости
компонент плазмы, некоторую найденную в работе область. Анализ этой области
показывает, что в двухжидкостной плазме, в отличие от одножидкостной (МГД),
возможны ударные волны как сжатия, так и
разрежения. В последнем случае плотность плазмы и давления компонент за фронтом
ударной волны меньше, чем перед фронтом. Такие ударные волны возможны, если
электроны и ионы пересекают фронт ударной волны в противоположных направлениях
и определяются отношением температур 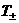 ионов и электронов
перед фронтом. В работе показано, что для существования ударных волн разрежения
необходимо и достаточно выполнения условий: ионов и электронов
перед фронтом. В работе показано, что для существования ударных волн разрежения
необходимо и достаточно выполнения условий:
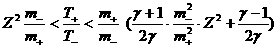 , ,
где 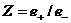 – кратность заряда
ионов. В частности, ударные волны разрежения отсутствуют только в сильно
неизотермической плазме. – кратность заряда
ионов. В частности, ударные волны разрежения отсутствуют только в сильно
неизотермической плазме.
МГД –
предел соответствует переходу 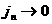 . При этом полученные в работе соотношения на разрыве
переходят в известные из газовой динамики условия Гюгонио, совпадающие с МГД –
соотношениями на разрыве в случае непрерывности магнитного поля на поверхности
разрыва. При . При этом полученные в работе соотношения на разрыве
переходят в известные из газовой динамики условия Гюгонио, совпадающие с МГД –
соотношениями на разрыве в случае непрерывности магнитного поля на поверхности
разрыва. При 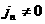 выведенные соотношения
на разрыве значительно ближе к газодинамическим, чем аналогичные соотношения в
МГД, однако построение конкретных разрывных течений сильно осложняется
отсутствием в ДЖЭМГД автомодельных решений. выведенные соотношения
на разрыве значительно ближе к газодинамическим, чем аналогичные соотношения в
МГД, однако построение конкретных разрывных течений сильно осложняется
отсутствием в ДЖЭМГД автомодельных решений.
Авторы признательны К.В.Брушлинскому, В.В.Савельеву, А.Н.Козлову за обсуждение
различных аспектов двухжидкостной плазмодинамики, а также РФФИ за финансовую
поддержку работы.
§ 1. Интегральные законы сохранения в ДЖЭМГД.
Как уже говорилось, в ДЖЭМГД существуют
разрывные течения, параметры которых претерпевают скачок на некоторой подвижной
поверхности, а вне её удовлетворяют уравнениям ДЖЭМГД. Наша цель – найти связь
между параметрами течения по разные стороны от поверхности разрыва. Для этого
перепишем уравнения ДЖЭМГД в интегральной форме и расширим понятие решения,
потребовав от обобщенного решения
обращения в тождество ДЖЭМГД – уравнений,
записанных в интегральном виде.
Для
реализации первой части этого плана перепишем, используя (1. д, е, ж), уравнение (1. г) в дивергентном
виде:
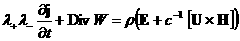 (1.г´) (1.г´)
и учтем, что на решении системы (1) выполнен закон сохранения энергии
[2]:
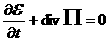 , (1,з) , (1,з)
где
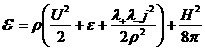
объемная плотность полной энергии плазмы, а
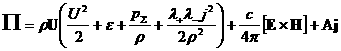
поток энергии. Выражения для объемной плотности
внутренней энергии 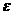 и плотности и плотности 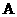 имеют вид: имеют вид:
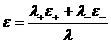
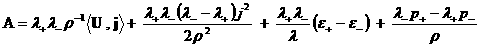
Уравнения 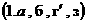 однотипные и имеют
вид: однотипные и имеют
вид:
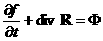 .
(5) .
(5)
Рассмотрим 3
– форму в
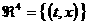
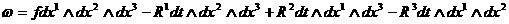  . .
и следующие условия:
 * для любой области * для любой области 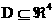 с кусочно–гладкой границей выполнено
равенство: с кусочно–гладкой границей выполнено
равенство:
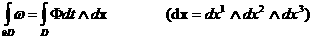 (5') (5')
*
для любой области 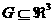 с кусочно–гладкой
границей и любых с кусочно–гладкой
границей и любых 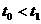 выполнено
равенство: выполнено
равенство:
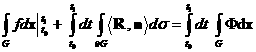 (5'')
(5'')
где  – единичная внешняя нормаль к – единичная внешняя нормаль к 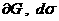 – элемент объема на – элемент объема на 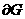 . Для . Для 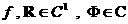 условия (5), (5'), (5'') эквивалентны, что вытекает из формулы Стокса
и равенства: условия (5), (5'), (5'') эквивалентны, что вытекает из формулы Стокса
и равенства:
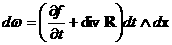 . .
Для негладких 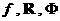 условие (5) теряет
смысл, а (5') равносильно (5''): условие (5'') получается из (5') для условие (5) теряет
смысл, а (5') равносильно (5''): условие (5'') получается из (5') для 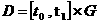 . .
Далее, рассмотрим 2–форму в 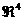 : :
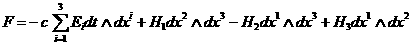 . .
Для 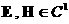 уравнения (1. д , е)
равносильны равенству: уравнения (1. д , е)
равносильны равенству:
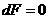 ,
(6) ,
(6)
которое, согласно формуле Стокса, дает для любой
трехмерной поверхности 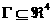 с кусочно–гладкой
границей тождество: с кусочно–гладкой
границей тождество:
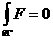 (6´)
(6´)

Если 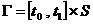 , где , где 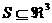 двумерная поверхность
с кусочно–гладкой границей, то (6') переходит в равенство: двумерная поверхность
с кусочно–гладкой границей, то (6') переходит в равенство:
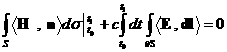 , (6'') , (6'')
ٰкоторое обычно переписывают в виде закона
Фарадея:
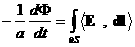 , , 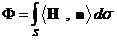 . .
Величина 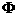 называется магнитным
потоком через поверхность называется магнитным
потоком через поверхность 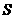 . .
Для 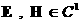 условия (6) и (6')
эквивалентны, а для негладких условия (6) и (6')
эквивалентны, а для негладких 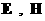 условие (6) теряет
смысл, а (6´) условие (6) теряет
смысл, а (6´)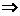 (6´´), хотя обратное неверно. (6´´), хотя обратное неверно.
Наконец,
для получения интегральной формы (1.ж) рассмотрим 1– и 2– формы в 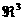 , зависящие от , зависящие от 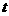 как от параметра: как от параметра:
 , , 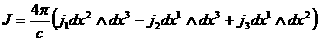
Для 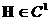 уравнение (1.ж)
равносильно равенству: уравнение (1.ж)
равносильно равенству:
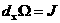 (7) (7)
справедливому в каждый момент времени, где индекс  указывает, что внешний дифференциал действует в указывает, что внешний дифференциал действует в 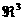 . Согласно формуле Стокса для любой двумерной поверхности . Согласно формуле Стокса для любой двумерной поверхности 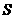 с кусочно – гладкой
границей условие (7) дает равенство: с кусочно – гладкой
границей условие (7) дает равенство:
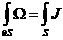 ,
(7') ,
(7')
которое
равносильно соотношению (закон
Ампера):
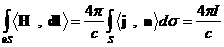 , , 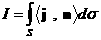 , (7'') , (7'')
а величина 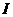 называется полным
током , протекающим через поверхность называется полным
током , протекающим через поверхность 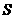 . Для . Для 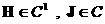 условия (7) и (7')
эквивалентны. Для негладких полей условие (7) теряет смысл. условия (7) и (7')
эквивалентны. Для негладких полей условие (7) теряет смысл.
Физические
законы постулируют соотношения (5'') ÷ (7''). Поэтому для определения
негладкого обобщенного решения воспользуемся интегральными соотношениями (5')
÷ (7').
Определение
1. Обобщенным решением
системы (1) ÷ (3) называются функции 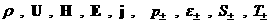 для которых найдется гладкая гиперповерхность для которых найдется гладкая гиперповерхность
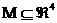 удовлетворяющая
условиям: удовлетворяющая
условиям:
1) в 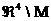 все перечисленные
функции непрерывно дифференцируемы и удовлетворяют системе (1)
÷ (3) а на все перечисленные
функции непрерывно дифференцируемы и удовлетворяют системе (1)
÷ (3) а на 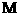 имеют разрыв
1–го рода имеют разрыв
1–го рода
2) для любой области 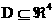 с кусочно – гладкой
границей имеют место равенства: с кусочно – гладкой
границей имеют место равенства:
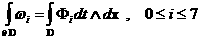 , ,
где
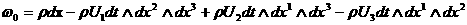 , ,
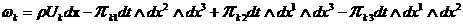 , ,
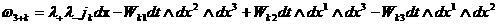 , ,
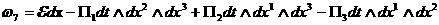
 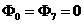  
  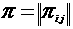 , , 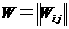 – компоненты тензоров – компоненты тензоров 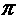 и и 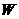 в декартовых
координатах, в декартовых
координатах,
3) для
любой трехмерной поверхности 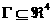 и двумерной
поверхности и двумерной
поверхности 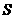 с кусочно –
гладкими границами выполнены соотношения: с кусочно –
гладкими границами выполнены соотношения:
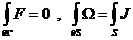 (9) (9)
где 2 – формы 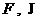 и 1 – форма и 1 – форма
 определены выше. определены выше.
В число интегральных законов (8), (9) не
входят интегральные соотношения, получаемые из закона сохранения энтропии
(1.в), поскольку энтропия единичной масс плазмы 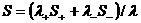 , как и энтропии
компонент , как и энтропии
компонент 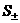 , при переходе через
поверхность разрыва не сохраняются (ибо поверхность разрыва формализует узкий
диссипативный – вязкий, теплопроводный и т.д. – слой, в котором энтропия
возрастает). Сохраняется только полная энергия , при переходе через
поверхность разрыва не сохраняются (ибо поверхность разрыва формализует узкий
диссипативный – вязкий, теплопроводный и т.д. – слой, в котором энтропия
возрастает). Сохраняется только полная энергия 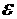 плазмы. При соблюдении
законов (8), (9) вне поверхности плазмы. При соблюдении
законов (8), (9) вне поверхности 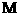 будут иметь место все
законы сохранения (1), кроме (1,в), и закон (1,з). Закон сохранения энергии
(1,з) является следствием уравнений (1), однако из (1,з) энтропийные уравнения (1,в) не вытекают.
Поэтому в определении обобщенного решения мы требовали справедливости уравнений
(1) ÷ (3) вне будут иметь место все
законы сохранения (1), кроме (1,в), и закон (1,з). Закон сохранения энергии
(1,з) является следствием уравнений (1), однако из (1,з) энтропийные уравнения (1,в) не вытекают.
Поэтому в определении обобщенного решения мы требовали справедливости уравнений
(1) ÷ (3) вне  , хотя это требование иэбыточное, и можно, например, считать,
что вне , хотя это требование иэбыточное, и можно, например, считать,
что вне 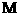 выполнены только уравнения (1,в) (или даже одно из них). выполнены только уравнения (1,в) (или даже одно из них).
§2.
Соотношения на разрыве.
Наша цель – получить соотношения между
предельными значениями параметров плазмы на поверхности разрыва 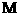 для произвольного
обобщенного решения системы (1) ÷ (3). Эти соотношения основаны на теореме,
доказанной в [5]. Для ее формулировки
введем следующие понятия. Пусть для произвольного
обобщенного решения системы (1) ÷ (3). Эти соотношения основаны на теореме,
доказанной в [5]. Для ее формулировки
введем следующие понятия. Пусть 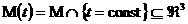 – двумерная
поверхность, – двумерная
поверхность,  – единичная нормаль
к – единичная нормаль
к 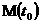 в точке в точке 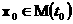 . Рассмотрим пересечение прямой . Рассмотрим пересечение прямой 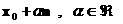 с с  и пусть и пусть 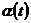 – наименьшее по
модулю – наименьшее по
модулю 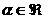 , для которого , для которого 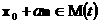 . .
Определение 2. Величина 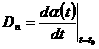 называется нормальной скоростью
движения поверхности называется нормальной скоростью
движения поверхности  в момент времени в момент времени 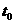 в точке в точке 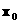 на этой поверхности в направлении на этой поверхности в направлении  . .
Пусть, например, 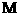 задается уравнением задается уравнением 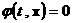 , причем , причем 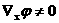 всюду на всюду на 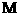 . Тогда . Тогда 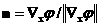 – единичная нормаль
к – единичная нормаль
к 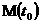 в точке в точке 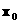 и, дифференцируя тождество и, дифференцируя тождество 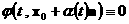 в точке в точке 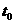 , получим: , получим:
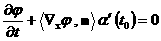 . .
Откуда 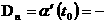 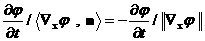 .
Если изменить направление у нормали, то изменится и знак у .
Если изменить направление у нормали, то изменится и знак у 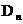 . .
Вернемся к общему случаю.
Пусть 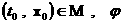 имеет разрыв первого
рода на имеет разрыв первого
рода на 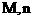 – единичная нормаль к – единичная нормаль к 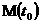 в точке в точке 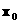 . Величина . Величина
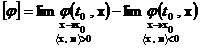 
называется скачком
функции 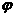 на поверхности на поверхности 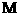 в точке в точке 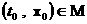 в направлении нормали в направлении нормали  . Если изменить знак
у . Если изменить знак
у  , то изменится знак и , то изменится знак и 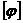 . .
Теорема 1. [5] Если 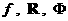 имеют разрыв
1–го рода на гиперповерхности имеют разрыв
1–го рода на гиперповерхности
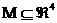 , а вне её
непрерывно дифференцируемы и для любой области , а вне её
непрерывно дифференцируемы и для любой области 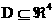 с кусочно –
гладкой границей справедливо тождество: с кусочно –
гладкой границей справедливо тождество:
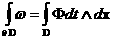 , ,
то в каждой точке 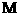 имеет место
равенство: имеет место
равенство:
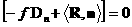 (10) (10)
где 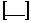 обозначает скачок
величины в скобке на поверхности обозначает скачок
величины в скобке на поверхности  в направлении
нормали в направлении
нормали  , а , а  – форма
(5). – форма
(5).
Заметим,
что условие (10) не зависит от функции 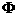 и выбора нормали и выбора нормали  . Из определения обобщенного решения и интегральных законов
(8) следует, что на разрыве имеет место соотношения, получаемые применением
равенства (10): . Из определения обобщенного решения и интегральных законов
(8) следует, что на разрыве имеет место соотношения, получаемые применением
равенства (10): 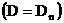
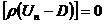 , , 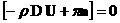
(11)
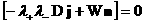 , , 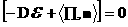
Из равенства
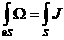
стандартным образом [6], учитывая отсутствие поверхностных токов,
выводится соотношение 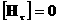 , а из равенства , а из равенства
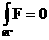
выводятся соотношения 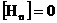 , , 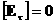 . Таким образом, из интегральных законов (9) следуют
тождества: . Таким образом, из интегральных законов (9) следуют
тождества:
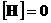 , , 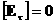 ,
(12) ,
(12)
где здесь и ниже для любого вектора 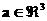 через через 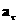 обозначается
тангенциальная составляющая обозначается
тангенциальная составляющая  : : 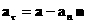 , , 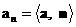 . .
Из соотношений (11) с учетом явных выражений
(2) для тензоров 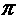 и и 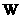
(а также величин
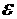 и и 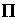 ) следуют равенства: ) следуют равенства:
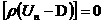 , , 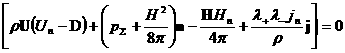 , , 
(13)
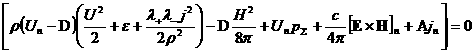
Преобразуем соотношения (13). Прежде всего, из (12)
следуют равенства:
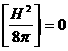 , , 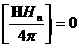 , , 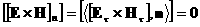
С другой стороны, если в интегральном законе (9) положить 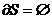 ( ( 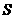 – замкнутая двумерная поверхность), то (9) дает – замкнутая двумерная поверхность), то (9) дает
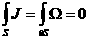 . .
Но отсюда, точно так же, как это делается при выводе
соотношения 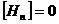
выводится равенство
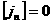 . .
Поэтому
соотношения (13) преобразуются к виду, в котором отсутствует электромагнитное
поле:
 , ,
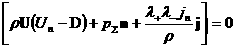 ,
,
(14)
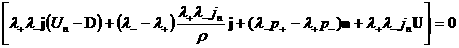 , ,
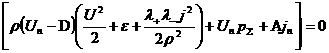 . .
Обозначим 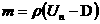 и спроектируем второе
и третье соотношения (14) на плоскость, касательную к и спроектируем второе
и третье соотношения (14) на плоскость, касательную к 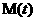 : :
 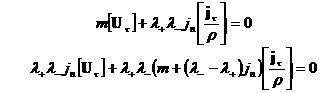 (*)
(*)
Детерминант полученной
линейной системы уравнений относительно скачков 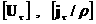 равен : равен :
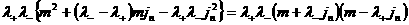 . .
Значит при 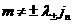 имеют место
равенства: имеют место
равенства:
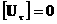 , , 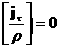 (15) (15)
В дальнейшем случай,
когда 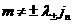 будем называть невырожденным. Проектируя второе и третье соотношения (14)
на нормаль, получим: будем называть невырожденным. Проектируя второе и третье соотношения (14)
на нормаль, получим:
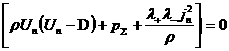 , ,
(16)
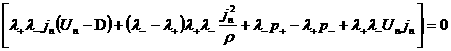 . .
Поскольку
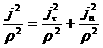 , , 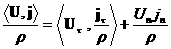 , , 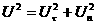
то в невырожденном случае из (15) следует:
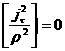 , , 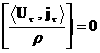 , , 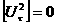 . .
Поэтому четвертое соотношение в (14) и выражение для
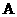 перепишутся в
следующем упрощенном виде: перепишутся в
следующем упрощенном виде:
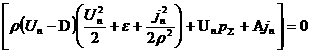 , ,
(17)
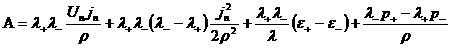 . .
Наконец, переходя в первом соотношении (14) и
соотношениях (16), (17) к переменной 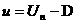 , получим искомые соотношения на разрыве в ДЖЭМГД: , получим искомые соотношения на разрыве в ДЖЭМГД:
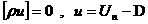 , ,
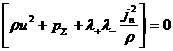 , ,
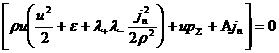 ,
(18) ,
(18)
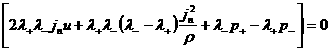 , ,
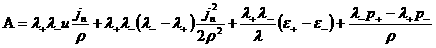 . .
К этим соотношениям надо добавить уравнения
состояния для электронного и ионного газов, позволяющих выразить 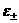 через через 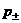 и и 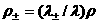 . Таким образом, если известны величины . Таким образом, если известны величины 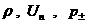 по одну сторону от
поверхности разрыва, то соотношения (18) позволяют найти их по другую сторону.
При этом по одну сторону от
поверхности разрыва, то соотношения (18) позволяют найти их по другую сторону.
При этом 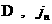 – константы,
одинаковые по обе стороны от – константы,
одинаковые по обе стороны от  . Нетрудно показать, что в
вырожденном случае получаются те же самые соотношения (18). Пусть,
например, . Нетрудно показать, что в
вырожденном случае получаются те же самые соотношения (18). Пусть,
например, 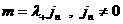 . Тогда из (*) следует равенство: . Тогда из (*) следует равенство:
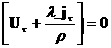 . (**) . (**)
С другой стороны, соберем в четвертом соотношении
(14) с учетом выражений для 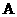 и и  все члены, куда входят все члены, куда входят
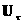 и и 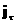 : :
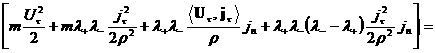
=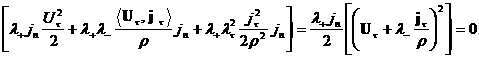 , ,
учитывая (**). Поэтому четвертое соотношение (14)
переходит в третье соотношение (18), в котором 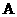 вычисляется по
укороченной формуле. вычисляется по
укороченной формуле.
В случае 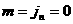 (контактный разрыв)
из (14) получим (контактный разрыв)
из (14) получим 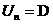 , , 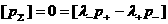 , откуда , откуда 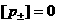 а скачки а скачки 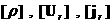 произвольные. произвольные.
В случае 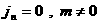 соотношения дают: соотношения дают:
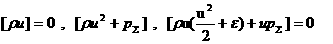
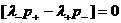 (19)
(19)
Уравнения первой строчки (19) это в точности условия
Гюгонио на разрыве в газовой динамике. При этом, однако, 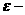 функция не от функция не от 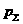 и и 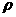 (как в газовой
динамике), а от (как в газовой
динамике), а от 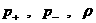 . Если электроны и ионы
– идеальные политропные газы с
общим показателем адиабаты, то: . Если электроны и ионы
– идеальные политропные газы с
общим показателем адиабаты, то:
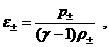 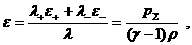
т.е. тогда 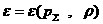 и из соотношений первой строчки (19) стандартным способом [5]
ищутся скачки и из соотношений первой строчки (19) стандартным способом [5]
ищутся скачки 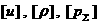 . Тогда вторая строка (19) позволяет найти скачки . Тогда вторая строка (19) позволяет найти скачки 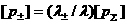 . Кроме того, согласно (15), . Кроме того, согласно (15), 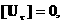 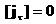 и значит, учитывая
(4), и значит, учитывая
(4), 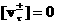 . Итак, при . Итак, при 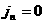 исследование
соотношений на разрыве практически такое же как в газовой динамике. исследование
соотношений на разрыве практически такое же как в газовой динамике.
Заметим,
что предельный переход 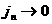 совпадает с МГД – пределом [2] в соотношениях (18). Известно,
что МГД – соотношения на разрыве в случае совпадает с МГД – пределом [2] в соотношениях (18). Известно,
что МГД – соотношения на разрыве в случае 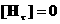 совпадает с соотношениями
Гюгонио в газовой динамике. Поэтому МГД – предел полученных соотношений (18) на
разрыве в ДЖЭМГД дает, как и следовало ожидать, МГД – соотношения на
разрыве. совпадает с соотношениями
Гюгонио в газовой динамике. Поэтому МГД – предел полученных соотношений (18) на
разрыве в ДЖЭМГД дает, как и следовало ожидать, МГД – соотношения на
разрыве.
§ 3. Уравнения
ударной адиабаты.
Установим
связь между термодинамическими параметрами плазмы по разные стороны от
разрыва в случае 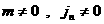 . .
Из
первых двух соотношений (18):
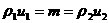
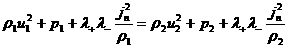
исключим скорости 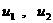 : :
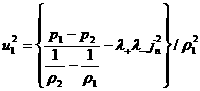 , , 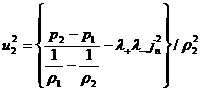 . .
(Ниже предполагается 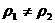 , в противном случае скачки
всех параметров плазмы равны нулю.) В более удобном виде, используя обозначения , в противном случае скачки
всех параметров плазмы равны нулю.) В более удобном виде, используя обозначения
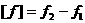 , получим: , получим:
 (20) (20)
Отсюда, в частности, следует, что величина
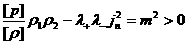 (21) (21)
положительна. Четвертое соотношение (18) дает:
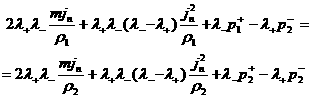 . .
Отсюда
находим  : :
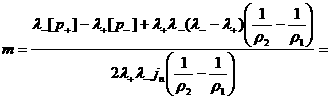
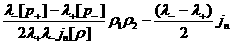 . (22)
. (22)
Подставляя это выражение в правую часть (21),
получим:
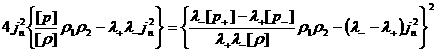
Раскрывая квадрат и учитывая равенство 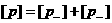 , имеем: , имеем:
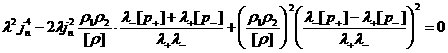
Откуда:
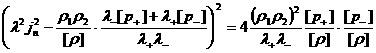 . .
Из этого равенства следует 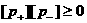 , т.е. скачки , т.е. скачки 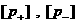 одного знака, а
т.к. одного знака, а
т.к. 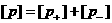 , то знак , то знак 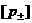 совпадает со
знаком совпадает со
знаком 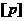 и значит, согласно (21), со знаком и значит, согласно (21), со знаком 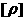 . Поэтому . Поэтому 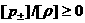 . Теперь из последнего равенства, извлекая
корень, получим: . Теперь из последнего равенства, извлекая
корень, получим:
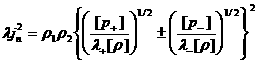 .
(23) .
(23)
Соотношение (23), связывающее только независимые
термодинамические параметры по разные стороны от разрыва, не имеют аналога в
газовой и магнитной гидродинамике.
Теперь установим соотношение между
термодинамическими параметрами по разные стороны от разрыва, аналогичное
гидродинамической ударной адиабате. Из третьего соотношения (18) с учетом
выражения для  получим: получим:
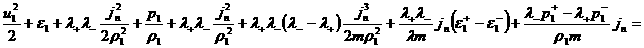 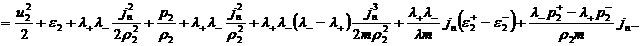 . .
Подставляя сюда выражения (20) для 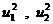 , получим: , получим:
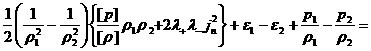
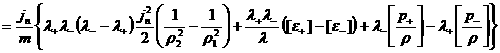 . .
Наконец, подставляя сюда полученное ранее выражение
(22) для  , получим аналог классической ударной адиабаты в газовой
динамике: , получим аналог классической ударной адиабаты в газовой
динамике:
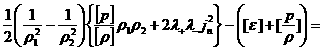
(24)
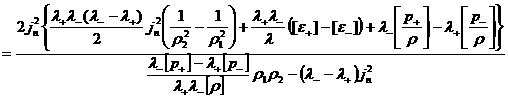 . . 
При 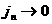 уравнение (24)
переходит в уравнение газодинамической ударной адиабаты [5]. Появление
дополнительного соотношения (23), связывающего термодинамические параметры по
разные стороны от разрыва вызвано увеличением на 1 числа независимых
термодинамических параметров. Поэтому теперь плазменная ударная адиабата
состоит из двух уравнений (23), (24), а не из одного, как это было в магнитной
гидродинамике. При уравнение (24)
переходит в уравнение газодинамической ударной адиабаты [5]. Появление
дополнительного соотношения (23), связывающего термодинамические параметры по
разные стороны от разрыва вызвано увеличением на 1 числа независимых
термодинамических параметров. Поэтому теперь плазменная ударная адиабата
состоит из двух уравнений (23), (24), а не из одного, как это было в магнитной
гидродинамике. При 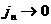 дополнительное уравнение
(23) дает либо дополнительное уравнение
(23) дает либо 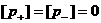 , либо , либо 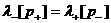 . С помощью соотношения (23) величину . С помощью соотношения (23) величину  можно записать в виде: можно записать в виде:
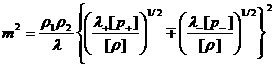 . .
Если электроны и ионы представляют собой идеальный
политропный газ с общим показателем адиабаты, то
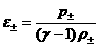 , , 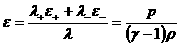 , , 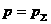 , ,
(25)
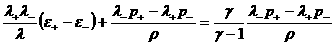
и второе уравнение ударной адиабаты (24) немного
упрощается:
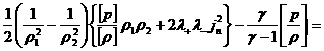
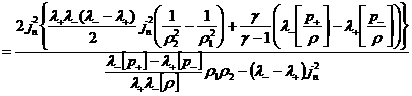 . .
Если электроны ионы имеют двучленные уравнения
состояния [4] с общим показателем
адиабаты
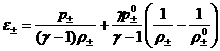 , , 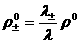 , , 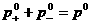 , (26) , (26)
где 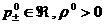 –
заданные константы, то –
заданные константы, то
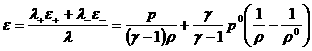
(27)
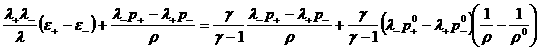
и уравнение ударной адиабаты (24) принимает вид:
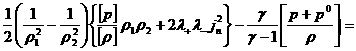
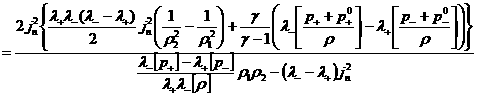 . .
§ 4. Разрешение соотношений на разрыве.
Пусть известны параметры
течения 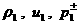 по одну сторону от разрыва,
а также скорость движения разрыва по одну сторону от разрыва,
а также скорость движения разрыва 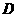 и нормальная компонента
плотности тока и нормальная компонента
плотности тока 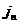 . Найдем параметры . Найдем параметры 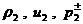 по другую сторону разрыва, исходя из
соотношений (18). Сначала для определенности считаем электроны и ионы
идеальными политропными газами с общим показателем адиабаты, затем обсудим
общий случай. Тогда справедливы тождества (25), а соотношения (18) немного
упростятся: по другую сторону разрыва, исходя из
соотношений (18). Сначала для определенности считаем электроны и ионы
идеальными политропными газами с общим показателем адиабаты, затем обсудим
общий случай. Тогда справедливы тождества (25), а соотношения (18) немного
упростятся:
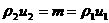 , ,
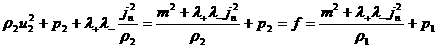 ,
,
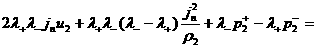
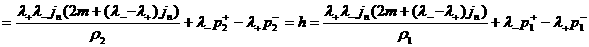 .
.
(28)
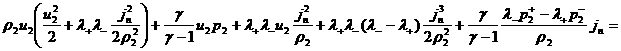
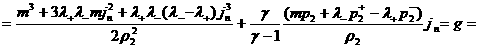
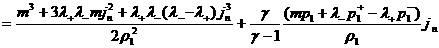 . .
Из двух первых левых соотношений
(28) получим:
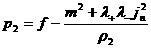 , , 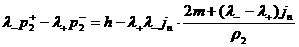 . (29) . (29)
Подставляя эти выражения в
последнее левое соотношение
(28) после несложных
преобразований получим квадратное относительно
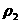 : :
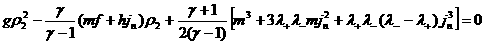 . (30) . (30)
Величины 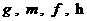 выражаются через выражаются через 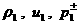 по правым соотношениям
(28). Рассуждая, как и выше, получим
равенство (30), где по правым соотношениям
(28). Рассуждая, как и выше, получим
равенство (30), где 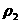 заменено на заменено на 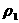 , откуда: , откуда:
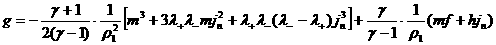
а из соотношений (29), где 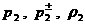 заменены на заменены на 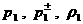 получим: получим:
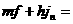 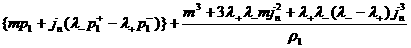
Подставляя
последнее равенство в выражение для 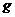 и обозначая и обозначая
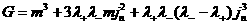 , , 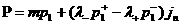 (31) (31)
получим:
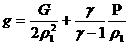 , , 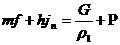 . .
Теперь
квадратное уравнение (30) переписывается в компактном виде:
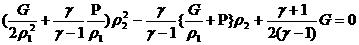 , ,
откуда его корни ищутся в явном виде:
 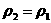 , , 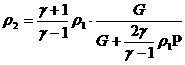 , ,
где выражения
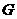 и и 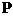 (с учетом (с учетом 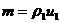 ) через ) через 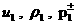 указаны в (31). Первый
корень указаны в (31). Первый
корень 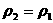 приводит к тривиальному
решению, когда все параметры по разные стороны от поверхности разрыва
совпадают. Второе решение, представляющее
основной интерес, дает явное выражение приводит к тривиальному
решению, когда все параметры по разные стороны от поверхности разрыва
совпадают. Второе решение, представляющее
основной интерес, дает явное выражение 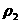 через через 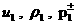 (а также (а также 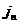 и и 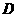 ). Теперь легко вычисляются остальные параметры течения.
Давления ). Теперь легко вычисляются остальные параметры течения.
Давления  ищутся из линейной
системы (с учетом ищутся из линейной
системы (с учетом 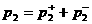 ) (29) с ненулевым детерминантом: ) (29) с ненулевым детерминантом:
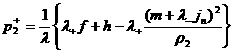 , , 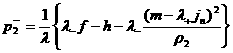 . .
В итоге
получаются следующие формулы разрешения соотношений (18) на разрыве для случая идеального
газа:
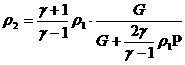 , , 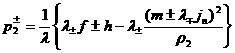 , , 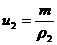 , (32) , (32)
где 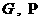 вычисляются по (31), вычисляются по (31), 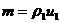 . а . а
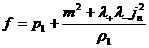 , , 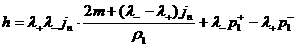 . (33) . (33)
В
случае произвольных уравнений состояния электронов и ионов процесс разрешения
соотношений (18) на разрыве такой же. Из
линейной системы (29) находим  как функции как функции 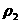 и подставляем
полученные выражения в последнее левое равенство (28): и подставляем
полученные выражения в последнее левое равенство (28):
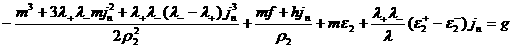 , (34) , (34)
где 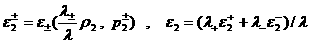 – известные функции.
В итоге получается нелинейное уравнение относительно – известные функции.
В итоге получается нелинейное уравнение относительно 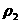 , откуда в принципе
находится , откуда в принципе
находится 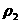 , а
значит уже по явным формулам и , а
значит уже по явным формулам и 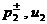 . Выше эта процедура была
проведена для случая идеальных газов, и тогда нелинейное уравнение (34) сводилось к квадратному. . Выше эта процедура была
проведена для случая идеальных газов, и тогда нелинейное уравнение (34) сводилось к квадратному.
Рассмотрим
два примера.
Случай
двучленных уравнений состояния [4].
Пусть функции 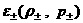 имеют вид (26). Тогда
для имеют вид (26). Тогда
для 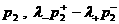 получим те же формулы
(29), а третье соотношение (18), переписанное в виде (34), используя (27),
сводится к квадратному уравнению относительно получим те же формулы
(29), а третье соотношение (18), переписанное в виде (34), используя (27),
сводится к квадратному уравнению относительно 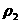 : :
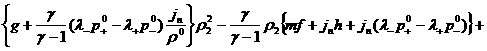
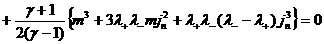
Ясно, что такое же соотношение с заменой 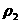 на на 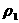 тоже будет
справедливо, откуда: тоже будет
справедливо, откуда:
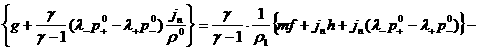
 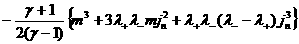 
Из формул (29), где 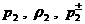 заменены на заменены на 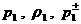 ,
находим: ,
находим:
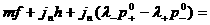 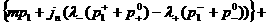
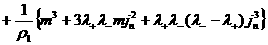
Подставляя это выражение в предыдущее равенство и
обозначая
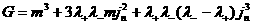
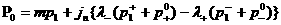 , ,
получим:
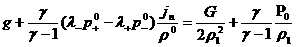
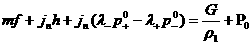
Поэтому квадратное уравнение относительно 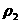 перепишется в том же
виде, что и для случая идеальных газов: перепишется в том же
виде, что и для случая идеальных газов:
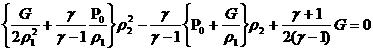
Отсюда получаем единственное нетривиальное
решение:
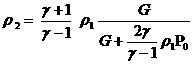 . .
Остальные параметры течения восстанавливаются по тем
же формулам (32), (33) , что и в случае идеальных газов.
Изотермический
случай. В этом случае из
интегральных законов (8) надо выбросить закон сохранения полной
энергии, поскольку при изотермическом
течении необходимо извне подводить или отводить от плазмы тепло, дабы
гарантировать неизменность температуры. Поэтому количество соотношений на
разрыве (18) уменьшится на 1: исчезнет
третье соотношение. Но уменьшится на 2 и количество термодинамических
параметров, поскольку при постоянной температуре 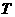 (для простоты
ограничимся случаем идеального газа): (для простоты
ограничимся случаем идеального газа):
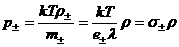 , , 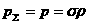 , , 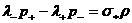 , ,
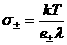 , ,
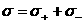 , , 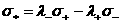  , ,
где 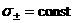 . Поэтому три оставшиеся соотношения на разрыве (18) позволяют по известным величинам . Поэтому три оставшиеся соотношения на разрыве (18) позволяют по известным величинам 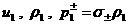 найти не только найти не только 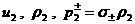 но и но и 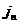 . Действительно, согласно
(18): . Действительно, согласно
(18):
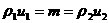
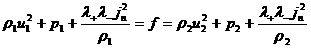 (35)
(35)
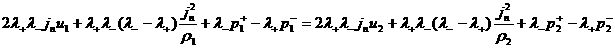 ,
,
из первых двух соотношений (35)
получим:
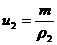 , , 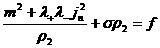 , ,
откуда получаем квадратное уравнение для нахождения 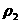 : :
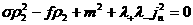 
Еще раз пользуясь
(35), выводим:
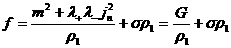 , , 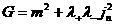 , ,
откуда
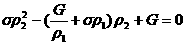 . .
Это уравнение имеет два корня: тривиальный
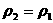 и и 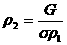 . .
Таким образом, получаем:
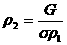 , , 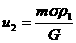 , , 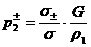 ,
(36) ,
(36)
где 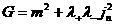 , , 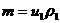 . Но это ещё не окончательное выражение,
поскольку . Но это ещё не окончательное выражение,
поскольку 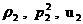 зависят от зависят от 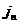 , которое находится
подстановкой выражений (36) в последнее соотношение (35): , которое находится
подстановкой выражений (36) в последнее соотношение (35):
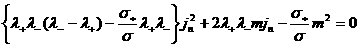 . .
Итак, для нахождения
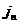 имеем квадратное
уравнение, корни которого имеют следующий вид: имеем квадратное
уравнение, корни которого имеют следующий вид:
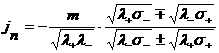 ` . ` .
Подставляя это выражение в 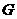 , получаем
окончательные формулы для величины , получаем
окончательные формулы для величины 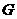 и, согласно (36),
для параметров и, согласно (36),
для параметров 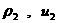 : :
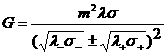 , , 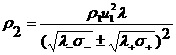 , , 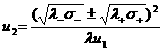
§5. Исследование устойчивости разрыва.
До сих
пор стороны разрыва были равноправны, что математически выражалось в
симметричном вхождении параметров течения по разные стороны от разрыва в
соотношения (18). Однако есть физические ограничения, нарушающие это
равноправие. Поскольку разрыв формализует тонкий диссипативный слой, в котором
энтропии электронов и ионов могут только расти, а вне разрыва плазма
бездиссипативна, то при перемещении единичной массы электронов или ионов в
соответствующем поле скоростей её энтропия
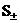 не меняется пока эта
масса находится вне разрыва и увеличивается при пересечении поверхности
разрыва. Математически это условие записывается в виде: не меняется пока эта
масса находится вне разрыва и увеличивается при пересечении поверхности
разрыва. Математически это условие записывается в виде:
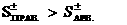 при при 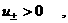 (37) (37)
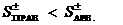 при при 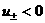 , ,
где 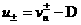 и фиксирована
нормаль и фиксирована
нормаль  к поверхности
разрыва, причем правым считается положительное направление нормали, левым –
отрицательное. Поскольку к поверхности
разрыва, причем правым считается положительное направление нормали, левым –
отрицательное. Поскольку 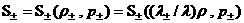 , то параметры , то параметры 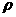 и и 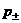 по разные стороны от
разрыва, помимо соотношений на разрыве (18), должны удовлетворять неравенствам
(37), которые, следуя газодинамической традиции, назовем условием
устойчивости разрыва. по разные стороны от
разрыва, помимо соотношений на разрыве (18), должны удовлетворять неравенствам
(37), которые, следуя газодинамической традиции, назовем условием
устойчивости разрыва.
При 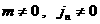 разрывное обобщенное
решение называется ударной волной, а поверхность разрыва – фронтом ударной
волны. При разрывное обобщенное
решение называется ударной волной, а поверхность разрыва – фронтом ударной
волны. При 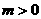 сторона слева от разрыва называется передней (или
стороной перед фронтом ударной
волны), а сторона справа от разрыва – задней (или стороной за фронтом
ударной волны). При сторона слева от разрыва называется передней (или
стороной перед фронтом ударной
волны), а сторона справа от разрыва – задней (или стороной за фронтом
ударной волны). При 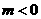 указанные стороны
меняются местами. указанные стороны
меняются местами.
Если
электроны и ионы пересекают поверхность разрыва в одном направлении, то
условие (37) означает, что энтропия
каждой компоненты за фронтом ударной волны больше, чем перед фронтом. Для таких
ударных волн как показано ниже, давления компонент и плотность за фронтом также
больше , чем перед фронтом т.е. они являются ударными волнами сжатия. Вместе с
тем, оказывается, возможны и ударные волны , в которых электроны и ионы
пересекают поверхность разрыва в противоположных направлениях, причем эти волны
могут быть как волнами
сжатие, так и волнами разрежения, что является важным
двухжидкостным эффектом динамики плазмы (как известно, в газовой [5] и
магнитной [7] гидродинамике ударные
волны являются всегда волнами сжатия). Для таких волн энтропия одной из
плазменных компонент за фронтом волны будет больше, а другой меньше, чем перед
фронтом.
Отметим,
что различить стороны разрыва посредством энтропии 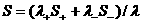 единичной массы плазмы (≡ электронов и ионов) нельзя, поскольку при движении с массовой
скоростью единичной массы плазмы (≡ электронов и ионов) нельзя, поскольку при движении с массовой
скоростью 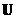 эта энтропия не сохраняется, несмотря на бездиссипативность
течения, что вытекает из уравнения эта энтропия не сохраняется, несмотря на бездиссипативность
течения, что вытекает из уравнения
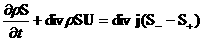 , ,
являющегося следствием уравнений (1.в).
Проведем
анализ условий устойчивости (37) для случая, когда электроны и ионы являются
идеальными газами с общим показателем адиабаты. Тогда
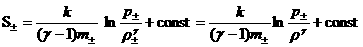 . .
Фиксируем нормаль к поверхности разрыва и обозначим
индексом ″2″ параметры течения справа от разрыва, а индексом
″1″ – слева. Тогда условия
устойчивости (37) запишутся в виде:
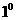 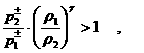 если если
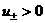
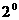 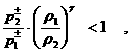 если если
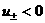
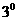 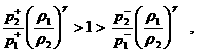 если если
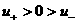
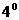  если если 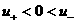 . .
Наша цель – получить
ограничения на параметры плазмы перед фронтом ударной волны, которые налагает на них условие
возрастания энтропии (37). Поэтому в условия 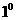 – – 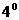 в зависимости от
знака и надо подставить или выражения
(32) для в зависимости от
знака и надо подставить или выражения
(32) для 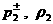 через через 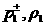 , полученные выше (при , полученные выше (при 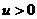 ) или аналогичные выражения
для ) или аналогичные выражения
для 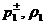 через через 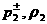 (при (при 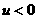 ), которые при
перестановке индексов совпадают с (32). Ввиду сказанного, ясно, что достаточно разобрать только случай ), которые при
перестановке индексов совпадают с (32). Ввиду сказанного, ясно, что достаточно разобрать только случай 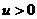
Экономя индексы, опустим
у параметров течения перед фронтом ударной волны 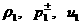 и т.д. индекс "1". Далее от переменных и т.д. индекс "1". Далее от переменных 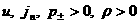
перейдем сначала к
переменным 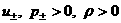 : :
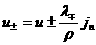 , , 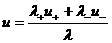 , , 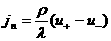 , (38) , (38)
а затем от переменных 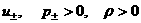 перейдем к
переменным перейдем к
переменным 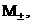 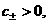 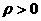 : :
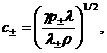 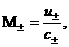 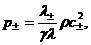 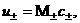 (39) (39)
имеющими простой физический
смысл: 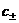 – звуковые скорости электронов и ионов, – звуковые скорости электронов и ионов, 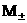 – число Маха электронов и ионов перед фронтом
ударной волны. В новых переменных,
согласно формулам (31) ÷
(33), куда надо подставить (38), (39), получим: – число Маха электронов и ионов перед фронтом
ударной волны. В новых переменных,
согласно формулам (31) ÷
(33), куда надо подставить (38), (39), получим:
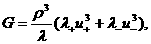 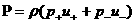 , ,
 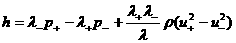 , ,
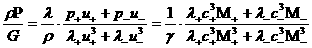 ,
(40) ,
(40)

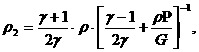 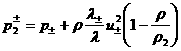 , ,
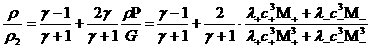 ,
,
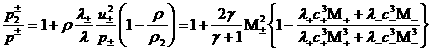 . .
Итак, в новых переменных
исчезла зависимость от  , и условия , и условия
 перепишутся в виде: перепишутся в виде:
(с1) 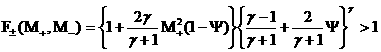 , , 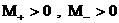 , ,
(с2)
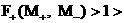 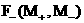 , , 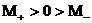  , , 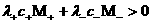 , ,
(с3)
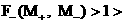 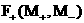 , , 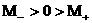  , , 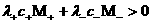 , ,
где
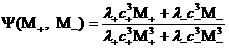
Построение областей (с1) ÷ (с3)
сводится к построению множеств 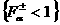 , , 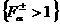 , где в обозначениях учтена параметрическая зависимость
функций , где в обозначениях учтена параметрическая зависимость
функций 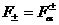 от от 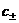 , причем в комбинации , причем в комбинации 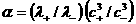 . При этом . При этом 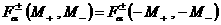 , , 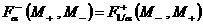 .Отсюда вытекает, что
в 1 – м квадранте ( .Отсюда вытекает, что
в 1 – м квадранте (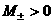 ) множество ) множество 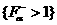 получается из множества получается из множества
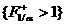 его отражением
относительно биссектрисы его отражением
относительно биссектрисы 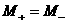 , а в 4 – м квадранте , а в 4 – м квадранте 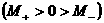 множество множество 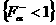 (соответственно (соответственно 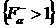 ) получается из множества ) получается из множества 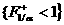 (соответственно (соответственно 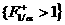 ) его отражением относительно биссектрисы ) его отражением относительно биссектрисы 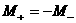 . Наконец, множество (с3) . Наконец, множество (с3) во втором квадранте получается из множества во втором квадранте получается из множества 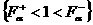 , , 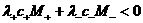 в 4 – м квадранте его
отражением относительно начала координат 0. Эти замечания сводят построение
области (с1)÷(с3) к построению только множеств в 4 – м квадранте его
отражением относительно начала координат 0. Эти замечания сводят построение
области (с1)÷(с3) к построению только множеств 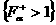 , , 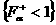 в полуплоскости в полуплоскости 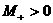 с последующим
выполнением указанных отражений и пересечений. Каждое из множеств с последующим
выполнением указанных отражений и пересечений. Каждое из множеств 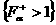 , , 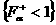 ограничено кривой ограничено кривой 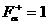 и осями координат и
строится по его пересечениям с лучами и осями координат и
строится по его пересечениям с лучами 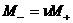 , , 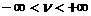 , , 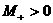 . При этом частью границы . При этом частью границы
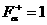 является кривая является кривая 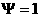 , которая, согласно
(40), разделяет ударные волны сжатия и
разрежения: при , которая, согласно
(40), разделяет ударные волны сжатия и
разрежения: при 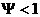 имеет место ударная
волна сжатия, при имеет место ударная
волна сжатия, при 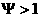 – разрежения. Наконец,
к условиям возрастания энтропии (37) надо добавить условия неотрицательности
давлений и плотности, – разрежения. Наконец,
к условиям возрастания энтропии (37) надо добавить условия неотрицательности
давлений и плотности, 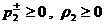 , за фронтом ударной волны, дополнительно ограничивающие
выбор параметров течения перед фронтом. Эти условия с учетом формул (40)
выписываются в явном виде в проективных координатах , за фронтом ударной волны, дополнительно ограничивающие
выбор параметров течения перед фронтом. Эти условия с учетом формул (40)
выписываются в явном виде в проективных координатах 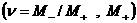 на полуплоскости
на полуплоскости 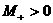 : :
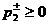 : : 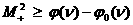 , , 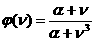 , , 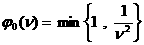
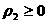 : : 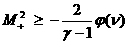 (41)
(41)
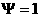 : : 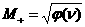 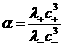
Опуская технические детали, приведем
результаты построения области (с1)÷(с3) , которые зависят от параметра 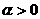 . В зависимости от соотношения между . В зависимости от соотношения между 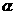 и и 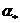 , где , где 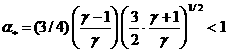 область (с1) ÷
(с3) заштрихована на Рис. 1÷4, причем границы область (с1) ÷
(с3) заштрихована на Рис. 1÷4, причем границы 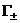 в область не входят.
Искомая
область распадается на 4 подобласти в область не входят.
Искомая
область распадается на 4 подобласти 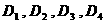 . Для . Для 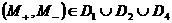 имеем ударную волну
сжатия, а для имеем ударную волну
сжатия, а для 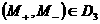 – разрежения. Для
точек из области – разрежения. Для
точек из области 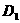 электроны и ионы
пересекают фронт ударной волны в одном направлении (слева направо), а для точек
из электроны и ионы
пересекают фронт ударной волны в одном направлении (слева направо), а для точек
из 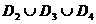 – в разных, причем для точек из – в разных, причем для точек из 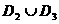 электроны пересекают
фронт справа налево, а ионы – слева
направо, а для точек из электроны пересекают
фронт справа налево, а ионы – слева
направо, а для точек из 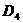 наоборот. Границы наоборот. Границы 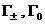 пересекаются с любым
лучом пересекаются с любым
лучом 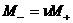 ( (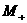 знакоопределено) не более чем в одной точке. Граница знакоопределено) не более чем в одной точке. Граница 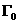 имеет явное описание: имеет явное описание: 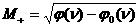 , и на ней электронное давление , и на ней электронное давление 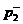 за фронтом ударной
волны равно нулю. Модули абсцисс точек пересечения за фронтом ударной
волны равно нулю. Модули абсцисс точек пересечения 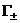 с лучом с лучом 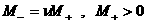 (или (или 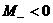 для луча во втором
квадранте) являются квадратным корнем решения уравнения для луча во втором
квадранте) являются квадратным корнем решения уравнения 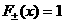 , большего или меньшего , большего или меньшего 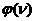 (такое есть, можно
показать, и единственно), в зависимости от того, лежит ли граница (такое есть, можно
показать, и единственно), в зависимости от того, лежит ли граница 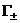 вне или внутри кривой вне или внутри кривой 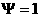 , изображенной на Рис. 1÷4. Здесь , изображенной на Рис. 1÷4. Здесь
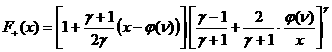 , ,
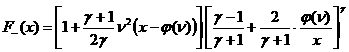 , ,
причем  . Части области попавшие внутрь кривой . Части области попавшие внутрь кривой  (они дважды
заштрихованы) отвечают ударным волнам разрежения. Существование таких ударных
волн зависит от расположения прямой (они дважды
заштрихованы) отвечают ударным волнам разрежения. Существование таких ударных
волн зависит от расположения прямой 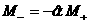 , , 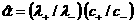 . Для электрон–ионной
плазмы всегда . Для электрон–ионной
плазмы всегда
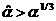 . Поэтому при . Поэтому при 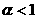 , как следует из Рис. 1,2, существование ударных волн
разрежения равносильно выполнению неравенства , как следует из Рис. 1,2, существование ударных волн
разрежения равносильно выполнению неравенства 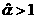 . Условия . Условия 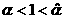 дают: дают:
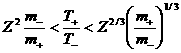 , (42) , (42)
где 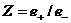 – кратность заряда
ионов, – кратность заряда
ионов, 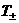 – температуры
электронов и ионов перед фронтом ударной волны. При – температуры
электронов и ионов перед фронтом ударной волны. При 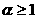 граница граница 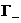 дважды заштрихованной
области на Рис. 3.4 расположены в секторе дважды заштрихованной
области на Рис. 3.4 расположены в секторе
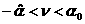 (причем любой луч из
этого сектора пересекает границу (причем любой луч из
этого сектора пересекает границу 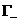 ), где ), где 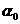 – наименьший
отрицательный корень уравнения – наименьший
отрицательный корень уравнения 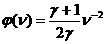 , сводящегося к кубическому , сводящегося к кубическому  . Поэтому при . Поэтому при 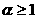 существование ударных
волн разрежения равносильно требованию существование ударных
волн разрежения равносильно требованию 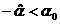 , а последнее,
учитывая , а последнее,
учитывая 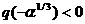 , эквивалентно неравенству , эквивалентно неравенству 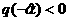 . Условия . Условия 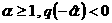 дают дают
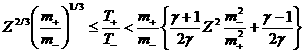 . (43) . (43)
Для реальных показателей адиабаты,
скажем 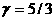 , условия (42), (43)
одновременно нарушается только для сильно неизотермической плазмы, , условия (42), (43)
одновременно нарушается только для сильно неизотермической плазмы,
когда
примерно на три порядка 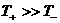 или или 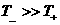 . В частности, только в сильно неизотермической плазмы
отсутствуют ударные волны разрежения. . В частности, только в сильно неизотермической плазмы
отсутствуют ударные волны разрежения.
В газодинамическом случае 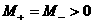 , , 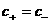 и пересечение
заштрихованных областей на Рис. 1÷4 с лучом и пересечение
заштрихованных областей на Рис. 1÷4 с лучом 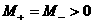 дает одномерную
область дает одномерную
область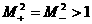 , что совпадает с известным газодинамическим условием [5]
возрастания энтропии на разрыве. , что совпадает с известным газодинамическим условием [5]
возрастания энтропии на разрыве.
Литература.
1. Гавриков М.Б. Линейные волны в нерелятивистской магнитной
гидродинамике. // Препринт ИПМ им. М.В. Келдыша АН СССР, 1988, N199.
2. Гавриков М.Б. Основные уравнения двухжидкостной
электромагнитной
гидродинамики. Часть I. // Препринт ИПМ им. М.В.
Келдыша РАН, 2006,
N59.
3. Гавриков
М.Б., Сорокин Р.В.. Однородные движения плазменного шнура в
электромагнитной гидродинамике. // Препринт ИПМ им. М.В. Келдыша
РАН,
2006, N40.
4. Куликовский
А.Г., Погорелов Н.В., Семенов А.Ю.
Математические вопросы численного решения гиперболических систем
уравнений. // М.: Физматлит, 2001,
стр.148.
5. Овсянников Л.В. Лекции по основам газовой динамике. // М.:
"Наука",
1981.
6. Тамм И.Е.
Основы теории электричества. // М.: "Наука", 1966.
7. Куликовский А.Г., Любимов Г.А.
Магнитная гидродинамика.
// М.: "Логос", 2005.
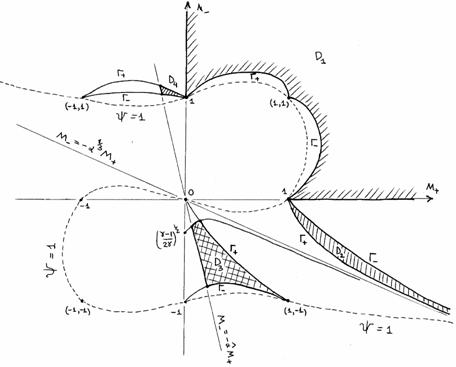
Рис. 1.  
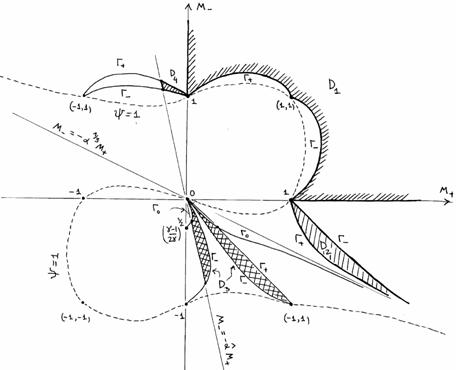
Рис. 2. 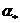  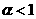
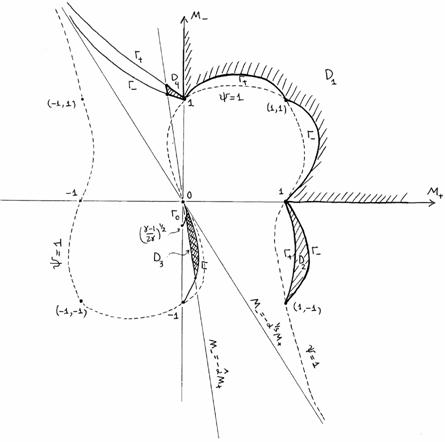
Рис. 3 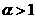
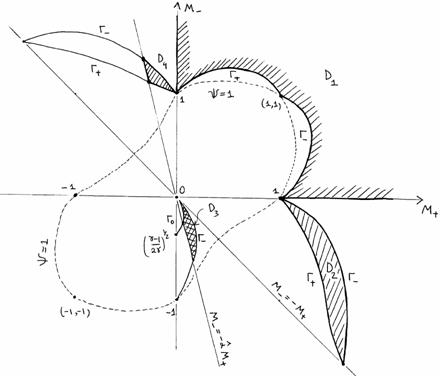
Рис. 4 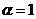
|