Аннотация
Рассмотрено кинетическое уравнение для релятивистских электронов в газовой среде и
самосогласованном электромагнитном поле. Построено приближенное решение в виде, аналогичном
дельта-подстановке. Приближение состоит в том, что для электронов, существенно отклонившихся
от траектории, определяемой уравнениями движения в самосогласованном электромагнитном поле,
рассматривается пространственно однородное кинетическое уравнение. Конструкция решения
обосновывает применимость для математического моделирования потока электронов метода частиц,
несмотря на наличие столкновений. Построена оценка точности приближенного решения, показавшая
его применимость для широкого класса задач моделирования релятивистских электронных пучков.
Abstract
The kinetic equation for relativistic electrons in gas and self-consistent electromagnetic
field is considered. The approximate solution in the form of δ–substitution is constructed.
The approximation consists in follows. The spatially uniform kinetic equation is considered
for electrons, essentially deviated from trajectory, movement equations in self-consistent
electromagnetic field determined by. The structure of solution substantiates the applicability
of particles method for mathematical modeling the electron’s flux, in spite of collisions.
The estimation of approximate solution accuracy, which shows it’s applicability for wide class
of problems of relativistic electron’s beams simulation, is constructed.
Введение
Релятивистские электронные пучки (РЭП), производимые,
например, ускорителями электронов [1], используются в экспериментальных работах
по исследованию свойств вещества [2]. При распространении РЭП в газовой среде
от выхода ускорителя до преграды, исследуемой в эксперименте, образуется самосогласованное
электромагнитное поле. Оно может влиять на измерительную аппаратуру и вносит
погрешности в результаты эксперимента. Математическое моделирование такого поля
и электронов в газе заданной плотности актуально для определения параметров
пучка на преграде и правильной интерпретации результатов эксперимента.
Данная работа посвящена построению функции
распределения электронов РЭП в виде, аналогичном дельта-подстановке [3]. Такое
представление позволяет использовать для моделирования РЭП метод частиц [4].
1 Построение приближенного решения
Рассмотрим поток релятивистских электронов в газовой
среде. Для функции распределения первичных электронов потока 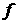 будем считать справедливым
[5] кинетическое уравнение будем считать справедливым
[5] кинетическое уравнение
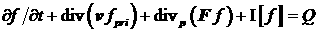 (1)
(1)
где 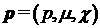 – импульс электрона, – импульс электрона, 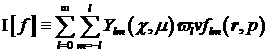 – интеграл углового рассеяния электронов за счет
всех столкновительных процессов, – интеграл углового рассеяния электронов за счет
всех столкновительных процессов, 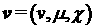 – скорость. Представление этого интеграла в виде
разложения по сферическим функциям – скорость. Представление этого интеграла в виде
разложения по сферическим функциям 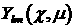 рассмотрим на примере
рассеяния с дифференциальным сечением рассмотрим на примере
рассеяния с дифференциальным сечением 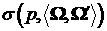 . Здесь . Здесь 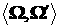 – косинус угла между
направлением движения электрона до ( – косинус угла между
направлением движения электрона до (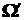 ) и после столкновения ( ) и после столкновения ( ). Сечение раскладывается в ряд по полиномам Лежандра ). Сечение раскладывается в ряд по полиномам Лежандра 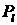 переменной переменной 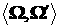 : :
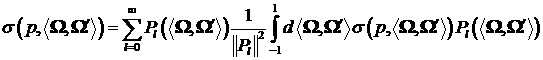 . .
Полиномы Лежандра
представляются в виде суммы сферических функций с помощью теоремы сложения [6]:
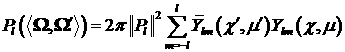 . .
Поэтому 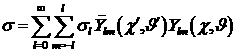 , где , где 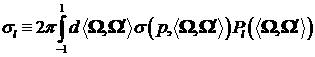 . .
Представим 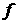 в виде ряда по
сферическим функциям в виде ряда по
сферическим функциям
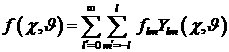 , ,
и подставим в интеграл
столкновений, обозначив 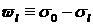 : :
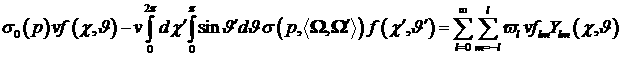
Все неупругие столкновительные процессы в уравнении
(1) учтены в третьем слагаемом правой части. Векторная функция 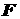 представляет собой
сумму силы Лоренца и «силы» ионизационного торможения [5]: представляет собой
сумму силы Лоренца и «силы» ионизационного торможения [5]:
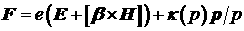
где 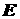 и и 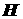 – напряженности электрического и магнитного поля, – напряженности электрического и магнитного поля, 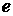 – заряд электрона, а – заряд электрона, а 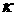 – тормозная
способность электронов. Так столкновения описываются в приближении малой
передачи энергии [5] при ионизации [7]. – тормозная
способность электронов. Так столкновения описываются в приближении малой
передачи энергии [5] при ионизации [7].
2 Приближение однородного рассеяния электронов на
характеристиках
Представим решение уравнения (1) в виде разности 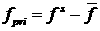 , где , где
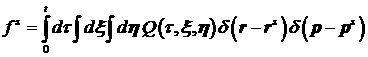
является решением уравнения
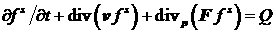 .
(2) .
(2)
Тогда для 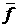 справедливо уравнение справедливо уравнение
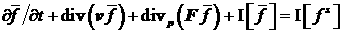 .
(3) .
(3)
Рассмотрим
характерные размеры задачи. Взаимодействие электронного потока с
самосогласованным электромагнитным полем характеризуют плазменная частота
электронов 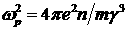 и дебаевский радиус и дебаевский радиус 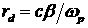 , где , где 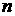 – концентрация электронов. Взаимодействие
отдельных электронов с рассеивающей средой описывается длиной пробега электрона
до полной потери энергии – концентрация электронов. Взаимодействие
отдельных электронов с рассеивающей средой описывается длиной пробега электрона
до полной потери энергии 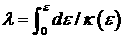 , до первого столкновения , до первого столкновения 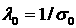 или или 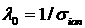 , и транспортной длиной пробега относительно углового
рассеяния , и транспортной длиной пробега относительно углового
рассеяния 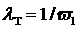 . .
Указанные
группы характерных размеров связаны между собой, поскольку в самосогласованном
поле электроны теряют энергию, от которой зависят сечения, определяющие длины
пробега. Пусть параметры 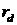 , , 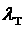 и и 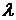 , характеризующие величины слагаемых в исходном уравнении (1)
сравнимы. , характеризующие величины слагаемых в исходном уравнении (1)
сравнимы.
Обратим
внимание на важное свойство электронного рассеяния на нейтральных молекулах
[8]. В каждом акте взаимодействия наиболее вероятно малое изменение не только
абсолютного значения импульса электрона, но и направления его движения. Это
свойство выражается в том, что 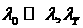 . .
Источником для
функции 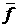 в (3) является в (3) является 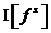 . Такой источник становится существенным по сравнению с
источником . Такой источник становится существенным по сравнению с
источником 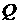 в уравнении (2) на расстояниях
порядка в уравнении (2) на расстояниях
порядка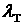 , то есть при , то есть при 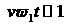 . Поэтому функция . Поэтому функция 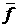 становится сопоставимой
по величине с функцией становится сопоставимой
по величине с функцией 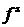 только на временах
порядка только на временах
порядка  . .
Поскольку для
газовых сред 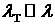 , функция , функция 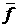 описывает электроны,
успевшие сбросить энергию. Сечения рассеяний при этом резко возрастают и
столкновения начинают превалировать над взаимодействием с самосогласованным
электромагнитным полем, поскольку радиус Дебая уменьшается пропорционально скорости
электрона, а тормозная способность описывает электроны,
успевшие сбросить энергию. Сечения рассеяний при этом резко возрастают и
столкновения начинают превалировать над взаимодействием с самосогласованным
электромагнитным полем, поскольку радиус Дебая уменьшается пропорционально скорости
электрона, а тормозная способность 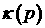 растет быстрее –
обратно пропорционально квадрату скорости. Поэтому слагаемое растет быстрее –
обратно пропорционально квадрату скорости. Поэтому слагаемое 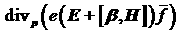 в (3) мало по сравнению
с в (3) мало по сравнению
с 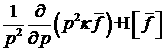 . .
В силу этого,
будем рассматривать вместо (3) приближенное уравнение:
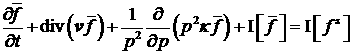 (4)
(4)
Решение
уравнения (4) будем искать в следующем виде:
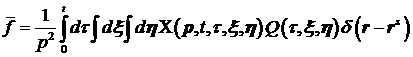 . (5) . (5)
Подставим 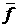 в уравнение (3).
Рассмотрим частную производную: в уравнение (3).
Рассмотрим частную производную:
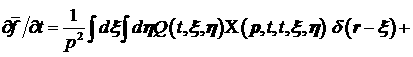
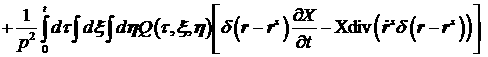 . .
Наложим на
функцию 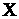 условие условие 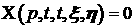 . Тогда . Тогда
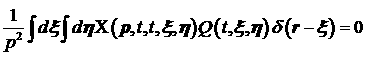 . .
Уравнение (4)
преобразуется к виду:
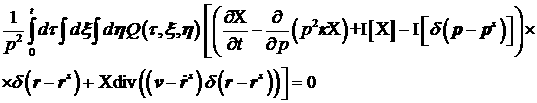 (6) (6)
К тому
времени, когда источник в уравнении (3) становится существенным по сравнению с 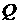 , столкновения начинают преобладать и над свободным переносом
электронов в пространстве. Действительно, размер области, занятой электронами
определяется длинами пробега, соответствующими начальной энергии, а сечения в
интеграле столкновений определяются текущей энергией. Поэтому слагаемое , столкновения начинают преобладать и над свободным переносом
электронов в пространстве. Действительно, размер области, занятой электронами
определяется длинами пробега, соответствующими начальной энергии, а сечения в
интеграле столкновений определяются текущей энергией. Поэтому слагаемое
в левой части
уравнения (3) мало по сравнению со слагаемым
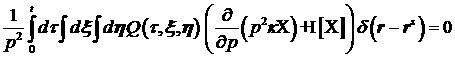 . .
Пренебрежем в
уравнении (6) отклонением электронов от траекторий, определяемых уравнениями
движения, за счет переноса в пространстве, по сравнению с отклонениями за счет
столкновений:
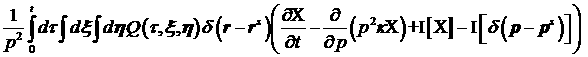 . (7) . (7)
Рассмотрим
уравнение для функции 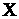 . .
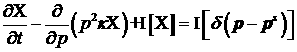 .
(8) .
(8)
Для того,
чтобы пользоваться в дальнейшем сферическими гармониками функции 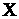 , представим , представим 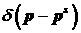 следующим образом [9]: следующим образом [9]:
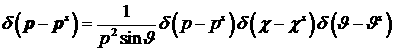 , ,
и формально разложим в ряд по
сферическим функциям:
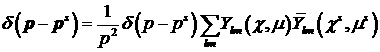
Такое
представление обобщенной функции 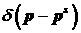 корректно, поскольку
она действует на любую финитную бесконечно дифференцируемую функцию корректно, поскольку
она действует на любую финитную бесконечно дифференцируемую функцию 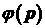 из основного
пространства следующим образом: из основного
пространства следующим образом:
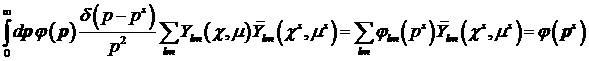
Заметим, что
введенное определение 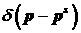 позволяет корректно
представить обобщенную функцию позволяет корректно
представить обобщенную функцию 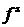 в виде ряда: в виде ряда:
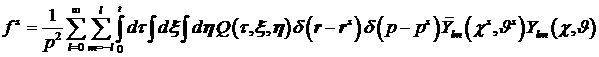 . .
Для
коэффициентов разложения 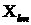 функции функции 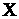 в силу ортогональности
сферических функций, обозначив в силу ортогональности
сферических функций, обозначив 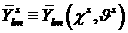 , получим следующее уравнение: , получим следующее уравнение:
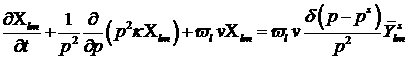 , (9) , (9)
Введенное
выше условие на функцию 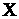 определяет начальное
условие определяет начальное
условие 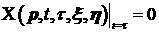 . В совокупности с этим условием уравнение (9) составляет задачу
Коши. Ее решение имеет вид: . В совокупности с этим условием уравнение (9) составляет задачу
Коши. Ее решение имеет вид:
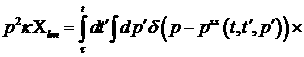
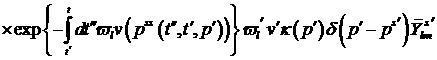 (10)
(10)
Здесь 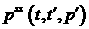 есть решение уравнения есть решение уравнения
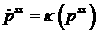 , если , если 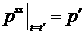 . .
Выполним в
(10) интегрирование по 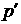 : :
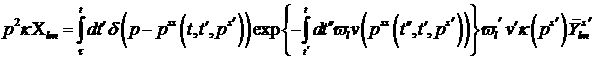 .(11) .(11)
Рассмотрим
величину 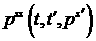 . Она отлична от . Она отлична от 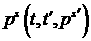 тем, что при ее
вычислении в уравнении движения отсутствует компонента силы Лоренца,
действующая по направлению движения электрона. Поскольку для электронов,
описываемых функцией тем, что при ее
вычислении в уравнении движения отсутствует компонента силы Лоренца,
действующая по направлению движения электрона. Поскольку для электронов,
описываемых функцией 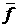 , эта компонента мала по сравнению с тормозной способностью,
можно считать, что , эта компонента мала по сравнению с тормозной способностью,
можно считать, что 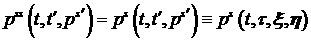 . Тогда . Тогда
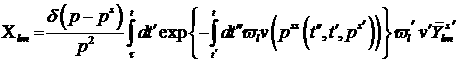 ,
(12) ,
(12)
В
соответствии с принятым приближением величина 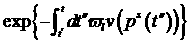 , как функция переменной , как функция переменной 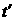 меняется быстрее, чем меняется быстрее, чем 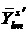 . Поэтому приближенно . Поэтому приближенно
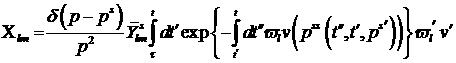 ,
(13) ,
(13)
Выполним
интегрирование по 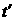 и подставим полученное
решение в (6): и подставим полученное
решение в (6):
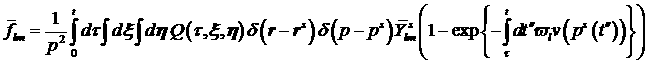
Вычитая
коэффициенты 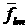 из из 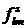 , получим , получим
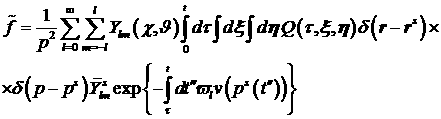 (14)
(14)
2 Уравнение непрерывности
Потребуем, чтобы для приближенного решения (9)
выполнялось спектральное уравнение непрерывности:
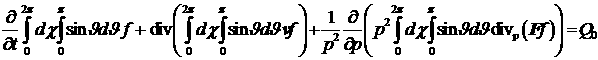 (15) (15)
Данное уравнение получено интегрированием уравнения
(1) по  и и  с весом с весом  . Выполнения условия (15) для приближенного решения (14)
можно добиться путем корректировки нулевого члена суммы (14). Вычислим его из
уравнения (10), подставив в него . Выполнения условия (15) для приближенного решения (14)
можно добиться путем корректировки нулевого члена суммы (14). Вычислим его из
уравнения (10), подставив в него 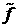 вместо вместо 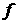 : :
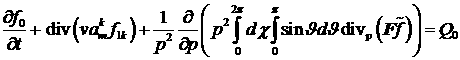 . .
Здесь 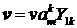 , где индекс , где индекс 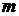 принимает значения
(1,-1,0), а принимает значения
(1,-1,0), а
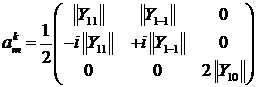 . .
Заметим следующее.
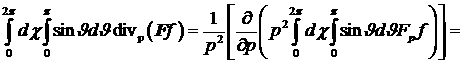
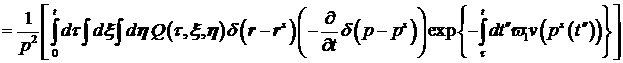
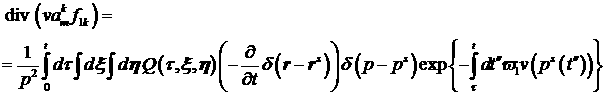
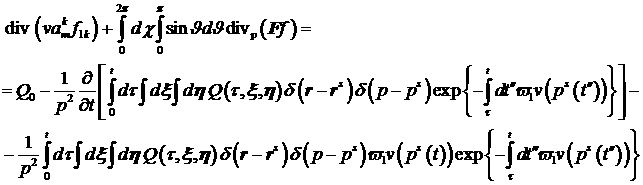
С учетом этих промежуточных выкладок
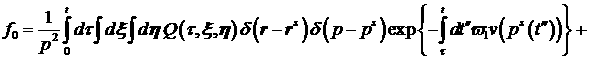 (16) (16)
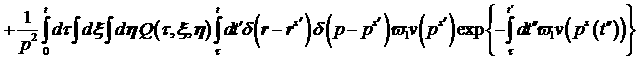 . .
Заметим, что интеграл по переменной 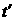 во втором слагаемом
правой части (11) может быть вычислен в соответствии с принятым приближением: во втором слагаемом
правой части (11) может быть вычислен в соответствии с принятым приближением:
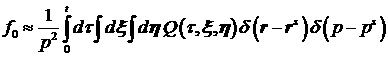 . .
Тогда 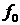 полностью совпадет с
нулевым членом ряда (9). Для электродинамической модели приближенное вычисление
интеграла не допустимо, поскольку приводит к нарушению полного уравнения непрерывности
заряда. полностью совпадет с
нулевым членом ряда (9). Для электродинамической модели приближенное вычисление
интеграла не допустимо, поскольку приводит к нарушению полного уравнения непрерывности
заряда.
Таким образом, окончательно приближенное решение
уравнения (1) рассматривается в следующем виде:
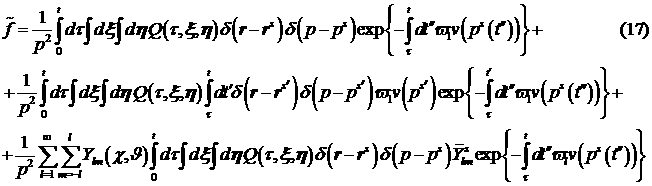
Для (17) выполнено спектральное уравнение
непрерывности заряда.
3 Точность приближенного решения
Подставим (17) в уравнение (1) и вычислим невязку:
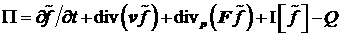 (18)
(18)
Для вычисления невязки, прежде всего, заметим
следующее. В производной 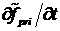 присутствуют
слагаемые, образующиеся при дифференцировании по верхнему пределу интеграла по
переменной присутствуют
слагаемые, образующиеся при дифференцировании по верхнему пределу интеграла по
переменной 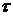 . Их сумма образует источник . Их сумма образует источник 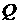 , представленный в виде разложения по сферическим функциям.
Выражения, образующиеся дифференцированием по времени экспоненты в первом слагаемом , представленный в виде разложения по сферическим функциям.
Выражения, образующиеся дифференцированием по времени экспоненты в первом слагаемом
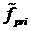 и по верхнему пределу
интеграла по переменной и по верхнему пределу
интеграла по переменной 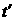 во втором слагаемом во втором слагаемом 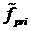 , равны с обратным знаком. Дифференцирование по времени
экспоненты в третьем слагаемом дает , равны с обратным знаком. Дифференцирование по времени
экспоненты в третьем слагаемом дает 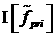 с обратным знаком.
Таким образом, с обратным знаком.
Таким образом,
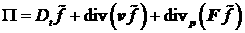 .
(19) .
(19)
Здесь символ 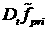 означает сумму
слагаемых, входящих в производную означает сумму
слагаемых, входящих в производную 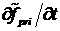 , образующихся при дифференцировании по , образующихся при дифференцировании по 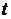 только компонент векторов только компонент векторов
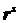 , и , и 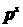 . .
Представим невязку (19) в виде ряда по сферическим
функциям:
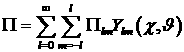 , ,
умножим на произвольную бесконечное число раз
дифференцируемую функцию из основного пространства 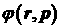 и проинтегрируем по
переменным и проинтегрируем по
переменным 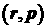 : :
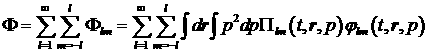 . (20) . (20)
Для вычисления 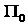 проинтегрируем (19): проинтегрируем (19):
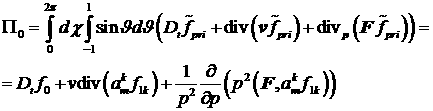 , ,
и вычислим
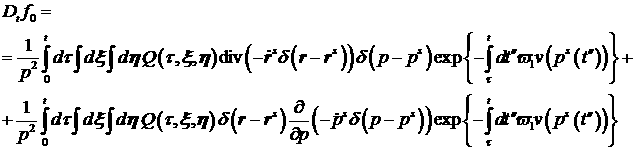 , ,
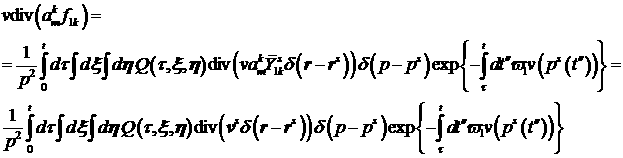 , ,
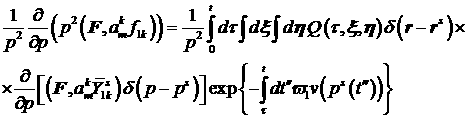 . .
Получим, что нулевой член в сумме (20) равен нулю.
Этот результат очевиден, поскольку при построении 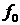 использовалось
спектральное уравнение непрерывности, и означает, что функция распределения использовалось
спектральное уравнение непрерывности, и означает, что функция распределения 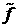 является точным
решением уравнения (1) в пространстве обобщенных функций, заданных на основном
пространстве финитных бесконечно дифференцируемых, сферически симметричных по
переменной является точным
решением уравнения (1) в пространстве обобщенных функций, заданных на основном
пространстве финитных бесконечно дифференцируемых, сферически симметричных по
переменной 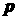 функций функций 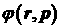 [10]. [10].
Для дальнейших оценок обозначим символом 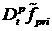 сумму слагаемых, образующихся
при дифференцировании по сумму слагаемых, образующихся
при дифференцировании по 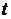 только компонент
вектора только компонент
вектора 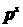 , можно записать невязку в виде , можно записать невязку в виде
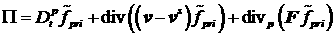 (20) (20)
Далее, обозначив символом 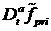 сумму слагаемых,
образующихся при дифференцировании
только величин сумму слагаемых,
образующихся при дифференцировании
только величин 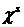 и и 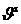 , можно записать невязку в виде: , можно записать невязку в виде:
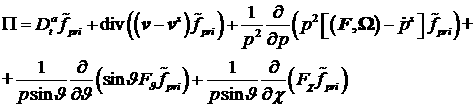 (21) (21)
С учетом того, что 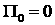 , после ряда промежуточных вычислений, невязку можно
представить в следующем виде: , после ряда промежуточных вычислений, невязку можно
представить в следующем виде:
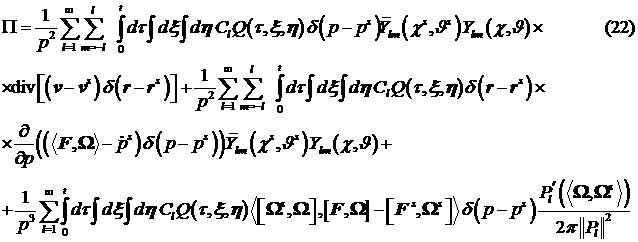
В формуле (22) суммирование по индексу 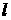 ведется от единицы до
бесконечности. Введено обозначение ведется от единицы до
бесконечности. Введено обозначение 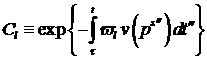 . .
Ограничим класс функций 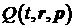 , исходя из простого физического соображения. Будем считать,
что , исходя из простого физического соображения. Будем считать,
что 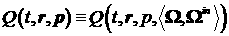 , где , где 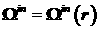 – поле направлений в координатном пространстве. – поле направлений в координатном пространстве.
Это дает возможность ограничить для дальнейшего
рассмотрения класс функций основного пространства, на которых оценивается
невязка решения. Ограничимся положительными функциями 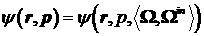 , представимыми в виде ряда, сходящегося равномерно для всех
значений , представимыми в виде ряда, сходящегося равномерно для всех
значений 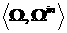 : :
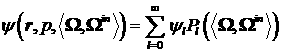 (23)
(23)
где 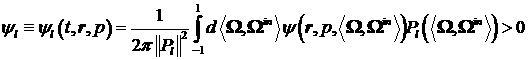 . .
Рассмотрим функцию
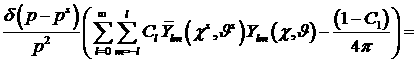
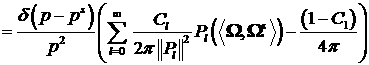 (24). (24).
Заметим следующее. Функции 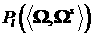 ортогональны на
единичной сфере. Действительно: ортогональны на
единичной сфере. Действительно:
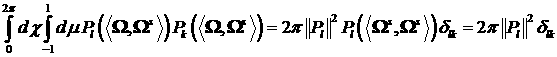
Заметим также, что
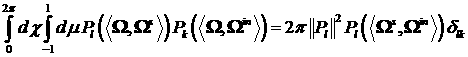
При 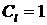 для всех для всех 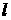 , то есть при , то есть при 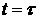 функция (24)
приобретает вид расходящегося ряда: функция (24)
приобретает вид расходящегося ряда:
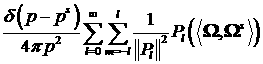 (25).
(25).
Этот ряд может рассматриваться как 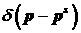 . Действительно: . Действительно:
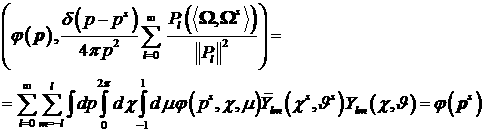 (26) (26)
Вычислим следующую величину:
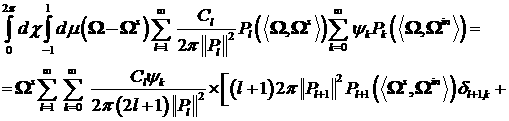
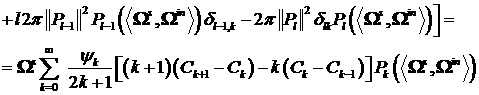 (27) (27)
Рассмотрим выражение 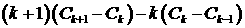 . Оценим его по модулю
значения: . Оценим его по модулю
значения:
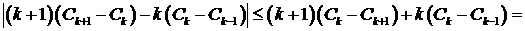
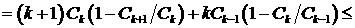
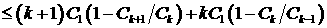
Рассмотрим величину 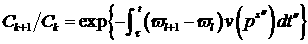 . Поскольку . Поскольку 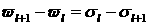 , то из свойств сечения
углового рассеяния, резко возрастающего при нулевом угле рассеяния, следует,
что , то из свойств сечения
углового рассеяния, резко возрастающего при нулевом угле рассеяния, следует,
что 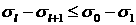 . Тогда . Тогда 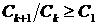 . В силу этого . В силу этого 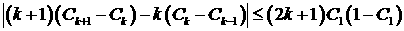 . .
При 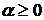 справедливо равенство справедливо равенство 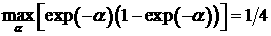 , поэтому оценка (27) может быть продолжена следующим
образом: , поэтому оценка (27) может быть продолжена следующим
образом:
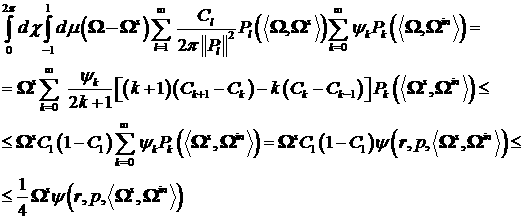 (28) (28)
Аналогично можно получить оценку
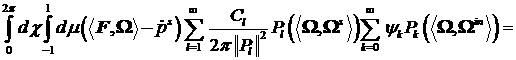
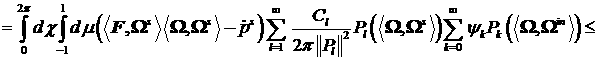 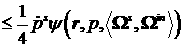 (29)
(29)
Подействуем невязкой (22) на функцию 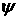 из основного
пространства, учитывая, что третье слагаемое после интегрирования по
компонентам импульса обратиться в ноль: из основного
пространства, учитывая, что третье слагаемое после интегрирования по
компонентам импульса обратиться в ноль:
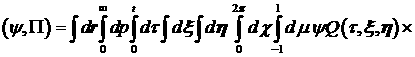
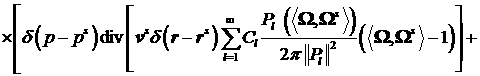 (30)
(30)
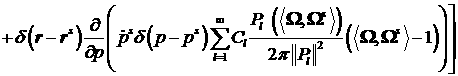
Выполним интегрирование по частям в правой части:
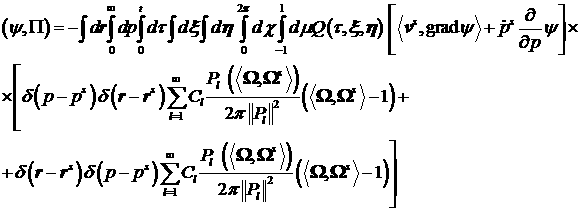
В силу оценок (28) и (29) получим неравенство:
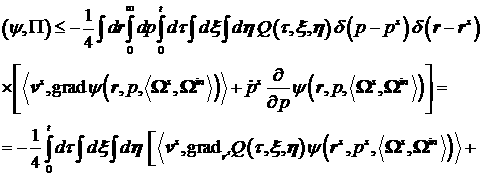
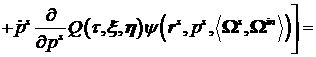
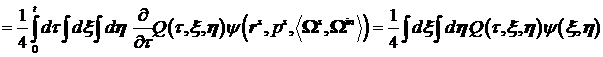
Таким образом, окончательно оценка имеет вид:
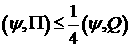 (31)
(31)
Физический смысл данной оценки состоит в следующем.
Подстановка приближенного решения в уравнение приводит к образованию невязки 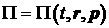 . Поэтому приближенное решение является точным для уравнения
(1) с правой частью . Поэтому приближенное решение является точным для уравнения
(1) с правой частью 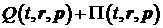 . В соответствии с оценкой (31) такая правая часть отличается
от . В соответствии с оценкой (31) такая правая часть отличается
от 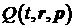 не более, чем на
четверть в обобщенном смысле. Задача вычисления электромагнитного поля путем
решения задачи Коши с однородными начальными данными для уравнения (1) в
совокупности с уравнениями Максвелла для самосогласованного электромагнитного
поля и уравнений газовой динамики для вторичных электронов [11] существенно отличается
от аналогичной задачи для уравнения Власова. Отличие заключается в том, что
соответствующая линейная задача имеет ограниченное решение. Причиной этого
отличия является наличие столкновений в сочетании с импульсным по времени
характером правой части. Ограниченность линейного решения обеспечивает
устойчивость по правой части. не более, чем на
четверть в обобщенном смысле. Задача вычисления электромагнитного поля путем
решения задачи Коши с однородными начальными данными для уравнения (1) в
совокупности с уравнениями Максвелла для самосогласованного электромагнитного
поля и уравнений газовой динамики для вторичных электронов [11] существенно отличается
от аналогичной задачи для уравнения Власова. Отличие заключается в том, что
соответствующая линейная задача имеет ограниченное решение. Причиной этого
отличия является наличие столкновений в сочетании с импульсным по времени
характером правой части. Ограниченность линейного решения обеспечивает
устойчивость по правой части.
Оценка точности является мажоритарной и ее можно
уточнить. Погрешность при этом будет существенно уменьшена. Однако в широком
классе практически важных задач точность задания источника электронов не
превышает порядка величины, что делает точность моделирования вполне приемлемой.
Заключение
Приближение однородного рассеяния электронов на
траекториях позволяет существенно снизить объемы вычислений по сравнению, как с
методом Монте-Карло, так и методом дискретных ординат. Приближение имеет ограничения.
Главное из них состоит в том, что функция распределения представляется в виде
ряда. Для применения метода частиц достаточно вычисления плотности тока и
концентрации. Остальные моменты функции распределения не вычисляются.
Организовать их вычисление возможно, однако полиномы Лежандра сходятся медленно
и преимущества в скорости вычисления утрачиваются.
Литература
1. Д.М. Иващенко, А.А. Федоров. Российские ускорители
электронов, использующиеся в качестве моделирующих установок. – Вопросы атомной науки и
техники, серия «Физика радиационного воздействия на радиоэлектронную аппаратуру»,
2002.- вып. 3, c. 120-128.
2. В.И.Бойко,
В.А.Скворцов, В.Е.Фортов, И.В.Шаманин. Взаимодействие импульсных пучков
заряженных частиц с веществом. – М.: Физматлит, 2003.
3. В.В.Веденяпин. Кинетические
уравнения Больцмана и Власова. М., ФИЗМАТЛИТ, 2001.
4. Hockney R.W., Eastwood J.W. Computer
Simulation Using Particles.– McGraw-Hill, New York,
1981.
5. Н.С. Келлин, М.Б. Марков, С.В. Паротькин.
Столкновения в математических моделях электромагнитного поля электронного
потока. – Препринт ИПМ им. М.В. Келдыша № 33, Москва, 2006.
6. А.Ф. Никифоров, В.Б. Уваров. Специальные функции
математической физики. – М.: Наука, 1984.
7. Н. Мотт,
Г. Мэсси. Теория атомных столкновений. М.: МИР, 1969.
8. Г. Мэсси, Е. Бархоп. Электронные
и ионные столкновения. М.: МИР, 1958.
9. В.Я. Арсенин. Методы математической
физики и специальные функции. – M.: Наука,
1984.
10. И.М. Гельфанд, И.М. Шилов.
Обобщенные функции и действия над ними. – М.: Добросвет, 2000.
11. А.В.Березин, Н.С.Келлин, М.Б.Марков,
С.В.Паротькин, А.В.Сысенко. О математических моделях вторичной
ионизации. – Препринт ИПМ им. М.В. Келдыша РАН, 2002,
№29.
|