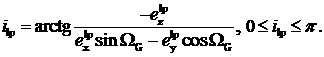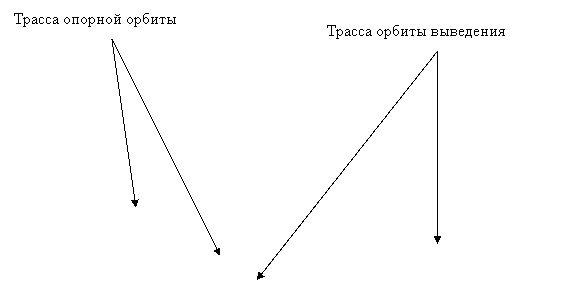Аннотация
Располагая данными о начальной орбите КА (орбите выведения или промежуточной орбите сложной
схемы выведения), координатах точки старта и временем старта, можно восстановить схему
выведения: оценить параметры опорной орбиты, на которую выводится КА вместе с разгонным блоком
или с последней ступенью ракеты-носителя (РН) перед проведением маневра, азимут запуска и
затраты характеристической скорости на маневр перехода на начальную орбиту. Препринт посвящен
построению алгоритма получения этих оценок.
Располагая данными о начальной орбите, можно оценить долготу восходящего узла на момент первого
пересечения плоскости экватора после момента старта. По оценке долготы восходящего узла,
времени старта и координатам точки старта оцениваются азимут запуска и наклонение опорной
орбиты РН. Если наклонение опорной орбиты отличается от наклонения начальной орбиты, то
произошел запуск с изменением наклонения. Другие параметры опорной орбиты и затраты
характеристической скорости оцениваются с использованием задачи Ламберта, которая позволяет
определять параметры орбиты по двум положениям и моментам времени. Положение на левом конце
находится на некоторой высоте над точкой старта. Момент времени, соответствующий левому концу,
принадлежит интервалу времени справа от момента старта. Выполняется перебор по возможным
положениям и моментам времени на левом конце. Параметры опорной орбиты при переборе выбираются
из условий на минимальную высоту опорной орбиты и модуль вектора характеристической скорости.
В докладе приведены примеры анализа выведений с космодромов: Мыс Канаверал, Ванденберг, Куру,
Сичан.
Abstract
Information about the orbital motion of spacecraft is available via Internet where one can find
the two- line elements of the primary orbit. If we know the primary orbit, the coordinates of
the launch site and the time we can restore the launch profile: we can evaluate the launch
azimuth and the characteristic velocity required for the transition to the primary orbit.
The work is presenting the procedure for evaluation of these parameters. With available data
on the primary orbit we can evaluate the longitude of the ascending node for the time of
the first crossing of the equator plane. Using the estimates of the ascending node, the time
of the launch and the coordinates of the launch site we can evaluate the azimuth and
the inclination of the launch.
If the inclination of the launch orbit differs from the inclination of the primary deployment
orbit then we have the case of launch with change of the inclination. The other parameters
of the launch orbit and the characteristic velocity can be evaluated by solving Lambert problem
for determination of orbital parameters using two positions and two reference times.
The position for the left end should be above the launch site. The time corresponding to the
left end belongs to the interval, which is located to the right from the time of the launch.
Then we perform the search on possible positions and the times at the left end. The parameters
of the launch orbit are selected to satisfy the conditions for the minimum altitude of
the launch orbit and minimum module of characteristic velocity.
The paper presents the analysis for the launches from Canaveral, Vandenberg, Kuru and Sychuan
launch sites.
Введение. Данные об
орбитальном движении космических аппаратов (КА) доступны по каналам Internet в виде двустрочных
элементов (TLE)
[1,2,8]. Располагая данными о начальной (первой) орбите КА, выведенного
ракетой-носителем (РН) и разгонным блоком (РБ), координатах точки старта и
временем старта, можно восстановить схему выведения: оценить параметры орбиты,
на которую выводится КА вместе с разгонным блоком (опорной орбиты), азимут
запуска и затраты характеристической скорости на маневр перехода на начальную орбиту.
Препринт посвящен построению алгоритма получения этих оценок.
Начальной орбитой может быть
орбита выведения или промежуточная орбита в случае сложной схемы выведения.
Располагая данными о начальной орбите, можно оценить долготу восходящего узла
на момент первого пересечения плоскости экватора после момента старта. По
оценке долготы восходящего узла, времени старта и координатам точки старта
оцениваются азимут запуска и наклонение опорной орбиты. Под опорной орбитой
понимается орбита, по которой двигался КА после завершения основной части
активного участка. Если наклонение опорной орбиты отличается от наклонения
начальной орбиты, то произошел запуск с
изменением наклонения. Параметры опорной орбиты и затраты характеристической
скорости оцениваются с использованием задачи Ламберта [3-6], которая позволяет
определять параметры орбиты по двум положениям и моментам времени. Маневр
изменения наклонения может быть модельно представлен в виде мгновенного
импульса, выданного в момент прохождения узла орбиты. Будем считать, что
маневр, изменивший наклонение, произошел в момент, когда начальная орбита в
первый раз после момента старта пересекает экваториальную плоскость. Тем самым
определено положение на правом конце и соответствующий момент времени,
необходимые как исходные данные для задачи Ламберта. Положение на левом конце
находится на некоторой высоте над точкой старта. Момент времени,
соответствующий левому концу, принадлежит интервалу справа от момента старта.
Выполняется перебор по возможным положениям и моментам времени на левом конце.
Параметры опорной орбиты при переборе определяются из условий на высоту
перицентра и затрат характеристической скорости, необходимой для перехода с
опорной на начальную орбиту.
В докладе приведены примеры
анализа выведений с космодромов: Мыс Канаверал, Ванденберг, Куру, Сичан.
Авторы выражают
признательность В.А. Степаньянцу, оказавшему существенную помощь в работе над
препринтом
Формализация и постановка
задачи. Рассмотрим
следующую модель. После старта КА и разгонный блок (или последняя ступень РН)
движутся по опорной траектории до момента пересечения экватора. При пересечении
экватора разгонный блок выдает импульс, который изменяет наклонение. Возможные
моменты времени приложения мгновенного импульса, изменившего наклонение, и
соответствующие положения КА можно определить по начальной орбите как моменты
времени прохождения восходящих и нисходящих узлов.
Рассмотрим теперь движение
КА по опорной орбите. Двигаясь по этой орбите, КА должен был бы пройти над
точкой старта в некоторый момент времени, который наступил позже момента старта
на несколько минут. Задав возможный диапазон высот прохождения над точкой
старта опорной орбиты, получим множество моментов времени и положений КА.
Таким образом, для опорной
орбиты определено множество возможных положений (в районе точки старта) и
соответствующих им моментов времени (левый конец) и множество возможных
положений и соответствующих им моментов времени в момент изменения наклонения
(правый конец). Для каждой пары из множеств на левом и правом конце можно
определить опорную орбиту, решив задачу Ламберта. Выполняя перебор по элементам
множеств на левом и правом концах, получим различные опорные орбиты. По опорной
и начальной орбитам можно вычислить характеристическую скорость, необходимую
для изменения наклонения. Среди множества опорных орбит, получаемых в
результате перебора, следует рассматривать только такие, которые удовлетворяют
ограничению по высоте перицентра. Из множества опорных орбит, удовлетворяющих
ограничению, выбирается такая, для которой минимален импульс изменения
наклонения.
Метод решения задачи. Введем следующие
обозначения: 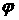 - широта полигона
старта, - широта полигона
старта, 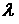 - долгота полигона
старта, - долгота полигона
старта,  - момент старта (дата
и время старта), - момент старта (дата
и время старта), 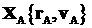 - вектор состояния
начальной орбиты (орбиты выведения или промежуточной орбиты в случае сложной
схемы выведения), - вектор состояния
начальной орбиты (орбиты выведения или промежуточной орбиты в случае сложной
схемы выведения), 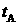 - момент времени,
соответствующий вектору состояния - момент времени,
соответствующий вектору состояния 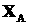 . .
Вначале проверяется:
изменилось ли наклонение. Для этого по начальным условиям начальной орбиты
численным интегрированием вычисляется 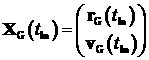 вектор состояния на
момент старта в гринвичской системе координат, фиксированной на этот же момент.
Вычисляются долгота восходящего узла вектор состояния на
момент старта в гринвичской системе координат, фиксированной на этот же момент.
Вычисляются долгота восходящего узла 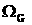 и наклонение и наклонение 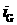 орбиты, определяемые
вектором состояния орбиты, определяемые
вектором состояния 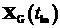 . .
Далее с использованием
широты 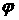 и долготы и долготы 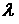 точки старта вычисляется вектор точки старта вычисляется вектор 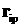 — положение точки
старта в ГСК и орт этого вектора: — положение точки
старта в ГСК и орт этого вектора: 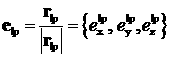 . Оценка наклонения орбиты вычисляется по формуле: . Оценка наклонения орбиты вычисляется по формуле:
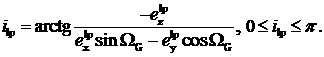
Если 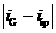 модуль разности
наклонения начальной орбиты и наклонения, вычисленного по точке старта, больше
заданного порога, то в процессе выведения произошло изменение наклонения. Рассмотрим
алгоритм, позволяющий для этого случая восстановить схему выведения, оценить
азимут запуска, затраты характеристической скорости на маневр изменения
наклонения и параметры орбиты до изменения наклонения. модуль разности
наклонения начальной орбиты и наклонения, вычисленного по точке старта, больше
заданного порога, то в процессе выведения произошло изменение наклонения. Рассмотрим
алгоритм, позволяющий для этого случая восстановить схему выведения, оценить
азимут запуска, затраты характеристической скорости на маневр изменения
наклонения и параметры орбиты до изменения наклонения.
Рассмотрим более подробно
этот алгоритм.
Входная информация:
|
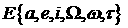
|
-
|
элементы
опорной орбиты,
|
|
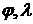
|
-
|
широта
и долгота точки старта,
|
|

|
-
|
момент
старта (дата и время старта),
|
|
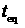
|
-
|
момент прохождения экватора, на котором ожидается
маневр изменения наклонения.
|
Выходная информация:
|
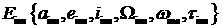
|
-
|
элементы
орбиты выведения,
|
|
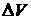
|
-
|
модуль импульса перехода с опорной орбиты
выведения на начальную орбиту,
|
|
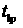
|
-
|
время прохождения над точкой старта при движении
по опорной орбите.
|
1. Вычисляется матрица 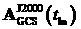 перехода из ГСК в СК J2000 на
момент времени перехода из ГСК в СК J2000 на
момент времени  . .
2. По элементам орбиты 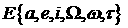 и моменту прохождения экватора и моменту прохождения экватора 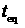 вычисляется вектор
состояния КА: вычисляется вектор
состояния КА: 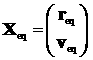 . Устанавливаются начальные состояния признаков: . Устанавливаются начальные состояния признаков:
|
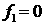
|
-
|
признак наличия решения, удовлетворяющего
ограничениям по высоте перицентра;
этот признак используется для поиска решения с минимальной высотой апоцентра
среди решений, удовлетворяющих ограничению по высоте перицентра;
|
|
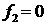
|
-
|
признак наличия решения; этот признак используется
для поиска решения с максимальной высотой перицентра среди всех решений.
|
3. Выполняется перебор по возможным моментам 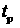 прохождения над точкой старта в диапазоне от прохождения над точкой старта в диапазоне от 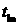 до до 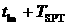 с шагом с шагом 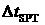 . Например, . Например, 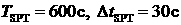 . .
4. Выполняется перебор по высоте прохождения над
полигоном 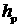 в диапазоне от в диапазоне от 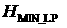 до до 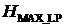 с шагом с шагом 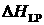 . .
Например, 
Для каждой пары значений 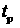 и и 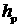 выполняются пункты: 5
– 10. выполняются пункты: 5
– 10.
5. Вычисляется 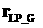 положение КА над точкой старта в ГСК по координатам полигона положение КА над точкой старта в ГСК по координатам полигона 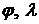 и высоте и высоте 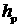 . .
6. Вычисляется матрица перехода из ГСК в СК J2000 на
момент 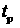 : :
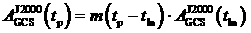 , ,
где
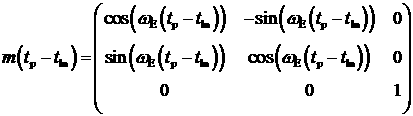 . .
7. Вычисляется положение КА в момент прохождения над
точкой старта в СК J2000:
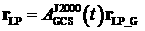 . .
8. Решается задача Ламберта для определения орбиты,
обеспечивающей перелет из точки  в момент в момент  в точку в точку 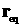 в момент в момент 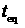 . В результате решения задачи Ламберта будут получены два,
одно или ни одного решения. Если не получено ни одного решения, то происходит
переход к следующей паре значений. . В результате решения задачи Ламберта будут получены два,
одно или ни одного решения. Если не получено ни одного решения, то происходит
переход к следующей паре значений.
9. Предварительный анализ решений задачи Ламберта.
Если имеется два решения:
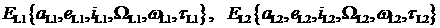 , ,
то выбирается то, для которого наклонение ближе к
наклонению заданной орбиты:
|
если 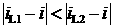
|
-
|
выбирается решение 1,
|
|
если 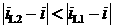
|
-
|
выбирается решение 2.
|
Если имеется одно решение,
то решение проверяется по критерию:
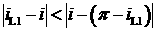 . .
Если решение не
удовлетворяет критерию, происходит переход к следующей паре значений.
Если решение найдено, то
переход к его анализу (п. 10). Обозначим найденное решение как 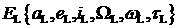 . .
10. Вычисляется высота перицентра:
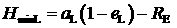 . .
Если выполняется условие 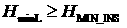 , то проверяется признак , то проверяется признак 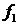 . Если . Если 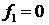 , то это первое найденное решение, удовлетворяющее
ограничению по высоте перицентра. В этом случае элементы орбиты , то это первое найденное решение, удовлетворяющее
ограничению по высоте перицентра. В этом случае элементы орбиты 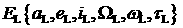 сохраняются в сохраняются в 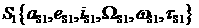 , момент времени , момент времени 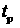 сохраняется в сохраняется в 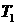 ( (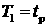 ), а признак ), а признак 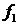 устанавливается в устанавливается в 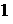 . .
Если 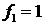 , то уже имеется отобранное решение. В этом случае
сравнивается высота апоцентра сохраненного решения с высотой апоцентра
анализируемого решения. Сохраняется решение с меньшей высотой апоцентра, т.е.
проверяется условие: , то уже имеется отобранное решение. В этом случае
сравнивается высота апоцентра сохраненного решения с высотой апоцентра
анализируемого решения. Сохраняется решение с меньшей высотой апоцентра, т.е.
проверяется условие: 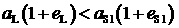 . Если условие выполнено, то в . Если условие выполнено, то в 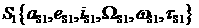 сохраняются элементы орбиты сохраняются элементы орбиты 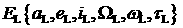 , в , в 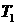 − значение − значение 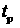 . .
Далее проверяется признак 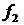 , который управляет поиском решения с максимальной высотой
перицентра среди всех решений. Если , который управляет поиском решения с максимальной высотой
перицентра среди всех решений. Если 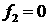 , это первое найденное решение. В этом случае найденное
решение , это первое найденное решение. В этом случае найденное
решение 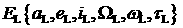 сохраняется в сохраняется в 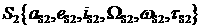 , момент времени , момент времени 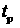 сохраняется в сохраняется в 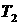 ( (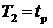 ), а признак ), а признак 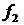 устанавливается в устанавливается в 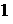 . .
Если 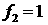 , то проверяется условие: , то проверяется условие: 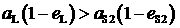 . Если это условие выполнено, то в . Если это условие выполнено, то в 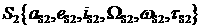 сохраняется сохраняется 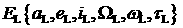 , а , а 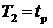 . .
На этом анализ пары 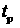 и и 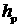 завершается. завершается.
11. Выбор решения. Если 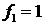 , то выбирается решение , то выбирается решение 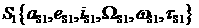 . Если . Если 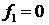 , а , а 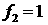 , выбирается решение , выбирается решение 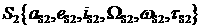 . .
Если одновременно 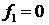 и и 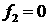 , то решение не найдено. , то решение не найдено.
Если решение найдено, то
переход к п. 12. Найденное решение — это и есть искомая опорная орбита 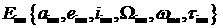 . Соответственно выбранному решению выбирается значение . Соответственно выбранному решению выбирается значение 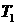 или или 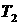 . Выбранное значение — это время прохождения над точкой
старта при движении по орбите выведения . Выбранное значение — это время прохождения над точкой
старта при движении по орбите выведения 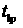 . .
12. Расчет модуля импульса. Вычисляется вектор
состояния на момент 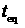 по орбитальным данным по орбитальным данным 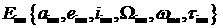 : : 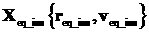 . Вычисляется модуль импульса перехода: . Вычисляется модуль импульса перехода: 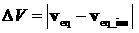 . .
Замечание. Поиск решений,
удовлетворяющих условию 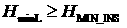 , может выполняться не только по критерию высоты перицентра
опорной орбиты, но и по критерию минимума характеристической скорости или по
комбинации этих критериев. , может выполняться не только по критерию высоты перицентра
опорной орбиты, но и по критерию минимума характеристической скорости или по
комбинации этих критериев.
Результаты. Примеры результатов,
полученных в результате работы алгоритма, описанного выше, приведены в таблицах
1-4 для запусков с космодромов: Мыс Канаверал, Вандерберг, Куру и Сичан.
Таблицы содержат следующие столбцы:
|
1
|
-
|
международное
обозначение пуска,
|
|
2
|
-
|
дата
пуска,
|
|
3
|
-
|
номер объекта
в Каталоге Космического командования ВВС США,
|
|
4
|
-
|
наклонение
начальной орбиты, град,
|
|
5
|
-
|
наклонение
опорной орбиты, град,
|
|
6
|
-
|
минимальная
высота начальной орбиты, км,
|
|
7
|
-
|
максимальная
высота начальной орбиты, км,
|
|
8
|
-
|
азимут
выведения, град,
|
|
9
|
-
|
интервал времени между достижением минимального расстояния между
трассой и точкой старта и моментом старта, сек,
|
|
10
|
-
|
модуль
импульса, м/с,
|
|
11
|
-
|
высота
перицентра опорной орбиты, км,
|
|
12
|
-
|
высота
апоцентра опорной орбиты, км.
|
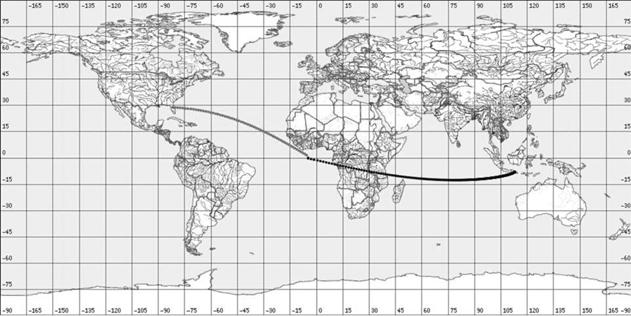
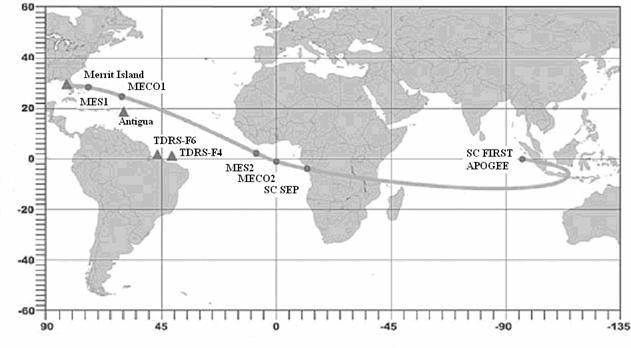
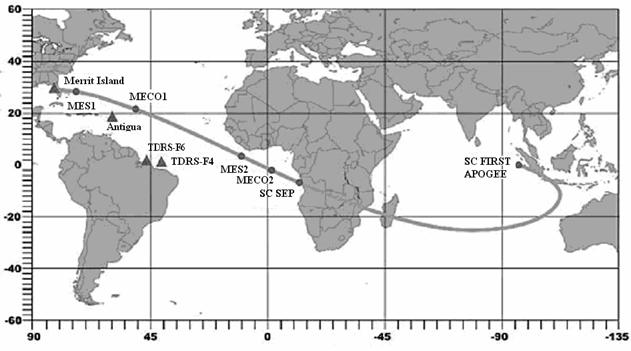
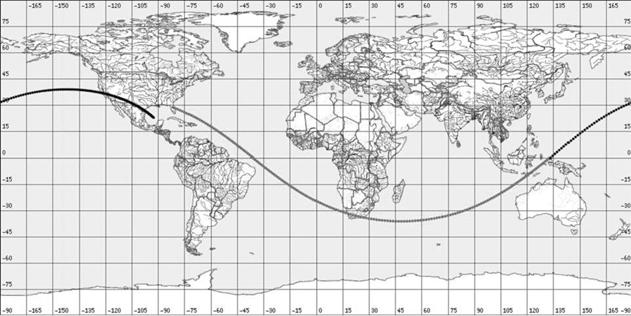
Для некоторых запусков в открытых официальных
материалах организаций, осуществляющих запуски КА, приведены трассы орбит
выведения и опорных орбит КА. В этих случаях можно сравнить трассу найденной
опорной орбиты и трассу опорной орбиты, приведенную в официальных материалах.
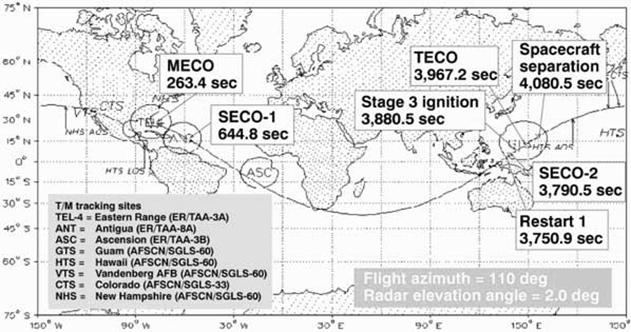
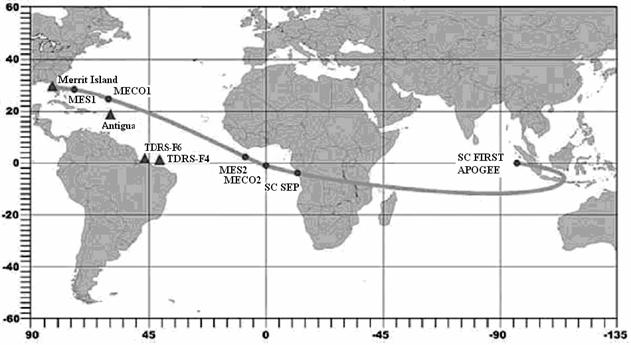
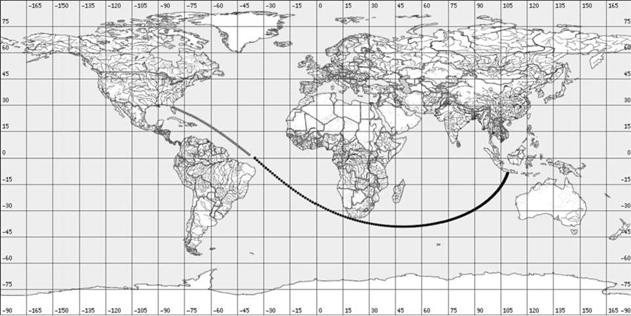
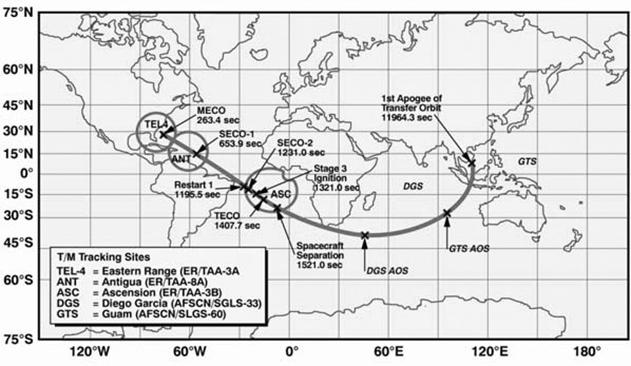
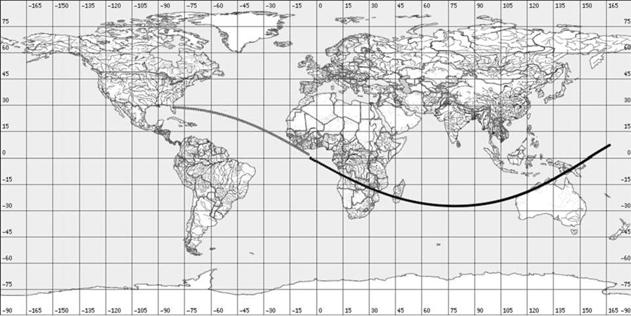
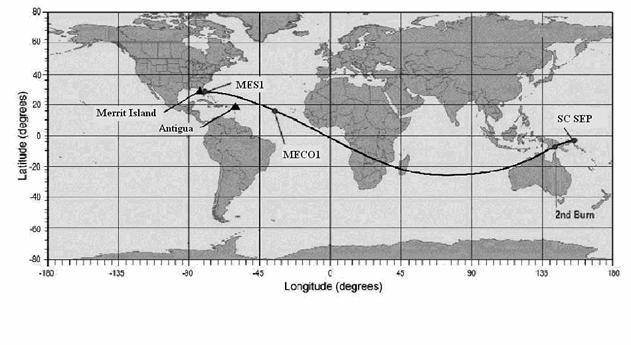
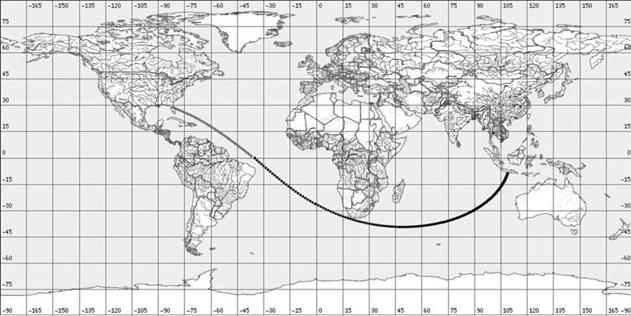
На рис. 1a,1b – 7a,7b приведены трассы найденных опорных орбит и приведенных в
материалах компаний Boeing
и International Launch Services
(ILS) по запускам с
международными номерами: 2004-003 (рис. 1), 2004-007 (рис. 2), 2004-009 (рис.
3), 2004-017 (рис. 4), 2004-023 (рис. 5), 2004-023 (рис. 6), 2004-045 (рис. 7).
Рисунки, номера которых заканчиваются на букву a, содержат трассы найденных орбит, а на
букву b — трассы из
официальных материалов.
|
![]() перехода из ГСК в СК J2000 на
момент времени
перехода из ГСК в СК J2000 на
момент времени ![]() .
.![]() и моменту прохождения экватора
и моменту прохождения экватора ![]() вычисляется вектор
состояния КА:
вычисляется вектор
состояния КА: 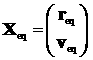 . Устанавливаются начальные состояния признаков:
. Устанавливаются начальные состояния признаков:![]() прохождения над точкой старта в диапазоне от
прохождения над точкой старта в диапазоне от ![]() до
до ![]() с шагом
с шагом ![]() . Например,
. Например, ![]() .
. ![]() в диапазоне от
в диапазоне от ![]() до
до ![]() с шагом
с шагом ![]() .
.
![]()
![]() и
и ![]() выполняются пункты: 5
– 10.
выполняются пункты: 5
– 10.![]() положение КА над точкой старта в ГСК по координатам полигона
положение КА над точкой старта в ГСК по координатам полигона ![]() и высоте
и высоте ![]() .
.![]() :
:![]() ,
,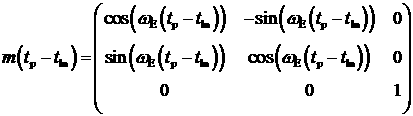 .
.![]() .
.![]() в момент
в момент ![]() в точку
в точку ![]() в момент
в момент ![]() . В результате решения задачи Ламберта будут получены два,
одно или ни одного решения. Если не получено ни одного решения, то происходит
переход к следующей паре значений.
. В результате решения задачи Ламберта будут получены два,
одно или ни одного решения. Если не получено ни одного решения, то происходит
переход к следующей паре значений. ![]() ,
, ![]() .
. ![]() .
.![]() .
. ![]() , то проверяется признак
, то проверяется признак ![]() . Если
. Если ![]() , то это первое найденное решение, удовлетворяющее
ограничению по высоте перицентра. В этом случае элементы орбиты
, то это первое найденное решение, удовлетворяющее
ограничению по высоте перицентра. В этом случае элементы орбиты ![]() сохраняются в
сохраняются в ![]() , момент времени
, момент времени ![]() сохраняется в
сохраняется в ![]() (
(![]() ), а признак
), а признак ![]() устанавливается в
устанавливается в ![]() .
.![]() , то уже имеется отобранное решение. В этом случае
сравнивается высота апоцентра сохраненного решения с высотой апоцентра
анализируемого решения. Сохраняется решение с меньшей высотой апоцентра, т.е.
проверяется условие:
, то уже имеется отобранное решение. В этом случае
сравнивается высота апоцентра сохраненного решения с высотой апоцентра
анализируемого решения. Сохраняется решение с меньшей высотой апоцентра, т.е.
проверяется условие: ![]() . Если условие выполнено, то в
. Если условие выполнено, то в ![]() сохраняются элементы орбиты
сохраняются элементы орбиты ![]() , в
, в ![]() − значение
− значение ![]() .
.![]() , который управляет поиском решения с максимальной высотой
перицентра среди всех решений. Если
, который управляет поиском решения с максимальной высотой
перицентра среди всех решений. Если ![]() , это первое найденное решение. В этом случае найденное
решение
, это первое найденное решение. В этом случае найденное
решение ![]() сохраняется в
сохраняется в ![]() , момент времени
, момент времени ![]() сохраняется в
сохраняется в ![]() (
(![]() ), а признак
), а признак ![]() устанавливается в
устанавливается в ![]() .
.![]() , то проверяется условие:
, то проверяется условие: ![]() . Если это условие выполнено, то в
. Если это условие выполнено, то в ![]() сохраняется
сохраняется ![]() , а
, а ![]() .
.![]() и
и ![]() завершается.
завершается.![]() , то выбирается решение
, то выбирается решение ![]() . Если
. Если ![]() , а
, а ![]() , выбирается решение
, выбирается решение ![]() .
.![]() и
и ![]() , то решение не найдено.
, то решение не найдено.![]() . Соответственно выбранному решению выбирается значение
. Соответственно выбранному решению выбирается значение ![]() или
или ![]() . Выбранное значение — это время прохождения над точкой
старта при движении по орбите выведения
. Выбранное значение — это время прохождения над точкой
старта при движении по орбите выведения ![]() .
.![]() по орбитальным данным
по орбитальным данным ![]() :
: ![]() . Вычисляется модуль импульса перехода:
. Вычисляется модуль импульса перехода: ![]() .
.![]() , может выполняться не только по критерию высоты перицентра
опорной орбиты, но и по критерию минимума характеристической скорости или по
комбинации этих критериев.
, может выполняться не только по критерию высоты перицентра
опорной орбиты, но и по критерию минимума характеристической скорости или по
комбинации этих критериев.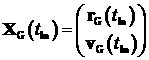
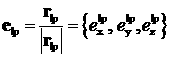 . Оценка наклонения орбиты вычисляется по формуле:
. Оценка наклонения орбиты вычисляется по формуле: