Исследование движения иглы туннельного микроскопа относительно поверхности
|
|
Введение |
3 |
|
§ 1. Конструкция
туннельного микроскопа НПО АЛМАЗ |
4 |
|
§ 2. Расчет туннельного
тока, проходящего через иглу туннельного микроскопа |
6 |
|
§ 3. Оценка размеров
конца иглы |
6 |
|
§ 4. Взаимодействие иглы
с поверхностью |
7 |
|
§ 5. Измерение рельефа
поверхности с помощью туннельного микроскопа |
9 |
|
Результаты и рекомендации |
12 |
|
Литература |
12 |
Введение
В работе
рассматривается задача интерпретации изображений, получаемых с помощью
туннельного микроскопа конструкции НПО АЛМАЗ, который используется в РХТУ им
Д.И.Менделеева. Интерес к туннельной микроскопии связан с тем, что она позволяет
получать сравнительно простым способом изображение рельефа подложки с разрешением
порядка 1 нм и менее.
В настоящее время используется метод механической развертки,
т.е. построчное сканирование поверхности. Поверхность как бы «ощупывается» концом
иглы на расстоянии примерно 1 нм. Измеренные относительные высоты
преобразуются в изображение рельефа и выводятся на дисплей.
Восстановление
реальной формы рельефа по получаемым результатам является достаточно сложной
математической задачей, так как требуется учитывать различные физические
факторы, которые влияют на туннельный ток, работу системы управления и
приводов. В общей постановке она сводится к решению уравнений в частных производных,
где неизвестным является рельеф поверхности, т.е. граничные условия. Сложность
прямого решения этой задачи приводит к необходимости поиска приближенных решений,
которые учитывают действующие факторы частично.
В настоящее
время штатное программное обеспечение для визуализации поверхности дает
достаточно грубое приближение, так как в нем в качестве рельефа принимается
траектория движения зонда. Точность такого решения зависит от точности
отслеживания заданной величины туннельного тока и выполнимости предположении,
что величина туннельного тока не зависит от рельефа и формы конца иглы.
В предлагаемой работе проведено исследование влияния
размеров конца иглы и физики туннельного
тока. Результаты исследования показывают,
что оба этих фактора вносят существенный вклад (порядка нанометра) в картину
получаемого изображения, что позволяет сделать вывод о необходимости коррекции
получаемого изображения в тех случаях, когда требуется получить разрешение 1 нм
и менее.
§ 1. Конструкция туннельного микроскопа НПО АЛМАЗ
 Микроскоп конструкции НПО АЛМАЗ
(рис. 1, 2) состоит из:
Микроскоп конструкции НПО АЛМАЗ
(рис. 1, 2) состоит из:
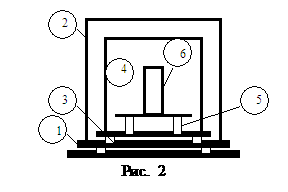 массивного основания (1),
кожуха (2), упругих опор (3, 5), камера для проведения экспериментов (4), блока
приводов (6).
массивного основания (1),
кожуха (2), упругих опор (3, 5), камера для проведения экспериментов (4), блока
приводов (6).
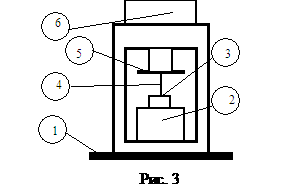
Блок приводов (рис. 3)
представляет собой: основание (1), ![]() пьезоприводы точных
перемещений (с разрешением 0,1 нанометра), устройства (3) крепления зонда (иглы
с радиусом закругления порядка 1 нанометра) (4), устройства крепления образца
(5), микрометрического механизма (6) для выведения образца в рабочую зону пьезоприводов.
пьезоприводы точных
перемещений (с разрешением 0,1 нанометра), устройства (3) крепления зонда (иглы
с радиусом закругления порядка 1 нанометра) (4), устройства крепления образца
(5), микрометрического механизма (6) для выведения образца в рабочую зону пьезоприводов.
§ 2. Расчет туннельного тока,
проходящего через иглу туннельного микроскопа
Основным способом получения рельефа
поверхности является сканирование при постоянной величине туннельного тока. В
этом режиме на иглу микроскопа подается постоянное напряжение. Система
управления поддерживает такую высоту до поверхности, чтобы величина туннельного
тока оставалась постоянной. Если поверхность является однородной, и между иглой
и подложкой нет других веществ, то в отсутствие возмущений конец иглы отслеживает
рельеф поверхности.
Неточности в отслеживании туннельного
тока и особенности его протекания приводят к тому, что расстояние между острием
иглы и подложкой не является постоянной величиной. В результате измеряемый
рельеф поверхности отличается от реального.
Рассмотрим зависимость плотности
туннельного тока от расстояния до подложки. Эта зависимость получена в работе
[2]:
j = ![]() (exp(-kz)
– (1+
(exp(-kz)
– (1+![]() )exp(-
)exp(-![]() , k =
, k = ![]() ,
,
где j
- плотность туннельного тока, k - константа затухания волновой функции в области потенциального
барьера, m = 9,1.10-31 кГ- масса
электрона, e = 1,6.10-19 Кл - заряд
электрона, j* » 4 эВ = 6,4.10-19
дж -
работа выхода электрона, h = 6,6 .10-34 дж/Кл - постоянная Планка, V -
подводимое напряжение, z – расстояние до поверхности.
При
указанных значениях констант k = 0,2 нм-1. В процессе сканирования
подводимое напряжение меньше 1 В.
Следовательно, eV < 1,6.10-19 дж << j*.
Используем
эту зависимость для упрощения формулы плотности туннельного тока, линеаризовав
его по параметру ![]() . В итоге получим:
. В итоге получим:
j = ![]() exp(-kz).
exp(-kz).
Подставив типичное значение подводимого
напряжения V = 0,3 В,
находим, что j = ![]() exp(-kz). Эту формулу удобно исследовать, если расстояние до поверхности z измерять в ангстремах.
Тогда j =
exp(-kz). Эту формулу удобно исследовать, если расстояние до поверхности z измерять в ангстремах.
Тогда j = ![]() 7-z А/Å2.
7-z А/Å2.
Диаметр
атома приблизительно равен 2Å. Если в процессе сканирования расстояние
между иглой и подложкой больше диаметра атома, т.е. z > 2Å,
то в этом случае 7-z << 1/z и, следовательно, зависимость туннельного тока от расстояния
определяется исключительно скоростью убывания показательной функции.
Отсюда можно
сделать вывод о том, что удаление иглы от поверхности на 1
Å приводит к уменьшению туннельного тока в семь раз, т.е. почти на
порядок. Расстояние между атомами составляет порядка 3 Å. Отсюда
делается вывод, что бо′льшая часть туннельного тока течет через ближайший
к сканируемой поверхности слой атомов, так как величина туннельного тока для
второго слоя меньше в 7-3 = 350 раз. Для того, чтобы существенная
доля туннельного тока приходилась на второй слой атомов, форма конца иглы
должна быть такой, чтобы диаметр второго слоя был бы в ![]() ≈ 18 раз больше, чем первого.
≈ 18 раз больше, чем первого.
Рабочая величина туннельного тока
равняется примерно 10-9А.
Обозначив через S площадку на
игле, через который протекает большая часть тока, получаем оценку для расстояния до подложки z,
которое должно удовлетворять условию
![]() . (1)
. (1)
Если условно принять, что площадь S равна площади атома (4 Å2),
то из этого неравенства следует, что расстояние, на котором должен двигаться кончик
иглы для того, чтобы туннельный ток оказался равным 10-9А,
составляет 4Å. В литературе (в том
числе в [2]) гипотетически считается возможной такая ситуация, когда весь
туннельный ток течет через атом, находящийся на конце иглы.
§ 3. Оценка размеров конца иглы
Случай, когда весь туннельный ток
течет через иглу, толщиной в один атом,
представляется маловероятным, так как плотность тока окажется такой же
как, если бы продолжительное время ток 10 000 А протекал по проводу диаметром
Для того,
чтобы уменьшить плотность тока на два
порядка, во столько же раз необходимо увеличить площадь сечения проводника.
Отсюда следует, что средний диаметр усика на конце иглы при величине туннельного
тока 1 нА должен иметь диаметр не менее 5 нм.
Учет ограничений на плотность тока
позволяет оценить снизу и размеры площадки, через которую туннельный ток
попадает в иглу. Естественно предположить, что плотность тока через площадку не
может быть более, чем на порядок выше тока, протекающий через конец иглы,
т.е.300 А/мм2. При величине тока 10-9 А
площадка должна иметь диаметр не менее 2 нм. Если, как было показано
выше, почти весь туннельный ток течет через один слой атомов, то, принимая во
внимание размеры площадки можно сделать вывод о том, что ближе к поверхности может находиться всего
лишь несколько атомов. Это условие накладывает ограничение на радиус
закругления иглы.
 Для оценки радиуса закругления воспользуемся рис. 4.
Здесь обозначены: r- радиус
атома, u - расстояние между
атомами, s - радиус
площадки, R – радиус закругления
иглы. Тогда
Для оценки радиуса закругления воспользуемся рис. 4.
Здесь обозначены: r- радиус
атома, u - расстояние между
атомами, s - радиус
площадки, R – радиус закругления
иглы. Тогда
s2 = R2-(R-(u + r))2, и R = 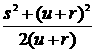 .
.
Принимая во внимание, что r =0,1 нм,
u = 0,3 нм, s = 1 нм, получим R = 10 нм. Полученная оценка радиуса закругления
площадки существенно больше оценки диаметра иглы. Однако, противоречия не
возникает, так как эти величины не связаны друг с другом функциональной зависимостью.
При некоторых технологиях производства
игл, на конце иглы получается сверхтонкий волосок. Ток, который может
пропустить этот волосок, ограничен его толщиной. Тонкие медные проводники
способны длительно пропускать ток порядка 10 А на каждый квадратный
миллиметр сечения. Следовательно, через медный проводник диаметром 1 нм
можно пропустить ток порядка 10 .10-12 А.
Для того, чтобы длительно пропускать ток 10-9 А волосок
должен иметь толщину несколько нанометров. Этот вывод находится в согласии с
полученными выше оценками.
Аналогичные рассуждения можно провести
относительно размеров области на поверхности, через которую проходит основная
часть туннельного тока. Разница состоит в том, что область перемещается по
поверхности вслед за иглой и, следовательно, в каждой точке оно существует
кратковременно. Поэтому, хотя его размер может быть в несколько раз меньше
диаметра площадки на игле, он все же конечен и составляет доли нанометра.
Таким образом, величина туннельного
тока является одним из ограничений чувствительности туннельного микроскопа.
Детали, которые меньше диаметра площадки, через которую туннельный ток попадает
на сканируемую поверхность, («пятна проводимости») воспроизводятся с
искажениями. Они как бы осредняются с соседними областями. Восстанавливать
реальный рельеф поверхности с разрешением меньше диаметра «пятна проводимости»
можно только при учете физических законов распространения туннельного тока.
Рассмотренные
особенности воспроизведения рельефа поверхности туннельным микроскопом могут
объяснить причину того, что стабильное изображение получается только после
нескольких сканирований. По-видимому, это связано с тем, что форма иглы и
субнанометровый рельеф поверхности изменяется (как бы отжигаются или
оплавляются) под воздействием высокой плотности туннельного тока.
Уравнение (1) позволяет получить
оценку на высоту сканирования. При диаметре площадки, через которую проходит
туннельный ток, в 2 нм она оказывается равной около 0,6 нм
(6 Å).
§ 4. Взаимодействие иглы с поверхностью
Особенности
прохождения туннельного тока проявляются в получаемых изображениях поверхности.
Туннельный ток протекает через слой атомов, и поэтому он является интегральной
величиной рельефа поверхности, находящегося под слоем атомов.
На первый взгляд это означает, что разрешение не может быть лучше линейных
размеров «пятна проводимости». Однако, если структура поверхности имеет
периодический характер, то результат осреднения будет также периодическим даже,
если период меньше размеров проводящей области. По этой причине, по-видимому,
удается увидеть атомную структуру поверхности. Если поверхность не является
периодической, то ее форму можно попытаться восстановить преобразованием,
обратным к осреднению.
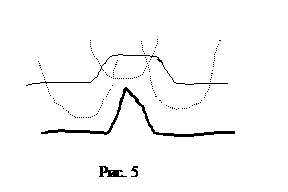
Рассмотрим теперь, как влияют размеры конца иглы на получаемое изображениие. На рис. 5 - 9 рассмотрены примеры огибания иглой поверхности для различных случаев.
Рис. 5 соответствует огибанию объекта,
имеющего вид пирамиды, размер которой больше диаметра иглы.
Непосредственно из рисунка можно сделать следующие выводы:
·
ширина
изображения рельефа больше пирамиды на ширину иглы и удвоенную величину
туннельного зазора;
·
на изображении
нет острого угла;
·
 относительная высота изображения пирамиды
приблизительно равна истинной высоте пирамиды.
относительная высота изображения пирамиды
приблизительно равна истинной высоте пирамиды.
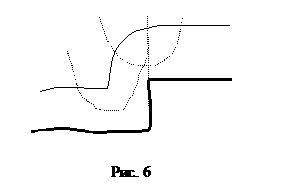
На рис. 6 рассмотрен случай огибания
ступеньки. Из рисунка можно сделать следующие выводы:
·
на изображении
уступ имеет вид дуги;
·
эта дуга совпадает с половиной поверхности иглы,
перевернутой концом вверх;
·
высота уступа
на изображении равна его истинной высоте;
·
дуга сдвинута
относительно уступа против направления сканирования на половину толщины иглы и
туннельный зазор (0,6 нм).
 На рис. 7 изображен случай огибания двух пирамид,
расстояние между которыми меньше размеров конца иглы. Из рисунка можно сделать
вывод о том, что о наличии двух рядом расположенных пирамид можно судить по
наличию щели на изображении рельефа. Глубина щели на порядок меньше реальной. С
учетом шумов определить наличие небольшой щели достаточно сложно.
На рис. 7 изображен случай огибания двух пирамид,
расстояние между которыми меньше размеров конца иглы. Из рисунка можно сделать
вывод о том, что о наличии двух рядом расположенных пирамид можно судить по
наличию щели на изображении рельефа. Глубина щели на порядок меньше реальной. С
учетом шумов определить наличие небольшой щели достаточно сложно.
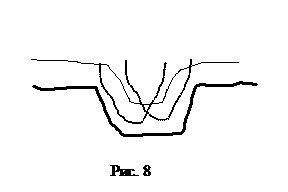 На
рис. 8 показано изображение впадины, которая шире конца иглы. Рисунок позволяет
сделать следующие выводы:
На
рис. 8 показано изображение впадины, которая шире конца иглы. Рисунок позволяет
сделать следующие выводы:
·
впадины на изображении
уже на ширину иглы и удвоенный туннельный зазор;
·
глубина впадины
равна глубине реальной впадины только, если ее ширина больше ширины конца иглы
и удвоенного туннельного зазора.
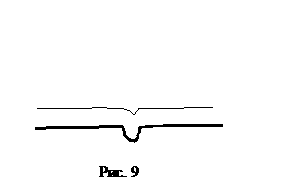
На
рис. 9 изображен случай, когда ширина впадины меньше диаметра иглы. Поскольку
туннельный ток является интегральной характеристикой проводящего слоя атомов,
ширина и глубина впадины на изображении окажется во много раз меньше, чем реальности.
Это позволяет сделать вывод о том, что без специальной обработки полученного
изображения сложно увидеть такие детали, размер которых меньше не только «пятна
проводимости», но и диаметра иглы.
§ 5. Измерение рельефа поверхности с помощью туннельного микроскопа
 Применим
результаты теоретического исследования для анализа изображений рельефа
поверхности, получаемого с помощью туннельного микроскопа.
Применим
результаты теоретического исследования для анализа изображений рельефа
поверхности, получаемого с помощью туннельного микроскопа.
На рис. 10 показан скан рельефа поверхности меди, который
получен с помощью туннельного микроскопа НПО «Алмаз» [1]. Скан имеет размеры
128 х 128 нм.
На рис. 11 представлена палитра, с помощью которой
кодируется высота поверхности. Для кодирования используются спектр всех цветов.
На рисунке представлены яркостные характеристики красного, зеленого и синего
цветов палитры.
Рис. 12 дает изображение в монохроматическом
свете. Яркость точки пропорциональна высоте. Рис. 12 отличается от рис. 10 тем,
что в нем высота кодируется не цветом, а яркостью.
Для анализа
изображений поверхности полезным оказалось представление рельефа в виде
вертикальных срезов (рис. 13). По вертикали отложена высота рельефа,
которая вычислена с помощью яркостной
палитры. В нижней части рисунка отложены ошибки такого пересчета. Непосредственно
из рисунка следует, что ошибки пренебрежимо малы. Рисунок показывает срез поверхности
при сканировании поверхности слева направо вдоль на отрезке длиной 128 нм.
Вертикальные полосы расставлены с шагом 1 нм. Их яркость меняется с
шагом 5 нм. Масштаб по вертикали и горизонтали одинаков. Вверху рисунка
изображена полоса, длина которой пропорциональна номеру скана на рис. 10.
Кроме рельефа с заданным номером показан также предыдущий.
Возможно также одновременное изображение последующего. Это позволяет выделять
ошибки, возникающие в измерительном тракте, так как, если на соседних
изображениях пик отсутствует, то, вероятно, он является ошибкой измерения.
Перейдем к обсуждению срезов рельефа.
Рис. 13 позволяет сделать вывод о том, что рассмотренная математическая модель
взаимодействия иглы с подложкой достаточно хорошо описывает наблюдаемые особенности
изображения. Как и предсказывает теория,
большинство пиков имеют сглаженные вершины. Напомним, что это связано с тем, что игла имеет
конечный радиус закругления, в результате чего туннельный ток протекает через слой атомов
иглы диаметром несколько нанометров. Для наклонных участков сглаженные участки представляют
собой наклонные прямые. В большинстве случаев рельеф на
соседних срезах отличается не более, чем на 1 нм, однако, достаточно
часто отклонения достигают 3-4 нм. Эти случаи находятся в противоречии с
выводом о том, что рельеф должен иметь сглаженный характер. Можно предположить, что отклонения являются результатом
ошибок измерения рельефа. Механизм их возникновения связан с тем, что в
качестве высоты принимается осредненный сигнал, подающийся на двигатель
вертикального перемещения иглы. Импульсные помехи в этом тракте приводят к
скачкам в измерениях высоты. Следует также обратить внимание на то, что
практически все скачки сосредоточены на горизонтальных участках. Это,
по-видимому, связано с особенностями позиционной системы управления, в которой
режимы колебаний имеют наибольшую амплитуду при нулевой уставке. Фактически
достоверными является только нижние зубцы изображения, так как система
управления стремится не допустить контакта иглы с поверхностью. Особенность изменения туннельного тока
(в 7 раз на каждые 0,1 нм) приводит к тому, что управление можно
сравнить с отслеживанием рельефа твердой поверхности в непосредственной
близости от нее, при условии, что касание поверхности требуется полностью
исключить. Известно, что возникающая при этом задача управления является достаточно
сложной. Примеры возможных решений и результаты экспериментов для систем с
программным управлением можно найти в работе [3]. Для того, чтобы представить себе
изменения в изображении, к которым приводит учет размеров иглы, графики срезов
были скорректированы. В основе алгоритма коррекции положены следующие соображения. Фактический рельеф поверхности
располагается относительно поверхности иглы на расстоянии приблизительно равном
сумме радиуса закругления и туннельного зазора. Обозначим это расстояние через d.
Точное решение задачи об определении рельефа среза поверхности
связано с построением огибающей к множеству окружностей, центр каждой из которых
находится в точке измеренного среза поверхности и имеет радиус, равный d. Алгоритм,
точно решающий эту задачу, оказывается достаточно сложным и связан с большим
объемом вычислений. На
рассматриваемом этапе исследований оказался достаточным следующий алгоритм.
Измеренная кривая срезов представляет собой ломаную, узлы которой имеют одинаковый
шаг по горизонтали. Каждый отрезок ломаной смещается по нормали вниз на d и строится новая ломаная, которая является нижней
границей всех получившихся точек. Затем
полученный график поднимается на d с тем, чтобы скомпенсировать опускание горизонтальных
участков, которые при сравнении исходной и построенной ломанной удобно располагать
рядом. Значение d является варьируемым параметром и задается вначале
работы корректирующей программы. На
практике оно близко к радиусу закругления. Результаты коррекции показаны на рис. 15 и 16.
Нетрудно заметить, что учет радиуса закругления приводит к расширению вогнутых
и сужению выпуклых участков кривой. Это видно на рис. 14, на котором
скорректированный рельеф построен для d = 10 нм. Возможность изменять значение d позволяет оценивать точность получаемого изображения. В
частности было найдено, что при d > 5 нм исчезают пики неровностей, которые,
как было сказано выше, скорее всего, являются ошибками измерений. На рис. 15 и 16 показаны
изменения в монохромном изображении, к которым
приводит учет радиуса закругления иглы. На рисунках заметно увеличение темных
(низких) областей и сужение светлых (высоких). Исчезли также пятна, связанные
пиками колебаний высоты. Наглядно это заметно на рисунках после проведения линий
уровня.(на рис. 17 и 18 они проведены с шагом 20 нм). На правом рисунке, полученном после коррекции, исчезли также
области, которые целиком состоят из точек линий уровня. Из
проведенных экспериментов можно сделать вывод о том, что получаемое изображение
имеет разрешение порядка нескольких нанометров. Детали, размер которых менее этой величины, по-видимому,
нельзя считать существующими в реальности. Результаты и выводы Туннельная микроскопия является
сравнительно дешевым средством получения изображений с нанометровым
разрешением. Вместе с тем, проведенное исследование показывает, что для того, чтобы достичь разрешения 1 нм
и менее, необходим учет размеров конца иглы, физических процессов взаимодействия
иглы с поверхностью и процессов управления движением иглы. В работе даны оценки влияния
особенностей протекания туннельного тока на разрешающую способность микроскопа. Разработаны способы интерпретации
изображений с учетом геометрии иглы. Эти методы могут использоваться для
восстановления истинного рельефа поверхности и оценки возмущений, которые
возникают в процессе сканирования. Литература 1. В.А. Карташев, Т.Ф. Бурухина. Исследование влияния
нерезонансных периодических возмущений на положение иглы туннельного
микроскопа. Препринт ИПМ РАН. М.: ИПМ РАН, 2004.
2.
В. Миронов. Основы
сканирующей зондовой микроскопии. М.: Техносфера, 2004.
3.
А.М.Гориневский,
А.М.Формальский, А.Ю.Шнейдер.
Управление манипуляционными системами на основе
информации об усилиях.


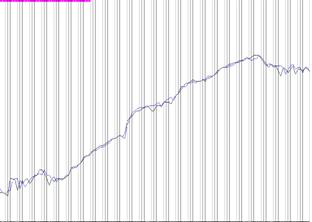

Рис.13
Рис.14