Аннотация
Сравниваются два способа вычисления главного вектора и главного момента сил светового давления,
действующих на космический аппарат с составным солнечным парусом. Первый способ основан на
аналитических формулах, полученных без учета затенения одних частей паруса другими.
Второй способ использует детальную геометрическую модель паруса, которая позволяет учесть
такое затенение. Предполагается, что часть фотонов, попадающих на парус, отражаются от него
зеркально, а остальные полностью поглощаются. Установлена область изменения параметров
ориентации паруса относительно падающих на него солнечных лучей, в которой первый способ
оказывается достаточно точным.
Abstract
We compare two way of calculation of light pressure force and torque acting on a composite
solar sail. The first way is based on analytical formulas, which were derived without taking
into account shading some parts of the sail by its other parts. The second way uses a detail
geometric model of the sail which allows taking proper account of such shading. We assume
photons interact with the sail in two ways. Some of them have a specular reflection,
the others are absorbed. We ascertain the range of spacecraft attitudes with respect to solar
rays in which the analytical formulas are sufficiently exact.
1.
Космический аппарат с солнечным парусом.
В [1 – 4] исследованы режим одноосной солнечной ориентации
искусственного спутника Земли, несущего солнечный парус, и закон управления парусом,
увеличивающий большую полуось орбиты такого спутника. Указанные работы
существенно используют аналитические формулы для главного вектора и главного
момента действующих на парус сил светового давления, причем эти формулы
получены без учета затенения одних частей паруса другими. Поскольку учет такого
затенения заведомо необходим при некоторых положениях паруса относительно
падающих на него солнечных лучей, была выполнена проверка использованных
упрощенных формул средствами геометрического моделирования, развитыми в [5].
Результаты этой проверки описаны ниже. По постановке задачи и методам ее
решения данная работа восходит к работе [6].
2. Форма паруса и аналитические выражения
для главного вектора
и главного момента действующих на
него сил светового давления
КА представляет собой небольшое центральное тело в
форме прямого кругового цилиндра, к которому прикреплен солнечный парус. Парус
состоит из восьми одинаковых плоских лепестков, имеющих форму равнобочной трапеции.
Чтобы нагляднее описать расположение лепестков относительно центрального тела,
примем на время, что это тело вырождается в отрезок прямой, совпадающий с его
осью, а каждый лепесток представляет собой равнобедренный треугольник. Все
лепестки без перекрытия можно уложить в правильный восьмиугольник. Форму паруса
опишем следующим образом. С КА свяжем систему координат 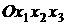 , на оси , на оси 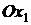 которой поместим отрезок,
играющий роль центрального тела. Указанный выше правильный восьмиугольник расположим
в координатной плоскости которой поместим отрезок,
играющий роль центрального тела. Указанный выше правильный восьмиугольник расположим
в координатной плоскости 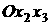 так, чтобы точка так, чтобы точка  являлась центром
восьмиугольника, а ось являлась центром
восьмиугольника, а ось 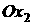 проходила через
середину одной из его сторон. Лепестки последовательно занумеруем числами 1, 2,
… , 8, приписав номер 1 лепестку, содержащему отрезок положительной полуоси проходила через
середину одной из его сторон. Лепестки последовательно занумеруем числами 1, 2,
… , 8, приписав номер 1 лепестку, содержащему отрезок положительной полуоси 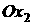 , номер 2 лепестку, содержащему биссектрису первого квадранта
системы координат , номер 2 лепестку, содержащему биссектрису первого квадранта
системы координат 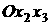 , и т. д. Лепестки с нечетными номерами перенесем вдоль оси , и т. д. Лепестки с нечетными номерами перенесем вдоль оси 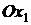 параллельно самим себе
в плоскость параллельно самим себе
в плоскость 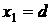 , лепестки с четными номерами перенесем точно также в
плоскость , лепестки с четными номерами перенесем точно также в
плоскость 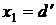 , , 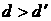 . Затем каждый лепесток повернем на угол . Затем каждый лепесток повернем на угол 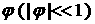 вокруг прямой,
проходящей через вершину лепестка на оси вокруг прямой,
проходящей через вершину лепестка на оси 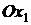 параллельно его
противолежащей стороне. Поворот выполним в сторону отрицательной полуоси параллельно его
противолежащей стороне. Поворот выполним в сторону отрицательной полуоси 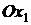 . Получим солнечный парус «вырожденного» КА. . Получим солнечный парус «вырожденного» КА.
Приведем некоторые геометрические характеристики
такого паруса. Нормаль к лепестку с номером 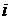 обозначим обозначим  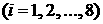 и положим и положим 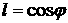 , , 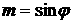 . Тогда в системе координат . Тогда в системе координат 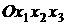 будем иметь будем иметь
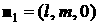 , , 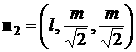 , ,
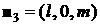 , , 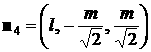 , ,
 , , 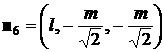 , ,
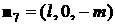 , , 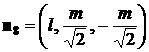 . .
Радиус-вектор
геометрического центра 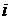 -го лепестка (точки пересечения медиан соответствующего
треугольника) относительно точки -го лепестка (точки пересечения медиан соответствующего
треугольника) относительно точки  обозначим обозначим 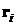 . В системе . В системе 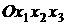
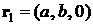 , , 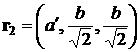 , ,
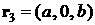 , , 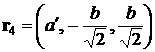 , ,
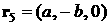 , , 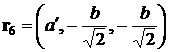 , ,
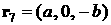 , , 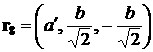 . .
В случае центрального тела в
виде отрезка и треугольных лепестков 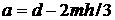 , , 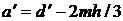 , , 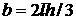 , где , где 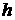 – высота
лепестка-треугольника, опущенная на его основание. – высота
лепестка-треугольника, опущенная на его основание.
Полученные формулы
остаются справедливыми и для «невырожденного» КА, если ось центрального тела
совпадает с осью 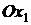 , а лепестки паруса получаются из лепестков-треугольников
отсечением от них одинаковых частей, примыкающих к оси , а лепестки паруса получаются из лепестков-треугольников
отсечением от них одинаковых частей, примыкающих к оси 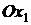 (отсекаемые части
представляют собой равнобедренные треугольники, подобные исходным лепесткам).
Разумеется, параметры (отсекаемые части
представляют собой равнобедренные треугольники, подобные исходным лепесткам).
Разумеется, параметры  , , 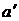 и и 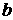 имеет в этом случае
другой смысл. Ниже будем считать, что точка имеет в этом случае
другой смысл. Ниже будем считать, что точка  принадлежит одному из
оснований этого тела (напомним, центральное тело – цилиндр), а само тело
расположено в полупространстве принадлежит одному из
оснований этого тела (напомним, центральное тело – цилиндр), а само тело
расположено в полупространстве 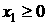 . .
Поскольку центральное тело мало, при расчете
главного вектора и главного момента сил светового давления, приложенных к КА,
будем учитывать действие этих сил только на парус. Примем, что доля  попавших на парус фотонов
отражается от него зеркально, доля фотонов попавших на парус фотонов
отражается от него зеркально, доля фотонов 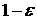 полностью им поглощается.
Будем рассматривать только такие положения КА, в которых угол между ортом полностью им поглощается.
Будем рассматривать только такие положения КА, в которых угол между ортом 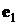 оси оси 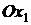 и ортом и ортом 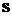 направления «Земля –
Солнце» меньше направления «Земля –
Солнце» меньше 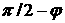 . Взаимное затенение лепестков учитывать не будем. При сделанных
предположениях главный вектор приложенных к парусу сил светового давления определяется
формулами . Взаимное затенение лепестков учитывать не будем. При сделанных
предположениях главный вектор приложенных к парусу сил светового давления определяется
формулами
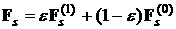 , ,
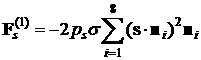 , , 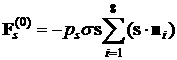 . .
Здесь  Н/м Н/м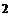 – давление света на абсолютно черную пластинку, расположенную
перпендикулярно солнечным лучам на гелиоцентрической орбите Земли, – давление света на абсолютно черную пластинку, расположенную
перпендикулярно солнечным лучам на гелиоцентрической орбите Земли,  – площадь одного
лепестка паруса. Суммы в выражениях для – площадь одного
лепестка паруса. Суммы в выражениях для 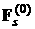 и и 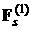 вычислялись в скалярной
форме в системе координат вычислялись в скалярной
форме в системе координат 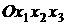 . Простые преобразования позволяют привести формулу для . Простые преобразования позволяют привести формулу для 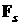 к виду [2] к виду [2]
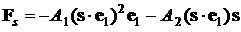 , (1) , (1)
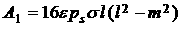 , , 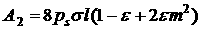 . .
Формула (1) – приближенная:
в ней в коэффициенте при 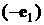 опущено слагаемое опущено слагаемое 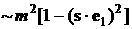 . Абсолютная величина этого слагаемого существенно меньше . Абсолютная величина этого слагаемого существенно меньше 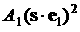 , так как, во-первых, , так как, во-первых, 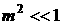 , во-вторых, при движении КА в режиме одноосной солнечной ориентации , во-вторых, при движении КА в режиме одноосной солнечной ориентации
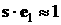 . .
Главный момент приложенных к парусу сил светового
давления определяется формулами
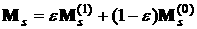 , ,
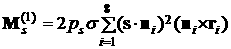 , , 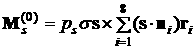 . .
В качестве полюса приведения
здесь принята точка  . Выписанные суммы вычислялись в скалярном виде в системе
координат . Выписанные суммы вычислялись в скалярном виде в системе
координат 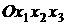 . Суммирование проводилось раздельно по четным и нечетным
индексам. При этом выражения для сумм по четным индексам получаются из
выражений для сумм по нечетным индексам заменой . Суммирование проводилось раздельно по четным и нечетным
индексам. При этом выражения для сумм по четным индексам получаются из
выражений для сумм по нечетным индексам заменой 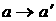 . После несложных, но громоздких выкладок для момента сил
светового давления была получена формула [1, 3] . После несложных, но громоздких выкладок для момента сил
светового давления была получена формула [1, 3]
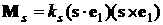 ,
(2) ,
(2)
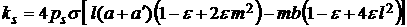 . .
Приведем числовые оценки.
Параметры конструкции паруса возьмем следующие: 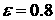 , , 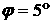 , , 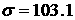 м м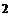 , , 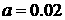 м м 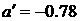 м, м, 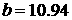 м. этом случае м. этом случае 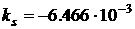 Нм, Нм, 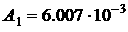 Н, Н, 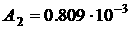 Н. Н.
Солнечный парус, рассмотренный выше, обладает одним замечательным
свойством – действующий на несущий его КА момент светового давления 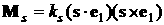 потенциален. А именно,
этот момент можно представить в виде потенциален. А именно,
этот момент можно представить в виде
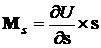 , , 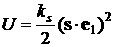 . .
Функция 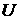 называется силовой.
Этот факт во многом определяет свойства вращательного движения КА [1, 2, 3]. называется силовой.
Этот факт во многом определяет свойства вращательного движения КА [1, 2, 3].
Погрешности в изготовлении и установке солнечного
паруса могут привести к нарушению свойства потенциальности действующего на КА
момента светового давления и, как следствие, к существенному изменению
движения. В качестве примера рассмотрим изменение параметров установки
лепестков паруса, приводящее к возникновению так называемого пропеллерного
момента. Для простоты расчетов будем считать, что это изменение одинаково для
всех лепестков. Предположим, что все лепестки повернуты на один и тот же угол в
одну и ту же сторону вокруг своих продольных осей. При этом указанные выше
радиусы-векторы 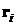 центров лепестков
остаются прежними, а нормали к лепесткам принимают вид центров лепестков
остаются прежними, а нормали к лепесткам принимают вид
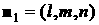 , , 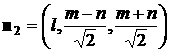 , , 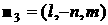 , ,
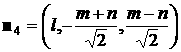 , , 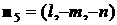 , , 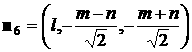 , ,
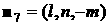 , ,  . .
Здесь 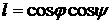 , , 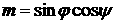 , , 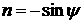 . В этом случае для момента сил светового давления можно
получить формулу . В этом случае для момента сил светового давления можно
получить формулу
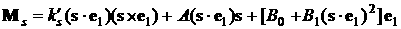 , (3) , (3)
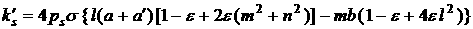 , ,
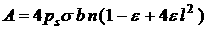 , , 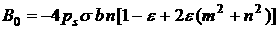 , ,
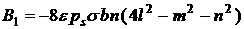 . .
Эта формула отличается от формулы для  , приведенной в разделе 2, несколько измененным выражением
для коэффициента в первом слагаемом и наличием двух дополнительных слагаемых.
При , приведенной в разделе 2, несколько измененным выражением
для коэффициента в первом слагаемом и наличием двух дополнительных слагаемых.
При 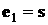 прежняя формула дает прежняя формула дает 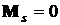 , новая формула дает , новая формула дает
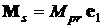 , , 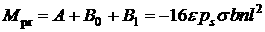 . .
Последнее соотношение означает, что если продольная
ось КА направлена на Солнце и 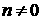 , то на КА относительно этой оси действует постоянный момент.
КА подобен пропеллеру, раскручиваемому ветром. Для приведенных выше параметров
паруса и , то на КА относительно этой оси действует постоянный момент.
КА подобен пропеллеру, раскручиваемому ветром. Для приведенных выше параметров
паруса и 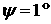 получаем получаем 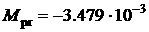 Нм. Нм.
Выражение
для 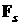 в рассматриваемом
примере по-прежнему имеет вид (1), где теперь в рассматриваемом
примере по-прежнему имеет вид (1), где теперь
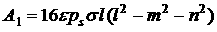 , , 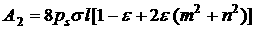 . .
При 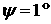 изменения в этих
коэффициентах практически не заметны. изменения в этих
коэффициентах практически не заметны.
3. Численный расчет главного
вектора и главного момента
действующих на КА сил светового
давления
Более точный расчет величин  и и 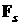 выполнялся с
использованием достаточно детальной геометрической модели КА (рис. 1, 2). Модель состояла из девяти многогранников. Один из них
моделировал центральное тело КА, а восемь других, одинаковых, – лепестки
паруса. Центральное тело представляло собой правильную призму, вписанную в
прямой круговой цилиндр высотой 0.8
м и диаметром 1 м. Призма имела 180 боковых граней, ее
поверхность разбивалась на 216 треугольных граней. Лепесток моделировался
прямой призмой, которая имела высоту 0.02 м и основание в виде равнобочной трапеции.
Размеры трапеции: меньшее основание – 1.52 м., большее основание – 13 м, высота – 14.2 м. Поверхность такой
призмы разбивалась на 12 треугольных граней. выполнялся с
использованием достаточно детальной геометрической модели КА (рис. 1, 2). Модель состояла из девяти многогранников. Один из них
моделировал центральное тело КА, а восемь других, одинаковых, – лепестки
паруса. Центральное тело представляло собой правильную призму, вписанную в
прямой круговой цилиндр высотой 0.8
м и диаметром 1 м. Призма имела 180 боковых граней, ее
поверхность разбивалась на 216 треугольных граней. Лепесток моделировался
прямой призмой, которая имела высоту 0.02 м и основание в виде равнобочной трапеции.
Размеры трапеции: меньшее основание – 1.52 м., большее основание – 13 м, высота – 14.2 м. Поверхность такой
призмы разбивалась на 12 треугольных граней.
Модели центрального тела и лепестков разрабатывались
в среде трехмерного моделирования 3d Studio MAX. Программная реализация модели
КА позволяла использовать в качестве центрального тела и лепестков любые 3d max
модели. Каждый лепесток можно было поворачивать вокруг своей оси симметрии
(высоты трапеции) на любой угол.
Сравним результаты численных расчетов  и и 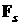 с использованием описанной
модели с результатами, полученными по формулам предыдущего раздела. В расчетах
примем с использованием описанной
модели с результатами, полученными по формулам предыдущего раздела. В расчетах
примем 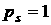 , , 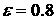 . Пусть в системе . Пусть в системе 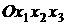 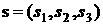 , , 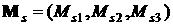 , , 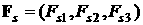 . Компоненты орта . Компоненты орта 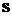 параметризуем углами параметризуем углами 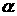 и и  с помощью формул с помощью формул
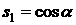 , , 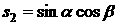 , , 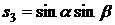 . .
Поскольку парус
представляет собой (почти) осесимметричную конструкцию с осью симметрии 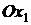 , удобно вместо компонент , удобно вместо компонент 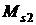 , , 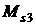 , ,  , , 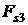 рассматривать их линейные
комбинации рассматривать их линейные
комбинации
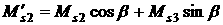 , , 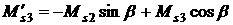 , ,
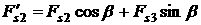 , , 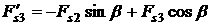 . .
Введенные
обозначения сохраним за компонентами векторов  и и 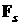 , рассчитываемых с помощью геометрической модели. Те же
компоненты, рассчитываемые по аналитическим формулам предыдущего раздела, обозначим , рассчитываемых с помощью геометрической модели. Те же
компоненты, рассчитываемые по аналитическим формулам предыдущего раздела, обозначим
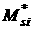 , , 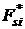 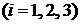 . При этом величины . При этом величины 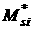 , , 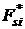 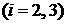 соответствуют величинам соответствуют величинам
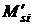 , , 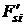 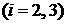 . Формулы (1), (2) позволяют найти . Формулы (1), (2) позволяют найти
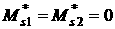 , , 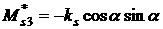 , ,
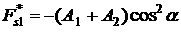 , , 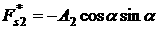 , , 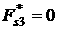 . .
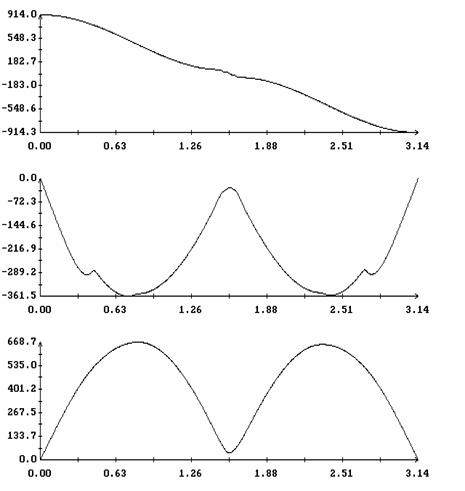
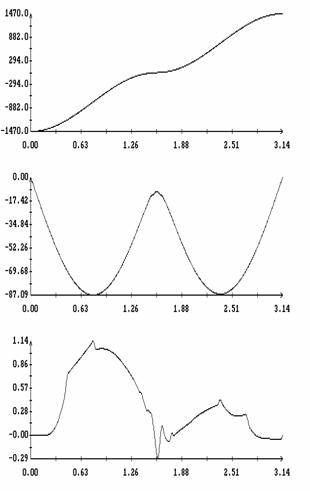
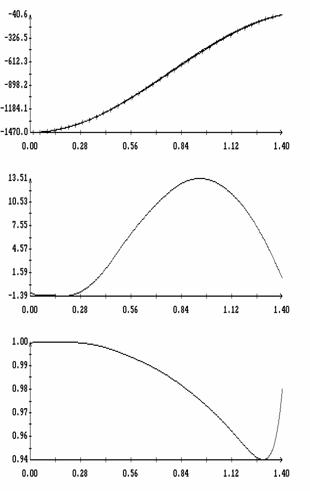
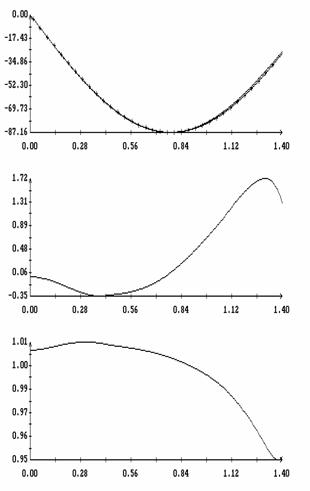
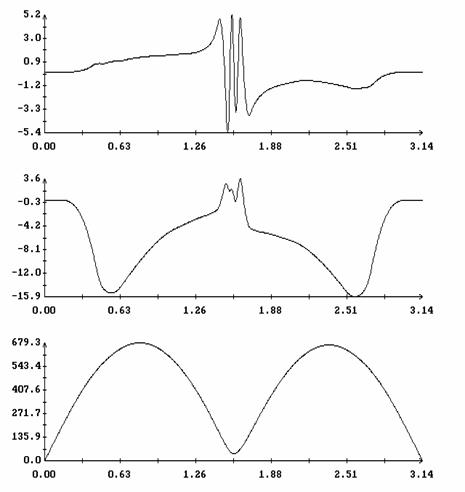
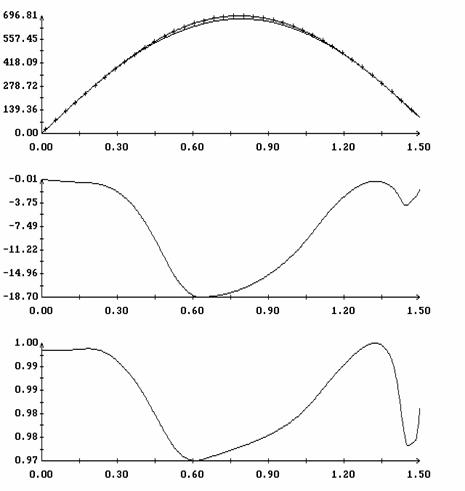
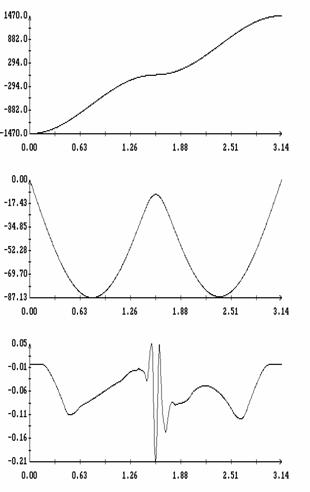
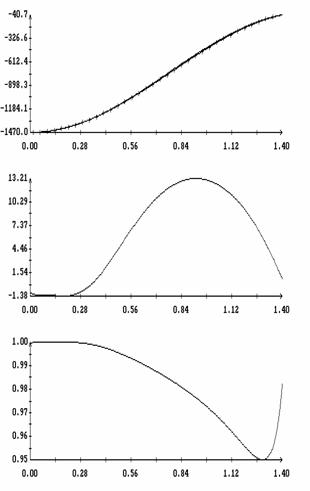
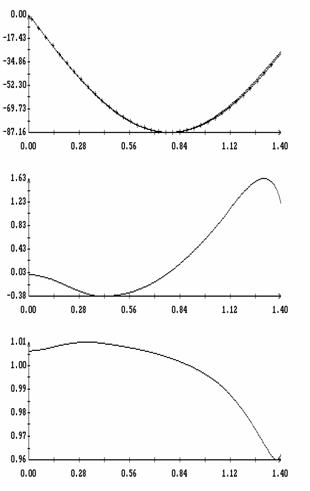
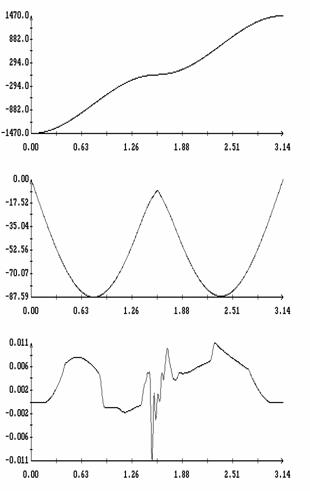
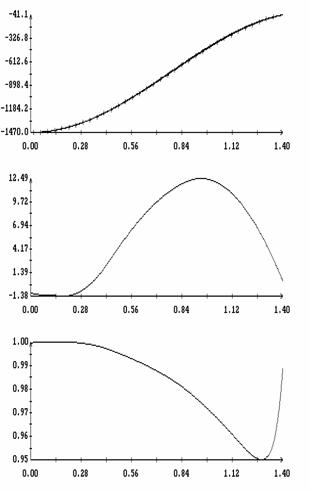
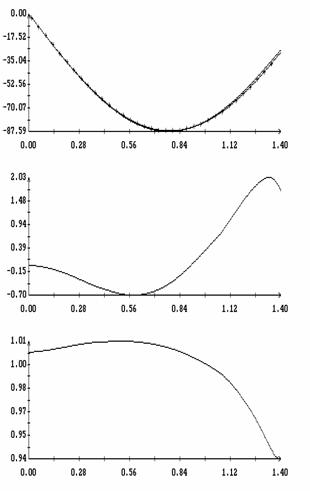
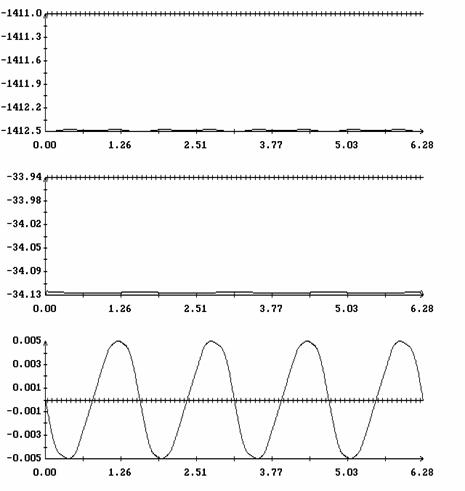
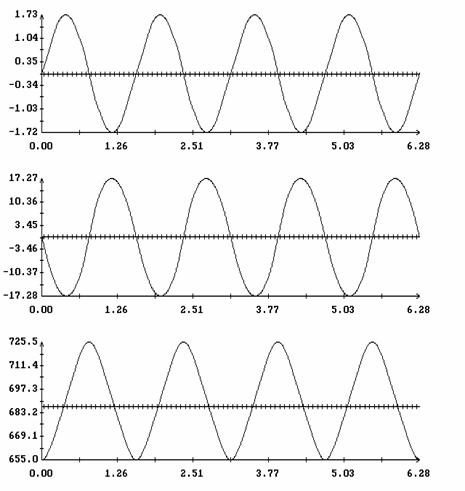
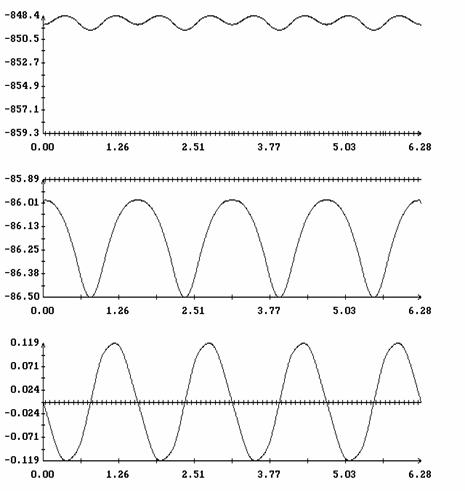
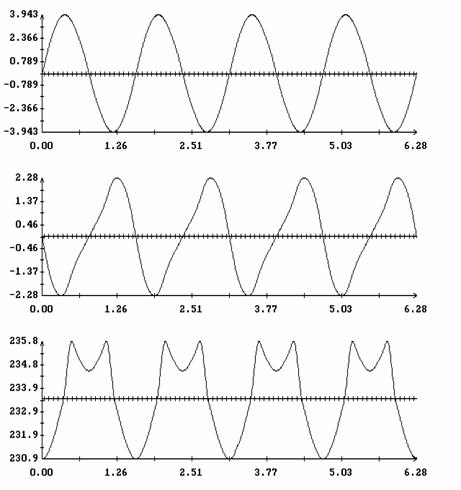
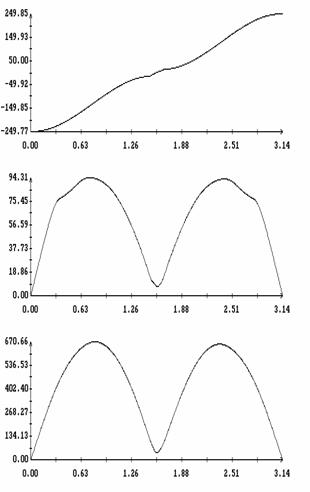
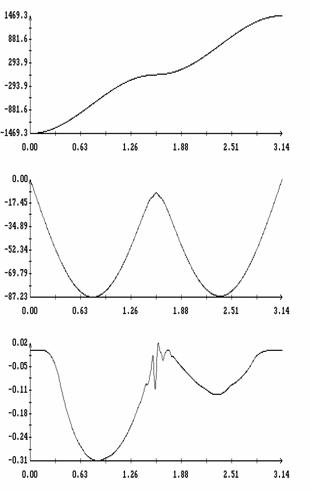
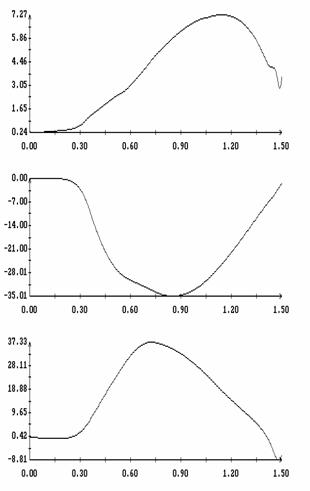
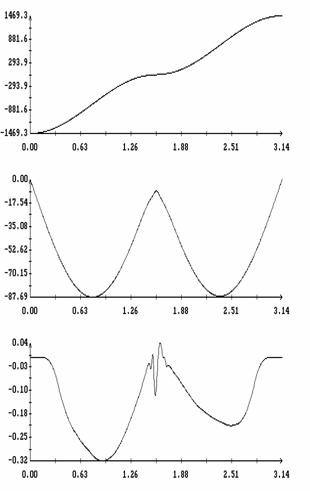
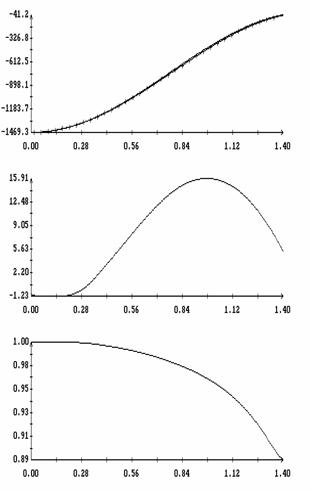
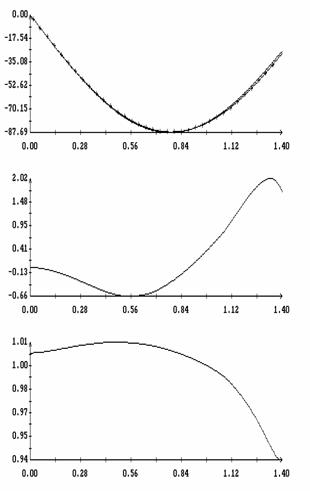
Сравнение результатов расчета компонент векторов  и и 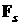 численным и аналитическим
способами представлено на рис. 3 – 11. Эти рисунки относятся к рассмотренному
выше парусу без пропеллерного эффекта. Рис. 3 – 8 содержат графики зависимости
компонент численным и аналитическим
способами представлено на рис. 3 – 11. Эти рисунки относятся к рассмотренному
выше парусу без пропеллерного эффекта. Рис. 3 – 8 содержат графики зависимости
компонент  и и 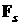 , а также некоторых характеристик совпадения аналитических и
численных результатов в зависимости от угла , а также некоторых характеристик совпадения аналитических и
численных результатов в зависимости от угла 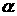 при нескольких
значениях при нескольких
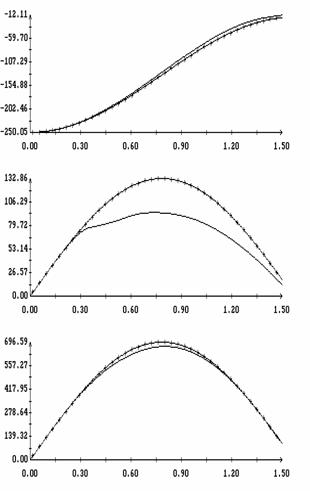
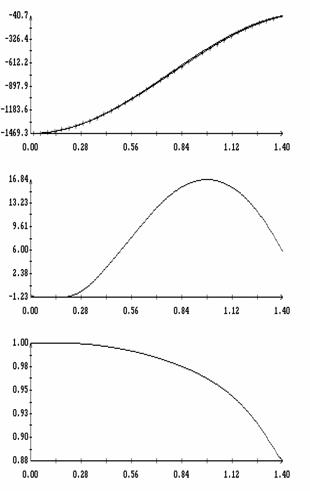
значениях  . Рис. 9 – 11 содержат графики зависимости аналогичных
величин от угла . Рис. 9 – 11 содержат графики зависимости аналогичных
величин от угла  при фиксированных значениях при фиксированных значениях
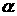 . Графики, построенные по аналитическим формулам, отмечены
маркерами. В подписях к рис. 9 – 11 приведены числовые значения отличных от
нуля соответствующих величин . Графики, построенные по аналитическим формулам, отмечены
маркерами. В подписях к рис. 9 – 11 приведены числовые значения отличных от
нуля соответствующих величин 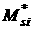 , , 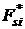 (они не зависят от (они не зависят от  ) и средних значений ) и средних значений
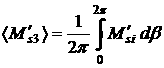 , , 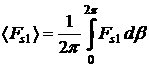  . .
Указанные средние значения
представляют наибольший интерес, поскольку КА вместе с парусом вращается вокруг
оси 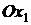 с угловой скоростью примерно с угловой скоростью примерно
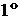 /с и действие светового давления на КА усредняется по этому
вращению [1 – 4]. Как следует из приведенных
рисунков, при малых значениях угла /с и действие светового давления на КА усредняется по этому
вращению [1 – 4]. Как следует из приведенных
рисунков, при малых значениях угла 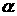 , примерно при , примерно при  (это наиболее практически
важный случай), имеет место весьма точное совпадение аналитических и численных
способов расчета векторов (это наиболее практически
важный случай), имеет место весьма точное совпадение аналитических и численных
способов расчета векторов  и и 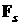 . Указанное совпадение оправдывает использование приближенных
аналитических формул (1), (2) в работах [1 – 4]. . Указанное совпадение оправдывает использование приближенных
аналитических формул (1), (2) в работах [1 – 4].
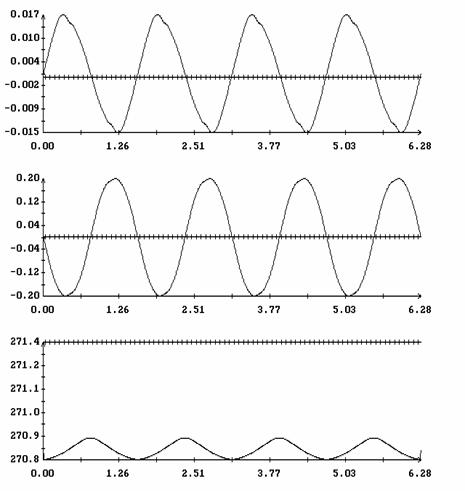
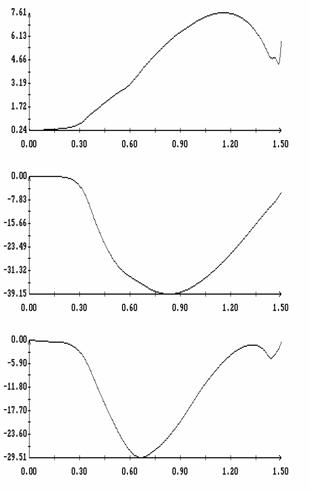
Сравнение результатов расчета компонент  и и 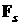 численным и аналитическим
способами в случае паруса с пропеллерным эффектом показано на рис. 12 – 17. Эти
рисунки аналогичны рис. 3 – 11, только аналитические формулы в данном случае
имеют вид численным и аналитическим
способами в случае паруса с пропеллерным эффектом показано на рис. 12 – 17. Эти
рисунки аналогичны рис. 3 – 11, только аналитические формулы в данном случае
имеют вид
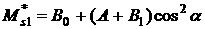 , , 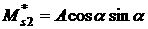 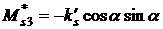 , ,
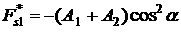 , , 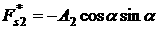 , , 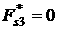 , ,
причем выражения для 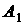 и и 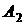 должны быть
соответствующим образом модифицированы. В подписях к рис. 16, 17 дополнительно
приведены числовые значения величин должны быть
соответствующим образом модифицированы. В подписях к рис. 16, 17 дополнительно
приведены числовые значения величин 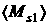 и и 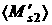 , которые определяются аналогично величине , которые определяются аналогично величине 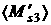 . Как видим область совпадения аналитических и численных
способов расчета векторов . Как видим область совпадения аналитических и численных
способов расчета векторов  и и 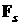 в случае пропеллерности
паруса несколько уменьшилась. Теперь достаточно точное совпадение имеет место
примерно при в случае пропеллерности
паруса несколько уменьшилась. Теперь достаточно точное совпадение имеет место
примерно при 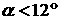 . .
Согласно [1 – 4] движение КА должно происходить в режиме
одноосной солнечной ориентации. В этом режиме, если не предпринимать управления
парусом по углу 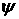 для увеличения большой
полуоси орбиты КА или коррекции угловой скорости его собственного вращения,
предельные значения угла для увеличения большой
полуоси орбиты КА или коррекции угловой скорости его собственного вращения,
предельные значения угла 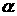 не превосходят не превосходят 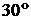 . В этом случае, результаты работ [1 – 4] не требуют пересмотра
с использованием более точной модели паруса. Если же предпринимать такие управления,
то максимальные значения угла . В этом случае, результаты работ [1 – 4] не требуют пересмотра
с использованием более точной модели паруса. Если же предпринимать такие управления,
то максимальные значения угла 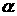 достигают достигают  , а иногда даже несколько превосходят этот предел. В этом
случае результаты [1 – 4] желательно уточнить с использованием более точных
выражений для , а иногда даже несколько превосходят этот предел. В этом
случае результаты [1 – 4] желательно уточнить с использованием более точных
выражений для  и и  . .
Данная работа выполнена при финансовой поддержке РФФИ
(грант 05-01-00451).
Литература
1.
Лихачев В.Н., Сазонов В.В., Ульяшин А.И.
Одноосная солнечная ориентация искусственного спутника Земли. Космические
исследования, 2003,
т. 41, N 2, с. 174-185.
2.
Лихачев В.Н., Сазонов В.В., Ульяшин А.И. Эволюция
орбиты искусственного спутника Земли с солнечным парусом. Космические
исследования, 2004, т. 42, N 1, с. 83-87.
3.
Лихачев В.Н., Сазонов В.В., Ульяшин А.И. Режим
одноосной солнечной ориентации искусственного спутника Земли. Препринт
Института прикладной математики им. М.В.Келдыша РАН, 2001, № 15.
4.
Лихачев В.Н., Сазонов В.В., Ульяшин А.И. Исследование
режима одноосной солнечной ориентации искусственного спутника. Препринт
Института прикладной математики им. М.В.Келдыша РАН, 2002, № 65.
5.
Сазонов Вас. В. Алгоритм отыскания освещенных
участков многогранных поверхностей в плоскопараллельном световом потоке.
Математическое моделирование, 2007, т. 19, № 6, с. 16-30.
6.
Комаров М.М., Климович Д.Н., Сазонов В.В. Расчет
сил и моментов светового давления, действующих на роторный солнечный парус.
Препринт Института прикладной
математики им. М.В. Келдыша РАН, 1995,
№ 59.
|
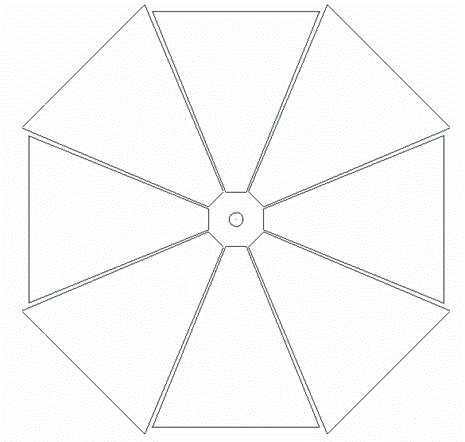
![]() . Изображение дано в перспективной проекции, поэтому дальние
лепестки выглядят меньше ближних.
. Изображение дано в перспективной проекции, поэтому дальние
лепестки выглядят меньше ближних.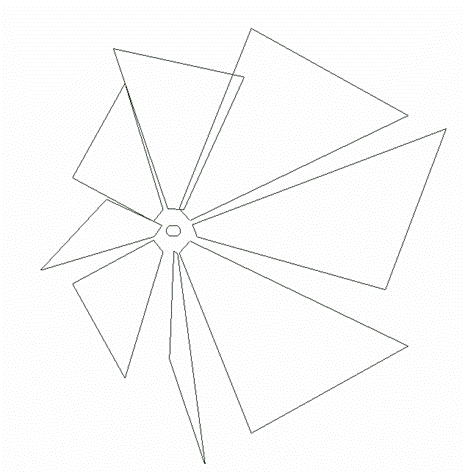
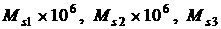

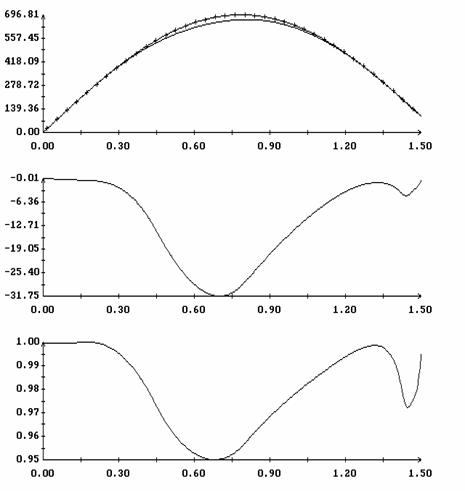
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)![]() при
при ![]() ;
;![]() этого момента формулой
этого момента формулой
![]() .
.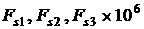
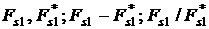
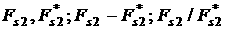
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)![]() при
при ![]() ; (б), (в) аппроксимация
компонент
; (б), (в) аппроксимация
компонент ![]() ,
, ![]() этой силы формулами
этой силы формулами ![]() ,
, ![]() .
.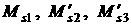
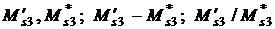
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)![]() при
при ![]() ;
;![]() этого момента формулой
этого момента формулой
![]() .
.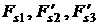
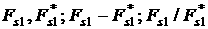
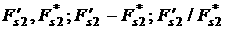
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)![]() при
при ![]() ;
(б), (в) аппроксимация компонент
;
(б), (в) аппроксимация компонент ![]() ,
, ![]() этой силы формулами
этой силы формулами ![]() ,
, ![]() .
.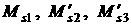
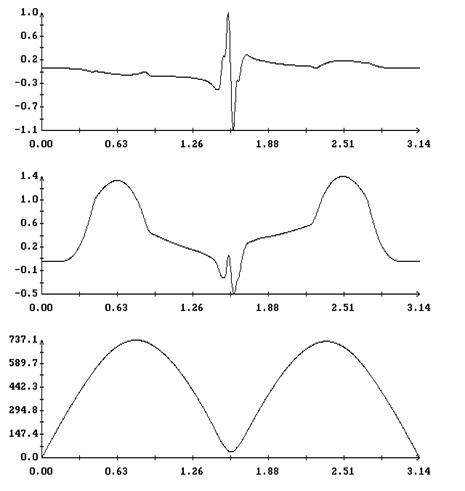
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)![]() при
при ![]() ;
;![]() этого момента формулой
этого момента формулой
![]() .
.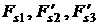
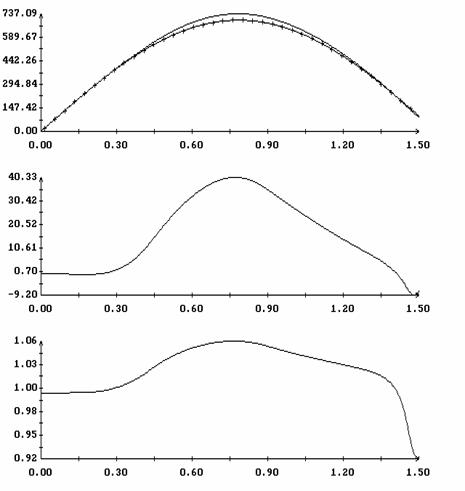
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)![]() при
при ![]() ; (б), (в) аппроксимация
компонент
; (б), (в) аппроксимация
компонент ![]() ,
, ![]() этой силы формулами
этой силы формулами ![]() ,
, ![]() .
.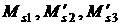
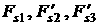
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)![]() при
при ![]() ;
;![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.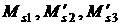
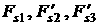
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)![]() при
при ![]() ;
;![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.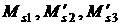
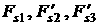
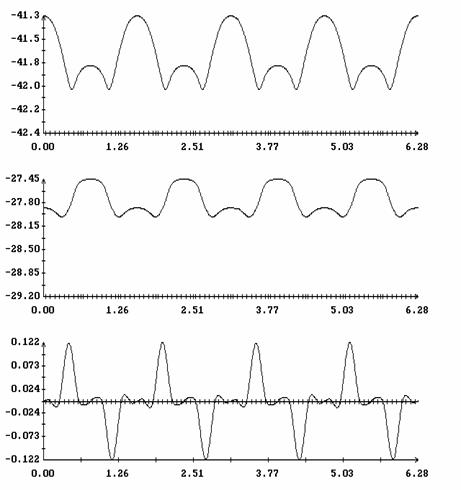
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)![]() при
при ![]() ;
;![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.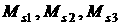
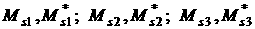
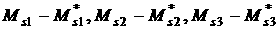
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)![]() при
при ![]() ; (б), (в) аппроксимация
момента формулами
; (б), (в) аппроксимация
момента формулами ![]() ,
, ![]() ,
, ![]() .
.
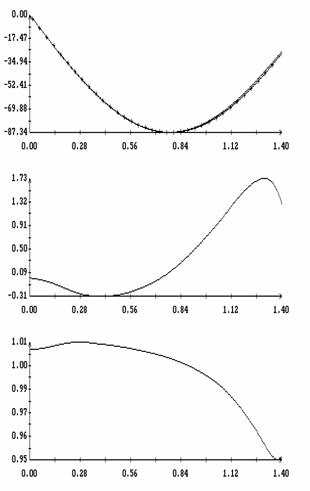
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)![]() при
при ![]() ; (б), (в) аппроксимация
компонент
; (б), (в) аппроксимация
компонент ![]() ,
, ![]() этой силы формулами
этой силы формулами ![]() ,
, ![]() .
.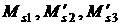

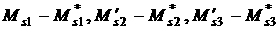

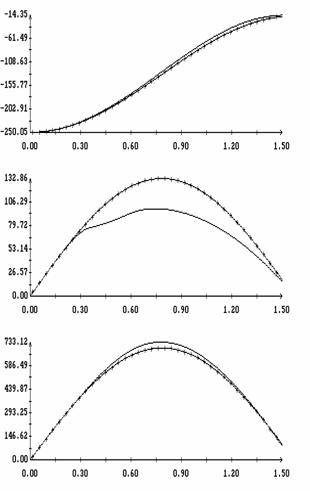
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)![]() при
при ![]() ; (б), (в) аппроксимация момента формулами
; (б), (в) аппроксимация момента формулами ![]() ,
, ![]() ,
, ![]() .
.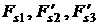
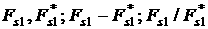
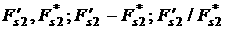
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)![]() при
при ![]() ; (б), (в) аппроксимация
компонент
; (б), (в) аппроксимация
компонент ![]() ,
, ![]() этой силы формулами
этой силы формулами ![]() ,
, ![]() .
.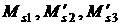
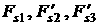
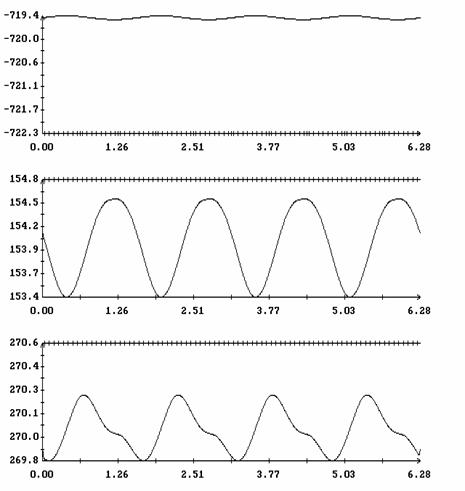
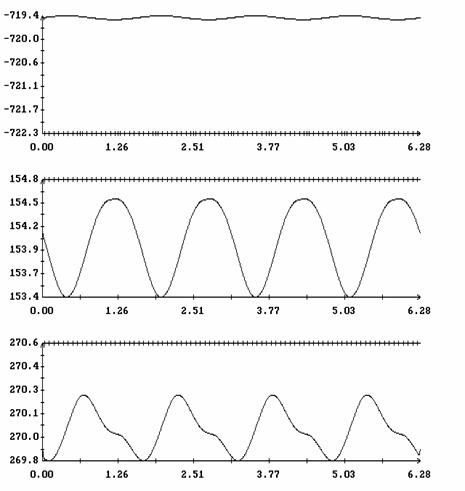
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)![]() при
при ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.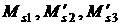
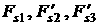
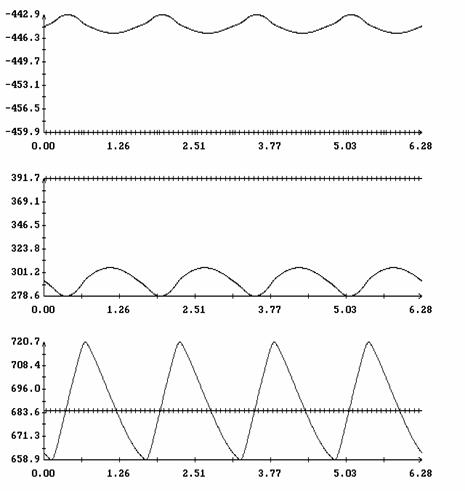
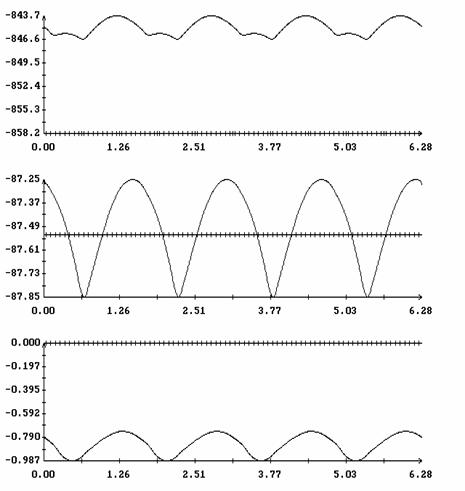
![]() (рад.)
(рад.)
![]() (рад.)
(рад.)![]() при
при ![]() ;
; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.