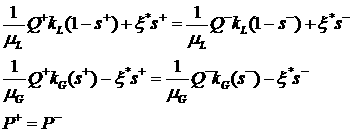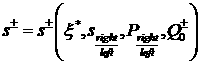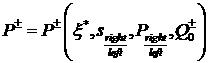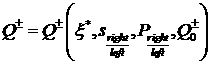Аннотация
Для системы уравнений двухкомпонентной, двухфазной фильтрации, которая не является ни
параболической, ни гиперболической системой уравнений, описано решение задачи Римана.
Задача Римана понимается как задача Коши с постоянными начальными данными для положительных
и отрицательных значений пространственной переменной. Получены соотношения Гюгонио,
предложены условия устойчивости, основанные на формулировке П.Лакса. В предложенной постановке
получены некоторые свойства решений задачи Римана, подтверждающие двойственный характер
рассматриваемой системы уравнений. Также описан процесс построения решения и приведены
соображения в пользу справедливости теорем существования и единственности для рассматриваемой
постановки задачи. Доказательства строгих теорем на этот счет пока не завершены и в
настоящей работе не приводятся.
Abstract
For the system of equations of two-component, two-phase filtration, which in fact is not
parabolic neither hyperbolic, the solution of the Riemann problem is described.
The Riemann problem is thought of as the Cauchy problem with constant initial function
for positive and negative values of space coordinate. The Hugoniot relations are obtained
and stability conditions are proposed in the framework of P.Lax stability conditions.
For this setting some qualitative properties of Riemann problem solutions are inferred
that confirm the intermediate character of the system under consideration. Also the process
of solutions construction is described and the arguments about the validity of existence
and uniqueness theorems are shown. The rigorous proofs are not given in the present study.
Введение
В настоящей работе рассматриваются вопросы постановки
и существования решений задачи Римана для одномерной системы уравнений
двухкомпонентной двухфазной фильтрации в пористых средах. Эта система
представляет собой систему двух законов сохранения массы (для каждой из двух
компонент). При этом неизвестными функциями являются молярные концентрации
компонент 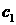 , , 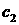 и давление и давление 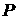 , при этом , при этом 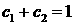 (последнее равенство
непосредственно следует из определения понятия концентрации). Значит, в
рассматриваемой системе двух законов сохранения в качестве неизвестных функций
можно взять давление (последнее равенство
непосредственно следует из определения понятия концентрации). Значит, в
рассматриваемой системе двух законов сохранения в качестве неизвестных функций
можно взять давление 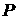 и одну из
концентраций, которую в дальнейшем будем обозначать через и одну из
концентраций, которую в дальнейшем будем обозначать через 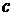 . .
Отметим, что указанная система уравнений не относится
к системам гиперболического типа, для которых традиционно ставится и решается
задача Римана. Не относится она также и к системам параболического типа, но ее
можно рассматривать как вырожденную параболическую систему уравнений.
Вследствие этого для этой системы можно определить понятие автомодельной
переменной и автомодельного решения и рассмотреть классическую постановку
задачи Римана: найти решение задачи Коши в случае, когда начальные функции
постоянны при отрицательных и положительных значениях пространственной
переменной, а в точке ноль имеет место разрыв. При этом, в отличие от уравнений
параболического типа, при решении подобной задачи могут возникать разрывы
неизвестных функций как в нелинейных гиперболических системах уравнений.
Здесь мы рассматриваем систему уравнений только для
двух компонент, т.е., как уже было сказано, систему уравнений 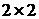 . Много работ было посвящено изучению системы уравнений
фильтрации, включающей . Много работ было посвящено изучению системы уравнений
фильтрации, включающей 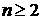 компонент,
предполагая, что среда несжимаема. Подробное изложение и обширную библиографию
можно найти, например, в [6]. В случае сжимаемых сред автору известны лишь
немногие отдельные результаты, которые не предполагают достаточной общности
постановки и решения задачи Римана. компонент,
предполагая, что среда несжимаема. Подробное изложение и обширную библиографию
можно найти, например, в [6]. В случае сжимаемых сред автору известны лишь
немногие отдельные результаты, которые не предполагают достаточной общности
постановки и решения задачи Римана.
В работе [1] была
рассмотрена система уравнений двухфазной фильтрации (без учета состава фаз) с
возможностью сжимаемости одной из фаз. Однако там фактически предполагалось,
что функция давления известна, и решалась возникающая задача Римана для одного неавтономного
уравнения для насыщенности (концентрации). Решение этой задачи Римана детально
описано, и оно обладает довольно сложной структурой, что затрудняет обобщение
теории на многокомпонентный случай (размерность системы, даже при наличии
только двух фаз, растет с ростом числа компонент). Заметим, что в [1] давление
фактически не рассматривается в качестве независимой переменной.
В работе [2] сделана попытка
описать условия устойчивости в случае 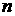 -компонентной смеси, исходя из физического условия убывания
свободной энергии на скачке. Далее для двухкомпонентной смеси приводится
решение задачи Римана. Здесь давление уже играет роль независимой переменной.
Однако, указанное условие устойчивости не дает никаких ограничений на
направление скачка при скачкообразном переходе из двухфазной области в
двухфазную. Таким образом, при данном условии устойчивости возникнет проблема
единственности решения.
-компонентной смеси, исходя из физического условия убывания
свободной энергии на скачке. Далее для двухкомпонентной смеси приводится
решение задачи Римана. Здесь давление уже играет роль независимой переменной.
Однако, указанное условие устойчивости не дает никаких ограничений на
направление скачка при скачкообразном переходе из двухфазной области в
двухфазную. Таким образом, при данном условии устойчивости возникнет проблема
единственности решения.
В предлагаемом препринте
рассматривается система уравнений фильтрации, где независимыми переменными
являются давление и концентрация одного из компонент. Для этой системы
формулируется задача Римана в классической постановке и условия устойчивости.
Условия устойчивости формулируются на основе условий Лакса для гиперболических
систем уравнений [4], а именно: «скачок, соответствующий определенному
семейству характеристик, возникает при пересечении характеристик этого
семейства, т.е. слабые возмущения, соответствующие данному семейству
характеристик приходят с двух сторон на скачок». Учитывая приведенные
условия устойчивости, далее описывается решение задачи Римана в случае, когда
начальные данные и решение лежат в двухфазной области (строгое доказательство
теоремы существования при соответствующих ограничениях будет дано в последующей
публикации). Построенное решение, по-видимому, является единственным для данной
постановки, однако строгого доказательства пока не получено.
Далее в §1 приводится общая формулировка для системы уравнений
двухкомпонентной, двухфазной фильтрации и ставится задача Римана. В §2 система
уравнений конкретизируется на случай двухфазной области, вводится автомодельная
переменная, и описываются непрерывные автомодельные решения – волны разрежения.
При этом доказывается теорема об отсутствии глобальных непрерывных решений
задачи Римана. В §3 приводятся соотношения Гюгонио для разрывных решений,
формулируется и исследуется условие устойчивости на разрывах. Наконец, в §4 на
базе предшествующих параграфов описан процесс построения обобщенных решений
задачи Римана, и приводятся соображения в пользу справедливости теорем
существования и единственности решения задачи Римана в предложенной постановке.
Попутно выводится теорема о бесконечной скорости распространения возмущений.
§1.
Общая формулировка системы уравнений двухкомпонентной, двухфазной фильтрации в
пористой среде. Постановка задачи Римана
Рассмотрим поток двухкомпонентной, двухфазной смеси
углеводородов с концентрациями 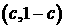 и имеющую давление и имеющую давление 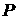 и температуру и температуру 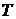 . Будем считать, что смесь находится в равновесном
состоянии в каждый момент времени. Предположим, что концентрация . Будем считать, что смесь находится в равновесном
состоянии в каждый момент времени. Предположим, что концентрация 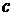 относится к более легкой (т.е. более летучей)
компоненте. Для каждого фиксированного значения давления рассмотрим равновесные
концентрации и плотности: относится к более легкой (т.е. более летучей)
компоненте. Для каждого фиксированного значения давления рассмотрим равновесные
концентрации и плотности: 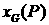 – кривая конденсации; – кривая конденсации; 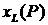 – кривая кипения; – кривая кипения; 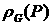 – равновесная плотность газа; – равновесная плотность газа; 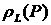 – равновесная плотность жидкости. Для многих
физических ситуаций можно считать, что все эти функции являются монотонными по – равновесная плотность жидкости. Для многих
физических ситуаций можно считать, что все эти функции являются монотонными по 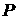 и и  . Обозначим через . Обозначим через 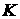 абсолютную проницаемость, через абсолютную проницаемость, через 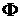 – пористость, через – пористость, через 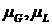 – вязкости газовой и жидкой фаз
соответственно; в настоящем исследовании мы предполагаем, что эти величины
являются постоянными. – вязкости газовой и жидкой фаз
соответственно; в настоящем исследовании мы предполагаем, что эти величины
являются постоянными.
Смесь лежит в двухфазной области, если 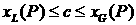 . Пусть . Пусть 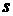 представляет собой насыщенность газовой фазы,
тогда имеет место соотношение представляет собой насыщенность газовой фазы,
тогда имеет место соотношение
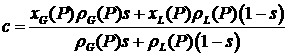 , ,
откуда
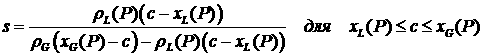 . (1.1) . (1.1)
Теперь
условие того, что смесь лежит в двухфазной области можно переформулировать так 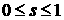 . .
Введем функции относительной
проницаемости (они возникают из рассмотрения физики процессов просачивания) 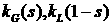 для газовой и жидкой
фаз соответственно. Эти функции являются монотонными, положительными и
принимают значения на отрезке для газовой и жидкой
фаз соответственно. Эти функции являются монотонными, положительными и
принимают значения на отрезке 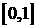 . .
Введем также функции плотности 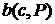 следующим образом следующим образом
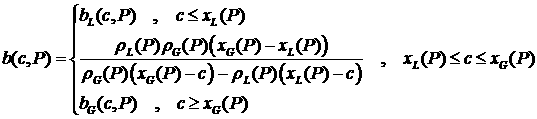 , ,
где 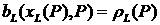 и и 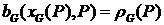 . Определим функции
потока . Определим функции
потока 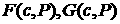 в соответствии с формулами в соответствии с формулами
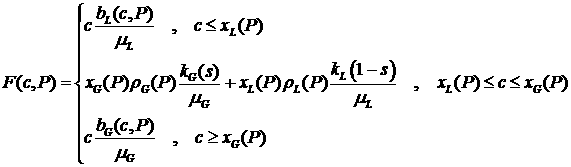
и
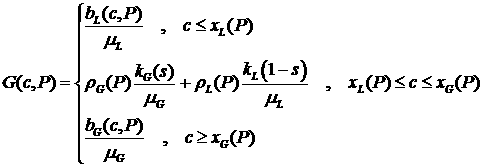 , ,
здесь 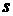 выражено через выражено через 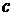 в соответствии с
формулой (1.1). в соответствии с
формулой (1.1).
ЗАМЕЧАНИЕ. Поскольку здесь мы главным образом интересуемся
поведением решений, лежащих в двухфазной области, то можно положить 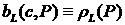 и и 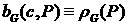 . .
Наконец
введем градиент давления в следующей нормировке
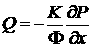 . .
Теперь можно записать наш объект исследования –
систему уравнений двухкомпонентной, двухфазной фильтрации в пористой среде – в
следующей форме
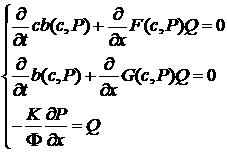 . (1.2) . (1.2)
Мы будем изучать решения так называемой задачи Римана
для системы (1.2), т.е. мы будем искать решения для начальных функций
следующего вида:
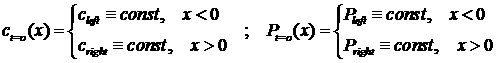 (1.3) (1.3)
Как
легко видеть система уравнений (1.2) не является ни гиперболической, ни
параболической, т.е. задача Римана (1.2), (1.3) требует специальных
рассмотрений.
Еще раз напомним, что в настоящем
исследовании мы будем изучать наиболее интересный случай, когда все начальные
константы (1.3) и получаемое в дальнейшем решение лежат в двухфазной области (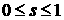 ). Это предположение не
ограничивает общность рассмотрений, но существенно упрощает обозначения и более
ясно демонстрирует основные особенности рассматриваемой задачи. ). Это предположение не
ограничивает общность рассмотрений, но существенно упрощает обозначения и более
ясно демонстрирует основные особенности рассматриваемой задачи.
§2. Вид системы уравнений
двухкомпонентной фильтрации в двухфазной области. Волны разрежения
В
двухфазной области общая система уравнений (1.2) имеет вид
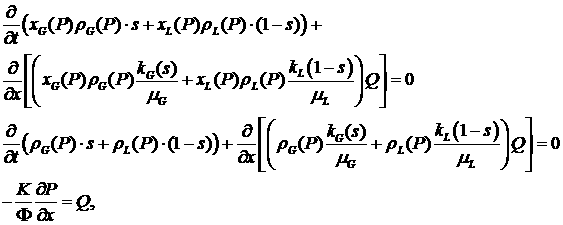 (2.1) (2.1)
здесь
использована переменная 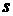 вместо вместо 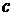 , т.к. мы находимся в
двухфазной области (см. (1.1)). Соответственно начальные данные для задачи
Римана теперь будут выглядеть так , т.к. мы находимся в
двухфазной области (см. (1.1)). Соответственно начальные данные для задачи
Римана теперь будут выглядеть так
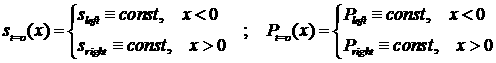 , (2.2) , (2.2)
где
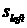 и и 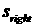 вычисляются по
значениям вычисляются по
значениям 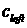 и и 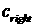 в соответствии с
формулой (1.1). В последующем мы будем иметь дело, главным образом, с задачей
Римана (2.1), (2.2). Также мы будем предполагать, что все функции от в соответствии с
формулой (1.1). В последующем мы будем иметь дело, главным образом, с задачей
Римана (2.1), (2.2). Также мы будем предполагать, что все функции от 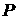 и и 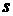 , используемые в (2.1), обладают достаточной гладкостью. , используемые в (2.1), обладают достаточной гладкостью.
Сначала исследуем непрерывные части решения задачи
(2.1), (2.2). Что означает в настоящем контексте слово ‘непрерывные’? Из вида
уравнений (2.1) ясно, что давление 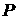 всегда является непрерывной функцией. Если производная
давления, т.е. функция всегда является непрерывной функцией. Если производная
давления, т.е. функция 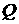 , терпит разрыв, то поскольку уравнения (2.1) записаны в
дивергентной форме и давление является непрерывной функцией, то насыщенность , терпит разрыв, то поскольку уравнения (2.1) записаны в
дивергентной форме и давление является непрерывной функцией, то насыщенность 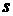 тоже терпит разрыв.
Отсюда получаем следующее тоже терпит разрыв.
Отсюда получаем следующее
ОПРЕДЕЛЕНИЕ 1. Решение (или
часть решения) системы (2.1) назовем непрерывным,
если непрерывны функции 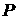 , ,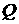 и и 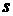 . В противном случае решение назовем разрывным. . В противном случае решение назовем разрывным.
Для того, чтобы найти непрерывные части решения задачи
(2.1), (2.2), введем автомодельную переменную 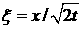 . Эта переменная отличается от соответствующей переменной для гиперболических систем . Эта переменная отличается от соответствующей переменной для гиперболических систем 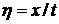 . Пусть ‘штрих’
обозначает дифференцирование по переменной . Пусть ‘штрих’
обозначает дифференцирование по переменной 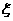 , тогда система (2.1)
для функций, зависящих только от , тогда система (2.1)
для функций, зависящих только от 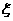 , сводится к следующей
системе обыкновенных дифференциальных уравнений , сводится к следующей
системе обыкновенных дифференциальных уравнений
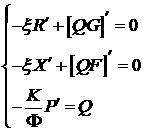 ,
(2.3) ,
(2.3)
где
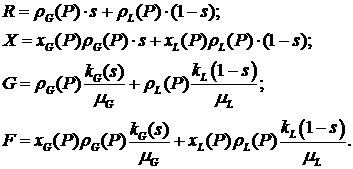 (2.4) (2.4)
Выполнив дифференцирования в системе (2.3) и используя
выражения (2.4), находим выражения для производных 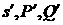
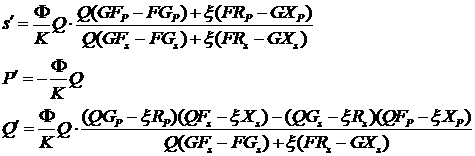 . (2.5) . (2.5)
Далее, запишем систему (2.5) в автономной форме, вводя
новую независимую переменную 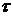 с помощью формулы с помощью формулы 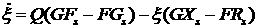 , где ‘точка’ обозначает дифференцирование по , где ‘точка’ обозначает дифференцирование по 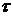
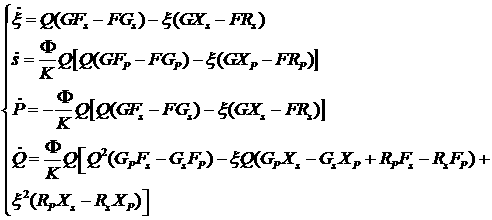 . (2.6) . (2.6)
Поведение
решений системы (2.5) оказывается существенно более сложным, чем поведение
решений соответствующей системы из двух уравнений в случае гиперболической
системы уравнений 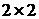 . Для анализа этого поведения необходимо также использовать систему (2.6). . Для анализа этого поведения необходимо также использовать систему (2.6).
Найдем также конкретный вид общих выражений в (2.6),
для упрощения записи опуская зависимость функций от 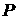 и и 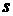
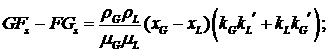
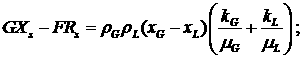
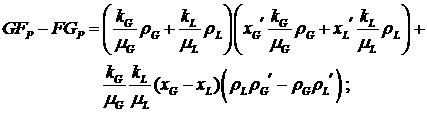
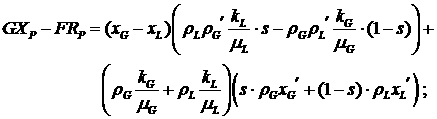
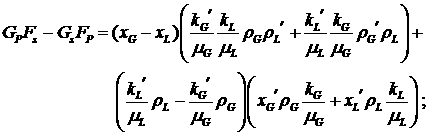
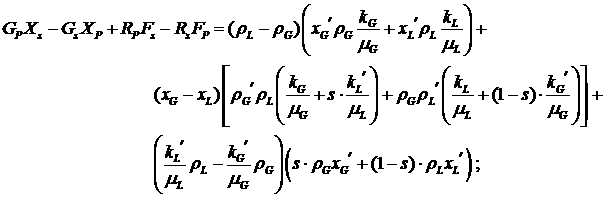
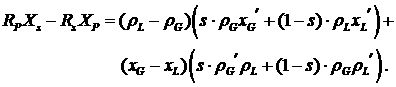
Эти
формулы показывают, что, скорее всего, невозможно найти какие-нибудь
содержательные предположения (при наличии фазовых переходов и сжимаемости),
упрощающие вид формул. Т.е. систему (2.6) необходимо исследовать в той форме,
как она есть, с помощью качественных методов.
Мы
начнем со следующего простого наблюдения.
ЛЕММА 1. Решение задачи (2.1), (2.2) не может иметь
следующего вида: постоянное при 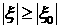 , , 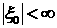 и непрерывное, отличное
от постоянной, в окрестности и непрерывное, отличное
от постоянной, в окрестности 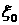 . .
ДОКАЗАТЕЛЬСТВО. Пусть непрерывное решение, отличное от постоянной,
начинается с конечного значения 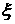 . Т.е. существует такое . Т.е. существует такое 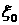 , , 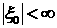 , что решение постоянно при , что решение постоянно при 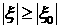 и в соответствии с Определением 1 и в соответствии с Определением 1  при при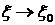 . Заметим, что . Заметим, что
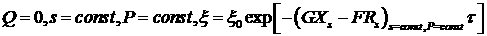
представляет
собой локальное решение системы (2.6). Система (2.6) удовлетворяет условиям,
гарантирующим локальное существование и единственность решений, т.е. решение
либо остается постоянным, либо 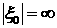 . , . ,
Возвращаясь к системе (2.5), ясно, что
для этой системы также выполнены условия теоремы существования и
единственности, кроме тех областей, где
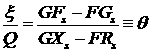 ,
(2.7) ,
(2.7)
Отметим,
что функция 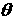 зависит только от зависит только от 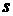 (это легко проверяется
непосредственным вычислением) а выражение (это легко проверяется
непосредственным вычислением) а выражение 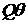 , на самом деле, является скоростью распространения ‘слабых
возмущений’ в терминологии работ [3], [7]. Поэтому назовем поверхность (2.7)
‘характеристической поверхностью’. , на самом деле, является скоростью распространения ‘слабых
возмущений’ в терминологии работ [3], [7]. Поэтому назовем поверхность (2.7)
‘характеристической поверхностью’.
ТЕОРЕМА 1. Не
существует глобальных непрерывных решений задачи (2.1), (2.2).
ДОКАЗАТЕЛЬСТВО. Рассмотрим систему уравнений (2.6) и введем новую
величину 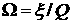 . Тогда для этой
величины имеем следующее уравнение . Тогда для этой
величины имеем следующее уравнение
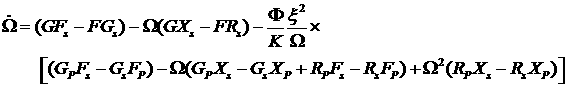 . (2.8) . (2.8)
Непосредственной
проверкой убеждаемся, что 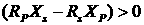 . Далее, из (2.8)
теперь легко видеть, что для больших значений . Далее, из (2.8)
теперь легко видеть, что для больших значений  и и  верно соотношение верно соотношение 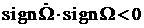 . .
Пусть
теперь 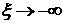 . Тогда в соответствии
с Леммой 1 . Тогда в соответствии
с Леммой 1  . Заметим также, что
если . Заметим также, что
если 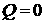 при конечном при конечном 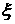 , то, аргументируя также, как при доказательстве Леммы 1,
получим противоречие с теоремой единственности решения. То есть величина , то, аргументируя также, как при доказательстве Леммы 1,
получим противоречие с теоремой единственности решения. То есть величина 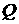 не может менять знак.
Предположим для определенности, что не может менять знак.
Предположим для определенности, что 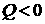 при при 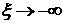 . Тогда . Тогда  и велико, т.е. и велико, т.е. 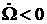 . До тех пор, пока мы
не пересечем характеристическую поверхность (2.7) . До тех пор, пока мы
не пересечем характеристическую поверхность (2.7) 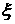 возрастает, и
непрерывное решение может быть построено. Если мы хотим получить глобальное
решение, то при возрастает, и
непрерывное решение может быть построено. Если мы хотим получить глобальное
решение, то при 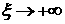 мы должны оставаться с
той же стороны от характеристической поверхности, с какой стартовали, т.е. мы должны оставаться с
той же стороны от характеристической поверхности, с какой стартовали, т.е.  . Значит . Значит 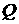 должно быть
положительным и стремиться к нулю, а величина должно быть
положительным и стремиться к нулю, а величина  должна стремиться к должна стремиться к  . Однако в этом случае . Однако в этом случае 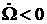 . Получили
противоречие, которое означает, что при попытке продолжения непрерывной
траектории необходимо обязательно пересечь характеристическую поверхность, что
невозможно при сохранении непрерывности траектории. Случай, когда . Получили
противоречие, которое означает, что при попытке продолжения непрерывной
траектории необходимо обязательно пересечь характеристическую поверхность, что
невозможно при сохранении непрерывности траектории. Случай, когда 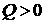 при при 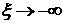 , рассматривается таким
же образом. , рассматривается таким
же образом.
§3. Распространение
разрывов. Условия Гюгонио
Используя наблюдение, сделанное при формулировке
Определения 1, мы будем считать решение разрывным, если рвутся функции 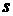 и и 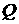 , а функция , а функция 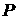 остается непрерывной.
Тогда, используя стандартные приемы теории обобщенных решений квазилинейных
уравнений, получим следующие соотношения на разрыве (соотношения Гюгонио) для
разрывных решений системы (2.1) остается непрерывной.
Тогда, используя стандартные приемы теории обобщенных решений квазилинейных
уравнений, получим следующие соотношения на разрыве (соотношения Гюгонио) для
разрывных решений системы (2.1)
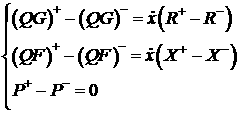 ,
(3.1) ,
(3.1)
где
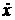 обозначает скорость распространения некоторого
разрыва, а обозначает скорость распространения некоторого
разрыва, а 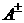 обозначает значения некоторой функции обозначает значения некоторой функции 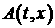 ‘справа’ и ‘слева’ от
этого разрыва, т.е. величины ‘справа’ и ‘слева’ от
этого разрыва, т.е. величины 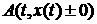 . В уравнениях (3.1)
использованы функции, определенные в (2.4). . В уравнениях (3.1)
использованы функции, определенные в (2.4).
При использовании автомодельной
переменной 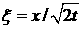 разрыв представляет
собой кривую разрыв представляет
собой кривую 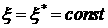 . При этом . При этом 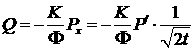 и и 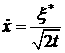 . Таким образом, в
случае автомодельных решений получаем (величина . Таким образом, в
случае автомодельных решений получаем (величина 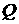 теперь обозначает
выражение теперь обозначает
выражение 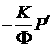 ) )
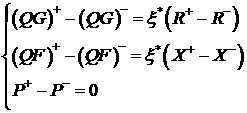 .
(3.2) .
(3.2)
Система
(3.2) записана в автомодельных переменных и явно демонстрирует тот факт, что
давление остается непрерывным, а рвутся градиент давления и насыщенность. Это
свойство отражает смешанный характер системы (2.1): можно сказать, что она
‘параболична’ по давлению и ‘гиперболична’ по насыщенности (концентрации).
Таким образом, можно помнить о непрерывности давления и (для удобства)
исключить третье уравнение из системы (3.2). Тогда, вспоминая вид входящих в (3.2) функций, получим
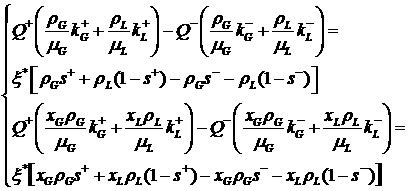 . (3.3) . (3.3)
Легко
видеть, что система (3.3) может быть преобразована к следующему, более простому
виду
 .
(3.4) .
(3.4)
Из
(3.4) следует выражение для адиабаты Гюгонио в случае системы (2.1), которая
фактически представляет собой условие непрерывности скорости фильтрации 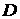
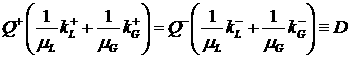 . .
Тогда соотношения Гюгонио могут быть переписаны в
форме
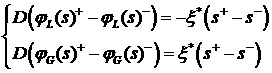 ,
(3.5) ,
(3.5)
где
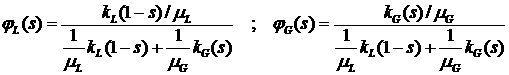 . .
Отметим также, что функция 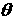 из (2.7) удовлетворяет
соотношениям из (2.7) удовлетворяет
соотношениям
 . .
Также
из (3.5) легко видеть, что 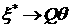 , т.е. к
характеристической скорости, при , т.е. к
характеристической скорости, при 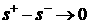 . .
Хорошо известно, что, вообще говоря,
условий Гюгонио недостаточно для выделения единственного решения в случае
систем гиперболического типа, необходимо добавить в какой-либо форме так
называемые условия устойчивости (см., например, [4]). Мы ожидаем подобную
ситуацию и в общем случае системы (1.2), а значит и в частном случае системы
(2.1). Для системы (2.1) сформулируем условия устойчивости, исходя из принципа
[4]: ‘слабые возмущения должны приходить на скачок с обеих сторон’. То есть
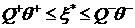 . (3.6) . (3.6)
Заметим,
что из уравнения для адиабаты Гюгонио (следствие (3.4)) вытекает, что 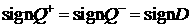 . .
Условие устойчивости (3.6) говорит
нам, что разрыв является ‘допустимым’, если он соединяет соответствующие
значения 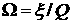 , которые расположены по разные стороны от характеристической
поверхности (2.7) ( , которые расположены по разные стороны от характеристической
поверхности (2.7) (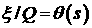 ). Посмотрим, что это означает в терминах функции ). Посмотрим, что это означает в терминах функции 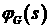 , которая в большинстве приложений представляет собой
невыпуклую функцию с одной точкой перегиба. Пусть для определенности , которая в большинстве приложений представляет собой
невыпуклую функцию с одной точкой перегиба. Пусть для определенности 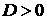 . Тогда из (3.5), (3.6) получим . Тогда из (3.5), (3.6) получим
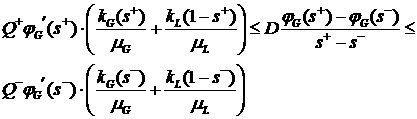
или
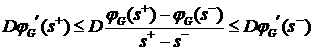 . (3.7) . (3.7)
В
случае 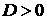 соотношение (3.7) принимает вид соотношение (3.7) принимает вид
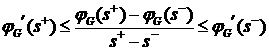 .
(3.8) .
(3.8)
В
случае 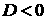 неравенства
(3.8) должны быть обращены. Таким образом, мы приходим к некоторому обобщению
классического условия Олейник [5] для невыпуклых функций потока с одной точкой
перегиба. неравенства
(3.8) должны быть обращены. Таким образом, мы приходим к некоторому обобщению
классического условия Олейник [5] для невыпуклых функций потока с одной точкой
перегиба.
§4. Построение решения
задачи Римана
Теперь
опишем способ построения решений для задачи Римана (2.1), (2.2). Без
ограничения общности мы будем предполагать, что 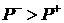 (в случае обратного
неравенства рассмотрения полностью аналогичны). Сначала докажем одно утверждение относительно бесконечной скорости
распространения возмущений в задаче Римана. (в случае обратного
неравенства рассмотрения полностью аналогичны). Сначала докажем одно утверждение относительно бесконечной скорости
распространения возмущений в задаче Римана.
ТЕОРЕМА 2. Для
автомодельных решений задачи Римана (2.1), (2.2) скорость распространения
возмущений бесконечна, т.е. для любой точки 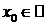 не существует
полуокрестности точки не существует
полуокрестности точки 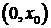 на полуплоскости на полуплоскости  , в которой , в которой 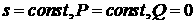 . .
ДОКАЗАТЕЛЬСТВО. Пусть существует такая окрестность 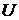 . Это значит, что в ‘окрестности’, скажем, . Это значит, что в ‘окрестности’, скажем, 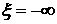 решение задачи Римана
постоянно. Обозначим максимальное решение задачи Римана
постоянно. Обозначим максимальное 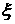 , при котором решение задачи Римана постоянно, через , при котором решение задачи Римана постоянно, через 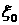 . Если . Если 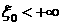 , то решение должно быть каким-то образом продолжено для , то решение должно быть каким-то образом продолжено для 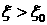 . Согласно Лемме 1, это продолжение не может происходить с
помощью непрерывных решений системы (2.6). Если же при . Согласно Лемме 1, это продолжение не может происходить с
помощью непрерывных решений системы (2.6). Если же при 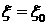 имеет место разрыв, то имеет место разрыв, то
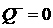 и, в соответствии со
следствием из (3.4) (уравнение для адиабаты Гюгонио), и, в соответствии со
следствием из (3.4) (уравнение для адиабаты Гюгонио), 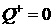 . Тогда и . Тогда и 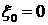 . Т.к. подобные рассуждения могут быть проведены и для . Т.к. подобные рассуждения могут быть проведены и для 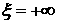 , то нашим предположениям удовлетворяет единственный набор
функций (решение задачи Римана) – постоянных при , то нашим предположениям удовлетворяет единственный набор
функций (решение задачи Римана) – постоянных при  и при и при  и имеющих разрыв при и имеющих разрыв при 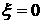 . Но в этом случае мы получили решение с разрывным давлением,
что не соответствует условиям (3.2). , . Но в этом случае мы получили решение с разрывным давлением,
что не соответствует условиям (3.2). ,
Теорема 2 утверждает, что в отличие от
гиперболических систем система (2.1) частично обладает свойствами
параболических уравнений, например, – бесконечной скоростью распространения
возмущений. Т.е. решение задачи Римана (2.1), (2.2) при 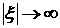 определяется решениями
системы (2.6) (или (2.5)). определяется решениями
системы (2.6) (или (2.5)).
Итак, теперь приступим к общему
построению решения задачи Римана. Будем строить это решение последовательно в соответствии
с ростом 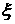 , начиная от области , начиная от области 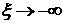 . Согласно Теореме 2 решение начинается с волны разрежения,
определяемой как решение системы (2.6). При этом . Согласно Теореме 2 решение начинается с волны разрежения,
определяемой как решение системы (2.6). При этом 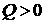 (поскольку (поскольку
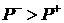 ), ), 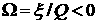 велико по модулю ( велико по модулю ( ) и возрастает (см. (2.8)). Из
формул (2.6) следует, что пока ) и возрастает (см. (2.8)). Из
формул (2.6) следует, что пока  лежит ниже
характеристической поверхности (2.7), величина лежит ниже
характеристической поверхности (2.7), величина 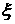 возрастает, и волна
разрежения может быть продолжена. В то же время, согласно Лемме 1, волна
разрежения не может переходить в постоянную величину. Напомним, что по Теореме
1 решение обязано иметь по крайней мере один скачок, чтобы величина возрастает, и волна
разрежения может быть продолжена. В то же время, согласно Лемме 1, волна
разрежения не может переходить в постоянную величину. Напомним, что по Теореме
1 решение обязано иметь по крайней мере один скачок, чтобы величина  преодолела
характеристическую поверхность. Условия устойчивости (3.6) показывают, что
скачок является устойчивым, только если величины преодолела
характеристическую поверхность. Условия устойчивости (3.6) показывают, что
скачок является устойчивым, только если величины 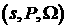 с разных сторон
разрыва лежат по разные стороны характеристической поверхности (2.7). с разных сторон
разрыва лежат по разные стороны характеристической поверхности (2.7).
Таким образом, волна разрежения должна
заканчиваться скачком, при этом величина  оказывается лежащей
выше характеристической поверхности (2.7). При этом согласно формулам для
адиабаты Гюгонио (следствие из (3.4)) значение оказывается лежащей
выше характеристической поверхности (2.7). При этом согласно формулам для
адиабаты Гюгонио (следствие из (3.4)) значение 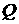 по другую сторону
разрыва останется положительным. Далее, после разрыва параметр по другую сторону
разрыва останется положительным. Далее, после разрыва параметр 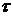 из системы (2.6)
должен начать убывать, т.к. из системы (2.6)
должен начать убывать, т.к. 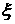 теперь убывает при
росте теперь убывает при
росте 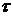 (это ничему не мешает,
т.к. (это ничему не мешает,
т.к. 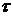 является автономным
параметром, который из-за разрыва никак не связан с соответствующим параметром,
который мы использовали при является автономным
параметром, который из-за разрыва никак не связан с соответствующим параметром,
который мы использовали при 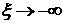 ). ).
Рассуждая аналогичным образом, мы
приходим к выводу, что после разрыва решение будет опять же волной разрежения,
определяемой формулами (2.6) вплоть до значения 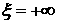 . .
Итак, мы приходим к следующей
конструкции. Имеется пучок траекторий (решений системы уравнений (2.6)),
которые удовлетворяют условиям: 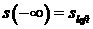 , , 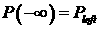 , , 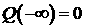 . Этот пучок можно параметризовать, например, величиной . Этот пучок можно параметризовать, например, величиной 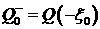 , где , где 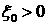 достаточно велико.
Двойственным образом имеется пучок траекторий (также решений системы уравнений
(2.6)), удовлетворяющих условиям: достаточно велико.
Двойственным образом имеется пучок траекторий (также решений системы уравнений
(2.6)), удовлетворяющих условиям: 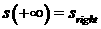 , , 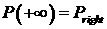 , , 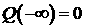 . Этот пучок опять же можно параметризовать величиной . Этот пучок опять же можно параметризовать величиной 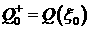 . Выбор траекторий, которые будут входить в решение задачи
Римана, определяется соотношениями на разрыве (3.2). А именно, . Выбор траекторий, которые будут входить в решение задачи
Римана, определяется соотношениями на разрыве (3.2). А именно,
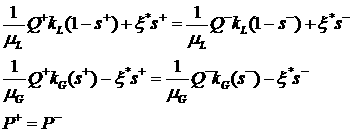 , (4.1) , (4.1)
где 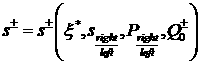 ; ; 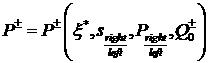 ; ;
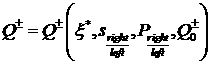 . Эти функции
определяются решениями системы (2.5) (или (2.6)). Система (4.1) состоит из трех
уравнений и содержит три неизвестных: величины . Эти функции
определяются решениями системы (2.5) (или (2.6)). Система (4.1) состоит из трех
уравнений и содержит три неизвестных: величины 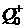 , , 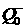 и положение скачка и положение скачка 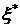 , поэтому, вообще говоря, имеет решение. , поэтому, вообще говоря, имеет решение.
Далее, система (4.1), вообще говоря,
имеет единственное решение. Поэтому неединственность в задаче Римана (2.1),
(2.2) может лишь возникнуть при наличии большего, чем один, числа скачков.
Напомним, что согласно нашим рассмотрениям знак 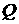 всегда сохраняется.
Отсюда следует, что (при условии всегда сохраняется.
Отсюда следует, что (при условии 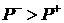 , т.е. , т.е. 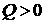 ) при скачке величины ) при скачке величины 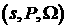 ‘слева’ от скачка
всегда лежат ниже характеристической поверхности (2.7), а эти же величины
‘справа’ от скачка всегда лежат выше характеристической поверхности (2.7), см.
(3.6). Т.е., попав один раз выше характеристической поверхности, нельзя
(благодаря условиям устойчивости (3.6)) снова посредством скачка попасть в
область ниже характеристической поверхности. Итак, скачок, а с ним и все
решение задачи Римана, оказывается единственным. ‘слева’ от скачка
всегда лежат ниже характеристической поверхности (2.7), а эти же величины
‘справа’ от скачка всегда лежат выше характеристической поверхности (2.7), см.
(3.6). Т.е., попав один раз выше характеристической поверхности, нельзя
(благодаря условиям устойчивости (3.6)) снова посредством скачка попасть в
область ниже характеристической поверхности. Итак, скачок, а с ним и все
решение задачи Римана, оказывается единственным.
Список Литературы
|
[1]
|
Бедриковецкий
П.Г., Каневская Р.Д., Лурье М.В. Автомодельные решения задач двухфазной
фильтрации с учетом сжимаемости одной из фаз. Механика жидкости и газа, № 1,
с. 71 – 80 (1990).
|
|
[2]
|
A.V. Koldoba, E.V. Koldoba,
The discontinuous solutions of the transport equations for compositional flow
in porous media. Transport in porous Media, v.52, pp. 267 – 277 (2003).
|
|
[3]
|
А.В.
Колдоба, Е.В. Колдоба, Разрывные решения уравнений многокомпонентной
фильтрации. Институт прикл. матем. им. М.В.Келдыша РАН, Препринт № 85 (1999).
|
|
[4]
|
P.D. Lax, Hyperbolic systems of conservation laws
and the mathematical theory of shock waves, No. 11, SIAM, Philadelphia
(1973).
|
|
[5]
|
Олейник О. А. Разрывные решения нелинейных
дифференциальных уравнений. Успехи Матеем. Наук, т. 12, вып. 3, с. 3 – 73
(1957).
|
|
[6]
|
F.M. Orr, Theory of Gas Injection Processes, Stanford
University, Stanford, California (2005).
|
|
[7]
|
Радвогин Ю.Б.
Характеристические свойства уравнений двухкомпонентной фильтрации. Институт
прикл. матем. им. М.В.Келдыша РАН, Препринт № 37 (2001).
|
|
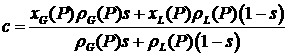 ,
,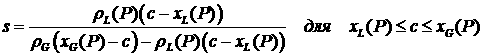
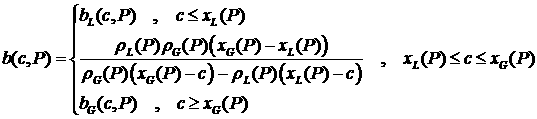 ,
,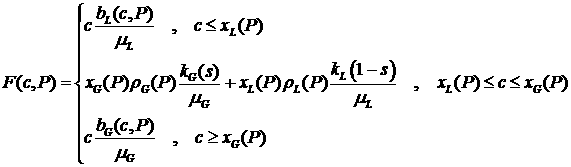
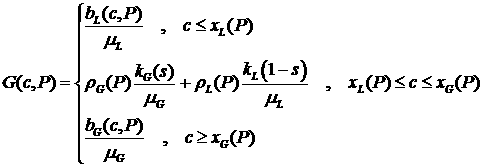 ,
,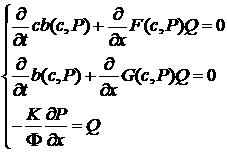
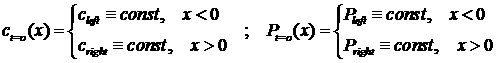
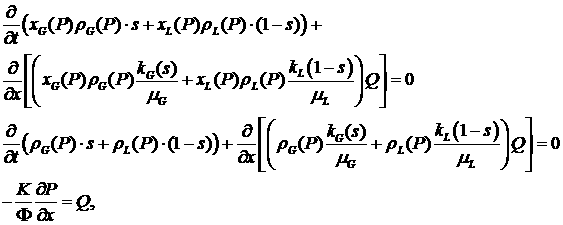
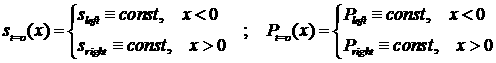
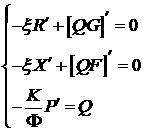
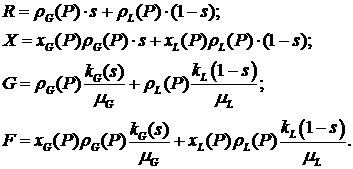
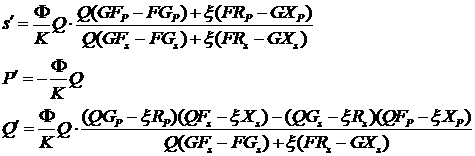
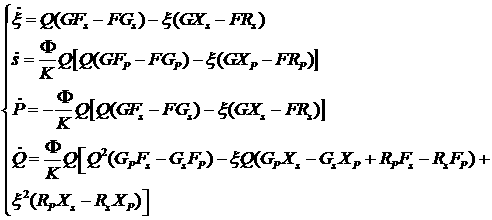
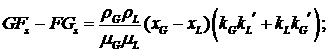
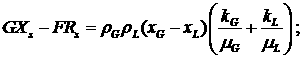
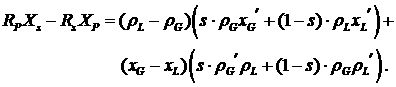
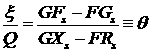 ,
,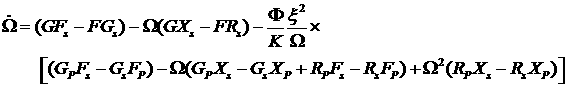 .
.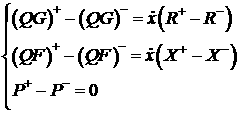
 .
.

 .
. ,
,
 .
.
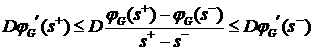
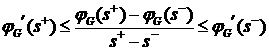 .
.