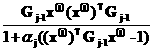О некоторых свойствах метода распознавания символов, основанного на полиномиальной регрессии
|
|
символ |
true_min |
true_max
|
false_min
|
false_max |
средняя оценка неправильного распознавания |
|
0 |
35,41
|
113,59
|
56,34
|
101,09
|
106,61 |
|
1 |
42,58 |
173,80 |
52,22 |
131,38 |
128,17 |
|
2 |
38,33 |
105,57 |
61,62 |
109,43 |
120,19 |
|
3 |
39,92 |
103,10 |
55,63 |
95,53 |
118,84 |
|
4 |
50,76 |
106,34 |
56,02 |
123,47 |
131,78 |
|
5 |
36,28 |
130,66 |
52,68 |
98,26 |
126,65 |
|
6 |
44,60 |
115,07 |
55,17 |
103,11 |
105,26 |
|
7 |
40,56 |
101,70 |
53,45 |
93,89 |
114,43 |
|
8 |
50,15 |
119,80 |
57,23 |
115,19 |
121,27 |
|
9 |
47,36 |
120,58 |
54,28 |
117,37 |
127,45 |
Были проведены расчеты и получены
средние оценки распознавания и дискретные аналоги функции распределения при
делении отрезка [true_min, true_max] на 50 равных частей. Результаты аналогичны приведенным на
рис.2-11.
Итак, можно сделать следующие
выводы. В среднем оценка распознавания
не зависит от удаленности растра символа от «среднестатистического» растра
данного символа по рассматриваемой базе обучения и распознавания. Средняя оценка правильного распознавания
существенно выше (приблизительно в два раза), чем средняя оценка неправильного
распознавания.
4. Анализ качества распознавания на различных базах символов
Интуитивно
понятно, что любая база распознавания – это каким-либо образом «испорченная»
база обучения. На практике бывает трудно определить, существует ли некая закономерность
преобразования базы обучения в базу распознавания. В настоящей работе мы сами
предлагаем четыре модели «разрушения» базы обучения, и в рамках каждой из них
исследуем зависимость качества распознавания от степени «искажения» обучающей
базы.
Будем анализировать поведение таких
характеристик качества распознавания символов, как оценка распознавания
(средняя по всем верно распознанным растрам базы), а также число неправильно распознанных образов по базе.
Скорость (абсолютная, средняя) между двумя точками на графике
равна модулю изменения величины, откладываемой по оси ординат, отнесенному к
модулю изменения величины, откладываемой по оси абсцисс.
Модель «наихудшего»
разрушения. В обучающей базе на этапе распознавания для каждого растра
выбирается случайным образов определенное количество пикселей, в которых vi, лежащие в полуинтервале 0≤vi <0,5, заменяются значением 1: [0;
0,5)→1, а при 0,5≤vi≤1 величиной 0: [0,5; 1]→0. Число пикселей, в которых производятся такие модификации,
варьируется от 1 до некоторого значения, в данном случае 10, при котором
преодолевается «порог» количества неправильно распознанных растров (мы
устанавливаем его равным удвоенному числу изображений, нераспознанных на самой
базе обучения, а именно, 881 ∙ 2 = 1762). При каждом фиксированном
количестве k (1≤k≤10) заменяемых
пикселей осуществляется распознавание по всей базе. При построении графиков
формально добавляется значение числа измененных пикселей, равное 0, что соответствует распознаванию обучающей
базы.
Модель «случайного»
разрушения. В обучающей базе на этапе распознавания для каждого растра
выбирается случайным образов определенное количество пикселей, в которых vi, лежащее на отрезке 0≤vi ≤1, заменяется на случайное значение,
также принадлежащее отрезку [0,1]. Число пикселей, в которых производятся такие модификации,
варьируется от 1 до 256, поскольку в данном случае не преодолевается «порог»
количества неправильно распознанных растров (881 · 2 = 1762).
Здесь и выше используется
генератор псевдослучайных чисел. Так в каждом текущем растре для случайного
выбора k различных пикселей из имеющихся перенумерованных
от 0 до 255 (т.е. всего 256 пикселей), выполняются следующие действия. Для
натурального числа, предлагаемого генератором псевдослучайных чисел, находим
остаток от деления на 256. Он является целым и принадлежит требуемому отрезку
[0,255]. Дополнительно проводится проверка отличия нового номера от полученных
прежде.
Аналогично, при выборе случайного значения vi, принадлежащего отрезку [0,1], для
натурального числа, предлагаемого генератором псевдослучайных чисел, находим
остаток от деления на 101. Он является целым и принадлежит отрезку [0,100]. Делим его на 100. Результат
принадлежит отрезку [0,1].
На рис.12а,б для сравнения приводятся результаты, полученные при
«наихудшем» и «случайном» разрушении для числа пикселей, в которых производятся
такие модификации, изменяющемся от 1 до 10. Также добавлен 0, что соответствует
отсутствию модификаций.
На рис.12а на отрезке для числа «испорченных» пикселей [0, 10]
показано линейное падение средней оценки распознавания для «наихудшего»
разрушения; для «случайного» разрушения убывание почти линейное, но средняя скорость его приблизительно в два
раза меньше. В обоих случаях зависимости являются строго монотонными.
На рис.12б можно видеть монотонное нарастание количества неправильно
распознанных растров при увеличении числа «испорченных» «наихудшем» образом
пикселей. Когда их количество становится равным 10, число неправильно
распознанных растров преодолевает «пороговое» значение и становится равным
1835. Для «случайного» разрушения график является почти монотонно нарастающим
(наблюдаются небольшие колебания) и близким к линейному. При 10
модифицированных пикселях количество нераспознанных растров увеличивается
незначительно, до значения 994. Т.е. на рассматриваемом отрезке для числа «испорченных»
пикселей [0, 10] средняя скорость увеличения числа неправильно распознанных
растров для «наихудшего» разрушения более чем в семьдесят три раза превышает
соответствующий показатель при «случайном» разрушении.
Как уже было отмечено ранее, при «случайном» разрушении пикселей
«пороговое» количество нераспознанных растров не достигается даже при модификации
всех пикселей. На рис 13а видно, что средняя оценка распознавания монотонно
убывает на максимально возможном отрезке для числа «испорченных» пикселей [0,
256], но скорость падения этой величины на участке [16, 40] существенно
замедляется и далее остается очень незначительной. Количество нераспознанных
растров увеличивается немонотонным образом, но в среднем на участке [0, 16]
увеличивается с большой скоростью, средняя скорость нарастания этой величины на
участке [16, 40] существенно замедляется и далее становится равной нулю, но при этом наблюдаются
колебания около оценки 205,7.
Анализ поведения оценки распознавания и числа нераспознанных растров
на моделях «наихудшего» и случайного разрушения позволяют нам делать выводы о
поведении аналогичных характеристик для моделей разрушения, лежащих «между»
двумя изученными. Очевидно, что с увеличением числа разрушенных пикселей
средняя оценка распознавания будет монотонно падать, а число нераспознанных
символов увеличиваться, но в среднем, немонотонно. Сделанные выводы позволяют
строить следующие модели разрушения уже для всех пикселей растра, без
дополнительного анализа влияния увеличения их числа.
Модели затемнения
(засветления). На этапе распознавания все пиксели растра постепенно затемняются:
vi→
vi+0,01 ∙ n, где n=0,1,2,..,nтемн . Если для каких-то
пикселей начиная с некоторого n имеем: vi≥1, то считаем, что
vi=1. При засветлении аналогично vi→ vi-0,01 ∙ n,
где n=0,1,2,.. ,nсветл . Если для каких-то пикселей
начиная с некоторого n имеем: vi≤0, то считаем, что
vi=0. При n= nтемн =12 и аналогично при n= nсветл =20 число неправильно
распознанных растров преодолевает «пороговое» значение (881 · 2 = 1762).
На рис.14а,б для сравнения приводятся результаты распознавания,
полученные при затемнении и засветлении растров. По оси абсцисс откладывается
число n, определяющее степень затемнения (засветления).
Распознаванию обучающей базы соответствует n=0.
На рис.14а показано почти линейное падение оценки распознавания
для затемнения и засветления, причем на
отрезке [0, 12] средняя скорость второго в 4,2 раза меньше. В обоих случаях
зависимости являются строго монотонными.
На рис.14б можно видеть немонотонное изменение количества
неправильно распознанных растров при затемнении. Дополнительные расчеты
показали, что при n=2,5 достигается минимальное число 823 неправильно
распознанных символов. При n= nтемн =12 число неправильно
распознанных растров преодолевает «пороговое» значение и становится равным
1783. Для засветления график является монотонным. При n= nсветл =20 число неправильно
распознанных растров преодолевает «пороговое» значение и становится равным
1747.
Итак, затемнение и засветление растров оказывают различное влияние
на распознавание. Оказывается, при небольшом затемнении (до n =
6) количество нераспознанных символов даже меньше, чем в немодифицированной
базе. Однако, в результате наблюдающегося затем стремительного роста количества
нераспознанных символов при затемнении, увеличение их числа по сравнению с
распознаванием исходной базы для n =12 при затемнении приблизительно в 4 раза больше,
чем при засветлении. Оценка распознавания как для затемнения, так и для
засветления, монотонно уменьшается с ростом степени изменения исходных растров,
причем при 0≤n ≤12 для второго процесса в 4,2 раза
медленнее, чем для первого.
Модель «дискретизации». В рассматриваемых «серых» растрах для каждого
пикселя 0≤vi ≤1. Поделим отрезок [0,1] на 256 равных по длине частей –
отрезок и 255 полуинтервалов: [0, dv], (dv, 2∙dv], … , (255∙dv, 256∙dv], где dv = 1/256. Осуществим следующее преобразование
для всех пикселей растра. Если 0≤vi ≤ dv, то vi → dv /2 (иначе [0, dv] → dv /2 ); в полуинтервале k∙dv <vi≤(k+1)
∙dv, где к=1, …, 255, производится замена: vi → (k+1/2)
∙dv (иначе (k ∙dv, (k+1)
∙dv] → (k+1/2) ∙dv ). Мы осуществили
дискретизацию бесконечного множества значений 0≤vi ≤1, в результате
которой vi будет принимать только 256 значений:{dv/2, (1+1/2)∙dv, … , (255+1/2)∙dv} Выполним распознавание
полученной базы символов, которая, как нетрудно понять, очень незначительно
отличается от исходной базы.
Произведем аналогичную дискретизацию с делением отрезка [0,1] на 128 частей, затем на 64
части, далее на 32 части, на 16, на 8 и наконец на 4. От базы к базе количество
отрезков дискретизации уменьшалось в 2 раза, Каждая последующая база все больше
отличается от исходной.
На рис.15а,б приводятся результаты, полученные при
«дискретизации». По оси абсцисс откладывается число отрезков дискретизации, а
именно 256, 128, 64, 32, 16, 8. Распознаванию обучающей базы соответствует
число 256.
На рис.15а показано строго монотонное падение оценки распознавания
при уменьшении количества отрезков дискретизации.
На рис.15б изображен график немонотонного изменения количества
неправильно распознанных растров. Дополнительные расчеты при 12 и 24 отрезках
дискретизации подтвердили, что на 16 отрезках дискретизации достигается
минимальное число 815 неправильно распознанных символов. Их количество увеличивается
(не достигая порогового значения) при дальнейшем уменьшении числа отрезков дискретизации
вплоть до 8.
На рис.16а,б также приводятся результаты, полученные при
дискретизации, но уже для числа отрезков
дискретизации 256, 128, 64, 32, 16, 8, 4 (добавилось число 4).
На рис.16а по-прежнему строго монотонное падение оценки
распознавания при уменьшении количества отрезков дискретизации.
На рис.16б изображен график немонотонного изменения количества
неправильно распознанных растров. При 4 отрезках дискретизации число
неправильно распознанных растров преодолевает «пороговое» значение и становится
равным 2806. Скорость роста на отрезке [8, 4] по оси абсцисс существенно выше
(в 40 раз), чем на отрезке [16, 8].
Итак, анализ результатов распознавания, полученных с
использованием модели «дискретизации», показывает, что оценка распознавания
монотонно уменьшается по мере «удаления» базы распознавания от базы обучения,
соответствующего убыванию числа отрезков дискретизации. Количество
нераспознанных символов ведет себя немонотонным образом. Вначале при уменьшении
числа отрезков дискретизации оно уменьшается и достигает минимума при
количестве таких отрезков, равном 16. Затем число нераспознанных символов увеличивается
(причем с нарастающей скоростью) и преодолевает пороговое значение.
5. Выводы
Изучение «поведения» описанного
метода распознавания, основанного на полиномиальной регрессии, при
распознавании рукопечатных цифр по базе, совпадающей с базой обучения, для
каждого из рассматриваемых символов показало следующее. В среднем оценка
распознавания не зависит от «удаленности» растра символа от
«среднестатистического» растра данного символа по рассматриваемой базе. Средняя оценка правильного распознавания
символа существенно выше (приблизительно в два раза), чем средняя оценка
неправильного распознавания.
«Превращение» базы обучения в базу
распознавания формализовано в виде четырех моделей. Для каждой из них получено,
что по мере увеличения степени «искажения» обучающей
базы оценка распознавания монотонно уменьшается,
а количество нераспознанных символов в целом
увеличивается, но этот процесс может протекать существенно немонотонным образом.
При реальном распознавании можно использовать полученные наработки
для улучшения качества распознавания, но уже в «обратном» порядке. Разумеется,
имеются в виду только те модели, что применяются для всех пикселей растра, а не
для некоторых случайным образом выбранных. Предложенные способы преобразования
(затемнение, засветление, «дискретизацию») можно применить к распознаваемой
последовательности символов. Из вышеописанного следует, что результатом может
быть либо улучшение оценок распознавания, либо уменьшение числа нераспознанных
символов, либо и то, и другое. Возможно комбинированное использование
затемнения (засветления) и «дискретизации».
Литература
[1] Гавриков М.Б., Пестрякова Н. В.
"Метод полиномиальной регрессии в задачах распознавания печатных и
рукопечатных символов", //Препринт ИПМатем. АН СССР, М., 2004, №22, 12 стр.
[2] Гавриков М.Б., Мисюрев А.В., Пестрякова
Н.В., Славин О.А. Развитие метода полиномиальной регрессии и практическое
применение в задаче распознавания символов. Автоматика и Телемеханика. 2006,
№3, С. 119-134.
[3] Sebestyen
G.S. Decision Making Processes in
Pattern Recognition, MacMillan, New York, 1962.
[4] Nilson N. J. Learning Machines, McGraw-Hill, New York, 1965.
[5] Schürmann J. Polynomklassifikatoren,
Oldenbourg, München, 1977.
[6] Schürmann J. Pattern
Сlassification, John Wiley&Sons,
Inc., 1996.
[7] Albert
A.E. and Gardner L.A. Stochastic
Approximation and Nonlinear Regression // Research Monograph 42. MIT Press,
Cambridge, MA, 1966.
[8] Becker
D. and Schürmann J. Zur
verstärkten Berucksichtigung schlecht erkennbarer Zeichen in der Lernstichprobe
// Wissenschaftliche Berichte AEG-Telefunken 45, 1972, pp. 97 – 105.
[9] Pao Y.-H. The Functional Link Net: Basis for an Integrated Neural-Net
Computing Environment // in Yoh-Han Pao (ed.) Adaptive Pattern Recognition and
Neural Networks, Addisson-Wesley, Reading, MA, 1989, pp. 197-222.
[10] Franke
J. On the Functional Classifier, in
Association Francaise pour la Cybernetique Economique et Technique (AFCET),
Paris // Proceedings of the First International Conference on Document Analysis
and Recognition, St. Malo, 1991, pp.481-489.
[11] Дж.Себер. Линейный регрессионный анализ.
М.:”Мир”, 1980.
[12]
Ю.В.Линник. Метод наименьших квадратов и основы математико -
статистической теории обработки наблюдений. М.:”Физматлит”, 1958.
Рисунки
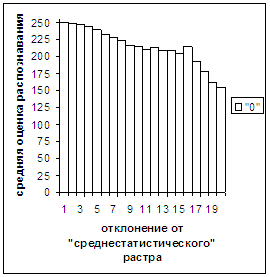
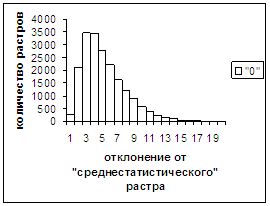
Рис. 2а
Рис. 2б
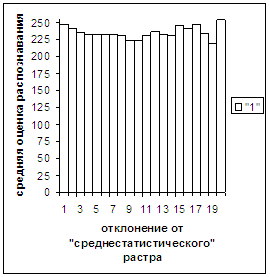
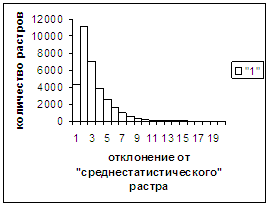
Рис. 3а
Рис. 3б
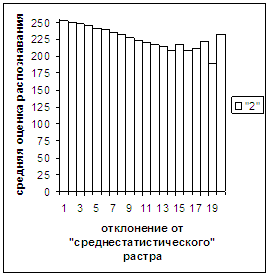
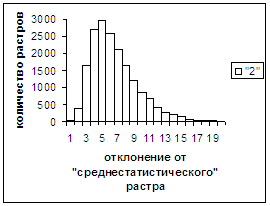
Рис. 4а
Рис. 4б

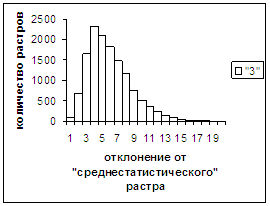
Рис. 5а
Рис. 5б
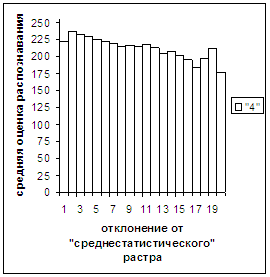
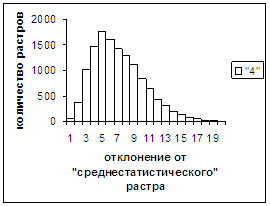
Рис. 6а
Рис. 6б
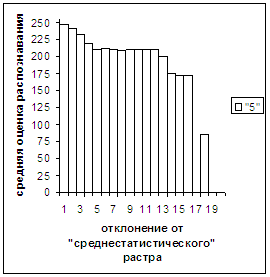
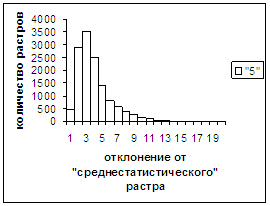
Рис. 7а
Рис. 7б
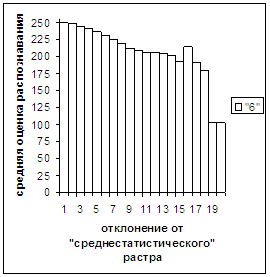
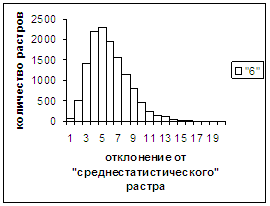
Рис. 8а
Рис. 8б
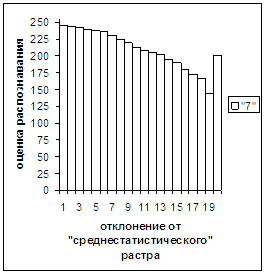
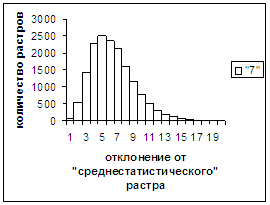
Рис. 9а
Рис. 9б
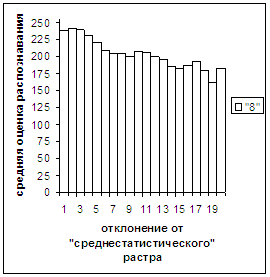
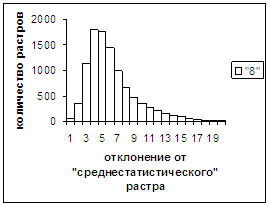
Рис. 10а
Рис. 10б
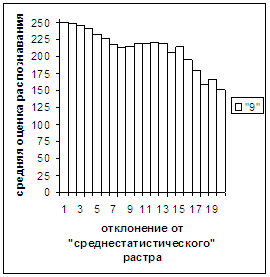
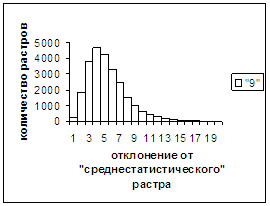
Рис. 11а
Рис. 11б
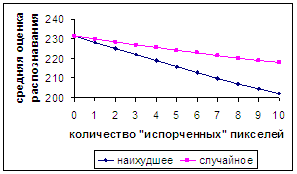
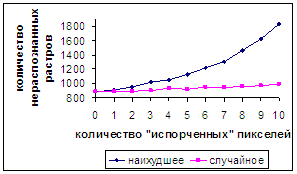
Рис. 12а
Рис. 12б
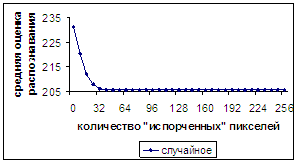

Рис. 13а
Рис. 13б
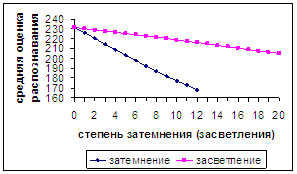
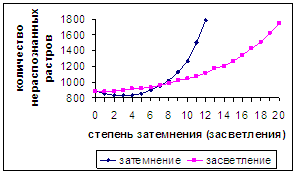
Рис. 14а
Рис. 14б
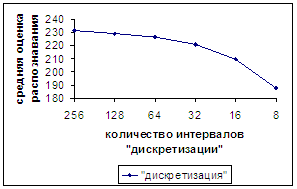
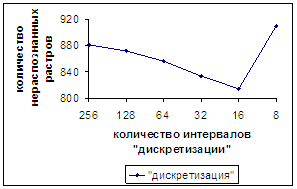
Рис. 15а
Рис. 15б
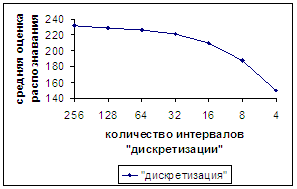
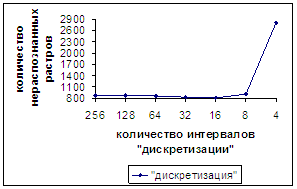
Рис. 16а
Рис. 16б