Динамика роста областей достижимости рикошетирующих механических систем

( The investigation of range regions growing dynamic of the rebounding mechanical systems
Preprint, Inst. Appl. Math., the Russian Academy of Science)

         Оглавление

Введение .........................................................................................  3

1.                Общая постановка задачи ............................................... 3

2.                Динамика роста дальности............................................   7

3.                Динамика развития областей роста.............................. 10

4.                Динамика прироста объемов .......................................  13

Заключение .................................................................................... 17

Литература ..................................................................................... 18

          Введение

          Оценки предельных линейных размеров областей достижимости механических систем с отражениями получены в целом ряде работ [1-4]. Однако значительный интерес представляет возможный анализ именно динамики развития зон роста из первоначально строго локализованного “источника возмущений”. Здесь важны также и оценки прироста площадей зон каждого рикошета и их пространственных характеристик. Исследованию этого вопроса и посвящена настоящая работа.

Общая постановка задачи.

Рассмотрим "квазипотенциальный"  биллиард  -  материальную точку с анизотропными упругими свойствами движущуюся в поле потенциальных сил  на участках между   квазисингулярными   отражениями   от некоторой   поверхности.

В рамках квазисингулярного подхода [1-5] считаем участок рикошета пренебрежимо малым по сравнению с участком свободного движения.

 Отражения   предполагают некоторую диссипацию энергии движения. Будем описывать  характер отражения путем сопоставления каждому вектору скорости  тела  Vº до отражения некоторой области  M в ³, состоящей  из  всевозможных  векторов скорости тела V¹ после отражения . Внешнюю границу такой области,  в случае   ее   существования,   по   аналогии   с   введенным   в геометрической оптике обозначением множества локальных скоростей света в неизотропной среде  [6,7], естественно  назвать индикатрисой  I  . Отметим, что рикошеты в ряде задач могут описываться достаточно сложным образом (например-  поверхность шарика квазисферична и имеет сложную форму, площадка соприкосновения тела с отражающей поверхностью на рикошете отлична от точки и, вообще говоря, не обязательно является компактом).

Зададимся целью описать динамику рикошета как преобразование входного вектора скорости (скорости падения) в вектор выходной скорости (скорость отражения) с помощью некоторого функционала отражения I:³®Â³:

                 V¹º =  I  ( Vº )

     Синтез областей достижимости может сильно меняться и приводить к структурно иным результатам в  зависимости от расположения  проекций скорости отражения  на поверхности рикошета относительно "точки  нулевой  скорости" O*.

В зависимости от этого составим следующую таблицу индикатрис рикошетирования.

         Т а б л и ц а   1

__________________________________________________________

упругость                 -                     -                 -               -                  -

__________________________________________________________

изотропия                -                     -                 +               +                -

__________________________________________________________

O*Î I                        0                    +                 -               +                 -

__________________________________________________________

          Можно выделить следующие классы индикатрис, описывающих характер взаимодействия тела со средой.

        (A). ”Слои” ("Мячик"). Точка O не лежит в I. Характеризует близкий  к упругому и близкий к плоскому характер отражения ("мячик" все время отскакивает в постоянной продольной плоскости).

           (B).”Лист” ("Камешек на воде").  Точка  O  лежит  на  границе  I   и характеризует наличие эффекта поглощения:  существуют  движения, при которых "камешек" тонет и отражения не происходит. Описывает наличие рикошетов в виде отскоков вбок.

        (C)."Эхо". Точка O лежит внутри I . "Выходные" скорости тела имеют  больший  модуль  в  направлении   вектора   скорости   до отражения. Характеризует наличие отражения "назад".

          (D)."Маяк". Точка O лежит в центре  области.  Характеризует изотропное  распространение  волнового   фронта   от   точечного источника света.

        Численно посчитанная модельная ОД для класса  индикатрис (B) (“лист”, "камешек на воде") получена в [1-3].  На рис.2 приведены модельные области достижимости  для наиболее характерных классов  индикатрис.

          Отметим,   что   "классическому"   случаю   гравитационного биллиарда  [8] соответствует индикатриса I  в  виде  одной  точки,  определяющая вектор скорости после  отражения,  равный  исходному  вектору  и характеризующая процесс бесконечного рикошетирования, а редукции этого случая на наличие анизотропного трения - продольный отрезок, не содержащий точку отражения.

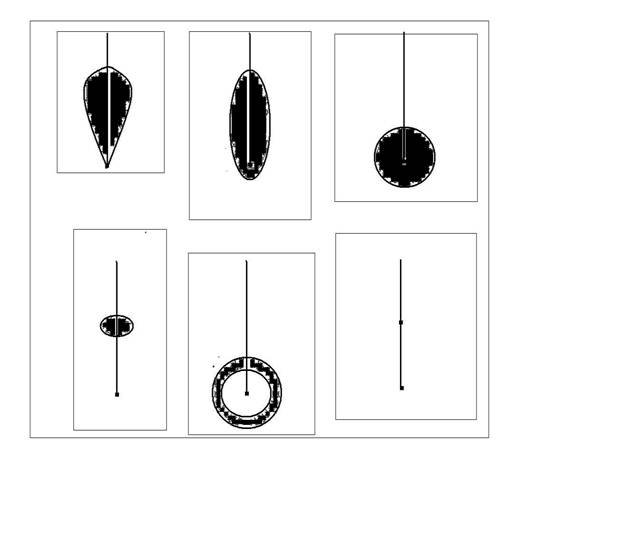
Рисунок 1. Классификация индикатрис по расположению концов возможных векторов отраженной скорости относительно скорости до отражения. Верхний ряд: В (“лист”), С (“эхо”), D (“маяк”). Нижний ряд: А (“слои”), Е (“фронт”), F (“плоский неупругий рикошет”)

        Анализ прироста мер областей достижимости на рикошетах.

        Рассмотрим на плоскости рикошета область достижимости при движении, состоящем из цепочки изотропных неупругих рикошетов, то есть при наличии диссипации при отражении, не зависящей от ориентации вектора отскока (отсутствии дополнительного затухания скорости при развороте).

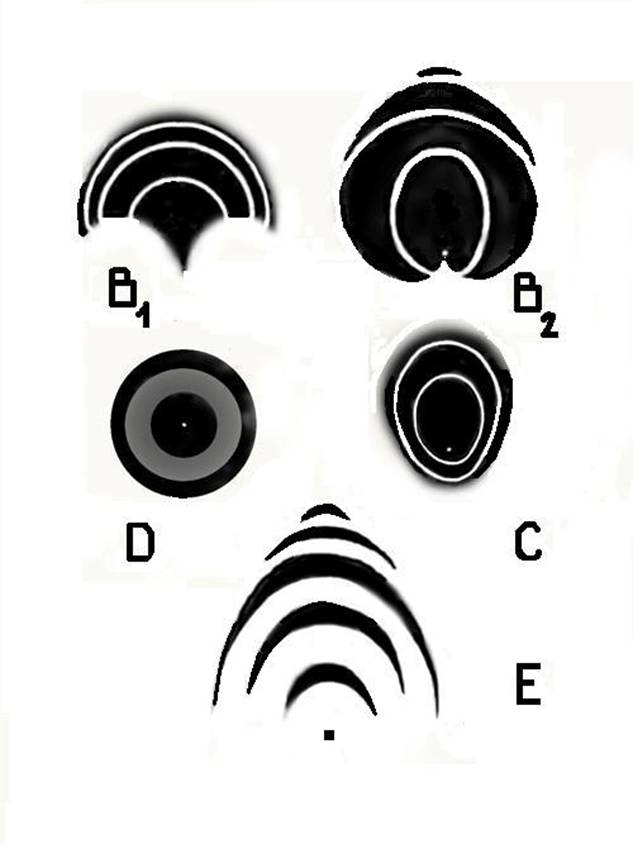
Рисунок 2. Модельные области достижимости для наиболее характерных классов индикатрис

Для гиперповерхности всевозможных скоростей после отражения можно записать:

             V((Vº,qº ,q¹,y¹) = V(Vº,qº ,q¹,0) = l Vº

   В поле сил тяжести для одного рикошета  индикатриса будет порождать, очевидно,  круговую  область достижимости одинаково скачущего во все стороны на поверхности воды камешка - сечение пространственного параболоида безопасности  поверхностью отражения.

  Площадь круга, заметаемого одним рикошетом на отражающей плоскости, очевидно, запишется как 

        S1 = p (l²Vº²sin½p/g)² = gl⁴ ,

          g = p V₀⁴  /g²

Внутренность круга заметается неоптимальными по углу отражения отскоками (a ¹ p¤4).

Зададимся целью изучить динамику прироста области достижимости на последующих рикошетах.

        Динамика роста дальности.

    Выпишем в ряд величины дальности после i-го рикошета:

        l₁ = pl²,  l₂ = pl² (1+l²),  ....,

         l_i+1 = pl² (1+l²+...+ l ²ⁱ ) = p l² (1-l²ⁱ ) / (1-l²),  

        p = Vº²  /g

Итоговая дальность:

         l¥ = pl²/(1-l²)

          Нетрудно видеть, что приращения дальности на каждом новом рикошете всегда меньше предыдущих приращений:

                           dl_i+1 > dl_i

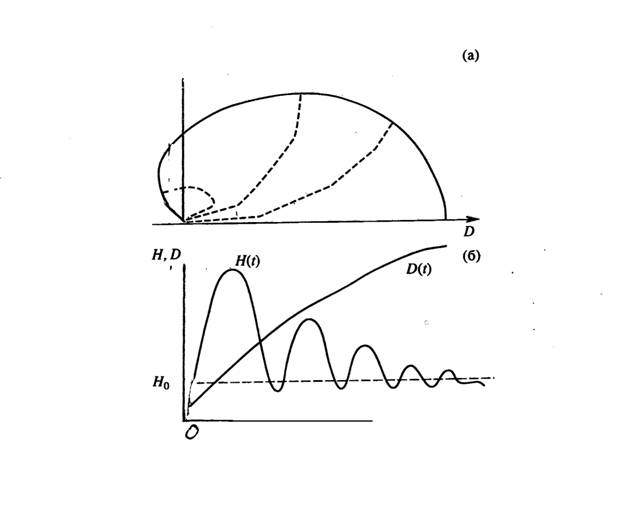
Рисунок 3. Квазисингулярное представление формирования области достижимости при спуске КА в атмосфере: а – следы траекторий на одном из симметричных сегментов поверхности роста; б – структура траекторий, приходящих на границу зоны роста.

         Динамика прироста площадей.

Выпишем в ряд величины соответствующих площадей достижимости после i-го рикошета:

                 s₁= gl⁴ ,  s₂ = gl⁴ (1+l²)²,  ....,

          s_i+1 = gl⁴ (1+l²+...+ l ²ⁱ )² = gl⁴ (1-l²ⁱ )²/(1-l²)²

          Выпишем в ряд по номерам рикошета соответствующие приращения областей достижимости.

        Приращение площади после первого рикошета - площадь круга:

                    ds₂ = gl⁴

          Приращение площади области достижимости после 2-го рикошета будет определяться как площадь кольца:

                 ds₃ = g l⁴ ((1+ l )² -  1 ) =  g l⁶  (2+ l²  ) 

Приращение площади области достижимости после 3-го и 4-го рикошетов будут так же определяться как площади кольца:

           ds₄ = g l⁴ ((1+ l⁴ +l⁶)² - (1+l⁴ )²) =

                          = g l⁸  (2+ 2l² + l⁴ )

           ds₅ = g l¹⁰  (2+ 2l² + 2l⁴+ l⁶ )

Аналогично вычисляется разность площадей i+1-й и i-й  зон отражения, причем с учетом формулы суммы геометрической прогрессии можно показать, что:

        ds_i+1 = g l²ⁱ⁺⁴   (l²ⁱ⁺²  - l²ⁱ - 2l²+ 2 )/(1-l²)²

или, произведя деление полиномов, получим:

        ds_i+1 = g l²ⁱ⁺⁴ (l²ⁱ⁺²  + l²ⁱ - 2)/(1-l²)

        Соотнесем приращения площадей на соседних зонах отражения:

        ds_i+1  - ds_i = g (l²ⁱ⁺² (2+ 2l² + ...+2l^2i-4+ l^2i-2)  -

         - l²ⁱ (2+ 2l² +...+ 2l^2i-6+ l^2i-4 )) =

               = g l²ⁱ  (l²ⁱ + 2l^2i-2  + l^2i-4   - 2 )

        Для разности 2-го и 1-го прироста площади имеем:

                 ds₂ - ds₁  = g l² (l⁴ + 2l² -1)

          Уравнение ds₂ - ds₁ = 0 помимо кратных корней l=0, отвечающих вырожденному случаю абсолютной неупругости, приводит к поиску корней биквадратного уравнения , относительно l:

                  l ⁴+ 2l²  -1 = 0

Это уравнение имеет один корень в области определения lÎ[0,1]:

           l² = -1+Ö2 » 0.41,  l= (-1+Ö2)½ » 0.64

Для разности 3-го и 2-го прироста площади имеем:

          ds₃ - ds₂  = g l²  (l⁶  + 2l⁴    + l²   - 2  )

Анализ полученных многочленов показывает, что при идеальном отражении l=1 приращение рикошетных площадей все время возрастает:

        dS₀<dS₁<dS₂<...<dS_n

         Наоборот, при ничтожно малых l выражение в скобках

         (l²ⁱ + 2l^2i-2   +  l^2i-4   - 2 )

много меньше 1 и приращения площадей уменьшаются с каждым новым рикошетом:

          dS₀>dS₁>dS₂>...>dS_n

При l³0.64 площадь второй области больше площади первого рикошета.

Площадь финальной области достижимости, вычисленная с использованием полученных выше  оценок максимальной конечной дальности неупругого рикошета, запишется как

       S =   g  l ⁴ /(1- l²)²,          g = p V₀⁴  /g²

       Динамика развития областей роста.

          Учитывая описанные выше эффекты, в рамках используемой модельной задачи получаем следующую общую картину динамики роста области достижимости в процессе рикошетирования .

  1. Приращения площади увеличиваются с каждым новым рикошетом. Области расширяются и фронтально, и вбок.

2. Приращения площади на соседних рикошетах сопоставимы по величине и максимальны. Области разворачиваются. Боковые и тыльные участки застывают.

  3. Приращения площади постепенно затухают и становятся ничтожно малыми заканчивается,

  4. после момента времени t* рост области достижимости прекращается. Область достижимости застывает.

                       t* = g l²/(1- l²)

Величину указанного времени естественно назвать временем роста системы (но - не временем жизни, поскольку область достижимости “застывает” в фазовом пространстве, но никуда не исчезает).

          Нетрудно вычислить, проводя аналогичные выкладки, оценки для нерикошетных перманентных областей достижимости катящихся по поверхности тел с сингулярно меняющимся  сухим трением.

Следующим пунктом представим основные фазы роста областей достижимости для другого типа “слабонеупругих” рикошетов, отвечающих классу индикатрис скорости А,  не содержащих в себе саму точку отражения. Область достижимости для таких систем будет многосвязной, не содержащей, очевидно, точку первого рикошета. Она будет состоять из системы постепенно расширяющихся вбок и утолщающихся слоев.

1. Зоны покрытия расширяются и утолщаются. Приращения площади увеличиваются с каждым новым рикошетом. Слои расширяются и фронтально, и вбок, но не слипаются.

2. Приращения площади на соседних рикошетах сопоставимы по величине и максимальны. Слои развертываются и загибаются.

3. Начинается слипание соседних слоев (то есть появляются точки на отражающей поверхности, куда можно попасть за разное количество рикошетов). Возможно образование полостей. Боковые и тыльные участки застывают.

4. Слои постепенно утончаются. Приращения площади постепенно затухают

5. Слои разлепляются  и вырождаются

6. После момента времени t* рост “слоистой” области достижимости заканчивается

Рисунок 4. Формирование полостей в области достижимости для случая слабонеупругих индикатрис. На поздних стадиях развития зоны соседних рикошетов могут слипаться.

          Оценки прироста областей достижимости для классической æ-c модели отражения вычисляются аналогичным образом и приводят к  идентичным результатам.

          Полученные оценки прироста размеров, площадей и объемов области достижимости могут иметь в терминах  оптико-механической аналогии смысл  области “видимости” точечного источника света  в оптической неоднородной (поглощающей) среде.

Для различных значений механической энергии Еi системы на на наборе этих непересекающихся пучков строятся фронты волны как проекции фазовой лагранжевой поверхности, соответствующей Еi на x-пространство [6]. При наличии мгновенной диссипации на рикошете система переходит на лагранжеву поверхность с более низким уровнем Еi и соответствующий волновой фронт Фi на участке свободного полета до следующего отражения (склейка непересекающихся фазовых пучков). Исходя из скрытого, но фундаментального принципа выпуклости в задачах вариационного исчисления и оптимального управления рассматриваемого типа, связанного с выпуклостью образа множества с непрерывной мерой при интегральных отображениях, можно утверждать, что совокупность всех промежуточных режимов на достаточно малом промежутке времени можно оценивать указанной дискретной выборкой. При этом экстремальная точка регулярным образом эволюционирует, образуя “поле экстремалей” при изменении параметров возмущения. 

Таким образом, финальную область достижимости системы можно рассматривать как сглаженную границу дискретного  набора волновых фронтов, построенных на рикошетах с постепенно понижающимся уровнем энергии. В этом смысле такой подход близок к методам описания областей достижимости дискретных объектов фрактальной геометрии. В рамках квазисингулярного подхода считаем участок рикошета пренебрежимо малым по сравнению с участком свободного движения.

        Динамика прироста объемов.

          Проводя аналогичные выкладки, можно получить оценки для  объемных областей достижимости в отсутствии массовых сил при наличии сингулярных изотропных диссипативных воздйствий:

          Выпишем объемы областей роста на первоначальных этапах роста области достижимости.

                    V₁ = 4/3 p(Vº²/g)³ l⁶  = r l⁶ ,

                 V₂ = r l  (l²+l⁴ )³,

                  V₃ = r l  (l²+l⁴ +  l⁶ )³, ....

                  Vµ=  r (l²/ (1-l²))³

Соответствующие  приращения объемов роста запишутся как

                  dV₁ =  r l⁶  ,

                  dV₂ = V₂ - V₁ = r l⁸  (l⁴  +3l² +3 ),

                 dV₃ = V₃ – V₂ = r l¹⁰(l¹² + 3l¹⁰ +3l⁸ + 3l⁴  + 6l²+3  )

Рассмотрим  условие dV₂ -  dV₁ = 0. Оно приводит к уравнению

                 r l⁶  (l⁶  +3l⁴ +3l² -1 ) = 0,

из которого непосредственно вытекает кубическое уравнение относительно l²:

                 l⁶  +3l⁴ +3l² -1  = 0

          Из анализа этого уравнения видно, что в случае малых l выражение слева отрицательно, а в случае l=1 -  положительно. Соответственно на интервале lÎ[0,1] находится корень этого уравнения и, кроме того, немедленно следует вывод, что при малой диссипации (l»1-e) приращения объемов роста нарастают, а при значительной потере энергии (l»e) приращение объемов роста резко затухает.

        Заключение.

          Изучены модельные задачи о камешке, рикошетирующе скользящем по поверхности воды и о неупругом мячике, скачущем либо катящимся по неидеальной поверхности. Получены оценки их предельной дальности. Получены оценки прироста мер областей рикошетирования.

          Прирост дальности неупругих рикошетов все время убывает, тогда как с приростом площадей (и - объемов) эта закономерность может не выполняться и зависит от величины диссипации. Полученные оценки прироста размеров, площадей и объемов области достижимости могут иметь в терминах оптико-механической аналогии смысл области “видимости” точечного источника света в оптической неоднородной (поглощающей) среде.

          Приведены основные фазы роста областей достижимости в процессе неупругих рикошетирований: мажорирование прироста площади области достижимости, оптимум, затухание прироста, застывание. Для “слабонеупругих” рикошетов выявлен эффект расширения и слипания первоначально фрагментированных фазовых слоев областей рикошетирования с возможным образованием внутренних полостей недостижимости.

         ПРИЛОЖЕНИЕ I.

          Опишем вкратце возможные пути использования полученной структуры динамики роста областей достижимости рикошетных систем.

1. Согласно описанным фазам роста более продолговатые формы объектов характерны начальным фазам, более широкие, с закрученной задней частью - конечным стадиям роста. По общей форме объекта можно, следовательно, пытаться делать оценки текущей стадии его эволюции и - возможности роста. В этом смысле эволюционно огурец был раньше арбуза, а яйцо - курицы.

2. Обратная “закрученная” часть формируется на начальных рикошетах и застывает на начальной стадии эволюции. Передняя же фронтальная часть продолжает формироваться даже после этого и застывает в последнюю очередь. Таким образом, “околоствольные” обратные участки являются реликтовыми в областях роста, а передние фронтальные – самыми последними. Можно говорить о том, что дыня наиболее сочна не у черенка, а - против него. Кора березы тверже и старше на дне глубоких борозд, а не на тонкой бересте между ними.

3. Реликтовые объекты областей роста (например - россыпи золота в интрузиях, локализацию старых звездных скоплений в галактиках) следует искать сбоку-сзади начальной точки роста.

4. Если необходимо перекрыть рост некоторого бокового сегмента растущего листа, то внутри необходимо блокировать не направление от него к центру (точке роста), а сопряженное по индикатрисе роста к этому направлению (то есть несколько ближе к основной “оси дальности” системы).

То же самое можно сказать при поиске внутренних зон, отвечающих за нарушения роста определенного граничного сегмента листа.

         Литература

1.       Голубев  Ю.Ф.,  Хайруллин   Р.З.   Метод   последовательной             линеаризации в задачах оптимального управления при входе  в                        атмосферу.-      Препринт ИПМ им.М.В.Келдыша АН СССР, 1985,                   N157.

2.       Ю.Ф.Голубев,    А.В.Грушевский,    Р.З.Хайруллин.    Законы             управления,     обеспечивающие  максимальную   дальность   при             спуске космического аппарата  в  атмосфере.-  Препринт  ИПМ               им.М.В.Келдыша АН СССР, 1988, N3.

3.   Голубев Ю.Ф., Грушевский А.В., Хайруллин Р.З.  О  структуре            области  достижимости  при   спуске   КА.-   Препринт   ИПМ         им.М.В.Келдыша РАН, 1993,N 78.

4.       Голубев Ю.Ф., Грушевский А.В., Хайруллин Р.З.  О  структуре                   области  достижимости  при   спуске   КА. - Космические исследования, 1996, т.34, N2, с. 180-189.

5.       Л.М.Шкадов,   Р.С.Буханова,   А.Ф.Илларионов,   В.П.Плохих.          Механика    оптимального     пространственного     движения               летательных аппаратов.- М.: Машиностр., 1972.

6.       Арнольд В.И. Математические методы классической  механики.-      М.:       Наука, 1974.

7.       Г.С.Ландсберг. Оптика. М.: Наука, 1976.

8.       Белецкий В.В. Регулярные и хаотические движения      твердых тел. –          М.: РХД, 2007.