Оценки потери дальности механических систем на неупругих рикошетах

Аннотация

Поставлены и изучены модельные задачи о камешке, рикошетирующе скользящем по поверхности воды и о неупругом мячике, скачущем либо катящимся по неидеальной поверхности. Получены оценки их предельной дальности. В зависимости от отношения коэффициентов трения качения и мгновенного трения рикошеты приводят дальше перманентного движения.

Abstract

Two model problems of the non-elastic rebounding mechanical systems are investigated: the problem of the stone rebounding on the water surface, and the problem of the non-elastic ball rebounding, The evaluations of their range are investigate.

Введение ........................................................................................ 3

достижимости.......................................................................... 4

2. Изотропная модель удара....................................................... 5

3. Сингулярность и перманентность ……................................ 12

4. Мультипараболоид безопасности......................................... 14

Заключение .................................................................................. 15

Литература ................................................................................... 16

Оптимальное управление находится гораздо ближе к широкому классу неуправляемых механических систем, чем это может показаться на первый взгляд. В частности, классическое вариационное исчисление можно рассматривать как подраздел теории оптимального управления [1], и значительный ряд соответствующих теорем (например- уравнение Эйлера) может быть выведен из принципа максимума Л.С.Понтрягина.

Движение рикошетирующих механических систем проходит в двух (или - нескольких ) зонах, различных по масштабу внешних воздействий. На участках между отражениями движение близко к свободному, то есть невозмущенному движению в поле консервативных сил (например - гравитационных, электростатических). На участках рикошетирования возмущающие воздействия максимальны.

Для достаточно протяженных в фазовом пространстве траекторий можно считать перемещения системы собственнно на рикошетах пренебрежимо малыми по-сравнению с перемещениями на участках свободного движения. Такой подход, как редукция сингулярности абсолютно упругого удара (или - с точки зрения изучения траекторных параметров - динамического биллиарда) на случай “мягкого удара” был использован Ю.Ф.Голубевым, А.В.Грушевским, Р.З.Хайруллиным как основа синтеза полуаналитического описания структуры области достижимости спускаемого космического аппарата, где оптимальными оказались траектории квазисингулярные, затухающие по-времени [2-6].

В качестве еще одной базовой задачи определения фазовых параметров системы с мягким ударом представим задачу о неупругом мячике, скачущем по неидеальной поверхности, для которого ставится задача оценки его текущего и- предельного фазового состояния. Указанная задача поставлена и решена в настоящей работе, наряду с другими модельными задачами.

Классический удар и плоская область достижимости.

В качестве модельной квазисингулярной механической системы рассмотрим рикошетирующее движение неупругого мячика в пространстве Â³ при наличии отражающей плоскости, в поле сил тяжести . При отсутствии боковых сил трения и аэродинамического сопротивления движение, очевидно, будет происходить в неизменяемой плоскости, содержащей вектор начальной скорости.

Из классической теории удара [7] следует, что нормальная и касательная составляющие скорости падения и отражения связаны через коэффициент восстановления Ньютона æ и коэффициент мгновенного трения c соответственно:

Введем в полетной плоскости декартовы координаты XOY с началом координат в точке первого рикошета. Тогда движение между рикошетами будет описываться уравнениями парабол

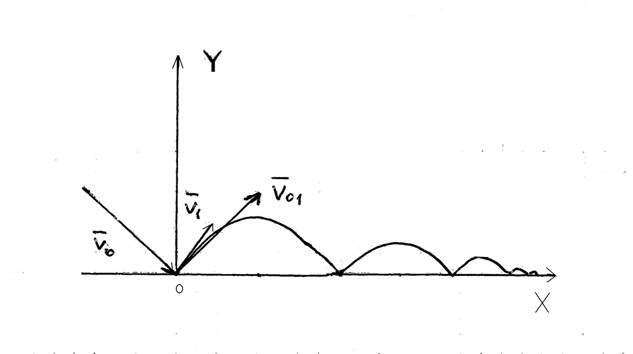
Рисунок 1. Построение рикошетирующих движений в полетной плоскости.

Оказывается возможным в рамках классической теории удара вычислить итоговую рикошетную область достижимости (в случае æ<1 рикошетное движение становится финитным по времени).

Итак, время жизни рикошета ограничено, зависит только от коэффициента восстановления æ и не превосходит величины

Классическая модель удара с использованием коэффициента восстановления Ньютона является первым, иногда очень грубым приближением к действительным закономерностям, описывающим соударение реальных тел [8]. Очевиден тот факт, что рикошеты в ряде задач могут описываться достаточно сложным образом (например- поверхность рикошета неидеальна, поверхность шарика квазисферична и имеет сложную форму, площадка соприкосновения тела с отражающей поверхностью на рикошете отлична от точки). Но многие закономерности динамики рикошетов сложных механических систем выявляются уже при использовании достаточно простых, но- “структурно адекватных” моделей отражения.

Рассмотрим “изотропную” модель рикошета, которая описывает потери энергии при ударе с помощью коэффициента затухания 0£l£1:

Нетрудно видеть, что в терминах классической теории удара [7] , введенный коэффициент связан с коэффициентом восстановления Ньютона æ и коэффициентом мгновенного трения c:

В случае l<1 рикошетное движение становится финитным по времени. Действительно, можно показать, что

Отсюда можно получить выражение для важного модельного параметра - коэффициента потери дальности, введенного как отношение максимально возможного пути системы с учетом диссипации к пути "невозмущенной эталонной" системы за это же время. Получим

Для характерного коэффициента затухания l=0.8 получим

то есть дальность при остановке гасится почти вдвое по отношению к пути невозмущенной системы за это же время.

Кроме того, видим, что с точностью до коэффициентов результирующие оценки области достижимости и времени окончания движения для двух моделей отражения совпадают.

Рассмотрим камень, рикошетирующий с затуханием по поверхности воды, и поставим модельную задачу определения всех точек на этой поверхности, в которые он может попасть при фиксированном векторе начальной скорости Vº . Поверхность будем для простоты считать горизонтальной плоскостью. Очевидно, вид искомой области будет определяться характером отражения камешка при каждом его соприкосновении с водой, которое, в свою очередь, зависит от текущих скорости камешка, его вращения и ориентации в пространстве. Громоздкая задача оптимизации в сложной среде - построение области достижимости указанного движения, становится разрешимой, если использовать следующие модельные допущения.

1. Приращения функционалов продольной дальности D и бокового отклонения B на участках непосредственного отражения от воды малы по сравнению с участками свободного полета.

2. Сопротивлением воздуха на участках свободного полета можно пренебречь.

Фазовое управление вектором скорости после рикошета вводится как способ описать всевозможные "маневры" камешка произвольной формы при взаимодействии с водой на участке отражения. Отличие от описанных выше модельных задач состоит в том, что рикошет описывается более громоздким, но - и более полным образом и, кроме того, возможно не отражение камешка от воды, а погружение на любом "неудачном" рикошете.

В этом случае форма ОД параметрически определится как

где n - число отражений, Vi(V,qº,q¹,y¹) - скорость камня после i-го отражения, зависящая как от траекторного угла на выходе q¹ и курсового угла y¹ , так и от значения qº до отражения, g- ускорение свободного падения. Динамические свойства затухания скорости при неупругом отражении и дополнительные потери скорости при развороте от текущей траекторной плоскости формально запишутся как

Таким образом, указанная задача сводится к определению зависимости

которая может находиться несколькими способами: из расчетов по модели взаимодействия тела со средой; в виде эмпирической таблицы; по оптимальности выбора пар (qi ,yi), рассматриваемых как дискретные управления на участках отражения.

Точную верхнюю грань множества всех динамически допустимых V(Vº,qº,q¹,y¹) (“индикатрису одного погружения”) будем называть в дальнейшем оптимальным маневром (ОМ). Таким образом, обозначив ее как I(Vº,qº ,q¹,y¹), можно записать:

Очевидно, что динамические возможности ОМ покрывают возможности внутренних точек индикатрисы.

Для предельного случая изотропности ОМ- отсутствии затухания скорости при развороте, можно записать:

и формулы (1.1) будут описывать, очевидно, круговую область достижимости одинаково скачущего во все стороны на поверхности воды камешка - сечение пространственного мультипараболоида безопасности поверхностью отражения (этот случай разобран выше).

где l, введенный выше коэффициент затухания 0£l<1 .

Можно показать, что максимальное число отражений (которое имеет место для продольной траектории) не превосходит числа

где квадратные скобки означают операцию взятия целого числа, V°- начальное, а Vc- "критическое" (минимальное) значение скорости, при которой еще происходит отражение камешка от поверхности и он не тонет.

Редукция вышерассмотренной модельной задачи о неупругом мячике на случай неупругого удара при наличии бокового рассеяния проводится аналогично и приводит к аналогичным результатам.

Задача о камешке может служить достаточно хорошим приближением задачи об оптимизации области достижимости при спуске космического аппарата в атмосфере [2-6], где оптимальные траектории также оказываются рикошетирующими на коротких погружениях в плотные слои атмосферы.

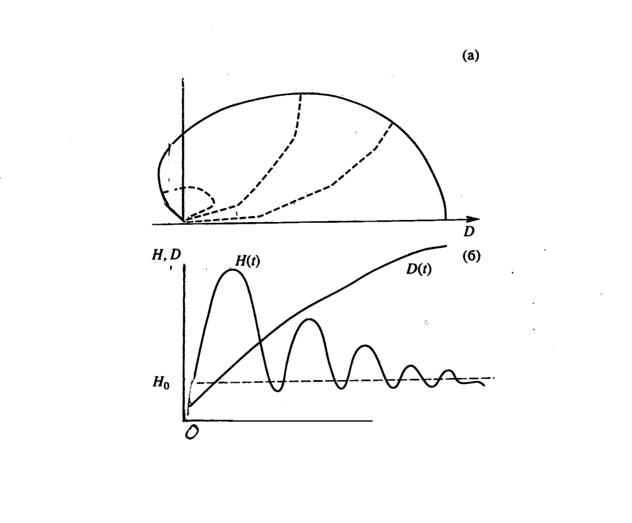
Рисунок 2. Задача определения области достижимости при входе КА в атмосферу, как задача построения области лостижимости неупругого биллиарда.

Полученные в [2,6] при построении ОД численными методами оптимальные законы движения КА можно представить как структурно отличающиеся от законов, найденных в предположении гипотезы квазистационарного планирования (либо малого отклонения от такого движения) и малости гравитационных воздействий по сравнению с аэродинамическими. Опорные траектории [2] оказываются состоящими из участков "изломов" трасс в плотных слоях атмосферы, где происходит основное торможение КА и аэродинамические воздействия доминируют, и чередующихся с ними, существенно более протяженных участков полета в разреженных слоях атмосферы, где главными являются гравитационные силы.

Отражение на участках погружения происходит за счет резкого роста подъемной силы в Зонах Маневра (ЗОМ)- плотных слоях атмосферы, которая "выкидывает" КА на последующие балллистические участки.

Вышеуказанное представление класса опорных оптимальных траекторий, названное квазисингулярным представлением [3-5], спользуется для полуаналитического конструирования ОД с помощью Метода Виртуального Управления (МВУ). Основа метода - сведение задачи поиска оптимума на всем интервале движения КА к выбору управления только на участках погружения в плотные слои атмосферы - с использованием заранее известного на этих участках функционального множества оптимальных маневров, с аналитическим восполнением оптимальных траекторий на баллистических участках

Таким образом параметры области достижимости представимы в виде суммы аналитических членов и малых табличных добавок при любой сконструированной последовательности ориентаций скоростей выхода КА из зон оптимального маневра на баллистические участки. При этом исчезает необходимость использования для процесса оптимизации протяженных траекторий большого числа узловых точек [2], а также проводить идентичные и трудоемкие расчеты оптимизации на участках погружения для получения новой точки ОД.

Основой Метода Виртуальных Управлений (МВУ) является решение серии оптимальных задач для КА с конкретными аэродинамическими характеристиками строится банк его оптимальных маневров . Для этого для табличных значений параметров скорости входа в рикошет Vºk и входного траекторного угла - qº и значений на вылете из рикошета траекторного и курсового углов q¹i , y¹j необходимо решить серию оптимальных задач на конечном отрезке времени 0<t<T.

Банк множества оптимальных маневров, найденный в процессе выполнения процедуры МВУ можно представить как сечения гиперповерхности в Â5 V(Vº ,qº ,q¹,y¹) "табличными" поверхностями уровня {Vº=Vºi ; qº=qºj }. Тогда каждое сечение будет представлять собой некоторую поверхность в Â³ локальной выходной скорости КА I =V (q¹,y¹), зависящую только от направления вылета и определяемую сферическими координатами q и y. Такую поверхность, по аналогии с введенным в геометрической оптике обозначением множества локальных скоростей света в неизотропной среде [9], было бы естественно назвать ндикатрисой. Вид такой индикатрисы, однако, как уже указывалось выше, может меняться в зависимости от входных параметров V и q.

Рассмотрим индикатрису рикошета, полученную эмпирическими, аналитическими, полуаналитическими, либо численными методами оптимизации (например - [3-5] ):

Без ограничения общности положим, что для вектора скорости падения курсовой угол будет нулевым:

Рассмотрим сечение индикатрисы I соответствующей гиперповерхностью (1.5.1). Оно будет являться некоторым множеством в Â³ V(q , y ). Из соображений гладкости и выпуклости [1] будем считать это множество компактным. Тогда по любому из заданных в Â³ направлений это множество будет достигать максимума расстояния от точки (0,0,0) (то есть максимума величины вектора выходной скорости V¹ ). (по некотрым “вырожденнным” направлениям может быть V¹ = 0). Выберем соответствующие максимальные значения по продольному и боковым направлениям рикошета Vd и Vb. Тогда всевозможные движения системы после рикошета будут, очевидным образом, заключены между двумя сферическими фронтами Фd и Фb изотропных движений с Vd и Vb. Причем действительное движение системы после рикошета будет ограничено поверхностью, касающейся каждого из этих фронтов и непрерывно расширяющейся от внутреннего к внешнему. С помощью указанного построения можно получать оценки движения в анизотропной среде через более простые изотропные.

Сравним экстремальные свойства перманентно движущихся по поверхности систем и аналогичных им систем с рикошетами об эту поверхность.

Коэффициент потери дальности для перманентного случая gp найдем из решения уравнения динамики катящегося шарика при наличии силы трения:

Видим, что дальность пробега xk и дальность рикошета Dmax соотносятся как

Аналогично при сравнении моделей перманентного движения и движения по классической модели удара можно получить

Множество b£1 на плоскости параметров l, m имеет вид

При характерных значениях коэффициента трения качения m=0.25 и l=0.8 значение b = 0.94<1 .

Итак, результаты анализа модельной задачи показывают, что для достаточно шероховатых поверхностей рикошеты уходят дальше, чем качение по плоскости.

Сведем полученные результаты в одну таблицу.

Областью достижимости в координатном пространстве движения в поле параллельных сил при фиксированном значении начальной скорости будет параболоид безопасности [7, с.174] . В нашем случае цепочки отражений результирующей областью будет, очевидно, суперпозиция усеченных поверхностью отражения начального параболоида вращения и последующих квазипараболических торов , соответственно, с финальным радиусом основания

Следует, однако, отметить отличие получающейся гиперповерхности от простой суперпозиции параболических торов с вершинами в точках рикошетов, порождаемыми концентрическими окружностями, содержащими соответствующие точки отражений для полета на максимальную дальность. Указанное отличие порождается тем, что динамически возможны перекрывания текущего параболоида безопасности отраженными после рикошета обратными траекториями при не очень сильном коэффициенте затухания скорости.

Данные свойства итоговой пространственной области достижимости подтверждаются соответствующими результатами численной оптимизации рикошетирующих движений [2,3]. При этом уточненный «пространственный мультипараболоид» получается вращением вокруг вертикальной оси графика численно найденной плоской задачи определения области динамически возможных движений соответствующего баллистического процесса [2,3,6].

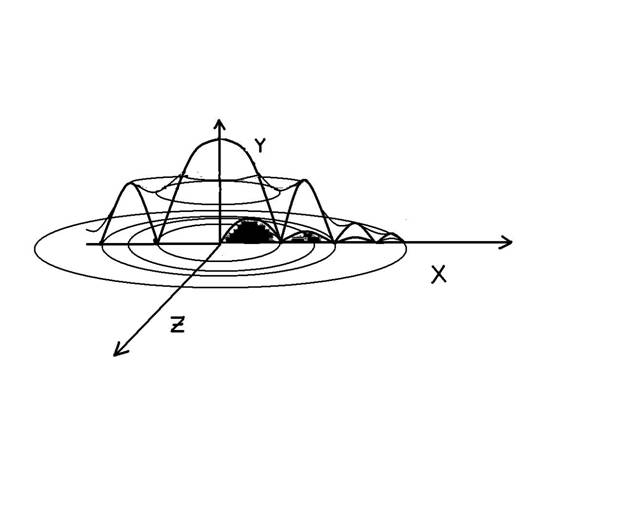
Рисунок 3. «Мультипараболоид безопасности» для объемной задачи баллистики при наличии отскока.

Поставлены и изучены модельные задачи о камешке рикошетирующе скользящем по поверхности воды и о неупругом мячике, скачущем либо катящимся по неидеальной поверхности. Получены оценки их предельной дальности. В зависимости от отношения коэффициентов трения качения и мгновенного трения c рикошеты приводят дальше перманентного движения. Время существования рикошета зависит от коэффициента восстановления Ньютона æ (и не зависит от коэффициента мгновенного трения). Представлен вид объемного «мультипараболоида безопасности» при наличии изотропной диссипации при отскоке.

1. В.В.Александров, В.Г.Болтянский, С.С.Лемак, Н.А.Парусников, В.М.Тихомиров. Оптимизация динамики управляемых систем. - М.: МГУ, 2000.

2. Голубев Ю.Ф., Хайруллин Р.З. Метод последовательной линеаризации в задачах оптимального управления при входе в атмосферу. - Препринт ИПМ им.М.В.Келдыша АН СССР, 1985, N 157.

3. Ю.Ф.Голубев, А.В.Грушевский, Р.З.Хайруллин. Законы управления, обеспечивающие максимальную дальность при спуске космического аппарата в атмосфере. - Препринт ИПМ им.М.В.Келдыша АН СССР, 1988, N 3.

4. Голубев Ю.Ф., Грушевский А.В., Хайруллин Р.З. О структуре области достижимости при спуске КА. - Препринт ИПМ им.М.В.Келдыша РАН, 993, N 78.

5. Голубев Ю.Ф., Грушевский А.В., Хайруллин Р.З. О структуре области достижимости при спуске КА. - Космические исследования, 1996, N 2, с.180-189.

6. Л.М.Шкадов, Р.С.Буханова, А.Ф.Илларионов, В.П.Плохих. Механика оптимального пространственного движения летательных аппаратов. - : Машиностр., 1972.

7. Ю.Ф.Голубев. Основы теоретической механики. - М.: МГУ,2000.

8. А.П.Маркеев. Теоретическая механика. - Москва-Ижевск: Регулярная и хаотическая динамика, 2001.

9. Арнольд В.И. Математические методы классической механики. - М.: Наука, 1974.

10. Белецкий В.В. Регулярные и хаотические движения твердых тел. М.:РХД, 2007.

Оценки потери дальности механических систем на неупругих рикошетах

( To the evaluations of the range loss for the non-elastic rebounding mechanical systems
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Грушевский А.В.
(A.V.Groushevski)

ИПМ им. М.В.Келдыша РАН

Москва, 2007

Аннотация

Abstract

Оценки потери дальности механических систем на неупругих рикошетах ( To the evaluations of the range loss for the non-elastic rebounding mechanical systems Preprint, Inst. Appl. Math., the Russian Academy of Science)

Грушевский А.В. (A.V.Groushevski) ИПМ им. М.В.Келдыша РАН

Москва, 2007

Аннотация

Abstract

Оценки потери дальности механических систем на неупругих рикошетах

( To the evaluations of the range loss for the non-elastic rebounding mechanical systems
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Грушевский А.В.
(A.V.Groushevski)

ИПМ им. М.В.Келдыша РАН