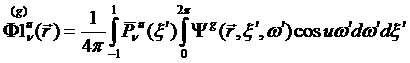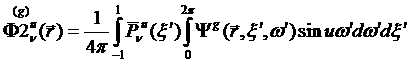Численные методы решения уравнения переноса в многогрупповом приближении в трехмерной геометрии
в пакете «РЕАКТОР»
|
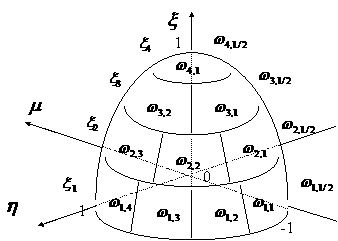 |
Рис. 1. Диаграмма расположения точек угловой
квадратуры ![]() на октанте.
на октанте.
4. Конечно-разностные методы решения.
Система многогрупповых уравнений переноса решается
итерационным способом. При решении задач на ![]() используются как
внешние итерации по источнику деления, так и внутренние итерации по источнику
рассеяния в каждой группе. В качестве начального приближения для потоков
используется численное решение, полученное в диффузионном приближении методом
верхней релаксации. При решении задач защиты задается распределенный источник
делений, сосчитанный ранее либо заданный извне.
используются как
внешние итерации по источнику деления, так и внутренние итерации по источнику
рассеяния в каждой группе. В качестве начального приближения для потоков
используется численное решение, полученное в диффузионном приближении методом
верхней релаксации. При решении задач защиты задается распределенный источник
делений, сосчитанный ранее либо заданный извне.
В пакете «РЕАКТОР» используются эффективные конечно-разностные схемы.
Численные методы различаются набором дополнительных соотношений, замыкающих
систему уравнений. Для решения задач на ![]() используется известная схема fix-up с обнулением отрицательных
потоков на выходе и последующим учетом баланса в ячейке. Для решения задач
защиты используется схема WDIF, которая хорошо зарекомендовала
себя при расчетах по американской программе TORT [11]. Практические расчеты
показали, что схема WDIF наиболее приспособлена для
расчета этих задач, особенно в криволинейной геометрии. Хотя эта схема не
является положительной для отдельно взятого направления, но в скалярных потоках
дает практически всюду положительное решение при оптимальном выборе параметра
используется известная схема fix-up с обнулением отрицательных
потоков на выходе и последующим учетом баланса в ячейке. Для решения задач
защиты используется схема WDIF, которая хорошо зарекомендовала
себя при расчетах по американской программе TORT [11]. Практические расчеты
показали, что схема WDIF наиболее приспособлена для
расчета этих задач, особенно в криволинейной геометрии. Хотя эта схема не
является положительной для отдельно взятого направления, но в скалярных потоках
дает практически всюду положительное решение при оптимальном выборе параметра ![]() .
Рассмотрим эту схему более подробно.
.
Рассмотрим эту схему более подробно.
Балансное уравнение метода дискретных ординат в X-Y-Z геометрии имеет вид:
![]() (1)
(1)
где
коэффициенты ![]() - площади боковых
поверхностей ячейки. Соответствующие дополнительные соотношения имеют вид:
- площади боковых
поверхностей ячейки. Соответствующие дополнительные соотношения имеют вид:
![]() (2)
(2)
Подставляя
соотношения (2) в (1), получим формулу для расчета плотности потока в ячейке.
Существует проблема выбора параметров ![]() (
(![]() ), которые принадлежат
интервалу
), которые принадлежат
интервалу ![]() . В схеме WDIF выбор весовых параметров осуществляется на основе
решения вспомогательных задач. Например, для направления по оси X значение
. В схеме WDIF выбор весовых параметров осуществляется на основе
решения вспомогательных задач. Например, для направления по оси X значение ![]() берется из решения
берется из решения ![]() следующей системы
уравнений:
следующей системы
уравнений:
![]()
![]()
![]()
![]()
Из
системы видно, что выходящий поток в направлении X полагается равным нулю. В двух других направлениях
выходящий поток определяется в зависимости от величины параметра ![]() . Полученное решение
. Полученное решение ![]() определяет выбор
весового параметра:
определяет выбор
весового параметра:
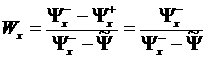
Окончательно
берется следующее значение ![]() .
.
Выбор параметра ![]() существенно влияет на
результаты расчета. Параметр
существенно влияет на
результаты расчета. Параметр ![]() эмпирически
подбирается так, чтобы получить более точное решение. В пакете «РЕАКТОР» по
умолчанию полагается
эмпирически
подбирается так, чтобы получить более точное решение. В пакете «РЕАКТОР» по
умолчанию полагается ![]() .
.
5. Ускорение внутренних
итераций.
Для ускорения внутренних итераций в пакете «РЕАКТОР»
первоначально [2] использовался диффузионный синтетический метод (DSA) [12]. В некоторых задачах использование этого
линейного метода приводило к сокращению времени счета. К сожалению, существуют
задачи, для решения которых использование этого метода может привести к
неустойчивому алгоритму. К таким задачам относятся задачи с оптически толстыми
областями, а также с областями с высокой анизотропией рассеяния. Именно для
этих задач наиболее необходимо использовать ускорение.
В настоящее время в пакете «РЕАКТОР» реализован
нелинейный метод ребаланса [13]. Существенное различие между этими двумя
методами состоит в том, что в методе ребаланса используется поправка,
полученная из решения диффузионной системы уравнений, коэффициенты которой
находятся из угловых потоков, полученных на этой же внутренней итерации.
Усовершенствование метода ребаланса, предложенное в работе [13] в одномерной
плоской геометрии, позволило повысить его эффективность. Численные расчеты
показали, что метод ребаланса эффективнее DSA метода. Ниже приводится описание этого метода.
На первых итерациях эффективно работает Метод группового ребаланса. Разобьем
источник в правой части уравнения переноса на две части, отделяя
внутригрупповое рассеяние (![]() ) от остальной части источника (
) от остальной части источника (![]() ):
):
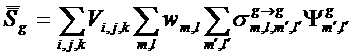 (1)
(1)
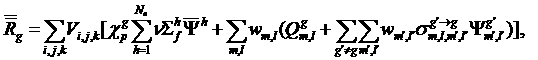 (2)
(2)
Просуммируем
уравнение переноса для группы ![]() по пространственной
области и по направлениям. Результат может быть записан в операторном виде:
по пространственной
области и по направлениям. Результат может быть записан в операторном виде:
![]() (3)
(3)
где
двойная черта означает двойное суммирование. Оператор ![]() представляет собой
утечку через границы,
представляет собой
утечку через границы, ![]() - утечка в результате
всех взаимодействий внутри ячейки.
- утечка в результате
всех взаимодействий внутри ячейки.
Рассмотрим итерационный цикл. Для итерации потока с
номером ![]() источник
внутригруппового рассеяния определяется с предыдущей итерации
источник
внутригруппового рассеяния определяется с предыдущей итерации ![]() . Если
. Если ![]() близок к
близок к ![]() , то итерации сходятся очень медленно. Реально получается
решение следующего уравнения:
, то итерации сходятся очень медленно. Реально получается
решение следующего уравнения:
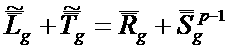 , (4)
, (4)
Для
того чтобы сбалансировать потоки и источники, вводится множитель ![]() , на который умножаются все потоки. Операторы
, на который умножаются все потоки. Операторы ![]() будут пропорциональны
будут пропорциональны ![]() , а
, а ![]() нет:
нет:
![]() . (5)
. (5)
Исключая
из (4) и (5) ![]() и
и ![]() , получим формулу для вычисления множителя
, получим формулу для вычисления множителя ![]() :
:
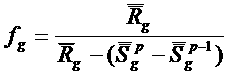 (6)
(6)
Итерация
![]() начинается с потоков:
начинается с потоков:
![]() (7)
(7)
Таким
образом, множитель ![]() служит показателем
общей сходимости.
служит показателем
общей сходимости.
На последующих итерациях ускорение сходимости
осуществляется с помощью метода Пространственного
ребаланса. Суммируя уравнение переноса только по направлениям, получим для
скалярных токов:
![]()
![]()
![]()
![]()
![]()
![]()
балансное
уравнение:
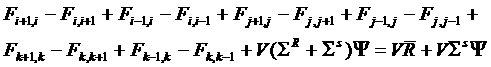 (8)
(8)
Результатом
итерации с номером ![]() является следующее
уравнение, где волной обозначен неребалансный результат, который не
удовлетворяет уравнению (8):
является следующее
уравнение, где волной обозначен неребалансный результат, который не
удовлетворяет уравнению (8):
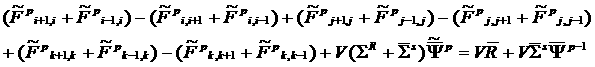 (9)
(9)
Если
предположить, что скалярный ток пропорционален потоку в ячейке:
![]() ,
, ![]() ,
, ![]()
и
подставить эти выражения в уравнение (8), а затем из двух уравнений (8) и (9)
исключить члены, содержащие ![]() , то, делая замену:
, то, делая замену:
![]() , (10)
, (10)
получим
линейную систему уравнений относительно ![]() для внутренних точек
пространственной области:
для внутренних точек
пространственной области:
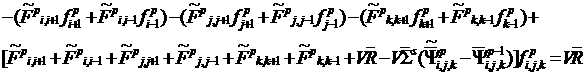 (11)
(11)
Разница в решении на двух ![]() и
и ![]() итерациях приводит к
ошибке в источнике рассеяния, которая перераспределяется с помощью уравнения
ребаланса (11) с коэффициентами в виде частичных токов. Если бы даже не было
этого перераспределения или оно было бы не существенным, решение уравнения (11)
итерациях приводит к
ошибке в источнике рассеяния, которая перераспределяется с помощью уравнения
ребаланса (11) с коэффициентами в виде частичных токов. Если бы даже не было
этого перераспределения или оно было бы не существенным, решение уравнения (11)
![]() все равно служило бы
для нового лучшего начального приближения на следующей итерации:
все равно служило бы
для нового лучшего начального приближения на следующей итерации:
![]()
Одновременно производится корректировка всех моментов
угловых потоков путем умножения на соответствующие поправки в каждой
пространственной точке, что позволяет сохранять первоначальное угловое
распределение.
Учет граничных условий необходимо осуществлять
согласованным способом. Если на внутренней границе заданы условия отражения, то
входящий поток равен выходящему. В уравнении (11), записанном для точки ![]() , полагаем
, полагаем ![]() .
.
Если на внешней границе заданы нулевые значения
входящего потока, то в уравнении (11) соответствующий ток равен нулю. Например,
для направления по оси X полагаем
входящий ток нулевым ![]() .
.
Если на внешней границе заданы условия отражения, то,
например, для направления по оси X в уравнении
(11) полагаем член с входящим током извне ![]() равным члену с выходящим током изнутри с предыдущей
итерации
равным члену с выходящим током изнутри с предыдущей
итерации ![]() . В результате замены получаем
в левой части член со вкладом, аналогичным вкладу от рассеяния:
. В результате замены получаем
в левой части член со вкладом, аналогичным вкладу от рассеяния:
![]()
Как уже отмечалось выше, при решении уравнения (11)
может быть получено отрицательное, либо расходящееся решение ![]() , если значения сечения рассеяния
, если значения сечения рассеяния ![]() велики. Благодаря
усовершенствованию метода ребаланса, предложенному в работе [13], эта
неустойчивость должна исчезнуть. Как известно, необходимым и достаточным
условием сходимости итерационного метода является условие, при котором все
собственные значения матрицы перехода по модулю меньше 1. Применительно к
диффузионному уравнению (11) это условие выполняется только при достаточном
увеличении его коэффициентов. Тогда амплитуда ребалансных поправок уменьшится,
что позволит приблизить поправки к значению 1 в тех областях, где они велики.
велики. Благодаря
усовершенствованию метода ребаланса, предложенному в работе [13], эта
неустойчивость должна исчезнуть. Как известно, необходимым и достаточным
условием сходимости итерационного метода является условие, при котором все
собственные значения матрицы перехода по модулю меньше 1. Применительно к
диффузионному уравнению (11) это условие выполняется только при достаточном
увеличении его коэффициентов. Тогда амплитуда ребалансных поправок уменьшится,
что позволит приблизить поправки к значению 1 в тех областях, где они велики.
Процедура усовершенствования заключается в следующем.
Сначала как обычно вычисляются скалярные токи. Затем каждый из них
увеличивается на фиктивный ток следующим образом:
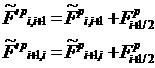 ,
, 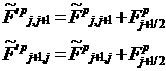 ,
, 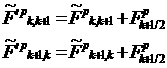 ,
,
где
увеличенный ток помечен штрихом, а фиктивные токи вычисляются по формулам:
![]() ,
, ![]() ,
, ![]()
С
учетом этих изменений уравнение ребаланса (11) примет следующий вид:
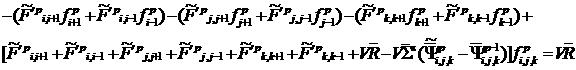 (12)
(12)
Полученная система уравнений (12) решается
итерационным методом верхней релаксации с автоматическим выбором параметра
релаксации в каждой группе.
На первой внутренней итерации используется стандартное
для трехмерной геометрии значение параметра ![]() . Проблема заключается в выборе оптимального значения
параметра
. Проблема заключается в выборе оптимального значения
параметра ![]() . Оптимальное значение увеличивается с увеличением сложности
задачи. В работе [14] было показано, что увеличение значения параметра
. Оптимальное значение увеличивается с увеличением сложности
задачи. В работе [14] было показано, что увеличение значения параметра ![]() надо осуществлять
только в случае необходимости.
надо осуществлять
только в случае необходимости.
Для того чтобы понять, как ведет себя процесс
ускорения внутренних итераций, рассчитываются следующие величины:
1) максимальная относительная ошибка решения уравнения
переноса до ускорения:
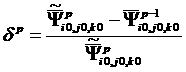 , (13)
, (13)
если
в точке ![]() достигается ее
максимум
достигается ее
максимум 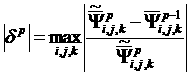 ;
;
2) относительная ошибка в этой же точке после ускорения
методом ребаланса:
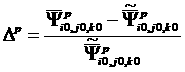 . (14)
. (14)
Возможны
следующие случаи:
а)
![]() , т.е. ребаланс действует в противоположную сторону, чем
основная итерация,
, т.е. ребаланс действует в противоположную сторону, чем
основная итерация,
б)
![]() , т.е. ребаланс осциллирует,
, т.е. ребаланс осциллирует,
в)
![]() , т.е. ребаланс расходится.
, т.е. ребаланс расходится.
При
выполнении одного из этих критериев необходимо увеличить значение ![]() на постоянную величину
на постоянную величину
![]() .
.
Несмотря на некоторую степень свободы в выборе
значения параметра ![]() , этот метод является надежным средством для решения задач
глубокого проникновения, особенно при высоких энергиях и высокой анизотропии
рассеяния. В худшем случае решение сходится со скоростью не меньшей, чем без
ускорения. Если значение параметра
, этот метод является надежным средством для решения задач
глубокого проникновения, особенно при высоких энергиях и высокой анизотропии
рассеяния. В худшем случае решение сходится со скоростью не меньшей, чем без
ускорения. Если значение параметра ![]() слишком велико, то
ускорение не будет происходить.
слишком велико, то
ускорение не будет происходить.
6. Ускорение внешних итераций по
источнику деления.
Рассмотрим степенной метод вычисления ![]() и источника деления
и источника деления ![]() :
:
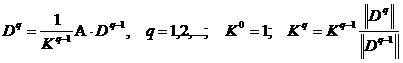 , где
, где 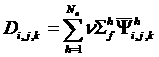
Известно, что для корректно поставленных задач для
любого произвольного положительного начального приближения ![]() этот метод сходится.
Будем считать, что система собственных функций
этот метод сходится.
Будем считать, что система собственных функций ![]() матрицы
матрицы ![]() полна, а все ее
собственные числа
полна, а все ее
собственные числа ![]() положительны и
положительны и ![]() . В конечномерном пространстве число собственных значений
. В конечномерном пространстве число собственных значений ![]() и собственных функций
и собственных функций ![]() матрицы перехода
матрицы перехода ![]() совпадает с числом
пространственных точек.
совпадает с числом
пространственных точек.
В пакете «РЕАКТОР» для ускорения внешних итераций до
недавнего времени использовался метод полиномов Чебышева. Для использования
этого метода ускорения надо предварительно оценить отношение двух наибольших
собственных чисел матрицы перехода ![]() , что является затруднительным. С другой стороны, этот
алгоритм слишком чувствителен к вычислительной погрешности [15].
, что является затруднительным. С другой стороны, этот
алгоритм слишком чувствителен к вычислительной погрешности [15].
В настоящее время используется более эффективный
алгоритм ускорения внешних итераций в задачах на ![]() . Алгоритм основан на экстраполяции компонент ошибки решения
к нулю, а самого решения соответственно к точному решению.
. Алгоритм основан на экстраполяции компонент ошибки решения
к нулю, а самого решения соответственно к точному решению.
Представим ошибку начального приближения в точке ![]() в виде ряда по собственным функциям матрицы
в виде ряда по собственным функциям матрицы ![]() :
:
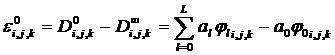 .
.
В
каждой пространственной точке все собственные функции вносят вклад в ошибку.
Величина этого вклада зависит от номера итерации, от ошибки начального приближения
и от матрицы перехода. Запишем выражение для ошибки, накопленной за ![]() итераций:
итераций:
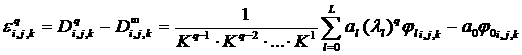 (1)
(1)
Так
как все члены ряда (1) за исключением первого члена (![]() ) стремятся к нулю
) стремятся к нулю ![]() при
при ![]() , то с увеличением числа итераций постепенно ошибка
, то с увеличением числа итераций постепенно ошибка ![]() уменьшается. Члены с
наименьшими собственными значениями исчезают быстрее.
уменьшается. Члены с
наименьшими собственными значениями исчезают быстрее.
Часто на практике возникают случаи, когда в процессе
итераций с ростом ![]() собственное значение
собственное значение ![]() практически не
меняется, а в источнике еще велика относительная ошибка:
практически не
меняется, а в источнике еще велика относительная ошибка:
![]() ,
, 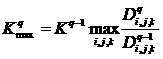 ,
, 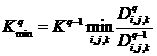 .
.
Это
означает, что расчет вышел на псевдо асимптотический режим, т.е. близкие по
величине собственные значения матрицы ![]() получаются в качестве
решения
получаются в качестве
решения ![]() . В таком случае возникает необходимость в ускорении, чтобы
сдвинуть итерационный процесс с мертвой точки. Если предположить, что
сходимость достигнута, то на асимптотике будут справедливы два выражения для
доминантного соотношения:
. В таком случае возникает необходимость в ускорении, чтобы
сдвинуть итерационный процесс с мертвой точки. Если предположить, что
сходимость достигнута, то на асимптотике будут справедливы два выражения для
доминантного соотношения:
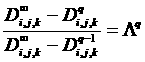 и
и 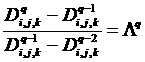
Из
этих соотношений следует формула:
![]() , (2)
, (2)
где
символом ![]() обозначено значение
параметра экстраполяции:
обозначено значение
параметра экстраполяции:
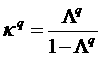 (3)
(3)
Алгоритм ускорения внешних итераций основан на
использовании формул (2) и (3) для линейной экстраполяции источника деления в
каждой точке пространства. Одновременно экстраполируются скалярные потоки по
такой же формуле. Для вычисления доминантного соотношения ![]() более удобно
использовать глобальную величину ошибки
более удобно
использовать глобальную величину ошибки ![]() :
:
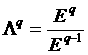 ,
, ![]() .
.
Так как экстраполяция источника вводит дополнительное
возмущение, необходимо продолжить процесс внешних итераций. Будем считать, что
с этого момента начинается новый итерационный цикл, основанный на новом
начальном приближении источника деления. Так может повторяться несколько раз,
пока относительная ошибка расчета ![]() ни достигнет заданной
малой величины, а значение
ни достигнет заданной
малой величины, а значение ![]() практически ни
совпадет со значениями
практически ни
совпадет со значениями ![]() и
и ![]() .
.
Экспериментальным путем подтверждено, что этот
алгоритм ускорения внешних итераций является эффективным. Например, при решении
реальной задачи для системы многогрупповых диффузионных уравнений расчет
ускорился в несколько раз.
Важно правильно эмпирически подобрать критерии
применения процедуры экстраполяции. Очевидно, что для значений ![]() и
и ![]() не надо делать
экстраполяцию. Экстраполяция делается, если три последовательные оценки
параметра экстраполяции
не надо делать
экстраполяцию. Экстраполяция делается, если три последовательные оценки
параметра экстраполяции ![]() близки между собой,
например удовлетворяют следующему критерию:
близки между собой,
например удовлетворяют следующему критерию:
 .
.
Кроме
того, значение ![]() определяется таким
образом, чтобы источник деления не изменился больше, чем на заданную
максимальную величину.
определяется таким
образом, чтобы источник деления не изменился больше, чем на заданную
максимальную величину.
В заключение заметим, что в [15] этот метод ускорения
описан для решения систем линейных уравнений и называется ![]() - процесс ускорения
сходимости.
- процесс ускорения
сходимости.
7. Ускорение внешних итераций для подкритических систем.
Для подкритических задач на размножение для ускорения
внешних итераций используется метод глобального ребаланса. Если обозначить
через ![]() полную сумму (по
энергетическим группам, по пространству и направлениям) внешнего источника и
через
полную сумму (по
энергетическим группам, по пространству и направлениям) внешнего источника и
через ![]() - полную сумму
источника деления
- полную сумму
источника деления
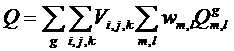 (1)
(1)
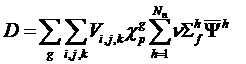 (2)
(2)
то
уравнение переноса может быть записано в операторном виде:
![]() (3)
(3)
где
![]() - номер внешней
итерации. Для того чтобы сбалансировать потоки и источники, вводится множитель
- номер внешней
итерации. Для того чтобы сбалансировать потоки и источники, вводится множитель ![]() , на который умножаются все потоки. Операторы
, на который умножаются все потоки. Операторы ![]() будут пропорциональны
будут пропорциональны ![]() , а
, а ![]() нет:
нет:
![]() (4)
(4)
Исключая
из (3) и (4) ![]() , получим формулу для вычисления множителя
, получим формулу для вычисления множителя ![]() :
:
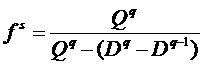 (5)
(5)
Результаты
внешней итерации умножаются на множитель ![]() . Этот метод эффективен, если источник распределен по всей
области размножения.
. Этот метод эффективен, если источник распределен по всей
области размножения.
8. Результаты расчета реактора СВБР 75/100.
Результаты расчетов по пакету «РЕАКТОР» показали
хорошее совпадение с расчетами реактора СВБР 75/100 по программе TORT [7] на одинаковых константах.
Расчет эффективного коэффициента размножения
выполнялся в HEX-Z геометрии в диффузионном приближении и в кинетическом
S4P1 приближении
для 30 групп нейтронов. В задаче использовалось 18 различных горизонтальных
картограмм. Общее число ячеек сетки 1791582. На Рис. 1 и 2 показаны результаты
расчета энерговыделения в диффузионном и кинетическом S4P1 приближениях
соответственно.
На Рис. 3 показано поведение значений ![]() на внешних итерациях
при решении этой задачи в диффузионном приближении. Задавалось ограничение на
число внутренних итераций не больше 9. На рисунке видно влияние экстраполяции
источника деления при ускорении внешних итераций (кривая немонотонно изгибается
и поднимается вверх к точному решению).
на внешних итерациях
при решении этой задачи в диффузионном приближении. Задавалось ограничение на
число внутренних итераций не больше 9. На рисунке видно влияние экстраполяции
источника деления при ускорении внешних итераций (кривая немонотонно изгибается
и поднимается вверх к точному решению).
Расчет защиты для реакторной
установки СВБР 75/100 выполнялся в X-Y-Z и R-FI-Z
геометриях в приближении S8P3, 30 групп нейтронов и 19
групп g-квантов. В X-Y-Z
геометрии 2417637 пространственных точек: 237 слоев по Z, 101 точек по X и 101
точек по Y. В R-FI-Z геометрии рассчитывались меньшие
по объему области с более подробной сеткой. На Рис. 4. показано поведение
плотности полного потока нейтронов в R-FI-Z геометрии.
Заключение
Описанные выше методы решения уравнения
переноса в многогрупповом приближении в трехмерной геометрии позволяют
эффективно решать как реакторные задачи, так и задачи защиты в едином пакете
программ «РЕАКТОР».
Литература
1.
A.V.
Voronkov, A.N. Chebeskov, E.P. Sychugova, I.Y. Krivitsky, E.V. Matveeva, Y.N.
Mironovich, A.D. Knipe. Low Reactivity Sodium-Void Benchmark Study in an
Annular Heterogeneous Assembly. Proceeding
of the International Topical Meeting on Sodium Cooled Fast Reactor Safety,
IPPE, Obninsk, 1994.
2.
А.В. Воронков, Л.П. Басс, Е.П. Сычугова. Пакет программ
KINRZ для решения многогруппового уравнения переноса нейтронов и γ –
квантов в двумерной R-Z геометрии методом дискретных ординат. Препринт ИПМ РАН, 1999, №83.
3.
А.В. Воронков, Е.П. Сычугова, Е.В. Матвеева, А.Н. Чебесков.
Расчетные исследования натриевого пустотного коэффициента реактивности (НПЭР),
измеренного в экспериментах «ZEBRA». Препринт
ИПМ РАН, 1996, №65.
4.
А.В. Воронков, Е.П. Сычугова. Решение уравнения переноса
нейтронов в двумерной R-Z и трехмерной X-Y-Z геометриях методом дискретных
ординат. Препринт ИПМ РАН, 1995, №6.
5.
А.В. Воронков,
Е.П. Сычугова, А.С. Голубев. Решение
стационарного уравнения переноса нейтронов в трехмерной Hex-Z геометрии. Отчет ИПМ РАН, 2004, № 7-03-2004 (37c.)
6.
А.В. Воронков,
Е.П. Сычугова, П.Б. Афанасьев, А.В. Дедуль, В.В.Кальченко. Трехмерные расчеты
радиационной защиты в пакете программ РЕАКТОР-ГП. Тезисы
доклада на IX Российской научной конференции «Радиационная защита и
радиационная безопасность в ядерных технологиях» 24-26 октября
7.
Е.В. Аверченков, П.Б. Афанасьев, А.В. Дедуль, В.В. Кальченко, А.В.Воронков, Е.П. Сычугова. Трехмерные
расчеты радиационной защиты реакторной установки СВБР 75/100. Тезисы доклада на IX Российской научной конференции
«Радиационная защита и радиационная безопасность в ядерных технологиях» 24-26
октября
8. Аверченков Е.В., Афанасьев П.Б., Дедуль А.В.,
Кальченко В.В., ВоронковА.В., Сычугова Е.П. Совместные расчеты «РЕАКТОР» + «ЗАЩИТА» реакторной установки СВБР 75/100 в
трехмерной геометрии. Тезисы докладов на 17-м семинаре «НЕЙТРОНИКА
– 2006» Нейтронно-физические проблемы атомной энергетики, 30 октября -03 ноября
9. «Вычислительные методы в
физике реакторов», Сб. статей под ред. Х. Гринспена, К. Келбера, Д. Окрента,
Москва, Атомиздат, 1972.
10.
B.G. Carlson «A Method of
Characteristics and Other Improvements in Solution Methods for the Transport
Equation», Nucl. Sci.
11.
DOORS3.2 One, Two- and Tree
Dimensional Discrete Ordinates Neutron/Photon Transport Code System. RSIC Computer Code Collection CCC-650, 1998.
12.
E.M. Gelbard and
13.
W. H. Reed. The Effectiveness of acceleration
Techniques for Iterative Methods in Transport Theory. Nucl. Sci.
14.
W.A. Rhoades. Improvements in
Discrete Ordinates Acceleration. Trans.
Am. Nucl. Soc., v. 39, 753 (November 1981).
15.
Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. Численные
методы. Изд-во МГУ им. М.В. Ломоносова,
3-е издание, дополненное и переработанное, Москва, 2004.
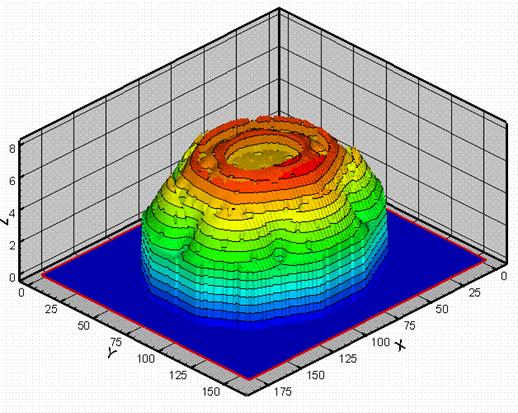
Рис. 1. Энерговыделение в центральной плоскости на
начало кампании
(в диффузионном приближении).
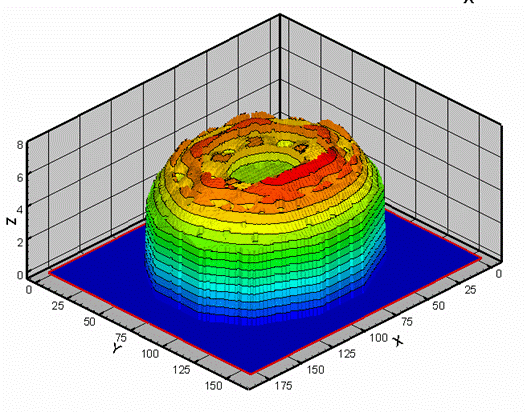
Рис. 2. Энерговыделение в центральной плоскости на
начало кампании
(в кинетическом приближении).
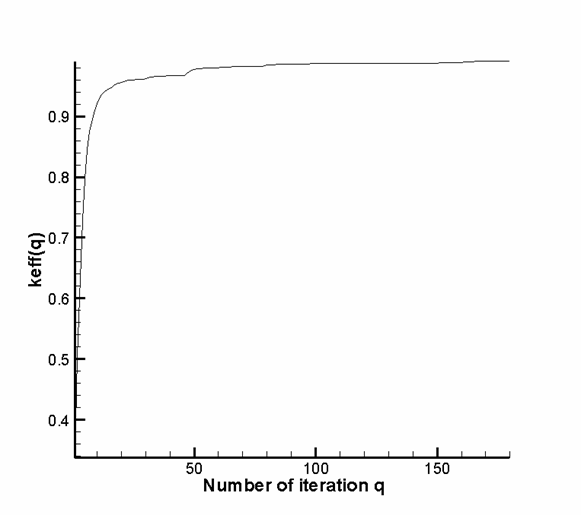
Рис. 3. Поведение приближенного значения ![]() на внешних итерациях
на внешних итерациях
в диффузионном приближении.
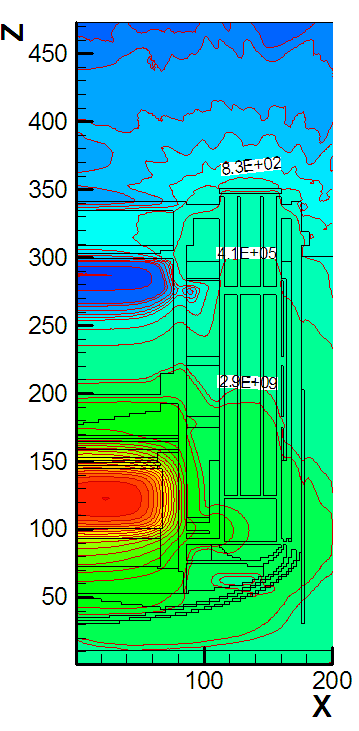
Рис. 4. Плотность
полного потока нейтронов (нейтр/см2с) в задаче защиты
в R-FI-Z геометрии.
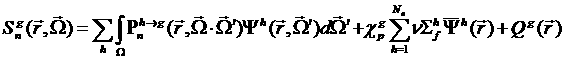
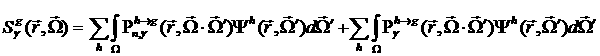 (3)
(3)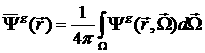
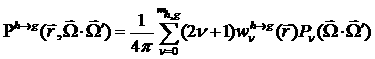 ,
, 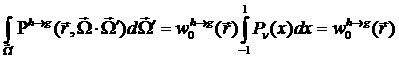
 ,
,