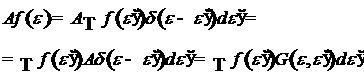Применение метода Монте-Карло для реконструкции спектров проникающих излучений и
аппаратных функций регистрирующей аппаратуры
|
|
|
Таким образом, информация о спектре
излучения источника ИИ и знание аппаратной функции регистрирующей аппаратуры,
являются необходимыми условиями адекватного математического моделирования
экспериментов с проникающим излучением.
Источники ионизирующего
излучения и используемая регистрирующая аппаратура обычно являются сложными
программно–аппаратными комплексами, которые не всегда могут поддаваться прямому
математическому моделированию, как вследствие незнания их внутреннего
устройства (например, структура некоторых ускорителей заряженных частиц
является коммерческой тайной), так и в случае сложности преобразования регистрируемого
излучения в измеряемую величину (например, многоступенчатый процесс
преобразования ионизирующего излучения в плотность почернения рентгеновской пленки).[3]
Поэтому в радиографии, радиоскопии и даже в радиометрии используют метод
сравнения данных, полученных при просвечивании контрольных образцов, с
образцами данных, получаемыми при просвечивании эталонных образцов.
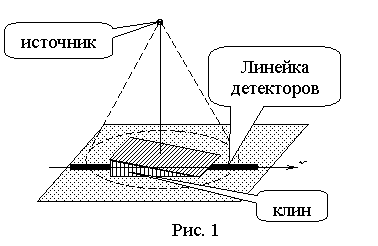
Рассмотрим стандартную схему
использования ионизирующего излучения для задач неразрушающего контроля,
изображенную на Рис. 1. Основные блоки математического моделирования
соответствующего эксперимента следующие:
-
моделирование тормозного излучения в рентгеновской трубке;
-
моделирование трансформации ионизирующего излучения при
взаимодействии ионизирующего излучения с фильтром и коллиматором;
-
моделирование трансформации ионизирующего излучения при
взаимодействии ионизирующего излучения с объектом контроля;
-
моделирование трансформации ионизирующего излучения при
взаимодействии ионизирующего излучения с усилительным экраном;
-
моделирование преобразования потока частиц регистрируемого
излучения в измеряемую величину для рентгеновской плёнки.
Как указывалось выше, для
адекватного математического моделирования рассматриваемых экспериментов
необходимо знание энергетического распределения источника излучения и функции
отклика измерительной аппаратуры.
Методы определения спектров
источников и функций откликов регистрирующей аппаратуры основаны на регистрации
различных измеряемых величин, являющихся функционалами от искомого
энергетического распределения, с последующей математической обработкой
результатов экспериментальных измерений [5; 6]. При этом, первостепенное значение имеет выбор
способа построения операторного уравнения, связывающего искомое спектральное
распределение ионизирующего излучения и совокупность измеряемых величин. Эти
задачи относятся к классу обратных задач, являются некорректно поставленными и
требуют при решении использования специальных алгоритмов. Подобные методы можно
отнести к косвенному математическому моделированию, поскольку они позволяют
находить функции отклика системы по косвенным признакам (отклику системы) не
вдаваясь во внутреннее устройство сложных систем или комплексов.
В
настоящей работе описывается методика реконструкции спектров используемого в
экспериментах гамма-излучения широкого энергетического диапазона и
реконструкция функции отклика регистрирующей системы, которая включает в себя:
-
метод построения операторных уравнений, связывающих искомые
распределения и измеряемые величины, который конструируется с учетом
особенностей физических процессов, характерных для соответствующих экспериментальных
работ;
-
алгоритмы определения спектральных распределений
гамма-излучения, обеспечивающие возможность одновременного использования
измеряемых величин различного типа в процессе решения соответствующей обратной
задачи, а также различных функциональных зависимостей указанных величин.
Разработанный способ
построения операторов связи между искомыми функциями и измеряемыми в экспериментах
величинами учитывает основные физические процессы взаимодействия ионизирующего
излучения с веществом для широкого энергетического диапазона фотонов (процессов
когерентного и некогерентного рассеяний, фотоэлектрического поглощения, рождения
электрон-позитронных пар и т.д.).
Построение искомого
операторного уравнения проводится следующим образом:
-
В соответствии с условиями проведения конкретного эксперимента,
определяется набор параметров, с помощью которых записывается искомое
операторное уравнение. Такими параметрами могут быть, например, толщина
просвечиваемого материала, координаты детекторов, регистрирующих излучение,
энергетическая шкала группового спектра регистрируемого излучения и т.п.
-
Строится оператор, связывающий спектры исходного и регистрируемого
излучения. Для этого используется понятие функции Грина, с помощью которой
конструируется ядро соответствующего интегрального оператора. Непосредственно
функция Грина для различных экспериментов может быть определена как
аналитически, так и расчетным путем (например, Методом Монте-Карло), в
зависимости от физических условий проведения опытов, от вида измеряемых величин
и используемых приближений.
-
Вычисляется функционал от спектра регистрируемого излучения,
соответствующий измеряемой в эксперименте величине.
Для
решения полученных систем операторных уравнений разработан устойчивый алгоритм,
позволяющий учитывать априорную информацию об искомом решении как
количественного, так и качественного типа. В основу разработанного алгоритма
положены результаты работ А.Н.Тихонова, В.Я.Арсенина, В.П.Загонова. Созданный
алгоритм основывается на вариационном принципе и дает возможность использовать
различную априорную информацию об искомом решении и может применяться для
решения систем линейных интегральных уравнений первого рода [7; 13].
Построение операторов преобразования спектров исходного излучения.
Конструирование и
анализ свойств операторов, связывающих распределения энергетических
распределений используемого излучения и измеряемых в рассматриваемых
экспериментах величин, подразумевают моделирование процесса трансформации проникающего
излучения в веществе опытного объекта и построение соответствующих функционалов
от спектров регистрируемого излучения.
Для упрощения изложения будем рассматривать трансформацию только энергетического спектра приходящих в детекторы фотонов, то есть сделаем предположение, что показания регистрирующей аппаратуры реагирует только на энергию приходящих частиц ионизирующего излучения и не зависят от интенсивности и направления приходящего излучения.
Пусть f(e) - спектральное распределение фотонов излучения,
падающего на объект (e ‑ энергия
излучения). В соответствии с конструктивными особенностями экспериментальной
установки, а также в результате взаимодействия с веществом опытного объекта, на
регистрирующую аппаратуру попадает излучение с распределением j(e), т.е. в ходе эксперимента происходит преобразование
спектра исходного излучения f(e) в спектр регистрируемого излучения j(e).
Будем рассматривать
преобразование функции f(e) в соответствующее распределение регистрируемого
излучения j(e) как действие оператора A в некотором функциональном пространстве U, j=Af, f, jÎU.
Отметим основные физические
допущения, в рамках которых проводится моделирование процессов трансформации
проникающего излучения в материалах объектов:
-
предполагается, что фотоны, проходящие сквозь объект, не изменяют
свойств используемых материалов;
-
предполагается также, что фотоны не взаимодействуют друг с
другом.
Очевидно, что в этом случае
траектории фотонов можно рассматривать независимо, поэтому оператор A является линейным.
Рассмотрим теперь некоторую
фиксированную конфигурацию и соответствующий набор параметров ![]() эксперимента (такими
параметрами могут быть характеристики облучаемого объекта, детектирующих
устройств, функциональные зависимости измеряемых величин и т.д.).
эксперимента (такими
параметрами могут быть характеристики облучаемого объекта, детектирующих
устройств, функциональные зависимости измеряемых величин и т.д.).
Будем считать ниже, что
опытный объект облучается фотонами с энергетическим распределением f(e). Соответственно, регистрируемое излучение будет
иметь спектр j(e). Это излучение взаимодействует с измеряющей аппаратурой,
результатом чего являются показания детектора F (измеряемая величина), которые при фиксированном наборе параметров
![]() представляют собой
функционал от j(e):
представляют собой
функционал от j(e):
где g(e) является функцией отклика и характеризует измеряемую
в эксперименте величину (доза рентгеновского или гамма-излучения, групповой
спектр комптоновских или фотоэлектронов и т.п.) и способ ее измерения
(конкретный тип регистрирующей аппаратуры и конкретная её настройка). Например,
если некоторое гипотетическое устройство «умеет» измерять всю попавшую на это устройство энергию излучения, то g(e)=e.[4]
Таким образом, формально проведение эксперимента можно
разделить на два этапа:
-
облучение объекта проникающим излучением, результатом которого
является преобразование спектра исходного излучения в спектр регистрируемого
излучения;
-
измерение величины F,
при котором происходит преобразование регистрируемого излучения в измеряемую
величину.
Первый из этих этапов
описывается с помощью преобразования j=Af, второй – с помощью
преобразования F=Pj, причем оператор ![]() определяется видом
функционалов .
определяется видом
функционалов .
Такой подход дает
возможность описывать регистрируемое излучение независимо от выбора измеряемой
величины и способа ее измерения, а затем на основе такого описания построить
преобразование j®F для конкретной измеряемой величины. Причем для различных
типов измерений используется одно и тоже описание регистрируемого излучения,
что является удобным и эффективным при математическом моделировании экспериментов.
Оператор A преобразования энергетического распределения фотонов
исходного излучения в спектр регистрируемого излучения будем строить следующим
образом.
Рассмотрим в качестве
спектра излучения источника функцию ![]() . Обозначим через
. Обозначим через ![]() результат действия
оператора
результат действия
оператора ![]() на указанную функцию:
на указанную функцию: ![]() . Функция
. Функция ![]() имеет смысл плотности
спектрального распределения регистрируемого излучения от моноэнергетического
источника фотонов с энергией
имеет смысл плотности
спектрального распределения регистрируемого излучения от моноэнергетического
источника фотонов с энергией ![]() .
.
Для произвольной функции f(e) запишем очевидное равенство:
Соотношение показывает, что для произвольного энергетического распределения
источника f(e) спектральное распределение регистрируемого излучения
j(e) можно найти по формуле ![]() .
.
Таким образом, построение
оператора A сводится к нахождению функции
![]() (функцию
(функцию ![]() можно интерпретировать
как функцию Грина оператора переноса
можно интерпретировать
как функцию Грина оператора переноса ![]() [8]). Определение этой функции является нетривиальной
задачей, требующей всякий раз учета конкретных физических условий проведения
соответствующих экспериментов и различных факторов, играющих определяющую роль
в формировании измеряемых характеристик изучаемых процессов. В некоторых
случаях удается записать
[8]). Определение этой функции является нетривиальной
задачей, требующей всякий раз учета конкретных физических условий проведения
соответствующих экспериментов и различных факторов, играющих определяющую роль
в формировании измеряемых характеристик изучаемых процессов. В некоторых
случаях удается записать ![]() аналитически, однако,
наиболее общим подходом для конструирования функции
аналитически, однако,
наиболее общим подходом для конструирования функции ![]() является
математическое моделирование процессов трансформации проникающего излучения в
материалах объектов с помощью эффективных вычислительных алгоритмов (см.,
например, [9; 10]). В [10] для дискретного описания объектов разработан поверхностно
ориентированный подход, основанный на точном задании замкнутых оболочек, разделяющих
гомогенные части объекта. Дискретизация оболочек проводится с помощью
экономичной модификации триангуляционного метода. Алгоритмы этой работы основаны
на сочетании указанного способа дискретного описания многокомпонентных объектов
сложной геометрии и различных модификаций метода Монте-Карло.
является
математическое моделирование процессов трансформации проникающего излучения в
материалах объектов с помощью эффективных вычислительных алгоритмов (см.,
например, [9; 10]). В [10] для дискретного описания объектов разработан поверхностно
ориентированный подход, основанный на точном задании замкнутых оболочек, разделяющих
гомогенные части объекта. Дискретизация оболочек проводится с помощью
экономичной модификации триангуляционного метода. Алгоритмы этой работы основаны
на сочетании указанного способа дискретного описания многокомпонентных объектов
сложной геометрии и различных модификаций метода Монте-Карло.
Как известно, метод
Монте-Карло основан на моделировании случайных траекторий фотонов, имеющих
исходное энергетическое распределение f(e). Результатом моделирования
является итоговое распределение фотонов j(e). Таким образом, применение алгоритма метода
Монте-Карло можно рассматривать как действие оператора A на функцию f(e) . С другой стороны, введя дискретную энергетическую сетку ![]() , можно проследить за траекториями фотонов из выделенного
энергетического интервала
, можно проследить за траекториями фотонов из выделенного
энергетического интервала ![]() и получить
распределение
и получить
распределение 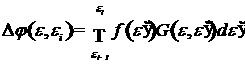 .
.
Тогда матрица 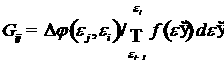 представляет собой дискретный
аналог функции
представляет собой дискретный
аналог функции ![]() . В этом случае значения спектра рассеянного излучения
. В этом случае значения спектра рассеянного излучения ![]() на дискретной
энергетической сетке
на дискретной
энергетической сетке ![]() можно также вычислять
путем свертки вектора
можно также вычислять
путем свертки вектора ![]() на сетке
на сетке ![]() с матрицей
с матрицей ![]() :
: ![]() . Возможность одновременного вычисления спектра рассеянного
излучения и ядра линейного оператора
. Возможность одновременного вычисления спектра рассеянного
излучения и ядра линейного оператора ![]() , которую предоставляет стандартный метод Монте-Карло,
позволяет свести целую серию расчётов с различными источниками излучения к
одному расчёту матрицы
, которую предоставляет стандартный метод Монте-Карло,
позволяет свести целую серию расчётов с различными источниками излучения к
одному расчёту матрицы ![]() (например, при f(e)=const) и дальнейшему её
многократному использованию при варьировании спектра исходного излучения или
при решении обратной задачи о его реконструкции.
(например, при f(e)=const) и дальнейшему её
многократному использованию при варьировании спектра исходного излучения или
при решении обратной задачи о его реконструкции.
Приведем примеры.
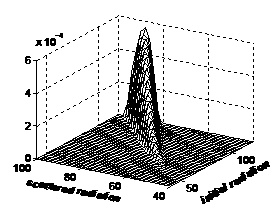
На Рис. 2 изображена функция ![]() , полученная для случая, когда в эксперименте измеряется
групповой спектр обратно рассеянного излучения. Указанная функция рассчитана с
использованием методики работы [10] на многопроцессорном вычислительном комплексе
МВС ‑ 15000.
, полученная для случая, когда в эксперименте измеряется
групповой спектр обратно рассеянного излучения. Указанная функция рассчитана с
использованием методики работы [10] на многопроцессорном вычислительном комплексе
МВС ‑ 15000.
При
проведении некоторых экспериментов вместо фотонного излучения, прошедшего
сквозь объект, регистрируется, например, электронный поток, порожденный при
взаимодействии квантов ионизирующего излучения с веществом объекта. В этом
случае строится оператор преобразования фотонного спектра в электронный.
Указанное построение проводится путем математического моделирования процессов
трансформации проникающего излучения в электронные потоки с использованием
физических моделей комптоновского рассеяния, фотоэлектрического поглощения,
рождения электрон-позитронных пар и т.д.
|
|
|
|
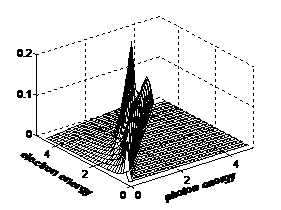
Рис. 3 |
В качестве примера на Рис. 3 изображено ядро оператора преобразования спектра ионизирующего излучения в энергетическое распределение электронов, рассчитанное с помощью методики работы [3].
Как указывалось выше, в процессе
измерения регистрируемого излучения происходит преобразование спектрального
распределения j этого излучения в
измеряемую детектором величину F(j).
Комбинируя соотношения и , получим:
|
|
Из следует, что, если известна функция отклика регистрирующей
системы, мы можем получить операторное уравнение I-го рода относительно
спектра исходного спектра и, наоборот, если известен спектр исходного излучения,
мы можем получить операторное уравнение I-го рода относительно
функции отклика регистрирующей системы.
|
|
В дальнейшем мы будем
рассматривать только реконструкцию энергетических спектров, в предположении,
что нам известна функция отклика регистрирующей аппаратуры.
Приведем примеры.
Предположим, что для
регистрации прошедшего через объект излучения используется детекторная
плоскость, имеющая N
детекторов по x и M детекторов по y (например, можно провести подобную дискретизацию
рентгеновской пленки). В этом случае в качестве параметра эксперимента удобно
использовать, например, координаты центров элементарных детекторов ![]() . Если измеряемой величиной при этом является интенсивность
регистрируемого излучения (g(e)=1), то:
. Если измеряемой величиной при этом является интенсивность
регистрируемого излучения (g(e)=1), то:
|
|
если
измеряется поглощенная энергия (g(e)=e), то:
|
|
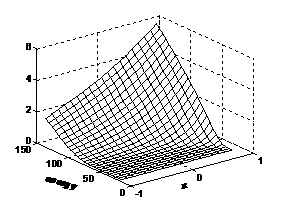
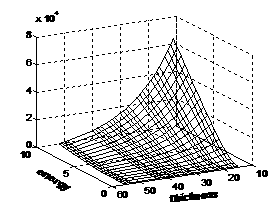
На Рис. 4 и Рис. 5 изображена функция ![]() для следующей конфигурации
эксперимента. На железный клин падает конический поток ионизирующего излучения,
измерения регистрируемого излучения проводятся линейкой детекторов,
расположенных вдоль центральной линии клина (Рис. 4). На Рис. 4 представлен случай, когда измеряется интенсивность
прошедшего сквозь
для следующей конфигурации
эксперимента. На железный клин падает конический поток ионизирующего излучения,
измерения регистрируемого излучения проводятся линейкой детекторов,
расположенных вдоль центральной линии клина (Рис. 4). На Рис. 4 представлен случай, когда измеряется интенсивность
прошедшего сквозь
клин излучения с
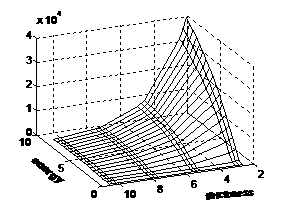
учетом процессов рассеяния и фотопоглощения фотонов , на Рис. 5 – случай, когда измеряемой величиной является поглощенная
энергия регистрируемого излучения .
|
|
|
|
Рис. 5 |
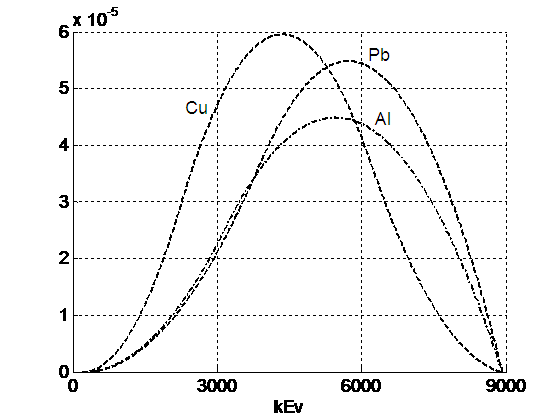
В качестве другого примера рассмотрим ситуацию, когда в
экспериментах используются наборы образцов различной толщины из разных материалов.
Здесь в качестве параметров используются пары ![]() , где
, где ![]() обозначает вид материала. На Рис. 6 и Рис.
7 приведены результаты расчета функции
обозначает вид материала. На Рис. 6 и Рис.
7 приведены результаты расчета функции ![]() для алюминия (Рис. 6) и свинца (Рис.
7), в случае, когда измеряемой величиной является
поглощенная энергия регистрируемого излучения.
для алюминия (Рис. 6) и свинца (Рис.
7), в случае, когда измеряемой величиной является
поглощенная энергия регистрируемого излучения.
|
|
|
Вычисления в приведенных примерах проводились на многопроцессорной системе МВС-15000 (http://www.jscc.ru/cgi-bin/show.cgi?path=/hard/scomputer.html&type=1).
Предположим, что пластина из некоторого материала
толщиной d облучается проникающим
излучением (при этом, происходит преобразование j(e)=Af(e)), и пусть за пластиной находится детектор, регистрирующий
прошедшее излучение j путем измерения некоторой
величины F(j). Если в качестве
изменяемого параметра эксперимента выбрать d, то в результате серии экспериментов можно получить
конечномерную аппроксимацию функции F(d) (такого рода эксперименты используются
на практике, например, для определения спектра тормозного излучения). Таким
образом, оператор P в
этом случае преобразует функцию j(e) (которая характеризует спектр регистрируемого
излучения) в функцию F(d): F(d)=P(d) j(e).
Вариационный принцип решения некорректно поставленных задач.
Для решения некорректно поставленных задач определяющее
значение имеет дополнительная информация об искомом решении. Такая информация
может быть достаточно разнообразной, например информация о принадлежности
решения к определённому классу гладкости или информация о знакопостоянстве
функции или её производной на определённом интервале, мажорантные оценки на
функцию и её производные, краевые условия. Отметим, что интегральные уравнения
вида 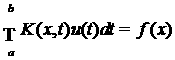 , где правая часть задана с некоторой погрешностью d в
метрике F можно рассматривать, как задание
множества определения решения,
, где правая часть задана с некоторой погрешностью d в
метрике F можно рассматривать, как задание
множества определения решения, 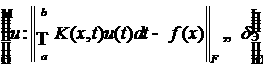 .
.
Существует также естественное разделение информации на полученную в ходе эксперимента и несущую в себе некоторую погрешность и информацию о решении, вытекающую из знаний об исследуемом процессе.
Следуя [11], будем рассматривать операторное уравнение Au=f, где A ‑ непрерывный оператор, и единственному решению ![]() соответствует точная
правая часть
соответствует точная
правая часть ![]() . Также будем считать, что правая часть задана с некоторой
погрешностью d,
. Также будем считать, что правая часть задана с некоторой
погрешностью d,
![]() . Тогда естественно искать решение на множестве
. Тогда естественно искать решение на множестве ![]() . Вследствие того, что множество Ud достаточно широко, оно может содержать
функции, для которых
. Вследствие того, что множество Ud достаточно широко, оно может содержать
функции, для которых ![]() , где C – любое
наперед заданное число (см. например [12]). Для сужения этой области необходимо использовать
дополнительную информацию об исходном
решении.
, где C – любое
наперед заданное число (см. например [12]). Для сужения этой области необходимо использовать
дополнительную информацию об исходном
решении.
Рассмотрим
неотрицательный функционал Ω[u], определенный на всюду плотном в Θ
подмножестве Θ 1.
Если решение ![]() принадлежит его области
определения и для всякого числа K>0 множество Θ1,K
элементов u из Θ1 для которых Ω[u]
принадлежит его области
определения и для всякого числа K>0 множество Θ1,K
элементов u из Θ1 для которых Ω[u]![]() K, компактно на Θ, то такой
функционал называется стабилизирующим. Будем рассматривать только такие элементы
множества Ud, на которых определен
функционал Ω[u],
K, компактно на Θ, то такой
функционал называется стабилизирующим. Будем рассматривать только такие элементы
множества Ud, на которых определен
функционал Ω[u], ![]() . Среди элементов этого множества найдем такой (такие)
элемент ud, который минимизирует
функционал Ω[u]. Элемент ud
можно рассматривать как результат применения к правой части уравнения некоторого
оператора R, зависящего от параметра d, т.
е. ud = R( fd, d). В
предположении, что такой элемент существует для любых d>0 и fdÎF, доказывается теорема, что оператор R( fd, d)
является регуляризирующим для уравнения Au=f.
. Среди элементов этого множества найдем такой (такие)
элемент ud, который минимизирует
функционал Ω[u]. Элемент ud
можно рассматривать как результат применения к правой части уравнения некоторого
оператора R, зависящего от параметра d, т.
е. ud = R( fd, d). В
предположении, что такой элемент существует для любых d>0 и fdÎF, доказывается теорема, что оператор R( fd, d)
является регуляризирующим для уравнения Au=f.
Представляется удобным и целесообразным подойти к построению алгоритма решения некорректной задачи следующим образом: в основу регуляризирующего алгоритма заложить некоторый вариационный принцип построения приближенного решения задачи [7], учитывающий лишь необходимую, наименее обременительную информацию о гладкости решения и о погрешности входных данных. Имеющуюся в той или иной прикладной задаче дополнительную априорную информацию предлагается использовать для сужения области допустимых решений.
При такой реализации происходит условное разделение всей априорной информации на следующие "уровни":
1. информация «первого уровня» о гладкости решения составляет основу алгоритма. Выбор принципа отбора регуляризованных приближенных решений, заложенный в базовый блок алгоритма, играет особую роль и определяет качество всего программного комплекса.
2. информация «второго уровня» или экспериментальная, вытекающая из операторных уравнений и погрешности входных данных, наряду с информацией «первого уровня» дает регуляризирующий эффект.
3. дополнительная априорная информация «третьего уровня» не используется для регуляризации задачи, а лишь сужает класс возможных решений, повышая качество приближений, и может придать решению физический смысл.
В своих работах В.П. Загонов разработал подход, учитывающий лишь необходимую, наименее обременительную информацию о гладкости решения, где в качестве стабилизирующего функционала используется вариация первой или второй производной в зависимости от имеющейся информации о гладкости искомого решения. Эта информация служит для построения базового блока алгоритма.
Основные принципы построения алгоритма,
дискретизация и приёмы решения изложены, например, в работах [7; 13].
Отметим следующие особенности предложенного подхода.
• Размерность матрицы равна параметру дискретизации.
• Рассмотрение систем интегральных уравнений первого рода и учет дополнительной информации о решении не усложняет логику алгоритма, а в некоторых случаях может ускорять процесс нахождения искомого решения.
• Рассмотренный вычислительный алгоритм позволяют учитывать задание погрешности правых частях в равномерной метрике или поточечное задание d(x).
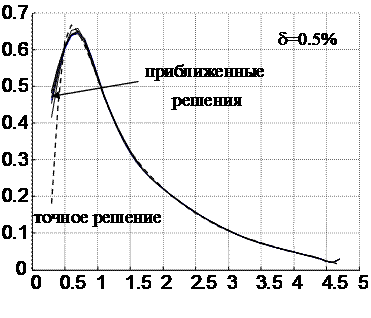
Ниже приведены некоторые модельные примеры восстановления спектров исходного ионизирующего излучения. На Рис. 8 приведен пример восстановления исходного спектра ионизирующего излучения, где в качестве функции Грина использовалась функция, приведённая на Рис. 3 . Исходные данные заданы с относительной погрешностью 0.5% и использована дополнительная информация о положительности решения.
|
|
|
|
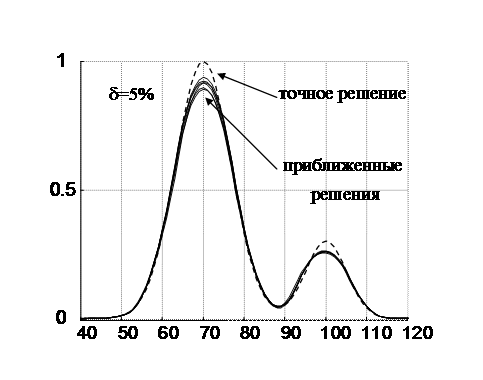
На Рис. 9 приведен результат восстановления спектра из модельного эксперимента, схема которого изображена на Рис. 4 с относительной погрешностью исходных данных в 5% и с дополнительной информацией о положительности решения.
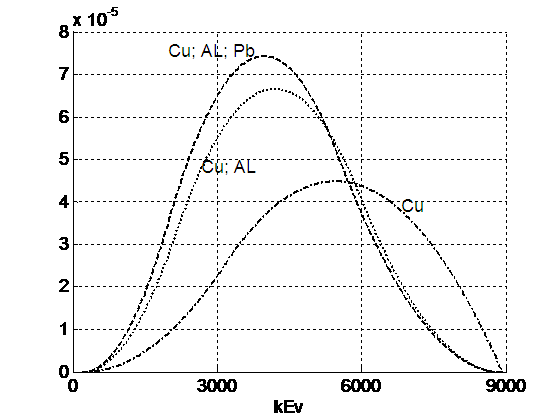
На Рис. 10 и Рис. 11 приведены результаты реальной реконструкции спектра линейного ускорителя. В качестве образцов брались пластины различной толщины трёх различных материалов медь, свинец и алюминий.
|
|
На Рис. 10 приведены результаты реконструкции отдельно для каждого материала, а на Рис. 11 приведены результаты реконструкции спектра, полученные при решении системы линейных операторных уравнений первого рода.
|
|
Заключение. В работе предложен
эффективный способ
построения операторных уравнений, связывающих искомые распределения и измеряемые
величины, который конструируется на основе статистического моделирования
физических процессов, сопровождающих облучение опытных объектов ионизирующим
излучением.
Разработаны устойчивые алгоритмы определения спектральных распределений используемого излучения, обеспечивающие возможность одновременного учета измеряемых величин различного типа в процессе решения соответствующей обратной задачи, а также различных функциональных зависимостей указанных величин.
Литература.
1.
Неразрушающий
контроль. Россия. 1900-2000 гг.:
Справочник. Под ред. В.В.Клюева. – 2-ое изд., исправ. и доп. М.:
Машиностроение, 2002.
2.
Д.М.
Иващенко, А.А. Федоров.
Российские ускорители электронов, использующиеся в качестве моделирующих
установок. Вопросы атомной науки и техники, серия: Физика радиационного
воздействия на радиоэлектронную аппаратуру. 2002, вып.3, с. 120 - 128,.
3.
М.Е.Жуковский,
С.В. Подоляко, Р.В.Усков.
Алгоритм расчета пространственного и спектрального распределений электронов,
порожденных при взаимодействии проникающего излучения с объектами. Препринт
Института прикладной математики им. М.В.Келдыша РАН, №89 за 2004г.
4.
А.А.Крюков,
М.В.Скачков, А.А.Егорушкин.
Численное моделирование возбуждения электромагнитных полей в цилиндрической
полости потоком релятивистских электронов. Препринт Института прикладной
математики им. М.В.Келдыша РАН, №41 за 2005г.
5.
G.A.Carlson. A differential absorption spectrometer for determining flash X-ray
spectra from 10 to 2000 keV. IEEE Trans.
Nucl. Sci., V. 36, pp. 1255 - 1259, 1988.
6. N.V.
Filippov, T.I. Filippova, V.I. Kraus, V.F.Zinchenko. Filippov type plasma focus as intense source of hard
X-rays. IEEE Trans. Plasma Sci., V. 24, pp. 1215 - 1233, 1996.
7.
Загонов
В.П.
Некоторые вариационные методы построения приближений негладких решений
некорректно поставленных задач. // ЖВМ и МФ. 1987, Т. 27, К 11, стр. 1614-1627.
8.
Кольчужкин
А.М., Учайкин В.В.
Введение в теорию прохождения частиц через вещество, М.: Атомиздат, 1978
9.
А.Ф.
Аккерман. Моделирование
траекторий заряженных частиц в веществе. М., 1991, 200 с.
10.
В.П.Загонов, М.Е.Жуковский, С.В.Подоляко, М.В.Скачков, Г.‑Р.Тиллак,
К.Беллон. Применение поверхностно ориентированного описания объектов для
моделирования трансформации рентгеновского излучения в задачах вычислительной
диагностики. М., Математическое моделирование. 2004, т.16, №5, с.103-116.
11.
Тихонов
А.Н., Арсенин В.Я. Методы решения
некорректно поставленных задач. М.: Наука. 1986.
12.
Васин
В.В., Агеев А.Л.
Некорректные задачи с априорной информацией, Уральская издательская фирма
«Наука», Екатеринбург, 1993.
13.
Загонов
В.П., Подоляко С.В. Некоторые алгоритмы
приближенного решения интегральных уравнений первого рода при наличии априорных
ограничений, Математическое моделирование, 1992г., т.4, N 4, с. 89-100.
[1] Так, по данным на 2006 год средняя
стоимость рентгенографических комплексов на пару рабочих мест колебалась от 2
до 7 миллионов российских рублей.
[2] Наиболее известные из них это ‑ MCNP, GEANT.
[3] Можно отметить, что даже в тех
случаях, когда спектр источника известен, энергетическое распределение фотонов
излучения, падающего на объект контроля, может заметно отличаться от спектра
излучения источника при использовании различного оборудования (контейнеров,
коллиматоров, усиливающих экранов и т.д.).
[4] Согласно [1], подобные устройства принято называть идеальным
детектором, который обладает квантовым выходом Q равным
единице.