Статистические модели электронной эмиссии. Модель «Утолщенных траекторий»

( Statistical Models of Electron Emission. "Thickened Paths" Model
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Введение

Математическое моделирование процессов взаимодействия ионизирующего излучения с объектами сложной геометрии и внутренней структуры имеет важное значение во многих приложениях. В частности, в рамках задач рентгеновской диагностики материалов и конструкций требуется определить и исследовать рентгеновские изображения объектов [1], а при изучении электромагнитного воздействия проникающего излучения необходимо проанализировать распределение потоков релятивистских электронов, возникающих в результате взаимодействия ионизирующего излучения с материалами объектов [2].

Математическое моделирование процессов трансформации проникающего излучения в материалах объектов проводилось в большом количестве работ. В одних работах используются и развиваются сеточные методы решения уравнения переноса излучения [3-5]. В других разрабатываются вычислительные алгоритмы, основанные на статистическом моделировании методом Монте-Карло процессов переноса и взаимодействия излучения с веществом [6,7]. Преимущество метода Монте-Карло перед альтернативными методами, основанными на численном решении кинетического уравнения, определяется удобством и приспособленностью этого метода к решению сложных граничных задач в многокомпонентных средах. Кроме того, метод Монте-Карло оказывается удобным при построении интегральных операторов связи между характеристиками исходного проникающего излучения и измеряемых в эксперименте величин, что дает возможность эффективного проведения массовых расчетов и решения обратных задач реконструкции характеристик исходного излучения по результатам экспериментальных измерений [8].

Эффективность применения метода Монте-Карло определяется в настоящее время, во-первых, развитием в самом методе способов уменьшения дисперсии расчетов; во-вторых, прогрессом в области создания быстродействующих многопроцессорных вычислительных систем.

С участием авторов настоящей статьи была разработана вычислительная методика [9], предназначенная для моделирования трансформации рентгеновского излучения в многокомпонентных объектах сложной геометрии и внутренней структуры. Эта методика включает в себя:

-       Поверхностно ориентированное описание многокомпонентных объектов сложной формы, основанное на точном определении границ гомогенных составляющих внутренней структуры объекта и задании соответствующих разделяющих замкнутых оболочек. Такой способ описания строится с учетом принципа инвариантности максимально возможной части описания объектов относительно линейных преобразований координат;

-       Эффективный алгоритм «трассировки» объекта для определения оптической толщины вдоль направления движения фотона, основанный на определении точек пересечения луча «источник-детектор» с разделяющими гомогенные части объекта поверхностями;

-       Методика расчета трансформации рентгеновского излучения в объектах сложной формы с учетом спектрального состава ионизирующего излучения, а также эффектов фотопоглощения, комптоновского и рэлеевского рассеяния. Эта методика построена на основе явного выделения граничных поверхностей с использованием триангуляционных моделей в сочетании с методом Монте-Карло, допускающим эффективное распараллеливание на многопроцессорных вычислительных системах.

В работе [10] авторами разработано несколько приемов увеличения эффективности расчетов методом Монте-Карло для важных частных случаев постановок задач о трансформации рентгеновского излучения на основе принципа максимальной информационной ценности фотонных траекторий.

Статистическое моделирование переноса электронов и других заряженных частиц представляет значительно большую трудность, чем моделирование переноса фотонов. Взаимодействие нейтральных частиц с материалами объектов характеризуется небольшим числом независимых столкновений с атомами вещества и участками свободного и прямолинейного движения этих частиц между столкновениями. При столкновении происходит один из возможных элементарных процессов взаимодействия (поглощение, упругое или неупругое рассеяние). Сечения этих процессов в настоящее время хорошо изучены и по ним имеются апробированные базы данных. Для заряженных частиц такой базы данных по сечениям элементарных процессов взаимодействия в настоящее время, по-видимому, нет [6]. Перенос электронов и других заряженных частиц происходит при постоянном действии кулоновских сил, приводящих к большому числу элементарных взаимодействий. Например, фотон в алюминии теряет энергию 500 кэВ, испытывая при этом около десяти столкновений, а электрон теряет ту же энергию, испытывая около 10⁵ элементарных взаимодействий.

Для статистического моделирования переноса заряженных частиц широко используется теория многократного рассеяния. Основу этой теории составляют функция Гоудсмита–Саундерсона распределения углов упругого рассеяния частиц, прошедших некоторый путь  в веществе, линейная тормозная способность частицы и функция Ландау распределения энергетических потерь на пути  . Модели, использующие теорию многократного рассеяния, сталкиваются с необходимостью постоянно контролировать выбор параметра  , поскольку теория не применима как при малых  , так и при больших значениях пути, пройденного частицей в веществе.

Настоящая работа посвящена описанию методики статистического моделирования переноса электронов в веществе и ее реализации при решении задач об электронной эмиссии с поверхности объектов, облучаемых ионизирующим излучением. Методика включает в себя ряд моделей, построенных по иерархическому принципу. При этом, пространственные и энергетические распределения, необходимые для расчетов в следующей модели, рассчитываются с использованием предыдущей.

Центральным звеном методики является модель утолщенных траекторий (МУТ). Преимущество этой модели заключается в отказе от использования приближенных распределений теории многократного рассеяния при сохранении экономичности вычислений. Распределения для расчетов с использованием МУТ получают путем расчетов по модели индивидуальных соударений (МИС), которая, имея примерно одинаковую с МУТ точность, значительно проигрывает в быстродействии.

С помощью МУТ строятся распределения для расчетов по упрощенной инженерной модели электронной эмиссии с поверхности объекта под действием ионизирующего излучения. Эта модель теряет в точности по сравнению с МУТ, но выигрывает в быстроте расчетов.

§1. Физическая модель

Задача переноса электронов в веществе ставится при следующих достаточно общих предположениях:

1)    рассеивающие центры среды (атомы) расположены случайно;

2)    электрон взаимодействует одновременно только с одним рассеивающим центром;

3)    электроны не взаимодействуют между собой.

В этих предположениях можно говорить о достаточно чёткой пространственной локализации взаимодействия и прийти к понятию траектории частицы как некоторой ломаной, в точках излома которой происходит взаимодействие и изменение состояния частицы, т.е. направления её движения и энергии.

Дифференциальное сечение упругого рассеяния аппроксимировалось формулой Мота [6,7]:

,

где  – параметр экранирования, α – постоянная тонкой структуры, Z – заряд ядер атомов среды, N – концентрация атомов среды,  – классический радиус электрона, β – отношение скорости электрона к скорости света, θ – угол между направлениями движения электрона до и после столкновения.

Потери энергии электрона в процессе неупругих столкновений учитывались в приближении непрерывного замедления, т.е. предполагалось, что за пройденный путь  электрон теряет энергию

,

где  – линейная тормозная способность электрона, значения которой для разных материалов и энергий электрона имеются, например, в базе данных на сайте www.nist.gov. Использование этого приближения обусловлено отсутствием у авторов доступа к апробированной базе данных по сечениям элементарных неупругих взаимодействий электронов с атомами среды.

Кроме приближения непрерывного замедления в некоторых расчётах использовалась функция Ландау распределения ионизационных потерь энергии электрона на пути  , заимствованная из теории многократного рассеяния [6,7]. Согласно Ландау, распределение потерь энергии  имеет следующий вид:

,

где

.

Здесь m и v – масса и скорость электрона, δ – поправка на эффект плотности, I – средний потенциал ионизации атома, , e – заряд электрона,

,

.

§2. Математические модели переноса электронов в веществе

Как известно, метод Монте-Карло в задачах переноса частиц в веществе сводится к построению большого числа траекторий частиц, представляющих некоторые ломаные линии, прямолинейные участки которых соответствуют свободным пробегам до столкновений. Свободный пробег, результат столкновения (поглощение или рассеяние), а также характеристики электрона после столкновения (энергия и направление движения рассеянной частицы) разыгрываются из соответствующих вероятностных распределений. Результаты выборки из конечного числа траекторий обрабатываются статистическими методами. Результатом моделирования является распределение частиц, вылетевших из объекта, по энергии и направлению движения.

Для использования метода Монте-Карло не требуется, вообще говоря, формулировать математическую модель в виде уравнений. Но фактически всегда можно говорить о том, что с помощью этого метода решается один из вариантов кинетического уравнения. Кинетическое уравнение Больцмана в общем случае нестационарного переноса записывается в виде:

,   (1)

где  – дифференциальная плотность потока частиц в момент времени t, в точке с координатами  и движущихся в направлении  с энергией E,  – плотность источников,  и  – полное и дифференциальное сечения взаимодействия, индекс k указывает на конкретный элементарный процесс взаимодействия. Предполагается только бинарный характер соударения.

В стационарном случае и в приближении непрерывного замедления (частица теряет энергию малыми порциями, не рассеиваясь при этом) уравнение (1) переходит в уравнение Левиса – Спенсера [11,12]

,(2)

где  – линейная тормозная способность электрона,  и  – полное и дифференциальное сечения упругого рассеяния.

Далее в работе будут рассмотрены общие схемы метода Монте-Карло, которые будут формулироваться в виде статистических моделей переноса электронов в веществе. Эти статистические модели соответствуют математическим задачам для кинетического уравнения переноса (1) в стационарном случае или его упрощённого варианта (2).

§3. Модель индивидуальных соударений (МИС)

МИС [6] является наиболее простой и очевидной моделью переноса частиц в веществе. В ней осуществляется прямое моделирование траекторий частиц, начальные координаты, энергия и направление движения которых выбираются или разыгрываются в соответствии с распределением источников S. Считается, что в каждой узловой точке траектории (рис.1) происходит один из возможных элементарных процессов взаимодействия. Вероятность каждого из этих процессов пропорциональна его вкладу в полное сечение взаимодействия. Распределения угла рассеяния и потери энергии частицы описываются дифференциальными сечениями соответствующих элементарных процессов.

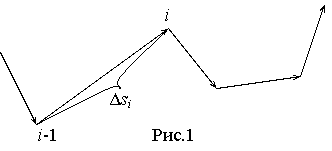Алгоритм построения i-го звена траектории частицы в МИС имеет следующий вид:

1)    розыгрыш пробега частицы в соответствии с законом ослабления

,

где  – полное сечение взаимодействия электрона с веществом (см. формулу (1)) или полное сечение упругого рассеяния (см. формулу (2))  – средний свободный пробег частицы в материале объекта,  – случайное число, равномерно распределённое на отрезке [0,1];

2)    вычисление координат точки взаимодействия:

,

где  – единичный вектор, указывающий направление движения частицы;

3)    проверка вылета частицы из объекта, вычисление вклада частицы в плотность потока, угловые и энергетические распределения частиц на границе объекта (регистрация частицы);

4)    розыгрыш вида взаимодействия, вероятность каждого из которых есть

,

где  – сечение взаимодействия k-го типа;

5)    розыгрыш потери энергии частицы или вычисление потери энергии по схеме непрерывного замедления:

;

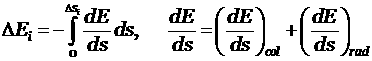6)    розыгрыш полярного угла рассеяния частицы в точке взаимодействия из распределения

,

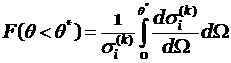где  – дифференциальное сечение рассеяния при k-м взаимодействии;

7)    розыгрыш азимутального угла рассеяния ;

8)    определение нового направления движения рассеянной частицы  в заданной системе координат.

Модель индивидуальных соударений (МИС) широко используется при моделировании нейтронных и фотонных траекторий. Применение МИС для заряженных частиц связано с большими затратами машинного времени, поскольку взаимодействие заряженных частиц обычно сопровождается малыми углами рассеяния и небольшими передачами энергии, а также очень большим числом соударений.

§4. Модель укрупнённых соударений (МУС)

Для описания движения электронов в веществе широко используется модель укрупненных соударений (МУС) [6]. При построении МУС предполагается, что на каждом из звеньев укрупненной траектории частицы происходит большое число индивидуальных соударений. Распределения углов рассеяния и потерь энергии в конце каждого из звеньев траектории берутся из теории многократного рассеяния. Распределения этой теории являются приближенными и имеют ограниченную область применимости. Длина звена траектории не разыгрывается, а выбирается определенным образом в соответствии с областью применимости теории многократных соударений. Чтобы избежать систематических погрешностей, вычислительные схемы МУС приходится тщательно сопоставлять с результатами расчетов по более детальной МИС.

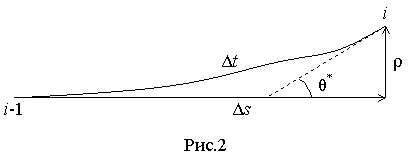
Алгоритм построения i-го звена траектории электрона (рис.2) в МУС имеет следующий вид:

1)    выбор криволинейного шага траектории ;

2)    розыгрыш угла многократного рассеяния  из распределения Гоудсмита – Саундерсона:

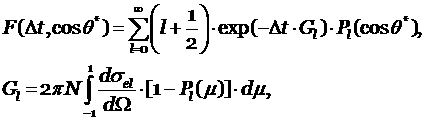
где  – дифференциальное сечение упругого рассеяния,  – полином Лежандра,  – плотность атомов среды;

3)    вычисление или розыгрыш прямолинейного шага траектории  и радиального смещения  каким-либо приближённым способом;

4)    розыгрыш азимутального угла рассеяния ;

5)    определение новых координат электрона ;

6)    регистрация электрона, если он вылетел из объекта;

7)    розыгрыш потери энергии из интегральных распределений Ландау, Блунка – Лейзеганга или вычисление энергии электрона  по схеме непрерывного замедления;

8)    определение нового направления движения электрона  в заданной системе координат.

МУС значительно экономичнее МИС по вычислительным затратам. Недостатком МУС является наличие в расчётах систематической погрешности, обусловленной приближениями теории многократного рассеяния и использованием приближённых формул для вычисления прямолинейного шага траектории  и радиального смещения  (см. рис.2).

§5. Модель утолщённых траекторий (МУТ)

В настоящей работе для описания движения электронов в веществе предлагается модель утолщенных траекторий (МУТ) [13]. Идея МУТ аналогична МУС, но в отличие от МУС в МУТ не используются приближенные распределения теории многократных соударений. Вычислительная схема МУТ аналогична МИС. В ней также сначала производится розыгрыш длины прямолинейного участка траектории, а затем энергии и направления движения рассеянной частицы. Все распределения, необходимые для розыгрышей, получают заранее численно по МИС в задаче о рассеянии электронов, движущихся вдоль трубки (рис.3), толщина которой является ключевым параметром модели. В этой задаче вклад электрона в распределения на границе трубки вычисляется при выполнении одного из трёх условий: 1) , где n – заданное целое число,  – средний свободный пробег электрона; 2)  (электрон начал движение в обратном направлении); 3) .

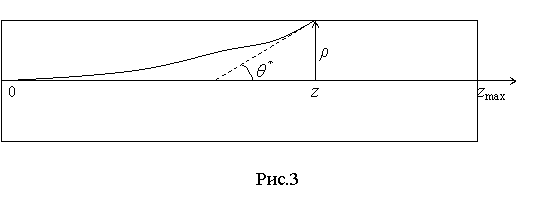
Таким образом, получают 1) функцию распределения электронов по координате и начальной энергии , 2) функцию распределения электронов по координате, косинусу угла рассеяния и начальной энергии , 3) функцию распределения электронов по координате, конечной энергии и начальной энергии  или среднюю конечную энергию электронов  (для схемы непрерывного замедления). Эти распределения используются для розыгрышей всех необходимых величин в алгоритме построения i-го звена «утолщённой» траектории электрона (рис.4), который имеет следующий вид:

1)    розыгрыш пробега электрона  ;

2)    вычисление координат i-го узла траектории

;

3)    розыгрыш энергии электрона в i-м узле траектории  (для схемы непрерывного замедления энергия электрона находится по таблице );

4)    розыгрыш азимутального угла рассеяния ;

5)    смещение i-го узла траектории в поперечном направлении на полуширину траектории , проверка вылета электрона из объекта;

6)    розыгрыш косинуса полярного угла рассеяния ;

7)    определение направления движения рассеянного электрона  в заданной системе координат;

8)    определение расстояния  от i-го узла траектории до границ объекта в направлении движения электрона . Если , то:

а) находится энергия электрона, вылетевшего из объекта, также как в п.3; б) электрон регистрируется с весом , равным вероятности прохождения электроном расстояния .

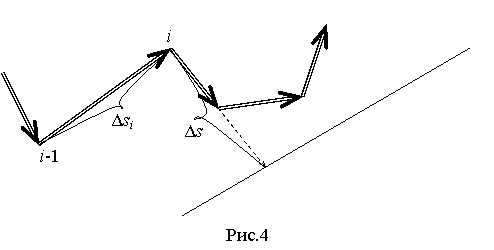
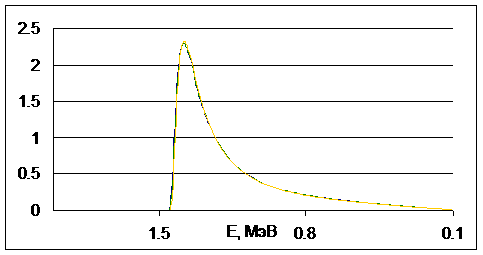
Рис.5

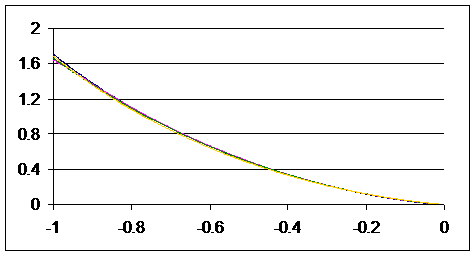
Рис.6

МУТ реализована на многопроцессорной вычислительной системе с распределенной памятью МВС-15000. В качестве примера рассмотрена модельная задача о прохождении плоскопараллельного потока электронов с начальной энергией 2 МэВ через железную (Fe) пластину толщиной 0.5 мм. Результаты расчетов по МУТ сравнивались с результатами расчетов, полученных с использованием МИС. На рис.5 представлен график плотности распределения электронов, прошедших пластину, по энергии, а на рис.6 – плотности распределения электронов по косинусу полярного угла вылета из пластины. Кривые на графиках соответствуют МИС, МУТ с полутолщиной траектории , МУТ с полутолщиной траектории , МУТ с полутолщиной траектории . Здесь полутолщина траектории измеряется в средних свободных пробегах электрона в материале мишени. Отношение прошедшего пластину потока электронов к падающему потоку равно 0,6.

На рис.5,6 видно, что кривые практически не различимы. Существенное различие наблюдается во времени расчётов. Время расчётов на 200 процессорах МВС-15000 приведено во втором столбце следующей таблицы.

Согласно таблице, наблюдается почти линейная зависимость времени расчёта от среднего числа звеньев траектории электрона в МУТ, указанного в первом столбце таблицы. Время расчётов по МИС во много раз превышает время расчётов по МУТ. В третьем столбце указано время, затраченное на получение распределений для МУТ в результате предварительного расчета по МИС на 200 процессорах. Это время растёт с ростом толщины «утолщённой» траектории и связано с ростом среднего числа индивидуальных столкновений электронов на одном звене траектории в МУТ. График зависимости среднего числа столкновений на одном звене траектории в МУТ от энергии электрона для рассматриваемых толщин траекторий приведён на рис.7. Кривая, отмеченная крестиком, соответствует МУТ с полутолщиной траектории , кривая с треугольником – МУТ с , кривая с кружочком – МУТ с .

Обращает на себя внимание тот факт, что время, затраченное на получение распределений для МУТ, сравнимо или превышает время расчётов по МИС (150 мин) и составляет значительную величину даже на современном суперкомпьютере. Вместе с тем очевидно и преимущество МУТ перед МИС, которое заключается в том, что трудоёмкий расчет распределений для МУТ проводится только один раз для конкретного материала (например, железа). В дальнейшем эти распределения в виде двумерных и трёхмерных таблиц могут многократно использоваться при решении различных задач переноса частиц в веществе.

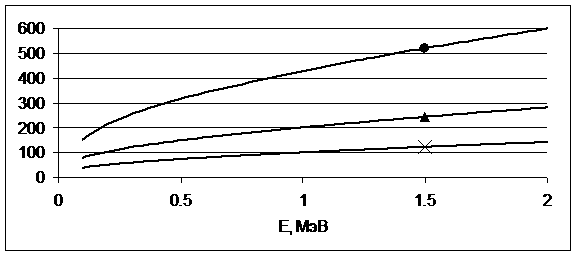
Рис.7.

§6. Упрощённая инженерная модель электронной эмиссии из плоского приграничного слоя объекта под действием ионизирующего излучения

Под действием ионизирующего рентгеновского или γ-излучения на поверхности объектов формируются потоки релятивистских электронов. Как правило, пробеги электронов в материале объекта много меньше его размеров. Поэтому можно считать, что из объекта вылетают электроны, образовавшиеся в его тонком приграничном слое. В связи с этим можно упростить статистическую модель переноса электронов в приграничном материале объекта, если заранее получить функцию распределения вылетающих электронов по глубине рождения h, начальной энергии E₀, начальному направлению движения θ₀, конечной энергии E и конечному направлению движения θ (рис. 8). Такую модель будем называть в дальнейшем «инженерной».

Функция распределения  оказывается в этом случае пятимерной и требует огромного количества памяти для хранения таблицы её значений. Дальнейшим упрощением указанной инженерной модели является переход к распределениям вероятности вылета  и средней энергии  электрона, вылетающего из объекта. При этом, пятимерная функция распределения заменяется на две трёхмерные таблицы. Такое упрощение не дает возможности получить угловые распределения электронов эмиссии, а также не учитывает разброс энергий этих электронов, который тем больше, чем меньше вероятность вылета электрона.

Указанные таблицы построены для железа в результате серии расчётов по МУТ.

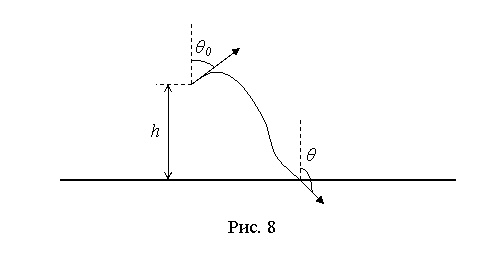
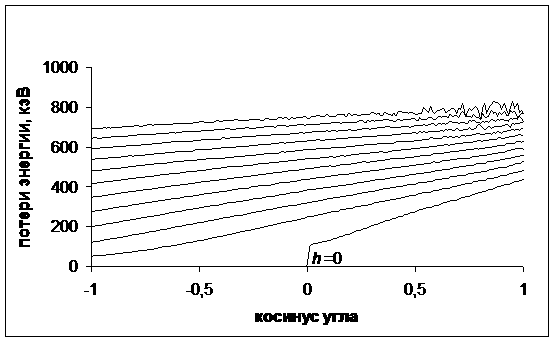
Рис. 9

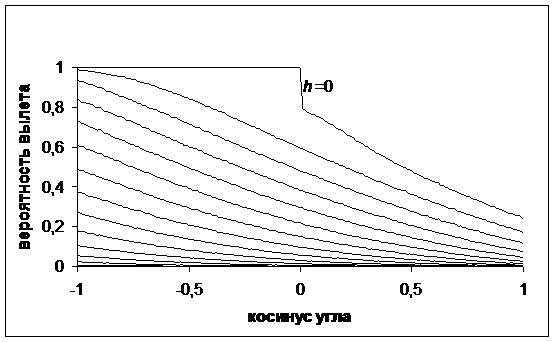
Рис. 10

На рис. 9 – 10 приведены графики фрагмента таблиц, относящегося к электрону с энергией 1 МэВ, образовавшегося на разных глубинах h от поверхности объекта. По оси абсцисс отложен косинус угла между направлением движения электрона и внутренней нормалью к поверхности объекта. По осям ординат отложены вероятность вылета из объекта и средние потери энергии. Линия с разрывом соответствует нулевой глубине h=0. Соседние кривые отвечают ближайшим значениям параметра h, отличающимся друг от друга на 0,05 от максимального расстояния, которое может пройти электрон в железе, теряя энергию в приближении непрерывного замедления.

Значительного улучшения описанной простейшей инженерной модели удается добиться введением искусственного среднеквадратичного отклонения (дисперсии):

, где  - вероятность вылета из объекта (весовой коэффициент электрона). Потери энергии электрона разыгрываются при этом по формуле

,

где 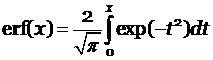 - функция ошибок,  - обратная функция ошибок. Предложенная аппроксимация энергетического распределения электронов не следует из каких-либо априорных данных. Её применимость и работоспособность проверяются эмпирически с помощью вычислительных экспериментов.

§7. Электронная эмиссия на границе объекта под действием ионизирующего излучения

С использованием рассмотренных моделей переноса электронов в веществе был построен алгоритм статистического моделирования эмиссии электронов с граничных поверхностей объектов, облучаемых ионизирующим излучением. В основу разработанного алгоритма положен принцип максимальной информационной ценности фотонных траекторий с точки зрения минимизации дисперсии получаемых статистических оценок характеристик электронных потоков. Некоторые особенности построенного алгоритма рассмотрены ниже.

Перенос фотонов излучения в веществе хорошо описывается моделью индивидуальных соударений (МИС), которая для многокомпонентных объектов сложной геометрии и внутренней структуры реализована, например, в работе [9]. Рождением электронов сопровождается два типа рассматриваемых взаимодействий фотонов излучения с веществом: фотоэлектрическое поглощение и комптоновское рассеяние фотона.

При комптоновском рассеянии фотона рождается электрон со следующими параметрами:

 – кинетическая энергия электрона: , где  и  – энергии фотона до и после рассеяния соответственно;

 – полярный угол движения электрона в системе координат, связанной с первоначальным движением фотона:

,

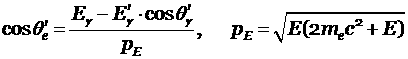где  – косинус угла рассеяния фотона;

 – азимутальный угол движения электрона: , где  – азимутальный угол рассеяния фотона;

При фотоэлектрическом поглощении фотона рождается электрон со следующими параметрами:

– кинетическая энергия электрона: , где  – энергии фотона до  поглощения,  – энергия связи К-оболочки в атоме вещества;

 – полярный угол движения электрона в системе координат, связанной с первоначальным движением фотона, разыгрывается с использованием углового распределения:

,

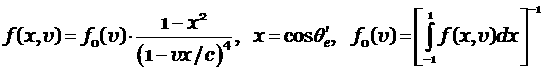где v – скорость электрона с энергией E, с – скорость света;

 – азимутальный угол движения электрона разыгрывается по формуле:

.

Таким образом, в узловой точке траектории фотона может родиться комптоновский или фото-электрон. Пробег электрона много меньше размеров объекта, поэтому лишь незначительная часть электронов, рождённых в тонком приграничном слое объекта, даст сколько-нибудь заметный вклад в формирование электронного потока на его границе. Следовательно, необходимо модифицировать алгоритм Монте-Карло, изменив статистику рождения электронов.

Естественным шагом в этом направлении является выделение «полезного» участка у границы объекта на продолжении каждого звена траектории фотона. На рис. 11 таким полезным участком является отрезок  . Расстояние от любой точки отрезка  до границы объекта не превышает максимального расстояния d (определяемого тормозной способностью электрона), которое может пройти электрон с известной начальной энергией в приграничном материале объекта. Точку рождения электрона можно разыгрывать на этом отрезке. Для этого используется условная плотность распределения точек взаимодействия фотона на отрезке:

, 

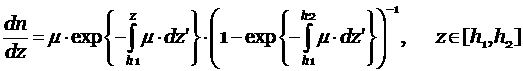полученная в соответствии с законом ослабления. Здесь μ – коэффициент ослабления излучения в веществе, пропорциональный полному сечению взаимодействия фотона. Можно считать, что в точке взаимодействия фотона рождается два электрона, начальные веса которых имеют вид:

,                   

.                       

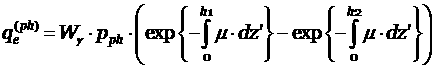Здесь разность экспоненциальных функций можно трактовать как вероятность взаимодействия фотона на отрезке ,  – вероятность фотоэлектрического поглощения,  – вероятность комптоновского рассеяния фотона,  – вес фотона до взаимодействия.

Для анализа эффективности рассмотренных статистических моделей переноса электронов проведены расчёты электронных потоков, образующихся при облучении квадратной железной (Fe) пластины .

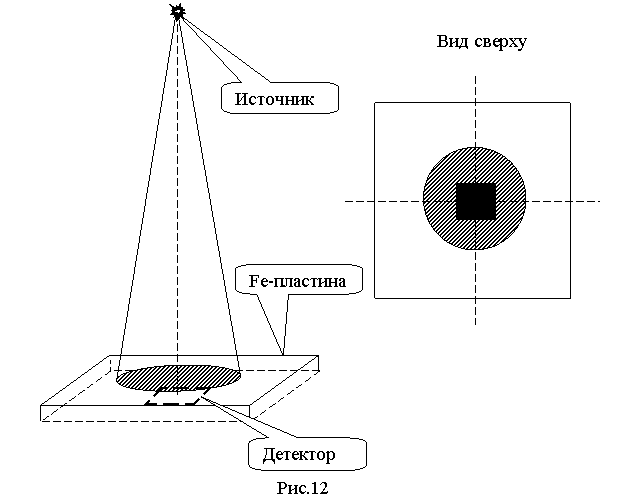
Схема вычислительного эксперимента представлена на рис.12.

В расчетах использовался точечный источник фотонов с энергией 500 кэВ и 100 кэВ. Расстояние от верхней границы пластины до источника 100 см; диаметр пятна засветки на верхней грани пластины – 5 см; детектор имеет размеры 2х2 см и расположен вплотную к нижней грани пластины. Детектор измеряет энергию электронов.

Результатом расчетов является нормированное энергетическое распределение электронов (фото- и комптоновских), т.е. функция  , причем .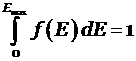

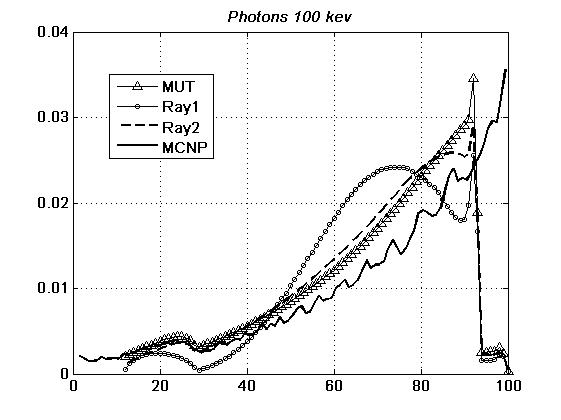
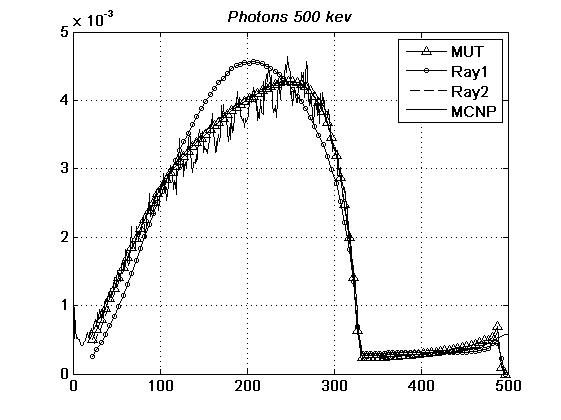
На рис. 13, 14 изображены графики спектральных зависимостей электронов, полученные при использовании трех моделей: МУТ (на рисунках – MUT), инженерной модели без дисперсии (Ray1), инженерной модели с дисперсией (Ray2) и результаты расчетов по MCNP [7], использующей МУС.

Сравнительный анализ результатов показывает, что инженерная модель без дисперсии дает неудовлетворительный результат, в то время как использование этой же модели с дисперсией позволяет получать спектры, близкие к результатам расчетов по МУТ и MCNP.

Отметим, что первый максимум спектра (около 25 кэВ при использовании фотонов с энергией 100 кэВ и около 250 кэВ для источника с энергией 500 кэВ) обусловлен главным образом комптоновскими электронами, а второй максимум (соответственно 90 и 490 кэВ) – фотоэлектронами.

Приведем в заключение оценки эффективности предложенных моделей. Расчеты по МУТ требуют примерно в 30-40 раз меньше времени, чем по MCNP, а по инженерной модели – примерно в 20 раз меньше, чем по МУТ при использовании одного и того же количества фотонных историй.

Заключение. Построены статистические модели переноса электронов, которые позволяют проводить эффективное моделирование процессов транспорта электронов в веществе на современных многопроцессорных вычислительных системах.

Литература

1.     Неразрушающий контроль. Россия. 1900-2000 гг.: Справочник. Под ред. В.В.Клюева. – 2-ое изд., исправ. и доп. М.: Машиностроение, 2002.

2.     С.Н. Ганага, Л.Н. Здуход, С.В. Пантелеев, Ю.В. Парфенов, О.Ф. Тарасов, А.В. Шапранов, Электродинамическое действие ионизирующих излучений // Физика ядерного взрыва под ред. В.М. Лоборева, т.2, с. 107.

3.     Р.М. Шагалиев и др. Математическое моделирование и методики решения многомерных задач переноса частиц и энергии, реализованные в комплексе САТУРН-3. // Вопросы атомной науки и техники, серия: Матем. моделирование физических процессов. 1999, вып. 4, с. 20-26.

4.     Л.П. Басс, О.В. Николаева, В.С. Кузнецов, А.В. Быков, А.В. Приезжев, А.А. Дергачев. Моделирование распространения оптического излучения в фантоме биологической ткани на суперЭВМ МВС1000/М. // Матем. моделирование. 2006, т.18, №1, с. 29-42.

5.     Т.А. Сушкевич. Математическое моделирование переноса излучения. М., 2005, 661 с.

6.     А.Ф. Аккерман. Моделирование траекторий заряженных частиц в веществе. М., 1991, 200 с.

7.     J.F.Briesmeister (ed.). MCNP - A General Monte Carlo N-Particle Transport Code. LANL Report LA-13709-M, Los Alamos, 2000.

8.     М.Е. Жуковский, С.В. Подоляко, М.В. Скачков, Г.-Р. Йениш.                      О моделировании экспериментов с проникающим излучением // Матем. моделирование. 2007, т.19, №1, с. 29-42.

9.     В.П.Загонов, М.Е.Жуковский, С.В.Подоляко, М.В.Скачков, Г.-Р.Тиллак, К.Беллон. Применение поверхностно ориентированного описания объектов для моделирования трансформации рентгеновского излучения в задачах вычислительной диагностики. // Матем. моделирование. 2004, т.16, №5, с.103-116.

10.            М.Е. Жуковский, М.В. Скачков, А.А. Егорушкин. Модификации метода Монте-Карло в задачах о трансформации ионизирующего излучения. Препринт ИПМ им. М.В. Келдыша РАН, 2005, № 85.

11.            Levis H.W. // Phys. Rev. 1950, Vol. 78, № 3, p. 526-533.

12.            Spencer L.V. // Ibid. 1955, Vol. 98, № 6, p. 1597-1611.

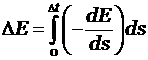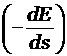
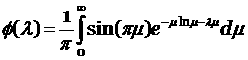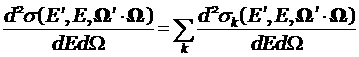
13.            М.В. Скачков. Модель «утолщенных траекторий» для описания движения электронов в веществе и ее реализация на МВС-5000М. Международный семинар «Супервычисления  и математическое моделирование». Саров, 2006, с. 91-92.