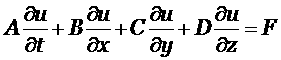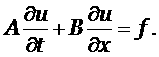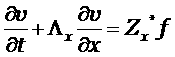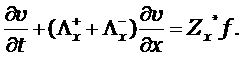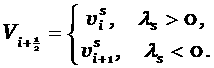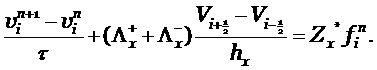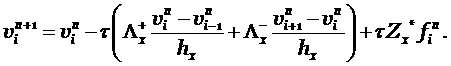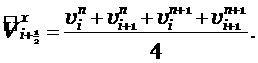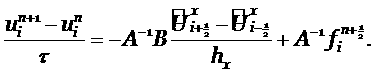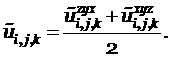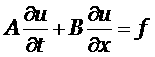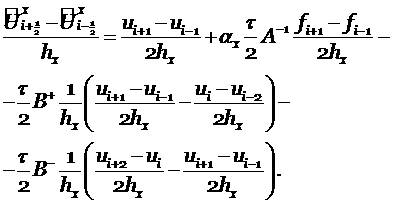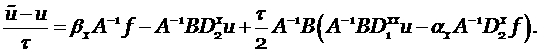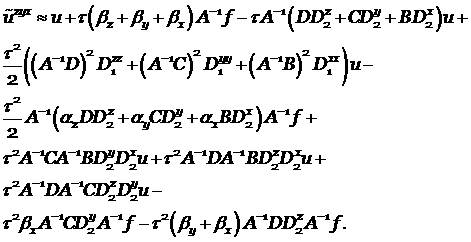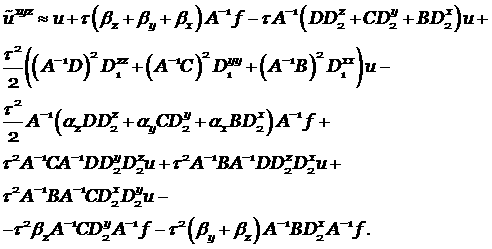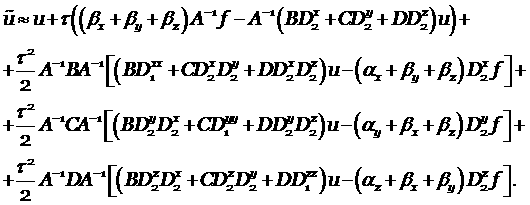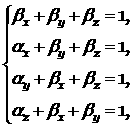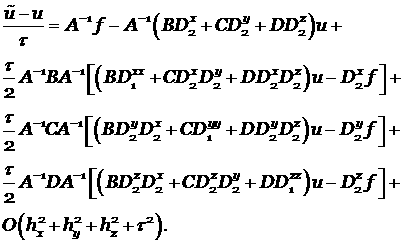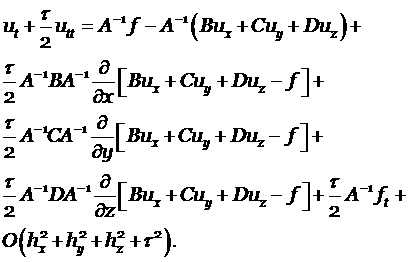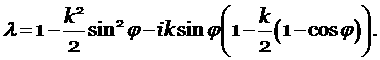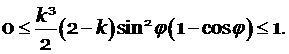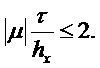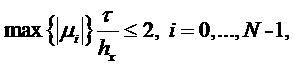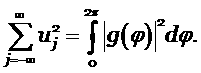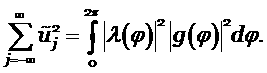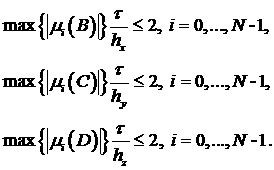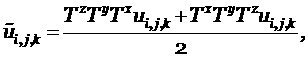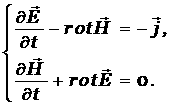Численный метод решения систем гиперболических уравнений в частных производных
|
|
|
(1.1) |
в области ![]() с заданными начальными
и граничными условиями, где
с заданными начальными
и граничными условиями, где ![]() - вектор неизвестных,
а
- вектор неизвестных,
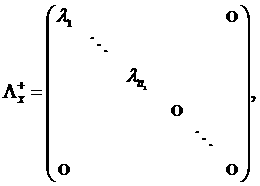
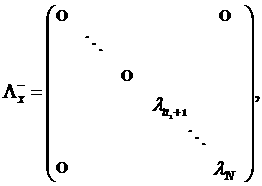
а ![]() - квадратные матрицы
- квадратные матрицы ![]() , отвечающие следующим условиям
, отвечающие следующим условиям
|
|
(1.2) |
Для простоты изложения будем считать, что заданы периодические краевые условия.
Для решения многомерной задачи решается отдельно задача по каждому из направлений, т.е. используется расщепление. Для решения одномерной системы уравнений её необходимо привести к каноническому виду [2]. Покажем алгоритм приведения на примере системы (1.3)
|
|
(1.3) |
Известно, что для матриц, отвечающим условиям (1.2),
существует невырожденная матрица ![]() такая, что
такая, что ![]() (единичная матрица) и
(единичная матрица) и ![]() (диагональная матрица)
[3]. Для нахождения матрицы
(диагональная матрица)
[3]. Для нахождения матрицы ![]() надо решить систему
линейных уравнений
надо решить систему
линейных уравнений
|
|
(1.4) |
где ![]() корни
характеристического уравнения
корни
характеристического уравнения
|
|
(1.5) |
Найдём эти корни и запишем их в следующем порядке ![]() . Обозначим через
. Обозначим через ![]() решение (1.4),
соответствующее
решение (1.4),
соответствующее ![]() , и построим матрицу
, и построим матрицу ![]() , состоящую из векторов
, состоящую из векторов ![]() в качестве столбцов
в качестве столбцов
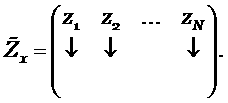
Из курса линейной алгебры известно, что такая матрица отвечает следующему условию
![]()
где
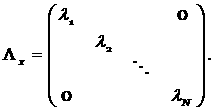
Перенормировкой векторов ![]() добьёмся выполнения
соотношения
добьёмся выполнения
соотношения
![]()
где ![]() единичная матрица, а
единичная матрица, а ![]() матрица после
нормировки векторов. Для такой матрицы выполняется следующее соотношение
матрица после
нормировки векторов. Для такой матрицы выполняется следующее соотношение
![]()
Подставим в систему (1.3)замену
|
|
(1.6) |
После такой замены получаем канонический вид системы (1.3)
|
|
(1.7) |
в переменных ![]() , которые являются Римановыми инвариантами для данной системы
, которые являются Римановыми инвариантами для данной системы
§2. Численная методика для одномерной системы уравнений
Введём пространственное разбиение с шагом ![]() и разбиение по времени
с шагом
и разбиение по времени
с шагом ![]() . Определим значения сеточной функции в центрах ячеек и целых
шагах по времени по следующему правилу:
. Определим значения сеточной функции в центрах ячеек и целых
шагах по времени по следующему правилу:
![]()
![]()
Ведём вспомогательные матрицы
|
|
(2.1) |
где![]() и перепишем систему (1.7) в удобном для дальнейших выкладок
виде
и перепишем систему (1.7) в удобном для дальнейших выкладок
виде
|
|
(2.2) |
Элементы вектора ![]() являются Римановыми
инвариантами и сохраняют своё значение на характеристиках
являются Римановыми
инвариантами и сохраняют своё значение на характеристиках ![]() , где
, где ![]() номер переменной в
векторе
номер переменной в
векторе ![]() . Используя это, получим значения переменных на полуцелом шаге
по времени (большие величины)
. Используя это, получим значения переменных на полуцелом шаге
по времени (большие величины)
|
|
(2.3) |
На границе области ![]() и
и ![]() большие величины определяются из граничных условий. С помощью
больших величин запишем разностную схему для системы уравнений (2.2)
большие величины определяются из граничных условий. С помощью
больших величин запишем разностную схему для системы уравнений (2.2)
|
|
(2.4) |
Полученная схема называется схемой Годунова [2], [4] и является схемой первого порядка аппроксимации. Мы ввели матрицы (2.1) по правилу, что все элементы матрицы имеют один знак. Используя это, подставим явно (2.3) в (2.4).
Получим разностную схему для системы уравнений в Римановых инвариантах
|
|
(2.5) |
Эта схема является предиктором численной методики. Полученный набор значений используется для уточнения решения на этапе корректора. На этапе корректора вычислим новые большие величины по формуле
|
|
(2.6) |
Подставив (2.6) в (2.5), получим большие величины, выраженные через Римановы инварианты с нижнего временного слоя
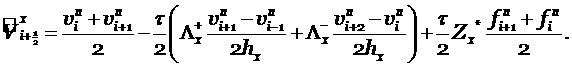
Выпишем разностную схему в исходных переменных ![]() , для этого сделаем преобразование
, для этого сделаем преобразование ![]() и введём
вспомогательные матрицы
и введём
вспомогательные матрицы
![]() .
.
Получим большие величины для исходных переменных
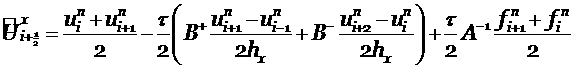
и используя их, запишем разностную схему аналогичную (2.4)
|
|
(2.7) |
§3. Численная методика для многомерной системы уравнений
В предыдущем параграфе был рассмотрен численный метод для
одномерного случая. Покажем, как построить решение для многомерного случая,
используя решения одномерных систем. Рассмотрим это на примере трёх измерений.
Введём пространственное разбиение с шагами ![]() и разбиение по времени
с шагом
и разбиение по времени
с шагом![]() . Определим значения сеточной функции в центрах ячеек и целых
шагах по времени, по правилу
. Определим значения сеточной функции в центрах ячеек и целых
шагах по времени, по правилу
![]()
Для каждого направления построим разностную схему, как было показано в предыдущем параграфе и запишем её в операторном виде
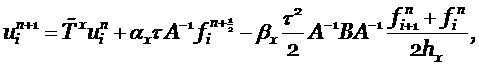
где ![]() разностный оператор
перехода на новый временной слой, а
разностный оператор
перехода на новый временной слой, а ![]() и
и ![]() весовые коэффициенты.
Добавление весовых коэффициентов в схему необходимо для правильной
аппроксимации функции, стоящей в правой части уравнения (1.1). В следующем
параграфе будет получено условие, которому должны отвечать эти веса для каждого
направления. Для удобства выкладок обозначим переход на новый временной слой
как действие одного разностного оператора
весовые коэффициенты.
Добавление весовых коэффициентов в схему необходимо для правильной
аппроксимации функции, стоящей в правой части уравнения (1.1). В следующем
параграфе будет получено условие, которому должны отвечать эти веса для каждого
направления. Для удобства выкладок обозначим переход на новый временной слой
как действие одного разностного оператора ![]() . Аналогично обозначим операторы перехода для других
направлений
. Аналогично обозначим операторы перехода для других
направлений ![]() . Последовательно действуя этими операторами, построим
вспомогательное решение
. Последовательно действуя этими операторами, построим
вспомогательное решение ![]() , где
, где
![]()
Аналогично построим ![]() . Решением будет полусумма вспомогательных решений [4]
. Решением будет полусумма вспомогательных решений [4]
|
|
(3.1) |
§4. Исследование порядка аппроксимации схемы
Для доказательства сходимости разностной схемы, используемой в методе, необходимо исследовать её устойчивость и аппроксимацию [5], [6].
Для исследования порядка аппроксимации, построим схему для системы
|
|
(4.1) |
в операторном виде. На этапе предиктора получаем разностную схему
|
|
(4.2) |
Функция ![]() в правой части (4.2)
берется на полуцелом шаге по времени. Веса, стоящие перед функцией
в правой части (4.2)
берется на полуцелом шаге по времени. Веса, стоящие перед функцией ![]() , будут найдены из условия, что корректор должен иметь второй
порядок аппроксимации.
, будут найдены из условия, что корректор должен иметь второй
порядок аппроксимации.
Выпишем разностную производную по пространству, стоящую в (2.7)
|
|
(4.3) |
Введём разностные операторы дифференцирования
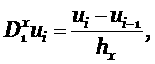
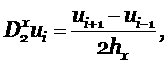
и перепишем (4.3) используя их, в виде
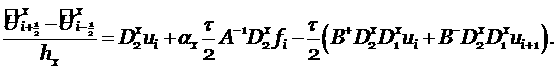
Рассмотрим отдельно выражение
|
|
(4.4) |
Если явно подставить в (4.4) разностные операторы и учесть, что
![]()
то получим произведение матрицы ![]() на разностную
производную второго порядка. Шаблон этой производной зависит от матриц
на разностную
производную второго порядка. Шаблон этой производной зависит от матриц ![]() и
и ![]() , но точность аппроксимации будет не ниже
, но точность аппроксимации будет не ниже ![]() . Выражение (4.4) можно заменить разностным оператором
. Выражение (4.4) можно заменить разностным оператором ![]() с точностью
с точностью ![]() , где оператор
, где оператор ![]() аппроксимирует
производную второго порядка с точностью
аппроксимирует
производную второго порядка с точностью ![]() . Опустим индекс
. Опустим индекс ![]() и запишем разностную
схему корректора в операторном виде
и запишем разностную
схему корректора в операторном виде
|
|
(4.5) |
Выпишем решение, как было показано в § 3:
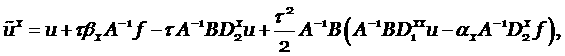

Члены выше второго порядка будем отбрасывать, т.к. нам надо показать второй порядок аппроксимации
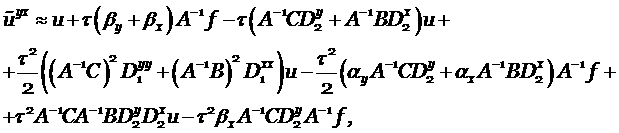
|
|
(4.6) |
Аналогично (4.6) получим выражение
|
|
(4.7) |
По формуле (3.1) запишем решение на верхнем временном слое
|
|
(4.8) |
Если в (4.8) веса будут удовлетворять следующему условию
|
|
(4.9) |
то схема будет иметь второй порядок аппроксимации.
Что бы показать это, предположим, что ![]() и
и ![]() достаточно гладкие
функции для разложения в ряд Тейлора в точке
достаточно гладкие
функции для разложения в ряд Тейлора в точке ![]() и
и ![]() являются решением
системы (1.1). Перепишем разностную схему(4.8) с учётом условия (4.9)
являются решением
системы (1.1). Перепишем разностную схему(4.8) с учётом условия (4.9)
|
(4.10) |
Подставив разложение в ряд Тейлора функций ![]() и
и ![]() в схему (4.10),
получим
в схему (4.10),
получим
|
|
(4.11) |
Сгруппируем выражения, стоящие в правой
части (4.11), с множителем ![]() . Учитывая, что
. Учитывая, что ![]() удовлетворяет системе
(1.1), получим
удовлетворяет системе
(1.1), получим
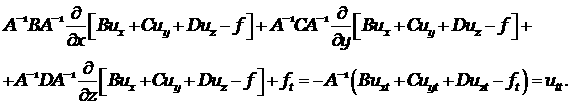
Перепишем (4.11) с учётом этого выражения
|
|
(4.12) |
Из (4.12) видно, что схема имеет второй порядок аппроксимации.
§5. Исследование устойчивости схемы
При построении решения многомерного уравнения мы используем одномерные разностные схемы, поэтому сначала найдём условие, при котором устойчива разностная схема для одномерного уравнения. Для поиска условий устойчивости решения многомерного уравнения, мы будем использовать энергетический подход [2], т.е. искать условия, при которых энергетическая норма решения не возрастает.
Найдём условие, при котором устойчива разностная схема (2.7) для одного однородного уравнения
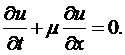
Для этого используем метод Фурье [5]. Подставим в разностную схему (2.5) решение в следующем виде
![]()
где ![]() - мнимая единица. Мы
также употребляем символ
- мнимая единица. Мы
также употребляем символ ![]() в качестве индекса
сеточной функции, но из контекста будет понятно, что он обозначает. Сократим
общий множитель
в качестве индекса
сеточной функции, но из контекста будет понятно, что он обозначает. Сократим
общий множитель ![]() и получим уравнение
для
и получим уравнение
для ![]()
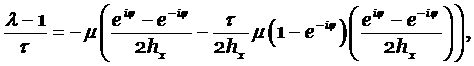
где 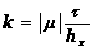 - число Куранта.
Разрешив его, получим, что
- число Куранта.
Разрешив его, получим, что
|
|
(5.1) |
На рис. 1 изображён график ![]() для различных чисел
Куранта
для различных чисел
Куранта ![]() .
.
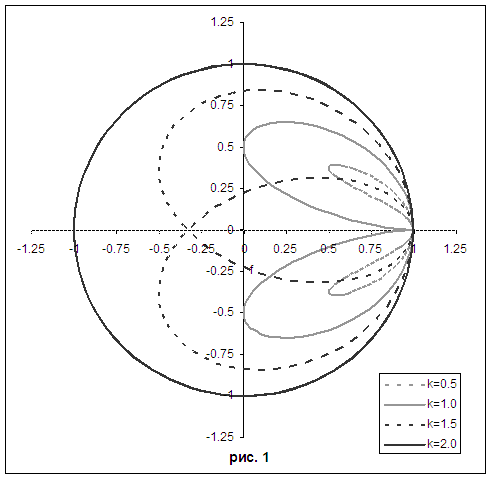
Для устойчивости схемы необходимо и достаточно выполнения условия
|
|
(5.2) |
Возведём (5.1) в квадрат
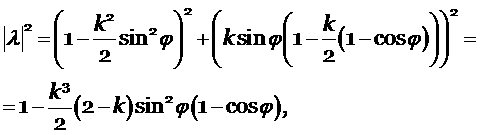
тогда условие (5.2) эквивалентно
|
|
(5.3) |
Очевидно, что выражение ![]() при
при ![]() . Максимум этого выражения достигается в точке
. Максимум этого выражения достигается в точке ![]() и равен
и равен ![]() . Выражение
. Выражение ![]() положительно при
положительно при ![]() . Максимум этого выражения достигается при
. Максимум этого выражения достигается при ![]() и равен
и равен ![]() . Получаем, что значения максимума для (5.3) равно
. Получаем, что значения максимума для (5.3) равно ![]() , а положительно оно при
, а положительно оно при ![]() . Из этого анализа получаем условие устойчивости
. Из этого анализа получаем условие устойчивости
|
|
(5.4) |
В случае нескольких переменных удобно рассматривать систему уравнений (1.3), записанную в Римановых инвариантах. Объединяя условие (5.4) для каждого из уравнений системы, получим
|
|
(5.5) |
где ![]() корни
характеристического уравнения
корни
характеристического уравнения ![]() . Мы получили необходимое и достаточное условие устойчивости
для одномерной схемы.
. Мы получили необходимое и достаточное условие устойчивости
для одномерной схемы.
Для доказательства устойчивости многомерной схемы нам надо ввести понятие энергетической нормы и устойчивости в энергетической форме. Энергетической норма для сеточной функции задаётся следующей формулой
|
|
(5.6) |
Суммирование производится по всей сетке. Для устойчивости схемы необходимо и достаточно выполнения условия
|
|
(5.7) |
где ![]() и
и ![]() - сеточная функция на
нижнем и верхнем временном слое соответственно.
- сеточная функция на
нижнем и верхнем временном слое соответственно.
Покажем, что условие (5.7) выполняется при условии (5.5) сначала для одномерного уравнения, а потом обобщим на случай системы. Запишем сеточную функцию через преобразования Фурье
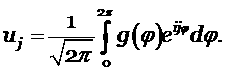
Для такой функции выполняется равенство Парсеваля
|
|
(5.8) |
Аналогично запишем сеточную функцию на следующем временном слое через преобразование Фурье и равенство Парсеваля для неё
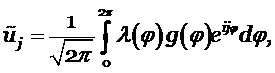
|
|
(5.9) |
С учётом условия (5.2) и равенства (5.8) и (5.9) , получим
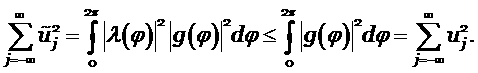
Мы доказали, что при условии (5.4) энергетическая норма не возрастает. Для системы (1.3) записанной в Римановых инвариантах, при выполнении условия (5.5), получаем неравенство
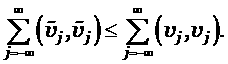
Делая обратное преобразование к (1.6), получим
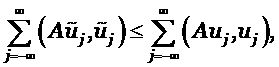
т.е. выполнение условия (5.7).
Для трёхмерного случая энергетическая норма имеет вид
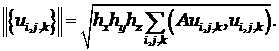
Докажем, что схема устойчива при выполнении следующих условий:
|
|
(5.10) |
Для этого запишем разностное решение в операторной форме
|
|
(5.11) |
где ![]() ,
,![]() ,
,![]() операторы перехода на следующий временной шаг по
соответствующему направлению. Для каждого из них при выполнении условий (5.11)
энергетическая норма не возрастает. Учитывая это и то, что норма – выпуклая
функция, последовательно получим соотношения для нормы решения
операторы перехода на следующий временной шаг по
соответствующему направлению. Для каждого из них при выполнении условий (5.11)
энергетическая норма не возрастает. Учитывая это и то, что норма – выпуклая
функция, последовательно получим соотношения для нормы решения
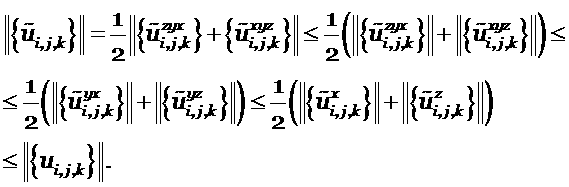
Этот приём подсказан С.К. Годуновым и использован в бакалаврской работе С.В. Селивановой при анализе устойчивости многомерных разностных схем.
Мы получили условия, при которых энергетическая норма не возрастает, т.е. схема устойчива. Из аппроксимации и устойчивости схемы следует её сходимость [5], [6].
§6. Тестовые расчеты
Рассмотрим задачу моделирования электромагнитных полей
внутри прямоугольной области. Граница области - идеальный проводник, т.е. ![]() , где
, где ![]() - электрическое поле,
а
- электрическое поле,
а ![]() - нормаль к границе.
Поля в начальный момент времени нулевые. Внутри находится газ, проводимость
которого равна нулю или постоянна. Аналитическое решение нестационарных
уравнений Максвелла, которые описывают поля, получено методом разделения
переменных [1], [7]. В качестве характеристики точности приводится ошибка
- нормаль к границе.
Поля в начальный момент времени нулевые. Внутри находится газ, проводимость
которого равна нулю или постоянна. Аналитическое решение нестационарных
уравнений Максвелла, которые описывают поля, получено методом разделения
переменных [1], [7]. В качестве характеристики точности приводится ошибка
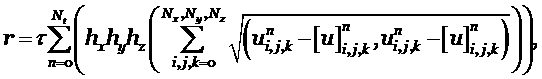
где ![]() - точное решение в
узлах сетки,
- точное решение в
узлах сетки, ![]() размерность сетки по
времени и пространству,
размерность сетки по
времени и пространству, ![]() шаги по времени и
пространству соотвестсвенно. Для каждого теста строится логарифмическая
зависимость ошибки от размерности сетки, коэффициент линейной зависимости
которой показывает порядок аппроксимации.
шаги по времени и
пространству соотвестсвенно. Для каждого теста строится логарифмическая
зависимость ошибки от размерности сетки, коэффициент линейной зависимости
которой показывает порядок аппроксимации.
Тестовая задача 1.
В проводящей полости с размерами
![]()
в начальный момент времени известными токами ![]() возбуждаются поля,
описываемые системой уравнений Максвелла
возбуждаются поля,
описываемые системой уравнений Максвелла
|
|
(6.1) |
При заданных токах
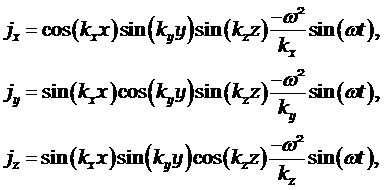
где
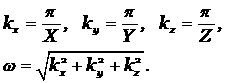
аналитическое решение этой системы имеет вид:
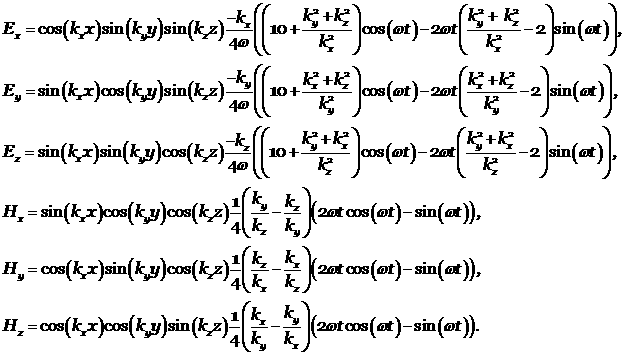
Проведены расчёты для области со следующей геометрией
![]()
На рис. 2 приведена логарифмическая зависимость ошибки ![]() от размерности сетки
от размерности сетки ![]() и коэффициент линейной зависимости.
и коэффициент линейной зависимости.
Тестовый расчет подтверждает второй порядок аппроксимации.
Тестовая задача 2.
Задача 1 дополняется уравнениями для векторного потенциала
![]() и скалярного
потенциала
и скалярного
потенциала ![]() , определяемых равенствами
, определяемых равенствами
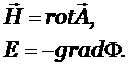
Расширенная система имеет вид:
|
|
(6.2) |
В разностной схеме электрическое поле,
стоящее справа в уравнении для потенциала ![]() рассматривается как
заданная функция и берётся с нижнего слоя по времени. Расчёты были сделаны для
двух геометрий полости:
рассматривается как
заданная функция и берётся с нижнего слоя по времени. Расчёты были сделаны для
двух геометрий полости:
1. ![]() , электрическое поле не возрастает по времени.
, электрическое поле не возрастает по времени.
2. ![]() , электрическое поле линейно возрастает по времени.
, электрическое поле линейно возрастает по времени.
Аналитическое решение задачи 1 дополняется аналитическими решениями для потенциалов

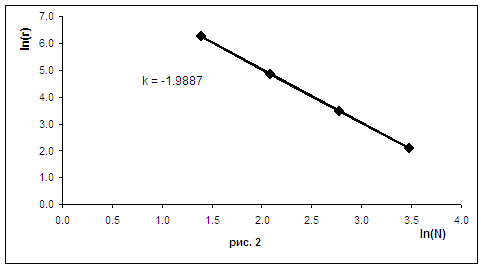
На рис. 3, рис. 4 приведена логарифмическая зависимость ошибки ![]() от размерности сетки
от размерности сетки ![]() и коэффициент линейной зависимости, для случая 1 и 2
соответственно.
и коэффициент линейной зависимости, для случая 1 и 2
соответственно.
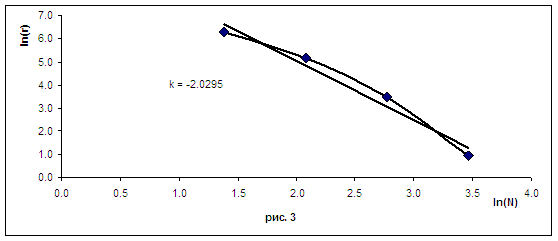
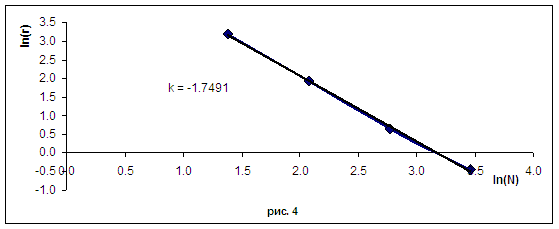
На рис. 4 видно, что схема теряет квадратичную сходимость и это объясняется тем, что мы берём электрическое поле не с полуцелого шага по времени, как это делается для токов, а с нижнего.
Тестовая задача 3.
Полость заполняется проводящим газом с постоянной проводимостью. Поля внутри полости описываются следующей системой
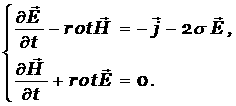
При заданных токах

где ![]()
аналитическое решение этой системы имеет вид:
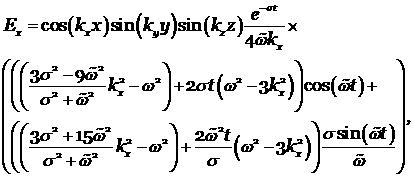
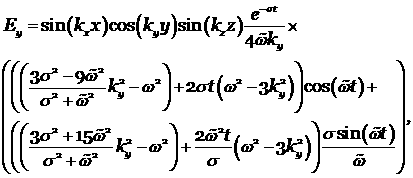
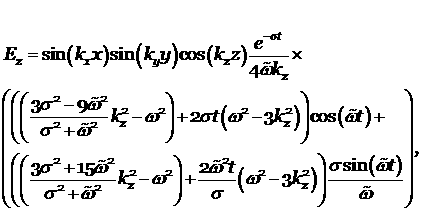
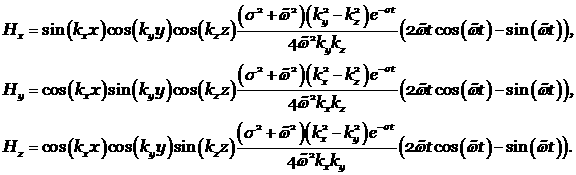
Были проведены расчёты для области со следующей геометрией
![]()
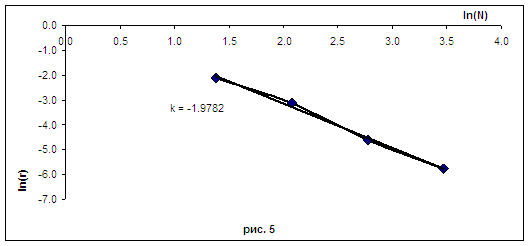
Проводимость в камере выбиралась такой, что бы за время расчета амплитуда экспоненты уменьшилась на порядок. На рис. 5 приведена логарифмическая зависимость ошибки от размерности сетки и показан коэффициент линейной зависимости.
Заключение
Построен численный метод решения системы гиперболических уравнений и доказана его сходимость, т.е. аппроксимация и устойчивость. Тестовые расчеты подтвердили второй порядок точности разностной схемы. Известно, что для разностных схем такого класса существенным становится требование дивергентности магнитного поля (нулевая дивергенция магнитного поля). По предложению С.К. Годунова вместо системы (6.1) планируется решать расширенную систему (6.2) с потенциалами и пересчитывать электрические и магнитные поля через них. Такая корректировка должна улучшить условие дивергентности для численного решения. С этой целью рассмотрена тестовая задача №2. Как было показано в расчётах, при таком дополнении может происходить потеря квадратичной сходимости, поэтому можно улучшить точность различными способами, например, сделать схему частично неявной, т.е. использовать электрическое поле с верхнего слоя по времени. Эту работу планируется провести в будущем как развитие предложенного алгоритма.
Автор выражает признательность С.К. Годунову за предложенные идеи и методы и В.Т. Жукову за постоянное внимание и помощь в работе.
Литература
1. А.Н.Тихонов, А.А.Самарский Уравнения математической физики.
М., Наука,
2. С.К.Годунов. Уравнения математической физики. Изд. 2-е.
М., Наука, Главная
редакция физ.-мат. литературы,
3. Ф.Р.Грантмахер. Теория матриц.
М., Наука, Главная
редакция физ.-мат. литературы,
4. А.Г.Куликовский, Н.В.Погорелов, А.Ю.Семенов. Математические вопросы численного решения гиперболических систем уравнений.
5. С.К.Годунов, В.С.Рябенький. Введение в теорию разностных схем.
М., Физматгиз,
6. А.А.Самарский. Теория разностных схем.
М., Наука, Главная
редакция физ.-мат. литературы,
М., Наука, Главная
редакция физ.-мат. литературы,