Аннотация
В работе представлена физико-математическая модель неравновесного микроволнового разряда в азотной среде, позволяющая
самосогласованно учитывать газодинамические, электродинамические и газоразрядные явления в потоках газа. Приведена общая
структура кинетической схемы, описывающая динамику неравновесных процессов в движущемся газе. В качестве иллюстрации
рассмотрена задача о разлете покоящегося молекулярного азота, подвергнутого воздействию мощного микроволнового излучения.
Abstract
In work the physical and mathematical model of the non-equilibrium microwave discharge in nitrogen medium permitting
is represented is self-consistent to take into account gasdynamics, electrodynamics and discharge phenomena in streams
of gas. The general scheme of the kinetic scheme circumscribing dynamics of non-equilibrium processes in driven gas
is indicated. A problem about a dispersion of molecular nitrogen subjected effect of a high-power microwave radiation
by way of illustration is considered.
Введение
Воздействие
микроволнового электрического разряда на высокоскоростные потоки молекулярных
газов имеет широкий прикладной интерес. В зависимости от прикладного характера
задачи большой интерес представляет возможность выбора разрядных режимов для
селективного возбуждения различных степеней свободы частиц газа. В быстро
проточных лазерных системах вложение
энергии поля в электронные и колебательные степени свободы газа является
задачей требующей точной оптимизации режимов накачки рабочей среды и
минимизации дестабилизирующих факторов, таких как, акустический и газодинамический
отклик среды (см. [1,2]). Вложение энергии микроволнового электрического поля в
нагрев движущегося газа представляет интерес для задач связанных с изменениями
характеристик и управлением потоками газов. В таких разрядах особенно эффективно
осуществляется нагрев молекулярных газов (например, воздушной смеси) в режимах
в которых основная доля энергии поля расходуется на возбуждение колебаний
молекул и в меньшей степени на прямой нагрев газа, его диссоциацию, ионизацию и
излучение (см., например, [3]). В этом
случае релаксация колебаний молекул в поступательные степени свободы частиц является
доминирующим фактором быстрого нагрева газа и изменения характеристик его
движения.
Ниже на примере
молекулярного азота, как основной компоненты воздушной смеси, рассматривается
воздействие микроволнового разряда на динамику разлета и газоразрядные
характеристики среды. Описание кинетических явлений в разряде производится в
рамках разветвленной кинетической схемы неравновесных плазмохимических процессов
[3].
Постановка задачи
Рассмотрим в плоской одномерной геометрии эволюцию состояния
молекулярного азота при воздействии на него плоской электромагнитной волны. В
начальный момент времени t=0 на покоящийся газ вдоль положительной
оси x падает электромагнитная волна c напряженностью поля 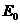 и длинной волны и длинной волны  . Газ занимает область
x>0 и отделен от полупространства x<0 радиопрозрачной перегородкой в точке x=0. В области
0< x <x1 находится слабый внешний источник
предионизации . Газ занимает область
x>0 и отделен от полупространства x<0 радиопрозрачной перегородкой в точке x=0. В области
0< x <x1 находится слабый внешний источник
предионизации  , который в отсутствие электрического поля формирует в
заданной области пространства начальное стационарное распределение свободных
электронов с концентрацией , который в отсутствие электрического поля формирует в
заданной области пространства начальное стационарное распределение свободных
электронов с концентрацией  , играющих роль «начальных затравочных» электронов. При t>0 в области предионизированного газа начинает
развиваться электрический разряд, в котором энергия электрического поля полностью
либо частично поглощается электронной компонентой плазмы. В столкновениях с
молекулами электроны передают свою энергию во внутренние степени свободы частиц
газа. При этом происходит возбуждение вращательных, колебательных и электронных
состояний молекул. Релаксация энергии, заключенной во внутренних степенях
свободы молекул определяет темп нагрева газа и динамику его разлета вдоль оси x. , играющих роль «начальных затравочных» электронов. При t>0 в области предионизированного газа начинает
развиваться электрический разряд, в котором энергия электрического поля полностью
либо частично поглощается электронной компонентой плазмы. В столкновениях с
молекулами электроны передают свою энергию во внутренние степени свободы частиц
газа. При этом происходит возбуждение вращательных, колебательных и электронных
состояний молекул. Релаксация энергии, заключенной во внутренних степенях
свободы молекул определяет темп нагрева газа и динамику его разлета вдоль оси x.
Самосогласованное
решение задачи описывается замкнутой системой уравнений электродинамики,
газодинамики и плазмохимической кинетики.
При
распространении электромагнитных волн в ионизированном газе свободные электроны
взаимодействуют с осциллирующим полем:

Взаимодействие определяет динамику
электронной компоненты и изменяет ее рассеивающие и поглощающие свойства. Если
поле поперечное, то уравнение для комплексной амплитуды поля имеет вид:
 , ,
где  - частота
электрического поля, с – скорость
света в вакууме, - частота
электрического поля, с – скорость
света в вакууме,  - комплексная диэлектрическая
проницаемость плазмы, - комплексная диэлектрическая
проницаемость плазмы,  и и  - диэлектрическая
проницаемость и проводимость среды, - диэлектрическая
проницаемость и проводимость среды, 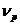 - эффективная частота
релаксации импульса электронов, - эффективная частота
релаксации импульса электронов,  , ,  - концентрация
электронов, - концентрация
электронов, 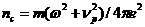 - критическая концентрация электронов (e и m
- заряд и масса электрона). - критическая концентрация электронов (e и m
- заряд и масса электрона).
Движение
газа, вызванное релаксацией внутренней энергии частиц в нагрев, описывается
системой уравнений газодинамики в которой уравнение непрерывности записано для
каждой компоненты плазмы в отдельности:
 , ,  , ,
 , ,  . .
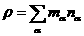 , ,  , , 
с начальными и граничными условиями:
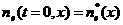 , , 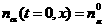 , ,  , , 
 , ,  , ,  , , 
где  - тяжелые компоненты
газоразрядной плазмы (молекулы в различных электронно-колебательных состояниях
и ионы), p и T – давление
и температура газа, v – скорость газа, - тяжелые компоненты
газоразрядной плазмы (молекулы в различных электронно-колебательных состояниях
и ионы), p и T – давление
и температура газа, v – скорость газа, 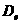 - коэффициент
амбиполярной диффузии электронов, члены в правых частях уравнений непрерывности - коэффициент
амбиполярной диффузии электронов, члены в правых частях уравнений непрерывности
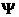 описывают изменения концентраций соответствующих частиц
вследствие протекания кинетических процессов в газе, Q – источник, описывающий релаксационный
нагрев газа, описывают изменения концентраций соответствующих частиц
вследствие протекания кинетических процессов в газе, Q – источник, описывающий релаксационный
нагрев газа, 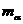 - массы частиц, к – константа Больцмана. - массы частиц, к – константа Больцмана.
Структура кинетической
схемы
Кинетическая
схема, используемая для описания неравновесного электрического разряда в
молекулярном азоте, в условиях значительного вложения энергии во внутренние
степени свободы молекул, включает в себя набор реакций между следующими компонентами
плазмы:
Колебательные уровни основного
электронного терма молекулы  : :
 
Электронно-возбужденные молекулы азота:
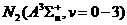 , ,  ; ;  , , , , ; ;
 , ,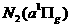 , , ; ;  . .
Электроны и ионы  и и  . .
В рассматриваемой кинетической модели зарядовая кинетика
определяется не только процессами прямой и ступенчатой ионизации, а также процессами
ассоциативной ионизации метастабильных состояний молекул:
 , ,  , , 
 , , 
Заселение метастабильных состояний  и и  происходит как за счет
непосредственного возбуждения молекул происходит как за счет
непосредственного возбуждения молекул  , так и за счет процессов тушения более высоких уровней
невозбужденными молекулами. , так и за счет процессов тушения более высоких уровней
невозбужденными молекулами.




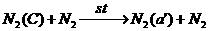
Содержание ионов  и и  в плазме определяется
реакциями конверсии и диссоциативной рекомбинации: в плазме определяется
реакциями конверсии и диссоциативной рекомбинации:


Колебательная
кинетика молекул азота в основном электронном состоянии 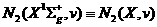 (где (где  - колебательное
квантовое число) описывается в рамках модели поуровневой кинетики
ангармонических осцилляторов, учитывающей колебательно-колебательные (VV) и колебательно-поступательные (VT) процессы, в приближении одноквантовых
переходов: - колебательное
квантовое число) описывается в рамках модели поуровневой кинетики
ангармонических осцилляторов, учитывающей колебательно-колебательные (VV) и колебательно-поступательные (VT) процессы, в приближении одноквантовых
переходов:


здесь  - молекула азота в
основном электронном состоянии с произвольным колебательным состоянием. В
рассматриваемой модели учитываются 48 колебательных энергетических уровней ( - молекула азота в
основном электронном состоянии с произвольным колебательным состоянием. В
рассматриваемой модели учитываются 48 колебательных энергетических уровней ( ) молекулы азота. ) молекулы азота.
При
описании возбуждения и девозбуждения колебательных уровней молекулы  электронным ударом
учитываются перекрестные переходы между первыми 11 колебательными состояниями: электронным ударом
учитываются перекрестные переходы между первыми 11 колебательными состояниями:
 , , 
Функция распределения
молекул азота по колебательным уровням основного электронного состояния
формируется за счет неупругих столкновений молекулы  с электронами и
другими молекулами с электронами и
другими молекулами  . При неупругом столкновении двух молекул . При неупругом столкновении двух молекул  учитываются процессы,
в которых происходит возбуждение одной их молекул и девозбуждение второй молекулы
VV-обмены, а
также процессы, протекающие с возбуждением и девозбуждением одной из молекул VT-релаксация. В рассматриваемой модели
диссоциацией сильно колебательно-возбужденных молекул при соударениях их с
другими молекулами пренебрегается. При неупругих столкновениях молекул учитываются процессы,
в которых происходит возбуждение одной их молекул и девозбуждение второй молекулы
VV-обмены, а
также процессы, протекающие с возбуждением и девозбуждением одной из молекул VT-релаксация. В рассматриваемой модели
диссоциацией сильно колебательно-возбужденных молекул при соударениях их с
другими молекулами пренебрегается. При неупругих столкновениях молекул  с электронами происходит
накачка энергии в колебательный резервуар молекул с электронами происходит
накачка энергии в колебательный резервуар молекул   -процессы, а также процессы возбуждения электронных термов
молекулы, диссоциация и ионизация молекул, которые описываются источниковым
членом -процессы, а также процессы возбуждения электронных термов
молекулы, диссоциация и ионизация молекул, которые описываются источниковым
членом  . .
Таким образом, система
уравнений, описывающая колебательную кинетику молекул азота, записывается в
виде:
 , ,  , ,
где:
 , ,  , ,
здесь  и и  - потоки молекул вдоль оси колебательных квантовых чисел,
вызванные VT- и VV- процессами: - потоки молекул вдоль оси колебательных квантовых чисел,
вызванные VT- и VV- процессами:
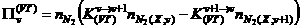 , ,
 , ,
 , ,  , ,  . .
 . .
Здесь выражения  и и  описывают заселение и
расселение колебательных состояний молекулы описывают заселение и
расселение колебательных состояний молекулы  ударом электрона: ударом электрона:
 = = и и  = = . .
Источниковый член  может быть представлен
в виде: может быть представлен
в виде:
 , ,
где символ z cсоответствует электронным состояниям:
 , и , и
Суммарная
скорость тепловыделения в результате протекания реакций в плазме может быть представлена
в виде:
 , ,
где слагаемое 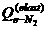 обусловлено упругим
рассеиванием электронов на молекулах; обусловлено упругим
рассеиванием электронов на молекулах;  - возбуждением
вращательных уровней молекулы - возбуждением
вращательных уровней молекулы  и их быстрой
последующей релаксацией; и их быстрой
последующей релаксацией;  - процессами релаксации
(тушения) электронно-возбужденных частиц - процессами релаксации
(тушения) электронно-возбужденных частиц  ; ;  - процессами нерезонансного
VV-обмена и VT- релаксации колебательно-возбужденных
молекул - процессами нерезонансного
VV-обмена и VT- релаксации колебательно-возбужденных
молекул  . .
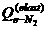 = = , ,
где  и и  - массы электрона и
молекулы азота; - массы электрона и
молекулы азота;  - транспортное сечение
рассеяния электрона на молекуле - транспортное сечение
рассеяния электрона на молекуле  ; ;  - функция распределения
электронов по энергии (ФРЭЭ); - функция распределения
электронов по энергии (ФРЭЭ);  - константа Больцмана. - константа Больцмана.
 = = , ,
где  - вращательная
постоянная молекулы азота; - вращательная
постоянная молекулы азота;  - сечение возбуждения
вращательных уровней основного электронного состояния молекулы азота. - сечение возбуждения
вращательных уровней основного электронного состояния молекулы азота.
 = = , ,
 = =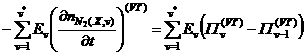 , ,
где  - энергия - энергия  -го колебательного состояния ангармонического осциллятора; -го колебательного состояния ангармонического осциллятора; 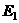 - энергия первого
колебательного уровня; - энергия первого
колебательного уровня;  - постоянная
ангармонизма. - постоянная
ангармонизма.
В
случаях интенсивного возбуждения электронных термов при относительно высоких
значениях напряженности электрического поля для описания быстрого нагрева газа
включен механизм тепловыделения, связанный с процессами столкновительного девозбуждения
электронно-колебательных уровней молекул частицами  в основном состоянии.
При этом происходят ступенчатые переходы возбужденных молекул из вышележащих
состояний в метастабильные состояния в основном состоянии.
При этом происходят ступенчатые переходы возбужденных молекул из вышележащих
состояний в метастабильные состояния  и и  . Выражение . Выражение  описывает выделение
небольших количеств внутренней энергии в поступательные степени свобода в
одиночных актах девозбуждения (соответствующим малым значениям параметра
Месси). описывает выделение
небольших количеств внутренней энергии в поступательные степени свобода в
одиночных актах девозбуждения (соответствующим малым значениям параметра
Месси).
Кинетика
электронной компоненты плазмы описывается квазистационарным уравнением
Больцмана для функции распределения электронов по энергии, записанным в
приближении двучленного разложения. Вычисление констант скоростей процессов неупругих
столкновений электронов с молекулами осуществляется путем свертки экспериментально
(либо теоретически) полученных сечений этих процессов с ФРЭЭ.
В
настоящей работе за основу принята база данных по сечениям и константам скоростей
элементарных процессов, протекающих с участием электрона в азотной плазме, приведенная
в [3].
Численная модель
Кинетические
характеристики процесса нагрева молекулярного азота, протекающего во время
неравновесного электрического разряда и в после разрядный период, описываются
жесткой задачей Коши для системы обыкновенных дифференциальных уравнений.
Большая жесткая система обыкновенных дифференциальных уравнений решается с помощью
специализированной программы DIFSUB с подключением высоко оптимизированного пакета
программ Intel®
Math Kernel Library 5.1.
При
расчете констант скоростей протекания элементарных процессов с участием
электронов решается уравнение Больцмана для ФРЭЭ, представляющее собой нелинейное
интегро-дифференциальное уравнение второго порядка со смещенными аргументами.
Как показывают расчеты, в условиях рассматриваемой задачи ФРЭЭ не является
однопараметрическим распределением Максвелла и чрезвычайно сильно зависит от
отношения напряженности электрического поля к концентрации молекул азота  , а также от состояния внутренних степеней свободы молекул (в
частности от степени возбуждения колебаний молекул). , а также от состояния внутренних степеней свободы молекул (в
частности от степени возбуждения колебаний молекул).
В данной работе во избежание чрезмерных затрат машинного времени
(чрезмерных даже для одномерных задач, описывающих динамику неравновесной
среды) проводится предварительный расчет ФРЭЭ и табулирование констант
скоростей процессов как функций от величин  и и  (где (где 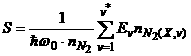 – среднее число колебательных квантов, приходящихся на одну
молекулу). Полученные константы скоростей процессов (в широком диапазоне
параметров – среднее число колебательных квантов, приходящихся на одну
молекулу). Полученные константы скоростей процессов (в широком диапазоне
параметров    , ,  ) аппроксимировались аналитическими зависимостями вида: ) аппроксимировались аналитическими зависимостями вида:
  , ,
что позволило снизить
затраты машинного времени на несколько порядков величины.
Уравнения
газодинамики решались на основе хорошо зарекомендовавшей себя полностью
консервативной частично-трехслойной разностной схемы (ПКС-1) [5].
Решение
уравнения электродинамики и формулировка граничных условий подробно описаны в
[4].
Обсуждение тестовых результатов
В качестве примера рассмотрим эффект
воздействия плоской электромагнитной волны с амплитудой  и длиной волны и длиной волны 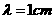 на покоящийся
молекулярный азот при высоком давлении ( на покоящийся
молекулярный азот при высоком давлении ( ). Начальная предионизация газа осуществляется в области ). Начальная предионизация газа осуществляется в области 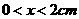 , где внешний источник ионизации поддерживает концентрацию
электронов на уровне , где внешний источник ионизации поддерживает концентрацию
электронов на уровне  . Электромагнитная волна, проходя через радиопрозрачную поверхность
(при x=0) частично поглощается
слабоионизованной плазмой, вызывая там лавинное размножение электронов –
развитие газового разряда. Электронная компонента возбуждает внутренние степени
свободы молекул: электронные уровни, вращение и колебания молекул. С течением
времени релаксация внутренней энергии молекул приводит к нагреву газа и его
движению. . Электромагнитная волна, проходя через радиопрозрачную поверхность
(при x=0) частично поглощается
слабоионизованной плазмой, вызывая там лавинное размножение электронов –
развитие газового разряда. Электронная компонента возбуждает внутренние степени
свободы молекул: электронные уровни, вращение и колебания молекул. С течением
времени релаксация внутренней энергии молекул приводит к нагреву газа и его
движению.
На
рисунке 1 в момент времени  50 мкс приведены
графики зависимостей амплитуды электрического поля и концентрации электронов в
пространстве. На рисунках 2 и 3 даны зависимости среднего числа колебательных
квантов приходящихся на одну молекулу S и
представлена динамика газа в различные
моменты времени 50 мкс приведены
графики зависимостей амплитуды электрического поля и концентрации электронов в
пространстве. На рисунках 2 и 3 даны зависимости среднего числа колебательных
квантов приходящихся на одну молекулу S и
представлена динамика газа в различные
моменты времени  20, 30, 40 и 50 мкс. 20, 30, 40 и 50 мкс.
Из
приведенных данных видно, что за короткий промежуток времени t~5 мкс вблизи радиопрозрачной стенки (x=0) формируется узкая область ( ~0,1-0,5 см) с концентрацией электронов близкой к
критической. В этой области происходит основное поглощение энергии волны, наиболее
сильное возбузждение внутренних степеней свободы молекул, интенсивный нагрев
газа (определяющий быстрый разлет газа). ~0,1-0,5 см) с концентрацией электронов близкой к
критической. В этой области происходит основное поглощение энергии волны, наиболее
сильное возбузждение внутренних степеней свободы молекул, интенсивный нагрев
газа (определяющий быстрый разлет газа).
Л и т е р а т у р а
1.
Силаков В.П., Чеботарев А.В. Стабильные режимы неравновесного импульсно-периодического
разряда в потоке молекулярного азота при высоком давлении. ПМТФ, 1992, N2 , с. 19-26.
2.
Богатов Н.А., Гитлин М.С. Экспериментальное исследование неустойчивости несамосогласованного
СВЧ- разряда. ЖТФ, 1987, т. 57, N 1.
3.
Русанов В.В., Силаков В.П., Чеботарев А.В. Кинетические характеристики процесса
нагрева молекулярного азота, протекающего во время неравновесного
электрического разряда и в послеразрядный период. –Препринт ИПМ N42/
4.
Безменов И.В., Русанов В.В., Силоков В.П. Динамика волнового СВЧ-разряда высокого
давления в молекулярном азоте. – Труды ИОФРАН, т. 47, 1994, с. 74-107.
5. Вычислительные методы в
математической физике. Под редакцией А.А. Самарского. Издательство Московского
Университета 1986.

Рис. 1

Рис. 2

Рис. 3
|