Динамические нагрузки на самолет-носитель при реализации воздушного старта ракеты-носителя (двухопорная схема).

( Dynamic loadings on the carrier aircraft at implementation of the vehicle air launch (the two-basic scheme).
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Введение

Идея воздушного старта ракеты с использованием самолета-носителя (СН) привлекает внимание разработчиков ракетно-космической техники последние 30 лет [1-4]. В частности, реализован старт трехступенчатой твердотопливной ракеты «Пегас» с доработанного бомбардировщика B-52G (или самолета L-1011) в горизонтальном полете, причем ракета с крылатой первой ступенью подвешена под крылом СН [5]. Последнее ограничивает массу и габариты ракеты.

Большие возможности открывает размещение ракеты внутри фюзеляжа СН. При таком решении существенно увеличивается дальность полета СН с ракетой к точке ее запуска, что расширяет оперативные возможности системы, масса и габариты ракеты могут быть увеличены для повышения массы выводимой полезной нагрузки. Указанный подход реализован в американском проекте Quick Reach [6, 7] и российском проекте Авиационно-ракетного комплекса космического назначения (АРК КН) «Воздушный старт». Комплекс включает СН Ан-124-100ВС и ракету космического назначения (РКН) «Полет» с космическим разгонным блоком (КРБ). Проект разработан Государственным ракетным центром «КБ имени академика В.П.Макеева», Авиационным научно-техническим комплексом имени О.К.Антонова и Аэрокосмической корпорацией «Воздушный старт»  с участием ведущих аэрокосмических предприятий России и Украины.

СН является бустерной многоразовой ступенью АРК КН, обеспечивая ненулевые начальные условия (высоту ~10 км, скорость ~0,2 км/с и угол наклона траектории ~20°). Это позволяет увеличить выводимую полезную нагрузку на 40-50% по сравнению с наземным стартом, в том числе за счет применения высотного сопла на двигателе первой ступени.

Двухступенчатая РКН с компонентами топлива кислород и керосин находится в транспортно-пусковом контейнере (ТПК) внутри СН и десантируется из него под действием порохового аккумулятора давления. Десантирование осуществляется после выполнения маневра «Горка» и создания условий квазиневесомости с вертикальной перегрузкой около 0,2 что необходимо для безопасного выхода РКН массой порядка 100000 кг. Время выхода составляет около 2,5 с.

РКН расположена в СН против направления полета и после выхода совершает разворот по тангажу с помощью РДТТ управления для получения начальной ориентации. На безопасном расстоянии от СН (~250 м) включается маршевый двигатель первой ступени и начинается ее выведение на орбиту.

Целью данной работы является определение динамических нагрузок на ТПК при классической двухопорной схеме его крепления к грузовому полу СН, а также реакций в опорах. Работа является частью общей задачи построения математической модели процесса десантирования РКН из СН, которая необходима для выбора оптимальной схемы крепления ТПК к грузовому полу СН с целью минимизации его массы, а также определения динамических нагрузок на РКН, ТПК и СН при обеспечении безударного выхода.

1. Постановка задачи

Рассматриваются две принципиально различающиеся схемы крепления:

·        двухопорная (в данной работе);

·        многоопорная (на следующем этапе).

Классическая двухопорная схема является статически определимой системой. В отличие от нее многоопорная схема с числом опор более двух является статически неопределимой системой. Двухопорная схема является исходным эталоном для сравнения нагрузок и условий выхода РН из ТПК и СН.

Математическая модель взаимодействия РН с ТПК в процессе десантирования, от момента страгивания РН (т.е. начала ее движения относительно ТПК) до момента покидания ТПК, не зависит от числа опор и включает следующие допущения. Движение РН относительно ТПК рассматривается в системе координат 0хуz, связанной с ТПК. Начало ее совпадает с передней (по направлению полета СН) точкой ТПК. Ось 0х направлена в сторону движения РН при выходе из ТПК, т.е. против направления полета СН. Ось 0y направлена вверх, а ось 0z замыкает правую систему координат.

ТПК принят в виде упругой балки трубчатого сечения длиной L с заданной погонной массой . В каждый фиксированный момент времени  известна нормальная перегрузка по длине ТПК: . РН рассматривается в виде цилиндрической упругой балки длиной , которая прилегает к ТПК по всей длине и в процессе выхода перемещается без трения на величину . Погонная масса РН задана: , где - связанная координата по оси РН от хвостовой части к головной. Соотношение связанных координат ТПК и РН:

                              .                                                                       (1.1)

Известна перегрузка, действующая на РН в каждый момент времени . Для общности постановки не предполагается тождественное равенство перегрузок  и .

Величины погонных нагрузок, приложенных к ТПК, определяются соотношением

                              ,                                                 (1.2)

где

                                                                                           (1.3)

- погонная сила от распределенной массы ТПК,

                                                                                        (1.4)

- погонная сила от распределенной массы РН, =9,81м/с² – ускорение свободного падения на уровне моря.

Величина  зависит также от взаимного положения РН и ТПК, т.е. от перемещения  в процессе выхода РН. Перемещение принято в качестве параметра квазистатической (т.е. статической в каждый момент времени t) задачи о нагружении ТПК при десантировании РН.

 2. Модель погонной массы

При близких длинах РН и ТПК, масса РН (~102000 кг) более чем на порядок превышает массу ТПК (~10000 кг в двухопорной схеме). Поэтому для сравнительного анализа действующих нагрузок на ТПК в двухопорной и многоопорной схемах можно в первом приближении принять погонную массу ТПК постоянной:

                              .

В целях упрощения задачи длины РН и ТПК приняты одинаковыми:

                                        31 м.

Эта величина соответствует длине РН без выступающей части сопла двигателя первой ступени. Тогда погонная масса ТПК в первом приближении составляет

                               .                                           (2.1)

Погонная масса заправленной РН существенно меняется по ее длине (на порядок и более), поэтому необходимо учитывать отмеченный фактор при построении модели . В основу модели положены предварительные данные об изменении погонной массы по длине РН при полной заправке, а также жесткостные характеристики поперечных сечений РН. Исходные данные скорректированы с учетом размещения в цилиндрической части головного обтекателя (ГО) космического разгонного блока (КРБ) с полезной нагрузкой (ПН). Масса КРБ включает конструкцию (1000 кг) и топливо (4500 кг), а масса ПН составляет 4000 кг. Принятая модель погонной массы РН и ее жесткостные характеристики приведены в табл. 2.1.

Таблица 2.1- Погонная масса и жесткостные характеристики РН

*) от хвостовой части РН.

Здесь Е– модуль упругости, – осевой момент инерции поперечного сечения РН, – модуль сдвига (модуль упругости второго рода), – площадь поперечного сечения РН. Средняя погонная масса РН составляет

                                      .                                       (2.2)

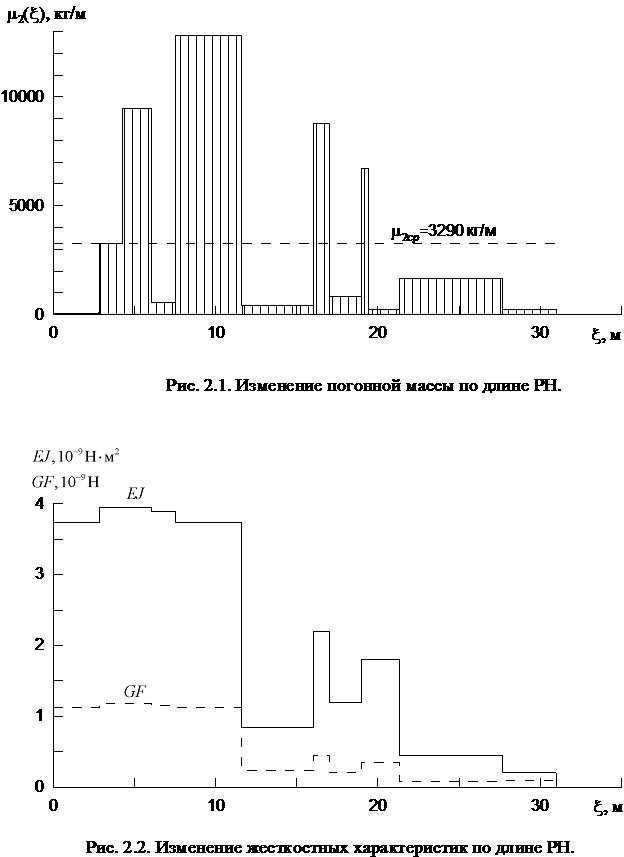
На рис. 2.1 показано изменение погонной массы РН по длине. Видно, что в местах расположения баков погонная масса на порядок больше, чем в местах расположения межбаковых и хвостовых отсеков. На рис. 2.2 дано изменение жесткостных характеристик на изгиб () и на срез () по длине РН. Эти характеристики необходимы для расчета эквивалентных напряжений и определения критических сечений при сравнении опорных схем ТПК для выбора оптимальной схемы.

3. Методика расчета двухопорной схемы крепления ТПК

На рис. 3.1 представлена принципиальная схема нагружения ТПК с двумя опорами под действием нагрузок от погонной силы тяжести самого ТПК  и погонной силы тяжести РН .

Предполагается, что в процессе выхода РН переместилась относительно ТПК на величину . Левая опора А ТПК является шарнирно неподвижной, правая опора В принята шарнирно подвижной. Здесь а₁ – расстояние от левого торца ТПК до опоры А, а₂ – расстояние между опорами, – реакция опоры А, – реакция опоры В.

Для определения внутренних усилий, возникающих в поперечном сечении ТПК от внешних нагрузок в вертикальной плоскости 0хуz, следует использовать принятые в сопротивлении материалов [8] следующие правила:

а) изгибающий момент относительно центральной оси z поперечного сечения ТПК равен (по величине и знаку) сумме моментов относительно этой оси всех внешних сил, приложенных к левой части ТПК, или сумме моментов всех внешних сил, приложенных к правой части, взятой с обратным знаком:

                                         ,

при этом моменты внешних сил положительны, когда они действуют по часовой стрелке;

б) поперечная сила равна (по величине и знаку) сумме проекций на ось 0y всех внешних сил, приложенных к левой части ТПК, или сумме проекций на ось 0y всех внешних сил, приложенных к правой части, взятой с обратным знаком:

                                ,

при этом проекции внешних сил положительны, когда они направлены вверх.

Часть РН длиной , которая вышла из ТПК, порождает на правом конце сосредоточенную перерезывающую силу

                                                                       (3.1)

и сосредоточенный изгибающий момент

                                        .                              (3.2)

В случае положительной перегрузки  перерезывающая сила , т.е. направлена вниз, а изгибающий момент , т.е. направлен по часовой стрелке.

Величина силы реакции в опоре В определяется из условия равенства нулю всех моментов относительно опоры А:

                               (3.3)

где  определяется условием (1.1).

Величина силы реакции в опоре А определяется из условия равенства нулю всех перерезывающих сил:

                                      (3.4)

Принято, что величина сдвига РН может меняться в диапазоне

                               0 £ Dх £ L.                                                                   (3.5)

При известных величинах реакций  и , а также величине сдвига  РН относительно ТПК, перерезывающая сила в произвольном сечении x ТПК задается уравнением

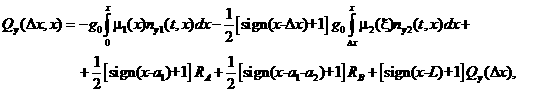            (3.6)

где

                                         0 £ х £ L.                                                                      (3.7)

Для вычисления изгибающего момента в сечении х предварительно вычислим момент внешних сил относительно начала координат

                                                                                         (3.8)

и равнодействующую внешних сил на участке то 0 до х

                                         .                                                             (3.9)

Тогда координата  точки приложения равнодействующей силы  будет определяться соотношением

                                         ,                                                                 (3.10)

а момент силы  относительно рассматриваемого сечения  вычисляется по формуле

                                         , где ,

или с учетом (3.8)-(3.10):

                                         .                                     (3.11)

Принимая во внимание соотношение (3.11), можно получить общую формулу для расчета изгибающего момента в сечении  при известной величине сдвига РН относительно ТПК:

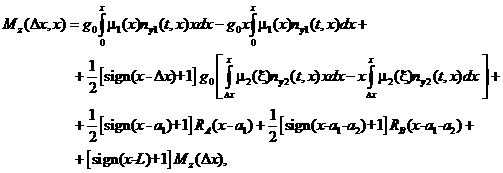                 (3.12)

где  меняется в диапазоне (3.7), а  меняется в диапазоне (3.5), но в каждый рассматриваемый момент времени величина  фиксирована.

4. Определение нагрузок при двухопорной схеме

При определении нагрузок для двухопорной схемы крепления ТПК к грузовому полу СН рассматривается тестовый набор следующих режимов нагружения:

по перегрузке

·        постоянная перегрузка;

·        линейно меняющаяся по длине РН и ТПК перегрузка;

по изменению погонной массы РН

·        средняя погонная масса РН;

·        переменная по длине погонная масса РН (рис.2.1);

по положению РН относительно ТПК

·        транспортировка заправленной РН в СН ();

·        выход РН из ТПК в условиях квазиневесомости ().

4.1. Действие постоянной перегрузки

Рассматриваются два режима нагружения. Первый режим связан с транспортировкой заправленной РН в СН, т.е. до начала выхода РН из ТПК (). Расчетная нормальная перегрузка составляет

                               .

Второй режим связан с выходом РН из ТПК в условиях квазиневесомости. Эксплуатационная нормальная перегрузка составляет

                                         ,

и с учетом коэффициента безопасности k=1,5 расчетная нормальная перегрузка

                                          .

В этом случае имеет место дополнительное нагружение ТПК вследствие сдвига РН относительно ТПК на величину . В принятой модели взаимодействия РН с ТПК в процессе выхода (РН – упругая цилиндрическая балка, ТПК – труба) РН не может поворачиваться относительно ТПК вплоть до полного выхода. Вышедшая часть РН будет создавать на срезе ТПК сосредоточенную силу и сосредоточенный момент , величины которых однозначно определяются длиной  вышедшей части РН из ТПК. Максимальные величины  и будут достигаться непосредственно перед выходом РН из ТПК, т.е. при . На следующем этапе модель взаимодействия будет уточнена за счет рассмотрения опорно-ведущих поясов РН. В этом случае РН будет вращаться относительно ТПК (вокруг последнего опорно-ведущего пояса) после выхода предпоследнего опорно-ведущего пояса из ТПК. Из-за вращения РН величины и будут меньше, чем в первой модели, но при этом возникает опасность соударения РН с ТПК или СН.

Для получения предварительных количественных оценок приняты следующие числовые данные:

-   погонная масса ТПК ;

-   средняя погонная масса РН ;

-   длина РН и ТПК =31 м;

-   расстояние от левого торца ТПК до опоры А ;

-   расстояние между опорами А и В .

Модель постоянной погонной массы РН () и ТПК () и постоянной перегрузки приводят к постоянной погонной нагрузке, что является общепринятым в сопротивлении материалов [8]. В исследуемой задаче эта модель рассматривается в качестве исходного эталона, с которым сравниваются другие случаи нагружения при переменной погонной массе РН и линейном изменении нормальной перегрузки по длине ТПК.

Два рассматриваемых случая по положению РН относительно ТПК (транспортировка РН к месту запуска со средней расчетной перегрузкой  при  и выход РКН из ТПК в процессе выполнения маневра «Горка» со средней расчетной перегрузкой  при ), безусловно, не исчерпывают всех расчетных случаев для выбора элементов конструкции ТПК из условия прочности. Однако оба случая являются достаточно «жесткими», так как в первом случае нормальная перегрузка является максимальной, а во втором случае перемещение РН относительно ТПК порождает дополнительные нагрузки.

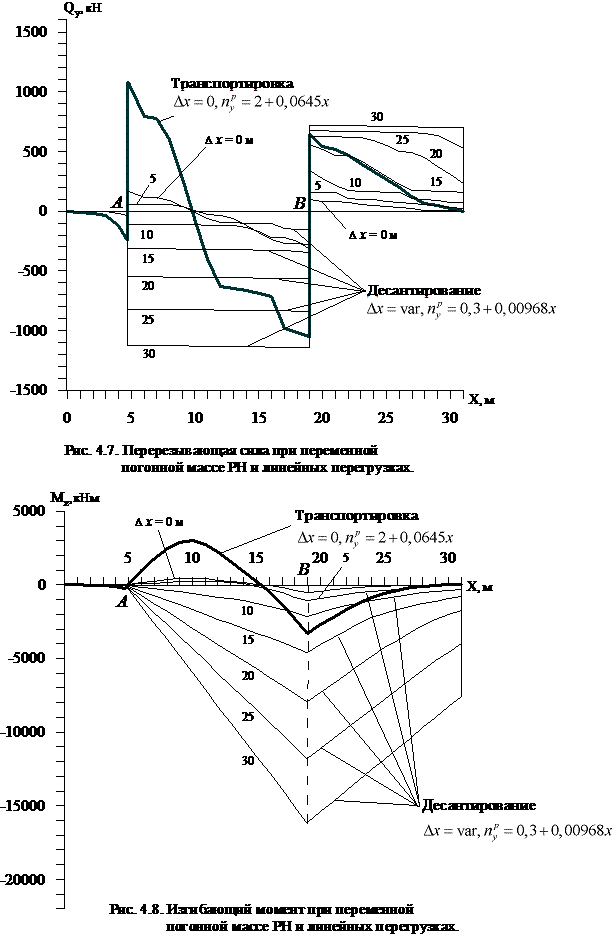
Ниже представлены результаты расчетов для рассмотренных режимов нагружения: эпюры перерезывающей силы  (рис. 4.1) и изгибающего момента        (рис. 4.2)    по    длине    ТПК.    Видно,  что   максимальная

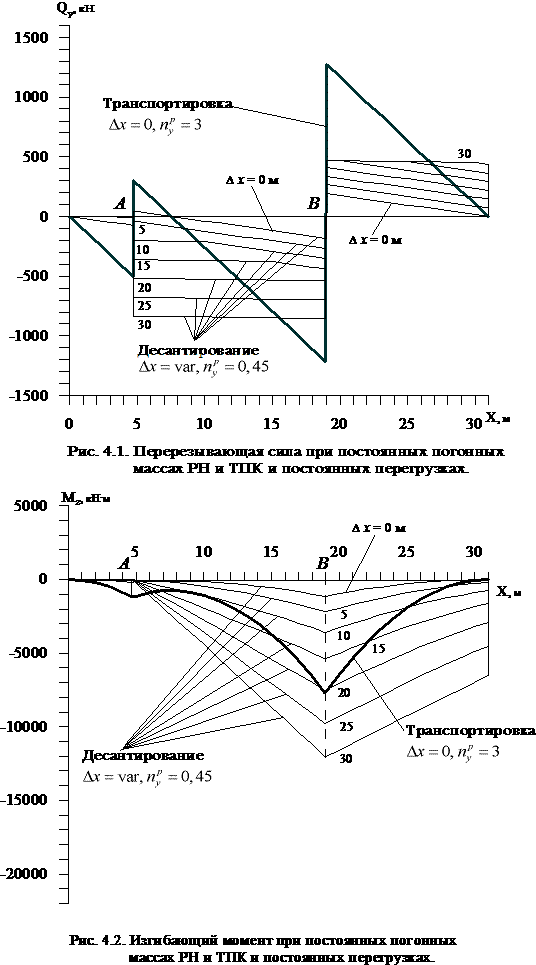
перерезывающая сила для режима транспортировки возникает в сечении над опорой В, которая расположена ближе к срезу ТПК. В этом случае перерезывающая сила оказывается больше, чем при выходе РН из ТПК для любых значений  в диапазоне .

Максимальный изгибающий момент при транспортировке РН в СН и при выходе РН из ТПК возникает в сечении над опорой В. При перемещении РН на величину  в процессе десантирования максимальный изгибающий момент оказывается больше, чем при транспортировке РН.

Величина максимальной перерезывающей силы, которая реализуется в режиме транспортировки, составляет Q_{y max}=1275 кН, что примерно в полтора раза превышает величину максимальной перерезывающей силы, достигаемой в режиме выхода РН из ТПК Q_{y max}=855 кН.

Величина максимального изгибающего момента, которая реализуется в режиме выхода РН из ТПК, составляет M_{z max}=12750 кНм, что примерно в 1,6 раза превышает максимальную величину изгибающего момента, достигаемо-го в режиме транспортировки, M_{z max}=7700 кНм.

При транспортировке, реакции в опорах ТПК составляют R_A=802 кН и R_B=2492 кН, т.е. наиболее нагруженной оказывается опора B, которая расположена ближе к срезу ТПК. При десантировании реакции в опорах ТПК имеют разные знаки: R_A=-828 кН (направлена вниз), R_B=1322 кН (направлена вверх).

Видно, что при расчете ТПК на прочность в рассматриваемой постановке (т.е. при постоянных погонных нагрузках) следует анализировать оба режима нагружения.

Реальное распределение погонной массы по длине РН (табл. 2.1, рис. 2.1) существенно отличается от равномерного. Поэтому происходит качественное и количественное перераспределение перерезывающих сил и изгибающих моментов по длине РН.

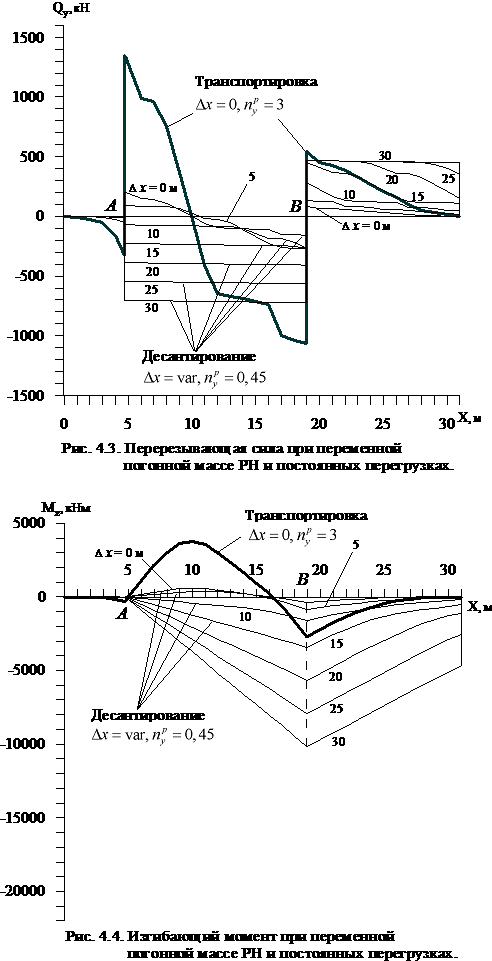
На рис. 4.3 показана перерезывающая сила, а на рис. 4.4 показан изгибающий момент по длине ТПК при переменной погонной массе РН и постоянных перегрузках. В этом случае распределенная погонная сила, действующая на ТПК, пропорциональна погонной массе РН.

Видно, что максимальная перерезывающая сила имеет место в режиме транспортировки и возникает в сечении над опорой А, которая расположена дальше от среза ТПК.

С учетом реального распределения массы по длине РН максимальный изгибающий момент при транспортировке возникает в сечении вблизи бака окислителя первой ступени «О1». Максимальный изгибающий момент при выходе РН из ТПК имеет место в сечении над опорой В, которая расположена ближе к срезу ТПК.

Сравнение двух режимов нагружения (транспортировка и выход РН) с учетом реального распределения массы РН по ее длине позволяет выявить максимальные величины перерезывающей силы и изгибающего момента.

Максимальное значение перерезывающей силы достигается при транспортировке и составляет Q_{y max}=1350 кН, что примерно в 1,9 раза больше величины перерезывающей силы при выходе РН из ТПК (Q_{y max}=720 кН).

Максимальное значение изгибающего момента достигается при выходе РН из ТПК на наибольшую длину. Это максимальное значение M_z max=10165 кНм примерно в 2,7 раза превышает максимальную величину изгибающего момента при транспортировке (M_{z max}=3765 кНм).

Видно, что переход от упрощенной модели распределения погонной массы по длине РН (средняя погонная масса) к реальной модели распределения при постоянной нормальной перегрузке приводит к изменению картины нагрузок как для перерезывающей силы Q_y, так и для изгибающего момента M_z. При этом величина максимальной перерезывающей силы Q_y меняется незначительно, с 1275 кН до 1350 кН (т.е. увеличивается на 6%), а величина максимального изгибающего момента M_z меняется существеннее, с 12750 кНм до  10165 кНм (т.е. уменьшается на 20%). В целом, при определении расчетных

нагрузок на ТПК в случае постоянной нормальной перегрузки, допускается использование в первом приближении модели постоянной погонной массы РН.

Учет реального распределения массы РН по длине приводит к изменению реакций в опорах ТПК. При транспортировке они меняются существенно и оказываются примерно равными: R_A=1684 кН и R_B=1610 кН. При десантировании реакции меняются несущественно по сравнению с моделью постоянной массы РН и составляют R_A=-696 кН, R_B=1190 кН.

4.2. Действие линейной перегрузки

Другая апробация вычислительных алгоритмов и случаев нагружения проводилась в предположении линейного изменения расчетной перегрузки по длине РН и ТПК. При построении линейной модели перегрузки принято, что в центре ТПК величина перегрузки равна расчетной перегрузке для случая транспортировки РН в СН () и для случая выхода РН из ТПК (), соответственно. На левом конце ТПК перегрузка на 1/3 меньше, а на правом конце на 1/3 больше. В результате получены следующие линейные модели расчетных перегрузок для случая транспортировки РН в СН и для случая выхода РН из ТПК:

                             ,                                     (4.1)

                             ,                                (4.2)

Для случая транспортировки РН в СН предполагается, что имеет место маневр в вертикальной плоскости с вращением СН относительно центра масс. В результате этого маневра СН происходит перераспределение перегрузки по линейному закону (4.1). Для случая выхода РН из ТПК предполагается, что имеют место угловая скорость и угловое ускорение, что также приводит к перераспределению перегрузки по линейному закону (4.2).

Расчеты проводились как для случая средней погонной массы РН , так и для случая переменной по длине погонной массы РН (табл .2.1, рис. 2.1).

Ниже представлены результаты расчетов:

·        эпюры перерезывающей силы  (рис. 4.5) и изгибающего момента  (рис. 4.6) по длине ТПК для случая средней погонной массы РН;

·        эпюры перерезывающей силы  (рис. 4.7) и изгибающего момента  (рис. 4.8) по длине ТПК для случая переменной по длине погонной массы РН;

Сравнение условий нагружения двухопорного ТПК под действием постоянной и линейной нормальных перегрузок в модельных задачах с постоянными погонными массами РН и ТПК и с переменной по длине погонной массой РН показывает значительное различие в величинах перерезывающей силы и изгибающего момента.

Линейная перегрузка, которая «в среднем» совпадает с постоянной и увеличивается к срезу ТПК, порождает существенно большие нагрузки на ТПК и грузовой пол СН, чем постоянная перегрузка, поэтому необходимо учитывать фактор возможного изменения перегрузки по длине ТПК и РН.

Перерезывающая сила достигает экстремальных значений Q_y max=1536 кН (для случая средней погонной массы РН) и Q_y max=1053 кН (для случая переменной по длине погонной массы РН) при транспортировке. Изгибающий момент достигает максимальных значений M_z max=20556 кНм (для случая средней погонной массы РН) и M_z max=16147 кНм (для случая переменной по длине погонной массы РН) при пуске когда РН почти полностью выходит из ТПК. Следовательно, при оценке условий нагружения необходимо рассматривать оба случая.

При постоянной и при линейной перегрузке перерезывающая сила Q_y и изгибающий момент M_z достигают экстремальных значений в сечении ТПК над опорой В, которая расположена ближе к срезу ТПК.

Линейная перегрузка приводит к изменению величин реакций в опорах ТПК по сравнению с постоянной перегрузкой. Это вызвано перераспределе-нием погонных сил по длине РН и ТПК. В случае постоянной погонной массы РН реакции в опорах ТПК при транспортировке составляют R_A=404 кН и R_B=2890 кН, а при десантировании (в конце выхода РН из ТПК) реакции имеют разные знаки: R_A=-1429 кН и R_B=2214 кН. Учет переменности погонной массы РН по длине существенно перераспределяет величины реакций в опорах ТПК. Так, при транспортировке реакции составляют R_A=1330 кН и R_B=1693 кН, а при выходе РН из ТПК почти на полную длину в процессе десантирования реакции составляют R_A=-1120 кН и R_B=1864 кН.

В табл. 4.1 представлены реакции в опорах ТПК, т.е. силы, приложенные к грузовому полу СН в точках опор, для всех рассмотренных случаев нагружения.

Таблица 4.1. Реакции в опорах ТПК при различных случаях нагружения

Выводы

Основные результаты выполненной работы состоят в следующем:

1.       Разработан вычислительный алгоритм и создано программное обеспечение, позволяющие определять нагрузки на ТПК и грузовой пол СН в классической двухопорной схеме при любом смещении РН относительно ТПК и при любой погонной нагрузке (из-за переменной погонной массы РН по ее длине или из-за переменной нормальной перегрузки по длине ТПК и РН).

2.       Показано, что учет изменения погонной массы по длине РН может значительно изменить распределение нагрузок на ТПК и реакции опор грузового пола, особенно в случае переменной по длине ТПК и РН перегрузки.

3.       Показана необходимость учета изменения перегрузки по длине ТПК и РН, так как при этом происходит существенное перераспределение нагрузок по сравнению со случаем постоянной перегрузки.

4.       Рассмотренная классическая двухопорная схема крепления ТПК к полу СН является хорошим исходным эталоном для сравнения при анализе многоопорных схем, которые, как предполагается, позволят уменьшить нагрузки на ТПК и грузовой пол СН.

Литература

1.     Государственный ракетный центр «КБ им. Академика В.П.Макеева». М.: Оружие и технологии, 2001.

2.     Godfrey D. Air-mobile ICBM systems // Flight International. 1974. V. 105. № 3391. P. 309, 310.

3.     Boeing VP stresses attractiveness of ICBM-carrying aircraft // Aerospace Daily, 1974. V. 65. № 21. P. 165, 166.

4.     USAF hopes to press advanced ICBM // Aviation Week and Space Tecnology. 1974. V. 100. № 6. P 60, 61.

5.     Flight International. 1977. V. 151. № 4569. P. 23.

6.     M.Sarigul-Klijn, N. Sarigul-Klijn, G.Hudson, B.McKinney, L.Menzel, E.Grabow. Trade Studies for Air Launching a Small Vehicle from Cargo Aircraft. AIAA-2005-0621, 2005.

7.     M.Sarigul-Klijn, N. Sarigul-Klijn, G.Hudson, L.Hoider, D.Fritz, C.Webber, G.Liesman, D.Shell, M.P.Gionfriddo. Flight Testing of a Gravity Air Launch Method to Enable Responsive Space Access. AIAA-2007-6146, 2007.

8.     Дарков А.В. Шпиро Г.С. Сопротивление материалов. «Высшая школа», М. 1965.