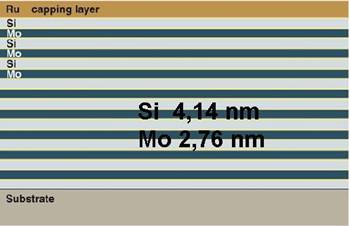
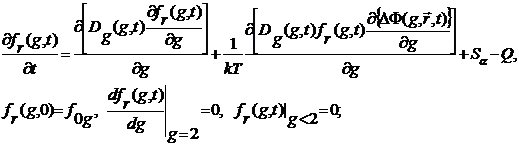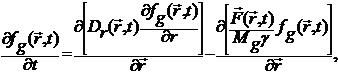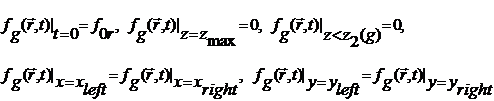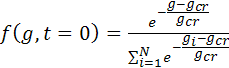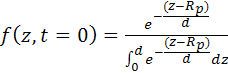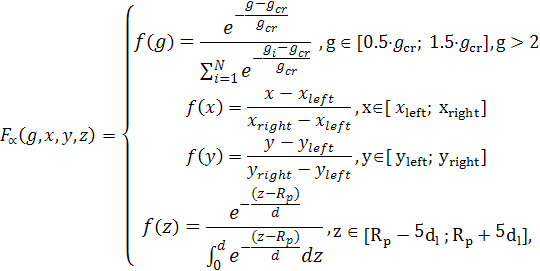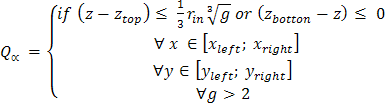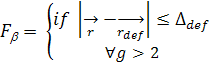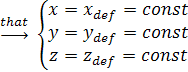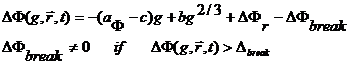Стохастическое моделирование флуктуационной стадии высокотемпературного блистеринга в слоистой среде

( Stochastic Computer Simulation of High-temperature Blistering at Fluctuation Stage into Multylayer Medium
Preprint, Inst. Appl. Math., the Russian Academy of Science)

Введение

Работа посвящена численному моделированию процессов деградации  свойств поверхностей, помещенных в радиационные потоки, в результате гетерогенного фазового перехода на начальной стадии, когда формирование дефектов представляет собой суперпозицию неравновесных физико-химических процессов, а время модификации свойств не превышает 10-100 мсек, в течение которого создаются начальные условия роста новой фазы и развиваются неустойчивости фазового перехода. Особенности блистеринга (образования вакансионно-газовых дефектов кристаллической решетки) могут быть рассмотрены, как пример фазового перехода 1-го рода на флуктуационной стадии

Технологические металлические зеркала используются для передачи оптичского сигнала детектору диагностических приборов в ТЯР [1,2], в рентгеновской литографии [3] и др. В работе [1] исследовались экспериментально зеркала разъемной структуры (монокристалл, поликристаллическая поверхность и др.), было показано что находясь под воздействием радиационной нагрузки поверхность зеркала, находящаяся в потоке ионов водорода,  теряет рабочие характеристики вследствие возникновения наноблистеров (вакансионно-газовых дефектов в кристаллической решетке металла), макроблистеров, локальных вздутий поверхности, трещин и возникновения микрорельефа. В установке ИТЭР первое зеркало будет подвергаться воздействию излучения, вышедшего непосредственно из термоядерной плазмы, включая атомы перезарядки, что  приводит к эрозии зеркала. В процессе работы ИТЭР замена зеркал будет крайне затруднена и может быть сделана не чаще, чем раз в год. Обеспечение стабильности оптических характеристик зеркал за весь срок эксплуатации с учетом режимов кондиционирования и предварительной очистки вакуумной камеры установки является обязательным для штатной работы диагностик.

Кинетический код блистеринга гелия на никеле при кэВ энергиях ионов в потоке на поверхность образца позволил обнаружить нелинейные эффекты в распределении среднего размера дефектов, в изменении распределения пористости и напряжений в решетке по глубине, по мере развития блистеринга  при различных температурах образца.

Процессы зародышеобразования, зависящие от температуры подложки и флюенса потока плазмы (или газа) на поверхность, от свойств кристаллической решетки образца (или его слоя), степени ее анизотропии и упругих свойств, плотности дефектов  (дислокаций и зерен), а также от потенциала поверхности раздела твердой подложки и плазмы, а также от начального распределения частиц (вакансий, атомов и др.) в объеме, представляют собой неравновесную стадию гетерогенного фазового перехода 1-го рода. Математическая модель и ее вычислительная реализация требуют решения систем квазилинейных интегродифференциальных уравнений математической физики в частных производных второго порядка. Метод стохастического аналога в форме стохастических дифференциальных уравнений Ито в форме Стратоновича позволяет анализировать нелинейную стадию зародышеобразования, а для учета химических превращений следует использовать уравнения Ито по точечной мере.

В работе рассматривается модификация кинетического кода «Блистер», необходимость которой связана с тем, что технологические зеркала  имеют слоистую структуру , состоящую из слоев металла и диэлектрика, например, “молибден-кремний”(Mo/Si).

Ранее разработанные методики моделирования блистеринга в материалах ТЯР необходимо изменить так, чтобы стал возможен  учет специфики накопления водорода в металле, возникновение пор и трещин, а также рассмотреть различные условия на внутренних границах металлических слоев Mo и пористой прослойки Si .

В результате модель деградации прочностных характеристик и шероховатости поверхности зеркала включает в себя формирование размеров дефектов, их миграцию в слоях зеркала нанометровых толщин, накопление дефектов и напряжений в решетке образца которые  должны оцениваться по неравновесным функциям распределения кластеров дефектов по размерам, и координатам. Скорость деградации свойств материалов подложки (разупрочение из-за образования слоев пористости, отшелушивание слоев, разрушение "крышек" блистеров на поверхности, переконденсация распыленного материала, оплавление трещин, загрязнение плазмы и др.) сопоставляется с картиной микрошероховатости поверхности. Результаты расчетов блистеринга при параметрах, близких к имитационным экспериментам, например, данные по распределению кратеров по размерам, по динамике образования дефектов на поверхности, степени разрушения и т.д. сопоставляются с визуализированными данными микроскопии образцов для создания программ прогноза степени деградации зеркала и размеров дефектов на отражающей плоскости при разных механизмах порообразования.

Вычислительные эксперименты на основе кинетических уравнений плазмы и плазмоподобных сред, в условиях “открытых” физических систем [4], которыми можно описывать модифицирующие поверхности фазовые переходы, на начальной неравновесной стадии, когда решается вопрос устойчивости роста тонкой пленки или сценарий развития блистеринга, актуальны.

В настоящее время существует большой интерес к проблемам гетерогенной нуклеации на неравновесной стадии [5], где рассматриваются пористые среды и поведение суспензий в них, в работе обобщаются теоретические кинетические модели нуклеации, но не содержит результатов вычислительных экспериментов на их основе. Модификация и усложнение имеющихся работающих вычислительных комплексов направлены на создание современного инструмента исследования сильно неравновесной стадии процессов образования и развития наноструктур на поверхности и в приповерхностном слое: образование пористости образца и напряжений, вызванных блистерингом. Деградацию прочности материалов слоев зеркал (разупрочение из-за образования пористости в металлическом слое, отшелушивание "крышек" блистеров на границах слоев металла и пористого кремния, переконденсация распыленного материала на поверхности, оплавление трещин поверхности, загрязнение плазмы над зеркалом и др.),  полученные в расчетах, можно сравнить с микрошероховатостью поверхности. Вычислительные эксперименты предоставляют возможность исследовать нелинейные процессы формирования дефектов в слоистой среде в широком диапазоне значений параметров физических  процессов, где неприменимы приближенные аналитические теории. С помощью расчетов могут быть выяснены пределы и степень эффективности приближенных теоретических подходов.

Создание комплекса программ для моделирования накопления водорода в пористых средах требует совершенствования кинетической и стохастической гибридной модели образования вакансионно-газовых дефектов и гетерогенных физико-химических процессов. Модификация алгоритмов решения систем стохастических дифференциальных уравнений Ито, объединяющих модели диффузии и скачков в фазовом пространстве задачи, изменяющих динамические стохастические переменные является актуальным направлением в решении задач математической физики, также как и создание высокопроизводительных кодов для современных вычислительных средств вместе с кинетическим уровнем описания явлений в пространственно-временных масштабах, характерных для быстропротекающих неравновесных явлений могут считаться конкурентоспособными, поскольку известные аналоги не сочетают в себе и сложность уровня постановки задач и реализацию в компьютерных кодах с проработкой достаточно общего формализма и оптимальной архитектуры приложения, охватывающих широкий спектр задач численного моделирования. Поэтому, создание на их основе пакета быстрой разработки приложений численного моделирования, обеспечивающего высокую производительность, масштабируемость (от одного персонального компьютера до кластера), и оптимальное автоматическое использование инструментальных средств операционной системы и параллельных алгоритмов пользователями различной квалификации исключительно важно.

Рис. 1 Система зеркал, используемая для фокусировки жесткого рентгеновского излучения.

Рис. 2 Схема зеркала, используемого для фокусировки жесткого рентгеновского излучения.

Известно, что растворимость гелия в металлах чрезвычайно мала, поэтому гелий, внедренный в металлы при ионной имплантации, имеет тенденцию к образованию гелий-наполненных пор или гелиевых пузырьков в металлах и диэлектриках, в кристаллических и аморфных материалах, что приводит к деградации свойств поверхности. Поскольку процесс образования гелиевых пузырьков при облучении поверхности образца приводит к нежелательным изменениям свойств материалов (охрупчиванию, изменению оптических, электромеханических, пластических и других свойств), он постоянно изучается с тех пор, как гелиевые пузырьки были обнаружены экспериментально. В данной статье рассматривается моделирование блистеринга в тонкой пленке, толщина которой ~ 100 нм.

Кинетическая и стохастическая модели.

Необходимо заметить, что вследствие флуктуационной неустойчивости процесса зародышеобразования фазовый переход зависит от начальных условий, но в случае рассмотрения начальных размеров зародышей в окрестности критического значения размера (при котором производная от величины потенциала Гиббса обращается в нуль) оказывается, что развитие флуктуаций может изменить и скорость образования зародышей новой фазы и функцию распределения зародышей по размерам. В случае “открытой” физической системы возможны заметные изменения в энергии образования кластеров зародышей по мере их роста/деградации. Изменение размера может происходить в результате слияний зародышей при их движении под действием дальнодействующих потенциалов взаимодействия зародышей друг с другом, возникает нелинейная броуновская диффузия. Пространственно-временные масштабы моделируемой флуктуационной неустойчивости сопоставимы с размерами микроструктуры поверхности и временем изменения ее свойств. В данной работе численная модель фазового перехода 1-го рода описывает его неравновесную стадию в условиях ``открытой'' физической системы, когда в течение ~ 10^-4 с происходит образование зародышей новой фазы, их кластеризация и формирование пространственно—временных структур блистеров в тонкой пленке никеля толщиной ~ 100 нм.

Для моделирования блистеринга применяется следующая модель: блистеры полагаются Броуновскими частицами /БЧ/ сферической формы, масса которых изменяется согласно (1). Причем координата центра масс БЧ изменяется под действием суммарного потенциала, действующего на блистер со стороны других БЧ, облучаемой и не облучаемой поверхностей и дефектов кристаллической решетки типа дислокаций и границ зерен. Данное взаимодействие является косвенным взаимодействием через акустические фононы решетки и Фриделевские осцилляции электронной плотности. Различные характерные времена образования зародыша блистера (10^-9 с) и броуновского движения (10^-8 с) позволили расщепить задачу по физическим процессам и представить каждое кинетическое уравнение его стохастическим аналогом. Кинетические уравнения Колмогорова-Феллера для флуктуационного зародышеобразования и Эйнштейна-Смолуховского для Броуновского движения являются интегро-дифференциальными уравнениями в частных производных. Уравнение Колмогорова-Феллера для эволюции размера блистера

           (1)

Уравнение Эйнштейна-Смолуховского с массой M_g, полученной из уравнения (1).

                (2)

здесь S_a(f_a) –функция источника,  ФР зародышей по размерам, g –размер блистера в единичных несжимаемых объемов атомов гелия V_l=4p/3 r³_w, где r_w радиус Вайскопфа, D_g  =D_g0g^2/3 коэффициент диффузии в пространстве размеров gÎ{G};  термодинамический потенциал образования зародыша, M_g его масса,  ФР зародышей по координатам кристаллической решетки_,  радиус-вектор кластера в ортогональной системе координат: x_left =-200, x_right=200, y_left =-200, y_right=200, z_top =0, z_botton=200 с периодическими граничными условиями по осям х и у: f(g,x_left,y,z)= f(g,x_right,y,z), f(g,x,y_left, z)= f(g,x,y_right z).  потенциала упругого взаимодействия дефектов между собой, с границами и дефектами решеток типа дислокаций, границ зерен и пор для пористой среды. Потенциал дальнодействующий, знакопеременный, реализующийся через возмущение акустических фононов решетки. Такое взаимодействие является косвенным, его зависимость от взаимного расположения центров масс дефектов выводится в предположении слабой анизотропии решетки, в которой происходит кластеризация дефектов. Другой пример такого взаимодействия приведен в моделях кластеризации дефектов легкой примеси (водорода) в металле косвенное взаимодействие осуществляется через фриделевские осцилляции электронной плотности, которое в случае сферической поверхности Ферми зависит от фермиевского импульса электронов, плотности их состояний на поверхности Ферми, и др. были использованы в работе [8-11]. Граничные условия для потенциала по х и у периодические: U(x_left, y,z)=U(x_right,y,z), U(x, y_left,z)=U(x,y_right,z). и  являются функционал-коэффициентами уравнение (1) и (2).

Ось z направлена вглубь образца. На верхней и нижней границах образца     (z_top =0 или z_botton=200) рассматривается граничное условие 1-ого рода: C_бл=0, здесь C_бл концентрация блистеров. Это соответствует f(g,x,y, z_top)=f(g,x,y, z_botton)=0. Численно это реализовано следующим образом: при выходе за верхнюю границу более 2/3 радиуса блистера моделируется его гибель, при выходе более радиуса блистера за нижнюю границу моделируется его гибель. При этом радиус образовавшегося кратера равен радиусу блистера.

На каждой внутренней границе слоев выполняется следующее условие:

<1 модельный параметр- вероятность блистеру перейти через границу слоев, C_{бл i}  и C_{бл j} концентрация блистеров в i и j слоях соответственно.

В начальный момент времени блистеры распределены согласно

 , g Î [0.5×g_cr; 1.5×g_cr], g>2

, _{z Î [Rp – 5dl ; Rp + 5dl],}

, xÎ[ x_left; x_right]

, xÎ[ y_left; y_right]

здесь использованы обозначения

g_cr критический размер зародыша, определяемый из условия _,

N- начальное число блистеров, модельный параметр, зависящей от дозы облучения и температуры образца,

R_p глубина слоя, отвечающая проекционному пробегу облучающих ионов,

d толщина всего образца,

d_l максимальная ширина слоя (для слоев разной толщины) ~ 4 нм,

 случайные величины, равномерно распределенные в интервале (0;1).

Используемый источник блистеров можно записать в виде:

S_a=I_a×F_a (g,x,y,z,t)

I_a интенсивность источника, в рассматриваемом случае число новых блистеров, появившихся во всем моделируемом объеме за шаг алгоритма.

I_a=I(доза облучения, температура)

В рассматриваемой системе существуют стоки 2-х типов:

_1.        Верхняя облучаемая и нижняя не облучаемая границы подложки, на которых моделируется гибель блистеров. Для них сток можно записать в следующем виде:

Здесь r_in радиус внедренного атома, N общее число блистеров, (x,y,z) координаты центра масс блистера.

2.        Дислокации, границы зерен и поры.

Q_b = h_b×N×F_b,

h_b Î (0;1] вероятность блистеру остаться на стоке, причем для каждого вида стока это своя величина.

Здесь D_def=2×a для дислокаций и D_def=2×a для пор, a наименьший параметр решетки.

Суммарный сток можно записать как

Q=Q_a+Q_b

Модель потенциала Гиббса

В уравнении (1) термодинамический потенциал (функционал-коэффициент уравнения) зависит от распределения дефектов по размерам f(g,x,y,z,t). Приведем его значение для g (2<g<g_®¥):

                                                                            ₍₃₎

здесь ,  разность химических  потенциалов фаз, - фактор формы, равный  для блистеринга (здесь и далее V_He- объем атома гелия)

s_bl поверхностное натяжение на границе “He в пузырьке- решетка”, с- эластичная реакция решетки на образование зародыша

Предполагается, что все связи при росте блистера рвутся одновременно, т.е. , где  энергия разрыва одной связи, N_b число связей у одного узла решетки.

                          (4)

Y модельный параметр

~ .

Если блистер находится на расстоянии ~ параметра решетки от дислокации или границы зерна, то  резко уменьшается (на порядки).

Все коэффициенты для каждого материала рассчитываются отдельно.

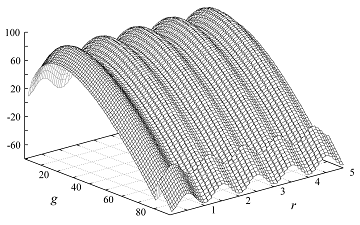Рис. 3 Изопроекция поверхности равных значений потенциала Гиббса (Дж/атом) в зависимости от размера блистера (в числе атомов Не) и его глубины от облучаемой поверхности (в параметрах решетки). Разрыв значений потенциала Гиббса соответствует первому разрыву связей в решетке.

Рис. 4 Зависимость потенциала Гиббса (Дж/атом, ось ординат) от размера зародыша (ось абсцисс), измеряемого в числе атомов.

Область неустойчивости образования зародышей ~ кТ, соответствует интервалу размеров островов [g_0min,g_0max], определяемых из условий: 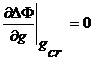, g_cr критический размер зародыша .

Модель взаимодействия блистеров.

Потенциал взаимодействия блистеров друг с другом, с облучаемой поверхностью и дефектами решетки учитывается в (2) как сумма

                                               (5)

соответствует взаимодействию блистеров друг с другом,  взаимодействию блистера со всеми поверхностями слоистой структуры, включая облучаемую поверхность,  - с дефектами решетки типа дислокаций, границ зерен,  потенциал взаимодействия блистер-пора для пористой среды.

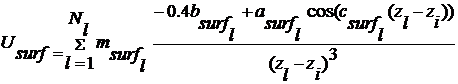              (6)

 Здесь N_l количество границ в слоистой среде, z_l глубина границы, z_lÎ [0;d], d –толщина пленки-подложки, z=0 облучаемая поверхность.

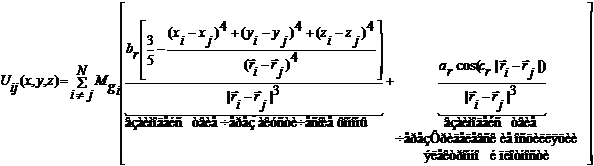(7)

M_gi это масса броуновской частицы, которая определяется из стохастического аналога уравнения (1).

При этом взаимодействие блистер-блистер гораздо слабее взаимодействия блистер-граница, поэтому на границах слоев рассматривается следующее граничное условие U_ij =0. Таким образом, выражение (7) действует только внутри одного слоя.

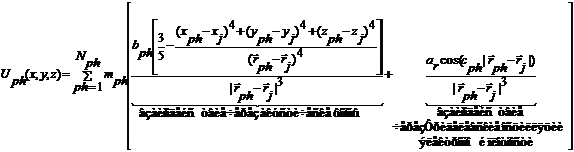 (8)

Здесь N_ph  рассматриваемое количество дислокаций, границ зерен во всем образце.

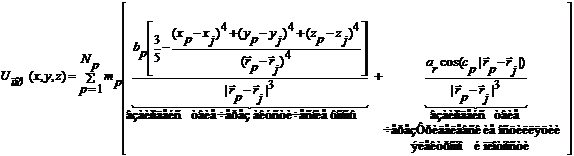         (9)

Здесь N_p  рассматриваемое количество пор в одном слое. Следует заметить, что взаимодействие с порами тоже имеет смысл только внутри одного пористого слоя, т.е. на верхней и нижней границах слоя U_пор=0.

 b_surf, a_surf, c_surf, m_surf, ,b_r, a_r, c_r, b_ph, a_ph, c_ph, m_ph , m_p, b_p, a_p, c_p параметры модели.

 непрерывно внутри всей подложки, т.е на каждой границе между l и ll  слоями выполняется условие .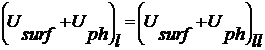

Условие на слияние блистеров друг с другом выглядит следующим образом:

. Слияние происходит, если D_f£0.5 (в параметрах решетки материала, внутри, которого находятся блистеры или если они по разные стороны от границы раздела металл-неметалл, то в берется наименьший параметр решетки).

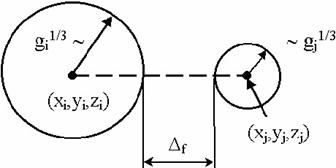
Рис. 5. Схема слияния блистеров.

Уравнения стохастического аналога

Стохастическое уравнение Ито в форме Стратоновича кинетического уравнения (1) имеет вид

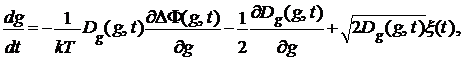                      (10)

где T_finish - длительность флуктуационной стадии, g_min и g_max - минимальное и максимальное значения начального размера пузырька (g₀), выбираются исходя из следующих условий: DF(g_min) = DF(g_max) = DF(g_cr) − kT, g_cr - критический размер зародыша, определяемый выражением 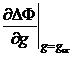= 0; x(t) - случайная функция (в данном случае это стандартный белый шум единичной интенсивности, поскольку здесь СДУ выписано в форме Ито - Стратоновича).

Кинетические уравнения решаются с помощью метода стохастического аналога. Используя наличие выделенного направления в задаче (направление падающего потока ионов) записываются уравнения для эволюции каждой координаты отдельно. Здесь и в дальнейшем под координатами блистера подразумевается координаты его центра масс. Уравнения для одной из координат x(t) записывается следующим образом

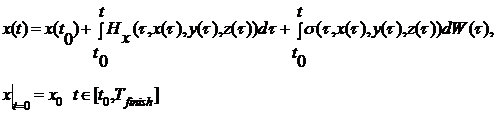                (11)

здесь

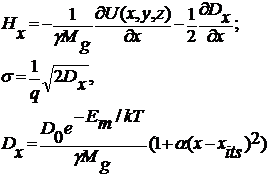                                                              (12)

x_its координата ближайшего междоузлия, E_m энергия миграции внедренного атома, D₀ коэффициент, соответствующий физическим параметрам задачи, q интенсивность белого шума.

Численная схема решения системы СДУ

Для решения системы 4-х взаимосвязанных СДУ с функционал- коэффициентами применяется метод не ниже 2-ого порядка точности в среднеквадратичном (модифицированный метод Артемьева).

Для i-ой траектории диффузионного Марковского процесса значения g_{n+1 и zn+1} в момент времени n+1 рассчитываются по следующим формулам:

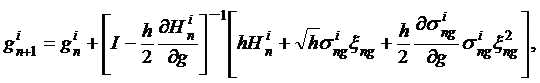
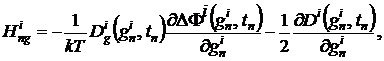                                      (13)

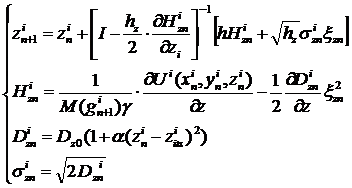                                             (14)

здесь I единичная матрица, h, h_z шаги по времени для эволюции размера и перемещения в пространстве (для всех трех пространственных направлений x, y, z шаг один и тот же).

СДУ в форме Ито - Стратоновича, то , где a_{1 и} a₂ случайные числа, равномерно распределенные в интервале(0,1).

Отношение разницы результатов, полученных с использованием формы Ито и с использованием формы Ито-Стратоновича, к результатам, полученным с использованием формы Ито-Стратоновича достигает 15%. Отношение разницы результатов, полученных с использованием метода Эйлера и с использованием метода Артемьева решения СДУ, к результатам, полученным с использованием метода Артемьева достигает 38%.

Программный код для моделирования блистеринга в тонкой пленке.

Образование пористости в материалах при имплантации ионов плохорастворимых газов актуально для оценки их прочности, для мониторинга деградации свойств материалов ТЯР. Образование пор (кластеров зародышей) можно анализировать как ``структуры'' самоорганизации, или долгоживущие пространственно-временные образования в многомерных фазовых пространствах.

Результаты численных исследований в указанном направлении являются актуальными, создание высокопроизводительных кодов для современных вычислительных средств вместе с кинетическим уровнем описания явлений в пространственно-временных масштабах, характерных для быстропротекающих неравновесных явлений могут считаться конкурентоспособными, поскольку известные аналоги не сочетают в себе и сложность уровня постановки задач и реализацию в компьютерных кодах с проработкой достаточно общего формализма и оптимальной архитектуры приложения, охватывающих широкий спектр задач численного моделирования. Поэтому, создание на их основе пакета быстрой разработки приложений численного моделирования, обеспечивающего высокую производительность, масштабируемость (от одного персонального компьютера до кластера), и оптимальное автоматическое использование инструментальных средств операционной системы и параллельных алгоритмов пользователями различной квалификации исключительно важно.

В настоящий момент существует ряд систем, использующихся для создания приложений численного моделирования. Эти системы предоставляют некоторый язык (фактически свой собственный язык программирования с возможностью подключения дополнительных библиотек), позволяющий реализовывать численные схемы и проводить расчеты. Наиболее часто используемые сложные специальные функции и некоторые алгоритмы реализованы в виде высокопроизводительных расширений языка (библиотек). Как правило присутствуют средства визуализации результатов, в том числе двумерных функций. К недостаткам существующих систем можно отнести их малую производительность в сложных вычислительных задачах, обусловленную невозможностью создания универсального высокоуровнего языка для реализации сложных массивнопараллельных численных схем работающих на больших сетках, отсутствие (или крайне слабые возможности) автоматического упорядоченного сохранения начальных параметров, результатов и исходных кодов с возможностью последующего многопараметрического поиска.

В настоящий момент оптимальным считается создание прототипа приложения на слаботипизированном интерпретируемом языке с автоматическим управлением памятью и развитыми возможностями функционального программирования (в данном случае Python), с дальнейшим переводом критичных по быстродействию частей кода на статически компилируемые языки (например С++). При этом верхний управляющий слой приложения и интерфейсные части, как наиболее часто модифицируемые, остаются написанными на Python-е. Для встраивания С++-кода в Python используется пакет SWIG (Simplified Wrapper and Interface Generator - упрощенный генератор оболочек и интерфейсов) [24].

Ивановым А.В. произведена автоматизация программирования на этапе технологического моделирования.

Исходные коды приложения хранятся под CVS (Concurrent Version System --- система контроля параллельных версий), сборка приложения производится с использованием утилиты automake, для визуализации результатов применяется gnuplot. Такой подход обеспечивает приемлемую скорость разработки и модификации приложения (благодаря Python-у, объектно-ориентированным возможностям С++ и другим использумеым утилитам); высокую производительность приложения, по сравнению с такими системами как mathlab, mathcad и mathematica (поскольку C++ позволяет наиболее более полно реализовывать машинные возможности); но все же требует от создателя приложения больших трудозатрат и высокой программисткой квалификации.

Интерпретация численного эксперимента реализации диффузионного Марковского процесса  в задачах моделирования блистеринга.

Математическая модель случайного процесса

{g(t), t³0}, "gÎ{G},

где g - размер кластера в фазовом пространстве {G} рассматривает условия  реализации МП: блистер должен содержать более чем 2 частицы g > 2 и меньше размера, при котором устойчивость блистера нарушается. Дискретная модель МП в [t₀, t] реализуется K траекториями МП, то есть на каждом шаге Dt необходимо перейти от определения точного числа траекторий МП (например, K) к с вероятностной мере. Физической интерпретацией этого может быть следующее: множество точек фазового пространства размеров {G} в численном эксперименте суммируется с учетом частичных фазовых объемов G_q. Для одномерного МП фазовое пространство размеров кластеров {G}:{g_min,g_max} содержит значение МП {g(t)}. Функция распределения /ФР/ по размерам g- f_r(g,t) по определению задает вероятность обнаружить среднее число элементов дискретной среды в заданной подобласти {G} фазового пространства и может быть рассчитана как

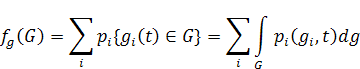
Здесь p_i - конечномерные меры, расчет которых производится с помощью СДУ Ито, индекс i обозначает бесконечное счетное множество элементов дискретной среды. По условиям численного эксперимента мы рассматриваем K траекторий МП и для каждого частичного фазового объема, входящего в {G}, мы обрываем бесконечное счетное множество конкретными конечными значениями числа элементов. Запишем процедуру восстановления ФР по расчетам траекторий случайного процесса. Для шага Dt: определяем g_min,g_max, задаем число q интервалов, определяем шаг Dg=|g_max-g_min|/q, вычисляем значения f_r(g) в момент времени t₁, t₂, ... Таким образом, схема метода стохастического моделирования может выглядеть так:

-по пространственно -временным масштабам физической проблемы рассчитываем функционал-коэффициенты уравнений (1), (2), выбираем виды источников и стоков

-формулируем граничные и начальные условия;

-уточняем дискретную модель среды, включающую в себя:

фазовые переменные и набор компонент,

потенциалы (сечения) взаимодействия и законы сохранения;

-формулируем соответствующие СДУ,

-при заданных начальных условиях, соответствующих физическим  параметрам задачи, решаем задачу Коши для полученной системы СДУ, так чтобы при этом порядок аппроксимации в с.к. пределе гарантировал достаточную точность расчетов;

-по траекториям случайного процесса X_i(t), i=1,…,N  рассчитываем математическое ожидание , дисперсию                               , а также и более высокие моменты случайного процесса X(t)

-по траекториям процесса X(t) восстанавливаем  МП и макроскопические физические параметры исследуемой среды, например, поток блистеров, рассчитываемые интегрированием неравновесных                 ФР .

Результаты стохастического моделирования блистеринга в пленке Ni.

В общем случае, концентрация атомов гелия в материале зависит от дозы облучения и глубины от облучаемой поверхности z. Блистеринг образуется, если концентрация внедренного гелия на глубине порядка проекционного пробега превысит предел растворимости гелия в никеле. В начале процесса образования блистеров, когда только наступило превышение предела растворимости газа в материале, происходит лавинообразное увеличение количества зародышей блистеров, после чего количество вновь образовавшихся блистеров в единицу времени можно считать постоянным. Рис. 6-10 соответствуют ситуации, когда количество вновь образовывающихся в ед. времени зародышей блистеров постоянно.

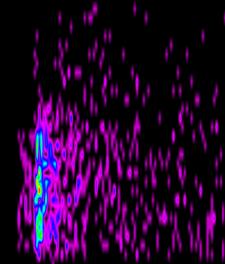
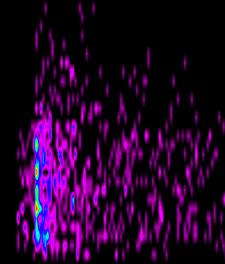
Цветная визуализация функции распределения блистеров в зависимости от их размеров (в Е) и глубины от облучаемой поверхности (в параметрах решетки) в момент времени 0,25 T_finish для рис.6, 0,5 T_finish для рис.7, 0,75 T_finish для рис.8 и T_finish=10^-5 с для рис.9. Функция распределения блистеров по размерам и глубине от облучаемой поверхности для T_finish= 10^-5 с приведена на рис.10. Расчет (рис.6-10) произведен для блистеринга He-Ni на тонкой подложки толщиной 200 параметров решетки, т.е. ~70 нм. Доза облучения 10¹⁷ ион/см², энергия ионов 5 кэВ, длина проекционного пробега приблизительно 30 нм, падение по нормали к поверхности. Температура 1000К, число траекторий 10⁶. На правой части рисунка представлена шкала соответствия цвета и значений функции распределения. Функция распределения нормирована на 1. Расчетная область 400х400х200 параметров решетки, причем на границах по х и у применяются периодические граничные условия, а на границах по z (z=0 облучаемая поверхность z=200 нижняя не облучаемая поверхность) рассматривается гибель блистеров. На рис. 10 представлена двумерная функция распределения блистеров по размерам (в Å) и глубины от облучаемой поверхности (в параметрах решетки) для описанных выше физических параметрах в момент времени T_finish=10^-5 с.

Рис. 11-12 соответствуют тестовым расчетам.

Для рис. 6-14 в начальный момент времени блистеры отсутствуют, затем рождаются равномерно с течением времени с размерами [3,99Å: 4,34Å] и распределены равномерно по глубине в интервале от 30 до 100 параметров решетки.

Распределение дефектов на поверхности образцов ("холмов", кратеров эрозии, цепочек островков жидкой фазы материала и др. структур на металлах, диэлектриках, сплавах, композитных материалах ) важно для прогнозирования  прочности и радиационной стойкости материалов. Полученные при воздействии на образец ионизирующего излучения  /ИИ/ повреждения структуры кристаллической решетки, образование объемных и поверхностных дефектов, можно сравнить с результатами моделирования процесса  их образования в численном эксперименте, по распределению структур поверхности можно предположить возможный сценарий их возникновения, основывающийся на  исходных предпосылках численной модели, а по степени совпадения или несовпадения картины шероховатости включать в рассмотрение  дополнительные факторы взаимодействия плазмы с поверхностью, создавая тем самым согласованную картину развития дефектов, которую  можно оценивать с точки зрения перспектив разрушения материала или определения предельных нагрузок данного образца,  либо рассматривая перспективы использования испытываемых материалов в установках с повышенными потоками ИИ.

Расчеты деградации свойств материалов (образование слоев пористости и отшелушивания материала, загрязнение плазмы и др.) и данные по микрошероховатости  поверхности, характеризующеся неравновесным распределением кратеров по размерам (ФР), динамикой образования дефектов на поверхности и степенью разрушения ее за счет  блистеринга представлены на графиках ( рис. 15-рис. 17), ранее сравнивались [25] с визуализированными данными микроскопии образцов, обработанных плазмой. Эти  исследования направлены на создание программ мониторинга прочностных свойств материалов в плазменных установках, методики могут быть использованы для анализа повреждаемости зеркал.

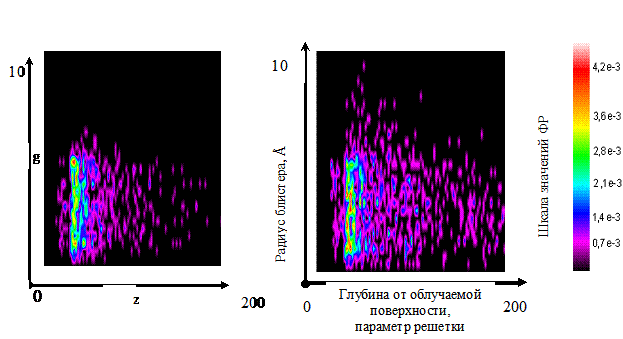
Рис.6                                                           Рис.7

Рис.8                                                          Рис.9

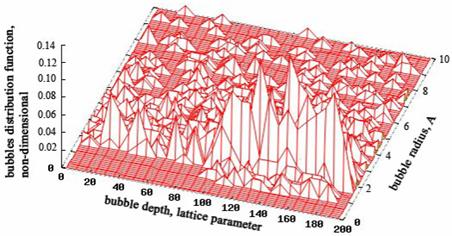
Рис.10

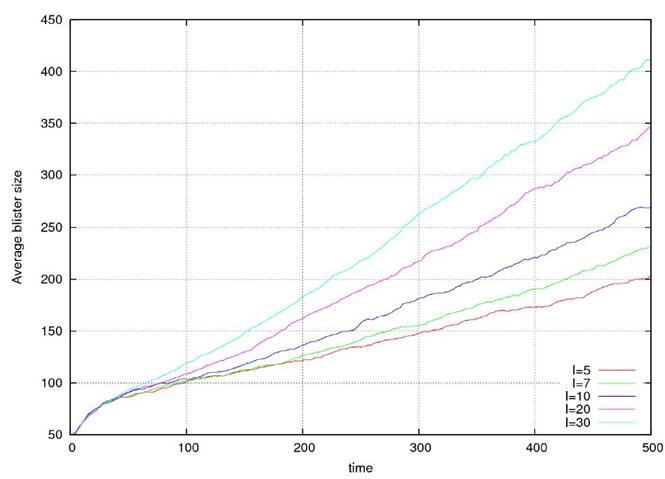
Рис. 11 Изменение среднего размера блистера (в числе атомов Не в нем) в зависимости от премени (в шагах алгоритма 2 ×10^-8 с.). Интенсивность источника (кол-во вновь образовавшихся блистеров  за шаг алгоритма) показана в нижнем правом углу графика.

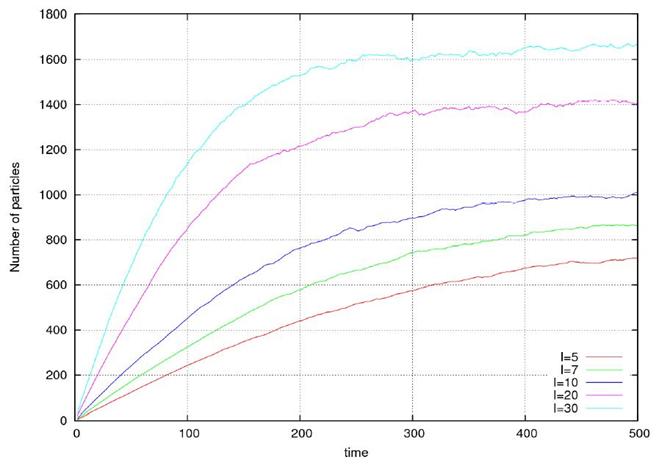
Рис. 12 Изменение общего количества блистеров (шт.) в зависимости от времени (в шагах алгоритма 2 ×10^-8 с.). Интенсивность источника (количество вновь образовавшихся блистеров  за шаг алгоритма) показана в нижнем правом углу графика.

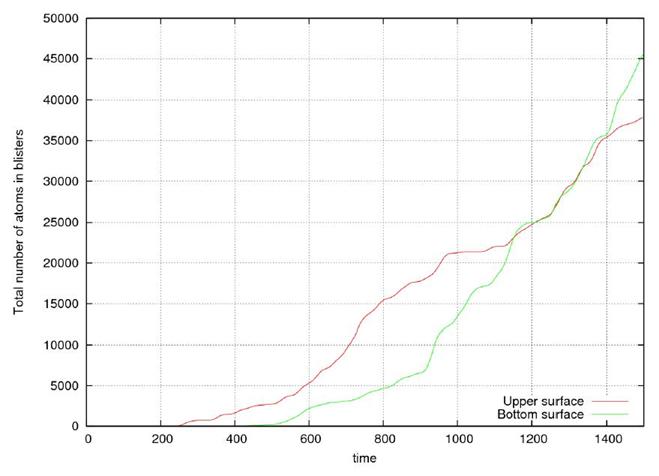
Рис.13 Зависимость среднего размера блистера, вышедшего на поверхность, от времени. Время измеряется в шагах алгоритма ~2 ×10^-9 с. Размер блистера измеряется в числе атомов гелия в нем. Блистеры, вышедшие на поверхность, контактирующую с плазмой, обозначены красной линией, на нижнюю, не облучаемую поверхность, зеленой линией.

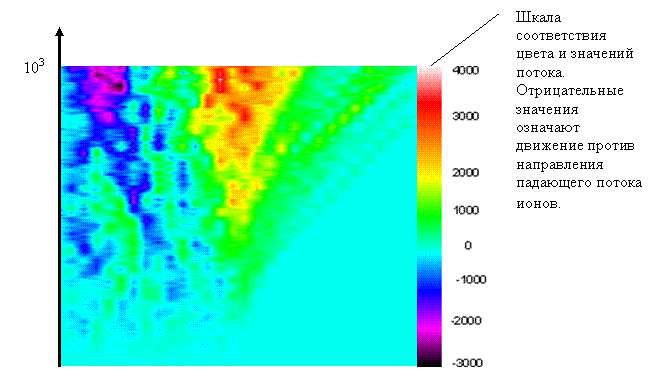
Рис.14 Цветная визуализация потока вещества вдоль оси z. По вертикали отложено время в шагах алгоритма ×10^-8 с, по горизонтали глубина от поверхности в параметрах решетки. При расчете значений потока принимаются следующие обозначения: масса – количество атомов в блистере, скорость определяется как параметр решетки деленный на шаг по времени.

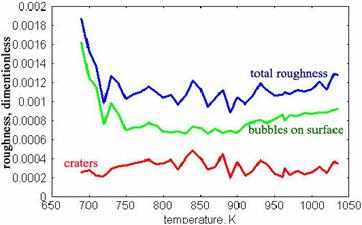
Рис. 15 Зависимость шероховатости в момент окончания флуктуационной стадии от температуры образца. Шероховатость – отношение площади неровностей поверхности (кратеров и вздутий) к общей площади поверхности. Шероховатость безразмерна. Температура измеряется в К.

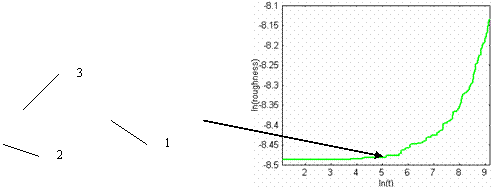
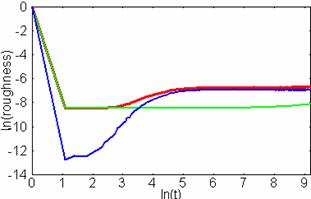
Рис. 16 Зависимость шероховатости от времени в двойном логарифмическом масштабе. Время измеряется в шагах алгоритма 10^-8 с. Линия 1 соответствует шероховатости за счет кратеров от погибших блистеров. Линия 2 соответствует шероховатости, обусловленной вышедшими на поверхность, но не погибшими на ней блистерами. Линия 3 показывает общую шероховатость поверхности. Температура подложки соответствует верхней температурной границе высокотемпературного блистеринга (0,6 температуры плавления материала подложки), в представленном случае это 1035К.

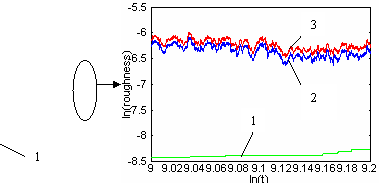
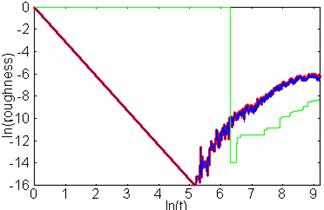
Рис. 17 Зависимость шероховатости от времени в двойном логарифмическом масштабе. Время измеряется в шагах алгоритма 10^-8 с. Линия 1 соответствует шероховатости за счет кратеров от погибших блистеров. Линия 2 соответствует шероховатости, обусловленной вышедшими на поверхность, но не погибшими на ней блистерами. Линия 3 показывает общую шероховатость поверхности. Температура подложки соответствует нижней температурной границе высокотемпературного блистеринга (0,4 температуры плавления материала подложки), в представленном случае это 690К.

Заключение.

—       С применением кинетической теории, модели Броуновского движения и метода стохастического аналога рассмотрена флуктуационная стадия высокотемпературного блистеринга в пленке толщиной порядка 100 нм.

—       Система из 4-х взаимосвязанных стохастических дифференциальных уравнений с функционал-коэффициентами решена численно. Численная схема реализована в виде высокоэффективного программного комплекса, написанного на языках С++ и Python, позволяющего рассчитать характеристики блистеринга в слоях металла и пористой армирующей прослойки.

—       Наблюдается нелинейный характер зависимости среднего размера блистера от времени. Замедление роста по всей видимости связвно с тем, что по мере своего роста блистер вынужден разрывать большое количество связей кристаллической решетки.

Благодарности

Работа частично поддержана грантами РФФИ 06-01-00569a и 07-01-00768, Программой «Наночастицы и нанотехнологии» Отделения математики РАН, грантом поддержки ведущих научных школ НШ-397.2008. Авторы выражают благодарность В.Д. Левченко, Т.В. Левченко за творческое сотрудничество.

Литература

[1] Рогов А.В., Вуколов К.Ю., Горшков А.В., Гуреев В.М.  Исследования методом магнетронного распыления деградации монокристаллических и напыленных молибденовых зеркал в условиях, подобных ИТЭР // Вопросы атомной науки и техники. Сер. Термоядерный синтез, 2005, вып. 2, с. 39—54.

[2] Voitsenya V.S., Bardamid A.F., Belyaeva A.I. et al. Diagnostic first mirrors for burning plasma experiments. Proc. of Intern. Conf. on Advanced Diagnostics for Magnetic and Inertial Fusion. Varenna, Italy, September 2001.— Kluwer Academic / Plenum Publishers, 2002, p. 285—294.

[3] Frank Goodwin, Yu-Jen Fan,Greg Denbeaux, Patrick Naulleau, Sven Trogisch, Markus Bender, Christian Schwarz,Bruno LaFontaine, Jeff Mackey.// Baselining the performance of a EUVL full field scanner through rigorous modeling.

[4] Сигов Ю.С. Вычислительный эксперимент :мост между прошлым и будущим физики плазмы. Избранные труды.//Сост.Змиевская Г.И., Левченко В.Д.-М.:Наука, ФИЗМАТЛИТ, 2001, 288 с)

[5] R.P.Sear//J.Phys.:Condens.Matter 19(2007) 033101(28 pp)

[6] Зельдович Я.Б.  К теории образования новой фазы, кавитация // ЖТЭФ, 1942, т. 12, N 11-12, с. 525-538

[7] Змиевская Г.И. Стохастические аналоги неравновесных столкновительных процессов// Физика плазмы, 1997, т.23, N 4, с.368-382

[8] Морозов А.И., Сигов А.С. //ЖЭТФ, 1989, т. 95, с.170-189

[9] Morosov A.I., Sigov A.S., Solid State Commun.,1988, т. 67, с. 841-856

[10] Морозов А.И., Овченков П.А., Сигов А.С. Взаимодействие дефектов в кристалле и процессы кластеризации//Дискретное моделирование плазмы, под ред. Сигов Ю.С. , 1990, Москва, Сборник трудов ИПМ им. М.В. Келдыша РАН

[11] Бeрзин А.А, Морозов А.И., Сигов, А.С. Диффузия легких атомов на поверхности кристалла и процессы кластеризации // ФТТ, т. 38, № 5, 1996, с. 1349-1356

[12] Bondareva A.L., Zmievskaya G.I.  Stochastic model applied to plasma-surface interaction's simulation // The Europ. Phys. Journ. D -Atomic, Molecular, Optical and Plasma Phys. vol.38, 2006, p.143-149.

[13] Бондарева А.Л., Змиевская Г.И. Стохастическое моделирование флуктуационной стадии образования тонких пленок // Доклады Академии Наук, изд. Наука, 2005, т.401, N 4, с. 471-475.

[14] Змиевская Г.И. "Стохастическое моделирование неравновесных процессов"//в кн."Будущее прикладной математики. Лекции для молодых ученых:от идей к технологиям".-- под ред. Г.Г. Малинецкого. М.: "КомКнига", 2008,  с.512 (сс.255-330)

[15] Змиевская Г.И., Бондарева А.Л. "Численное моделирование вакансионно-газовых дефектов поверхности твердого тела, возникающих после воздействия на неё горячей плазмы" в книге "Энциклопедия низкотемпературной плазмы." т. IX-2. "Радиационная плазмодинамика: физика, экспериментальные технологии, применения", серия Б, 2007, стр. 480-506.

[16] Бондарева А.Л., Змиевская Г.И. Моделирование флуктуационной стадии высокотемпературного блистеринга // Изв. Акад. Наук. Сер.физическая, 2004, т.68, N3, cc.336-339.

[17] Аверина Т.А., Артемьев С.С., Новое семейство численных методов решения стохастических дифференциальных уравнений //ДАН СССР, 1986, т.288, N4, с.777-780.

[18] Zmievskaya G.I., Bondareva A.L., Levchenko V. D., Levchenko T.V.  A kinetic stochastic model of blistering and nanofilm islands deposition: self organization problem // J. Phys. D: Appl. Phys., 2007, N 40, pp. 4842 – 4849

[19] Bondareva A.L., Zmievskaya G.I., Ivanov A.V. Plasma Surface Interaction: thin film formation // Proc. 25-th International Symposium of Rarefied Gas Dynamics “RGD25”, Saint-Peterburg, Russia, July 21-28 2006, ed: M.S.Ivanov and A.K. Rebrov, Novosibirsk, 2007, pp. 715-719

[20] Бондарева А.Л., Змиевская Г.И. Стохастическое моделирование образования тонких пленок на поверхности образца // Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2006, N 10, с. 1-6

[21] Бондарева А.Л., Змиевская Г.И. Radiation-induced defect's clustering and self-organization during surface modification // Вопросы атомной науки и техники, 2006, N 5, с. 248-253

[22] Бондарева А.Л., Змиевская Г.И. Численное моделирование вакансионно-газовых дефектов поверхности твердого тела, возникающих после воздействия на неё горячей плазмы// "Энциклопедия низкотемпературной плазмы". Гл. ред. серии В.Е. Фортов. Серия Б. "Справочные приложения, базы и банки данных". Тематический том IX - 3. "Радиационная плазмодинамика". Под ред. В.А. Грибкова. Москва, Янус-К, 2007, с. 480-506

[23] Бондарева А.Л., Змиевская Г.И. Исследование изменения свойств поверхности в результате высокотемпературного блистеринга методом стохастического моделирования// Изв. Акад. Наук. Сер.физическая, 2002, т. 66, N 7, cc. 994-997

[24] Иванов А.В. "Система контроля результатов и алгоритмов для задач численного моделирования" Автоматизация и современные технологии. М.: Машиностроение. 2007 12. С. 29-34

[25] А.Л.Бондарева, В.А.Грибков, А.В.Дубровский, Г.И. Змиевская, В.Н.Пименов Microstructure surface damaging:ionizing radiation damaging pulse fluxes surface treatment and computer simulation//Proc. of  XXXVIII Intern. Conf. on Phenomena in Ionized Gazes, July 15-20, 2007 Prague Czech Republic.-Ed.by J.Schmidt, M.Simek, S.Pekarek, V.Prucher.- 1P03-13, 2007 http://icpig2007.ipp.cas.cz , с.  1 -  4