Проектирование квазисинхронных орбит КА вокруг Фобоса для решения задачи посадки на его поверхность
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
– |
параметр
орбиты Фобоса, |
|
|
– |
гравитационные
постоянные Фобоса и Марса. |
Невозмущенное движение ![]() с нулевым
эксцентриситетом
с нулевым
эксцентриситетом ![]() описывается системой
дифференциальных уравнений:
описывается системой
дифференциальных уравнений:
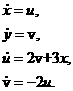 (2)
(2)
Решение уравнения (2) можно представить в виде:
![]() (3)
(3)
где
![]() – постоянные.
– постоянные.
Решение уравнения (1) можно рассматривать как движение
по эллипсу, центр которого имеет координаты: ![]() и
и ![]() .
.
Используя координаты центра эллипса, выражение (3)
можно представить в виде:
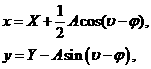 (4)
(4)
где
|
|
– |
большая
полуось оскулирующего эллипса, |
|
|
– |
разность
фаз между движением КА вокруг Фобоса и Фобоса вокруг Марса, определяемая из
условия: |
Используя (4), найдем, что ![]() (5)
(5)
Соотношения
(4) и (5) описывают замену переменных в уравнении (1), в результате которой
происходит переход от переменных ![]() к новым переменным
к новым переменным ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Полученная в результате система уравнений имеет вид:
. Полученная в результате система уравнений имеет вид:
![]() ,
,
![]()
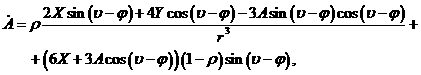 (6)
(6)
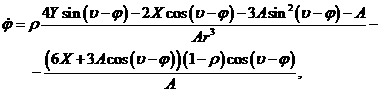
где
![]() .
.
Вычисляя производные от ![]() по
по ![]() , получим:
, получим:
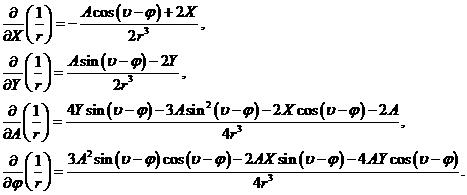 (7)
(7)
Упростим
(6) с использованием (7):
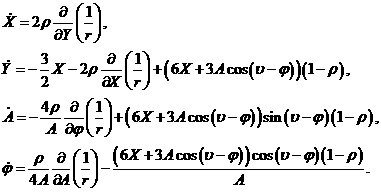 (8)
(8)
Эволюционное движение системы (8) изучено в работе [3]
для случая плоского кругового движения задачи Хилла (![]() ) в условиях удаления тела нулевой массы от тела меньшей
массы на расстояния, значительно превышающие радиус сферы Хилла. В этой работе
получены эволюционные уравнения движения центра эллипса вдоль оси
) в условиях удаления тела нулевой массы от тела меньшей
массы на расстояния, значительно превышающие радиус сферы Хилла. В этой работе
получены эволюционные уравнения движения центра эллипса вдоль оси ![]() . Найдены два интеграла эволюционных уравнений. Первый
интеграл – большая полуось орбиты. Второй интеграл – результат преобразования
интеграла Якоби к новым координатам. Получено соотношение для периода либрации
и его предельные значения для малых амплитуд либрации. Пространственный случай
эволюционного движения в аналогичных условиях исследован в работе [4]. В этих
работах с целью изучения эволюции вдоль оси
. Найдены два интеграла эволюционных уравнений. Первый
интеграл – большая полуось орбиты. Второй интеграл – результат преобразования
интеграла Якоби к новым координатам. Получено соотношение для периода либрации
и его предельные значения для малых амплитуд либрации. Пространственный случай
эволюционного движения в аналогичных условиях исследован в работе [4]. В этих
работах с целью изучения эволюции вдоль оси ![]() при упрощении системы
уравнений была исключена составляющая, описывающая эволюционное движение вдоль
при упрощении системы
уравнений была исключена составляющая, описывающая эволюционное движение вдоль ![]() . Тем самым отброшено множество движений, представляющих
практический интерес [1]. Поэтому, решая задачу построения системы эволюционных
уравнений для поиска решений системы (1), обладающих заданным свойством, нужно
специальным образом выбрать фазовые переменные.
. Тем самым отброшено множество движений, представляющих
практический интерес [1]. Поэтому, решая задачу построения системы эволюционных
уравнений для поиска решений системы (1), обладающих заданным свойством, нужно
специальным образом выбрать фазовые переменные.
Одним из основных элементов при построении системы
эволюционных уравнений является представление интеграла ![]() через выбранные
фазовые параметры. Такие представления с использованием полных эллиптических
интегралов 1-го и 2-го рода найдены в работах [3-6].
через выбранные
фазовые параметры. Такие представления с использованием полных эллиптических
интегралов 1-го и 2-го рода найдены в работах [3-6].
Рассмотрим теперь уравнение (1) и представим движение
вокруг Фобоса с использованием двух эллипсов. КА движется по эллипсу, полуоси
которого равны ![]() и
и ![]() . Разность фаз между движением КА вокруг Фобоса и Фобоса
вокруг Марса составляет
. Разность фаз между движением КА вокруг Фобоса и Фобоса
вокруг Марса составляет ![]() . Центр эллипса, по которому движется КА, также движется по
эллипсу, полуоси которого равны
. Центр эллипса, по которому движется КА, также движется по
эллипсу, полуоси которого равны ![]() и
и ![]() ;
; ![]() – константа. Разность
фаз между движением КА и движением центра эллипса составляет
– константа. Разность
фаз между движением КА и движением центра эллипса составляет ![]() . Такому представлению движения КА соответствует замена
переменных:
. Такому представлению движения КА соответствует замена
переменных:
 (9)
(9)
После
выполнения замены переменных (9) уравнение (1) преобразуется к виду:

(10.1)
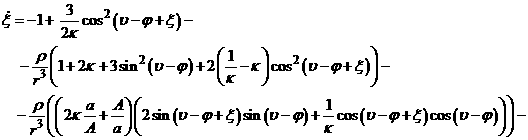
![]()
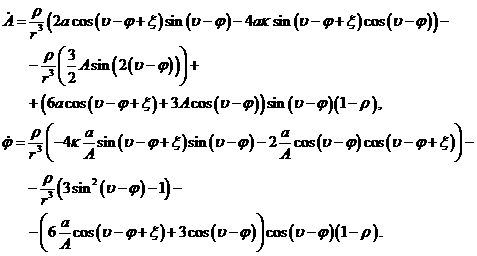 (10.2)
(10.2)
Интеграл
Якоби, для системы (10.1, 10.2) при ![]() , имеет вид:
, имеет вид:
![]() .
.
2. Предварительный численный анализ. Постановка
задачи аналитических исследований
В результате численного интегрирования системы
уравнений (10.1-10.2) по начальным условиям, найденным в работе [1], получены
траектории, имеющие вид, показанный на рис. 1. Положение центра эллипса ![]() определяется
формулами:
определяется
формулами:
![]() (11)
(11)
Положение
точки нулевой массы определяется формулами (4). Траектории, показанные на рис.
1, получены при ![]() по следующим начальным
условиям:
по следующим начальным
условиям: ![]()
Как видно из рис. 1, при начальных условиях, найденных
в [1], движение КА (точки нулевой массы) и центра эллипса происходит в узких
кольцеобразных областях, внешней и внутренней. КА имеет обратное движение по
отношению к движению Фобоса вокруг Марса, а центр эллипса – прямое. Внешнее
кольцо – это кольцо, в которое попадает траектория КА. КА движется по
перемещающемуся эллипсу, центр которого движется в противофазе по отношению к
КА. Поэтому КА всегда находится в области пересечения перемещающегося эллипса и
внешнего кольца. Большая полуось эллипса практически не меняется. Перемещение
эллипса происходит за счёт движения его центра в пределах внутреннего кольца.
При этом значения ![]() и
и ![]() близки к своим средним
значениям, а значение
близки к своим средним
значениям, а значение ![]() близко к
близко к ![]() .
.
Рассмотрим ![]() – средние значения
величин
– средние значения
величин ![]() и их производных
и их производных ![]() :
:
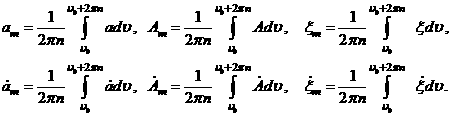 (12)
(12)
В таблицах 2.1, 2.2, 2.3 приведены результаты расчётов
величин ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() для трех вариантов
начальных условий (удаления начальной точки от поверхности Фобоса), найденных в
[1]. Таблицы содержат по три строки. Первая строка соответствует удалению на 50
км, вторая – на 55 км, третья – на 60 км. Из этих таблиц видно, что с удалением
орбиты от поверхности Фобоса среднее значение полуоси внешнего эллипса
для трех вариантов
начальных условий (удаления начальной точки от поверхности Фобоса), найденных в
[1]. Таблицы содержат по три строки. Первая строка соответствует удалению на 50
км, вторая – на 55 км, третья – на 60 км. Из этих таблиц видно, что с удалением
орбиты от поверхности Фобоса среднее значение полуоси внешнего эллипса ![]() возрастает, а
внутреннего
возрастает, а
внутреннего ![]() убывает. Средние
значения производных
убывает. Средние
значения производных ![]() близки к нулю. Среднее
значение разности фаз
близки к нулю. Среднее
значение разности фаз ![]() близко к
близко к ![]() , а
, а ![]() – среднее значение
производной – к нулю.
– среднее значение
производной – к нулю.
Из приведенных выше рассмотрений следует постановка
задачи для аналитических исследований. Нужно построить осредненную систему
уравнений для исходной системы (10.1) и (10.2) и найти ее решения, обладающие
свойствами: ![]()
Далее, используя найденное аналитическим способом
решение и разбросы мгновенных значений относительно средних, можно сканированием
в достаточно узкой области найти искомое решение системы (10.1), (10.2),
обладающее свойством попадания орбиты в узкую кольцеобразную область вокруг
Фобоса (тела меньшей массы).
Таблица 2.1. Диапазоны изменения средних и мгновенных значений полуоси
внешнего эллипса и ее производной
|
|
min |
max |
min |
max |
min |
max |
min |
max |
|
1 |
3.5224 |
3.5687 |
3.3286 |
3.8763 |
0.0000 |
0.0006 |
-0.6894 |
0.6894 |
|
2 |
3.6130 |
3.6720 |
3.4318 |
3.9590 |
0.0000 |
0.0007 |
-0.6237 |
0.6237 |
|
3 |
3.7150 |
3.7867 |
3.5444 |
4.0555 |
0.0000 |
0.0005 |
-0.5681 |
0.5681 |
Таблица 2.2. Диапазоны изменения средних и мгновенных значений
полуоси и производной внутреннего эллипса и ее производной
|
|
min |
max |
min |
max |
min |
max |
min |
max |
|
1 |
0.4416 |
0.4656 |
0.3929 |
0.5310 |
-0.0001 |
0.0000 |
-0.1570 |
0.1572 |
|
2 |
0.3984 |
0.4217 |
0.3464 |
0.4850 |
-0.0001 |
0.0001 |
-0.1501 |
0.1502 |
|
3 |
0.3607 |
0.3832 |
0.3054 |
0.4450 |
-0.0001 |
0.0000 |
-0.1460 |
0.1459 |
Таблица 2.3. Диапазоны изменения средних и мгновенных значений
разности фаз в движении по внутреннему и внешнему эллипсам и производной
разности фаз
|
|
min |
max |
min |
max |
min |
max |
min |
max |
|
1 |
3.1413 |
3.1416 |
2.8364 |
3.4468 |
-0.0003 |
0.0004 |
-0.4886 |
0.7620 |
|
2 |
3.1413 |
3.1416 |
2.8041 |
3.4793 |
-0.0004 |
0.0004 |
-0.4947 |
0.8404 |
|
3 |
3.1412 |
3.1416 |
2.7703 |
3.5127 |
-0.0005 |
0.0004 |
-0.5007 |
0.9262 |

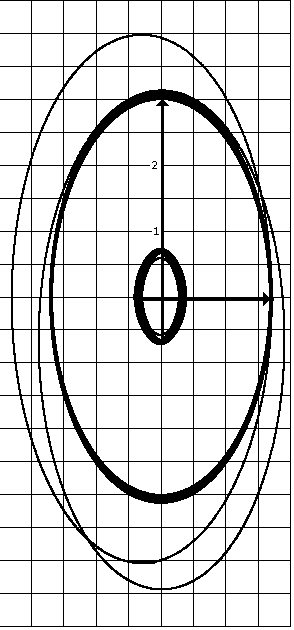
Рис. 1. Траектории движения точки нулевой массы (КА) и центра
перемещающегося эллипса. Мгновенные положения эллипсов, по которым движется КА,
показаны для двух моментов времени, когда ![]() (
(![]() ) и
) и ![]() (б). Центры этих
эллипсов находятся в точках внутреннего кольца, из которых начинаются стрелки.
(б). Центры этих
эллипсов находятся в точках внутреннего кольца, из которых начинаются стрелки.
3. Подготовка системы (10.1), (10.2) к
усреднению
Используя зависимость ![]() от
от ![]() , преобразуем систему (10.1), (10.2).
, преобразуем систему (10.1), (10.2).
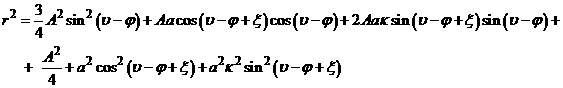 (13)
(13)
Вычислим производные ![]() по
по ![]() .
.
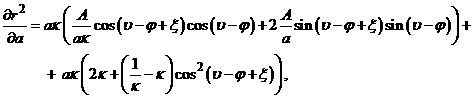 (14)
(14)
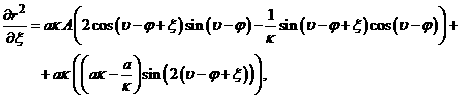 (15)
(15)
![]() (16)
(16)
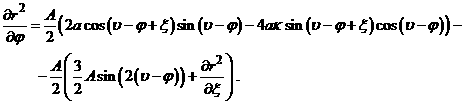 (17)
(17)
В каждом из 4-х уравнений (10.1) и (10.2) выделим
сумму членов в скобках, которые умножаются на ![]() . Заметим, что эта сумма в уравнении для
. Заметим, что эта сумма в уравнении для ![]() равна
равна ![]() , в уравнении для
, в уравнении для ![]() –
– 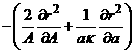 , в уравнении для
, в уравнении для ![]() –
– 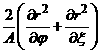 , в уравнении для
, в уравнении для ![]() –
– ![]() . Используя это, преобразуем систему (10.1) и (10.2) к виду:
. Используя это, преобразуем систему (10.1) и (10.2) к виду:
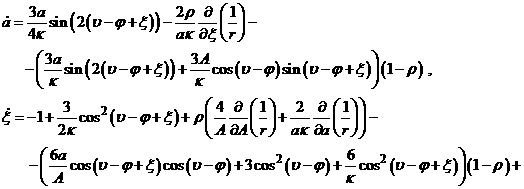 (18.1)
(18.1)
![]()
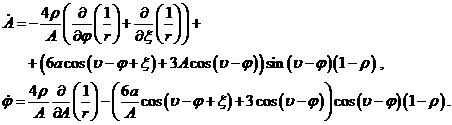 (18.2)
(18.2)
Правильность тождественных преобразований системы
(10.1), (10.2) к виду (18.1), (18.2) подтверждена численной проверкой, при
которой одновременно интегрировались указанные выше системы уравнений и
сопоставлялись полученные результаты.
4. Частный случай плоского кругового
движения задачи Хилла (![]() )
)
В случае плоской круговой задачи система (18.1),
(18.2) преобразуется к виду:
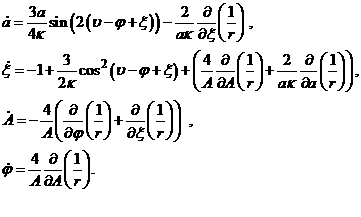 (19)
(19)
Усредним
систему (19) на интервале от 0 до 2π. Обозначим среднее значение ![]() , умноженное на 2π, как
, умноженное на 2π, как ![]() , т.е.
, т.е. 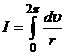 , а средние значения переменных как
, а средние значения переменных как ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Эти средние значения удовлетворяют следующей системе
дифференциальных уравнений:
. Эти средние значения удовлетворяют следующей системе
дифференциальных уравнений:
 (20)
(20)
Очевидно,
что ![]() не зависит от фазы
не зависит от фазы ![]() . Поэтому
. Поэтому ![]() . Отсюда следует, что справедливо равенство:
. Отсюда следует, что справедливо равенство: ![]() . Поэтому
. Поэтому ![]() — интеграл системы
(20). Интеграл Якоби для усреднённой системы (20) имеет вид:
— интеграл системы
(20). Интеграл Якоби для усреднённой системы (20) имеет вид: ![]() .
.
5. Вычисление значения интеграла ![]()
Введем обозначения: ![]() . Используя эти обозначения, преобразуем (13) к виду:
. Используя эти обозначения, преобразуем (13) к виду:
![]() , (21)
, (21)
где
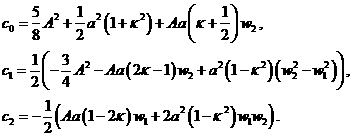
Обозначим
![]() . Пусть
. Пусть ![]() определяется как
определяется как ![]() , тогда (21) преобразуется к виду:
, тогда (21) преобразуется к виду:
![]() , (22)
, (22)
где
![]() , т. к. в рассматриваемом множестве решений
, т. к. в рассматриваемом множестве решений ![]() .
.
Рассмотрим:
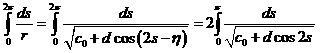 . (23)
. (23)
Т.к.
![]() , для
, для ![]() применима формула
2.571 пункт 4 из [16], которая позволяет представить неопределенный интеграл
применима формула
2.571 пункт 4 из [16], которая позволяет представить неопределенный интеграл ![]() через неполный
эллиптический интеграл первого рода:
через неполный
эллиптический интеграл первого рода:
 , (24)
, (24)
где
![]() – эллиптический
интеграл первого рода,
– эллиптический
интеграл первого рода, 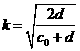 ‑ модуль
интеграла.
‑ модуль
интеграла.
Используя (24), преобразуем (23) к виду:
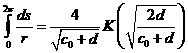 , (25)
, (25)
где
![]() – полный эллиптический
интеграл первого рода.
– полный эллиптический
интеграл первого рода.
6. Вычисление производных ![]()
Представим ![]() ,
, ![]() ,
, ![]() в виде:
в виде:
![]()
![]()
![]() . (26)
. (26)
Используя формулу 8.123 п. 2 [16] дифференцирования
полного эллиптического интеграла по его модулю и представление производной
через полные эллиптические интегралы первого и второго рода, получим:
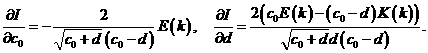 (27)
(27)
Далее вычислим производные ![]() и
и ![]() по
по ![]() и
и ![]() :
:
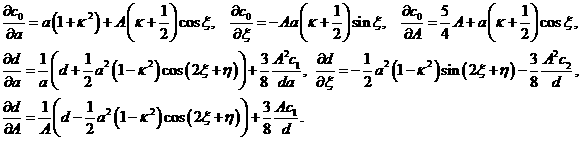 (28)
(28)
7. Усредненные уравнения движения
Усредняя систему (18.1) и (18.2) и используя
приближение ![]() , получим:
, получим:
 (29)
(29)
Система (29) имеет интеграл: ![]() .
.
Усредненная система (29) совпадает с усредненной
системой (20) для нулевого эксцентриситета.
8. Условие для поиска начального
приближения начальных условий. Выбор параметра ![]()
Условие для поиска начального приближения параметров
КСО, обладающих искомым свойством, позволяет получить уравнение для ![]() из системы (29).
Потребуем, чтобы
из системы (29).
Потребуем, чтобы ![]() . Тогда условие превращается в уравнение, связывающее
. Тогда условие превращается в уравнение, связывающее ![]() и
и ![]() :
:
![]() , (30)
, (30)
где 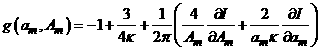 . (31)
. (31)
Используя (26), представим функцию ![]() в виде:
в виде:
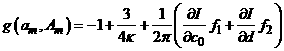 ,
(32)
,
(32)
где ![]() ,
, ![]() .
.
Заметим, что при ![]() и
и ![]() величину
величину ![]() можно было представить
полным квадратом:
можно было представить
полным квадратом: ![]() . Тогда модуль
эллиптического интеграла становится равным
. Тогда модуль
эллиптического интеграла становится равным ![]() , а функция
, а функция ![]() принимает вид:
принимает вид:
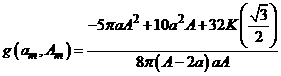 . (33)
. (33)
Для
определения зависимости ![]() нужно решить квадратное уравнение:
нужно решить квадратное уравнение:
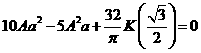 . (34)
. (34)
Корни
этого уравнения вычисляются по формуле:
 (35)
(35)
и
имеют действительные значения при выполнении условия: 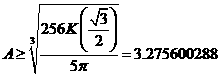 .
.
Расчеты показали, что движение по КСО можно получить
только при использовании меньшего корня, т.е. при знаке ″–″ в (35)
перед радикалом.
9. Алгоритм
формирования начального приближения
Компоненты вектора положения ![]() связаны с параметрами
связаны с параметрами ![]() и
и ![]() следующим
соотношением:
следующим
соотношением:
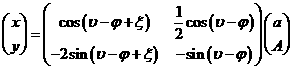 . (36)
. (36)
Решая
эту систему линейных уравнений при ![]() относительно
переменных
относительно
переменных ![]() и
и ![]() , получим:
, получим:
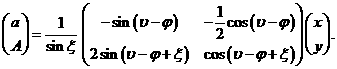 (37)
(37)
При ![]() система (36) имеет
решение, если выполняется условие:
система (36) имеет
решение, если выполняется условие: ![]() ,
, ![]() . В этом случае
. В этом случае ![]() и
и ![]() определяются из
решения уравнения:
определяются из
решения уравнения: ![]() .
.
Пусть теперь известно, что КСО должна пройти через
точку с координатами ![]() в момент времени, в который истинная аномалия Фобоса равна
в момент времени, в который истинная аномалия Фобоса равна ![]() . Тогда, при заданных
. Тогда, при заданных ![]() и
и ![]() , определяем
, определяем ![]() и
и ![]() .
.
Определение начального приближения при поиске
начальных условий КСО с искомыми свойствами определяется сканированием по ![]() и
и ![]() . Сканирование выполняется в два прохода. На первом проходе
сканирование по
. Сканирование выполняется в два прохода. На первом проходе
сканирование по ![]() выполняется на
интервале от 0 до 2π с шагом
выполняется на
интервале от 0 до 2π с шагом ![]() . На втором проходе сканирование выполняется на интервале
. На втором проходе сканирование выполняется на интервале ![]() , где
, где ![]() ‑ точка, в
которой была достигнута минимальная ширина кольца на первом проходе. Шаг
сканирования на втором проходе составляет
‑ точка, в
которой была достигнута минимальная ширина кольца на первом проходе. Шаг
сканирования на втором проходе составляет ![]() от длины интервала
перебора. Интервал сканирования по
от длины интервала
перебора. Интервал сканирования по ![]() на первом и втором
проходах одинаковый: от
на первом и втором
проходах одинаковый: от ![]() до
до ![]() , где
, где ![]() . Шаг сканирования составляет
. Шаг сканирования составляет ![]() от размера интервала
сконирования.
от размера интервала
сконирования.
На каждом шаге сканирования определяются ![]() и
и ![]() . Если
. Если ![]() и
и ![]() , формируется начальное приближение и вычисляется ширина
кольца.
, формируется начальное приближение и вычисляется ширина
кольца.
Указанный алгоритм за время расчета ~15 минут на Pentium 4 позволяет определить начальное приближение с
высокой точностью.
10. Вычислительная процедура поиска
минимума
Вычислительная процедура поиска минимума построена на
основе комбинированного применения метода градиентного спуска и метода золотого
сечения. Сначала применяется градиентный спуск, а затем метод золотого сечения.
Алгоритм градиентного спуска дополнен возможностями выхода из локального
минимума и идентификации попадания в овраг по одной из переменных.
При использовании градиентного спуска КСО исследуется
на небольшом интервале времени, который соответствует интервалу истинной
аномалии от ![]() до
до ![]() , где
, где ![]() . Локальный минимум, найденный методом градиентного спуска,
уточнялся методом золотого сечения для большего значения
. Локальный минимум, найденный методом градиентного спуска,
уточнялся методом золотого сечения для большего значения ![]() .
.
Вычислительные эксперименты показали, что искомые КСО
являются почти периодическими (квазипериодическими) с ошибкой не превосходящей ![]() по каждой канонической
полярной переменной. Квазипериод не превосходит 10000 оборотов Фобоса вокруг
Марса.
по каждой канонической
полярной переменной. Квазипериод не превосходит 10000 оборотов Фобоса вокруг
Марса.
Рассмотрим алгоритм градиентного спуска. Как и в [1]
будем рассматривать задачу в следующей постановке. Задано начальное положение
КА: ![]() в момент времени, в
который истинная аномалия Фобоса равна
в момент времени, в
который истинная аномалия Фобоса равна ![]() . Рассмотрим множество КСО, проходящих через заданную точку,
при различных значениях вектора скорости. Для каждой такой КСО определим
множество точек пересечения с отрицательной частью оси
. Рассмотрим множество КСО, проходящих через заданную точку,
при различных значениях вектора скорости. Для каждой такой КСО определим
множество точек пересечения с отрицательной частью оси ![]() и максимальное
удаление
и максимальное
удаление ![]() точек этого множества
от начальной точки. Найдём вектор начальной скорости , для которого минимально
значение максимального удаления
точек этого множества
от начальной точки. Найдём вектор начальной скорости , для которого минимально
значение максимального удаления ![]() . Численные эксперименты показали, что при использовании
градиентного спуска для поиска КСО с минимальным значением
. Численные эксперименты показали, что при использовании
градиентного спуска для поиска КСО с минимальным значением ![]() целесообразно
использовать уравнения в канонических полярных переменных:
целесообразно
использовать уравнения в канонических полярных переменных: ![]() :
:
![]()
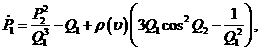 (38)
(38)
![]()
Начальное
положение задается условием:
![]() . (39)
. (39)
Определим функцию ![]() , которая каждой паре
, которая каждой паре ![]() начальных значений
обобщенных скоростей ставит в соответствие максимальную по абсолютной величине
разность между значениями
начальных значений
обобщенных скоростей ставит в соответствие максимальную по абсолютной величине
разность между значениями ![]() и
и ![]() в точках,
удовлетворяющих условию
в точках,
удовлетворяющих условию ![]() на интервале:
на интервале: ![]() , где
, где ![]() – заданная целая
константа:
– заданная целая
константа:
![]() . (40)
. (40)
Поиск минимума функции ![]() выполним методом
градиентного спуска. Начальные значения обобщенных скоростей определим
алгоритмом формирования начального приближения. Производные вычислим разностным
методом:
выполним методом
градиентного спуска. Начальные значения обобщенных скоростей определим
алгоритмом формирования начального приближения. Производные вычислим разностным
методом:
![]()
![]() (41)
(41)
где
![]() .
.
При вычислении производных должны проверяться условия
попадания в локальный минимум или овраг. Если одновременно выполнены условия:
 (42)
(42)
точка
![]() попала в локальный
экстремум.
попала в локальный
экстремум.
При попадании текущей точки в локальный экстремум
вычисляются значения функции в следующих четырех точках: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , где
, где ![]() ,
, ![]() . Если минимальное значение из этих четырех значений меньше,
чем
. Если минимальное значение из этих четырех значений меньше,
чем ![]() , происходит переход в соответствующую точку.
, происходит переход в соответствующую точку.
Если все четыре значения больше, чем ![]() , считается, что текущий локальный экстремум и есть искомый
глобальный экстремум, а значения
, считается, что текущий локальный экстремум и есть искомый
глобальный экстремум, а значения ![]() — искомые значения.
— искомые значения.
Если одновременно выполняются условия: ![]() и
и ![]() , текущая точка попала в овраг по переменной
, текущая точка попала в овраг по переменной ![]() . В этом случае при переходе к следующей точке должны
использоваться только производные по переменной
. В этом случае при переходе к следующей точке должны
использоваться только производные по переменной ![]() , значение
, значение ![]() обнуляется.
обнуляется.
При одновременном выполнении условий: ![]() и
и ![]() точка попадает в овраг
по переменной
точка попадает в овраг
по переменной ![]() . В этом случае обнуляется значение
. В этом случае обнуляется значение ![]() . Одновременное попадание в овраг по переменным
. Одновременное попадание в овраг по переменным ![]() и
и ![]() означает, что текущая
точка попадает в локальный экстремум. Этот случай уже рассмотрен выше.
означает, что текущая
точка попадает в локальный экстремум. Этот случай уже рассмотрен выше.
Вычисляется величина: ![]() . Если эта величина
меньше, чем
. Если эта величина
меньше, чем ![]() , считается, что достигнут минимум по малому модулю
градиента, а значения
, считается, что достигнут минимум по малому модулю
градиента, а значения ![]() — искомые.
— искомые.
Дальше ищется значение шага ![]() , при котором значение функции
, при котором значение функции
![]() меньше, чем
меньше, чем ![]() . Для этого выполняется цикл по величине шага
. Для этого выполняется цикл по величине шага ![]() , начиная со значения, использованного при численном
нахождении производных. При каждом новом проходе цикла величина шага
, начиная со значения, использованного при численном
нахождении производных. При каждом новом проходе цикла величина шага ![]() уменьшается вдвое.
Если найдено искомое значение шага
уменьшается вдвое.
Если найдено искомое значение шага ![]() , происходит переход к новым значениям обобщённых скоростей
, происходит переход к новым значениям обобщённых скоростей ![]() и повторение действий,
начиная с вычисления производных.
и повторение действий,
начиная с вычисления производных.
Если величина шага ![]() стала меньше, чем
стала меньше, чем ![]() , считается, что искомый минимум найден, а значения
, считается, что искомый минимум найден, а значения ![]() — искомые значения
обобщённых скоростей.
— искомые значения
обобщённых скоростей.
Особенность использования метода золотого сечения [17]
состоит в том, что он применяется к функции двух переменных ![]() и
и ![]() . Сначала фиксируется
. Сначала фиксируется ![]() и поиск выполняется по
переменной
и поиск выполняется по
переменной ![]() . После того, как минимум найден, фиксируется
. После того, как минимум найден, фиксируется ![]() и выполняется поиск по
и выполняется поиск по
![]() . Затем выполняется поиск по
. Затем выполняется поиск по ![]() и т. д. Другой
особенностью применения метода золотого сечения является то, что поиск
начинается из точки текущего найденного минимума. Для того чтобы попасть в
условия поиска по методу золотого сечения, границы интервала поиска задаются
асиметрично относительно текущего минимума. Если
и т. д. Другой
особенностью применения метода золотого сечения является то, что поиск
начинается из точки текущего найденного минимума. Для того чтобы попасть в
условия поиска по методу золотого сечения, границы интервала поиска задаются
асиметрично относительно текущего минимума. Если ![]() — точка, с которой
начинается поиск, то поиск минимума выполняется в интервале:
— точка, с которой
начинается поиск, то поиск минимума выполняется в интервале: 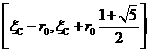 , где
, где ![]() — радиус поиска. При
поиске минимума методом золотого сечения использованы следующие значения параметров:
интервал поиска 0.1 и 0.4 по
— радиус поиска. При
поиске минимума методом золотого сечения использованы следующие значения параметров:
интервал поиска 0.1 и 0.4 по ![]() соответственно, порог
прекращения поиска 0.001 (одинаковый по
соответственно, порог
прекращения поиска 0.001 (одинаковый по ![]() ).
).
11. Результаты расчетов
Значения начальных удалений от точки ![]() , средняя ширина кольца, средняя разность относительных
угловых скоростей и квазипериод приведены в таблице 11.1.
, средняя ширина кольца, средняя разность относительных
угловых скоростей и квазипериод приведены в таблице 11.1.
Таблица 11.1.
Параметры КСО
|
Начальное удаление |
Средняя ширина кольца |
Средняя разность относит. угловых скоростей |
Квазипериод |
|
2.456423 |
0.10 – 0.11 |
0.215 – 0.235 |
65 – 787 |
|
2.654142 |
0.11 – 0.12 |
0.182 – 0.200 |
5 – 568 |
|
2.851861 |
0.13 |
0.155 – 0.171 |
19 – 547 |
|
3.0 |
0.13 – 0.14 |
0.137 – 0.153 |
7 – 866 |
|
3.5 |
0.16 – 0.17 |
0.095 – 0.107 |
19 – 870 |
|
4.0 |
0.19 – 0.20 |
0.067 – 0.077 |
14 – 915 |
|
4.5 |
0.20 – 0.25 |
0.049 – 0.057 |
18 – 756 |
|
5.0 |
0.24 – 0.25 |
0.037 – 0.043 |
26 – 968 |
|
5.5 |
0.27 – 0.29 |
0.028 – 0.033 |
31 – 1403 |
|
6.0 |
0.29 – 0.33 |
0.022 – 0.026 |
39 – 1223 |
|
6.5 |
0.32 – 0.34 |
0.017 – 0.021 |
49 – 1670 |
|
7.0 |
0.34 – 0.37 |
0.014 – 0.017 |
61 – 1014 |
|
7.5 |
0.36 – 0.39 |
0.011 – 0.014 |
74 – 2137 |
|
8.0 |
0.39 – 0.42 |
0.009 – 0.011 |
89 – 2122 |
В таблицах 11.2–11.15 приведены значения обобщенных
скоростей на начальный момент для начальных удалений от 2.456423 до 8. Значения
приводятся с учетом свойства симметрии рассматриваемой системы. Система
уравнений (1) обладает свойством симметрии: если ![]() — решение системы (1),
то
— решение системы (1),
то ![]() — тоже решение системы
(1). В канонических полярных переменных:
— тоже решение системы
(1). В канонических полярных переменных: ![]() симметричные решения уравнения
(1)
симметричные решения уравнения
(1) ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() ,
, ![]() связаны соотношениями:
связаны соотношениями:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
При поиске начальных условий рассматривается семейство
КСО, проходящее через точку ![]() с полярными координатами:
с полярными координатами:
![]() ,
, ![]() в момент времени,
соответствующий значению истинной аномалии
в момент времени,
соответствующий значению истинной аномалии ![]() . Для каждой КСО определяется множество точек пересечения с
отрицательной частью оси
. Для каждой КСО определяется множество точек пересечения с
отрицательной частью оси ![]() и максимальное
удаление точек этого множества от точки
и максимальное
удаление точек этого множества от точки ![]() . Для каждого начального
значения истинной аномалии
. Для каждого начального
значения истинной аномалии ![]() ищется КСО, для
которой максимальное удаление минимально. Начальные значения обобщенных
скоростей обозначим:
ищется КСО, для
которой максимальное удаление минимально. Начальные значения обобщенных
скоростей обозначим: ![]() и
и ![]() .
.
Решению уравнения (1) с начальными условиями: ![]() будет соответствовать симметричное решение с
начальными условиями:
будет соответствовать симметричное решение с
начальными условиями: ![]() . Очевидно, что
максимальные удаления симметричных решений равны между собой. При этом в одном
из симметричных решений истинная аномалия
. Очевидно, что
максимальные удаления симметричных решений равны между собой. При этом в одном
из симметричных решений истинная аномалия ![]() растет, в другом
убывает. Для периодических решений максимальное удаление от точки
растет, в другом
убывает. Для периодических решений максимальное удаление от точки ![]() не должно зависеть от
направления движения по траектории (вперед или назад). Поэтому, если бы
найденные симметричные решения были бы периодическими, максимальные удаления от
точки
не должно зависеть от
направления движения по траектории (вперед или назад). Поэтому, если бы
найденные симметричные решения были бы периодическими, максимальные удаления от
точки ![]() должны совпадать.
должны совпадать.
Найденные решения являются квазипериодическими.
Поэтому найденные значения начальных обобщённых скоростей связаны приближённой
зависимостью: ![]() ,
, ![]() , а в таблицах,
содержащих результаты расчетов, приведены одинаковые значения
, а в таблицах,
содержащих результаты расчетов, приведены одинаковые значения ![]() и
и ![]() для начальных значений
истинной аномалии:
для начальных значений
истинной аномалии: ![]() и
и ![]() .
.
На
рис. 2 показаны найденные КСО для начальных удалений 3 и 8.
Таблица 11.2. Значения обобщенных скоростей ![]() и
и ![]() для начального
удаления
для начального
удаления ![]()
|
|
|
|
|
|
град |
|
|
|
|
0 |
0.000 |
1.888 |
|
100 |
0.020 |
1.884 |
260 |
|
|
10 |
0.004 |
1.888 |
350 |
110 |
0.020 |
1.883 |
250 |
|
|
20 |
0.007 |
1.887 |
340 |
120 |
0.018 |
1.883 |
240 |
|
|
30 |
0.010 |
1.887 |
330 |
130 |
0.016 |
1.882 |
230 |
|
|
40 |
0.013 |
1.887 |
320 |
140 |
0.013 |
1.881 |
220 |
|
|
50 |
0.016 |
1.887 |
310 |
150 |
0.010 |
1.881 |
210 |
|
|
60 |
0.018 |
1.886 |
300 |
160 |
0.007 |
1.880 |
200 |
|
|
70 |
0.019 |
1.886 |
290 |
170 |
0.004 |
1.880 |
190 |
|
|
80 |
0.020 |
1.885 |
280 |
180 |
0.000 |
1.880 |
|
|
|
90 |
0.021 |
1.885 |
270 |
|
|
|
|
Таблица 11.3. Значения обобщенных скоростей ![]() и
и ![]() для начального
удаления
для начального
удаления ![]()
|
град |
|
|
|
|
град |
|
|
|
|
0 |
0.000 |
2.417 |
|
|
100 |
0.022 |
2.410 |
260 |
|
10 |
0.004 |
2.417 |
350 |
|
110 |
0.021 |
2.409 |
250 |
|
20 |
0.007 |
2.417 |
340 |
|
120 |
0.019 |
2.408 |
240 |
|
30 |
0.011 |
2.417 |
330 |
|
130 |
0.017 |
2.406 |
230 |
|
40 |
0.014 |
2.416 |
320 |
|
140 |
0.014 |
2.405 |
220 |
|
50 |
0.017 |
2.415 |
310 |
|
150 |
0.011 |
2.404 |
210 |
|
60 |
0.019 |
2.415 |
300 |
|
160 |
0.008 |
2.404 |
200 |
|
70 |
0.021 |
2.414 |
290 |
|
170 |
0.004 |
2.403 |
190 |
|
80 |
0.022 |
2.412 |
280 |
|
180 |
0.000 |
2.403 |
|
|
90 |
0.022 |
2.411 |
270 |
|
|
|||
Таблица 11.4. Значения обобщенных скоростей ![]() и
и ![]() для начального
удаления
для начального
удаления ![]()
|
град |
|
|
|
|
град |
|
|
|
|
0 |
0.000 |
2.990 |
|
100 |
0.023 |
2.978 |
260 |
|
|
10 |
0.004 |
2.990 |
350 |
110 |
0.022 |
2.976 |
250 |
|
|
20 |
0.008 |
2.989 |
340 |
120 |
0.021 |
2.975 |
240 |
|
|
30 |
0.012 |
2.989 |
330 |
130 |
0.018 |
2.973 |
230 |
|
|
40 |
0.015 |
2.988 |
320 |
140 |
0.015 |
2.971 |
220 |
|
|
50 |
0.018 |
2.987 |
310 |
150 |
0.012 |
2.970 |
210 |
|
|
60 |
0.020 |
2.985 |
300 |
160 |
0.008 |
2.969 |
200 |
|
|
70 |
0.022 |
2.984 |
290 |
170 |
0.004 |
2.968 |
190 |
|
|
80 |
0.023 |
2.982 |
280 |
180 |
0.000 |
2.968 |
|
|
|
90 |
0.024 |
2.980 |
270 |
|
||||
Таблица 11.5. Значения обобщенных скоростей ![]() и
и ![]() для начального
удаления
для начального
удаления ![]()
|
град |
|
|
|
|
град |
|
|
|
|
0 |
0.000 |
3.447 |
|
100 |
0.024 |
3.431 |
260 |
|
|
10 |
0.004 |
3.447 |
350 |
110 |
0.023 |
3.429 |
250 |
|
|
20 |
0.008 |
3.446 |
340 |
120 |
0.022 |
3.426 |
240 |
|
|
30 |
0.012 |
3.445 |
330 |
130 |
0.019 |
3.424 |
230 |
|
|
40 |
0.016 |
3.444 |
320 |
140 |
0.016 |
3.422 |
220 |
|
|
50 |
0.019 |
3.442 |
310 |
150 |
0.013 |
3.420 |
210 |
|
|
60 |
0.021 |
3.440 |
300 |
160 |
0.009 |
3.419 |
200 |
|
|
70 |
0.023 |
3.438 |
290 |
170 |
0.004 |
3.418 |
190 |
|
|
80 |
0.024 |
3.436 |
280 |
180 |
0.000 |
3.418 |
|
|
|
90 |
0.025 |
3.434 |
270 |
|
||||
Таблица 11.6. Значения обобщенных скоростей ![]() и
и ![]() для начального
удаления
для начального
удаления ![]()
|
град |
|
|
|
|
град |
|
|
|
|
0 |
0.000 |
5.157 |
|
|
100 |
0.028 |
5.127 |
260 |
|
10 |
0.005 |
5.157 |
350 |
|
110 |
0.027 |
5.122 |
250 |
|
20 |
0.010 |
5.156 |
340 |
|
120 |
0.025 |
5.117 |
240 |
|
30 |
0.014 |
5.154 |
330 |
|
130 |
0.022 |
5.113 |
230 |
|
40 |
0.018 |
5.152 |
320 |
|
140 |
0.019 |
5.109 |
220 |
|
50 |
0.021 |
5.149 |
310 |
|
150 |
0.015 |
5.106 |
210 |
|
60 |
0.024 |
5.145 |
300 |
|
160 |
0.010 |
5.104 |
200 |
|
70 |
0.027 |
5.141 |
290 |
|
170 |
0.005 |
5.102 |
190 |
|
80 |
0.028 |
5.136 |
280 |
|
180 |
0.000 |
5.101 |
|
|
90 |
0.028 |
5.131 |
270 |
|
|
|
|
|
Таблица 11.7. Значения обобщенных скоростей ![]() и
и ![]() для начального
удаления
для начального
удаления ![]()
|
град |
|
|
|
|
град |
|
|
|
|
0 |
0.000 |
7.123 |
|
100 |
0.032 |
7.072 |
260 |
|
|
10 |
0.005 |
7.123 |
350 |
110 |
0.030 |
7.064 |
250 |
|
|
20 |
0.011 |
7.121 |
340 |
120 |
0.028 |
7.057 |
240 |
|
|
30 |
0.016 |
7.117 |
330 |
130 |
0.025 |
7.050 |
230 |
|
|
40 |
0.020 |
7.113 |
320 |
140 |
0.021 |
7.044 |
220 |
|
|
50 |
0.024 |
7.108 |
310 |
150 |
0.016 |
7.039 |
210 |
|
|
60 |
0.027 |
7.102 |
300 |
160 |
0.011 |
7.035 |
200 |
|
|
70 |
0.030 |
7.095 |
290 |
170 |
0.006 |
7.033 |
190 |
|
|
80 |
0.032 |
7.087 |
280 |
180 |
0.000 |
7.032 |
|
|
|
90 |
0.032 |
7.080 |
270 |
|
||||
Таблица 11.8. Значения обобщенных скоростей ![]() и
и ![]() для начального
удаления
для начального
удаления ![]()
|
град |
|
|
|
|
град |
|
|
|
|
0 |
0.000 |
9.338 |
|
100 |
0.036 |
9.253 |
260 |
|
|
10 |
0.006 |
9.337 |
350 |
110 |
0.034 |
9.255 |
250 |
|
|
20 |
0.012 |
9.334 |
340 |
120 |
0.031 |
9.241 |
240 |
|
|
30 |
0.018 |
9.330 |
330 |
130 |
0.028 |
9.231 |
230 |
|
|
40 |
0.023 |
9.323 |
320 |
140 |
0.023 |
9.223 |
220 |
|
|
50 |
0.027 |
9.317 |
310 |
150 |
0.018 |
9.215 |
210 |
|
|
60 |
0.031 |
9.308 |
300 |
160 |
0.012 |
9.211 |
200 |
|
|
70 |
0.034 |
9.296 |
290 |
170 |
0.006 |
9.207 |
190 |
|
|
80 |
0.036 |
9.285 |
280 |
180 |
0.000 |
9.206 |
|
|
|
90 |
0.036 |
9.274 |
270 |
|
||||
Таблица 11.9. Значения обобщенных скоростей ![]() и
и ![]() для начального
удаления
для начального
удаления ![]()
|
град |
|
|
|
|
град |
|
|
|
|
0 |
0.000 |
11.800 |
|
|
100 |
0.039 |
11.698 |
260 |
|
10 |
0.007 |
11.799 |
350 |
|
110 |
0.038 |
11.683 |
250 |
|
20 |
0.013 |
11.795 |
340 |
|
120 |
0.035 |
11.668 |
240 |
|
30 |
0.019 |
11.789 |
330 |
|
130 |
0.031 |
11.655 |
230 |
|
40 |
0.025 |
11.781 |
320 |
|
140 |
0.026 |
11.643 |
220 |
|
50 |
0.030 |
11.770 |
310 |
|
150 |
0.020 |
11.634 |
210 |
|
60 |
0.034 |
11.758 |
300 |
|
160 |
0.014 |
11.626 |
200 |
|
70 |
0.037 |
11.744 |
290 |
|
170 |
0.007 |
11.622 |
190 |
|
80 |
0.039 |
11.730 |
280 |
|
180 |
0.000 |
11.621 |
|
|
90 |
0.040 |
11.714 |
270 |
|
|
|
|
|
Таблица 11.10. Значения обобщенных скоростей ![]() и
и ![]() для начального
удаления
для начального
удаления ![]()
|
град |
|
|
|
|
град |
|
|
|
|
0 |
0.000 |
14.508 |
|
|
100 |
0.043 |
14.376 |
260 |
|
10 |
0.007 |
14.506 |
350 |
|
110 |
0.041 |
14.357 |
250 |
|
20 |
0.015 |
14.502 |
340 |
|
120 |
0.038 |
14.335 |
240 |
|
30 |
0.021 |
14.494 |
330 |
|
130 |
0.034 |
14.320 |
230 |
|
40 |
0.027 |
14.482 |
320 |
|
140 |
0.028 |
14.305 |
220 |
|
50 |
0.033 |
14.469 |
310 |
|
150 |
0.022 |
14.293 |
210 |
|
60 |
0.037 |
14.452 |
300 |
|
160 |
0.015 |
14.282 |
200 |
|
70 |
0.040 |
14.436 |
290 |
|
170 |
0.008 |
14.277 |
190 |
|
80 |
0.043 |
14.418 |
280 |
|
180 |
0.000 |
14.279 |
|
|
90 |
0.043 |
14.394 |
270 |
|
|
|
|
|
Таблица 11.11. Значения обобщенных скоростей ![]() и
и ![]() для начального
удаления
для начального
удаления ![]()
|
град |
|
|
|
|
град |
|
|
|
|
0 |
0.000 |
17.463 |
|
100 |
0.047 |
17.294 |
260 |
|
|
10 |
0.008 |
17.461 |
350 |
110 |
0.045 |
17.272 |
250 |
|
|
20 |
0.016 |
17.454 |
340 |
120 |
0.041 |
17.249 |
240 |
|
|
30 |
0.023 |
17.444 |
330 |
130 |
0.037 |
17.227 |
230 |
|
|
40 |
0.030 |
17.431 |
320 |
140 |
0.031 |
17.208 |
220 |
|
|
50 |
0.036 |
17.414 |
310 |
150 |
0.024 |
17.194 |
210 |
|
|
60 |
0.040 |
17.394 |
300 |
160 |
0.017 |
17.182 |
200 |
|
|
70 |
0.044 |
17.371 |
290 |
170 |
0.008 |
17.175 |
190 |
|
|
80 |
0.046 |
17.348 |
280 |
180 |
0.000 |
17.173 |
|
|
|
90 |
0.047 |
17.322 |
270 |
|
||||
Таблица 11.12. Значения обобщенных скоростей ![]() и
и ![]() для начального
удаления
для начального
удаления ![]()
|
град |
|
|
|
|
град |
|
|
|
|
0 |
0.000 |
20.663 |
|
|
100 |
0.050 |
20.466 |
260 |
|
10 |
0.009 |
20.661 |
350 |
|
110 |
0.048 |
20.432 |
250 |
|
20 |
0.017 |
20.653 |
340 |
|
120 |
0.045 |
20.401 |
240 |
|
30 |
0.025 |
20.641 |
330 |
|
130 |
0.040 |
20.348 |
230 |
|
40 |
0.032 |
20.624 |
320 |
|
140 |
0.034 |
20.370 |
220 |
|
50 |
0.039 |
20.604 |
310 |
|
150 |
0.026 |
20.346 |
210 |
|
60 |
0.044 |
20.579 |
300 |
|
160 |
0.018 |
20.323 |
200 |
|
70 |
0.047 |
20.556 |
290 |
|
170 |
0.009 |
20.316 |
190 |
|
80 |
0.050 |
20.521 |
280 |
|
180 |
0.000 |
20.312 |
|
|
90 |
0.051 |
20.497 |
270 |
|
|
|
|
|
Таблица 11.13. Значения обобщенных скоростей ![]() и
и ![]() для начального
удаления
для начального
удаления ![]()
|
град |
|
|
|
|
град |
|
|
|
|
0 |
0.000 |
24.113 |
|
|
100 |
0.054 |
23.869 |
260 |
|
10 |
0.009 |
24.108 |
350 |
|
110 |
0.052 |
23.839 |
250 |
|
20 |
0.018 |
24.101 |
340 |
|
120 |
0.048 |
23.804 |
240 |
|
30 |
0.027 |
24.084 |
330 |
|
130 |
0.043 |
23.774 |
230 |
|
40 |
0.034 |
24.066 |
320 |
|
140 |
0.036 |
23.744 |
220 |
|
50 |
0.041 |
24.041 |
310 |
|
150 |
0.028 |
23.721 |
210 |
|
60 |
0.047 |
24.012 |
300 |
|
160 |
0.019 |
23.705 |
200 |
|
70 |
0.051 |
23.981 |
290 |
|
170 |
0.010 |
23.696 |
190 |
|
80 |
0.054 |
23.940 |
280 |
|
180 |
0.000 |
23.692 |
|
|
90 |
0.055 |
23.906 |
270 |
|
|
|
|
|
Таблица 11.14. Значения обобщенных скоростей ![]() и
и ![]() для начального
удаления
для начального
удаления ![]()
|
град |
|
|
|
|
град |
|
|
|
|
0 |
0.000 |
27.808 |
|
|
100 |
0.058 |
27.530 |
260 |
|
10 |
0.010 |
27.803 |
350 |
|
110 |
0.056 |
27.480 |
250 |
|
20 |
0.020 |
27.794 |
340 |
|
120 |
0.052 |
27.444 |
240 |
|
30 |
0.029 |
27.779 |
330 |
|
130 |
0.046 |
27.410 |
230 |
|
40 |
0.037 |
27.753 |
320 |
|
140 |
0.039 |
27.377 |
220 |
|
50 |
0.044 |
27.726 |
310 |
|
150 |
0.030 |
27.352 |
210 |
|
60 |
0.050 |
27.688 |
300 |
|
160 |
0.020 |
27.333 |
200 |
|
70 |
0.055 |
27.652 |
290 |
|
170 |
0.010 |
27.320 |
190 |
|
80 |
0.058 |
27.607 |
280 |
|
180 |
0.000 |
27.317 |
|
|
90 |
0.059 |
27.567 |
270 |
|
|
|
|
|
Таблица 11.15. Значения обобщенных скоростей ![]() и
и ![]() для начального
удаления
для начального
удаления ![]()
|
град |
|
|
град |
|
град |
|
|
|
|
0 |
0.000 |
31.753 |
|
|
100 |
0.062 |
31.430 |
260 |
|
10 |
0.011 |
31.747 |
350 |
|
110 |
0.059 |
31.380 |
250 |
|
20 |
0.021 |
31.736 |
340 |
|
120 |
0.055 |
31.335 |
240 |
|
30 |
0.031 |
31.717 |
330 |
|
130 |
0.049 |
31.292 |
230 |
|
40 |
0.039 |
31.688 |
320 |
|
140 |
0.041 |
31.252 |
220 |
|
50 |
0.047 |
31.656 |
310 |
|
150 |
0.032 |
31.227 |
210 |
|
60 |
0.053 |
31.618 |
300 |
|
160 |
0.022 |
31.205 |
200 |
|
70 |
0.058 |
31.570 |
290 |
|
170 |
0.011 |
31.192 |
190 |
|
80 |
0.061 |
31.526 |
280 |
|
180 |
0.000 |
31.184 |
|
|
90 |
0.063 |
31.476 |
270 |
|
|
|
|
|
12. Алгоритм проектирования КСО
Исходными данными при проектировании являются
следующие величины: ![]() максимальное удаление КА от поверхности Фобоса на долготе
270°,
максимальное удаление КА от поверхности Фобоса на долготе
270°, ![]() момент времени и
момент времени и ![]() долгота, которую должен проходить КА в этот момент времени.
Сначала по максимальному удалению
долгота, которую должен проходить КА в этот момент времени.
Сначала по максимальному удалению ![]() выбирается одна из
таблиц 11.2 – 11.15. Для этого заданное максимальное удаление пересчитывается в
безразмерную величину
выбирается одна из
таблиц 11.2 – 11.15. Для этого заданное максимальное удаление пересчитывается в
безразмерную величину ![]() по формуле:
по формуле:
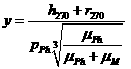 ,
,
где
|
|
– |
заданное
максимальное удаление КА в диапазоне от 50 до 200 км, |
|
|
– |
расстояние от
центра Фобоса до точки на его экваторе с долготой 270°, (11.1 км), |
|
|
– |
параметр
орбиты Фобоса, |
|
|
– |
гравитационная
постоянная Фобоса, |
|
|
– |
гравитационная
постоянная Марса, |
Далее выбирается таблица по найденной безразмерной
величине ![]() и значениям
и значениям ![]() максимальных
удалений, к которым эти таблицы относятся. Выбор выполняется из условия
близости
максимальных
удалений, к которым эти таблицы относятся. Выбор выполняется из условия
близости ![]() к
к ![]() .
Таблицы построены так, что диапазон удалений 50-60 км, номинального случая в
проекте Фобос-Грунт, покрыт с шагом 5 км, а остальной диапазон 60-200 км,
предназначенный для работы при отклонениях от номинального случая, – с шагом
12.5 км.
.
Таблицы построены так, что диапазон удалений 50-60 км, номинального случая в
проекте Фобос-Грунт, покрыт с шагом 5 км, а остальной диапазон 60-200 км,
предназначенный для работы при отклонениях от номинального случая, – с шагом
12.5 км.
По заданному моменту времени ![]() определяется
определяется ![]() истинная
аномалия Фобоса на этот момент времени. Эта величина используется для выбора
строки со значениями обобщенных скоростей из выбранной таблицы. Для этого по
начальным условиям, соответствующим строке таблицы, определим долготу
истинная
аномалия Фобоса на этот момент времени. Эта величина используется для выбора
строки со значениями обобщенных скоростей из выбранной таблицы. Для этого по
начальным условиям, соответствующим строке таблицы, определим долготу ![]() , которую проходит КА при истинной аномалии
, которую проходит КА при истинной аномалии ![]() .
Следует отметить, что каждой строке таблицы соответствует пара начальных
условий. Выбирается такая строка таблицы и формируются начальные условия, при
которых минимальна величина
.
Следует отметить, что каждой строке таблицы соответствует пара начальных
условий. Выбирается такая строка таблицы и формируются начальные условия, при
которых минимальна величина ![]() .
.
По выбранным начальным условиям вычисляется вектор
состояния КА в канонических полярных переменных на истинную аномалию ![]() :
: ![]() . На момент времени
. На момент времени ![]() по полной модели
движения Фобоса в инерциальной системе координат, в которой выполняются
проектные расчеты, вычисляются оскулирующие элементы его орбиты.
по полной модели
движения Фобоса в инерциальной системе координат, в которой выполняются
проектные расчеты, вычисляются оскулирующие элементы его орбиты.
С использованием оскулирующих элементов орбиты Фобоса
вектор состояния КА из канонических полярных переменных пересчитывается в орбитальную
систему координат Фобоса, а затем в инерциальную систему координат.
Центр орбитальной системы
координат совпадает с центром масс Фобоса. Ось ![]() направлена по линии визирования Марс – Фобос. Ось
направлена по линии визирования Марс – Фобос. Ось ![]() ортогональна оси
ортогональна оси ![]() , лежит в плоскости орбиты Фобоса и направлена в сторону его
орбитального движения.
, лежит в плоскости орбиты Фобоса и направлена в сторону его
орбитального движения.
Проектные расчеты [11] выполняются в системе
координат, центр которой совпадает с центром масс системы Марс-Фобос, плоскость
XY совпадает с плоскостью среднего
экватора Земли эпохи J2000, ось X направлена в точку весеннего равноденствия Земли этой
эпохи, ось Z направлена ортогонально плоскости XY в сторону
северного полюса, ось Y дополняет систему координат до правой.
Вектор состояния КА ![]() в орбитальной системе координат Фобоса вычисляется по
формулам:
в орбитальной системе координат Фобоса вычисляется по
формулам:
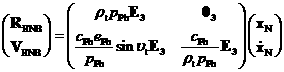 ,
,
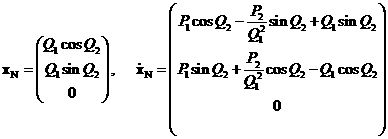 ,
,
где
|
|
− |
нулевая
матрица 3×3, |
|
|
− |
единичная
матрица 3×3, |
|
|
− |
переменная,
вычисляемая по формуле: |
|
|
− |
оскулирующий
интеграл площадей орбиты Фобоса, |
|
|
− |
оскулирующий
параметр орбиты Фобоса, |
|
|
− |
оскулирующий
эксцентриситет орбиты Фобоса. |
Вектор состояния КА в инерциальной системе координат
вычисляется по формулам:
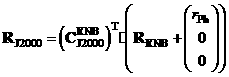 ,
,
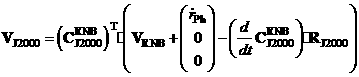 ,
,
где
|
|
− |
расстояние
от центра масс системы Марс-Фобос до центра масс Фобоса на момент времени |
|
|
− |
радиальная
скорость Фобоса на этот же момент времени. |
Матрица ![]() и ее производная по
времени вычисляются по формулам:
и ее производная по
времени вычисляются по формулам:
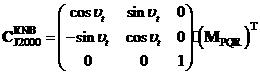 ,
,
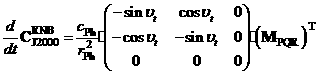 ,
,
где ![]() – матрица,
составленная из векторов Гаусса:
– матрица,
составленная из векторов Гаусса: ![]() и
и ![]() .
.
Векторы Гаусса вычисляются по
формулам:
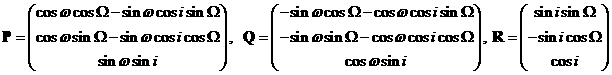 ,
,
где
|
|
− |
оскулирующее
наклонение орбиты Фобоса, |
|
|
− |
оскулирующая
долгота восходящего узла орбиты Фобоса, |
|
|
− |
оскулирующий
аргумент перицентра орбиты Фобоса. |
Алгоритм
проектирования КСО позволяет получить начальные условия, которые обеспечивают
прохождение над заданной долготой Фобоса в заданное время. Таблицы начальных
условий покрывают интервал от 50 до 200 км.
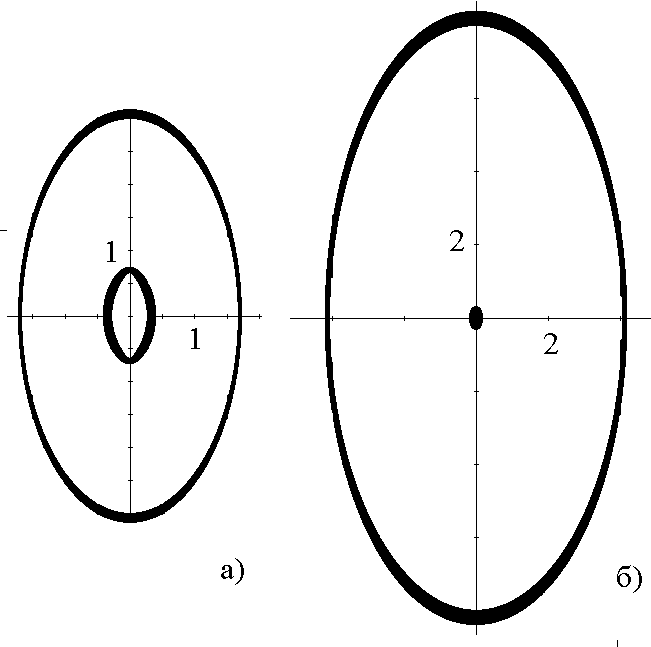
Рис. 2. Движение по КСО и движение центра эллипса: а) – начальное удаление ![]() , б) – начальное
удаление
, б) – начальное
удаление ![]()
Список литературы
1.
Тучин А.Г.
Квазисинхронные орбиты и их использование для сближения космического аппарата с
Фобосом // Космич. исслед. 2007. Т. 45. № 2. С. 144-149.
2.
Henon M. Numerical
Exploration of the Restricted Problem // VI. Hill’s Case: Non-Periodic Orbits.
Astronomy and Astrophysics. 1970. V. 24. № 9. P. 24-36.
3. Benest D. Libration effects for retrograde satellites in
the restricted three-body problem // Cel. Mech. 1976. V. 13. № 2. P. 203-215.
4. Коган А.Ю. Далекие спутниковые орбиты в ограниченной круговой
задаче трех тел // Космич. исслед. 1988. Т. 26. № 6. С. 813-818.
5. Лидов М.Л.,
Вашковьяк М.А. О квазиспутниковых
орбитах для эксперимента по уточнению гравитационной постоянной // Письма в АЖ.
1994. Т. 20. № 3. С. 229-240.
6. Лидов М.Л.,
Вашковьяк М.А. О квазиспутниковых
орбитах в ограниченной эллиптической задаче трех тел // Письма в АЖ. 1994. Т.
20. № 10. С. 781-795.
7. Лидов. М.Л. Об одном семействе пространственных периодических
орбит около Луны и планет // ДАН СССР. 1977. Т. 233. № 6. С. 1068-1071.
8. Лидов М.Л.,
Рабинович В.Ю. Исследование семейств
пространственных периодических орбит задачи трех тел // Космич. исслед. 1979.
Т. 17. № 3.
9. Лидов. М.Л. Метод построения семейств пространственных
периодических орбит в задаче Хилла // Космич. исслед. 1982. Т. 20. № 6. С.
787-807.
10. Лидов М.Л.,
Вашковьяк М.А. Теория возмущений и
анализ эволюции квазиспутниковых орбит в ограниченной задаче трех тел //
Космич. исслед. 1993. Т. 31. № 2. С. 75-99.
11. Аким Э.Л., Заславский Г.С., Морской И.М., Степаньянц В.А., Тучин А.Г. Баллистика, навигация и
управление полетом космического аппарата в проекте «Фобос-Грунт» // Изв. РАН.
Сер. ТиСУ. 2002. № 5.
12.
Шишов В.А. Модель движения Фобоса и
методика уточнения параметров в проекте «Фобос-Грунт». Препринт № 10. М.: ИПМ
им. М.В. Келдыша РАН, 2008.
13.
Akim E.L., Popov G.A., Tuchin A.G.
Mechanics and Motion Control of a Space Vehicle in the Project of Relict
Substance Delivery on Earth (The Project “Phobos-Grunt”) // Proc. 16th IFAC
Symposium on automatic control in Aerospace. Preprints. Saint Petersburg.
Russia. 2004. V. 1.
14.
Akim E.L., Botkin A.V., Stepaniants V.A., Shishov V.A., Ruzskiy E.G. and
Tuchin A.G. Orbit Selection, Navigation and Maneuvers before
the Landing on the Phobos Surface for Phobos Sample Return Project // Proc.
17th International Symposium on Space Flight Dynamics. 16-20 June, 2003.
Moscow. Russia. V. 1.
15. Akim E.L., Stepaniants V.A.,
Shishov V.A., Ruzskiy E.G. and Tuchin A.G. Ballisticks, navigation and motion control of the SC on
stages of the Phobos surface approaching and landing // Proc. 18th International Symposium on Space Flight Dynamics, 11-15
October, 2004. Munich. Germany.
16. Градштейн И.С., Рыжик И.М. Таблицы интегралов сумм,
рядов и произведений. М.: Наука, 1971.
17. Растригин
Л.А. Системы экстремального
управления. М.: Наука, 1974.
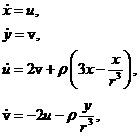
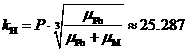 .
.