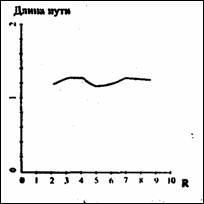
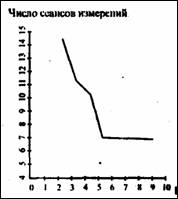
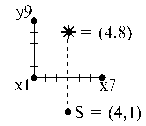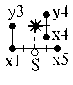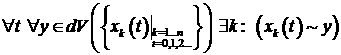Формальные подходы к проектированию алгоритмов информационного обеспечения мобильных систем
(выбор пути, навигация, надежность)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
N символ и название ситуации |
Типичная конфигурация |
Комментарий |
Эффект |
|
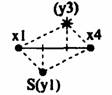
(а) "+" "Прямой крест" |
|
Полная симметрия двух наблюдаемых подцелей (х1 и
x4) по затратам на их достижение (b) и оценкам затрат на
дальнейшее движение до цели (g) |
Неустойчивость "нормальных" V‑алгоритмов:
Vb. Vg, V(b+g) и др. С‑алгоритм
в общем случае устойчив |
|
(b) “X” "Косой крест" |
|
Симметрия двух подцелей (x1 и x4) по
сумме b+g |
Неустойчивость V(b+g); Vb, Vg, С‑алгоритмы
-устойчивы. |
|
(с) «Т» "Касание" («Мимолет-ный поцелуй») |
|
Касание вершины препятствия (х1) текущей
"линией цели" |
Неустойчивость С-алгоритмов с соответствующим
направлением обхода(на рисунке С+); V‑алгоритм в общем
случае устойчив. |
|
(d) "+h" "Гомонеус" |
|
Симметрия типа (а), но достигаемая на краях
прохода, а не препятствия |
"Гомотопная неустойчивость" для
“нормальных" V‑алгоритмов; при вариации элемента задачи получаются
гомотопные пути. |
В пояснение этих теорем приводятся
реализации для ситуаций типа D4, D6, D10, D12 (см. Табл.2, рис. 2 и 3)
В Таблице 2 приведены
типы особых ситуаций доминирования (OCД) D’N’ для пары
алгоритмов. Здесь предполагается, что функция доминирования (обозначенная d) изначально - до вариации элемента задачи - d(a,b) = 1.
Символ “+” означает, что соответствующее отображение (a, b, La, Lb, d) непрерывно зависит от малых вариаций
параметров элемента задачи;
Символ “-” означает скачок (пути, длины пути), а
для функции доминирования этот символ означает
смену знака.
Символ “” - означает увеличение функции,
Символ “¯” - означает
уменьшение.
Основные типы
OCД описываются набором из 5 элементов
множества {+, -}, показанных в первых пяти столбцах таблицы.
Подтип типа определяется
видом скачка функции эффективности (длины пути) La, Lb или пары (La,Lb).
Из таблицы следует, что с учетом подтипов возможны
22 ситуации, в том числе 7 “неустойчивого доминирования”.
Пример. Полная формула OCД для
D83 запишется в виде:
(- - ↑)(- - ¯) => -
Таблица 2
Типы
особых ситуаций доминирования.
|
N |
a |
La |
b |
Lb |
d(a,b) |
Тип
OCД |
П о
д т и
п ы |
|||
|
1 |
- |
+ |
+ |
+ |
+ |
D1 |
|
|
|
|
|
2 |
- |
+ |
- |
+ |
+ |
D2 |
|
|
|
|
|
3 |
- |
+ |
- |
- |
+ |
D3 |
D31 (↑) |
D32 (↓) |
|
|
|
*4 |
- |
+ |
- |
- |
- |
D4(↓) |
|
|
|
|
|
5 |
- |
- |
- |
+ |
+ |
D5 |
D51 (↑) |
D52 (↓) |
|
|
|
*6 |
- |
- |
- |
+ |
- |
D6(↑) |
|
|
|
|
|
7 |
- |
- |
- |
- |
+ |
D7 |
D71 (↑↑) |
D72 (↓↓) |
D73 (↑↓) |
D74 (↑↓) |
|
*8 |
- |
- |
- |
- |
- |
D8 |
D81 (↑↑) |
D82 (↓↓) |
D83 (↑↓) |
|
|
9 |
- |
- |
+ |
+ |
+ |
D9 |
D91 (↑) |
D92 (↓) |
|
|
|
*10 |
- |
- |
+ |
+ |
- |
D10 (↑) |
|
|
|
|
|
11 |
+ |
+ |
- |
- |
+ |
D11 |
D111 (↑) |
D112 (↓) |
|
|
|
*12 |
+ |
+ |
- |
- |
- |
D12 (↓) |
|
|
|
|
|
13 |
+ |
+ |
- |
+ |
+ |
D13 |
|
|
|
|
Пары (D4,D6),(D10,D12) реализуются на одинаковых элементах задачи. Для
каждой ситуации неустойчивого доминирования приведена изначальная функция
доминирования d;
предполагается, что в начальной позиции первый алгоритм доминирует над вторым
(а после вариации параметров элемента задачи - наоборот). Вариации указаны
идентификатором var, далее идет
идентификатор точки вариации - начальной (b) или
целевой (g), после чего стрелкой указывается
направление малой вариации соответствующей точки. В полной формуле вместо (1) (-1) после W2=-1 поставлены соответственно стрелки вверх и вниз.
|
|
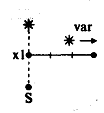
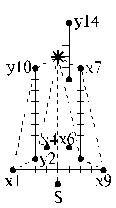
(HД1) S = (5, 0), * = (5, 11); s = 7; n = 32; l = 15; n = 3 D4: (- +)(- - ↓ ) => - d(Vb+, V(b + g) g +) var S <= |
||
|
a/b |
Ph |
Lph |
|
|
V b+ |
x9, (7, 2), x6 |
15.8 |
|
|
V b+ |
x1, y2, x4 |
15.8 |
|
|
V(b + g) g + |
x9, x7, y14 |
20.6 |
|
|
V(b + g) g + |
x1, y10 |
15.5 |
|
D6: (- -↑)(-
+) => -
d(V(b + g) g -, Vb -
); var
S =>
Характеристики путей
определяются по той же таблице, замена
w
= + на w = - в конце формулы алгоритма приводит к тому, что пути до и после вариации
старта S меняются местами.
Формула неопределенности:
“+”(“I”)&[“X”(“Г”)V”X”(“2ГГ”)]
![]()
|
|
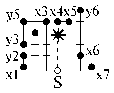
(HД2) s = 2; n = 11; l = 10; n = 1 D10: (- -↑)(+ +)
=> - var * <= d(V(b + g)+, C+ ) |
||
|
a/b |
Ph |
LPh |
|
|
V(b + g) g+ |
x7 |
9.2 |
|
|
V(b + g) g+ |
x1, y9 |
12.4 |
|
|
C+ |
(4,4) ↓, x7 |
11.0 |
|
D12: (+ +)(- - ↓) =>
-; d(C+,
V(b + g) -);
var *
=>
О путях V(b + g) g w замечание аналогичное (HД1)
Формула неопределенности: “+”(”Г”)
Рис.2 Атлас “неустойчивого доминирования”. I. D4, D6, D10, D12
|
|
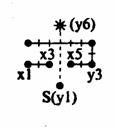
(HД3) S = (4, 1)↓; * = (4, 4) s = 8; n = 24; l = 8; n = 2 D81: (- -↑)(- -↑) => - d( V(b + g)+, C+); var * <= |
||
|
a/b |
Ph |
LPh |
|
|
V(b + g) g+ |
x7, y6 |
10.9 |
|
|
V(b + g) g+ |
x1, y2, (2, 4), y3,
y5, x3 |
13.0 |
|
|
C + |
x7, x6, y6 |
11.2 |
|
|
C + |
x7, x6, y6, x5, x4 |
11.8 |
|
Формула неопределенности:
![]() “+”(“Г4”V”Г”&“Т”(“I”))
“+”(“Г4”V”Г”&“Т”(“I”))
|
|
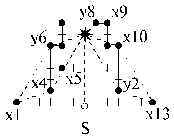
(HД4) S = (7, 1)↓; * = (7, 7) s = 9; n =
30; l =
14; n = 3 D82: (- -↓)(- -↓)
=> - d( V g+, V(b + g) b +); var *
=> Замечание: аналогично (HD1) для D81:
d(V(b + g) b -, V g-)var * => |
||
|
a/b |
Ph |
LPh |
||
|
V g+ |
X13, x10, x9, y8 |
16.4 |
||
|
V g+ |
x1, y6, (5, 8) |
16.2 |
||
|
V(b + g) b+ |
x13, y2, x10, x9, y8 |
17.8 |
||
|
V(b + g) b+ |
x1, x4, x5 |
15.0 |
||
Формула неопределенности:
“+”(“I”)&2”X”(“Г”V”2Г2”)
![]()
|
|
(HД5) S = (3, 1)↓; *
= (3, 3) s = 3; n
= 8; l = 6; n = 3 D83: (- -↑)(- -↑) => - d(C+,
V(b + g)
-) var *
=> |
||
|
a/b |
Ph |
LPh |
|
|
C+ |
x5 |
4.8 |
|
|
C+ |
x5, x4, y4 |
6.8 |
|
|
V(b + g)- |
x1, y3 |
6.0 |
|
|
V(b + g)- |
x5, x4 |
4.8 |
|
Формула неопределенности:
“+”(“Г”)&(0V“Т”(“I”))
Рис.
3. Атлас “неустойчивого доминирования”. II. D8.
В формуле V-алгоритма знак "+"или "-" в конце формулы
показывает направление предпочтительного выбора в случае равенства оценок у
видимых подцелей. Этот знак для данной ситуации имеет тот же смысл, что и для С-алгоритмов. В элементе задачи для D4 и D6
имеются три особые точки: один "прямой крест" и два "косых
креста". Ниже рисунка карты элемента приводится таблица путей, где в
столбцах соответственно указаны (слева направо): формула алгоритма (a/ b), вершины пути ph (кроме начальной b и конечной g), а также длины путей Lph. Если в формуле ситуации
"неустойчивого доминирования" W2="-"
для соответствующего алгоритма, то в таблице алгоритму соответствуют две
строки: до вариации элемента задачи и после. Алгоритмы для D6 те же, что и для D4,
за исключением знака обхода при равенстве оценок подцелей (он меняется на
противоположный). При этом и пути для алгоритмов с W2="-" меняются местами. Кроме того, меняются местами
алгоритмы в функции доминирования. То же остается справедливым для пары D10, D12. В случае, если в состав пути
входит точка, не обозначенная на карте, она указывается своими координатами,
например, точка (x4, y4) имеет
координату x, равную 4, и координату y, равную 4. Стрелкой при этом
указывается, с какой "стороны" отрезка расположена точка (поскольку
отрезок как препятствие нулевой толщины предполагается трехслойным).
В принципе можно доказать, что возможны реализации и всех трех возможных модификаций ситуации D8.
3.МЕТОД ЛОГИЧЕСКИХ ПОТЕНЦИАЛОВ
Метод потенциалов в задаче
выбора пути для мобильного робота (МР) был предложен в 1970 году [3].
В этом методе рассматривается случай, когда робот снабжен достаточно точной навигационной системой, чтобы ее ошибками можно было пренебречь, и системе управления известны как координаты робота и измерительного устройства, так и ориентация сектора обзора и направление производящихся измерений в некоторой абсолютной системе координат (АСК). Робот во всех случаях представляет собой точку с предписанным вектором ориентации.
Суть метода заключается в следующем. Предположим, что цель
имеет некоторый положительный заряд, препятствия заряжены отрицательно;
местоположения цели и препятствий фиксированы. Пусть также имеется некоторая
отрицательно заряженная точка, способная перемещаться. Поместим ее в исходную
точку. Под действием сил подвижная точка будет притягиваться к цели и
отталкиваться от препятствий, причем законы движения могут задаваться, в
принципе, различными способами. Логично предположить, что при некоторых
ограничениях на структуру местности и законы движения подвижной точки эта точка
достигнет цели.
В
зависимости от способа задания функций, можно получить трассы с обходом
препятствий с той или иной степенью «риска» (величины приближения к
препятствиям). Рассматриваемые ниже алгоритмы гарантируют от зацикливания в
случае, когда контуры препятствий выпуклы. Метод может также использоваться для
случая, когда препятствия разбиваются на группы, выпуклые оболочки которых не
пересекаются.
Основные вопросы, связанные с методом потенциалов, освещены в работах [2,3,4]. Две основные характеристики метода потенциалов составляют:
1)
Законы движения точки.
2)
Способы задания функции отталкивания от препятствий.
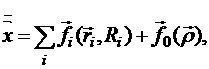
Согласно
теоретической механике, в данном случае уравнения движения задаются в виде
(будем считать, что препятствия представляют собой окружности радиуса ri):
где fi – сила отталкивания от i–ой окружности, f0 - сила притяжения к цели, r - вектор, направленный в
точку цели. Однако, как показано в [2],
такой способ задания уравнения движения является нецелесообразным, поскольку
траектория после «соударения» с препятствием будет сильно отбрасываться назад,
т.к. инерция в этом случае гасится не сразу. Поэтому путь робота строится на
основе решения специального уравнения движения, которое в простейшем случае
имеет вид:
![]()
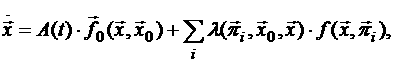
где x
– координаты робота, f0 – сила притяжения к целевой
точке, fi - сила
отталкивания от i-го препятствия. В общем
случае уравнение движения для построения трассы запишется в виде:
где x0– координаты цели, l - коэффициент зон влияния, pi - параметры i–го препятствия, A - матрица поворота системы. В простейшем случае
построение трассы представляет собой реализацию метода градиентного спуска с
постоянным шагом.
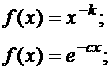
Пусть
цель притягивает подвижную точку все время с единичной силой. Тогда силу
отталкивания от каждого препятствия желательно задать так, чтобы на границе она
принимала единичное значение и была направлена по по нормали к препятствию, а
вне препятствия убывала пропорционально расстоянию. Были исследованы следующие
виды функций отталкивания:
k, c являлись варьируемыми параметрами. Изменяя их, можно
получить качественно различные виды траекторий. Так, взяв большое значение
параметра k, получим траекторию,
сходную с обходом препятствия по контуру – точка будет отклоняться от
препятствия лишь на небольшое расстояние. С другой стороны, при малых значениях
параметра k, точка будет отклоняться от
препятствия раньше, однако, сферы действия различных препятствий в этом случае
могут перекрываться (если препятствия расположены близко друг от друга) и
возможность прохода между ними может быть пропущена.
Проанализированы
возможности использования метода потенциалов для управления распределенной
мобильной системой (РМС). Исследовано пять способов организации такого
движения:
1. Движение по схеме «цепь».
В этом случае сила притяжения цели действует на «лидера», и каждый МР
«притягивается» к впереди идущему.
2. Движение типа «гонка за
лидером». В этом случае все элементы РМС «притягиваются» к «лидеру», который, в
свою очередь, «притягивается» к целевой точке.
3. Движение типа «расхождения».
В этом случае на МР, расположенные компактной группой или цепью, начинает
действовать сила отталкивания от «лидера». МР «разбегаются», исследуя каждый
свой участок.
4. Движение типа
«схождение». В этом случае «лидер» собирает все элементы РМС в компактную
группу.
5. Организация движения типа
«свободный поиск». В этом случае сила притяжения к цели отсутствует, и каждый
элемент РМС движется в свободном от препятствий направлении.
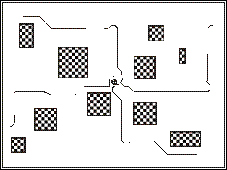
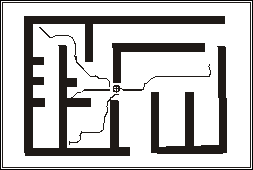
а) б)
а) Движение типа «расхождение». В этом случае на МР, расположенные компактной группой или цепью, начинает действовать сила отталкивания от «лидера». МР «разбегаются», исследуя каждый свой участок.
б) Движение типа «схождение». В этом случае «лидер» собирает все элементы РМС в компактную группу.

в)
Организация движения типа «свободный поиск». В этом случае сила притяжения к цели отсутствует, и каждый элемент РМС движется в свободном от препятствий направлении.
Рис 4
(а,б,в). Примеры движения РМС на основе метода потенциалов
4. ИНТЕРПРЕТИРУЮЩАЯ НАВИГАЦИЯ
Интерпретирующая навигация
использует не систему счисления пути, а анализ динамических изменений в
визуальной окрестности движущегося робота (например, относительных, т.е.
вычислимых на основе СИО, признаков ориентиров).
В настоящее время усложнение
навигационного обеспечения идет в направлении планирования действия в
динамической среде, активном использовании априорной информации и новых
представлений знаний о среде и функциональной задаче и построении логик для
представлений и рассуждений в условиях неопределенности.
В
реализации алгоритмов интерпретирующей навигации (ИН) мы ориентируемся на сенсорное
обеспечение, сочетающее как прямое лазерное дальнометрирование, так и осмотр пространства
традиционными ТВ-средствами. При движении внутри помещений активно используются
стандартные эталоны - ориентиры-маркеры с кодом, идентифицирующим их
расположение.
Организация
навигационных вычислений в перспективных проектах (например, для организации
движения телепрограммируемых МР -грузовиков при транспортировке с места добычи
полезных ископаемых) может быть представлена в виде следующей схемы (так
называемого "навигационного креста"):
|
|
|
ГРНС |
|
|
|
|
|
úê |
|
|
|
ИН |
¾ |
СУ МР |
¾ |
ТНС |
|
|
|
úê |
|
|
|
|
|
Оператор |
|
|
где использованы обозначения: ГРНС - глобальная
радионавигационная спутниковая система; ТНС - традиционная навигационная
система, включающая в себя процессы счисления пути и подкорректировки по
ориентирам; ИН - интерпретирующая навигация.
Аналогом количественной
модели в АСК в случае ИН выступает иная, качественная модель, - граф
информационной эквивалентности (ГИЭ). В таком описании вершинам графа
соответствуют связные районы местности с одинаковым информационно-визуальным
содержанием (районы информационной эквивалентности – И.Э.), а ребрам - изменение
этих описаний при переходе из района в район. В этом случае организация
передвижения МР основывается на фиксированном наборе информационно-двигательных
действий (ИДД). Подобный тип навигации иногда называется за рубежом
"качественной" навигацией.
Следует отметить, что в
данном случае каждому району И.Э. соответствует абсолютное описание -
упорядоченная по углу наблюдаемая видимая последовательность ориентиров -
кольцо. Интерпретирующая навигация, в отличие от качественной, использует точечные
ориентиры, а не ориентиры - протяженные объекты. Кроме того, каждому ориентиру
приписывается не абсолютный признак (например, номер или координаты в АСК), а
относительный, который вычисляется на основе локально действующей информационной
системы (ИС) с учетом затенения. Таким образом, на одном объекте может быть
расположено несколько ориентиров, и, кроме того, видимые признаки ориентиров
(относительные, а не абсолютные) могут совпадать.
Более подробно эти вопросы
рассмотрены в [5]
Районы И.Э. для 2D постановки порождаются разбиением
плоскости движения, в которой движется МР, “линиями действия”, которые проходят
через “ориентир-источник” и “ориентир-затенитель”.
Ориентир-источник - это такой ориентир, который либо появляется, либо исчезает при
выходе за пределы данного района И.Э (при пересечении линии действия).
Ориентир-затенитель, актуальный для данного ориентира-источника, находится на некоторой
части границы видимого контура препятствия, ответственного за затенение
ориентира-источника.
Особая точка - это такая точка на местности, что сколь угодно малое перемещение
вблизи нее в две разные точки может привести к пересечению нескольких линий
действия.
Существуют 4 типа подобных
ситуаций:
"клещи" - источник
виден только на линии действия ;
"навал"
- кратная совпадающая линия действия для ряда источников по данному затенителю;
"узел"
- пересечение в одной точке нескольких линий действия;
"веер"
- пересечение нескольких линий действия вблизи выпуклой вершины.
Излагаемый в [5] алгоритм
информационного слежения работает при достаточно общих предположениях о
структуре местности указанного типа. Запрещенными считаются только ситуации
типа "клещи".
Нетрудно видеть, что лишь в
ситуации типа "веер" наблюдается изменение типа наблюдаемого на
данной вершине скачка.
Для простоты ниже
полагается, что МР не производит сеансов на линиях действия ориентиров.
Следует отметить, что в
случае особой точки типа "клещи" определение остается в силе,
поскольку здесь происходит как бы слияние двух линий действия:
ориентир-источник появляется и сразу же исчезает.
Теорема 4.1. Все возможные типы особых точек для постановки 2D сводятся к перечисленным выше четырем случаям.
Доказательство. Итак, особая точка, по
определению, существует в случае наличия общих точек у линий действия. Здесь
могут быть два случая:
(1). Линии действия
совпадают на каком-то участке. В этом случае может получиться только особая
точка типа "навал", т.к. затенитель и источник расположены на одной
линии.
(2). Линии действия (более
двух) пересекаются в некоторой точке. Здесь возможны два подслучая:
(2.1). Эта многократная
точка пересечения совпадает с затенителем. Тогда получается особая ситуация
типа "веер" (передвижение МР вблизи затенителя).
(2.2). Точка пересечения не
совпадает с затенителем - получается точка типа "узел".
Наконец, особая точка типа
"клещи" возникает в случае, если источник и два затенителя с
различными признаками "скачка" расположены на одной прямой. Таким
образом, перебор по всем возможным ситуациям расположения источников и
затенителей дает только описанные выше типы особых точек.
Особые точки второго рода
возникают в случае, если особые точки первого рода (описанные выше) совпадают
друг с другом. Естественно, что совпадать могут только точки различных типов.
Таким образом, максимум может совпасть четыре особые точки различных типов.
Типы особых точек и их влияние на алгоритмы ИН иллюстрирует
таблица 2.
Таблица 3. Типы особых точек для описаний на основе видимых ориентиров в
интерпретирующей навигации.
Название
|
Содержание |
Влияние |
|
“Навал” |
Появление множества ориентиров
на одной ли- нии действия |
На абсолютную
интерпретацию не влияет, поскольку упорядочивание ориентиров по углу наблюдения
фиксировано |
|
“Веер” |
Пересечение нескольких
линий действия при движении вблизи ориентира-затенителя |
Недопустимо
в алгоритме определения начального местоположения |
|
“Узел” |
Пересечение нескольких
линий действия во внутренней точке среды |
Недопустимо
в алгоритме определения
начального местоположения |
|
“Клещи” |
Ориентир-источник в данной
окрестности виден только на линии |
Недопустимо
для всех алгоритмов ИН |
Приводимые ниже теоремы
являются основными положениями в теории алгоритма информационного слежения ИН.
Этот алгоритм позволяет по заданной в начальный момент времени абсолютной
интерпретации локальных относительных признаков ориентиров проводить в
дальнейшем в каждом из дальнейших сеансов измерения адекватную абсолютную
интерпретацию ориентиров без системы счисления пути.
Tеорема 4.2. Пусть e1 - минимум по всем
районам И.Э. данной местности расстояния между свободным контуром данного
района и "поясом" района
(свободный контур образуют граничные отрезки, не принадлежащие границе
препятствий, а "пояс" района образуют отрезки, которые не входят одновременно
в свободные контуры каких-либо двух соседних к данному району районов И.Э.) -
см. рис. 11. Пусть e2 - половина
минимального расстояния между вершинами препятствий. Пусть L - видимый диаметр местности. Пусть, далее, e < min(e1,e2). Алгоритм информационного слежения гарантирует
абсолютную интерпретацию и информационную привязку (в случае, если они заданы в
начальный момент времени) при частоте сеансов, не превышающей величину ( v + cL)/e, где v – максимальная скорость движения робота, с - максимальная угловая скорость вращения ориентации робота при условии,
что на местности не наблюдается ситуация типа "клещи" (источник виден
только на линии).
Tеорема 4.3. Пусть начальное относительное описание в виде кольца признаков
является самоналожимым и/или класс И.Э., которому принадлежит начальное
положение МР не является односвязным. Тогда, в случае, если на местности отсутствуют
особые ситуации типа "узел" с кратностью более 2, и движение МР
производится так, чтобы избежать особых ситуаций типа "веер",
возможно определение начального положения МР (района и.э.), в случае, если
указанные выше неопределенности могут быть сняты исследованием окрестности
некоторого порядка начального района И.Э.
5. УСЛОВИЯ СОГЛАСОВАНИЯ ИНФОРМАЦИОННОЙ И ДВИГАТЕЛЬНОЙ АКТИВНОСТЕЙ МОБИЛЬНОГО РОБОТА.
Надежность
алгоритмов СУ МР определяется в основном составом предположений о
характеристиках среды, эффективностью алгоритмов в случае выполнения этих
предположений и характером поведения СУ МР в случае нарушения этих
предположений (последнее имеет большое значение для обеспечения живучести МР).
Одним из важных обстоятельств здесь является выполнение условий согласования
(УС) информационных и двигательных параметров МР [6, 7].
Алгоритму
информационного обеспечения движения МР соответствует несколько неравенств,
связывающих функции параметров, характеризующих измеритель (высота положения,
частоты сканирования, угловые скорости вращения блока обзора и т.п.), с
параметрами, характеризующими движение робота (скорость движения, параметры
участка пути и т.п.). При выполнении этих неравенств гарантируется выполнение
текущей информационно-двигательной задачи (обнаружение в движении препятствий
заданных типов и размеров, слежение в движении за ориентиром и т.п.). В случае
нарушения какого-либо из неравенств необходимо либо менять алгоритм, либо
соглашаться с ухудшением качества и надежности работы СУ МР.
Учет УС необходим как на этапе проектирования, так и для уже
построенных МР. В обоих случаях основу методики составляют расчетные случаи
движения. Разработка таких расчетных случаев является задачей эксперта.
Совокупность расчетных случаев составляет основу для исследования УС. При этом
для каждого расчетного случая возможна постановка двух
задач:
(1).
Для заданных типов двигательного поведения и заданных экстремальных параметров
среды определить параметры ИС МР, гарантирующие выполнение УС.
(2).
Для ИС с фиксированными параметрами и заданными экстремальными параметрами
среды определить ограничения на возможное двигательное поведение МР при
выбранных УС.
К настоящему времени разработан ряд расчетных случаев для
движения МР по опорной базовой плоскости и методика соответствующих
исследований УС. Кратко охарактеризуем типы этих
расчетных случаев:
1. Сканирование ближней зоны обзора по ходу движения.
Основные
параметры среды для условий согласования:
-
характерный минимально допустимый размер обнаруживаемых препятствий (определяет
дискретность осмотра в проекции на базовую плоскость).
Возможные
последствия нарушений условий согласования:
а) Допустим фатальный исход.
б)
Возможно "нарушение без последствий" условий согласования при
дополнительной априорной информации о среде, в частности, за счет увеличения
размеров обнаруженных опасных зон.
2. Осмотр дальнего плана среды для выбора пути
Здесь предполагается, что непреодолимые
препятствия могут быть двух типов: "стена" и "яма".
Основные параметры среды для условий согласования:
- минимально допустимое расстояние до "стены" при
проведении сеансов измерений,
-
минимально возможная глубина "ямы",
-
характерный размер достаточного прохода.
Возможные последствия нарушений условий согласования:
а) Не
фатальные последствия, - если при движении к
выделенной подцели незамеченная яма или фиксированный ложный проход адекватно
идентифицируются ИС ближнего действия.
3. Проведение сеансов навигационных измерений для
выделения текущего множества ориентиров в среде.
Основные
параметры среды для условий согласования:
-характерное
расстояние между особенностями естественных ориентиров (например, вертикальными
ребрами предметов в помещении) или между искусственными маркерами;
-
расстояние, характеризующее пороговое ограничение на смещение робота, при
котором видимая часть среды не претерпевает "слишком значительных
изменений" (это означает, что для двух последовательных сеансов обзора существуют
общие ориентиры, что позволяет произвести интерпретацию как вновь появившихся,
так и исчезнувших ориентиров);
-
видимый диаметр среды - максимальное расстояние между двумя точками среды,
видимыми одна из другой (видимость понимается с учетом радиуса действия
информационной системы МР).
Возможные
последствия нарушений условий согласования:
а)
неадекватная интерпретация местоположения МР в среде, где допустимы несвязные
районы с одинаковыми описаниями видимой части среды для используемого типа ИС;
б)
неадекватное определение требуемого курса движения (ситуация типа
"буриданова осла"), если существуют районы с
"самоналожимыми" описаниями;
в)
"конфликтная ситуация" при наличии эффективной системы счисления пути
(ССП);
г)
фатальный исход, если уход ССП превысил допустимый предел в случаях a) и б).
Введём четвёртый тип расчётного случая УС.
Его общий вид выглядит
следующим образом: KxKyKz P(x,y,z),
где ![]() , P(x,y,z) -
предикат.
, P(x,y,z) -
предикат.
Заметим, что
кванторные префиксы вида ![]() широко используются в
математике. Например, в математическом анализе, наибольшей популярностью
пользуется кванторный префикс
широко используются в
математике. Например, в математическом анализе, наибольшей популярностью
пользуется кванторный префикс ![]() . Он используется, например, при определении предела, непрерывности функции
в точке, а также в дискретной математике при формулировании леммы о разрастании
для регулярных языков [8] .
. Он используется, например, при определении предела, непрерывности функции
в точке, а также в дискретной математике при формулировании леммы о разрастании
для регулярных языков [8] .
Пусть теперь ![]() - носитель террайна,
- носитель террайна, ![]() - видимая окрестность множества
- видимая окрестность множества ![]() ,
а
,
а ![]() - открытая граница множества
- открытая граница множества![]() ,
т.е. те участки границы множества
,
т.е. те участки границы множества ![]() ,
через которые МР может покинуть
,
через которые МР может покинуть ![]() .
Пусть
.
Пусть ![]() - положение
- положение ![]() -го МР в момент времени
-го МР в момент времени ![]() .
Тогда такт работы системы управления РМС заключается в выборе подцелей движения
для элементов РМС из множества [9]:
.
Тогда такт работы системы управления РМС заключается в выборе подцелей движения
для элементов РМС из множества [9]:
![]() .
.
Пусть ставятся следующие
задачи:
1. Достижимость целевой точки и
аналог информационного обхода для конечного графа. Пусть ![]() - множества вершин
графа возможных перемещений. Время дискретно,
- множества вершин
графа возможных перемещений. Время дискретно, ![]() - положения РМС.
- положения РМС. 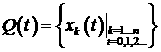 - пройденные вершины
графа возможных перемещений. Условие согласование выглядит следующим образом:
- пройденные вершины
графа возможных перемещений. Условие согласование выглядит следующим образом:
|
|
(1) |
2. Информационный обход в общем
случае. Пусть ![]() - носитель террайна
- носитель террайна
(графа с континуум рёбер вершин). В этом случае
условие согласования выглядит следующим образом:
|
|
(2) |
Следует особо отметить, что для этой задачи возможна
запись УС в следующем виде:
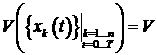 , где
, где ![]() - время окончания ИО.
- время окончания ИО.
3. Информационное блокирование
– усиление УС информационного обхода
|
|
(3) |
Это условие аналогично можно записать в виде:
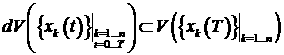
Следует особо подчеркнуть, что
приведённые выше УС являются инвариантами для любого допустимого алгоритма
данной функциональной задачи.
6. ВИРТУАЛЬНЫЕ ДАТЧИКИ
Виртуальные
датчики (ВД) [10-12], являются обобщением понятия логического датчика [10] и
вычислительного модуля. В
каждом ВД, наряду с сенсорными, выполняются вычислительные операции.
Непосредственно сенсорные операции ВД может и не выполнять, а использовать
информацию, полученную от других ВД. Нижний уровень информационной
системы робота составляют физические датчики (ФД). На следующем уровне
расположены ВД – программные системы,
обеспечивающие настройку на конкретные типы ФД (возможно с некоторой
предварительной обработкой информации). Это позволяет при программировании
верхнего уровня системы управления не учитывать специфики уровня ФД.
Среди основных типов ВД можно
выделить следующие:
- ВД, осуществляющие
фильтрацию информации (в т.ч. логические и пороговые перенастраиваемые
фильтры),
- ВД - “инспекторы”, осуществляющие регистрацию
изменений в заданном районе наблюдаемой среды,
- ВД - детекторы,
регистрирующие появление заданного объекта или комбинации заданных
характеристик среды,
- ВД – “обобщающие преобразователи”, которые по
заданному описанию характеристик среды производят их свертку и обобщение с
целью уменьшения количества информации, необходимой для принятия решения.
Концепция виртуальных датчиков, представленная в [11], является
дальнейшим развитием концепции логических датчиков, предложенной Хендерсоном
[10]. Она основана на том, что более
выгодно использование подсистем, обладающих собственными встроенными
элементами искусственного интеллекта. Это позволяет полнее обеспечить интерфейс
с управляющей ЭВМ на высоком уровне абстрагирования знаний. При этом
обеспечивается полный информационный обмен между супервизором и датчиками,
которые не связаны с ним непосредственно. Такой подход подразумевает, что
супервизор может координировать решение общей задачи управления при использовании
различных типов датчиков и приводов.
Термин
"виртуальные датчики" был введен в [11] с целью выявления аналогии
между предложенной концепцией и виртуальными машинами, где функционирование
системы не зависит от технической реализации. Например, виртуальные датчики
могут, используя различные сенсорные
комбинации, обеспечивать дополнительные функции очувствления по отношению к
реализуемым физическим датчикам.
Данный подход получил
отражение в области технологий интеллектуальных датчиков (smart-sensor), развиваемой
IEEE. Получило развитие семейства стандартов по интерфейсам интеллектуальных
преобразователей IEEE 1451, целью которых является внедрение технологии
интеллектуальных преобразователей. Стандарты
серии IEEE 1451 ищут пути упрощения взаимодействия интеллектуальных
преобразователей (датчиков и приводов) через развитие стандартных интерфейсов
[13].
Таким
образом, подсистемы интеллектуальных датчиков и приводов обеспечивают
сопряжение знаний низкого уровня, связанного с устройствами очувствления, со
знанием высокого уровня, совместимого с супервизором. Следовательно,
формируется иерархия концептуальных уровней, нижний уровень которой составляют
базисные концепции.
Учет
УС является основополагающим на этапе проектирования информационной системы
(ИС), т.е. при настройке на конкретный уровень ФД работа ИС должна происходить
с учетом соответствующих УС.
Иерархии ВД соответствует
иерархия моделей среды и, в случае мобильных роботов, иерархия соответствующих
информационно-двигательных действий.
Следует отметить, что три
характерные основные особенности информационной системы на базе ВД заключаются
в следующем:
1. Виртуальный датчик как основной элемент ИС;
2. Эффективное обеспечение мультисенсорных систем на базе общего перенастраиваемого интерфейса;
3. Наличие механизма выбора конфигурации и реконфигурации информационной системы.
Таблица 4.
Основные типы виртуальных датчиков
в сенсорной сети, построенной на основе данных физических датчиков. Первые
шесть даны по работе [12], остальные по данным авторов.
Типы |
Функции датчиков |
|
0.Основные датчики
(fundamental sensors). |
Основной датчик представляет собой физический датчик в совокупности с его драйвером. |
|
1. Датчики состояния (State sensors). |
Формирование опросов состояний физических датчиков при помощи соответствующих драйверов. |
|
2. Датчики событий (Event sensors). |
Сигнал от ВД события возникает в случае, если произошло заданное супервизором изменение уровня сигнала ФД. |
|
3. Триггерные датчики
(Trigger sensors). |
Осуществление заданной комбинации данных от датчика состояния и датчика события: данные от датчика состояния передаются в случае, если произошло срабатывание заданного датчика события в соответствии с предписанным условием супервизора. |
|
4. Трендовые датчики (Trend sensors). |
Осуществляют накопление данных (для статистической обработки) в случае осуществления заданного события. |
|
5. Датчики дрейфа (Drift sensors). |
Определяют событие как наличие систематического заданного дрейфа показаний заданного датчика. |
|
6. Датчики надежности данных (Health sensors). |
Проверяют наличие и работоспособность ФД и удовлетворение получаемого от ФД сигнала заданному рабочему диапазону. |
|
7. Детекторы. |
Логические фильтры, позволяющие выделить в последовательности данных ВД особенность типа скачка и скачка производной. |
|
8. Датчики обобщения информации |
“обобщающие преобразователи”, которые по заданному описанию характеристик среды производят их свертку и обобщение с целью уменьшения количества информации, необходимой для принятия решения |
|
9. Датчики ситуации |
Общая ситуация окружающей обстановки (или сцены) представляется в виде одного обобщенного признака ситуации. Значение данного признака ситуации может служить входом в словарь “ситуация-действие” при организации управления верхнего уровня |
7. МЕТОДЫ ПОВЫШЕНИЯ НАДЕЖНОСТИ
Таблица 5. Основные способы повышения надежности МС и РМС.
Данные взяты из обзоров,
приведенных в [14,15].
|
Концепция |
Реализация |
|
Изоляция одиночных сбоев |
Организация цикла управления с обновлением
информации и выработкой управляющих воздействий на каждом шаге. Такой цикл не
допускает распространения ошибок. |
|
Выбор частот процессов |
Составление и анализ условий согласования
процессов управления |
|
Аппаратная и программная реконфигурация систем управления |
1.Выделение участков программ, допускающих
эффективную аппаратную реализацию. 2.Перезагрузка программ бортового компьютера. 3.Реконфигурация сенсорной системы. |
|
Повышение надежности измерителей |
Спецконтроллеры или предварительная обработка сигнала для преодоления дефектов измерительной
аппаратуры. |
|
Диагностические проверочные требования |
1.Фоновая взаимопроверка аппаратных средств и
программных систем. 2.Тесты измерительных устройств. |
|
Технология блокирования и отключения |
1.Спецрежим экстренного прекращения действий. 2.Спецрежим "останов-осмотр-ожидание" 3.Спецрежим поиска и перемещения в безопасное
место с переходом в ждущий режим. |
|
"Плавная деградация" |
Наличие специализированных программных средств,
обеспечивающих ограниченное функционирование системы при программных или
аппаратных сбоях, выходящих по своей значимости за пределы циклов управления |
|
"Мягкий отказ" |
Резервирование ждущего режима, разрешающего
проведение тестов на основе специального монитора для диагностики отказа
системы. |
|
Защита программного обеспечения |
1.Схемы защиты системной памяти БЦВМ 2.Троекратное
дублирование системных таблиц. 3.Обработка данных в трех независимых каналах
с определением результата по схеме голосования "2 из 3" |
|
Анализ работы в наихудших условиях |
Обновляющаяся база данных о параметрах системы с
учетом их изменения в процессе эксплуатации в наихудших условиях |
|
Спецсредства программи-рования |
Специальные языковые средства для программной
обработки незапланированных событий. |
|
Локальная автономность и наглядность |
1.Реализация распределенных вычислений с
возможностью реконфигурации. 2.Наглядность системного описания системы |
ЗАКЛЮЧЕНИЕ
Формальный подход к исследованию алгоритмов информационного обеспечения мобильных систем базируется на обосновании алгоритмов, исследовании их сравнительной эффективности и адекватной интерпретации сенсорных данных. Выше в работе были изложены следующие методы и технологии этого подхода:
· исследование немонотонной зависимости длины пути от радиуса действия информационной системы,
· исследование сравнительной эффективности алгоритмов выбора пути,
· неустойчивое доминирование одного алгоритма над другим,
· использование метода потенциалов для задачи выбора пути,
· интерпретирующая навигация,
· виртуальные датчики
· способы повышения надежности.
Указанная базовая концепция позволяет не только разрабатывать систему информационного обеспечения для МР и МС, но и производить ее качественное обоснование, определять область допустимости и исследовать эффективность.
ПРИЛОЖЕНИЕ 1. ИСТОРИЧЕСКАЯ СПРАВКА О МЕТОДЕ ПОТЕНЦИАЛОВ
Наряду
с указанным названием – метод потенциалов (Potential Field Approach), он имеет следующие названия:
способа "искусственных потенциальных полей" (artificial potential fields), "полей виртуальных
сил" (virtual force field - VFF), "гистограммы векторных сил" (vector field histogram-VFH) и др. Суть этого
метода, напомним, заключается в том, что путь строится на основе решения
специального "уравнения движения", в которое входят "сила
притяжения к цели", "силы отталкивания от препятствий " и,
возможно, некоторые другие "силы". При ссылке на этот метод в
качестве пионерских упоминаются работы 1985 -1986 гг. [16,17]. Вместе с тем
работа фирмы Хитачи по управлению МР, в которой использованы идеи
"силового поля", выпущена в 1984 г. [18]. В [2] опубликовали
результаты подобного исследования в ИПМ АН СССР в 1974г. Вместе с тем
использование подобных физических аналогий при трассировке электронных плат
уходит корнями в глубь 50-х годов [19]. Правда, вычислительные аспекты при этом
имеют свою специфику.
Сам
архетип идеи движения в поле "информационных" (виртуальных) сил
восходит к работам 30-х-40-х годов одного из виднейших представителей
гештальтпсихологии Курта Левина. Он выступил с идеей применения в психологии
концепции физического поля для описания поведения и конфликтных ситуаций при
взаимодействии индивида с окружающим миром [20]. Современные психологи
критикуют К. Левина за физикализм концепции, акцент на динамический аспект в
ущерб содержательному и многое другое. Вместе с тем в указанных работах К.
Левина можно почерпнуть немало интересного. Экспериментальный материал, подтверждающий
разработанную концепцию, был получен в основном при наблюдении за детьми
разного возраста и документирован посредством киносъемок. Имеет смысл привести
четыре особенности поведения сил «психологического поля», выделенного К.
Левиным:
(1).
"...сила поля исчезает (или по крайней мере сильно ослабевает) как только
объект попадает в сферу "владений индивида".
(2).
"...в некоторых случаях величина валентности [заряда] увеличивается с ее
явной близостью. Это выражается как в продолжительности, так и в интенсивности
попыток к достижению цели".
(3).
"...величина сил поля, которые соответствуют отрицательной валентности,
уменьшаются намного быстрее с увеличением физического расстояния, чем это
происходит с силами поля, соответствующими положительной валентности".
(4).
Возможны колебания локомоций вблизи точек равновесия сил, которые называются
также "годологическим конфликтом".
Все они имеют аналоги при использовании метода
потенциалов для управления МР.
На
начальном этапе исследований в ИПМ рассматривались препятствия в виде
окружностей. Подобное представление после результатов работ Koditschek с
соавторами [21,22] можно считать основным. Сила притяжения к цели полагалась
постоянной по модулю и направленной к точке цели. Сила отталкивания от i-ого препятствия fi зависела
от аргумента Ri /ri
, где Ri -радиус
i-ой окружности, ri -расстояние
от центра i-ой окружности до
движущейся точки. fi считалась направленной от центра окружности.
Траектория ("локомоция") получалась в результате интегрирования
уравнений движения второго порядка, так как ускорение, действующее на
движущуюся точку, определялось суммой указанных сил. В ходе исследований
выяснилось, что инерционность, заложенная в указанную модель, приводит к тому,
что траектория движения становится малоприемлемой (препятствие
"отбрасывает" движущуюся точку очень сильно и траектория получается
чересчур "изрезанной"). Для того, чтобы избавиться от этого
недостатка и сделать метод годным для случая аппроксимации контуров препятствий
другими способами, было предпринято следующее. Во-первых, стали использоваться
уравнения движения первого порядка (т.е. действующие силы определяют скорость,
по сути дела речь идет об аналоге простого градиентного спуска). Во-вторых,
сила отталкивания стала определяться аргументом, равным расстоянию до
препятствия. При этом форма контура препятствия произвольна, а для приведенного
выше примера это разность ri
–
Ri. Направлена эта сила в сторону от ближайшей
точки препятствия. В ходе исследований было признано рациональным в случае
наличия нескольких препятствий использовать функции от указанного аргумента x типа x-k или e-cx,
которые быстро убывают с расстоянием. При этом коэффициенты k и c
могут быть варьируемыми параметрами.
Следует
особо подчеркнуть, что, варьируя параметры k
и c при определении сил отталкивания,
можно получать траектории для движения нескольких МР. Если ввести в этом
процессе запаздывание, то можно получить режим "следования друг за
другом".
Иногда среда, в которой расположено много
препятствий, "хорошо организована", например, препятствия разбиваются
на группы, выпуклые оболочки которых не пресекаются. В этом случае сила отталкивания
может вычисляться сразу для всей группы.
Таким образом, метод потенциалов позволяет
строить "размытые" модели среды и получать решение без учета ненужных
подробностей.
Анализируя разнообразие зарубежных работ по
методу потенциалов, можно выделить два интересных направления.
Первое является попыткой ответить на вопрос:
можно ли эффективно задавать силовое поле так, чтобы отсутствовали устойчивые
точки равновесия в принципе. Достаточно очевидно, что в общем случае ответ на
этот вопрос положительный. Действительно, функция потенциала в точке x, равная минимальной
длине допустимого пути от x к g - точке цели, задает такое поле.
Однако эту функцию в общем случае считать весьма непросто. Koditschek с
соавторами в серии работ [21,22] и др. предложили свой подход к этой проблеме,
который хотя и отличается оригинальностью, в итоге оказывается вряд ли намного
проще способа, указанного выше. Вначале рассматривается "сферический
мир". Для плоскости это окружности-препятствия, окруженные
окружностью-рамкой. В этом мире результирующая сила определяется не как сумма
сил, действующих от различных препятствий, а как произведение таких сил. Эти
два положения позволяют избежать наличия точек равновесия силового поля, что
зафиксировано теоретически.
Далее строится последовательность
диффеоморфизмов. Поначалу это – переход от
"сферического мира" к "звездному
миру" - в котором препятствия представляются
многоугольниками особого вида. Затем происходит
переход от "полигонального мира" ко
все более и более "общим мирам". При этом диффеоморфизм сохраняет
"безособенность" силовых полей, получающихся при поэтапных изменениях "сферического мира". Однако необходимо отметить,
что демонстрируемые иллюстрации подобных полей для постановок, более общих чем
"сферический мир", позволяют утверждать, что для них весьма характерны "овражные эффекты". Следовательно,
при фиксированном значении шага возможны в лучшем случае эффекты типа
"информационного дребезга", а в худшем - зацикливание в ложном
экстремуме. Возможно, что именно поэтому авторы не демонстрируют примеры
построения траекторий движения, а - лишь изображения полей линий уровня
потенциала.
Второе направление, берущее начало от работ
исследователей Оксфордского университета, заключается в представлении МР не точкой, а отрезком или прямоугольником.
Это позволяет рассчитывать не только результирующую силу, действующую на МР, но
и момент сил, т.е. управлять ориентацией.
Некоторые результаты
исследования алгоритмов, основанных на методе потенциалов, полученные в ИПМ в
70-80х гг. прошлого века, приводятся в работе [3].
ПРИЛОЖЕНИЕ 2. УПРАВЛЯЮЩИЕ СИСТЕМЫ МОБИЛЬНОГО РОБОТА
Среда,
в которой действует МР, предполагается: а) априорно неизвестной; б) большой; в)
сложной; г) динамической. После определенного времени обследования такой среды
МР должен быть способен к передвижению в любое место с доступной минимизацией
стоимости передвижения. Такая постановка задачи называется Максимальным
Навигационным Тестом (МНТ, Maximum Navigation Test)
и является в настоящее время общепринятой [23].
В наиболее общем подходе навигационная система
взаимодействует практически со всеми элементами системы управления (СУ) МР. В
последней можно выделить следующие основные модули:
-
Управление движением с локальным объездом препятствий (Motion control).
-
Локализация и построение моделей среды.
-
Планирование.
-
Архитектура.
Управление двигательным
поведением.
В
настоящее время упор делается на организацию двигательного поведения МР на
основе использования множества алгоритмов, реализующих такие режимы движения, как
следование по заданному курсу, объезд встреченного препятствия с возвращением
на курс, отслеживание контура (препятствия или поля) и
т.п. В то же время, всё более назревает вопрос о переходе от одноцелевых
алгоритмов, основанных на механизмах типа "стимул-реакция", к алгоритмическим механизмам многоцелевого
поведения, использующих понятийное описание состояния робота и его окружения.
Предполагается перспективным построение многоцелевого объединения
упомянутых рефлекторных алгоритмов одним из двух способов:
1) одновременное
функционирование нескольких аппаратно реализованных контроллеров (например, на
основе нейронных сетей) с автоматически получаемым согласованием целей и
режимов возможного движения и формированием так называемого комбинированного
поведения (combining behavior);
2) последовательное
поведение (sequencing behavior),
при котором верхний уровень управления с использованием сложных логических
алгоритмов осуществляет поочерёдное
переключение с одного типа движения на другой при появлении определенного
события.
Оба эти направления
требуют, прежде всего, развития логики интерпретации сигналов осмотра внешней
среды и методов её описания. Именно здесь полезно использование алгоритмики
описанных выше виртуальных датчиков свойств окружения робота.
Локализация и моделирование среды.
Эти
проблемы жестко взаимосвязаны между собой. Имея
хороший алгоритм пространственной локализации наблюдений, можно построить
эффективную модель местности и наоборот. Разрабатывать алгоритмы для
одновременного решения этих двух задач крайне тяжело. Объединение разнотипных
сенсорных данных (в том числе - с различных точек пространства в процессе
движения) может осуществляться статистически - с использованием правил Байеса,
фильтра Калмана и других аналогичных фильтров.
Существует
три общепринятых уровня моделей: верхний называется глобальным, средний –
локальным или проблемным, а на нижнем уровне располагается модель для
представления текущего сенсорного поля (обычно используется представление в
виде клеток-ячеек – cell
decomposition
model).
Используется
два основных типа моделей: геометрические и топологические. При геометрическом
моделировании объект определяется вектором характеристик, позиции, ориентации и
других отношений. При топологическом моделировании описываются качественные
аспекты отношения положения объекта с другими объектами. Обычно этот тип
моделей является связным графом. Существует два способа построения
топологической модели: либо из геометрической модели, либо непосредственно.
Аналогично описывается и локализация
положения МР:. Геометрическая локализация
определяет положение и ориентацию МР. Топологическое описание положения МР
определяется на основе описания его отношения со средой типа «в помещении А»,
«напротив двери» и т.п.
Существуют
три основные стратегии локализационных вычислений: 1) периодическое
совмещение локальной модели среды с заданной априори картой; 2) определение
позиции на основании априори известных реперов-ориентиров; 3) выделение
характеристик среды и оценка их позиций относительно робота с последующим
определением результирующего перемещения робота. В последней стратегии также
могут применяться либо геометрический, либо топологический подходы.
Планирование.
Перспективными считаются следующие подходы к планированию
пути:
1).
Методы, основанные на карте путей, здесь обычно используются графы видимости и
диаграммы Вороного.
2). Представление карты
среды в виде клеточного поля. Сюда относятся обобщенная триангуляция Делоне, а
также представление в виде квадратных и шестиугольных полей, на которых могут
реализовываться модели вероятностного прохождения, модели с накоплением
информации и т.п.
3). Движение в
виртуальных информационных полях. Сюда относятся алгоритмы, основанные на
методе потенциалов, а также ряд других эвристических алгоритмов.
4). Методы планирования
двигательного поведения. В этом случае план представляет собой
последовательность поведенческих актов, переход между которыми осуществляется
по наступлении определенного события.
Архитектура.
На
протяжении 70-80-х годов господствовал подход к действиям, основанный на планах
(plan based action) [23]. Иногда этот подход назывался SMPA (Sensor – Model – Plan – Act). Начиная с середины 80-х годов
разрабатываются архитектуры, основанные на рефлекторном подходе к формированию
двигательного поведения МР. В этом случае планы исключаются, и считается, что
внешняя среда сама по себе является лучшей своей моделью. Этот подход к формированию
действий называется основанным на сенсорике (sensor based action) [23].
В настоящее время
интенсивно разрабатываются гибридные архитектуры, сочетающие в себе черты обоих
подходов[23]. Обязательным в этом случае является трехуровневая система планирования:
на верхнем уровне находится общий планировщик, на среднем – контроллер выделенного класса дискретных событий и на
нижнем –
контроллеры для организации определенных типов двигательного поведения.
Разрабатываемая концепция интерпретирующей навигации предполагает использование
особенностей организации рефлекторного
двигательного поведения МР, использование моделей среды топологического типа,
организации передвижения на основе последовательности
информационно-двигательных действий (ИДД) и гибридной навигационной
архитектуры.
Серьезное внимание
уделяется вопросам трансляции из "топологического" представления
среды (на основе наблюдаемых отношений между препятствиями) в геометрическое,
удобное для классического задания пути в некоторой абсолютной системе координат
(АСК). Начиная с начала 90-х годов используется разбиение среды на
"перцептуально эквивалентные классы" ("perceptual equivalence classes" - термин предложен Dan Huttenlocker [6]), позволяющее организовать движение не только на основе
счисления пути, но и с учетом взаимосвязи расположения зон, где видно
"приблизительно одно и то же". Такой подход
лежит в основе описанной выше интерпретирующей навигации.
Следует особо отметить, что
для организации движения в индустриальных средах и по
естественной местности активно используются
лазерные дальномеры (хотя они и являются более дорогими устройствами по сравнению
с телекамерами и обладают рядом специфических недостатков). Это позволяет
существенно упростить выделение естественных ориентиров,
связанных с рельефом окружения робота. Вместе с этим, использование телекамер
позволяет выделять и пеленговать ориентиры по их фотометрическим особенностям -
без ограничений расстояний визирования. Комбинирование этих двух типов
наблюдения и измерения свойств окружения робота должно привести к расширению
возможностей и повышению надёжности процессов построения движения и поведения
мобильных роботов.
ЛИТЕРАТУРА
1.Платонов А.К., Зуева Е.Ю.,
Кирильченко А.А., Соколов С.М. Логический подход к проектированию алгоритмов
информационного обеспечения мобильных
систем. 1. Основные понятия.
2.Платонов А.К., Карпов И.И.,
Кирильченко А.А. Метод потенциалов в задаче прокладки трассы. // М.: Препринт
Ин-та прикл. матем. им. М.В.Келдыша АН СССР, 1974, № 124, 29 с.
3.Платонов А.К., Кирильченко А.А.,
Колганов М.А. Метод потенциалов в задаче выбора пути: история и перспективы. //
М.: Препринт Ин-та прикл. матем. им. М.В.Келдыша РАН, 2001, № 40, 32 с.
4.Барбашова Т.Ф., Кирильченко А.А.,
Колганов М.А. Некоторые аспекты использование метода потенциалов при управлении
мобильными роботами. // Препринт Ин-та прикл. матем. Им.М.В.Келдыша РАН, 2004, №
21, 26 с.
5.Кирильченко А.А., Платонов А.К.,
С.М.Соколов. Теоретические аспекты организации интерпретирующей навигации
мобильного робота. // М.: Препринт Ин-та прикл. матем. им. М.В.Келдыша РАН,
2002, № 5, 40 с.
6.Барбашова Т.Ф., Кирильченко А.А.,
Ярошевский В.С., Яшкичев И.В. Условия согласования информационно-двигательных
параметров мобильного робота при осмотре среды // М.: Препринт Ин-та прикл.
матем. им. М.В.Келдыша АН СССР, 1988, № 190, 29 с.
7.Каргашин А.Ю., Кирильченко А.А.,
Ярошевский В.С. Определение характеристик дискретного осмотра среды мобильным
роботом с использованием дальномерной информационной системы. //
Программирование прикладных систем. - М.: Наука, 1992.-С. 155-164.
8.Белоусов А.И., Ткачев С.Б.
Дискретная математика //М., МГТУ им. Н.Э.Баумана, 2002, 743с., с.538
9.Бакиров А.К., Кирильченко А.А.
Проблемы управления распределенными мобильными системами. // М.: Препринт Ин-та
прикл. матем. им. М.В.Келдыша РАН, 2000, №
64.-23 с.
10.Henderson
T.C, Shilcrat E. Logical sensor systems. // ”J. Robotic Systems”, 1984, v. 1,
No. 2, pp. 169 – 193.
11.Nicholls
H.R., Rowland J.J., Sharp K.A.I. Virtual devices and intelligent gripper сontrol
in robotics. //”Robotica”, 1989, v. 7, № 3, pp. 199-204.
12.Кирильченко А.А., Петрин А.А.
Свойство виртуальности в информационных системах робототехники. // М.: Препринт
Ин-та прикл. матем. им. М.В.Келдыша РАН, 2003, №
41 23 с.
13.Potter D., IEEE P1454.4’s
plug-and-play sensors. // Sensors, December 2002,www.sensormag.com
14.А.А.Кирильченко,
В.С.Ярошевский. Повышение надежности мехатронных систем. // "Технология,
сер. ГПС и робототехника", // Технология. Межотраслевой научно-технический
сборник. Серия "Гибкие производственные системы и робототехника",
1993, N 3-4.-С.19-24.
15.Платонов
А.К., Кирильченко А.А., Ястребов В.В. Проблемы разработки автономных подводных
аппаратов // М.: Препринт Ин-та прикл. матем. им. М.В.Келдыша РАН, 1997, N 45, 36 с.
16.Khatib O. Real-time obstacle
avoidance for manipulators and mobile robots. // “IEEE Int. Conf. Robotics and
Automation”, 1985, pp. 500-505.
17.Brooks R.A. Self calibration of
motion and stereo vision for mobile robots // “IEEE Int. Robotics and
Automation”, 1986, 2:14.
18.Ichikawa Y., Fujie M., Ozaki N.
On mobility and autonomous properties of mobile robots // Robot, 1984, №44. pp.
31-36.
19.Фиск К., Кэски Д., Уэст Л. Автоматическое проектирование печатных плат // ТИЭЭР, 1967, №11, т. 55, стр. 217-228.
20.Левин К. Топология и теория поля. // "Хрестоматия по истории психологии", М.: Издательство МГУ, 1980, с.122-131.
21.Rimon E., Koditschek D.E. The construction of analytic
diffeomorphisms for star worlds. // "IEEE Int. Conf. Rob. and Autom.,
1989: Proc. vol.1", - Waschington etc., 1989, pp. 21-26.
22.Koditschek D.E. Task encoding:
toward a scientific paradigm for robot planning and control // "Robotics
and Automation systems", 1992, v.9, № 1-2, pp. 5-39.
23.Salichs
M.A., Morena L. Navigation of mobil robots: open questions. //”Robotica”, 2000,
v.18, pp.227-234.//
СОКРАЩЕНИЯ
АСК – абсолютная система координат
ВД – виртуальные датчики
ГИЭ – граф информационной эквивалентности
ГРНС – глобальная радионавигационная спутниковая система
ИДД – информационно-двигательные действия
ИН – интерпретирующая навигация
ИО – информационный обход
ИС – информационная система
ИЭ – информационная эквивалентность
ИППП – исчисление
предикатов первого порядка
МР – мобильный робот
МС – мобильная система
ПНФ – предварённая нормальная форма
РМС – распределенная мобильная система
СИО – система информационного обеспечения
СРС – сенсорная распределенная система
ССП – система счисления пути
СУ – система управления
ТНС – традиционная навигационная система
УС – условия согласования
ФД – физические датчики