Аннотация
Двумерная компьютерная модель была применена для численного расчета разряда в высокочастотном
поле. Двухтемпературная модель учитывает ионизацию, диссоциацию, диффузию электронов и т.д.
Abstract
A two-dimensional computer code has been developed for numerical calculation of the
discharge in UHF fields. The two-temperature model takes into account ionization,
dissociation, electron diffusion etc.
Введение
Работа посвящена численному исследованию
процесса газового разряда стримерного типа и является продолжением работ [1 -
12]. Основное внимание уделено расчету формы и поведению фронта ионизации.
§1
Постановка задачи
Взаимодействие электромагнитного поля заданной частоты с проводящим частично
ионизованным газом описывается системой
Максвелла для комплексных амплитуд поля E, H
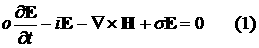
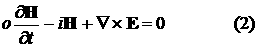
совместно с уравнениями ионизации и теплообмена
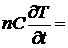 
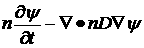 
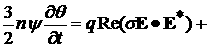 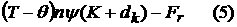
Здесь
n - плотность
газа (постоянная), T -
его
температура, ψ – относительная
концентрация электронов, θ – их
температура.
Используемые единицы измерения и выражения
для всех коэффициентов, проводимости
σ, диссоциации δ, теплоемкости C, диффузии D,
ионизации νi, рекомбинации νr, теплообмена
K и т.д.
приведены ниже.
При
выборе единиц измерения
[*] используем фиксированные
значения частоты внешнего поля ω = 2.2 ·1010 сек-1,
массы молекулы газа М = 3.3·10-24 г и
положим:
[x] = c/ω = 1.36 см,
[σ] = ω/4π = 1.75·109 сек-1,
[n] = 2.4
·1019 см-3,
[θ] = [T] = 4.1 ·10-14 эрг,
[H] =
[E] = 36 г1/2 см-1/2
сек -1,
[v] = ([T]/M)1/2 = 1.11· 105 см/сек,
[t] =
[x]/[v] = 1.22·
10-5 сек.
Для энергии системы, силы
тока и количества электронов используются единицы:
[W] = [Q] = [n][T][x]3
= 2.5 ·106 эрг,
[J] = [σ][E][x]2
= 1.2· 1011 г1/2 см3/2 сек
-2,
[S]= [n][x]3=6·1019
.
При этом
константы и функции, входящие в систему уравнений (1) - (5), принимают
следующий вид:
o=3.7 ·10-6 , 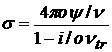 , , 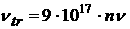 , a=0.026 , , a=0.026 ,
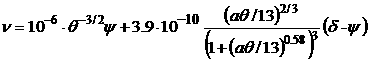 , ,
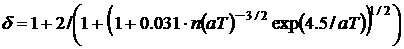 , ,
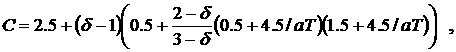
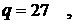 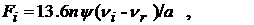
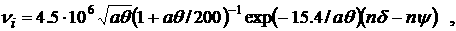
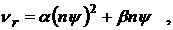 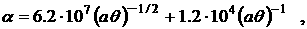
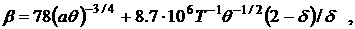
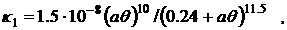 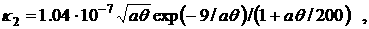
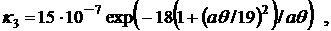 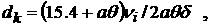
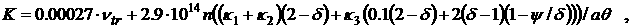
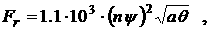 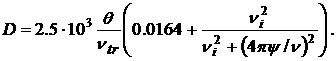
Ввиду малости коэффициента (o ~ 10-6) при производных по времени
в уравнениях (1), (2), пренебрегаем этими членами и решаем полученную систему Гельмгольца как
стационарную, при каждом t , с условиями Зоммерфельда на бесконечности для
возмущения поля.
В данной работе мы ограничиваемся
двумерным цилиндрически симметричным
( ∂/∂φ = 0 ) случаем с
внешним полем в виде стоячей волны, имеющим отличные от
нуля компоненты Ez = J0(r), Hφ = -iJ1(r),
выражаемые функциями Бесселя.
Газ считается неподвижным постоянной
плотности, принятой за единицу. В начальный момент равна единице и его
температура. Электронная компонента
отлична от нуля лишь в окрестности
начала координат, в шаре радиуса
0.01, где относительная концентрация ее порядка
10-5, а температура равна 69. Развитие этого возмущения и
составляет предмет задачи.
Симметрия задачи относительно плоскости z = 0 позволяет ограничиться расчетом в
области z > 0.
Чтобы
сделать задачу Гельмгольца ограниченной, используем интегральное представление решения соответствующей внешней однородной
задачи для связи значений решения на двух поверхностях, т.е. в качестве
нелокального граничного условия. Решение же внутренней неоднородной задачи
проведем методом матричной прогонки.
Остальные
уравнения системы решаются обычными разностными
методами.
§2 Результаты расчета
Полученные в результате расчета зависимости изображены на рисунках.
Рис.1 показывает динамику фронта ионизации.
Здесь, слева, изображено положение фронта на три момента времени. Справа -
график Z(t) - положение фронта на
оси z как функция времени.
Наблюдается резкое ускорение его перемещения на интервале 0.01 < t < 0.015, до одной тысячной скорости света. Последующее
замедление связано, по-видимому, с уменьшением остроты головки стримера и ее
расширением.
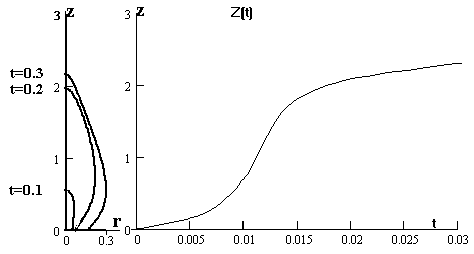
Рис.1 Положение фронта ионизации.
На рис.2 показаны распределения модулей поля
и проводимости вдоль оси на момент t=0.013. Максимум поля чрезвычайно
узок и располагается в районе, где проводимости, т. е. электронов, практически
нет.
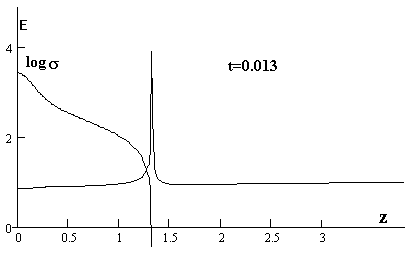
Рис.2 Распределение модулей поля и проводимости
Рис.3 демонстрирует распределения поля на
тот же момент поперек оси - линии
уровня |Е|=1 и =2 (слева) и вдоль двух указанных разрезов
(справа).
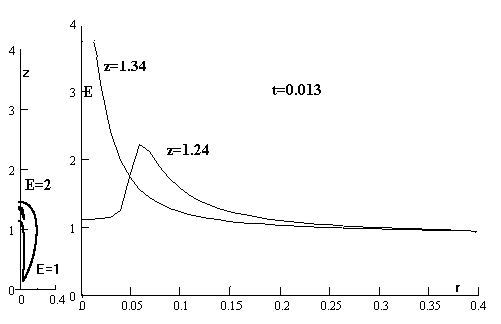
Рис.3 Распределение поля.
На
рис.4 изображено изменение максимума поля на оси со временем.
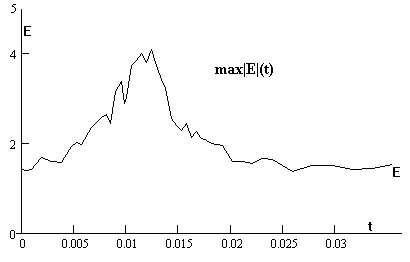
Рис.4 Максимум поля.
На рис.5 представлена z - компонента тока Jz = ∫σEzrdr, ее действительная и мнимая части. Слева - как
функция z, на момент t = 0.013, справа - как функция t в сечении z = 0. Ускорение фронта ионизации после t = 0.01 связано, в частности, с изменением фазы.
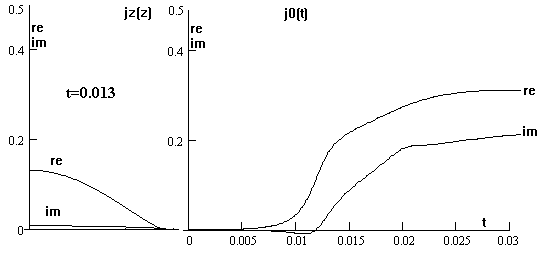
Рис.5 Z – компонента тока.
На
рис.6,7 представлены действительная и мнимая части возмущения поля на оси z в тот же момент t = 0.013.
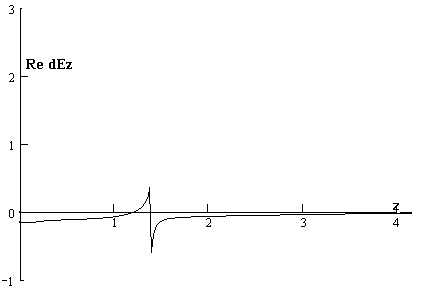
Рис.6 Re возмущения поля Ez на оси.

Рис.7 Im возмущения поля Ez на оси.
На
рис.8 показано поведение во времени количества S = ∫∫nψrdrdz и энергии W = 1.5∫∫nψθrdrdz электронов. Здесь же дана энергия, полученная
системой в результате джоулева нагрева Q(t) = ∫∫∫qRe(σEE*)rdrdzdt.
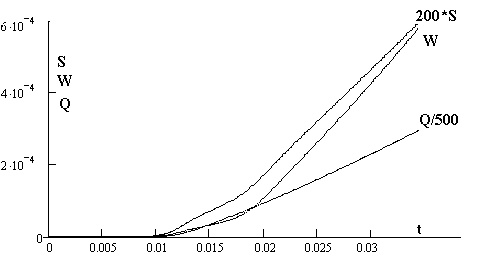
Рис.8 Количество и энергия электронов.
Литература
[1] О.И.
Воскобойникова, С.Л. Гинзбург, В.Ф. Дьяченко, К.В. Ходатаев. Инициация
микроволнового стримерного разряда в газе. // Препринт ИПМ им. М.В. Келдыша РАН, 2001, № 13.
[2] О.И.
Воскобойникова, С.Л. Гинзбург, В.Ф. Дьяченко, К.В. Ходатаев. Численное
исследование подкритического микроволнового разряда в газе высокого давления.
// ЖТФ, 2002, Т. 72, Вып. 8.
[3] О.И. Воскобойникова,
С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик,
К.В. Ходатаев. Расчеты микроволнового стримерного разряда в газе.
// Препринт ИПМ им. М.В. Келдыша РАН, 2002, № 35.
[4] О.И.
Воскобойникова, С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик. Расчеты
микроволнового разряда в газе. // Препринт ИПМ им. М.В. Келдыша РАН, 2003, №
30.
[5] С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик,
К.В. Ходатаев. Модель микроволнового разряда в газе. // Препринт ИПМ им. М.В.
Келдыша РАН, 2004, № 16.
[6] С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик,
К.В. Ходатаев. 2-D модель микроволнового разряда в газе. // Препринт
ИПМ им. М.В. Келдыша РАН, 2005, № 1.
[7] С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик,
К.В. Ходатаев. 3-D модель микроволнового разряда в газе. // Препринт
ИПМ им. М.В. Келдыша РАН, 2005, № 58.
[8] С.Л. Гинзбург, В.Ф. Дьяченко, В.В. Палейчик.
Численное исследование микроволнового разряда в газе. // Препринт ИПМ им. М.В.
Келдыша РАН, 2006, № 29.
[9] В.Ф. Дьяченко.
Численный метод решения системы
Гельмгольца. // Препринт
ИПМ им. М.В. Келдыша РАН, 2007, № 14.
[10] В.Ф. Дьяченко, Е.В. Шаханова. Взаимодействие
волны с проводящим волокном. // Препринт ИПМ им. М.В. Келдыша РАН, 1993, № 29.
[11] О.И. Воскобойникова. Итерационный метод решения
задачи о рассеянии волны. // Препринт ИПМ им. М.В. Келдыша РАН, 1997, № 38.
[12] О.И. Воскобойникова.
Несколько расчетов микроволнового стримерного разряда. // Препринт ИПМ им. М.В.
Келдыша РАН, 2001, №57.
|