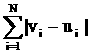Анализ метода распознавания символов, основанного на полиномиальной регрессии
|
|
символ |
v_true_ min |
v_true_ max |
v_true_max/ v_true_min |
v_false_ min |
v_false_ max |
┐v_ min |
┐v_ max |
Рfalse |
|
0 |
35,41
|
113,59
|
3,21
|
56,34 |
101,09 |
50,91 |
171,30
|
106,61
|
|
1 |
42,58 |
173,80 |
4,08 |
52,22 |
131,38 |
48,00 |
142,30 |
128,17 |
|
2 |
38,33 |
105,57 |
2,75 |
61,62 |
109,43 |
49,74 |
168,44 |
120,19 |
|
3 |
39,92 |
103,10 |
2,58 |
55,63 |
95,53 |
47,68 |
171,61 |
118,84 |
|
4 |
50,76 |
106,34 |
2,09 |
56,02 |
123,47 |
55,87 |
172,25 |
131,78 |
|
5 |
36,28 |
130,66 |
3,60 |
52,68 |
98,26 |
45,89 |
178,17 |
126,65 |
|
6 |
44,60 |
115,07 |
2,58 |
55,17 |
103,11 |
55,32 |
165,89 |
105,26 |
|
7 |
40,56 |
101,70 |
2,51 |
53,45 |
93,89 |
49,42 |
169,91 |
114,43 |
|
8 |
50,15 |
119,80 |
2,39 |
57,23 |
115,19 |
53,73 |
157,66 |
121,27 |
|
9 |
47,36 |
120,58 |
2,55 |
54,28 |
117,37 |
54,81 |
164,77 |
127,45 |
3.3. Поведение средней оценки распознавания и функции распределения
при отклонении от «среднестатистического» вектора. На рис.2в, 3в даны
диаграммы зависимости средней оценки распознавания символа (9 и 1 соответственно) от величины отклонения между полиномиальным
вектором х, построенным по его
растру, и «среднестатистическим»
полиномиальным вектором этого символа. Для остальных цифр диаграммы аналогичны
рис.2в.
Для «среднестатистического» полиномиального
вектора конкретного символа значение в каждой компоненте вектора, имеющей номер
i, равно среднему
арифметическому значений i-х компонент по всем растрам
рассматриваемого символа. Расстояние между векторами v=(v1,…,vL) и u=(u1,…,uL) определяется так:
вычисляется модуль разности значений в i-х компонентах и проводится
суммирование по всем L компонентам:
||v-u|| =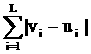 (17)
(17)
Диапазон
отклонений между полиномиальным вектором распознанного верно изображения
символа и «среднестатистическим» вектором этого символа по рассматриваемой базе
лежит от минимального х_true_min до максимального х_true_max. В
таблице 2 приведены значения этих величин.
Отрезок [х_true_min, х_true_max]
(оси абсцисс на рис.2в, 3в) был поделен на 20 равных по длине частей – отрезок
и 19 полуинтервалов: [х_true_min, х_true_min + хdv], (х_true_min + хdv, х_true_min + 2хdv], … ,
(х_true_min + 19хdv, х_true_min + 20хdv], где
хdv = (х_true_max – х_true_min)/20.
Затем для совокупности изображений, имеющих полиномиальные векторы, попадающие
в каждый такой участок, вычислялась средняя оценка распознавания (оси ординат
на рис. 2в, 3в). На этих рисунках видно, что средняя оценка
распознавания для каждого из рассматриваемых символов на
соответствующем этому символу отрезке [х_true_min, х_true_max] убывает монотонно (с
некоторыми шумовыми погрешностями) по мере «удаления» от
«среднестатистического» вектора, а для «1» сначала монотонно убывает, а затем монотонно увеличивается и принимает
максимальное значение 255 на предпоследнем интервале удаления от «среднестатистического»
вектора (также с некоторыми погрешностями). Уровень шумов в этих зависимостях существенно ниже, а
степень монотонности выше, чем в аналогичных зависимостях для средней оценки
распознавания при отклонении от «среднестатистического» растра.
На рис.2г, 3г приведены
диаграммы - «дискретный» аналог функции распределения для распознанных верно
изображений символов 0, 1 (для 2, … , 9 аналогично). А именно, ось абсцисс
такая же, как указано в предыдущем абзаце для рис.2в, 3в, а по оси ординат
отложено количество правильно
распознанных изображений, попавших в каждую двадцатую часть отрезка [х_true_min, х_true_max].
Для «1» при увеличении
отклонения от 0 сначала наблюдалось уменьшение оценки, а затем ее рост до
максимальной оценки 255 на наиболее удаленных участках. Возникла гипотеза о
том, что база единиц составлена из двух подбаз.
Дальнейшие действия были проделаны для
«среднестатистических» векторов, поскольку в использующих их зависимостях
уровень шумов существенно ниже, чем для «среднестатистических» растров. Найдя
первоначальное «среднестатистическое» значение полиномиального вектора х0, мы отделили ту часть изображений,
полиномиальные векторы которых удалены от соответствующего х_true_min
более чем на 2/3 величины х_true_max-х_true_min и построили для них «среднестатистическй»
вектор х1. Оказалось, что для изображений,
векторы которых к х1 ближе, чем к х0, при удалении от х1 оценка монотонно падает (рис.3ж).
Всего оказалось 714 таких изображений. Для оставшихся 32388 изображений построили
новый среднестатистический вектор х2,
при отклонении от которого имела место аналогичная закономерность (рис.3д). Для
каждой из выделенных подбаз построили функции распределения (соответственно
рис.3з, рис.3е), которые оказались схожи с функциями распределения других
символов. Дополнительные итерации, несомненно, улучшили бы степень разделения
подбаз.
Проанализировано, как
соотносится монотонный характер убывания средней оценки распознавания при
удалении от «среднестатистического» вектора с функциями распределения верно
распознанных изображений для различных оценок распознавания. Изучение указанных
закономерностей проведено на примере символа «8». Рассмотрены следующие
диапазоны оценок распознавания: [255, 250), [250, 240), [240, 230), [230, 220),
[220, 210), [210, 200), [200, 190), [190, 180), [180, 170), [170, 160), [160,
150), [150, 140), [140, 130), [130, 120). Проводить исследования для более
низких оценок нецелесообразно, поскольку количество оставшихся изображений, не
попавших в описанные полуинтервалы, невелико и сопоставимо с количеством
неправильно распознанных растров. Для изображений, получивших оценку
распознавания внутри каждого из этих полуинтервалов, построены соответствующие
функции распределения. На рис.4а-4д приведены графики - «дискретный» аналог
описанных функций распределения. А именно, ось абсцисс такая же, как указано
ранее в настоящем разделе 3.3 для рис.2в, 3в, 2г, 3г а по оси ординат отложено количество
правильно распознанных изображений,
получивших оценку из соответствующего диапазона и попавших в каждую
вышеописанную двадцатую часть отрезка [х_true_min, х_true_max].
На рис.4а приведен такой же
график для всего «совокупного» спектра оценок распознавания, полученных
изображениями цифры 8 (соответствующий диаграмме, аналогичной рис. 2г, 3г),
обозначенный в «легенде» диапазоном «0-255». Здесь же имеются графики функций
распределения для диапазонов [255, 250) и [250, 240), указанные в «легенде» как
«250-255» «240-250» соответственно.
Использование диапазона [255, 250), который вдвое меньше каждого из указанных
на рис. 4б, 4в, 4г, 4д объясняется тем, что в этот полуинтервал попадает
большое количество символов, как это нетрудно увидеть на рис.4а при сравнении
графиков «250-255» и «240-250».
В серии рис.4а – 4г для
удобства в проведении сопоставления каждый предыдущий и последующий рисунки
содержат по одному общему графику. Так для рис.4а, 4б общим является «240-250»,
рис.4б, 4в объединяет «210-220», а рис.4в, 4г роднит «180-190», а рис.4г, 4д -
«150-160».
Итак, на каждом из двадцати частей
отрезка [х_true_min, х_true_max] средняя оценка получается
суммированием оценок 1, 2, 3, …, 254, 255 с весами, определяемыми средней
величиной (по этому отрезку) функции вероятности соответствующей оценки. Из этого
становится понятным, что полученный результат, а именно, монотонное убывание
средней оценки распознавания, далеко не очевиден. Он соответствует наличию
структуры в ряду случайных событий.
Диапазон отклонений между
полиномиальным вектором неправильно распознанного изображения символа и «среднестатистическим»
вектором этого символа по рассматриваемой базе находится от минимального х_false_min до
максимального х_false_max. В таблице 2 приведены
значения этих величин для каждого из символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Для произвольного символа G из рассматриваемых цифр 0, 1, 2, 3, 4, 5, 6,
7, 8, 9 диапазон отклонений между полиномиальными векторами изображений всех
символов, кроме G, и «среднестатистическим» вектором цифры G по рассматриваемой
базе находится от минимального ┐х_min до максимального ┐х_max. В
таблице 2 приведены значения этих величин для каждого из возможных символов G: 0, 1,
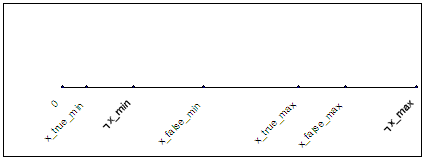
2, 3, 4, 5, 6, 7, 8, 9. Отметим, что для каждого из рассматриваемых цифр х_true_min <
┐х_min < х_false_min; кроме того, х_true_max <
┐х_max; а также х_false_max < ┐х_max. Следовательно, для каждого символа G можно
выделить полуинтервал [х_true_min, ┐х_min), в
котором находятся только правильно распознанные изображения этого символа;
внутри полуинтервала [┐х_min, х_false_min) имеются правильно
распознанные изображения символа G и изображения символов,
отличных от G; в полуинтервале (MAX(х_true_max, х_false_max), ┐х_max]
лежат только изображения символов, отличных от G; внутри отрезка [х_false_min, MIN(х_true_max, х_false_max)] содержатся
любые изображения (и правильно, и неправильно распознанные изображения символа G, а
также отличные от G символы); в полуинтервале (MIN(х_true_max, х_false_max), MAX(х_true_max, х_false_max)] - отличные от G символы,
а также при х_true_max > х_false_max (для
цифр 0, 1, 3, 5, 6, 8, 9)- правильно, а при х_true_max < х_false_max (для
2, 4, 7) - неправильно распознанные изображения символа G
(соответственно рис.5а, 5б).
Итак, при удалении от
«среднестатистического» полиномиального вектора любого рассматриваемого символа
выявлено структурированное расположение правильно и неправильно распознанных
изображений рассматриваемого символа, а также отличных от него символов.
Отметим, что соотношения,
приведенные в двух предыдущих абзацах, не выполняются для приведенных в таблице
1 аналогичных величин в терминах растров (v_true_min, ┐v_min, v_false_min, v_true_max, v_false_max,
┐v_max). Следовательно, выявленное для полиномиальных
векторов структурированное расположение символов при удалении от
«среднестатистического» вектора не имеет места в терминах растров.
Таблица 2
|
сим-вол |
х_true_ min |
х_true_ max |
х_true_max/ х_true_min |
х_false_ min |
х_false_ max |
┐х_ min |
┐х_ max |
|
0 |
2004
|
5290
|
3,21
|
3002 |
5119 |
2186 |
7754 |
|
1 |
2416 |
7917 |
4,08 |
3046 |
6437 |
2698 |
6915 |
|
2 |
2237 |
5265 |
2,75 |
3491 |
5523 |
2860 |
7710 |
|
3 |
2276 |
4954 |
2,58 |
3026 |
4936 |
2697 |
7723 |
|
4 |
2798 |
5158 |
2,09 |
3135 |
5619 |
3148 |
7729 |
|
5 |
2104 |
6300 |
3,60 |
3142 |
4909 |
2558 |
8057 |
|
6 |
2416 |
5161 |
2,58 |
3375 |
4966 |
3004 |
7437 |
|
7 |
2324 |
5276 |
2,51 |
2913 |
5621 |
2788 |
7645 |
|
8 |
2679 |
5505 |
2,39 |
3335 |
5188 |
2901 |
6977 |
|
9 |
2559 |
5482 |
2,55 |
3076 |
5313 |
2964 |
7458 |
3.4. Распознавание «среднестатистических» растров и векторов
различных символов. Вышеприведенные результаты получены с использованием
«среднестатистических» растров и векторов. Возникает естественный вопрос, а
будут ли они сами верно распознаны при помощи описанного метода? Если да, то
каковы оценки распознавания? Оказалось, что как «среднестатистические» растры,
так и векторы распознаются верно для всех символов. Очевидно, что любое
изображение распознается как перечень из десяти альтернатив для каждого из символов
0 - 9 с соответствующей оценкой. Альтернативы нумеруются по мере убывания
оценок. Для правильно распознанного символа оценка 0ой альтернативы,
естественно, и есть оценка распознавания.
Интерес представляет не только она, но и оценка 1ой
альтернативы. Соотношение между этими оценками говорит о «контрастности»
распознавания: чем больше различаются оценка 0ой альтернативы и
оценка 1ой альтернативы, тем больше контрастность распознавания. В
таблице 3 для каждой из цифр от 0 до 9 приведены оценки распознавания
«среднестатистических» растров Рv-средн
(0ая альтернатива), а также Рv-средн (1ая
альтернатива). Аналогично, даны оценки распознавания «среднестатистических»
векторов Рх-средн (0ая
альтернатива), а также Рх-средн
(1ая альтернатива). Для каждой цифры оценка
распознавания «среднестатистического» растра ниже, чем соответствующего
вектора. Оценка первой альтернативы для
любого «среднестатистического» растра выше, чем оценка первой альтернативы для любого
«среднестатистического» вектора (как того же символа, так и другого).
Следовательно, «среднестатистические» растры имеют меньшую контрастность, чем
соответствующие векторы. Разброс оценок (разница между максимальной и
минимальной оценками) при распознавании «среднестатистических» растров равен
229-105=124. Он намного выше, чем имеющийся у векторов (240-219=21). В таблице в двух последних столбцах для
каждого символа указано сначала общее количество изображений, а затем число /
доля (выраженная в процентах) неправильно распознанных изображений.
Таблица 3
|
символ |
Рv-средн (0ая
альтернтива) |
Рv-средн (1ая
аль-тернатива) |
Рх-средн (0ая
аль-тернатива) |
Рх-средн (1ая
аль- тернатива) |
количество
изображений |
число / доля (%) неправильно распознанных
изображений |
|
0 |
229
|
38
|
237
|
11 |
19580
|
42 / 0,215
|
|
1 |
133 |
44 |
242 |
7 |
33160 |
54
/ 0,163
|
|
2 |
189 |
61 |
240 |
4 |
17990 |
47
/ 0,261 |
|
3 |
134 |
29 |
229 |
7 |
13650 |
106 / 0,783 |
|
4 |
105 |
58 |
223 |
18 |
12900 |
163 / 1,264 |
|
5 |
152 |
31 |
228 |
12 |
13120 |
57 /
0,434 |
|
6 |
179 |
47 |
235 |
13 |
13041 |
48 / 0,368 |
|
7 |
157 |
54 |
238 |
8 |
16151 |
88 / 0,545 |
|
8 |
130 |
53 |
219 |
14 |
10121 |
174 / 1,719 |
|
9 |
176 |
47 |
236 |
10 |
25051 |
102 / 0,407 |
3.5. Расстояния между «среднестатистическими» растрами и векторами
различных символов. В дополнение к таблице 1 (п.3.2.) приведем данные о расстоянии между
«среднестатистическими» растрами различных символов. В таблице 4 по горизонтали
и по вертикали указаны цифры от 0 до 9. На пересечении столбцов и строк даны расстояния
между «среднестатистическими» растрами соответствующих цифр.
Расстояние между
«среднестатистическими» растрами цифр 4 и 9 является минимальным и равно 34,3,
а для 0 и 1 соответствующее расстояние - максимальное, его значение 81,6. Чисто
визуально это понятно.
Таблица 4
|
символ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
0 |
81,6 |
61,3 |
63,2 |
60,2 |
52,1 |
46,9 |
80,6 |
57,1 |
40,6 |
|
1 |
81,6 |
0 |
55,8 |
53,4 |
46,3 |
49,4 |
62,3 |
34,7 |
49,7 |
56,9 |
|
2 |
61,3 |
55,8 |
0 |
47,6 |
53,3 |
48,5 |
56,0 |
50,6 |
36,7 |
43,6 |
|
3 |
63,2 |
53,4 |
47,6 |
0 |
60,9 |
46,8 |
49,5 |
52,3 |
37,8 |
48,8 |
|
4 |
60,2 |
46,3 |
53,3 |
60,9 |
0 |
51,9 |
49,9 |
55,2 |
47,8 |
34,3 |
|
5 |
52,1 |
49,4 |
48,5 |
46,8 |
51,9 |
0 |
43,9 |
50,0 |
42,3 |
37,9 |
|
6 |
46,9 |
62,3 |
56,0 |
49,5 |
49,9 |
43,9 |
0 |
66,4 |
37,0 |
46,7 |
|
7 |
80,6 |
34,7 |
50,6 |
52,3 |
55,2 |
50,0 |
66,4 |
0 |
51,8 |
57,4 |
|
8 |
57,1 |
49,7 |
36,7 |
37,8 |
47,8 |
42,3 |
37,0 |
51,8 |
0 |
36,7 |
|
9 |
40,6 |
56,9 |
43,6 |
48,8 |
34,3 |
37,9 |
46,7 |
57,4 |
36,7 |
0 |
Аналогично, в дополнение к
таблице 2 (п.3.3.) приведем данные о расстоянии
между «среднестатистическими» векторами различных символов. В таблице 5 по
горизонтали и по вертикали указаны цифры от 0 до 9. На пересечении столбцов и
строк даны расстояния между «среднестатистическими» векторами соответствующих
цифр.
Таблица 5
|
символ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0 |
0 |
4358 |
3350 |
3426 |
3252 |
2924 |
2535 |
4202 |
3067 |
2244 |
|
1 |
4358 |
0 |
3127 |
3048 |
2509 |
2767 |
3396 |
1994 |
2662 |
3057 |
|
2 |
3350 |
3127 |
0 |
2517 |
2918 |
2817 |
2857 |
2721 |
1929 |
2354 |
|
3 |
3426 |
3048 |
2517 |
0 |
3254 |
2724 |
2651 |
2947 |
2120 |
2540 |
|
4 |
3252 |
2509 |
2918 |
3254 |
0 |
2837 |
2627 |
2850 |
2435 |
1803 |
|
5 |
2924 |
2767 |
2817 |
2724 |
2837 |
0 |
2366 |
2848 |
2333 |
2110 |
|
6 |
2535 |
3396 |
2857 |
2651 |
2627 |
2366 |
0 |
3447 |
1925 |
2347 |
|
7 |
4202 |
1994 |
2721 |
2947 |
2850 |
2848 |
3447 |
0 |
2659 |
2904 |
|
8 |
3067 |
2662 |
1929 |
2120 |
2435 |
2333 |
1925 |
2659 |
0 |
1902 |
|
9 |
2244 |
3057 |
2354 |
2540 |
1803 |
2110 |
2347 |
2904 |
1902 |
0 |
Расстояние между
«среднестатистическими» векторами цифр 8 и 9 является минимальным (что
отличается от случая с растрами) и равно 1902, а для 0 и 1 соответствующее
расстояние – максимальное (как и для растров), его значение 4358. Это также укладывается
в рамки визуального представления о сходстве и различии символов. Тот факт, что
пара наиближайших «среднестатистических» растров не совпадает с парой наиближайших
«среднестатистических» векторов горит о существенной перестройке «метрики» при
переходе от растрового к векторному подходу.
В этом же заключается
причина того, что между таблицами 4 и 5 не наблюдается заметного соответствия:
большему / меньшему значению расстоянию между «среднестатистическими» растрами
не всегда соответствует большее / меньшее расстояние между «среднестатистическими»
векторами.
3.6. Связь между распознаванием и степенью близости к
«среднестатистическим» растрам и векторам. Выше уже было показано
(п.3.2.), что для любого символа растры его верно распознанных изображений
могут находиться дальше от «среднестатистического» растра этого символа, чем
растры неверно распознанных изображений, а также аналогично (п.3.3.), что для
любого символа полиномиальные векторы его верно распознанных изображений могут
находиться дальше от «среднестатистического» вектора этого символа, чем полиномиальные
векторы неверно распознанных изображений.
Представляет интерес, для
какой части правильно распознанных символов расстояние между растрами их
изображений и соответствующим «среднестатистическим» растром меньше расстояний
до «среднестатистических» растров других символов. Аналогично, для какой части
правильно распознанных символов расстояние между полиномиальными векторами их
изображений и соответствующим «среднестатистическим» вектором меньше расстояний
до «среднестатистических» векторов других символов.
А также, для какой части
неправильно распознанных символов расстояние между растрами их изображений и
«среднестатистическим» растром символа, получившего при распознавании
наибольшую оценку, меньше расстояний до «среднестатистических» растров других
символов. Аналогично, для какой части
неправильно распознанных символов расстояние между полиномиальными векторами их
изображений и «среднестатистическим» вектором символа, получившего при распознавании
наибольшую оценку, меньше расстояний до «среднестатистических» векторов других
символов.
Расчеты показали, что среди верно
распознанных 173 897 изображений растры наименее удалены от
«среднестатистического» растра соответствующего символа для 152153 изображений,
что составляет 87,50% от их числа. Аналогично, полиномиальные векторы наименее
удалены от «среднестатистического» вектора соответствующего символа для 153720
изображений, что составляет 88,40% от их числа.
Соответственно, среди
неверно распознанных 881 изображений растры наименее удалены от «среднестатистического»
растра символа, получившего максимальную оценку всего лишь для 470 изображений,
что составляет 53,35% от их числа. Аналогично, среди неверно распознанных 881
изображений полиномиальные векторы наименее удалены от «среднестатистического»
вектора символа, получившего максимальную оценку всего лишь для 454
изображений, что составляет 51,53% от их числа.
Таблица 6(1)
|
|
ср.-стат. растр «0» |
ср.-стат. растр «1» |
ср.-стат. растр «2» |
ср.-стат. растр «3» |
ср.-стат. растр «4» |
|
0 |
19367 |
15 |
2 |
4 |
0 |
|
1 |
89 |
30063 |
79 |
321 |
780 |
|
2 |
106 |
310 |
15426 |
45 |
0 |
|
3 |
33 |
358 |
24 |
11997 |
1 |
|
4 |
25 |
2304 |
12 |
14 |
9291 |
|
5 |
142 |
66 |
1 |
1225 |
1 |
|
6 |
424 |
423 |
4 |
56 |
2 |
|
7 |
12 |
570 |
14 |
30 |
136 |
|
8 |
72 |
543 |
148 |
253 |
0 |
|
9 |
956 |
829 |
12 |
1066 |
56 |
Таблица 6(2)
|
|
ср.-стат. растр «5» |
ср.-стат. растр «6» |
ср.-стат. растр «7» |
ср.-стат. растр «8» |
ср.-стат. растр «9» |
доля min отклонен. |
|
0 |
34 |
22 |
1 |
19 |
73 |
0,991 |
|
1 |
192 |
158 |
168 |
656 |
601 |
0,908 |
|
2 |
51 |
211 |
178 |
1518 |
98 |
0,860 |
|
3 |
191 |
94 |
148 |
571 |
129 |
0,886 |
|
4 |
1 |
208 |
558 |
36 |
290 |
0,729 |
|
5 |
10857 |
620 |
62 |
65 |
31 |
0,831 |
|
6 |
265 |
11729 |
1 |
94 |
0 |
0,903 |
|
7 |
127 |
15 |
14825 |
22 |
312 |
0,923 |
|
8 |
9 |
755 |
45 |
8010 |
114 |
0,805 |
|
9 |
181 |
24 |
327 |
906 |
20588 |
0,825 |
Для правильно распознанных
символов описанные результаты получены раздельно по каждому из символов 0, 1,
…, 9 и представлены в таблицах 6(1) - 6(2) для растров, а также 7(1) - 7(2) для
полиномиальных векторов.
По таблицам 6(1) - 6(2)
видно, что для каждого из символов растры наибольшего количества изображений
ближе всего к «своему» «среднестатистическому» растру (их доля указана в
последнем столбце таблицы 6(2)).
По таблицам 7(1) - 7(2)
видно, что для каждого из символов полиномиальные векторы наибольшего количества
изображений ближе всего к «своему» «среднестатистическому» вектору (их доля
указана в последнем столбце таблицы 7(2)).
Таблица 7(1)
|
|
ср.-стат. вектор «0» |
ср.-стат. вектор «1» |
ср.-стат. вектор «2» |
ср.-стат. вектор «3» |
ср.-стат. вектор «4» |
|
0 |
19081 |
19 |
1 |
11 |
0 |
|
1 |
74 |
29534 |
151 |
605 |
1172 |
|
2 |
45 |
138 |
16962 |
52 |
2 |
|
3 |
10 |
152 |
52 |
12634 |
0 |
|
4 |
20 |
1381 |
5 |
13 |
10310 |
|
5 |
33 |
8 |
0 |
1062 |
5 |
|
6 |
220 |
294 |
16 |
156 |
2 |
|
7 |
0 |
201 |
43 |
72 |
215 |
|
8 |
10 |
622 |
531 |
704 |
1 |
|
9 |
529 |
689 |
27 |
1656 |
98 |
Таблица 7(2)
|
|
ср.-стат. вектор «5» |
ср.-стат. вектор «6» |
ср.-стат. вектор «7» |
ср.-стат. вектор «8» |
ср.-стат. вектор «9» |
доля min отклонен. |
|
0 |
293 |
26 |
1 |
31 |
74 |
0,977 |
|
1 |
424 |
75 |
258 |
574 |
240 |
0,892 |
|
2 |
188 |
104 |
86 |
321 |
45 |
0,945 |
|
3 |
319 |
37 |
135 |
97 |
110 |
0,933 |
|
4 |
18 |
58 |
860 |
16 |
58 |
0,809 |
|
5 |
11731 |
195 |
18 |
5 |
13 |
0,898 |
|
6 |
1297 |
10946 |
0 |
66 |
1 |
0,842 |
|
7 |
163 |
4 |
15169 |
2 |
194 |
0,944 |
|
8 |
128 |
593 |
84 |
7059 |
217 |
0,710 |
|
9 |
1006 |
14 |
475 |
157 |
20294 |
0,813 |
При сопоставлении таблиц 6(1)
- 6(2) и 7(1) - 7(2) видно, что они существенно различаются. Можно привести
огромное количество примеров несоответствия данных. Достаточно уже сравнить
вторые столбцы таблиц 6(2) и 7(2), относящиеся к «среднестатистическим» растру
и вектору символа 5. Значительные
расхождения имеются также и в последних столбцах таблиц 6(2) и 7(2), так что к
приведенным общим по всем символам цифрам о наименее удаленных от
«среднестатистического» растра изображениях (87,50%) и наименее удаленных от
«среднестатистического» вектора изображениях (88,40%) следует добавить данные о
разбросе по различным символам из последних столбцов таблиц.
Таблица 8(1)
|
|
ср.-стат. растр «0» |
ср.-стат. растр «1» |
ср.-стат. растр «2» |
ср.-стат. растр «3» |
ср.-стат. растр «4» |
|
0 |
29 |
0 |
1 |
4 |
0 |
|
1 |
0 |
193 |
1 |
8 |
16 |
|
2 |
1 |
14 |
13 |
1 |
0 |
|
3 |
0 |
11 |
2 |
54 |
0 |
|
4 |
1 |
17 |
1 |
1 |
12 |
|
5 |
2 |
1 |
0 |
5 |
0 |
|
6 |
20 |
3 |
0 |
8 |
0 |
|
7 |
0 |
17 |
1 |
5 |
8 |
|
8 |
2 |
5 |
1 |
5 |
0 |
|
9 |
29 |
14 |
7 |
7 |
3 |
Таблица 8(2)
|
|
ср.-стат. растр «5» |
ср.-стат. растр «6» |
ср.-стат. растр «7» |
ср.-стат. растр «8» |
ср.-стат. растр «9» |
|
0 |
1 |
3 |
0 |
1 |
5 |
|
1 |
0 |
2 |
10 |
5 |
2 |
|
2 |
12 |
8 |
7 |
8 |
9 |
|
3 |
6 |
3 |
1 |
5 |
9 |
|
4 |
0 |
1 |
8 |
6 |
6 |
|
5 |
9 |
3 |
2 |
0 |
1 |
|
6 |
3 |
37 |
0 |
1 |
1 |
|
7 |
8 |
9 |
66 |
6 |
5 |
|
8 |
0 |
2 |
2 |
29 |
1 |
|
9 |
6 |
6 |
2 |
13 |
28 |
Для неправильно распознанных
символов также соответствующие результаты получены раздельно по каждому из
получивших наивысшую оценку символов 0, 1, …, 9 и представлены в таблицах 8(1)
- 8(2) для растров, а также 9(1) - 9(2) для полиномиальных векторов.
По таблицам 8(1) -
8(2) видно, что не для каждого из символов растры наибольшего количества
изображений ближе всего к «своему» «среднестатистическому» растру.
По таблицам 9(1) - 9(2) видно, что не для каждого из символов
полиномиальные векторы наибольшего количества изображений ближе всего к «своему»
«среднестатистическому» вектору.
Таблица 9(1)
|
|
ср.-стат. вектор «0» |
ср.-стат. вектор «1» |
ср.-стат. вектор «2» |
ср.-стат. вектор «3» |
ср.-стат. вектор «4» |
|
0 |
27 |
0 |
3 |
5 |
0 |
|
1 |
0 |
173 |
3 |
13 |
23 |
|
2 |
1 |
6 |
17 |
3 |
1 |
|
3 |
1 |
4 |
1 |
58 |
1 |
|
4 |
1 |
10 |
2 |
1 |
20 |
|
5 |
1 |
1 |
0 |
4 |
0 |
|
6 |
13 |
2 |
0 |
17 |
0 |
|
7 |
0 |
9 |
4 |
6 |
9 |
|
8 |
1 |
5 |
1 |
9 |
0 |
|
9 |
24 |
16 |
10 |
14 |
7 |
Таблица 9(2)
|
|
ср.-стат. вектор «5» |
ср.-стат. вектор «6» |
ср.-стат. вектор «7» |
ср.-стат. вектор «8» |
ср.-стат. вектор «9» |
|
0 |
3 |
2 |
0 |
0 |
4 |
|
1 |
2 |
1 |
14 |
6 |
2 |
|
2 |
21 |
4 |
11 |
4 |
5 |
|
3 |
16 |
3 |
1 |
1 |
5 |
|
4 |
4 |
1 |
8 |
4 |
2 |
|
5 |
13 |
1 |
1 |
0 |
2 |
|
6 |
9 |
30 |
0 |
1 |
1 |
|
7 |
19 |
3 |
70 |
3 |
2 |
|
8 |
3 |
0 |
3 |
22 |
3 |
|
9 |
8 |
4 |
5 |
3 |
24 |
В таблицах 8(1) - 8(2) и
9(1) - 9(2) отсутствует последний столбец, имеющийся в таблицах 6(1) - 6(2) и
7(1) - 7(2). Это понятно, поскольку в первом столбце указаны не сами
распознаваемые символы, а те ошибочные символы, в качестве которых они были
распознаны.
Следует отметить, что между
таблицами 8(1) - 8(2) и 9(1) - 9(2) наблюдается определенное сходство, в
отличие от таблиц 6(1) - 6(2) и 7(1) - 7(2). Видимо, это говорит о том, что для
неправильно распознанных символов использование полиномиальных векторов вместо
растров добавляет небольшое количество информации о символах, в отличие от
ситуации с правильно распознанными символами, для которых переход от растров к
полиномиальным векторам существенно увеличивает количество информации и приводит
к перестраиванию структуры распознавания (таблицы 6(1) - 6(2), 7(1) - 7(2)).
4. Выводы
Изложенный в пп. 3.1.-3.6.
материал позволяет понять, что, во-первых, при описании метода распознавания
следует различать мелкомасштабные, среднемасштабные и крупномасштабные явления.
К мелкомасштабным следует
отнести те, при описании которых вообще не используется механизм осреднения.
Сюда нужно причислить распознавание и выставление оценок отдельным изображениям
символов.
К среднемасштабным следует
отнести те, при описании которых принципиальным является наличие (или
построение) «среднестатистических» растров и векторов различных символов,
но не используется механизм осреднения
оценок (или он является несущественным, служит каким-то второстепенным целям, и
от него легко отказаться). Сюда нужно причислить: 1) получение «среднестатистических»
растров и векторов различных символов, 2) их распознавание и нахождение оценок
распознавания, 3) определение расстояния
между ними (естественно, для растров и векторов отдельно), 4) построение функций
распределения (необязательно осредненных по частичным диапазонам отклонения –
это делалось исключительно для удобства рисования картинок) при отклонения от
«среднестатистических» растров / векторов, причем как для всей совокупности
оценок, так и для отдельных оценок или их частичных диапазонов, 5) обнаружение
наличия структуры при отклонении от «среднестатистического» растра / вектора
символа правильно, неправильно распознанных изображений этого символа, а также
«чужих» символов, 6) определение среди распознанных изображений символа доли
тех, для которых наиближайшим является «свой» «среднестатистический» растр /
вектор, 7) вычисление среди нераспознанных
изображений символа доли тех, для которых наиближайшим является получивший
максимальную оценку среднестатистический растр / вектор, 8) решение ориентироваться
на полиномиальные векторы, а не на растры, поскольку использование последних
сопряжено с присутствием существенных шумовых помех. Помимо указанных восьми
пунктов могут быть их комбинации и модификации. Следует только отметить, что
среднемасштабные явления надо поделить на те, в которых используются «среднестатистические»
растры / векторы различных символов – они «ближе» к мелкомасштабным, а также на ориентированные
только на «среднестатистический» растр / вектор одного символа – эти ближе к
крупномасштабным. Такое деление на две подгруппы сделать нетрудно. Уже на этом
среднемасштабном уровне над «хаосом» мелкомасштабных» явлений выявлено наличие
структуры – в расположении правильно, неправильно распознанных, а также «чужих»
символов при удалении от «среднестатистического» вектора.
К крупномасштабным явлениям
следует отнести те, при описании которых принципиальным является ориентация на
«среднестатистический» растр или вектор одного определенного символа (о наличии
остальных символов следует забыть), кроме того, используется механизм
осреднения оценок. Удивительным оказывается то, что над «хаосом»
мелкомасштабных и среднемасштабных явлений обнаруживается некий «порядок». А
именно, несмотря на то, что на всем диапазоне отклонений от «среднестатистического»
вектора имеются символы, получившие различные оценки распознавания, количество
которых определяется уже описанными функциями распределениями, результатом их
«коллективного» действия оказывается наличие
структуры, а именно, монотонное уменьшение средней оценки распознавания
при удалении от «среднестатистического» вектора.
Среднемасштабное описание
распознавания можно получить, если абстрагироваться
от взаимного расположения «среднестатистических» векторов, не отрицая, в то же
время, их наличие. Итак, есть «среднестатистический» вектор некоторого символа.
К нему «привязаны», иначе, от него отсчитываются зоны нахождения правильно
распознанных «своих» символов, неправильно распознанных «своих» символов, чужих
символов (это среднемасштабная структура). Следующий шаг – осреднение по
оценкам (для интервалов по признаку удаленности от «среднестатистического»
вектора) - дает крупномасштабное описание распознавания.
А именно, при удалении от «среднестатистического» вектора средняя оценка
распознавания монотонно падает.
Литература
[1] Гавриков М.Б., Пестрякова Н. В.
"Метод полиномиальной регрессии в задачах распознавания печатных и
рукопечатных символов", //Препринт ИПМатем. РАН, М., 2004, №22, 12 стр.
[2] Гавриков М.Б., Пестрякова Н. В., Славин О.А,
Фарсобина В.В.. "Развитие метода полиномиальной регрессии и
практическое применение в задаче распознавания", //Препринт ИПМатем. РАН,
М., 2006, №25, 21 стр.
[3] Гавриков М.Б., Мисюрев А.В., Пестрякова
Н.В., Славин О.А. Развитие метода полиномиальной регрессии и практическое
применение в задаче распознавания символов. Автоматика и Телемеханика. 2006,
№3, С. 119-134.
[4] Гавриков М.Б., Пестрякова Н. В., Усков А.В.,
Фарсобина В.В. "О некоторых свойствах метода распознавания символов,
основанного на полиномиальной регрессии", //Препринт ИПМатем. РАН, М.,
2007, №69, 20 стр.
[5] Гавриков
М.Б., Пестрякова Н. В., Усков А.В., Фарсобина В.В. "О некоторых свойствах
оценки метода распознавания символов, основанного на полиномиальной регрессии",
//Препринт ИПМатем. РАН, М., 2008,
№7, 28 стр.
[6] Sebestyen G.S. Decision Making Processes in Pattern Recognition, MacMillan,
New York, 1962.
[7] Nilson N. J. Learning
Machines, McGraw-Hill, New York, 1965.
[8] Schürmann J. Polynomklassifikatoren, Oldenbourg, München, 1977.
[9] Schürmann J. Pattern Сlassification,
John Wiley&Sons, Inc., 1996.
[10] Albert
A.E. and Gardner L.A. Stochastic
Approximation and Nonlinear Regression // Research Monograph 42. MIT Press,
Cambridge, MA, 1966.
[11] Becker
D. and Schürmann J. Zur
verstärkten Berucksichtigung schlecht erkennbarer Zeichen in der
Lernstichprobe // Wissenschaftliche Berichte AEG-Telefunken 45, 1972, pp. 97 – 105.
[12] Pao
Y.-H. The Functional Link Net:
Basis for an Integrated Neural-Net Computing Environment // in Yoh-Han Pao (ed.)
Adaptive Pattern Recognition and Neural Networks, Addisson-Wesley, Reading, MA,
1989, pp. 197-222.
[13] Franke
J. On the Functional Classifier, in
Association Francaise pour la Cybernetique Economique et Technique (AFCET),
Paris // Proceedings of the First International Conference on Document Analysis
and Recognition, St. Malo, 1991, pp.481-489.
[14]
Дж.Себер. Линейный регрессионный
анализ. М.:”Мир”, 1980.
[15] Линник Ю.В. Метод наименьших квадратов и
основы математико - статистической теории обработки наблюдений. М.:”Физматлит”,
1958.
стической теории обработки наблюдений.
М.:”Физматлит”, 1958.
Рисунки
Рис. 2а Рис. 2б
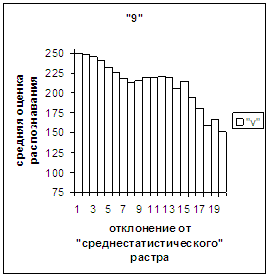
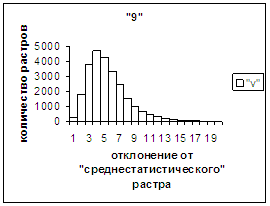
Рис. 2в Рис. 2г
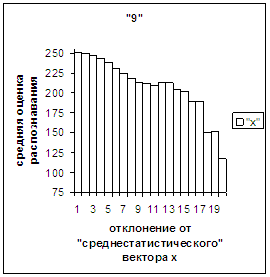
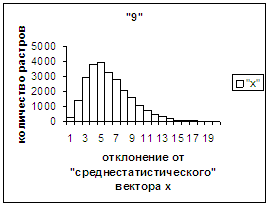
Рис. 3а Рис. 3б
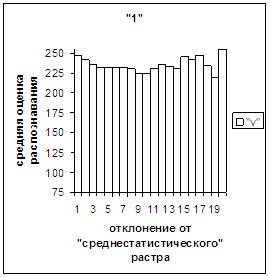
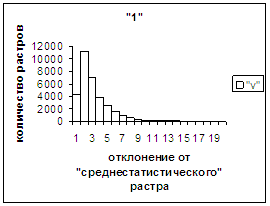
Рис. 3в Рис. 3г
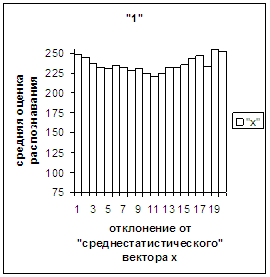
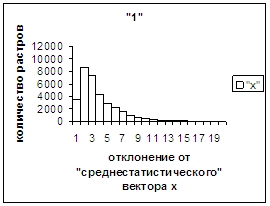
Рис. 3д Рис. 3е
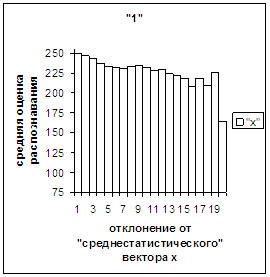
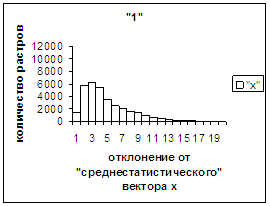
Рис. 3ж Рис. 3з
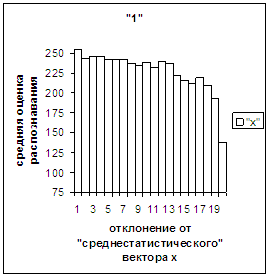
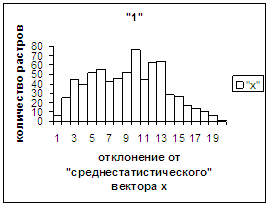
Рис. 4а
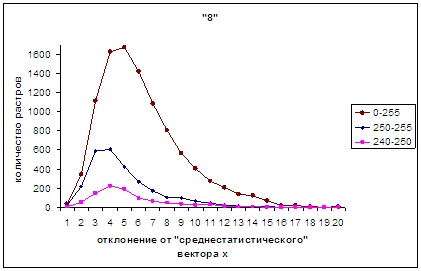
Рис. 4б
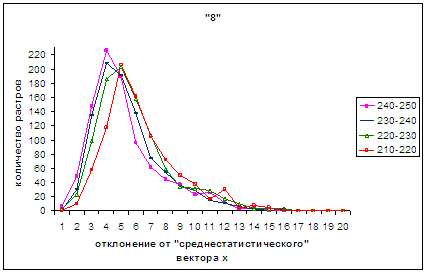
Рис. 4в
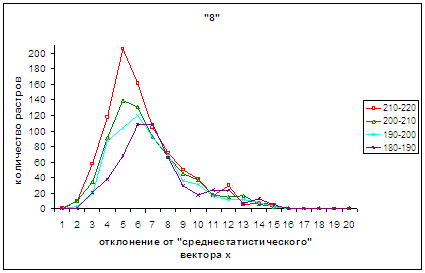
Рис. 4г
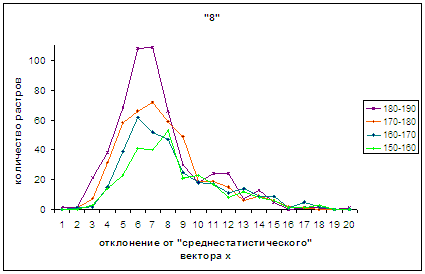
Рис. 4д
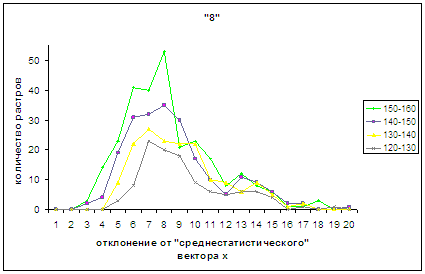
Рис. 5а
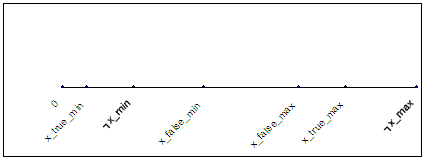
Рис. 5б
 +
+ +…
+… +
+ +…
+… +
+ +…
+…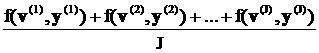
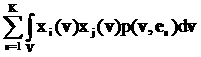 ]1
]1