Аннотация
Рассматривается математическая модель параллельного пучка электронов в экспериментальном объеме линейного
индукционного ускорителя ЛИУ-10. Кратко описаны основные уравнения и численные алгоритмы модели. Представлены
результаты расчетов распределений концентрации электронов и самосогласованного электромагнитного поля.
Выявлено развитие бетатронной неустойчивости пучка и ультрарелятивистский характер диаграммы направленности
его электромагнитного излучения. Приведено сравнение параметра неустойчивости с теоретической оценкой.
Abstract
The mathematical model of the parallel electron’s beam in the experimental volume of the linear inductive
accelerator LIA-10 is considered. The main equations and numerical algorithms of the model are briefly described.
The results of electron’s concentration and self-consistent electromagnetic field calculations are represented.
The development of the betatron fluctuation and ultrarelativistic behavior of the electromagnetic radiation’s polar
pattern are revealed. The comparison of fluctuation parameter with theoretical estimation is cited.
Введение
Распространение релятивистских электронных пучков
(РЭП) в газовых средах и их взаимодействие с различными объектами является
традиционным предметом исследования как экспериментальной, так и теоретической
физики. Трудно переоценить практическое значение этих работ, имеющих практические
приложения в таких отраслях, как исследование взаимодействия излучения с веществом
[1], обеспечение работы приборов в экстремальных условиях [2 –4] и т.д.
В настоящее время пространственно-энергетические,
угловые и другие характеристики РЭП определяются, как правило, с
помощью экспериментов. Это
связано, в частности, с тем, что теоретическое описание процессов взаимодействия
электронов со средой и создаваемым ими самосогласованным электромагнитным полем
достаточно сложны и поддаются теоретическому анализу только в существенных
приближениях [5]. Такие приближения ограничивают как размерность задач, так и
набор учитываемых физических эффектов.
Экспериментальные работы также ставят существенные
проблемы. Проведение детальных
экспериментальных исследований требует
существенных материальных затрат. Отдельную проблему представляют собой
измерения. Измерительная аппаратура, как правило, имеет весьма сложную
конструкцию и является дорогостоящей. Кроме того, правильная интерпретация
результатов измерений подразумевает учет влияния всех
вторичных электромагнитных эффектов, которые оказывает мощный
электронный пучок на чувствительные элементы измерительной аппаратуры.
Одним из путей повышения эффективности и достоверности
исследований характеристик РЭП является сочетание экспериментов с
математическим моделированием. С появлением современной высокопроизводительной
параллельной вычислительной техники возможности математического моделирования
существенно расширились. Появилась возможность трехмерного моделирования пучка
электронов на основе кинетической теории и уравнений Максвелла для
электромагнитного поля. С другой стороны, экспериментальная проверка самих
математических моделей является важнейшим этапом их разработки и единственным
значимым критерием, позволяющим доверять теоретическим результатам. Это весьма
существенно в ситуациях, когда эксперименты либо слишком затратны, либо невозможны
технически.
Целью данной работы является исследование средствами
математического моделирования физических эффектов, сопровождающих распространение
РЭП, выходящего из ускорительного тракта линейного индукционного ускорителя электронов ЛИУ-10,
эксплуатируемом ФГУП «НИИприборов» [6]. Ускоритель ЛИУ-10 используется для проведения
экспериментов по исследованию радиационной стойкости различных объектов при
воздействии непосредственно РЭП или интенсивного тормозного излучения, генерируемого
электронами пучка в мишени-конверторе.
Пучок электронов после прохождения ускорительного
тракта ЛИУ-10 через тонкий экран (около 50 мкм тантала) выводится в
помехозащищенный комплекс (ПЗК), в котором могут размещаться тестируемые
объекты. Внутренний объем ПЗК экранирован от внешних электромагнитных
воздействий металлическими стенками.
Характерная энергия электронов ускорителя ЛИУ-10
составляет порядка 10 МэВ при общем токе пучка до 25 кА. Самосогласованное
электромагнитное поле, образующееся при распространении такого пучка в
воздухе, существенно влияет на движение электронов. Это влияние приводит
к образованию неустойчивостей, параметры которых достаточно хорошо изучены в
физике релятивистских электронных пучков. В результате внутри ПЗК образуется
достаточно сложная электромагнитная обстановка, характеризующаяся трехмерными
распределениями электронов и электромагнитного поля. Математическое
моделирование неустойчивостей требует затрат вычислительных ресурсов, не
допустимых для последовательных ЭВМ, поскольку размеры ПЗК существенно превосходят
толщину пучка, а время его распространения превышает длительность импульса.
2. Модель
переноса электронов в газе и численные алгоритмы
Электромагнитная обстановка внутри ПЗК формируется
свободными электронами и ионами. Электроны пучка попадают в ПЗК через выходную
мембрану. Взаимодействуя с молекулами газов, составляющих воздух, они образуют
вторичные электроны и ионы. Функция распределения электронов 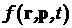 , зависящая от координат , зависящая от координат 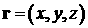 , импульса , импульса 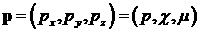 и времени и времени  , подчиняется кинетическому уравнению , подчиняется кинетическому уравнению
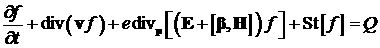 , (1) , (1)
где
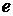 – заряд электрона, – заряд электрона,  – отношение скорости электрона – отношение скорости электрона  к скорости света к скорости света 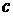 . . 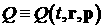 – источник электронов, описывающий их начальное распределение
на входной мембране. Напряженности электрического поля – источник электронов, описывающий их начальное распределение
на входной мембране. Напряженности электрического поля 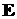 и магнитного поля и магнитного поля 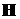 являются функциями координат
и времени. Они подчиняются уравнениям Максвелла [7]: являются функциями координат
и времени. Они подчиняются уравнениям Максвелла [7]:
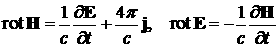 . (2) . (2)
В рассматриваемой модели ионы, образующиеся при
вторичной ионизации, дают вклад в плотность электрического тока 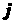 , совместно с электронами. При изложении модели будем
считать, что , совместно с электронами. При изложении модели будем
считать, что  , а ионы покоятся, не создавая тока. В расчетах ионный ток
учитывается как ток проводимости. , а ионы покоятся, не создавая тока. В расчетах ионный ток
учитывается как ток проводимости.
Уравнения (1 – 2) описывает
эволюцию электронного потока в приближении среднего поля [8]. Импульс электрона
изменяется под действием силы Лоренца. Степень ионизации газа считается малой,
в результате чего вероятность взаимодействия электрона с нейтральной молекулой
существенно превышает вероятность взаимодействия с ионом. Поэтому взаимодействие
электронов с молекулами газа описывается линейным интегралом столкновений. Дифференциальный
оператор уравнений определяет квазилинейную систему гиперболических уравнений
первого порядка в частных производных. Для нее рассматривается задача Коши [9]
с однородными начальными данными.
В работах [10-11] показано следующее. Задачу
(1) – (2) можно приближенно свести к отдельным моделям для электронов
пучка и вторичных электронов, образующихся в непрерывном спектре при ионизации
воздушной среды. Перенос пучка может рассматриваться в приближении малых
передач энергии при ионизационном рассеянии электронов высокой энергии. Построено
приближенное решение кинетического уравнения для 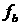 – функции распределения электронов пучка: – функции распределения электронов пучка:
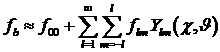 (3) (3)
где 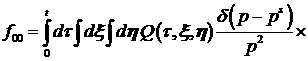
 , ,
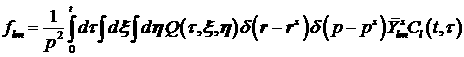 , ,
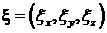 , , 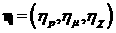 – переменные интегрирования, соответствующие по
физическому смыслу начальной координате и импульсу электрона, образовавшегося в
момент времени – переменные интегрирования, соответствующие по
физическому смыслу начальной координате и импульсу электрона, образовавшегося в
момент времени 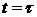 . Движение электрона описывается функциями . Движение электрона описывается функциями 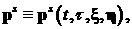 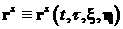 , которые являются решением уравнений движения , которые являются решением уравнений движения 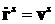 , , 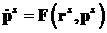 , , 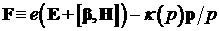 , с начальными данными , с начальными данными 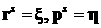 при при 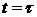 . Точка означает дифференцирование по времени. Величина . Точка означает дифференцирование по времени. Величина 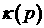 выражает тормозную
способность воздуха. выражает тормозную
способность воздуха.
В уравнении (3) используются следующие обозначения.
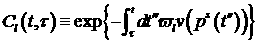 , , 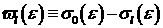 , ,
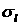 – коэффициенты разложения по полиномам Лежандра
дифференциального сечения углового рассеяния [1], – коэффициенты разложения по полиномам Лежандра
дифференциального сечения углового рассеяния [1], 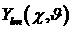 сферическая функция, сферическая функция, 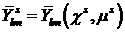 – сопряженная сферическая
функция переменных – сопряженная сферическая
функция переменных  и и  , ,  . .
Тормозная способность учитывает потери энергии за счет
всех, в том числе упругих столкновений, а коэффициенты  описывают угловое
рассеяние за счет всех, в том числе ионизационных столкновений. описывают угловое
рассеяние за счет всех, в том числе ионизационных столкновений.
Функцию распределения первичных электронов в таком
приближении можно вычислять методом частиц [12].
Точность приближенного решения исследуется путем
вычисления невязки кинетического уравнения для электронов пучка. Она [11]
является финитной обобщенной функцией, заданной на пространстве бесконечно дифференцируемых
финитных основных функций. Оценка невязки  на конусе положительных
функций основного пространства, которые представимы в виде на конусе положительных
функций основного пространства, которые представимы в виде  , где , где  – поле направлений в координатном пространстве,
показывает, что – поле направлений в координатном пространстве,
показывает, что 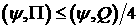 . .
Плотность тока электронов пучка имеет вид:
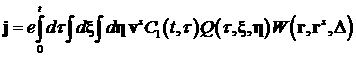 . (4) . (4)
Здесь 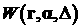 , , 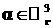 – бесконечно дифференцируемые функции, образующие
континуальное разложение единицы на пространстве – бесконечно дифференцируемые функции, образующие
континуальное разложение единицы на пространстве 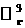 с диаметром покрытия с диаметром покрытия  . Символом . Символом 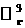 обозначено трехмерное
координатное пространство. обозначено трехмерное
координатное пространство.
Решение (3) имеет простой физический смысл. Частица,
появляющаяся в момент времени 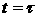 в точке в точке  с импульсом с импульсом 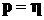 , и содержащая изначально электроны в количестве , и содержащая изначально электроны в количестве 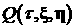 , двигается по траектории , двигается по траектории  , , 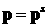 , определяемой электромагнитным полем и ионизационным
торможением. Количество электронов или вес частицы по ходу движения
экспоненциально (пропорционально , определяемой электромагнитным полем и ионизационным
торможением. Количество электронов или вес частицы по ходу движения
экспоненциально (пропорционально  ) уменьшается. Из-за углового рассеяния за электронным
потоком образуется изотропный шлейф, спектр которого продолжает деградировать
за счет ионизационного торможения. ) уменьшается. Из-за углового рассеяния за электронным
потоком образуется изотропный шлейф, спектр которого продолжает деградировать
за счет ионизационного торможения.
Модель вторичных электронов
строится на основе гидродинамического приближения пространственно-однородного
кинетического уравнения. Приближение обосновано тем, что средняя энергия
вторичных электронов не превышает сотен эВ. Дисперсия их спектра велика в
основном за счет электронов низкой энергии. Поэтому пробеги вторичных
электронов в воздухе малы по сравнению с характерными размерами задачи. Скорости
малы по сравнению со скоростью света.
В модели
вторичных электронов величины, необходимые для вычисления плотности тока
вторичных электронов 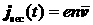 , определяются из системы уравнений «переноса Максвелла»
[13]: , определяются из системы уравнений «переноса Максвелла»
[13]:
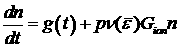 ; ;
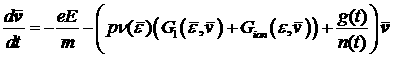 ; ;
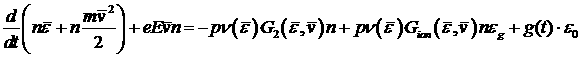
с начальными условиями
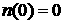 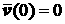 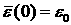 . .
Здесь  – температура среды, – температура среды, 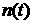 – концентрация вторичных электронов, – концентрация вторичных электронов,  – дрейфовая скорость, – дрейфовая скорость, 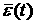 – средняя энергия, – средняя энергия,
Функция 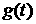 есть интенсивность
ионизации среды, вычисляемая по следующей формуле: есть интенсивность
ионизации среды, вычисляемая по следующей формуле:
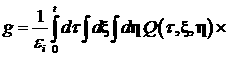
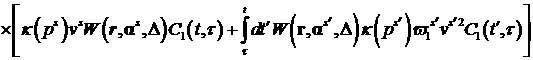 . .
где 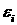 – цена ионизации среды. – цена ионизации среды.
Правые части
уравнений «переноса Максвелла» содержат функционалы от сечений столкновительных
процессов:
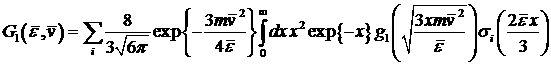 , ,
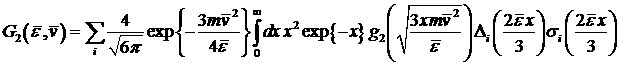 , ,
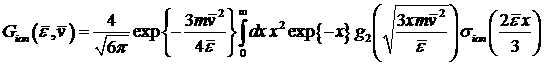 , ,
где 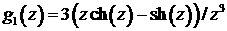 , , 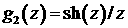 , ,
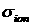 – полное сечение ионизационного рассеяния, – полное сечение ионизационного рассеяния, 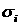 – сечения других неупругих процессов, – сечения других неупругих процессов, 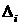 – энергия, теряемая электроном при столкновении i-ого типа, – энергия, теряемая электроном при столкновении i-ого типа,  – переменная интегрирования. – переменная интегрирования.
Численная
реализация метода частиц предполагает совместное решение уравнений Максвелла и
уравнений движения на трехмерной разностной сетке. В каждой ячейке сетки
локально вычисляется интенсивность вторичной ионизации и плотность тока
электронов. Сложность преград и элементов измерительной аппаратуры
обуславливают использование прямоугольных сеток в декартовых координатах.
Наиболее
надежной разностной схемой для уравнений Максвелла является схема «крест». Она
замечательна тем, что представляет собой аппроксимацию интегральной формы
уравнений Максвелла на каждой ячейке сетки. Схема является явной, поэтому
разностные уравнения решаются быстро. Преимуществом является относительная простота
распараллеливания вычислений, что искупает даже основной недостаток схемы –
условную устойчивость. Шаблон разностной схемы «крест» и принципы построения разностных
уравнений представлены в [14].
Численный
алгоритм решения уравнений движения и вычисления плотности тока рассмотрен в
[15]. От других реализаций метода частиц в варианте «cloud-in-cell» его отличают гарантированное выполнение уравнения непрерывности
и возможность использования неравномерной пространственной сетки. Основная идея
алгоритма состоит в том, что плотность электрического тока в ребрах ячеек
разностной сетки вычисляется через изменение заряда в ее вершинах за шаг по
времени. Система линейных уравнений относительно компонент тока при этом
замыкается дополнительным условием. Оно состоит в том, что в течение шага по
времени направление скорости частицы не изменяется и совпадает с направлением
создаваемого ею тока. Если частица пересекает границу ячейки, то ее движение
разбивается на два этапа – до границы и после. Координаты частицы вычисляются
путем численного решения обыкновенного дифференциального уравнения по явной
разностной схеме. Уравнение для импульса частицы на каждом временном слое
решается в два этапа. На первом с помощью центрированной разностной схемы
отслеживается изменение импульса за счет электромагнитного поля. На втором
учитывается изменение импульса частицы за счет ионизационного торможения.
Параллельная
версия расчетных программ составлена на алгоритмическом языке Фортран-90 с
библиотекой передачи сообщений MPI. Принципы
распараллеливания и оценки его эффективности представлены в [15]. Идея состоит
в следующем.
Расчет
самосогласованного электромагнитного поля подразумевает обмен данными на каждом
временном слое между подпрограммами, осуществляющими решение уравнений
Максвелла и уравнений движения частиц. Общая схема распараллеливания определяется
информационными зависимостями между вычисляемыми переменными.
Тип
зависимостей в алгоритме схемы «крест» определяется связью между значениями
переменной в точках с индексами 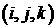 и и  . Наилучшие результаты при реализации алгоритмов с такими
зависимостями на статической прямоугольной сетке дает модель распараллеливания
по данным. Алгоритм вычисления плотности электрического тока путем решения
уравнений движения частиц определяет тот же тип информационных зависимостей.
Однако при этом количество частиц в ячейках сетки может существенно различаться.
Интенсивность генерации частиц неравномерна по ячейкам сетки. Эту
неравномерность можно оценить априорно, поскольку начальное распределение
электронов предполагается известным. В ходе вычислений частицы перемещаются
между ячейками в соответствии с уравнениями движения, распределяясь по ним также
неравномерно, причем это априорно оценить уже невозможно в силу нелинейности
задачи. Поэтому при расчете параметров частиц возникает дисбаланс загрузки
процессоров. . Наилучшие результаты при реализации алгоритмов с такими
зависимостями на статической прямоугольной сетке дает модель распараллеливания
по данным. Алгоритм вычисления плотности электрического тока путем решения
уравнений движения частиц определяет тот же тип информационных зависимостей.
Однако при этом количество частиц в ячейках сетки может существенно различаться.
Интенсивность генерации частиц неравномерна по ячейкам сетки. Эту
неравномерность можно оценить априорно, поскольку начальное распределение
электронов предполагается известным. В ходе вычислений частицы перемещаются
между ячейками в соответствии с уравнениями движения, распределяясь по ним также
неравномерно, причем это априорно оценить уже невозможно в силу нелинейности
задачи. Поэтому при расчете параметров частиц возникает дисбаланс загрузки
процессоров.
Неравномерность
распределения по ячейкам сетки не позволяет распределять данные «по месту», то
есть так, чтобы расчет параметров частиц проводился на тех же процессорах, где
они появляются. Такое распределение приводит к простою большинства процессоров
и резко снижает эффективность распараллеливания.
В программе
реализовано равномерное динамическое перераспределение работ по расчету
параметров частиц между процессорами. Для этого учитывается, что расчет параметров
данной частицы на каждом временном слое никак не связан с расчетами параметров
других частиц, а время расчета параметров частицы мало меняется при переходе с
одного временного слоя на другой. Еще более эффективно пропорциональное перераспределение
частиц. Для его реализации на следующем слое учитывается время расчета частицы
на предыдущем слое.
Подпрограммы,
реализующие решение уравнений Максвелла и уравнений движения частиц, включены в
единую параллельную программу на основе следующего принципа. Распараллеливание по данным на линейку процессоров,
номера которых связаны c узлами сетки
по одной из координат, сочетается с динамической
балансировкой загрузки процессоров при расчете параметров частиц.
Первым шагом расчетного воспроизведения
электромагнитной обстановки, создаваемой пучком электронов ускорителя в ПЗК,
является моделирование распространения параллельного пучка. Электроны вылетают
с поверхности выходной металлической мембраны, отделяющей объем камеры от канала
ускорителя, перпендикулярно ее поверхности. Размеры ПЗК составляют 200x200x200 см.
Электроны стартуют с кольца, расположенного в плоскости (ZY), в направлении оси Х. Расположение координатных осей
показано на рисунке 1. Начало системы координат
находится на левой стенке камеры, в центре кольца, с которого стартуют
электроны.
|

|

|
|
Рисунок 1 – Геометрия
расчета
|
Начальная энергия электронов составляет 8 МэВ.
Амплитуда интенсивности потока электронов равна – 1021
электронов/(см2 с), что соответствует полному току пучка 6 кА с
площади 12π см2. Начальный внутренний радиус пучка составляет 6.5 см,
внешний – 9.5 см. Зависимость интенсивности потока электронов от
времени выбрана в виде плавной функции, так, чтобы длительность по основанию
составила 20 нс. Все электроны выпускаются вдоль нормали к стенке камеры.
Расчет велся на разностной сетке 200х192х192.
Задействовано 10000 слоев по времени. Время расчета составило 4.5 часа на 60
процессорах.
3.1 Бетатронная
неустойчивость пучка
На рисунке 2 показано развитие пучка, полученное путем
расчета. Кадры рисунка отображают распределение концентрации электронов в
камере в различные моменты времени. Время изменяется от нуля, когда фронт пучка
начинает выходить из мембраны, до момента, соответствующего приходу максимума
пучка на противоположную стенку камеры.
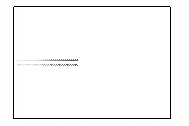
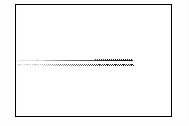
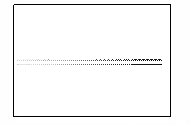
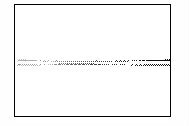
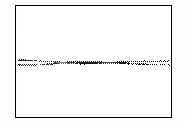
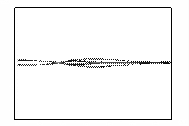




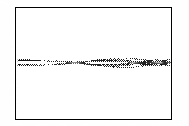
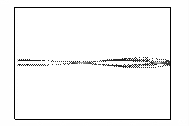
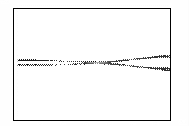
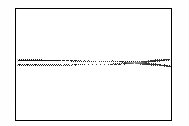
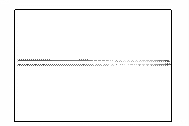
Рисунок 2 – Развитие пучка электронов в камере
(в плоскости XY,
последовательность кадров слева направо)
На кадрах отчетливо прослеживается развитие
бетатронной неустойчивости пучка. Пучок сжимается на определенных расстояниях
от мембраны под действием самосогласованного электромагнитного поля,
создаваемого электронами.
Природа возникновения бетатронной неустойчивости
состоит в следующем. Первоначально электроны летят параллельно оси Х, создавая
продольный ток пучка и генерируя продольную компоненту электрического поля.
Одновременно из-за вторичной ионизации электронами пучка воздушной среды
возникает радиационная проводимость, создается ток вторичных электронов,
направленный противоположно току электронов пучка. Ток смещения и суммарный ток
всех электронов создают поперечное магнитное поле, которое, в свою очередь
создает поперечное электрическое поле.
Поперечная компонента электрического поля стремиться
расширить пучок, а поперечная компонента магнитного поля его сжимает. Пока
электроны не взаимодействовали с молекулами воздуха, указанные влияния
компенсируют друг друга. По мере развития вторичной ионизации развивается
радиационная проводимость, которая гасит электрическое поле в пучке. Сжатие магнитным
полем начинает превалировать. Такая ситуация возможна только при релятивистских
энергиях электронов. Сила Лоренца 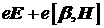 состоит из двух
слагаемых. Первое отражает действие электрического поля, второе – магнитного.
Поперечные компоненты, ответственные за движения электронов в поперечном
направлении в вакууме примерно равны по модулю. Если модуль скорости мало отличается
от скорости света, то и силы примерно равны. Для нерелятивистских электронов кулоновское
отталкивание электронов сразу разрушает пучок, поскольку состоит из двух
слагаемых. Первое отражает действие электрического поля, второе – магнитного.
Поперечные компоненты, ответственные за движения электронов в поперечном
направлении в вакууме примерно равны по модулю. Если модуль скорости мало отличается
от скорости света, то и силы примерно равны. Для нерелятивистских электронов кулоновское
отталкивание электронов сразу разрушает пучок, поскольку  , а , а 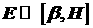 . .
Таким образом, уменьшение электрического поля за счет
обратного тока вторичных электронов приводит к сжатию пучка. За счет магнитного
поля электроны приобретают отрицательную поперечную компоненту импульса.
Электроны проходят через ось пучка и начинают расходиться, приобретая по
инерции положительную компоненту импульса. Далее процесс сжатия повторяется.
Длина бетатронной неустойчивости 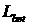 [32] в физике
релятивистских электронных пучков определяется следующим образом: [32] в физике
релятивистских электронных пучков определяется следующим образом:
 . .
Здесь
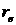 – радиус пучка, – радиус пучка, 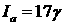 кА – ток Альфвена, кА – ток Альфвена,
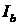 – ток пучка, – ток пучка,  – релятивистский фактор. – релятивистский фактор.
Для рассматриваемых исходных данных 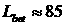 см, что неплохо согласуется
с расчетными данными. см, что неплохо согласуется
с расчетными данными.
3.2 Электромагнитное излучение
ультрарелятивистского пучка
На
рисунке 3 представлено развитие в камере модуля электрического поля.

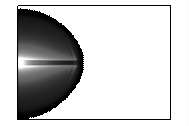




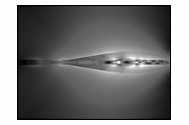

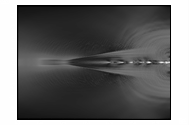
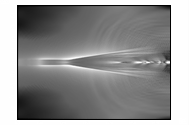


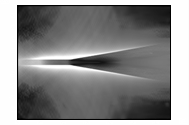





Рисунок 3 – Развитие электрического поля пучка
электронов в камере
(в плоскости XY,
последовательность кадров слева направо)
На
рисунке 4 показано развитие магнитного поля.
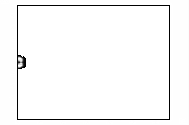
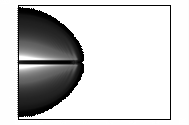
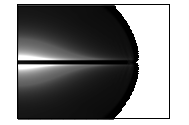
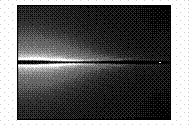
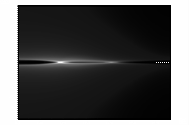
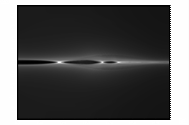


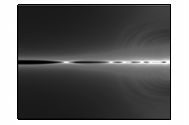


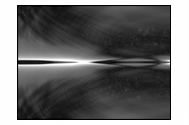






Рисунок 4 – Развитие магнитного поля пучка
электронов в камере
(в плоскости XY,
последовательность кадров слева направо)
Диаграмма направленности электромагнитного излучения
пучка вытянута в направлении его распространения. Это однозначно следует из
рисунков 5 и 6. Такая ситуация имеет место для ультрарелятивистских
пучков. В соответствии с потенциалами Льенара-Вихерта релятивистский электрон
излучает электрическое поле [7]
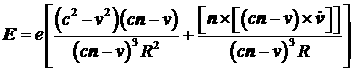 , ,
где  – единичный вектор в направлении движения
электрона; – единичный вектор в направлении движения
электрона;
R – расстояние от электрона до точки
наблюдения.
Таким
образом, 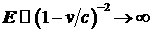 , если , если  . .
Поскольку начальная энергия электронов в расчете
составляет 8 МэВ, то  , а эффект вытянутости диаграммы направленности излучения
вдоль направления распространения пучка должен иметь место, что и наблюдается в
расчете, до тех пор, пока картина не начинает определяться отражениями волн от
стенок ПЗК. , а эффект вытянутости диаграммы направленности излучения
вдоль направления распространения пучка должен иметь место, что и наблюдается в
расчете, до тех пор, пока картина не начинает определяться отражениями волн от
стенок ПЗК.
Заключение
Результаты расчетов параллельного пучка демонстрируют
развитие классических эффектов, свойственных для РЭП – бетатронную
неустойчивость и вытянутую по направлению распространения пучка диаграмму направленности
электромагнитного излучения. Проявление этих эффектов в расчетах являются
необходимыми условиями адекватности математической модели.
Информация о распределении концентрации электронов
пучка в объеме ПЗК может быть использована для оптимального распределения
преград и более точного определения интенсивности падающего на них потока
электронов.
При проведении расчетов выявлен целый ряд недостатков
математической модели. Во-первых, недопустимо задавать моноэнергетический пучок
набором частиц с одинаковой начальной энергией. Это приводит к нефизичному
структурированию пучка с периодом структуры, равным шагу дискретизации по
времени. Необходимо разыгрывание энергии по заданному распределению. Во-вторых,
математическая модель плохо описывает электромагнитную обстановку в ПЗК на
больших временах. Образуется нефизичное распределение заряда в точках,
соответствующих границе прошедшего пучка. Этот факт прослеживается во всех
расчетах и является следствием пространственной однородности кинетического
уравнения для вторичных электронов. Условие пространственной однородности нарушается
на границе пучка, образуется нефизичный разрыв плотности тока проводимости и,
как следствие, накопление заряда. Этот заряд сохраняется в течение всего
расчетного времени и остается существенным после рекомбинации вторичных электронов
и ионов.
Литература
1.
В.И.Бойко,
В.А.Скворцов, В.Е.Фортов, И.В.Шаманин. Взаимодействие импульсных пучков
заряженных частиц с веществом. – М.: Физматлит, 2003.
2.
Д.М. Иващенко,
А.А. Федоров. Российские ускорители электронов, использующиеся в качестве моделирующих
установок. – Вопросы атомной науки и техники, серия «Физика радиационного воздействия на
радиоэлектронную аппаратуру», 2002.- вып. 3, c. 120-128.
3.
В.К. Федоров,
Н.П. Сергеев, А.А. Кондрашин. Контроль и испытания в проектировании
и производстве радиоэлектронных средств. М.: Техносфера, 2005.
4.
А.И. Чумаков.
Действие космической радиации на интегральные схемы. – М.: Радио
и связь, 2004.
5.
Генерация и
фокусировка сильноточных релятивистских электронных пучков./ под ред.
Л.И. Рудакова. – М.: Энергоатомиздат, 1990.
6.
Официальный сайт
ФГУП НИИПриборов http://www.niipriborov.ru/.
7.
Л.Д. Ландау,
Е.М. Лифшиц. Теоретическая физика. Т.2.Теория поля. – М.:Наука,
1979.
8. А.А. Власов. Теория многих частиц. – М.: ГИТТЛ, 1959.
9.
Р. Курант.
Уравнения с частными производными. – М.: МИР, 1964.
10.
Н.С. Келлин, М.Б. Марков,
С.В. Паротькин. Столкновения в
математических моделях электромагнитного поля электронного
потока. – Препринт ИПМ им. М.В. Келдыша № 33, Москва, 2006.
11.
М.Б. Марков. Приближение однородного рассеяния электронов на траекториях. Препринт
ИПМ им. М.В. Келдыша № 37, Москва, 2007.
12.
Hockney
R.W., Eastwood J.W. Computer Simulation Using Particles.– McGraw-Hill, New
York, 1981.
13.
С.В. Паротькин. Радиационная проводимость в потоке быстрых электронов.– Тихонов
и современная математика: Математическое моделирование: Международная
конференция, Москва, МГУ им. М.В. Ломоносова, 19-25 июня 2006 года.:
Тезисы докладов секции №2. М.: Издательский отдел ВМиК МГУ им.
М.В. Ломоносова, 2006.
14.
А.В. Березин, М.Б. Марков,
Б.Д. Плющенков. Локально-одномерная
разностная схема для электродинамических задач с заданным волновым
фронтом. – Препринт ИПМ им. М.В. Келдыша РАН, № 31, Москва, 2005.
15.
А.Н. Андрианов, А.В. Березин,
А.С. Воронцов, К.Н. Ефимкин, М.Б. Марков. Моделирование электромагнитных полей радиационного
происхождения на многопроцессорных вычислительных
системах. – Препринт ИПМ им. М.В. Келдыша РАН, № 74, Москва, 2006.
16.
Г. Бенфорд, Д. Бук. Равновесие релятивистского пучка. В кн. «Достижения физики плазмы».
М.: Мир, 1974, стр. 32.
|















![]() состоит из двух
слагаемых. Первое отражает действие электрического поля, второе – магнитного.
Поперечные компоненты, ответственные за движения электронов в поперечном
направлении в вакууме примерно равны по модулю. Если модуль скорости мало отличается
от скорости света, то и силы примерно равны. Для нерелятивистских электронов кулоновское
отталкивание электронов сразу разрушает пучок, поскольку
состоит из двух
слагаемых. Первое отражает действие электрического поля, второе – магнитного.
Поперечные компоненты, ответственные за движения электронов в поперечном
направлении в вакууме примерно равны по модулю. Если модуль скорости мало отличается
от скорости света, то и силы примерно равны. Для нерелятивистских электронов кулоновское
отталкивание электронов сразу разрушает пучок, поскольку ![]() , а
, а ![]() .
.![]() [32] в физике
релятивистских электронных пучков определяется следующим образом:
[32] в физике
релятивистских электронных пучков определяется следующим образом: ![]() .
.![]() – радиус пучка,
– радиус пучка, ![]() кА – ток Альфвена,
кА – ток Альфвена,
![]() – ток пучка,
– ток пучка, ![]() – релятивистский фактор.
– релятивистский фактор. ![]() см, что неплохо согласуется
с расчетными данными.
см, что неплохо согласуется
с расчетными данными.



































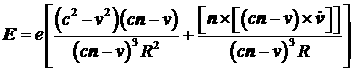 ,
,![]() – единичный вектор в направлении движения
электрона;
– единичный вектор в направлении движения
электрона;![]() , если
, если ![]() .
.![]() , а эффект вытянутости диаграммы направленности излучения
вдоль направления распространения пучка должен иметь место, что и наблюдается в
расчете, до тех пор, пока картина не начинает определяться отражениями волн от
стенок ПЗК.
, а эффект вытянутости диаграммы направленности излучения
вдоль направления распространения пучка должен иметь место, что и наблюдается в
расчете, до тех пор, пока картина не начинает определяться отражениями волн от
стенок ПЗК.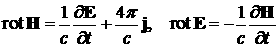 .
.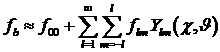
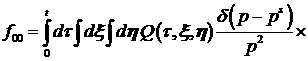
 ,
,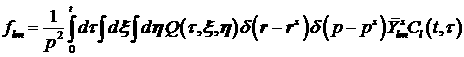 ,
,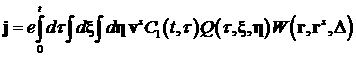
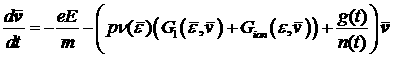 ;
;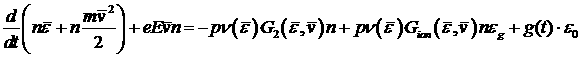
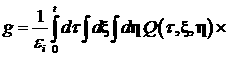
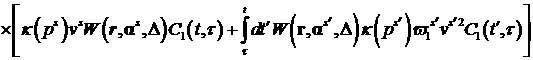 .
.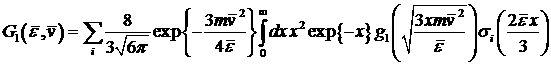 ,
,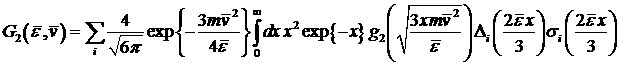 ,
, ,
,
