Угловое распределение релятивистского электронного пучка линейного индукционного ускорителя ЛИУ-10
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Энергия электрона (МэВ) |
Тормозная способность (МэВ см2/г) |
Массовая длина пробега (г/ см2) |
Длина пробега (см) |
||
|
Ионизационная |
Радиационная |
Общая |
|||
|
1.00 |
1.661 |
0.013 |
1.674 |
0.490 |
380 |
|
1.50 |
1.661 |
0.020 |
1.680 |
0.790 |
611 |
|
1.75 |
1.671 |
0.023 |
1.694 |
0.940 |
726 |
|
2.00 |
1.684 |
0.027 |
1.711 |
1.085 |
839 |
|
2.50 |
1.712 |
0.034 |
1.747 |
1.374 |
1063 |
|
3.00 |
1.740 |
0.047 |
1.783 |
1.658 |
1282 |
|
3.50 |
1.766 |
0.050 |
1.817 |
1.935 |
1496 |
|
4.00 |
1.790 |
0.060 |
1.850 |
2.208 |
1708 |
|
4.50 |
1.812 |
0.070 |
1.881 |
2.476 |
1915 |
|
5.00 |
1.833 |
0.080 |
1.911 |
2.74 |
2119 |
|
5.50 |
1.852 |
0.090 |
1.940 |
2.999 |
2319 |
|
6.00 |
1.870 |
0.100 |
1.967 |
3.255 |
2517 |
|
7.00 |
1.902 |
0.120 |
2.020 |
3.757 |
2906 |
|
8.00 |
1.931 |
0.140 |
2.068 |
4.246 |
3284 |
|
9.00 |
1.956 |
0.160 |
2.115 |
4.724 |
3654 |
|
10.00 |
1.979 |
0.180 |
2.159 |
5.192 |
4015 |
Данные таблицы свидетельствуют о следующем. Во-первых,
радиационными потерями энергии электронами и тормозным гамма-излучением при рассмотрении
распространения электронов в воздухе можно пренебречь. Во-вторых, длины
пробегов электронов с энергиями порядка 10 МэВ более чем на порядок превосходят
размер ПЗК. Под длиной пробега электрона здесь понимается расстояние, по
прохождении которого электрон теряет всю свою энергию в результате
ионизационного рассеяния на нейтральных молекулах.
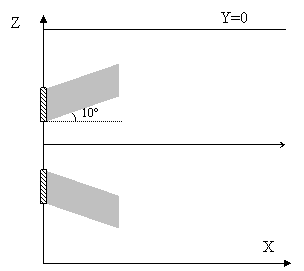
В расчете принято, что угол между направлением
начального импульса электронов и нормалью к поверхности мембраны составляет 10
градусов, как показано на рисунке 1.
Начальная энергия электронов составляет 8 МэВ.
Электрон с такой энергией имеет длину пробега порядка 30 метров. Интенсивно
взаимодействовать с воздушной средой он может только в том случае, если его
энергия существенно изменится за счет торможения в самосогласованном поле.
Начальный внутренний диаметр пучка составляет 6.5 см,
внешний – 9.5 см. Амплитуда интенсивности потока электронов равна 1021
электронов/(см2 с), что соответствует полному току пучка 6 кА с
площади 12π см2. Зависимость интенсивности потока электронов от
времени выбрана в виде плавной импульсной функции, так, чтобы длительность по
основанию составила 20 нс.
Расчет велся на разностной сетке 200х192х192.
Задействовано 10000 слоев по времени. Время расчета составило 4.5 часа на 60
процессорах параллельного компьютера МВС15000 в Межведомственном
суперкомпьютерном Центре РАН [10].
|
|
|
|
Рис.1 – Расходящийся пучок |
Рис.2 – Плотность заряда в плоскости YZ, X=80 см, T= 22 нс |
В качестве результатов расчета на характерных
временных слоях записывались распределения напряженностей электрического и
магнитного поля, а также концентрации электронов. Сравнение линий уровня
концентрации в различные моменты времени дает представление о динамике пучка.
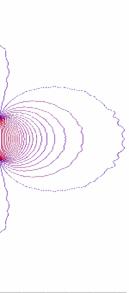
Такая иллюстрация развития пучка показана на рисунке
3. На нем изображены линии уровня концентрации электронов в плоскости XY, соответствующие различным последовательным моментам
времени.
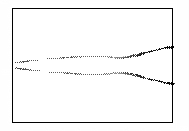
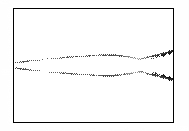
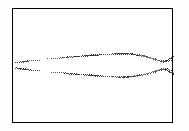

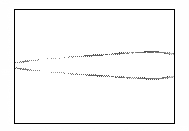
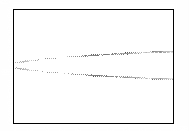
Рис.3 – Развитие пучка электронов с начальным угловым
распределением
(в плоскости XY,
последовательность кадров слева направо)
На последних кадрах видно, что в области,
соответствующей промежуточным значениям X, пучок как бы «исчезает». Это происходит вследствие
ухода электронов из плоскости из плоскости Z=0. Пучок структурируется, что хорошо видно на рисунке 3. Этот эффект
возникает из-за того, что начальное распределение электронов считается моноэнергетичным.
2. Внешнее магнитное поле в
помехозащищенном комплексе
Единственным объяснением углового распределения
представляется проникновение в ПЗК магнитного поля выводного устройства
ускорителя ЛИУ-10. Это поле
создается на выходе ускорительного тракта специальным соленоидом для
обеспечения прямолинейности траектории электронов в выводном устройстве.
Отметим, что магнитное поле выводного соленоида
является квазистатическим, поэтому проникает через стенки ПЗК и экран,
«провисая» в объем ПЗК.
Для того, чтобы определить величину внешнего
магнитного поля при задании геометрической модели ПЗК для расчета, выполнены
предварительные вычисления. Рядом со стенкой камеры помещен дополнительный
объект, моделирующий выводной соленоид. Длина соленоида составляет 45 см,
радиус – 26 см. В ячейках разностной сетки, соответствующих этому
объекту, задан постоянный сторонний электрический ток постоянной величины,
подобранной так, чтобы магнитное поле в центре соленоида равнялось 0,5 Тл –
величине, известной из эксперимента. Запущен расчет в режиме численного решения
уравнений Максвелла с заданным током в правой части. После стабилизации
магнитного поля во всей расчетной области, включая ПЗК, результаты сохранены. В
расчете динамики пучка на той же сетке они используются в качестве входных данных
о внешнем магнитном поле, действующем на заряженные частицы.
Рассмотрим
результат расчета «провисающего» магнитного поля. На рисунке 4 представлены
линии уровня компонент магнитного поля
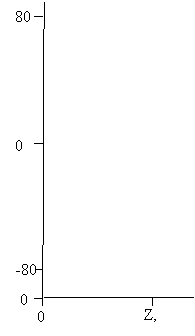
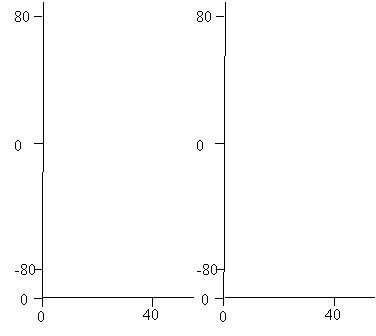
|
|
0 |
|
||
|
Нормальная Компонента |
Тангенциальная компонента |
Модуль |
Рис.4 – Линии уровня внешнего магнитного поля
(плоскость XY, см)
Значение поля вблизи левой границы ПЗК – порядка
4 103 ед. СГС, то есть
на 25 процентов меньше, чем в ускорительном тракте. Это соответствует имеющимся
экспериментальным данным. При удалении от границы поле падает пропорционально
1/r 2, где r – расстояние
от мембраны.
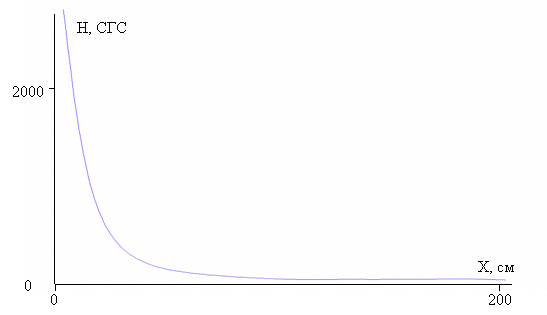
Рис.5 – График зависимости модуля внешнего магнитного
поля от расстояния до границы
3. Распространение пучка во внешнем
электромагнитном поле
Рассмотрим результаты расчета распространения пучка в
ПЗК с учетом внешнего магнитного поля, создаваемого выводным соленоидом на выходе
из ускорительного тракта. Электроны выпускаются по нормали к поверхности
выходного экрана. Остальные исходные данные расчета, такие как полный ток
пучка, начальное распределение интенсивности по поверхности экрана совпадают с
представленными в первом разделе. Расчет проведен на той же разностной сетке по
пространственным координатам и времени и потребовал того же объема ресурсов
МВС15000М.
На рисунке 6 показана геометрия расчета
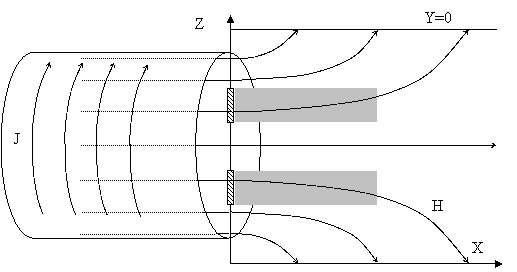
Рис.6 – Параллельный пучок во внешнем магнитном поле
Внешнее
магнитное поле существенно изменяет поведение параллельного пучка. Развитие
пучка показано на рисунке 7. Использован тот же способ представления данных –
последовательность кадров с линиями уровня концентрации электронов.
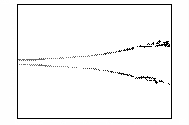
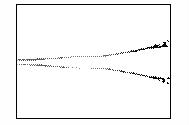
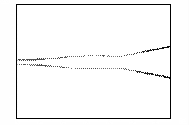
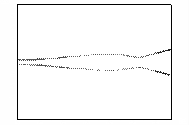
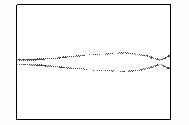
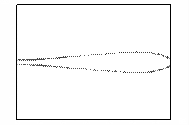
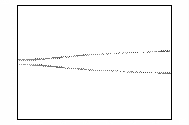
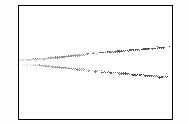
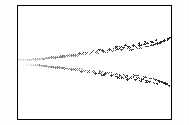
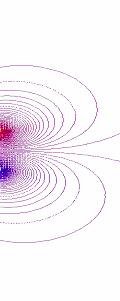
Рис.7 – Развитие пучка электронов во внешнем
магнитном поле
(в плоскости XY,
последовательность кадров слева направо)
На кадрах рисунка 7 прослеживаются следующие стадии
динамики пучка. Первоначально электроны летят параллельно оси абсцисс. Внешнее
магнитное поле закручивает их вокруг своих силовых линий, меняя направление
импульса. Электрон приобретает ненулевую поперечную компоненту импульса.
Поскольку внешнее магнитное поле быстро уменьшается с ростом расстоянием, это
воздействие носит кратковременный характер. В результате электроны как бы
испытывают небольшое угловое отклонение в самом начале своей траектории внутри
ПЗК. Рассмотрим два электрона, которые вылетают с поверхности выходного экрана параллельно друг другу в плоскости XZ с равными по модулю и противоположными по знаку
значениями Y. Такие электроны оказываются под
действием поперечных компонент внешнего магнитного поля противоположного знака
и отклоняются в разные стороны от оси X.
Структура пучка при этом сохраняет аксиальную симметрию. На некотором
расстоянии от выходного экрана внешнее магнитное поле уменьшается и становится
малым в сравнении с самосогласованным электромагнитным полем. Продольное
электрическое поле пучка генерирует поперечную компоненту магнитного поля,
которое сжимает пучок, противодействуя кулоновскому отталкиванию электронов.
Поперечные компоненты самосогласованного электрического поля уменьшаются из-за
тока медленных электронов, возникающего в результате вторичной ионизации
воздушной среды. В результате сжатие начинает превалировать над расталкиванием,
и пучок сжимается. Этот эффект отчетливо прослеживается на кадрах рисунка 7 и
называется [11] бетатронной неустойчивостью релятивистского электронного пучка.
Для теоретической оценки длины бетатронной
неустойчивости РЭП необходимы такие параметры как его радиус и полный ток [11].
В рассматриваемом случае влияние магнитного поля не позволяет выполнить такую
оценку, поскольку изменяет радиус и сообщает электронам дополнительную поперечную
компоненту импульса. Длина бетатронной неустойчивости ![]() параллельного пучка
вычисляется следующим образом:
параллельного пучка
вычисляется следующим образом:
![]() .
.
Здесь
![]() – радиус пучка,
– радиус пучка, ![]() кА – ток Альфвена,
кА – ток Альфвена,
![]() – ток пучка,
– ток пучка, ![]() – релятивистский фактор.
– релятивистский фактор.
В случае параллельного пучка ![]() см. Последние кадры
рисунка 7 показывают, что пучок сжимается на расстоянии примерно 1.3 метра от выходного
экрана. Это, очевидно, связано с приобретаемым пучком во внешнем магнитном поле
на начальном участке траектории нетривиальным угловым распределением.
Самосогласованному магнитному полю необходимо дополнительное время, чтобы
скомпенсировать поперечную компоненту импульса электрона.
см. Последние кадры
рисунка 7 показывают, что пучок сжимается на расстоянии примерно 1.3 метра от выходного
экрана. Это, очевидно, связано с приобретаемым пучком во внешнем магнитном поле
на начальном участке траектории нетривиальным угловым распределением.
Самосогласованному магнитному полю необходимо дополнительное время, чтобы
скомпенсировать поперечную компоненту импульса электрона.
Расчет пучка во внешнем магнитном поле демонстрирует
также, что диаграмма направленности его электромагнитного излучения является
ультрарелятивистской. Это иллюстрирует рисунок 8. Кадры этого рисунка представляют
линии уровня модуля напряженности электрического поля в последовательные
моменты времени. Отчетливо видно, что диаграмма направленности
электромагнитного излучения вытянута в направлении распространения пучка. Такой
эффект характерен для излучения релятивистских заряженных частиц, что следует
из вида потенциалов Льенара-Вихерта.

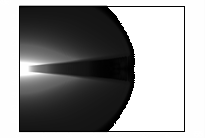
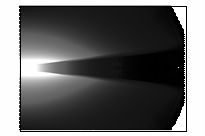





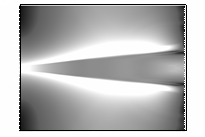


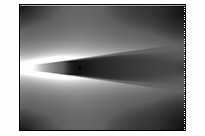

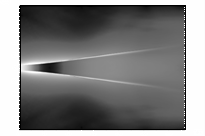
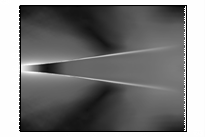
Рис. 8– Развитие модуля электрического поля
В этом расчете проявился еще один эффект. Оказалось,
что пучок не только сжимается, но и истончается в поперечном сечении. Этот факт
демонстрирует рисунок 9, на котором представлены линии уровня концентрации электронов
в плоскости YZ, X=160 см в последовательные моменты времени.
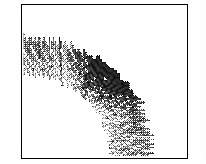
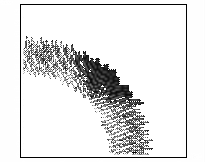
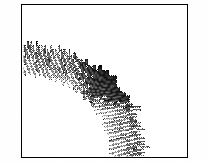
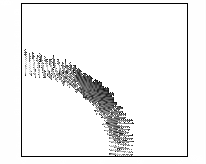
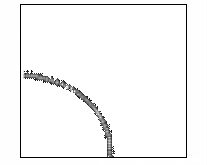

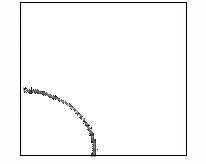
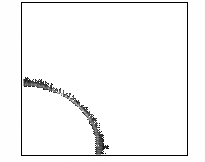
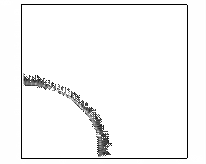
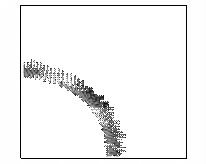
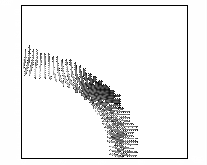
Рис. 9 – Развитие пучка электронов
(в плоскости YZ, X=160 см, последовательность кадров слева направо).
К истончению пучка приводит самосогласованное
магнитное поле. На начальном этапе вокруг пучка развивается сжимающее, а внутри
– расталкивающее самосогласованное магнитное поле. Сечение пучка поперечной плоскостью
представляет собой кольцо. При переходе из области пространства, внешней по
отношению к кольцу во внутреннюю область поперечное магнитное поле меняет знак.
В последующие моменты времени этот эффект практически исчезает в расчете с внешним
магнитным полем и существенно уменьшается в расчете с заданным угловым
распределением. Смену знака поперечной компоненты магнитного поля, приводящую к
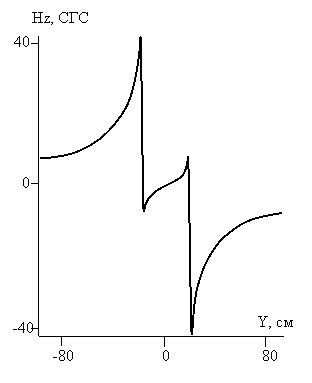
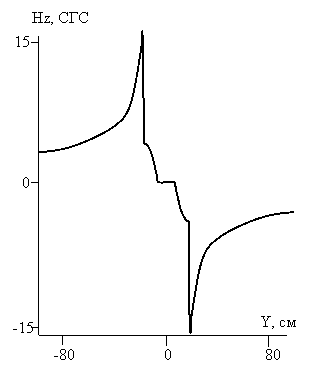
истончению пучка, и исчезновение этого эффекта демонстрирует рисунок 10.
|
|
|
|
T= 12 нс |
T= 20 нс |
|
Рис. 10 – Зависимость Hz от Y. X=160 см, Z = 0
см, |
|
Заключение
Результаты расчетов динамики пучка с учетов внешнего
магнитного поля, создаваемого соленоидом выводного устройства
ускорителя и «провисающего» в ПЗК, совпали с результатами расчетов с
измеренным в эксперименте начальным угловым распределением электронов. Это
свидетельствует о том, что причиной нетривиального углового распределения
является внешнее магнитное поле. Совпадение также подтверждает результаты
измерений углового распределения.
Литература
1.
Д.М. Иващенко,
А.А. Федоров. Российские ускорители электронов, использующиеся в качестве моделирующих
установок. – Вопросы атомной науки и техники, серия «Физика радиационного воздействия на
радиоэлектронную аппаратуру», 2002.- вып. 3, c. 120-128.
2. В.И.Бойко, В.А.Скворцов, В.Е.Фортов, И.В.Шаманин. Взаимодействие импульсных пучков заряженных частиц с веществом. – М.: Физматлит, 2003.
3.
Официальный сайт
ФГУП НИИПриборов http://www.niipriborov.ru/.
4. А.Н. Андрианов,
А.В. Березин, А.С. Воронцов, К.Н. Ефимкин, М.Б. Марков. Моделирование электромагнитных полей радиационного
происхождения на многопроцессорных вычислительных
системах. – Препринт ИПМ им. М.В. Келдыша РАН, № 74, Москва, 2009.
5. М.Б. Марков. Приближение однородного рассеяния электронов на
траекториях. Препринт ИПМ им. М.В. Келдыша № 37, Москва, 2007.
6. С.В. Паротькин. Радиационная проводимость в потоке быстрых
электронов.– Тихонов и современная математика: Математическое
моделирование: Международная конференция, Москва, МГУ им. М.В. Ломоносова,
19-25 июня 2006 года.: Тезисы докладов секции №2. М.: Издательский отдел ВМиК
МГУ им. М.В. Ломоносова, 2009.
7.
Hockney
R.W., Eastwood J.W. Computer Simulation Using Particles.– McGraw-Hill, New
York, 1981.
8. Н. Мотт,
Г. Мэсси. Теория атомных
столкновений. М.: МИР, 1969.
9.
Официальный сайт National Institute of Standarts and Technology
http://www.phys.nist.gov/
10.
Официальный сайт
Межведомственного Суперкомпьютерного Центра РАН http://www.jscc.ru/
11.
Г. Бенфорд, Д. Бук. Равновесие релятивистского пучка. В кн. «Достижения физики плазмы».
М.: Мир, 1974, стр. 32.