Аннотация
Исследуется динамика системы спутник-стабилизатор. Предполагается, что в шарнире,
соединяющем два тела, имеется вязкое трение, но отсутствует упругость. Рассматривается
движение в плоскости круговой орбиты и определяются параметры, при которых собственные
колебания около устойчивого положения равновесия в орбитальной системе координат затухают
максимально быстро. Скорость протекания переходных процессов оценивается величиной степени
устойчивости линеаризованных уравнений движения. В результате оптимизации по безразмерному
коэффициенту демпфирования пространство параметров системы разбивается на области,
в каждой из которых максимум степени устойчивости достигается на определенной конфигурации
корней характеристического уравнения. Показано, что глобальный максимум достигается в двух
точках пространства параметров. При этом одно из тел системы вырождается в пластину,
а характеристическое уравнение имеет четыре равных вещественных корня.
Abstract
Dynamics of a gravitational system satellite-stabilizer is studied. It is assumed that
there exists viscous friction in the hinge connecting the system components but there
is no spring resistance. The plane motion in a circular orbit is analyzed; the parameters
that provide the most rapid damping of the natural oscillations in the vicinity of
the equilibrium are determined. To estimate the duration of the transitional processes,
the degree of stability of the linearized equations of motion is used. As a result
of optimization with respect to dimensionless damping coefficient, the space of
the system’s parameters is divided into several domains. In each of these domains,
the maximum degree of stability takes place on a specific configuration of characteristic
equation roots. It is shown that the global optimum is achieved in the two points
of the parameter space. Here one of the system’s bodies degenerates into a plate,
and the characteristic equation has four equal real roots.
Введение
Принцип
работы пассивных систем ориентации спутников основан на взаимодействии с
внешними силовыми полями (например, с гравитационным или магнитным полем Земли)
или использовании гироскопических свойств вращающихся тел. При синтезе системы
и выборе значений ее параметров необходимо обеспечить не только устойчивость
требуемого положения равновесия, например,
в орбитальной системе координат, но и гарантировать достаточно
эффективное демпфирование собственных колебаний спутника, возникающих в
результате ошибок выведения и действия возмущений. В гравитационных системах
для гашения колебаний в окрестности устойчивого положения равновесия используется
относительное движение компонентов системы, при котором энергия колебаний
рассеивается за счет трения в шарнире [1]. Впервые такая схема была предложена
Д.Е. Охоцимским в 1956 г. При другом способе введения демпфировани на спутнике
устанавливаются двухстепенные гироскопы в вязкоупругой подвеске [2];
собственные колебания спутника вызывают прецессию роторов гироскопов и, таким
образом, также приводят к диссипации энергии.
Одним
из основных критериев качества пассивных систем ориентации является быстродействие,
т.е. скорость демпфирования собственных колебаний спутника. В свою очередь, для
оценки скорости демпфирования часто используется величина степени устойчивости 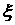 [3] - взятой с
обратным знаком действительной части ближайшего к мнимой оси корня
характеристического уравнения линеаризованной системы уравнений движения
спутника. Большой круг работ посвящён поиску таких значений параметров систем
ориентации, при которых достигается максимум [3] - взятой с
обратным знаком действительной части ближайшего к мнимой оси корня
характеристического уравнения линеаризованной системы уравнений движения
спутника. Большой круг работ посвящён поиску таких значений параметров систем
ориентации, при которых достигается максимум 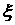 . При этом, поскольку характеристические уравнения
исследовавшихся систем имеют, как правило, высокий порядок, оптимизация в
основном проводилась численно. . При этом, поскольку характеристические уравнения
исследовавшихся систем имеют, как правило, высокий порядок, оптимизация в
основном проводилась численно.
Однако
следует отметить, что все используемые численные методы на финальной стадии
оптимизации теряют свою эффективность, что связано с неаналитичностью степени
устойчивости в экстремуме. Неаналитический характер обусловлен тем, что при
подходе к экстремуму корни характеристического уравнения стремятся подравнять
свои вещественные части. Последний факт был обнаружен в ходе численной
оптимизации целого ряда пассивных и полупассивных систем ориентации спутников и
был положен в основу специального алгоритма поиска оптимальных параметров таких
систем [4].
Напомним некоторые результаты исследования пассивных систем
ориентации, демонстрирующие отмеченную тенденцию выравнивания вещественных
частей корней характеристического уравнения в окрестности экстремума степени
устойчивости:
·
В
[5] рассматривалась система спутник-стабилизатор с демпфирующей пружиной,
допускающей поступательные перемещения стабилизатора относительно спутника.
Оказалось, что максимум степени устойчивости достигается в точке, где все корни
характеристического уравнения восьмого порядка имеют одинаковую вещественную
часть.
·
В
[6] исследовался спутник с двумя стабилизаторами, присоединенными при помощи
одностепенных шарниров. При оптимальных параметрах действительные части всех
корней характеристического уравнения десятого порядка совпадают.
·
В
[7] определены оптимальные параметры спутника, стабилизируемого вращением, с
демпфером маятникового типа. Максимальная степень устойчивости такой системы
достигается в точке, где все четыре корня характеристического уравнения
вещественны и равны.
·
В
[2] рассматривался спутник, стабилизируемый вращением, с гиродемпфером нутационных
колебаний. Показано, что при достаточно большой величине кинетического момента
ротора гироскопа максимум степени устойчивости достигается при таких значениях
параметров, когда все корни характеристического уравнения вещественны и равны.
Наряду
с численными исследованиями задач данного класса предпринимались попытки
аналитической оптимизации степени устойчивости. В [8] рассматривались характеристические
уравнения третьего и четвертого порядка специального вида:
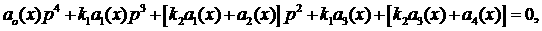 (1) (1)
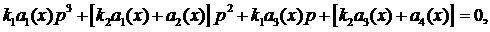 (2) (2)
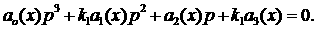 (3)
(3)
Их отличает характер зависимости
коэффициентов уравнений от двух выделенных параметров - 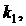 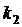 (для системы
спутник-стабилизатор (рис. 1) это коэффициенты вязкого трения и упругости в
шарнире); (для системы
спутник-стабилизатор (рис. 1) это коэффициенты вязкого трения и упругости в
шарнире); 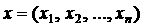 - остальные параметры системы. Необходимость
исследования уравнений (1)-(3) обусловлена тем, что для ряда систем ориентации
(см., например, [2, 7, 10-12]) именно такой вид принимают характеристические
уравнения. В [8] решена задача оптимизации степени устойчивости по - остальные параметры системы. Необходимость
исследования уравнений (1)-(3) обусловлена тем, что для ряда систем ориентации
(см., например, [2, 7, 10-12]) именно такой вид принимают характеристические
уравнения. В [8] решена задача оптимизации степени устойчивости по 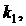 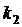 для уравнений (1)-(3).
Здесь же с использованием полученных результатов проведена аналитическая оптимизация
одной частной конфигурации системы спутник-стабилизатор по всем параметрам. для уравнений (1)-(3).
Здесь же с использованием полученных результатов проведена аналитическая оптимизация
одной частной конфигурации системы спутник-стабилизатор по всем параметрам.
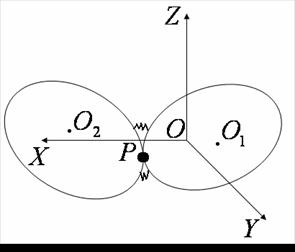
Рис. 1:
Система спутник-стабилизатор
В [9] рассмотрено характеристическое уравнение чётного
порядка. Показано, что для системы порядка 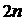 , зависящей от , зависящей от  параметров, локальный
максимум степени устойчивости достигается при таких значениях параметров, когда
характеристическое уравнение имеет n-кратный корень параметров, локальный
максимум степени устойчивости достигается при таких значениях параметров, когда
характеристическое уравнение имеет n-кратный корень 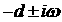 . .
Настоящая работа
посвящена исследованию уравнения
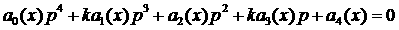 . (4) . (4)
Такой вид характеристическое уравнение
принимает, например, в задаче о малых колебаниях системы спутник-стабилизатор в
случае, когда пружина в шарнире отсутствует (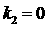 ). Параметр ). Параметр 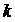 в (4) пропорционален
коэффициенту вязкого трения в шарнире. Цель исследования состоит в определении
оптимального значения коэффициента в (4) пропорционален
коэффициенту вязкого трения в шарнире. Цель исследования состоит в определении
оптимального значения коэффициента 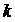 , при котором достигается максимум степени устойчивости.
Методически работа близка [8]. , при котором достигается максимум степени устойчивости.
Методически работа близка [8].
На
первом этапе решается задача максимизации степени устойчивости по 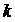 : устанавливаются все конфигурации корней, на которых может
достигаться оптимум; для каждой конфигурации определяются области в
пространстве безразмерных параметров системы, где она является оптимальной,
т.е. на ней достигается максимум степени устойчивости; получено значение
максимальной по : устанавливаются все конфигурации корней, на которых может
достигаться оптимум; для каждой конфигурации определяются области в
пространстве безразмерных параметров системы, где она является оптимальной,
т.е. на ней достигается максимум степени устойчивости; получено значение
максимальной по 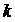 степени устойчивости и
определено оптимальное значение параметра степени устойчивости и
определено оптимальное значение параметра 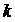 . .
На
втором этапе определяются оптимальные значения всех остальных безразмерных
параметров системы спутник-стабилизатор. Показано, что оптимум достигается в
двух точках пространства параметров. При этом в обоих случаях
характеристическое уравнение имеет четыре равных вещественных корня.
Первый этап оптимизации
Положение
равновесия системы является асимптотически устойчивым, если все корни уравнения
(4) имеют отрицательные вещественные части. Это накладывает ограничения на
коэффициенты 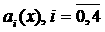 . В соответствии с критерием Рауса-Гурвица (полагаем . В соответствии с критерием Рауса-Гурвица (полагаем 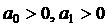 ) имеем ) имеем
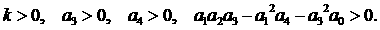 (5) (5)
Введем параметры 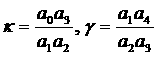 . Тогда, в соответствии с (5), . Тогда, в соответствии с (5),
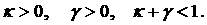 (6) (6)
Соответствующая область на рис. 2
выделена светло-серым цветом.
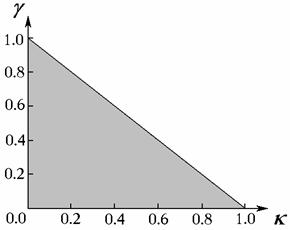
Рис. 2: Допустимая область изменения
параметров 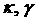
Обозначим 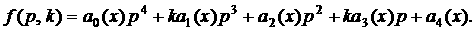 Известно, что комплекснозначные функции Известно, что комплекснозначные функции 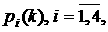 неявно определяемые
уравнением (4), непрерывны. Они также дифференцируемы, за исключением, быть
может, точек, где неявно определяемые
уравнением (4), непрерывны. Они также дифференцируемы, за исключением, быть
может, точек, где
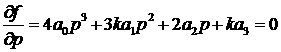 , ,
что соответствует случаю, когда
уравнение (4) имеет кратный корень. Аналогичные утверждения справедливы для 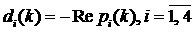 . Поскольку степень устойчивости определяется выражением . Поскольку степень устойчивости определяется выражением  , то её экстремальное значение достигается в точке, где , то её экстремальное значение достигается в точке, где 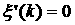 (т.е. в точке,
где (т.е. в точке,
где 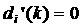 для некоторого для некоторого 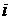 ), либо в точке недифференцируемости ), либо в точке недифференцируемости 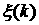 , либо на границе интервала изменения , либо на границе интервала изменения 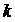 (при (при 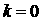 или или 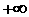 ). При ). При 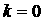 уравнение (4) принимает
вид уравнение (4) принимает
вид 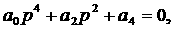 откуда откуда
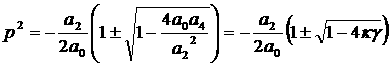 . .
Но, в силу (6), 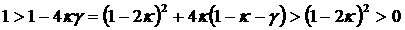 , т.е. , т.е. 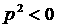 . Следовательно, все корни чисто мнимые и . Следовательно, все корни чисто мнимые и 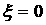 . Если . Если 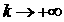 , то легко показать, что один из корней уравнения (4) имеет
вид , то легко показать, что один из корней уравнения (4) имеет
вид 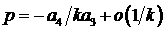 , и поэтому с ростом , и поэтому с ростом 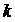 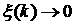 . В свою очередь, точки недифференцируемости . В свою очередь, точки недифференцируемости 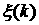 лежат среди точек
недифференцируемости лежат среди точек
недифференцируемости 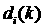 (соответствующих кратному
корню уравнения (4)), а также точек, где кривые (соответствующих кратному
корню уравнения (4)), а также точек, где кривые 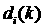 пересекаются под ненулевым
углом. Таким образом, максимальная по пересекаются под ненулевым
углом. Таким образом, максимальная по 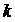 степень устойчивости
может достигаться в следующих случаях: степень устойчивости
может достигаться в следующих случаях:
§
совпадают
действительные части у двух пар комплексно сопряжённых корней: 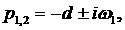 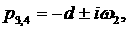 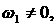 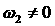 ; ;
§
совпадают
действительные части у двух вещественных корней (кратный вещественный корень, 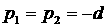 ); );
§
совпадают
вещественные части у пары комплексно сопряжённых корней и одного вещественного
корня: 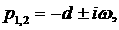 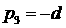 ; ;
§
для
действительной части одного из корней выполнено условие экстремальности: 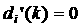 . .
Проанализируем
далее каждую из перечисленных возможностей.
1. Две пары комплексно сопряжённых корней с одинаковыми вещественными частями
Пусть при 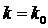 корни уравнения (4)
имеют вид корни уравнения (4)
имеют вид 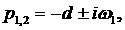 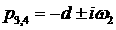 (для определенности, (для определенности, 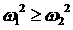 ). Представляя его в виде ). Представляя его в виде
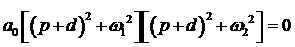 (7) (7)
и приравнивая коэффициенты при одинаковых степенях 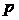 в (4) и (7), получаем в (4) и (7), получаем
 (8) (8)
откуда
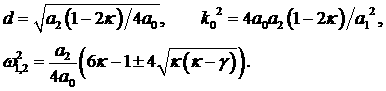 (9) (9)
Принимая во внимание
неотрицательность 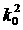 и и 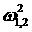 , получаем условия , получаем условия
 ,
(10) ,
(10)
при которых такая конфигурация корней
возможна (темно-серая область на рис. 3).
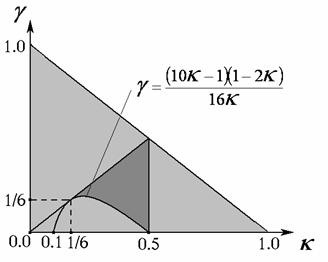
Рис. 3
Теперь
определим область, в которой 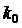 действительно является
оптимальным. Для этого перепишем (4) в виде действительно является
оптимальным. Для этого перепишем (4) в виде
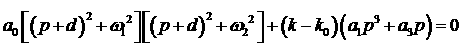
и сделаем подстановку 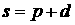 . Тогда получим . Тогда получим
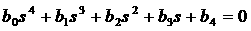 , ,
где
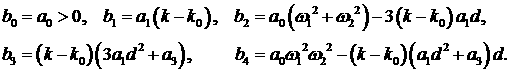
Необходимые и достаточные условия устойчивости имеют вид
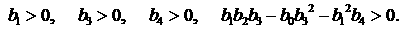
Из первого условия следует 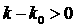 , а четвертое условие приводится к виду , а четвертое условие приводится к виду
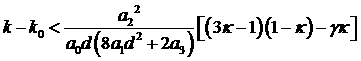 . .
Отсюда следует, что при 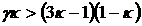 (область I на рис. 4) (область I на рис. 4) 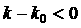 . Таким образом, в
области I при . Таким образом, в
области I при 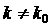 характеристическое
уравнение имеет корни, лежащие правее прямой характеристическое
уравнение имеет корни, лежащие правее прямой 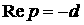 . Таким образом, при . Таким образом, при 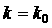 действительно
достигается максимум степени устойчивости и действительно
достигается максимум степени устойчивости и 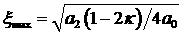 . .
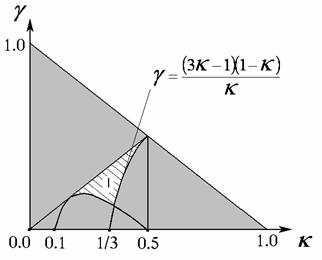
Рис. 4
2. Кратные корни
Проанализируем
случай кратных вещественных корней 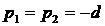 , при этом другие два корня ( , при этом другие два корня (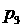 и и 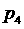 ) могут быть вещественными или комплексно сопряженными. Случай
кратных комплексно сопряжённых корней ( ) могут быть вещественными или комплексно сопряженными. Случай
кратных комплексно сопряжённых корней (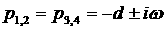 ) отдельно не исследуется, поскольку при ) отдельно не исследуется, поскольку при 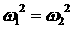 он сводится к уже
рассмотренному в предыдущем разделе случаю (такая конфигурация корней имеет
место на границе он сводится к уже
рассмотренному в предыдущем разделе случаю (такая конфигурация корней имеет
место на границе 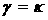 темно-серой
области на рис. 3). темно-серой
области на рис. 3).
Кратный корень 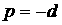 удовлетворяет
уравнению (4) и уравнению удовлетворяет
уравнению (4) и уравнению
 . (11) . (11)
Выражая из (11) 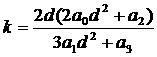 и вводя обозначение и вводя обозначение 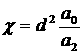 , преобразуем (4) к виду , преобразуем (4) к виду
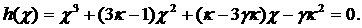 (12) (12)
Заметим, что уравнение (12) всегда
имеет хотя бы один положительный корень.
Определим,
при каких условиях максимальная степень устойчивости достигается на кратном
корне. Для этого перепишем уравнение (4) в виде
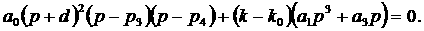
Здесь 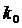 - значение - значение 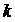 , соответствующее кратному корню. Если , соответствующее кратному корню. Если  и и 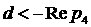 , то
при , то
при 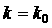 степень устойчивости
равна степень устойчивости
равна 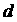 . Если сделать замену . Если сделать замену 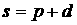 , то в получившемся уравнении коэффициент , то в получившемся уравнении коэффициент 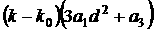 при при 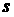 в первой степени, и
свободный член в первой степени, и
свободный член 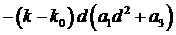 оказываются
противоположных знаков, т.е. нарушаются необходимые и достаточные условия
устойчивости. Таким образом, показано, что оказываются
противоположных знаков, т.е. нарушаются необходимые и достаточные условия
устойчивости. Таким образом, показано, что  достигается на кратном
корне, если достигается на кратном
корне, если 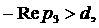 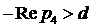 . .
При поиске области на
плоскости 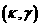 , где эти условия выполнены, удобно разделить всю допустимую
область изменения параметров , где эти условия выполнены, удобно разделить всю допустимую
область изменения параметров 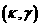 на две подобласти: в
одной уравнение (4) может иметь кратные
корни при трёх значениях параметра на две подобласти: в
одной уравнение (4) может иметь кратные
корни при трёх значениях параметра 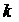 (т.е. (12) имеет три положительных корня), в другой –
только при одном значении (т.е. (12) имеет три положительных корня), в другой –
только при одном значении 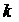 (т.е. (12) имеет один положительный корень); на границе,
разделяющей эти области, уравнение (12)
имеет два положительных корня.
Для нахождения границы необходимо разрешить систему двух уравнений – уравнения
(12) и уравнения (т.е. (12) имеет один положительный корень); на границе,
разделяющей эти области, уравнение (12)
имеет два положительных корня.
Для нахождения границы необходимо разрешить систему двух уравнений – уравнения
(12) и уравнения 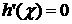 , имеющего вид , имеющего вид
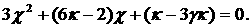 (13) (13)
Исключая из (12), (13) 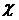 , получаем , получаем
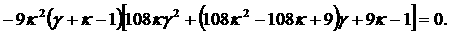 (14) (14)
В допустимой области 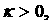 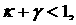 поэтому (14)
эквивалентно поэтому (14)
эквивалентно
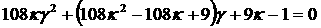 , ,
откуда
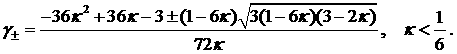 (15)
(15)
Заметим, что на кривых (15) кратные
корни (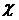 ) действительно положительны, поскольку коэффициент при ) действительно положительны, поскольку коэффициент при 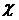 в уравнении (13)
отрицателен, а свободный член положителен. в уравнении (13)
отрицателен, а свободный член положителен.
Можно показать, что условие 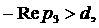 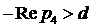 выполнено всюду в
области существования трёх положительных корней уравнения (12), включая её границы (рис. 5, область между кривыми выполнено всюду в
области существования трёх положительных корней уравнения (12), включая её границы (рис. 5, область между кривыми 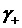 и и 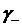 ), а также в области ), а также в области 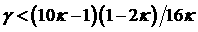 , где (12) имеет один положительный корень. На рис. 5 вертикальной штриховкой показана
вся область, где оптимум достигается на кратном корне, наклонной – где оптимум
достигается в случае двух пар комплексно сопряжённых корней с одинаковой
вещественной частью. Остается еще проанализировать случаи 3-х корней с
одинаковой вещественной частью и экстремума вида , где (12) имеет один положительный корень. На рис. 5 вертикальной штриховкой показана
вся область, где оптимум достигается на кратном корне, наклонной – где оптимум
достигается в случае двух пар комплексно сопряжённых корней с одинаковой
вещественной частью. Остается еще проанализировать случаи 3-х корней с
одинаковой вещественной частью и экстремума вида 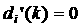 . .
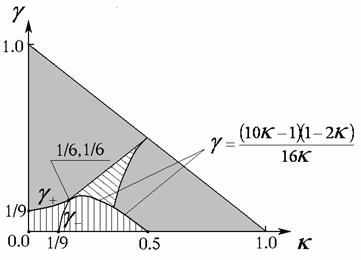
Рис. 5
3. Три корня с одинаковой
вещественной частью
Обозначим
корни характеристического уравнения 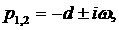 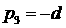 , , 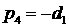 . Тогда уравнение (4) можно записать в виде . Тогда уравнение (4) можно записать в виде
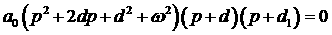 . .
Приравнивая коэффициенты при соответствующих степенях 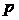 , получаем , получаем
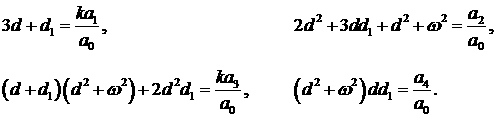
Вводя обозначение 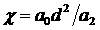 , после преобразований получаем , после преобразований получаем
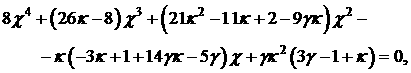 (16) (16)
а также
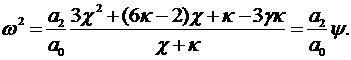 (17) (17)
Нас интересуют положительные корни
(16), для которых 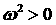 . Найдём сначала кривую, на которой . Найдём сначала кривую, на которой 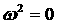 . Выразив из этого условия . Выразив из этого условия
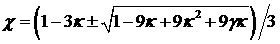
и подставив в (16), получим уравнение
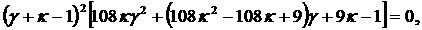
эквивалентное (14). Следовательно, 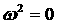 на кривых (15); на кривых (15); 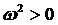 имеет место вне ограниченной
этими кривыми области, т.е. в области, где уравнение (4) имеет кратные вещественные
корни при одном значении имеет место вне ограниченной
этими кривыми области, т.е. в области, где уравнение (4) имеет кратные вещественные
корни при одном значении 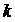 . .
Далее,
рассмотрим вопрос о числе положительных корней уравнения (16). Очевидно, (16)
имеет положительный корень при 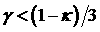 . При этом на самой прямой . При этом на самой прямой 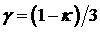 уравнение (16)
принимает вид уравнение (16)
принимает вид 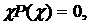 где где
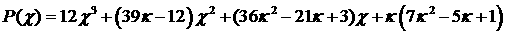 . .
Результаты численного
решения уравнения 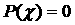 показывают, что
положительных корней в допустимой области не существует. Кроме того, можно
показать, что (16) не имеет кратных положительных корней в области, где показывают, что
положительных корней в допустимой области не существует. Кроме того, можно
показать, что (16) не имеет кратных положительных корней в области, где 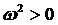 . Отсюда следует, что при . Отсюда следует, что при 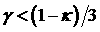 уравнение (16) имеет
положительный корень, и притом единственный, , а в оставшейся части области положительных
корней нет. Таким образом, рассматриваемая конфигурация корней возможна в
темно-серой области на рис. 6. уравнение (16) имеет
положительный корень, и притом единственный, , а в оставшейся части области положительных
корней нет. Таким образом, рассматриваемая конфигурация корней возможна в
темно-серой области на рис. 6.
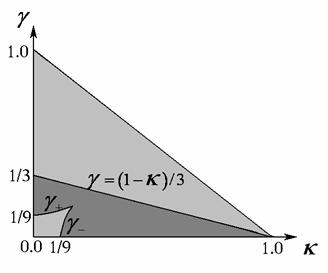
Рис. 6
Теперь
определим область, где данная конфигурация корней является оптимальной.
Перепишем уравнение (4) в виде
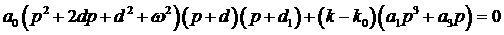 , ,
где 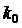 - значение - значение 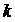 , соответствующее рассматриваемой конфигурации корней.
Условие , соответствующее рассматриваемой конфигурации корней.
Условие 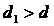 эквивалентно эквивалентно 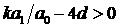 . Подставляя . Подставляя 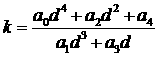 , преобразуем это
неравенство к виду , преобразуем это
неравенство к виду 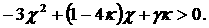 Исключая Исключая 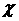 из из 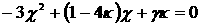 и (16), приходим к
соотношению и (16), приходим к
соотношению
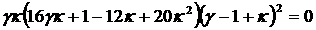 , ,
откуда
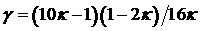 . .
Условие 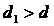 выполняется при выполняется при 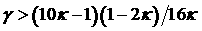 . .
Сделаем
замену 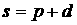 и выпишем необходимые
и достаточные условия устойчивости полученного в результате уравнения и выпишем необходимые
и достаточные условия устойчивости полученного в результате уравнения
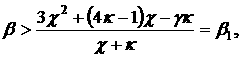 (18.1) (18.1)
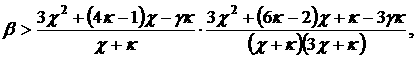 (18.2) (18.2)
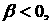 (18.3) (18.3)
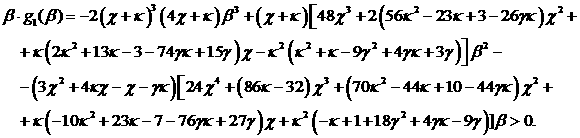 (18.4) (18.4)
Здесь введено обозначение 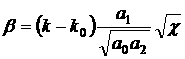 . .
С учётом 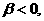 (18.4) эквивалентно (18.4) эквивалентно
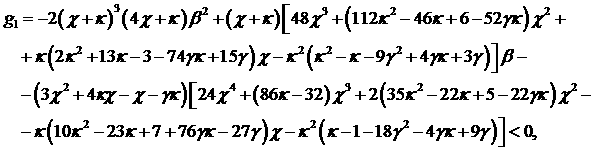 (18.5) (18.5)
где 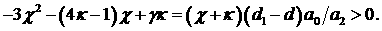 При этом При этом
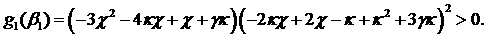
Поскольку график 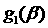 есть парабола, направленная
ветвями вниз, условия устойчивости несовместны тогда и только тогда, когда есть парабола, направленная
ветвями вниз, условия устойчивости несовместны тогда и только тогда, когда 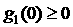 . Тем самым, для нахождения границы соответствующей области
нужно решать совместно (16) и уравнение . Тем самым, для нахождения границы соответствующей области
нужно решать совместно (16) и уравнение
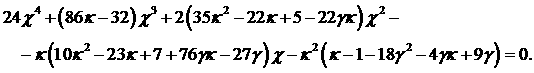 (19) (19)
Исключая 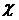 , приходим к уравнению , приходим к уравнению
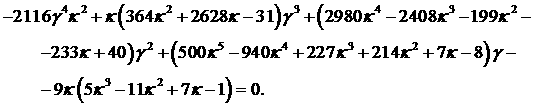
Его решения показаны на рис. 7
сплошными линиями (как и граница допустимой области); штриховыми линиями
показаны границы области существования исследуемой конфигурации корней, а также
кривая, где выполнено условие 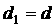 . .
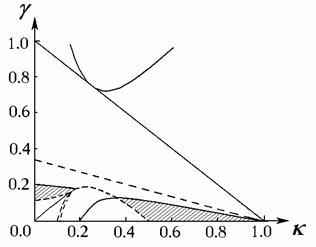 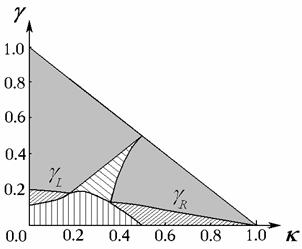
Рис. 7
Рис. 8
Область, в которой рассматриваемая
конфигурация корней является оптимальной, на рис. 7, 8 отмечена более плотной
наклонной штриховкой. Левая и правая части верхней границы этой области
обозначены 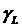 и и 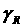 , соответственно. , соответственно.
4. Случай d’(k)=0
Предметом рассмотрения в данном
разделе вляются точки, в которых выполняется необходимое условие внутреннего
экстремума 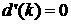 , где , где 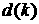 - действительная часть
орня уравнения (4), взятая с обратным знаком. Покажем сначала, что это условие
не может выполняться на вещественном корне - действительная часть
орня уравнения (4), взятая с обратным знаком. Покажем сначала, что это условие
не может выполняться на вещественном корне 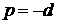 . .
Действительно,
для вещественного корня уравнения (4) имеет место
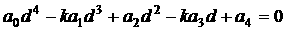 . (20) . (20)
Дифференцируя по 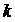 , получаем , получаем
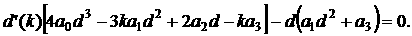
Таким образом, 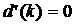 влечёт влечёт 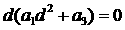 . Однако . Однако 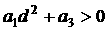 , а , а 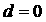 противоречит
предположению об устойчивости решения. противоречит
предположению об устойчивости решения.
Поэтому
далее будем рассматривать условие 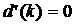 только для пары
комплексно сопряженных корней только для пары
комплексно сопряженных корней 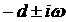 . Перепишем уравнение (4) в виде . Перепишем уравнение (4) в виде
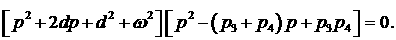
Приравнивая коэффициенты при соответствующих степенях 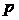 , получаем , получаем
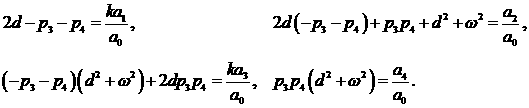 (21) (21)
Обозначим 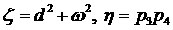 . Тогда из (21) находим . Тогда из (21) находим
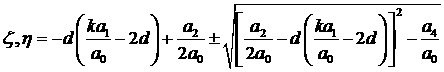 , ,
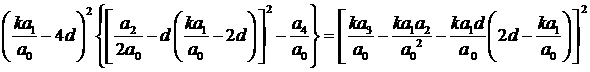 . .
Обозначая 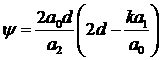 , получаем , получаем 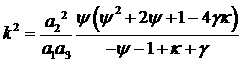 . .
Переменная  изменяется в интервале
от изменяется в интервале
от 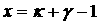 до 0; квадратичный сомножитель
в числителе обращается в нуль в точках до 0; квадратичный сомножитель
в числителе обращается в нуль в точках 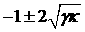 , лежащих вне этого интервала (поскольку , лежащих вне этого интервала (поскольку 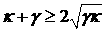 ); ); 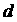 имеет вид имеет вид
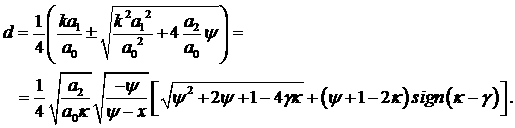 (22) (22)
Ответ на вопрос, почему
рассматриваются только зависимости 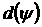 , соответствующие зависимостям , соответствующие зависимостям 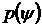 , остающимся комплексными при всех значениях , остающимся комплексными при всех значениях  (т.е (т.е 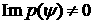 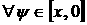 ; для таких ветвей выполнено условие ; для таких ветвей выполнено условие 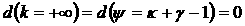 ), дают следующие два утверждения: ), дают следующие два утверждения:
Утверждение 1: Луч 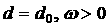 на комплексной
плоскости пересекает кривые на комплексной
плоскости пересекает кривые 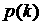 (решения (4)) не более трёх раз. (решения (4)) не более трёх раз.
Для
доказательства подставим в (4) 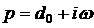 и выделим действительную
и мнимую части. Получим два уравнения: и выделим действительную
и мнимую части. Получим два уравнения:
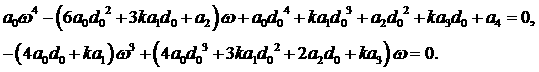
Из второго уравнения (с учётом 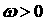 ) выражаем ) выражаем
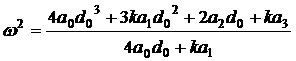
и подставляем в первое уравнение.
Обозначая 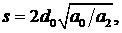 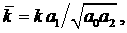 приходим к кубическому
по приходим к кубическому
по 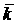 уравнению уравнению
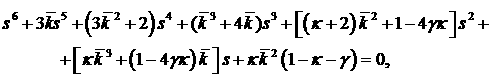
что и доказывает утверждение.
Утверждение 2: Если условие 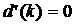 выполнено на ветви выполнено на ветви 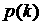 , содержащей кратный вещественный корень, то оптимум степени
устойчивости в этой точке не достигается. , содержащей кратный вещественный корень, то оптимум степени
устойчивости в этой точке не достигается.
Предположим,
что на ветви, содержащей кратный вещественный корень, 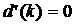 . Заметим, что достаточно ограничиться подобластью, где
конфигурация «кратный вещественный корень» достигается при единственном
значении . Заметим, что достаточно ограничиться подобластью, где
конфигурация «кратный вещественный корень» достигается при единственном
значении 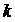 (в противном случае
оптимум всегда достигается на минимальном по модулю кратном корне, см. п. 2).
Для того, чтобы условие (в противном случае
оптимум всегда достигается на минимальном по модулю кратном корне, см. п. 2).
Для того, чтобы условие 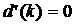 обеспечивало максимум
степени устойчивости, необходимо, чтобы, во-первых, обеспечивало максимум
степени устойчивости, необходимо, чтобы, во-первых, 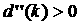 , а во-вторых, чтобы два остальных корня лежали левее этой
точки (они лежат на «чисто комплексных» ветвях, точка С в верхней полуплоскости и симметричная точка в нижней, рис.
9). , а во-вторых, чтобы два остальных корня лежали левее этой
точки (они лежат на «чисто комплексных» ветвях, точка С в верхней полуплоскости и симметричная точка в нижней, рис.
9).
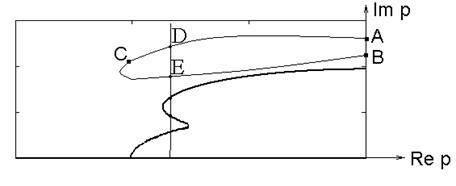
Рис. 9
Но тогда, очевидно, «чисто
комплексная» ветвь (начинающаяся в A и заканчивающаяся в B) пересекает луч 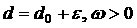 в двух точках (D и E); в результате будет по меньшей мере
4 пересечения, что противоречит Утверждению
1. в двух точках (D и E); в результате будет по меньшей мере
4 пересечения, что противоречит Утверждению
1.
Вернемся
к поиску экстремума. Поскольку 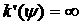 только при только при 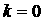 и и 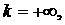 т.е. на границе
области определения, то условие т.е. на границе
области определения, то условие 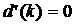 эквивалентно условию эквивалентно условию 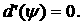 Последнее, в свою
очередь, сводится к уравнению Последнее, в свою
очередь, сводится к уравнению
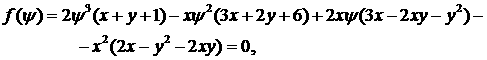 (23) (23)
где 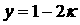 . Поскольку . Поскольку 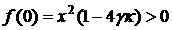 в допустимой области ( в допустимой области (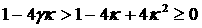 ), а ), а 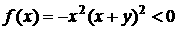 , то на допустимом интервале существует от одного до трех
экстремумов. В случае 3-х экстремумов рассматривается тот, для которого
соответствующее , то на допустимом интервале существует от одного до трех
экстремумов. В случае 3-х экстремумов рассматривается тот, для которого
соответствующее 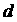 минимально; это правомерно,
поскольку, в силу Утверждения 2,
достаточно рассматривать «чисто комплексные» ветви; в силу Утверждения 1 они имеют единственный экстремум (в противном случае,
было бы по меньшей мере пять пересечений); в силу того же Утверждения 1, если экстремумов больше одного, то минимальный
находится на «чисто комплексной» ветви (в противном случае было бы пять пересечений). минимально; это правомерно,
поскольку, в силу Утверждения 2,
достаточно рассматривать «чисто комплексные» ветви; в силу Утверждения 1 они имеют единственный экстремум (в противном случае,
было бы по меньшей мере пять пересечений); в силу того же Утверждения 1, если экстремумов больше одного, то минимальный
находится на «чисто комплексной» ветви (в противном случае было бы пять пересечений).
Найдём
область оптимальности данной конфигурации. Представим (4) в виде
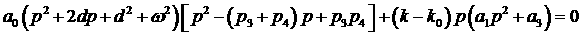 , ,
где 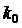 - значение - значение 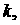 соответствующее
рассматриваемой конфигурации корней. Будем предполагать, что соответствующее
рассматриваемой конфигурации корней. Будем предполагать, что 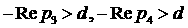 . Сделаем замену . Сделаем замену 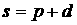 и выпишем два из
необходимых и достаточных условий устойчивости, а именно, условия и выпишем два из
необходимых и достаточных условий устойчивости, а именно, условия 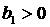 и и 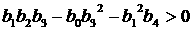 (здесь (здесь 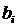 обозначают
коэффициенты полученного уравнения, обозначают
коэффициенты полученного уравнения, 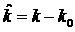 ). Имеем ). Имеем
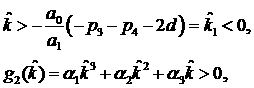 (24) (24)
где
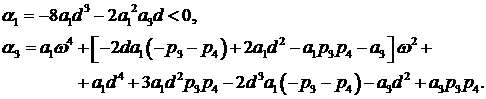 (25) (25)
При этом оказывается, что
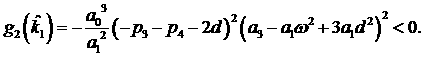
Кроме того, дифференцируя
выражения (21) по 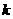 , исключая производные , исключая производные 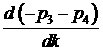 , , 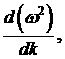 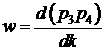 и учитывая, что и учитывая, что 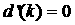 , получаем , получаем 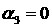 . .
Таким
образом, имеем
 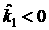 , , 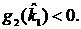
Это означает, что необходимые и
достаточные условия устойчивости несовместны (см. рис. 10).
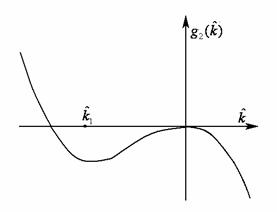
Рис. 10
Следовательно,
оптимум достигается в точке внутрннего экстремума только при 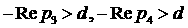 . При этом, на границах с областью, где оптимальной является
конфигурация «две пары комплексно сопряжённых корней с одинаковой вещественной
частью», имеет место . При этом, на границах с областью, где оптимальной является
конфигурация «две пары комплексно сопряжённых корней с одинаковой вещественной
частью», имеет место 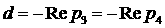 . На границах с областью, где оптимальной является
конфигурация «три корня с одинаковой вещественной частью», имеет место . На границах с областью, где оптимальной является
конфигурация «три корня с одинаковой вещественной частью», имеет место 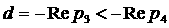 . Во всех точках внутри области . Во всех точках внутри области 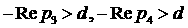 . .
5. Результаты первого этапа
оптимизации
Подводя
итог первого этапа оптимизации, сформулируем полученные результаты. Плоскость
параметров 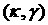 разбита на области, в
каждой из которых максимум степени устойчивости достигается на определенной
конфигурации корней (см. Таблицу, рис. 11). разбита на области, в
каждой из которых максимум степени устойчивости достигается на определенной
конфигурации корней (см. Таблицу, рис. 11).
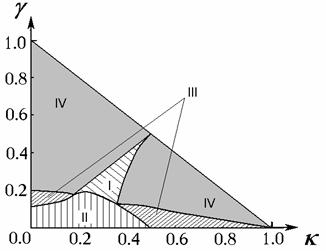
Рис. 11
Заметим, что в точках 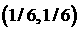 и и 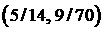 сходятся все типы областей.
В первом случае уравнение (4) имеет 4-х кратный вещественный корень, во втором
вещественные части кратного корня и экстремума сходятся все типы областей.
В первом случае уравнение (4) имеет 4-х кратный вещественный корень, во втором
вещественные части кратного корня и экстремума 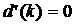 совпадают. совпадают.
Поскольку оптимальное
значение степени устойчивости всегда можно представить в виде 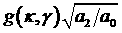 , интересно рассмотреть зависимости от , интересно рассмотреть зависимости от 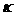 степени
устойчивости при фиксированном значении степени
устойчивости при фиксированном значении 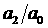 (положим его равным 1)
и нескольких фиксированных значениях (положим его равным 1)
и нескольких фиксированных значениях 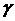 (рис. 12). (рис. 12).
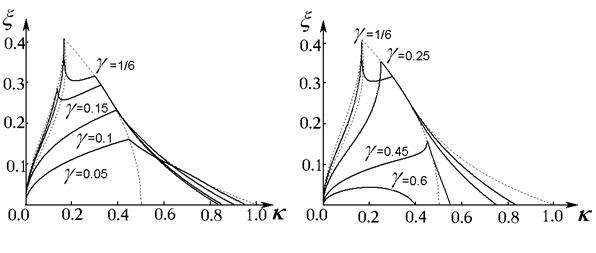
Рис. 12
Таблица
|
|
область
|
конфигурация
корней
|
|
I
|
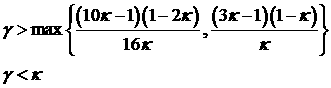
|
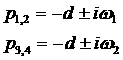
|
|
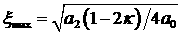 ; ; 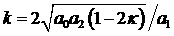
|
|
II
|
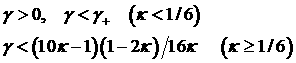
|
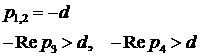
|
|
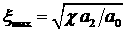 , где , где 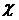 - минимальный
положительный корень уравнения - минимальный
положительный корень уравнения 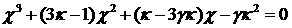 ; ; 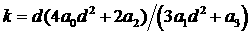
|
|
III
|
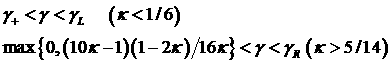
|
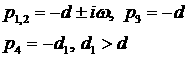
|
|
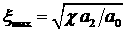 , где , где 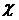 - положительный
корень уравнения - положительный
корень уравнения
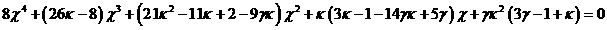
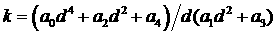
|
|
IV
|
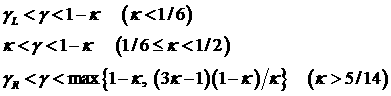
|
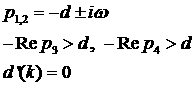
|
|
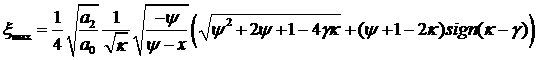 , ,
где  - корень уравнения - корень уравнения
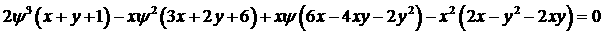 , ,
лежащий в интервале 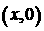 , , 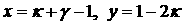 ; ;
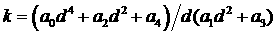
|
На рис. 12 штриховыми линиями
показаны образы границ областей I-IV (видно, что некоторые из них являются «огибающими» графиков 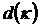 ; на некоторых происходит разрыв производной). Максимальное
значение степени устойчивости достигается при ; на некоторых происходит разрыв производной). Максимальное
значение степени устойчивости достигается при 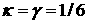 и, согласно (9),
составляет и, согласно (9),
составляет 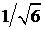 . Приведём также пример зависимости оптимального коэффициента
демпфирования от . Приведём также пример зависимости оптимального коэффициента
демпфирования от  при фиксированном при фиксированном 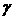 (на рис. 13, где (на рис. 13, где 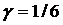 , штриховой линией обозначен образ области I). , штриховой линией обозначен образ области I).
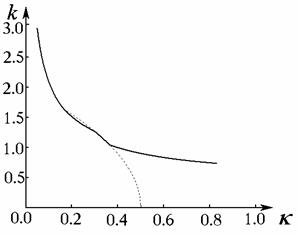
Рис. 13
Второй этап
оптимизации
На
втором этапе определим оптимальные значения всех параметров системы спутник-стабилизатор
(рассматривается равновесие, в котором спутник и стабилизатор ориентированы
вдоль касательной к орбите; шарнир совпадает с центром масс каждого из тел). В
случае, когда отсутствует упругая связь в шарнире, линеаризованные уравнения,
определяющие малые колебания системы спутник-стабилизатор в плоскости круговой
орбиты, имеют вид
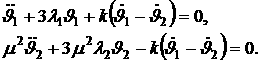 (26) (26)
Здесь
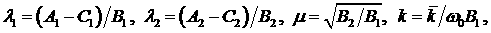 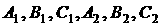 - главные центральные
моменты инерции спутника и стабилизатора, - главные центральные
моменты инерции спутника и стабилизатора, 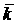 - коэффициент
демпфирования, - коэффициент
демпфирования,  - угловая скорость
движения центра масс системы по орбите, - угловая скорость
движения центра масс системы по орбите, 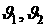 - углы тангажа,
определяющие ориентацию спутника и стабилизатора в орбитальной системе
координат; точкой обозначено дифференцирование по истинной аномалии. Характеристическое
уравнение системы (26) имеет вид (4), где - углы тангажа,
определяющие ориентацию спутника и стабилизатора в орбитальной системе
координат; точкой обозначено дифференцирование по истинной аномалии. Характеристическое
уравнение системы (26) имеет вид (4), где
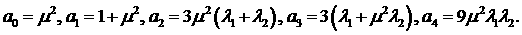 (27) (27)
Вместо использовавшихся выше
параметров 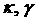 удобно перейти к таким
параметрам удобно перейти к таким
параметрам 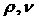 , что , что 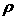 зависит только от зависит только от 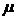 , а , а 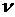 - только от - только от 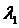 и и 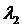 . Например, ведем параметры . Например, ведем параметры
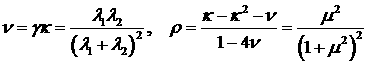 . (28) . (28)
На плоскости 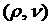 допустимая область
представляет собой квадрат допустимая область
представляет собой квадрат 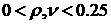 ; при этом каждой точке области соответствуют две точки области
на плоскости ; при этом каждой точке области соответствуют две точки области
на плоскости 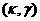 , абсциссы которых симметричны относительно 0.5. , абсциссы которых симметричны относительно 0.5.
Заметим,
что все полученные выше формулы для оптимальной степени устойчивости
представимы в виде
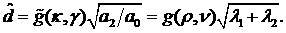
При этом величина 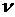 определяется лишь
отношением определяется лишь
отношением 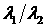 . Поэтому очевидно, что максимум степени устойчивости
достигается в точке . Поэтому очевидно, что максимум степени устойчивости
достигается в точке 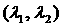 на границе допустимой
области на границе допустимой
области 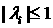 , т.е. либо , т.е. либо 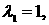 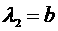 , либо , либо 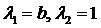 ( (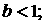 выражение для выражение для 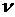 симметрично относительно симметрично относительно
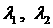 ). Физически это означает, что одно из тел вырождается в
пластину. При таких ). Физически это означает, что одно из тел вырождается в
пластину. При таких 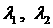 имеем имеем
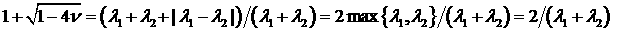 , ,
откуда 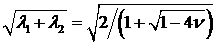 и, следовательно, и, следовательно,
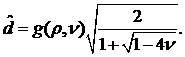 (29) (29)
Анализ выражения (29) удобно провести
лишь для случая двух пар комплексно сопряжённых корней с одинаковой
вещественной частью (заштрихованная область на рис. 14). В этом случае 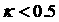 , и соответствие этой области с областью на плоскости , и соответствие этой области с областью на плоскости 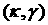 является взаимно
однозначным. является взаимно
однозначным.
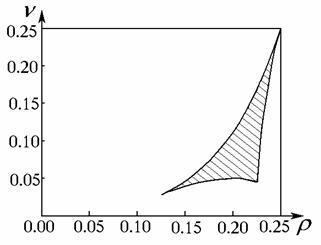
Рис. 14
В рассматриваемом случае формула (29) принимает вид
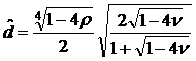 , ,
т.е.  монотонно убывающая
функция монотонно убывающая
функция 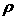 и и 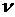 . Следовательно, максимум достигается на границе в точке . Следовательно, максимум достигается на границе в точке 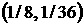 , которой в пространстве , которой в пространстве 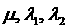 соответствует два
набора оптимальных параметров соответствует два
набора оптимальных параметров
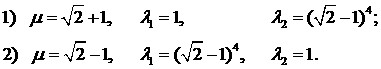
В первом случае оптимальное значение 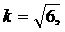 во втором во втором 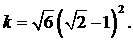 Степень устойчивости в
обоих случаях Степень устойчивости в
обоих случаях 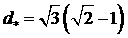 , при этом характеристическое уравнение имеет 4-х кратный
корень. , при этом характеристическое уравнение имеет 4-х кратный
корень.
Докажем,
что 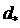 является глобальным
максимумом степени устойчивости. Подставляя в (4) является глобальным
максимумом степени устойчивости. Подставляя в (4) 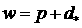 , получим , получим
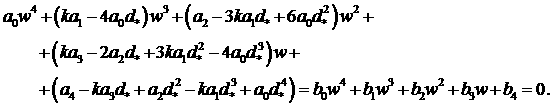 (30) (30)
Введём обозначения
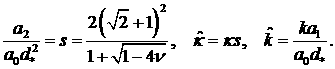 (31) (31)
Тогда необходимые и достаточные
условия устойчивости принимают вид
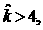 (32.1)
(32.1)
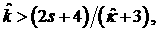 (32.2)
(32.2)
 (32.3) (32.3)
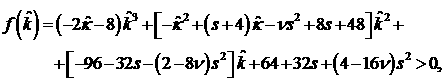 (32.4)
(32.4)
откуда, в частности, следует
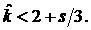 (32.5)
(32.5)
Сравнивая (32.1) и (32.5), получаем 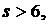 откуда откуда 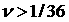 . Заметим далее, что . Заметим далее, что
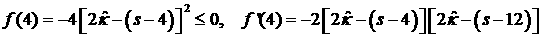 , (33) , (33)
т.е., при 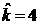 многочлен из условия
(32.4) отрицателен за исключением случая, когда многочлен из условия
(32.4) отрицателен за исключением случая, когда 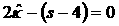 . Построим соответствующую кривую на плоскости . Построим соответствующую кривую на плоскости 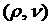 совместно с линией совместно с линией 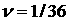 (рис. 15). (рис. 15).
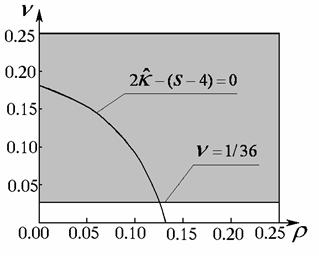
Рис. 15
Заметим, что кривая 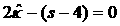 соответствует «листу»,
где соответствует «листу»,
где 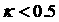 (поскольку из (поскольку из 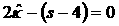 следует следует 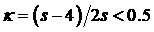 ). Правее этой кривой на данном листе, а также на всём листе,
где ). Правее этой кривой на данном листе, а также на всём листе,
где 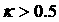 , как следует из (33), , как следует из (33), 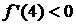 , поскольку при , поскольку при 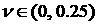 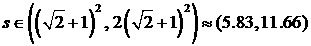 . Далее, график функции . Далее, график функции
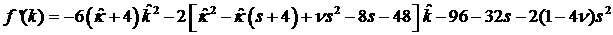
есть парабола, направленная ветвями
вниз.
Несложно показать, что
всюду в допустимой области точка 4 лежит правее вершины параболы, т.е.
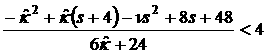 . (34) . (34)
Из (34) следует, что даже при наличии у
функции 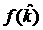 экстремумов точка экстремумов точка 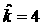 лежит в этом случае
правее них, а поэтому лежит в этом случае
правее них, а поэтому 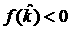 не только при не только при 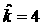 , но и при , но и при 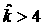 . Таким образом, показана несовместность условий (32). . Таким образом, показана несовместность условий (32).
Рассмотрим теперь область 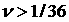 , лежащую левее кривой , лежащую левее кривой 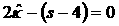 на листе на листе 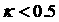 . В этой области . В этой области 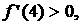 но, по-прежнему, но, по-прежнему, 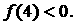 Поскольку, очевидно, Поскольку, очевидно, 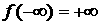 и и 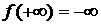 , то ситуация, когда , то ситуация, когда  в каких-то точках
правее в каких-то точках
правее 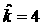 , возможна только,
если уравнение , возможна только,
если уравнение 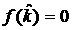 имеет более одного
корня. Найдём область, на плоскости имеет более одного
корня. Найдём область, на плоскости 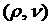 , в которой это имеет место. Для нахождения её границ решаем
совместно уравнения , в которой это имеет место. Для нахождения её границ решаем
совместно уравнения 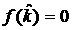 и и 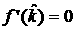 , что приводит к уравнению 4-го порядка, которое ввиду его
громоздкости здесь не приводится. Решая его численно, получаем область существования
3-х корней (на рис. 16 заштрихована). , что приводит к уравнению 4-го порядка, которое ввиду его
громоздкости здесь не приводится. Решая его численно, получаем область существования
3-х корней (на рис. 16 заштрихована).
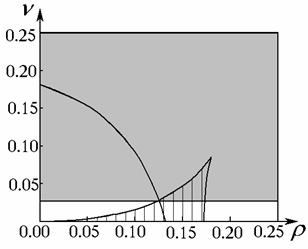
Рис. 16
Граница
полученной области проходит непосредственно через точку (1/8,1/36). Таким
образом, область левее кривой 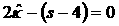 (и (и 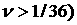 и область 3-х корней
не пересекаются. Поэтому из и область 3-х корней
не пересекаются. Поэтому из 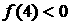 следует, что и при следует, что и при 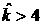 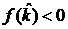 , т.е. и в этом случае условия (32) несовместны. , т.е. и в этом случае условия (32) несовместны.
Наконец, рассмотрим точки, лежащие
непосредственно на кривой 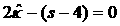 . Из проведенного выше анализа следует, что хотя теперь . Из проведенного выше анализа следует, что хотя теперь 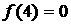 , но всюду правее , но всюду правее 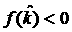 , и снова условия (32) несовместны. Тем самым, показано, что всюду в
допустимой области изменения параметров , и снова условия (32) несовместны. Тем самым, показано, что всюду в
допустимой области изменения параметров 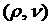 необходимые и
достаточные условия устойчивости уравнения (30) не выполнены, т.е. оно имеет
корни в правой полуплоскости. Это означает, что оптимум действительно
достигается в точке необходимые и
достаточные условия устойчивости уравнения (30) не выполнены, т.е. оно имеет
корни в правой полуплоскости. Это означает, что оптимум действительно
достигается в точке 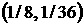 . При этом максимальная степень устойчивости . При этом максимальная степень устойчивости 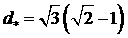 достигается при
следующих значениях параметров: достигается при
следующих значениях параметров:
1) 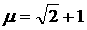 , , 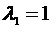 , , 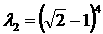 , ,  ; ;
2) 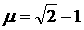 , , 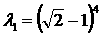 , , 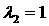 , ,  . .
Заключение
В настоящей работе
проведена оптимизация по 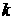 степени устойчивости
для характеристического уравнения вида (4). Установлено, что максимальное
значение степени устойчивости может достигаться на одной из четырёх конфигураций
корней. В пространстве безразмерных параметров системы определены
соответствующие области, для каждой из которых получены выражения, определяющие
максимальную величину степени устойчивости и оптимальное значение степени устойчивости
для характеристического уравнения вида (4). Установлено, что максимальное
значение степени устойчивости может достигаться на одной из четырёх конфигураций
корней. В пространстве безразмерных параметров системы определены
соответствующие области, для каждой из которых получены выражения, определяющие
максимальную величину степени устойчивости и оптимальное значение 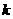 . .
Для частного случая
системы спутник-стабилизатор (шарнир совпадает с центрами масс спутника и
стабилизатора) определены оптимальные параметры, при которых собственные
колебания системы в плоскости круговой орбиты затухают максимально быстро.
Строго доказано, что в точке оптимума характеристическое уравнение имеет 4-х
кратный вещественный корень. При этом одно из тел вырождается в пластину.
Литература
1. Сарычев В.А. Вопросы ориентации
искусственных спутников, Итоги науки и техники. Серия “Исследование
космического пространства”. ВИНИТИ, т.11, 1978.
2. Мирер С.А. Оптимальное
гиродемпфирование нутационных колебаний спутника, стабилизируемого вращением.
Космич. исследования, т. 15, 1977, №5, с. 677-682.
3. Цыпкин Я.З., Бромберг П.В. О степени
устойчивости линейных систем. Изв. АН СССР, ОТН, 1945, №12, с. 1163-1168.
4. Сарычев В.А., Пеньков В.И., Яковлев
Н.И. Оптимизация параметров линейных систем. Препринт Института прикладной
математики им. М.В. Келдыша РАН, 1975, №124.
5. Сарычев В.А., Пеньков В.И.
Исследование гравитационной системы стабилизации спутника с демпфирующей
пружиной. Препринт Института прикладной математики им. М.В. Келдыша РАН, 1974,
№127.
6. Яковлев Н.И. Оптимизация по
быстродействию параметров гравитационных систем ориентации с двумя демпферами.
Препринт Института прикладной математики им. М.В. Келдыша РАН, 1976, №56.
7. Мирер С.А., Сарычев В.А. Оптимальные
параметры спутника, стабилизируемого вращением, с демпфером маятникового типа.
Космич. исследования, т. 35, 1997, № 6, с. 651-658.
8. Сарычев В.А., Сазонов В.В.
Оптимальные параметры пассивных систем ориентации спутников. Космич.
исследования, т. 14, 1976, №2, 1976, с. 198-208.
9. Сидорюк М.Е. К задаче нахождения
максимума степени устойчивости. Препринт Института прикладной математики им.
М.В. Келдыша РАН, 1981, №89.
10.
Sarychev V.A., Mirer S.A., Sazonov
V.V. Plane oscillations of a gravitational system satellite-stabilizer with
maximal speed of response. Acta Astronautica, vol.3, 1976, No.9-10, p. 651-669.
11.
Мирер С.А. Плоские колебания спутника с двумя гироскопами. Космич. исследования, т. 16, 1978, № 1, с. 137-139.
12.
Sarychev V.A., Mirer S.A., Isakov A.V. Dual-Spin Satellites with Gyro-Damping, Acta Astronautica, 1982, Vol. 9, №5, p. 285-289.
|
![]() ; на некоторых происходит разрыв производной). Максимальное
значение степени устойчивости достигается при
; на некоторых происходит разрыв производной). Максимальное
значение степени устойчивости достигается при ![]() и, согласно (9),
составляет
и, согласно (9),
составляет ![]() . Приведём также пример зависимости оптимального коэффициента
демпфирования от
. Приведём также пример зависимости оптимального коэффициента
демпфирования от ![]() при фиксированном
при фиксированном ![]() (на рис. 13, где
(на рис. 13, где ![]() , штриховой линией обозначен образ области I).
, штриховой линией обозначен образ области I). 
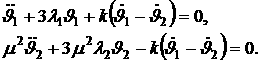 (26)
(26)![]()
![]() - главные центральные
моменты инерции спутника и стабилизатора,
- главные центральные
моменты инерции спутника и стабилизатора, ![]() - коэффициент
демпфирования,
- коэффициент
демпфирования, ![]() - угловая скорость
движения центра масс системы по орбите,
- угловая скорость
движения центра масс системы по орбите, ![]() - углы тангажа,
определяющие ориентацию спутника и стабилизатора в орбитальной системе
координат; точкой обозначено дифференцирование по истинной аномалии. Характеристическое
уравнение системы (26) имеет вид (4), где
- углы тангажа,
определяющие ориентацию спутника и стабилизатора в орбитальной системе
координат; точкой обозначено дифференцирование по истинной аномалии. Характеристическое
уравнение системы (26) имеет вид (4), где![]() (27)
(27)![]() удобно перейти к таким
параметрам
удобно перейти к таким
параметрам ![]() , что
, что ![]() зависит только от
зависит только от ![]() , а
, а ![]() - только от
- только от ![]() и
и ![]() . Например, ведем параметры
. Например, ведем параметры 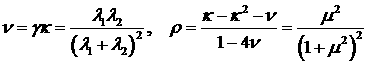 . (28)
. (28)![]() допустимая область
представляет собой квадрат
допустимая область
представляет собой квадрат ![]() ; при этом каждой точке области соответствуют две точки области
на плоскости
; при этом каждой точке области соответствуют две точки области
на плоскости ![]() , абсциссы которых симметричны относительно 0.5.
, абсциссы которых симметричны относительно 0.5.![]()
![]() определяется лишь
отношением
определяется лишь
отношением ![]() . Поэтому очевидно, что максимум степени устойчивости
достигается в точке
. Поэтому очевидно, что максимум степени устойчивости
достигается в точке ![]() на границе допустимой
области
на границе допустимой
области ![]() , т.е. либо
, т.е. либо ![]()
![]() , либо
, либо ![]() (
(![]() выражение для
выражение для ![]() симметрично относительно
симметрично относительно
![]() ). Физически это означает, что одно из тел вырождается в
пластину. При таких
). Физически это означает, что одно из тел вырождается в
пластину. При таких ![]() имеем
имеем![]() ,
,![]() и, следовательно,
и, следовательно, 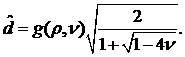 (29)
(29)![]() , и соответствие этой области с областью на плоскости
, и соответствие этой области с областью на плоскости ![]() является взаимно
однозначным.
является взаимно
однозначным.
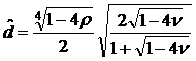 ,
, ![]() монотонно убывающая
функция
монотонно убывающая
функция ![]() и
и ![]() . Следовательно, максимум достигается на границе в точке
. Следовательно, максимум достигается на границе в точке ![]() , которой в пространстве
, которой в пространстве ![]() соответствует два
набора оптимальных параметров
соответствует два
набора оптимальных параметров 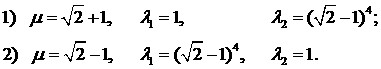
![]() во втором
во втором ![]() Степень устойчивости в
обоих случаях
Степень устойчивости в
обоих случаях ![]() , при этом характеристическое уравнение имеет 4-х кратный
корень.
, при этом характеристическое уравнение имеет 4-х кратный
корень.![]() является глобальным
максимумом степени устойчивости. Подставляя в (4)
является глобальным
максимумом степени устойчивости. Подставляя в (4) ![]() , получим
, получим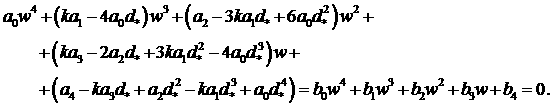 (30)
(30)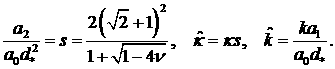 (31)
(31)![]() (32.1)
(32.1)![]() (32.2)
(32.2)![]() (32.3)
(32.3)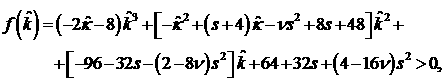 (32.4)
(32.4)![]() (32.5)
(32.5)![]() откуда
откуда ![]() . Заметим далее, что
. Заметим далее, что ![]() , (33)
, (33)![]() многочлен из условия
(32.4) отрицателен за исключением случая, когда
многочлен из условия
(32.4) отрицателен за исключением случая, когда ![]() . Построим соответствующую кривую на плоскости
. Построим соответствующую кривую на плоскости ![]() совместно с линией
совместно с линией ![]() (рис. 15).
(рис. 15).
![]() соответствует «листу»,
где
соответствует «листу»,
где ![]() (поскольку из
(поскольку из ![]() следует
следует ![]() ). Правее этой кривой на данном листе, а также на всём листе,
где
). Правее этой кривой на данном листе, а также на всём листе,
где ![]() , как следует из (33),
, как следует из (33), ![]() , поскольку при
, поскольку при ![]()
![]() . Далее, график функции
. Далее, график функции ![]()
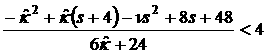 . (34)
. (34)![]() экстремумов точка
экстремумов точка ![]() лежит в этом случае
правее них, а поэтому
лежит в этом случае
правее них, а поэтому ![]() не только при
не только при ![]() , но и при
, но и при ![]() . Таким образом, показана несовместность условий (32).
. Таким образом, показана несовместность условий (32).![]() , лежащую левее кривой
, лежащую левее кривой ![]() на листе
на листе ![]() . В этой области
. В этой области ![]() но, по-прежнему,
но, по-прежнему, ![]() Поскольку, очевидно,
Поскольку, очевидно, ![]() и
и ![]() , то ситуация, когда
, то ситуация, когда ![]() в каких-то точках
правее
в каких-то точках
правее ![]() , возможна только,
если уравнение
, возможна только,
если уравнение ![]() имеет более одного
корня. Найдём область, на плоскости
имеет более одного
корня. Найдём область, на плоскости ![]() , в которой это имеет место. Для нахождения её границ решаем
совместно уравнения
, в которой это имеет место. Для нахождения её границ решаем
совместно уравнения ![]() и
и ![]() , что приводит к уравнению 4-го порядка, которое ввиду его
громоздкости здесь не приводится. Решая его численно, получаем область существования
3-х корней (на рис. 16 заштрихована).
, что приводит к уравнению 4-го порядка, которое ввиду его
громоздкости здесь не приводится. Решая его численно, получаем область существования
3-х корней (на рис. 16 заштрихована).
![]() (и
(и ![]() и область 3-х корней
не пересекаются. Поэтому из
и область 3-х корней
не пересекаются. Поэтому из ![]() следует, что и при
следует, что и при ![]()
![]() , т.е. и в этом случае условия (32) несовместны.
, т.е. и в этом случае условия (32) несовместны.![]() . Из проведенного выше анализа следует, что хотя теперь
. Из проведенного выше анализа следует, что хотя теперь ![]() , но всюду правее
, но всюду правее ![]() , и снова условия (32) несовместны. Тем самым, показано, что всюду в
допустимой области изменения параметров
, и снова условия (32) несовместны. Тем самым, показано, что всюду в
допустимой области изменения параметров ![]() необходимые и
достаточные условия устойчивости уравнения (30) не выполнены, т.е. оно имеет
корни в правой полуплоскости. Это означает, что оптимум действительно
достигается в точке
необходимые и
достаточные условия устойчивости уравнения (30) не выполнены, т.е. оно имеет
корни в правой полуплоскости. Это означает, что оптимум действительно
достигается в точке ![]() . При этом максимальная степень устойчивости
. При этом максимальная степень устойчивости ![]() достигается при
следующих значениях параметров:
достигается при
следующих значениях параметров: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;
;![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.![]() степени устойчивости
для характеристического уравнения вида (4). Установлено, что максимальное
значение степени устойчивости может достигаться на одной из четырёх конфигураций
корней. В пространстве безразмерных параметров системы определены
соответствующие области, для каждой из которых получены выражения, определяющие
максимальную величину степени устойчивости и оптимальное значение
степени устойчивости
для характеристического уравнения вида (4). Установлено, что максимальное
значение степени устойчивости может достигаться на одной из четырёх конфигураций
корней. В пространстве безразмерных параметров системы определены
соответствующие области, для каждой из которых получены выражения, определяющие
максимальную величину степени устойчивости и оптимальное значение ![]() .
. 
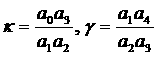 . Тогда, в соответствии с (5),
. Тогда, в соответствии с (5), 
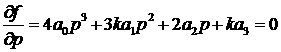 ,
, 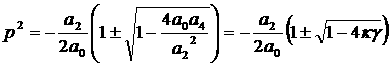 .
.
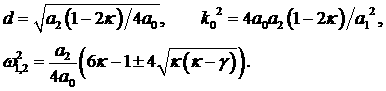

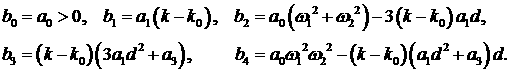
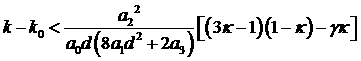 .
.
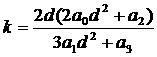
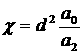 , преобразуем (4) к виду
, преобразуем (4) к виду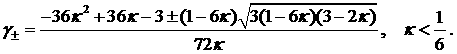

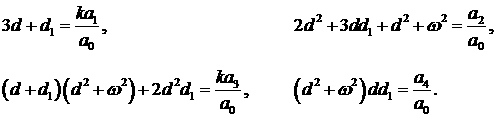
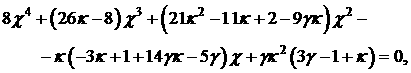
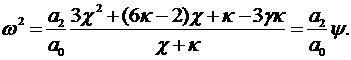

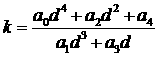 ,
,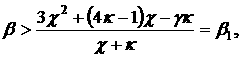
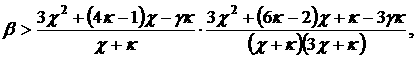
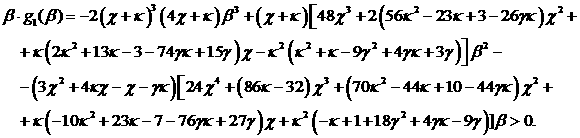
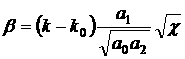 .
.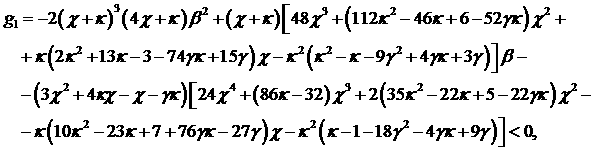 (18.5)
(18.5)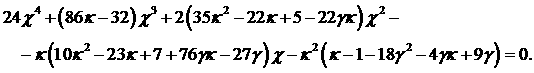
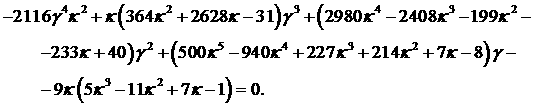


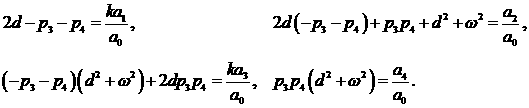
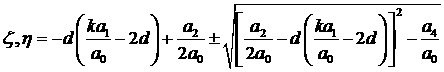 ,
,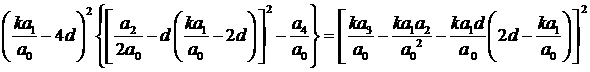 .
.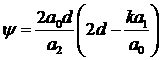 , получаем
, получаем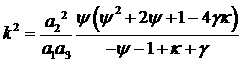 .
.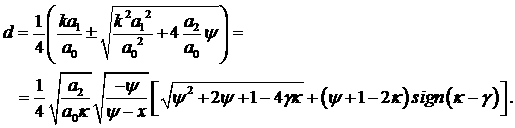
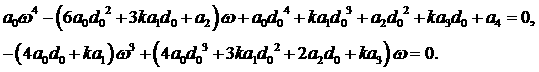
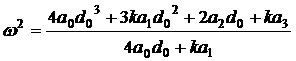
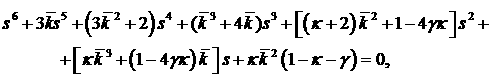

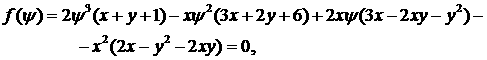
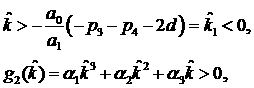
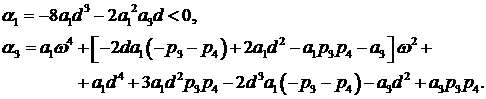
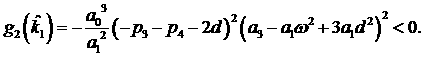
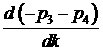 ,
, 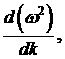
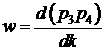



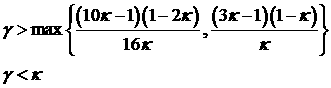
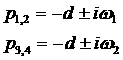
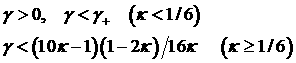
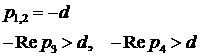
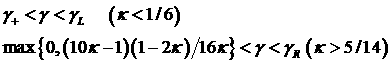
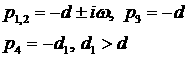
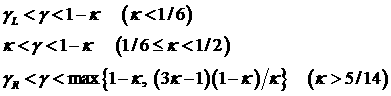
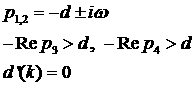
 ,
,