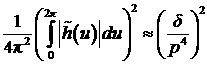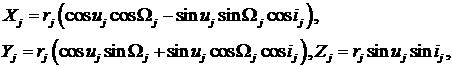Аннотация
Разработан алгоритм управления для устранения вековых уходов, возникающих из-за малых возмущений, в частности сжатия Земли
в относительном движении спутников, образующих конфигурацию Formation Flying. По предположению оскулирующая орбита главного
спутника – круговая, главный спутник не управляется. Дочерний спутник снабжен пассивной магнитной системой ориентации и
двигателем малой тяги, расположенным вдоль оси ориентации. Проведено исследование возможности устранения относительных
вековых уходов спутников при использовании управления с ограничением на величину и направление. Аналитически построено управление,
обеспечивающее устранение относительного векового смещения при движении по орбите. Аналитические результаты подтверждены численным
моделированием на примере орбиты первого российского технологического наноспутника ТНС-0 N1.
Abstract
The preprint is devoted to control algorithm development to nullify a relative secular drift due to the Earth oblateness in
Formation Flight motion. It is assumed a chief satellite orbit to be circular and its orbit not to be controlled to maintain the formation.
Deputy satellite is equipped with a passive magnetic attitude control system with permanent magnet alongwith the principal
inertia axis and low-propulsion thruster alongwith the same direction. The investigation how to eliminate the relative secular
drift by a limited control is carried out. The limitation consists in a constraint of direction and magnitude of feasible control.
In the present work the control to eliminate the relative secular drift is analytically developed. Analytical results are approved
by numerical simulation of the satellite motion like the first Russian nanosatellite TNS-0 N1.
1. Введение
Известно, что в отсутствие
внешних возмущений при определенных начальных условиях для формации спутников
существуют периодические траектории дочернего спутника относительно главного,
движущегося по круговой траектории, даже в отсутствие управления. Это следует
из уравнений Хилла, которые получаются путем линеаризации уравнений Ньютона при
движении спутников в центральном поле тяжести [1].
Реальное гравитационное поле
Земли не является центральным. Приближенная модель гравитационного поля Земли представляет
собой разложение в ряд по полиномам Лежандра, где первый член разложения
отвечает центральному ньютонову полю, а если предположить, что распределение
массы Земли симметричное, то следующим существенно ненулевым членом разложения
является гармоника J2 [2]. При этом, гармоника J2 в 1000
раз меньше, чем первая гармоника разложения, поэтому влияние сжатия Земли на
движение в гравитационное поле Земли можно рассматривать как возмущение.
Анализ влияния гармоники J2
на формацию спутников является весьма популярной темой исследования. Например,
в [3] исследуется влияние возмущения от сжатия Земли на ограниченное движение
формации спутников и показывается, что гармонику J2 при анализе движения
необходимо учитывать. В [4] проводится исследование модифицированных уравнений
Хилла, включающих в себя J2, а в [5] учитывается и сопротивление
атмосферы. В [6] и [7] предлагаются законы управления, необходимые для
поддержания формаций, при этом в [7] минимизируется затрачиваемое на
маневрирование топливо. Во всех указанных работах предполагается, что вектор
тяги может быть направлен произвольно в пространстве, то есть управление
трехосное. В [8] введено ограничение на направление возможного вектора тяги.
Для управления используется двигатель с вектором тяги в направлении «вдоль
касательной к траектории». При этом проводится исследование возможности
поддержания ограниченного относительного движения для невозмущенной задачи
Хилла в случае ошибок в начальных условиях, а также в зависимости от размера
формации, от эллиптичности траектории главного спутника и т.д. Возможность
применения одноосного в связанных со спутником осях управления для поддержания
необходимой конфигурации рассмотрена также в [9], где проведено построение
множества возможных траекторий при управлении вдоль одной оси для невозмущенной
задачи Хилла. В [10] приведен пример использования малой тяги для поддержания
заданной конфигурации.
В настоящей работе проведено
исследование возможности устранения относительного векового ухода двух
спутников при ограниченном управлении. Относительное движение рассматривается в
системе главный и дочерний спутники, начало координат связано с главным
спутником. Под главным спутником понимается неуправляемый спутник, а под
дочерним – спутник с двигателем. В качестве одного из основных требований к
системе управления выставляется простота ее исполнения.
Считается, что оба спутника
движутся в центральном ньютоновом поле. Отличие гравитационного поля от
центрального, например, из-за сжатия Земли рассматривается как возмущение, приводящее
к изменению орбит обоих спутников. Орбита главного спутника в начальный момент
времени - круговая.
В качестве системы
ориентации для маневрирующего дочернего спутника используется пассивная
магнитная система ориентации, которая не требует расхода рабочего тела и
энергии бортовых батарей и работает за счет стабилизирующего воздействия
момента внешних сил со стороны геомагнитного поля. Известно, что при
использовании такой системы ориентации спутник в каждой точке своей траектории
будет ориентирован практически по вектору напряженности магнитного поля Земли.
Для управления орбитальным движением дочернего спутника будем использовать
двигатель, развивающий тягу вдоль его оси ориентации, которая совпадает с одной
из его главных осей инерции спутника. Преимущество такой системы управления
заключается в том, при использовании двигателя вдоль оси ориентации спутника не
нужно заботиться об обеспечении ориентации вектора управления, так как в каждой
точке орбиты вектор управления будет направлен вдоль вектора напряженности
магнитного поля Земли.
Примером системы, в которой
для управления ориентации используется магнит, расположенный вдоль оси
симметрии, является первый российский наноспутник ТНС-0 №1 (рис.1) [11]. Постоянный магнит с
дипольным моментом 2.2 A·м2 ориентирует спутник вдоль местного вектора
напряженности поля Земли. Спутник был успешно выведен на почти круговую орбиту
вручную российским космонавтом с борта Международной космической станции 28-го
марта 2005 года. Параметры орбиты следующие: высота 350 км, наклонение 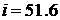 °, эксцентриситет °, эксцентриситет 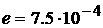 . Масса спутника составляет около 4.5 кг [12]. . Масса спутника составляет около 4.5 кг [12].
Попытка реализации системы орбитального маневрирования
для спутника, ориентированного по магнитному полю Земли, на базе одноосной
корректирующей двигательной установкой “Пульсар” была сделана в конце 1989 года
на микроспутнике Magion-2, запущенным на борту основного спутника
Интеркосмос-24, для проведения комплексных исследований процессов
распространения электромагнитных волн низкочастотного диапазона в магнитосфере
Земли и их взаимодействия с заряженными частицами радиационных поясов.
Выполнение научной программы проекта «Активный» с помощью этих двух спутников
позволило бы одновременно проводить пространственно разнесенные исследования
плазменных процессов в околоземном космическом пространстве. Фактически
планировались эксперименты с использованием конфигурации Formation Flying.
Однако возникли проблемы с двигательной установкой на микроспутнике. Из-за
этого через три месяца после старта, по состоянию на 01 января 1990 года
расстояние между спутниками вместо положенных 10 км, составляло уже 4000 км. К
августу 1990 года аппараты вообще разошлись на противоположные стороны орбиты
[13, 14].

Рис.1. Вид спутника ТНС-0 со стороны антенны GLOBALSTAR
без теплозащиты (фото РНИИ КП)
2. Вывод уравнений движения
и условия на управление
Пусть оскулирующая орбита
главного спутника – круговая, а оскулирующая орбита дочернего –
слабоэллиптическая. Чтобы при изучении движения не возникало вырождения по e
(эксцентриситету) и  (направлению на
перицентр), введем новые переменные (направлению на
перицентр), введем новые переменные 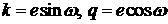 - проекции вектора
Лапласа на линию узлов и линию в плоскости орбиты, перпендикулярную линии узлов. - проекции вектора
Лапласа на линию узлов и линию в плоскости орбиты, перпендикулярную линии узлов.
Введем орбитальную систему
координат (ОСК) для каждого спутника следующим образом: ось Оx3 (или
Z) в направлении радиус-вектора спутника в каждой точке орбиты, ось Оx1
(X) выбрана в плоскости орбиты перпендикулярно Оx3 и
составляет со скоростью острый угол. Ось Оx2 (Y) –
дополняет систему координат до правой тройки. Точка О совпадает с центром масс
спутника. Направления осей ОСК приведены на рис.2.
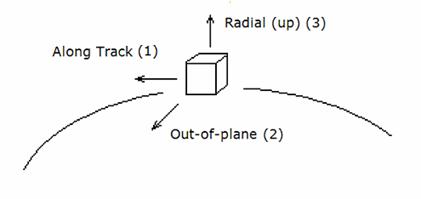
Рис.
2. Оси орбитальной системы координат
Запишем уравнения движения
каждого спутника в переменных 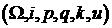 [15] [15]
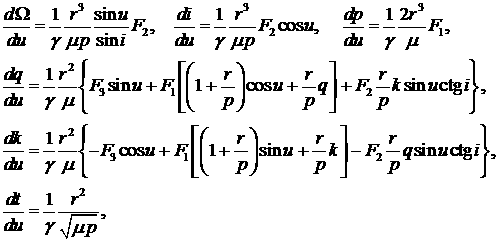 (1)
(1)
где {F1 F2 F3} – компоненты возмущения в
ОСК,  – долгота восходящего узла, – долгота восходящего узла, 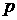 – параметр орбиты, – параметр орбиты, 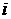 – наклонение орбиты, – наклонение орбиты, 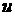 – аргумент широты, – аргумент широты, 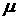 –
гравитационный параметр Земли. Здесь –
гравитационный параметр Земли. Здесь
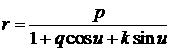 , , 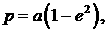 (2) (2)
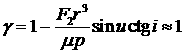 , при , при 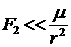 , a – большая полуось орбиты.
Элементы орбиты показаны на рис.3. , a – большая полуось орбиты.
Элементы орбиты показаны на рис.3.
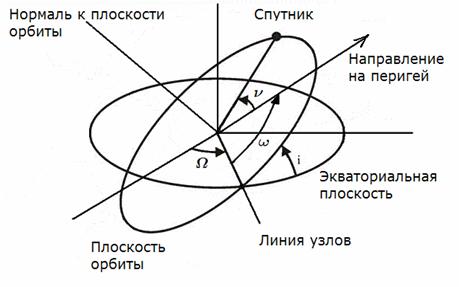
Рис.
3. Орбитальные элементы
Уравнения (1) для каждого
спутника имеют идентичный вид, в случае их использования для первого спутника в
обозначении переменных появится индекс «1», в случае второго – индекс «2».
Возмущение от сжатия Земли действует на оба спутника. Для исследования влияния
возмущения на элементы орбиты нужно подставить в уравнения движения (1)
возмущение от гармоники J2, представимое [16] в ОСК
следующим образом:
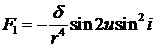 , , 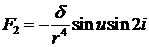 , , 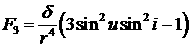 . (3) . (3)
Здесь 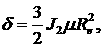 Re – радиус Земли. Re – радиус Земли.
Если возмущение мало по
сравнению с величиной ускорения центрального гравитационного поля, то из (1)
видим, что производные орбитальных элементов в таком случае малы. В случае
возмущения от сжатия Земли скорость изменения орбитальных элементов имеет
порядок J2. Следовательно, за время, в течение которого аргумент
широты изменится на величину равную 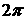 , орбитальные элементы изменятся мало. Поэтому, следуя методу
Ван-дер-Поля, можно заменить правые части системы (1) их средними значениями за
период [17] и таким образом, вычислить среднее изменение орбитальных элементов
за период по каждому спутнику. , орбитальные элементы изменятся мало. Поэтому, следуя методу
Ван-дер-Поля, можно заменить правые части системы (1) их средними значениями за
период [17] и таким образом, вычислить среднее изменение орбитальных элементов
за период по каждому спутнику.
Вычислим среднее изменение
элементов орбиты за период движения по орбите, учитывая выражение для
радиус–вектора орбиты (2), а также значения стандартных интегралов. Введем
символическое обозначение 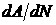 , обозначающее изменение параметра А за один оборот
спутника по орбите, то есть при изменении аргумента широты u от
0 до , обозначающее изменение параметра А за один оборот
спутника по орбите, то есть при изменении аргумента широты u от
0 до 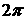 . .
Изменение угла восходящего
узла за период
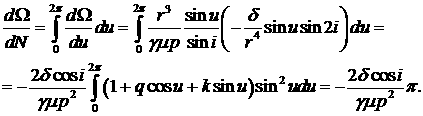
Аналогичным образом можно
вычислить среднее изменение за период остальных орбитальных элементов.
Несложный расчет показывает [18]
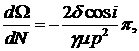 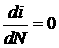 , , 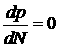 , ,  , , 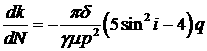 . .
Видим, что вековые уходы за период существуют только
по восходящему узлу  и аргументу перицентра и аргументу перицентра
 . Сжатие Земли не влияет на форму и размеры орбиты, а только
на ее положение в пространстве. . Сжатие Земли не влияет на форму и размеры орбиты, а только
на ее положение в пространстве.
Заметим, что в уравнениях
движения присутствуют уходы для каждого спутника. Проследим за разницей в
уходах. Эта разница за счет сжатия Земли равна
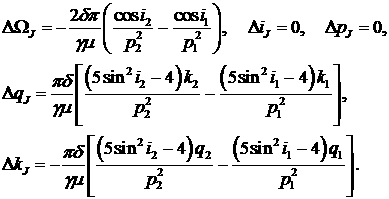 (4)
(4)
Индекс «J»
обозначает разницу в уходах за счет сжатия Земли.
Из системы (4) видим,
например, что в случае одинаковых наклонений, эксцентриситетов и фокальных
параметров, управление для поддержания формации не требуется, так как
относительные вековые уходы отсутствуют. Такое движение реализуется, например,
в формации leader-follower, то есть при движении по
одной орбите с разницей в аргументе широты. В остальных случаях для поддержания
относительной траектории и устранения вековых уходов необходимо управлять,
таким образом, чтобы изменение всех орбитальных элементов за период было равно
нулю.
В общем случае, чтобы менять
элементы 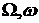 , не изменяя при этом форму и размеры орбиты, нужно
прикладывать бинормальное управление, как это видно из (1). Нужно учесть, что
при наличии бинормального ускорения будет меняться и наклонение. При этом, если
выбрать функцию управления, ортогональную функции , не изменяя при этом форму и размеры орбиты, нужно
прикладывать бинормальное управление, как это видно из (1). Нужно учесть, что
при наличии бинормального ускорения будет меняться и наклонение. При этом, если
выбрать функцию управления, ортогональную функции  , то наклонение за период в среднем не изменится. , то наклонение за период в среднем не изменится.
Далее построим такое
управление, которое позволит устранить вековые уходы. Для этого сначала опишем
используемое управление. Как было сказано во Введении, основным требованием для
системы управления спутника является ее простота. Поэтому в качестве системы
управления выбран двигатель, размещенный вдоль оси инерции спутника, которая в
свою очередь при наличии пассивной магнитной системы стабилизации,
ориентирована вдоль вектора напряженности магнитного поля в каждой точке
орбиты.
Если в качестве модели
магнитного поля Земли выбрать модель прямого диполя, то вектор магнитного поля
в ОСК будет выглядеть следующим образом:
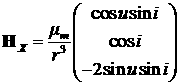 . .
Здесь 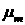 - магнитный параметр
Земли. - магнитный параметр
Земли.
Так как управление
реализуется только вдоль орта напряженности магнитного поля, то управление в
ОСК выглядит так:
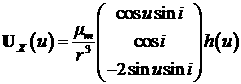 . (5) . (5)
Здесь
h(u) – искомая
скалярная функция величины тяги. Заметим, что тяга будет найдена с точностью до
множителя равного модулю вектора напряженности.
Оценим среднее значение 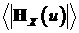 модуля вектора напряженности
за период. Модуль вектора напряженности магнитного поля может быть оценен
следующей цепочкой неравенств модуля вектора напряженности
за период. Модуль вектора напряженности магнитного поля может быть оценен
следующей цепочкой неравенств
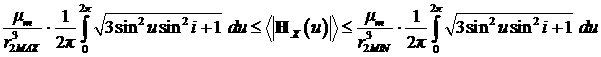 , ,
где 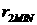 и и 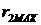 соответственно
минимальное и максимальное значения радиус-вектора второго спутника при
движении по орбите за период. Для оценки используем неравенство
Коши-Буняковского [19] соответственно
минимальное и максимальное значения радиус-вектора второго спутника при
движении по орбите за период. Для оценки используем неравенство
Коши-Буняковского [19]
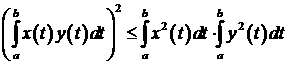 . (6) . (6)
Положим 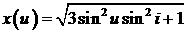 , , 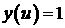 , тогда интеграл от x(u) будет оценен сверху так: , тогда интеграл от x(u) будет оценен сверху так:
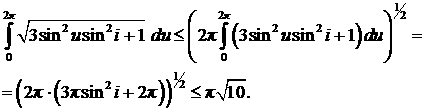
Тогда оценка «сверху» среднего значения вектора
напряженности равна
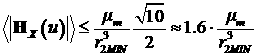 , ,
а оценка «снизу» среднего значения модуля вектора
магнитного поля следующая:
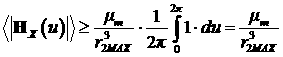 . .
Так как для получения значения управления необходимо
умножить найденное h(u) на модуль вектора
напряженности, то для оценки управления сверху логично взять оценку модуля
напряженности сверху. Тогда реальное управление 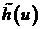 имеет вид имеет вид
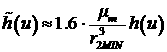 (7)
(7)
Исследуем влияние управления (5) на орбиту дочернего
спутника при разных наклонениях (без учета J2) при подстановке в
дифференциальные уравнения для оскулирующих элементов (1). Вычислим изменение
орбитальных элементов за период при наличии только такого управления в
предположении малости возмущающего ускорения
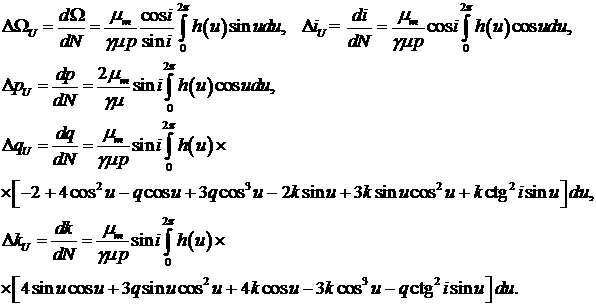
Так как управляется дочерний спутник, то уход за
счет управления возникает только для его орбитальных элементов. Для того чтобы
за счет управления компенсировать вековые уходы из-за нецентральности
гравитационного поля Земли, необходимо приравнять нулю сумму уходов по каждой
переменной за период из-за гармоники J2 и из-за управления. Тогда
получим систему интегральных уравнений
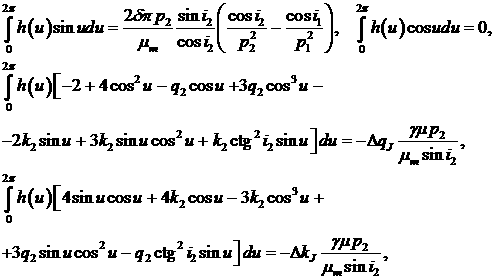 (8) (8)
с помощью которой необходимо найти искомое
управление h(u). На следующем этапе
необходимо разрешить систему (8), чтобы найти одну неизвестную скалярную
функцию h(u). Так как требуется
устранить уходы с помощью двигателей малой тяги, то интеграл от функции h(u) на периоде должен принимать
минимальное из всех возможных значение.
3. Построение управления
Будем искать решение
уравнений (8) в виде ряда Фурье
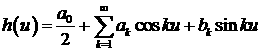 , (9) , (9)
где ak и bk искомые коэффициенты разложения.
Чтобы найти коэффициенты
разложения (9), требуется вычислить интегралы, входящие в систему интегральных
уравнений (8). Воспользуемся свойством ортогональности базисных функций ряда
Фурье на периоде, а также известными табличными значениями квадратов каждой
базисной функции
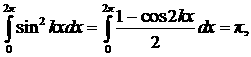
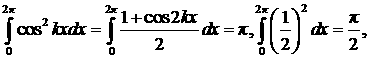
где k – натуральное. Кроме того,
воспользуемся определением коэффициентов ряда Фурье
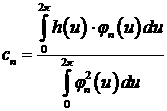 , где , где
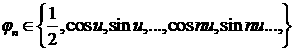 , и , и 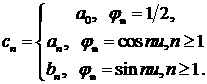
Тогда все слагаемые - интегралы в (8) - определяются
следующими выражениями, вычисляемыми с помощью определения коэффициентов ряда
Фурье:
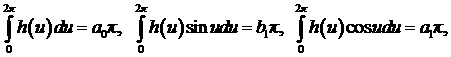
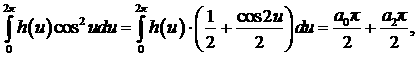 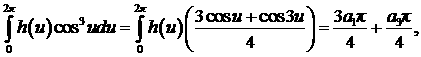
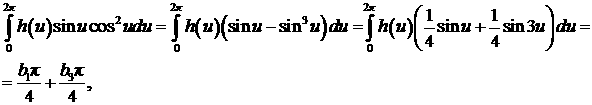
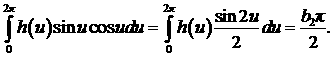
После подстановки значений интегралов в (8) получаем
систему равенств
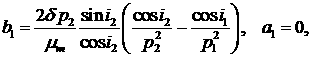 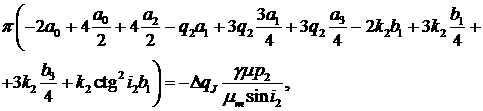
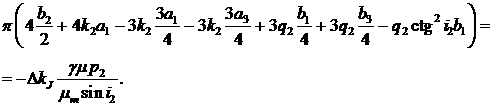
После некоторого упрощения находим
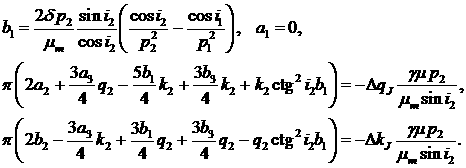 (10) (10)
Таким образом, получили систему (10), состоящую из
четырех алгебраических уравнений для определения шести коэффициентов a1,b1,a2,b2,a3,b3. Эта система является
переопределенной и определяет двумерное подпространство в шестимерном
пространстве всех возможных коэффициентов. Остальные коэффициенты из системы
интегральных уравнений (8) найти не удается, но так как требуется найти
минимальную функцию управления, то можно положить ненайденные коэффициенты
равными нулю, так как
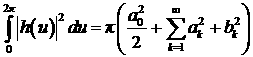 . .
Вообще, интегральное
управление, а значит и суммарный расход топлива равен 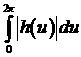 , но в выбранном классе функций квадрат функции представим
более простым выражением с использованием коэффициентов разложения в ряд Фурье,
чем модуль той же функции. Поэтому для обоснования использования квадрата от
функции вместо модуля обратимся к неравенству (6). Если , но в выбранном классе функций квадрат функции представим
более простым выражением с использованием коэффициентов разложения в ряд Фурье,
чем модуль той же функции. Поэтому для обоснования использования квадрата от
функции вместо модуля обратимся к неравенству (6). Если 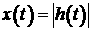 , , 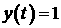 , а интервал равен , а интервал равен 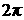 , то неравенство (6) принимает следующий вид: , то неравенство (6) принимает следующий вид:
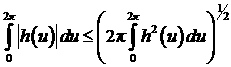 . .
Таким образом, рассматривая
интеграл по норме L2, найдем верхнюю оценку потребления топлива.
Преобразуем полученную
систему (10) к виду
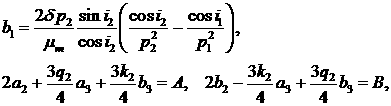 (11) (11)
введя обозначения
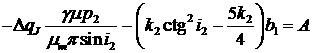 , ,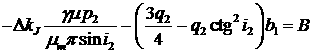 . .
Рассмотрим два последних
уравнения системы (11). Они описывают переопределенную систему алгебраических
уравнений, которую в матричном виде можно записать так:
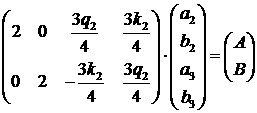 . .
Известно, что система алгебраических уравнений
совместна тогда и только тогда, когда ранг исходной матрицы A равен
рангу расширенной матрицы. В нашем случае ранг исходной матрицы равен двум, так
как существует ненулевой минор размерности два
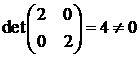 . .
Видим, что присоединение к матрице столбца (A,B)T
никак не влияет на ранг, а значит, система совместна. Так как уравнений два, а
неизвестных четыре, то можно выразить две переменные через две другие. Выразим,
например, a2 и b2 через a3 и b3 по формулам
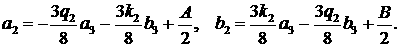 (12) (12)
Таким образом, получено решение системы (11) в общем
виде с произвольными переменными a3 и b3.
Теперь учтем то, что
управление должно быть минимально возможным за период, поэтому сумма квадратов
коэффициентов должна принимать минимально возможное значение. Запишем это в
виде цепочки соотношений
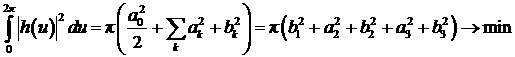 . .
Так как b1 константа, зависящая только
от начальных условий, а a2 и b2 выражаются через a3 и b3, то минимизация функционала может быть проведена только по переменным a3 и b3, а именно
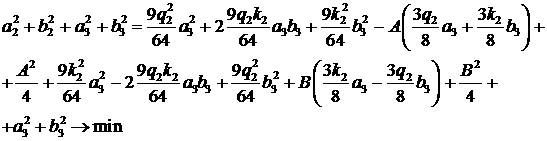 (13) (13)
Видим, что перекрестные члены в виде aibj в (13) сокращаются и после преобразований (13)
приводится к виду
 . .
Известно, что если квадратичная форма имеет вид 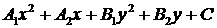 , то к сумме квадратов она приводится следующим образом: , то к сумме квадратов она приводится следующим образом:
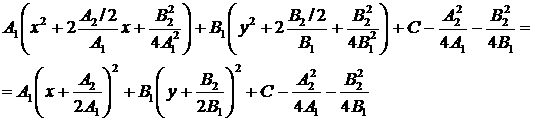 . .
Минимальное значение форма принимает при значениях 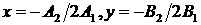 и это минимальное
значение равно и это минимальное
значение равно 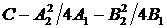 . В нашем случае минимум достигается при следующих значениях
параметров a3 и b3: . В нашем случае минимум достигается при следующих значениях
параметров a3 и b3:
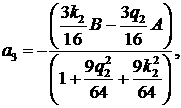 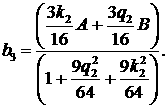
Значение функционала 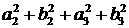 равно равно 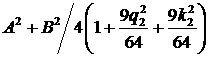 . .
С учетом соотношений 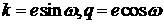 получаем искомое
значение для квадрата управления получаем искомое
значение для квадрата управления
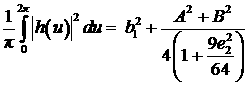 . (14) . (14)
4. Оценка величины
управления
Произведем оценку
получившегося выражения (14), учитывая то, что орбита главного спутника
круговая, а значит k1 = 0 и q1 = 0. Тогда с учетом
выражений из (4)
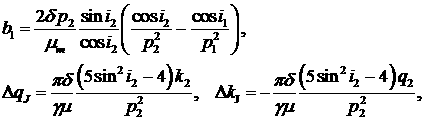
и после подстановки их в (11) получим значения для
коэффициентов A и B
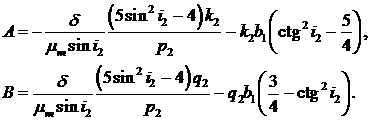 (15) (15)
Отдельно, квадраты коэффициентов определяются
выражениями
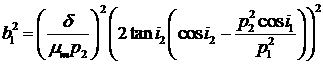
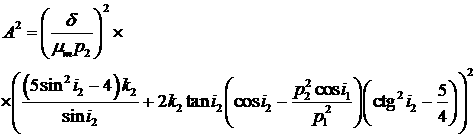 (16)
(16)
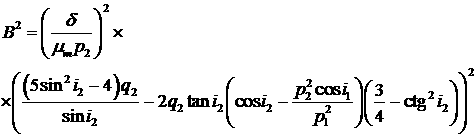
Используя формулу (14), соотношения (7) и (16),
оценим интеграл, используя следующую цепочку соотношений:
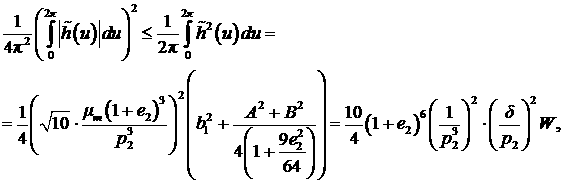 (17) (17)
где
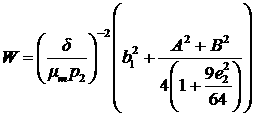 . (18) . (18)
Чтобы возмущение было мало и можно было использовать
метод усреднения, необходимо выполнение неравенства
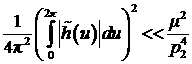 , ,
либо
приближенного соотношения
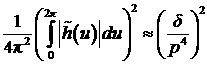 . .
С учетом выражения (3) для 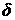 эти условия выполнено, если выражение (18) не превышает,
например, 100. А это выполнено в том случае, если тангенс и котангенс угла
наклонения в (16) ограничены. эти условия выполнено, если выражение (18) не превышает,
например, 100. А это выполнено в том случае, если тангенс и котангенс угла
наклонения в (16) ограничены.
Если ввести
обозначение 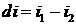 ,
то для (18) можно построить график зависимости W от наклонения дочернего
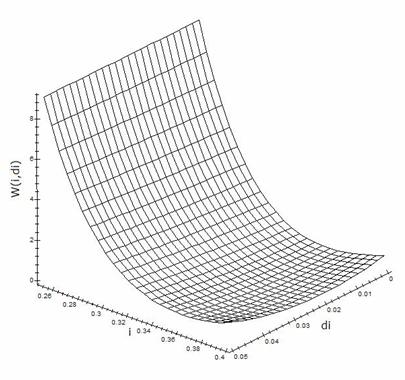
спутника и разницы наклонений дочернего и главного спутников (рис.4). Для
построения сумма квадратов была оценена сверху: q2 = 1, k2 = 1, p1=p2. Видим, что область значений параметров наклонения, необходимых для
реализации малой тяги, существует. На рис.4 показана часть поверхности,
значения функции W на которой не превышают 10.
Видим, что управлять относительным движением при использовании описываемого
алгоритма выгоднее в смысле затрат топлива на средних широтах. ,
то для (18) можно построить график зависимости W от наклонения дочернего
спутника и разницы наклонений дочернего и главного спутников (рис.4). Для
построения сумма квадратов была оценена сверху: q2 = 1, k2 = 1, p1=p2. Видим, что область значений параметров наклонения, необходимых для
реализации малой тяги, существует. На рис.4 показана часть поверхности,
значения функции W на которой не превышают 10.
Видим, что управлять относительным движением при использовании описываемого
алгоритма выгоднее в смысле затрат топлива на средних широтах.
5. Численная верификация
результатов
Построим траектории
относительного движения при найденном управлении. Для этого воспользуемся тем,
что в геоцентрической экваториальной системе координат координата центра масс
каждого спутника связана с орбитальными элементами при помощи соотношений
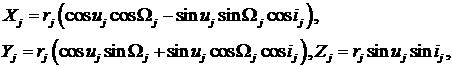
где j – номер спутника. Таким
образом, рассчитав численно изменение орбитальных элементов по (1) с учетом
выражений (3) и (5), в каждый момент времени можно найти координаты каждого из
спутников в ОСК при наличии и отсутствии управления. На всех последующих
рисунках главный спутник находится в точке с координатами (0,0,0).
|
|
|
Рис.
4. Поверхность для определения области параметров (углы - в радианах)
|
Построим относительную
траекторию и управление для одинаковых параметров орбиты p и
разных наклонений для случая круговой орбиты главного спутника и
слабоэллиптической орбиты дочернего спутника. Разницу в наклонениях выберем
такую, что максимальное расхождение спутников (при прохождении наивысшей точки
орбиты) не превосходит 1000 м, а значит, величина разницы в наклонениях для
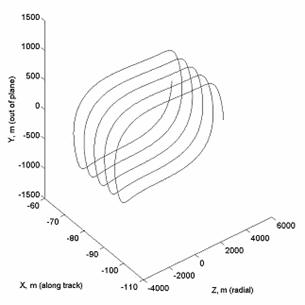
радиуса орбиты около 7000 км должна быть не более чем 1000/7000000 ~ 0,025o. На рис.5 показана
относительная траектория при отсутствии управления. Видим, что уход по
направлению «вдоль траектории» равен примерно 25 м на 5 витках. При этом
наклонение траектории главного спутника равно 51.61o, а дочернего 51.6o. Радиус орбиты равен 6700
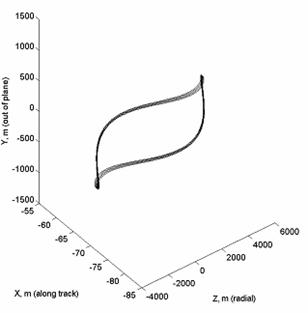
км, эксцентриситет орбиты дочернего спутника равен 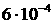 . На рис.6 показана относительная траектория при наличии
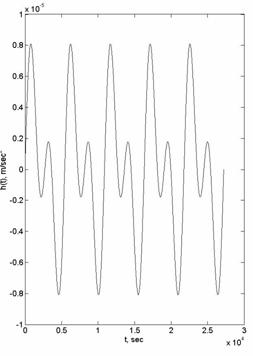
управления, на рис.7 построен график зависимости управления от времени. Видим,
что управление значительно уменьшило вековой уход с 25 м на 5-ти витках до 25
см. Характеристическая скорость, необходимая для управления на пяти витках,
рассчитывается как интеграл от модуля функции управления и равна в нашем случае
0.0998 м/сек. . На рис.6 показана относительная траектория при наличии
управления, на рис.7 построен график зависимости управления от времени. Видим,
что управление значительно уменьшило вековой уход с 25 м на 5-ти витках до 25
см. Характеристическая скорость, необходимая для управления на пяти витках,
рассчитывается как интеграл от модуля функции управления и равна в нашем случае
0.0998 м/сек.
|
|
|
|
|
Рис. 5. Относительное движение при
разности в наклонениях без управления
|
Рис. 6. Относительное движение в плоскости
орбиты при разности в наклонениях с управлением
|
Рис. 7. Управление для устранения вековых
уходов при разности в наклонениях
|
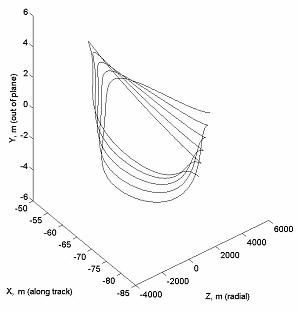
Теперь
рассмотрим случай, когда имеет место отличие в радиусах орбит для спутников.
Параметры орбиты возьмем следующими: радиус орбиты главного спутника 6700 км,
большая полуось орбиты дочернего спутника плюс 100 м к радиусу орбиты главного,
наклонения орбит одинаковы и равны 51.6o, эксцентриситет орбиты
дочернего спутника равен 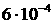 , направление на перигей составляет 90o с линией узлов. На рис.8
показано относительное движение при отсутствии управления. Видим, что в
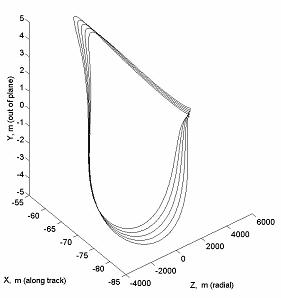
относительном движении есть незначительный уход. На рис.9 показан результат
применения управления к такой формации. Видим, что вековой уход исчез. Величина
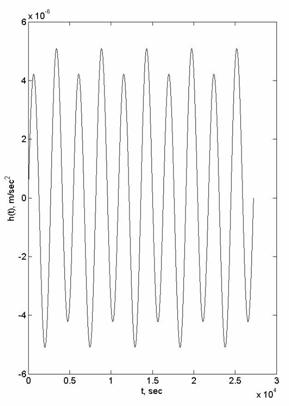
управления построена на рис.10. Все траектории также построены на пяти витках.
Характеристическая скорость на пяти витках рассчитывается как интеграл от
модуля функции управления и равна в этом случае 0.0810 м/сек. , направление на перигей составляет 90o с линией узлов. На рис.8
показано относительное движение при отсутствии управления. Видим, что в
относительном движении есть незначительный уход. На рис.9 показан результат
применения управления к такой формации. Видим, что вековой уход исчез. Величина
управления построена на рис.10. Все траектории также построены на пяти витках.
Характеристическая скорость на пяти витках рассчитывается как интеграл от
модуля функции управления и равна в этом случае 0.0810 м/сек.
|
|
|
|
|
Рис. 8. Относительное движение при отличии в радиусах
орбит без управления
|
Рис. 9. Относительное движение при отличии в радиусах орбит с
управлением
|
Рис. 10. Управление для устранения вековых уходов при
эксцентрической орбите дочернего спутника
|
6. Оценка времени жизни
спутника на орбите при использовании управления вдоль вектора напряженности
магнитного поля
Для того чтобы оценить время
жизни спутника, нужно знать его запас характеристической скорости. Необходимый
запас характеристической скорости для устранения влияния сжатия Земли на орбиту
спутника был оценен в предыдущем разделе. Для того, чтобы оценить время жизни,
следует сравнить его с известными значениями характеристической скорости для
реальных проектов наноспутников.
Примером двигателя малой
тяги является двигатель на наноспутнике SNAP – 1 (разработка SSTL).
Спутник был запущен в 2000 году. Масса аппарата – 6.5 кг, запас
характеристической скорости спутника – 3.4 м/сек. Тяга двигателя составляла 45
– 120 мН, масса жидкого бутана, используемого как рабочее тело, – 32.6 г,
удельный импульс всего 60 сек [20]. Оценочное время жизни превышало 5 лет. На
рис.11 показан двигатель малой тяги для спутника, он имеет форму трубки,
свернутой в спираль, суммарная длина трубки равна 1.1 м [21].

Рис.11. Двигатель для SNAP – 1 [22]
Запаса характеристической
скорости одного такого двигателя хватит на 12 дней непрерывной работы (~200
витков), если его использовать на дочернем спутнике подобном ТНС-0 N1 для
компенсации векового ухода, возникающего от сжатия Земли, согласно описанному
выше алгоритму управления.
7. Заключение
В работе проверена
возможность устранения вековых уходов, возникающих из-за сжатия Земли, с
помощью малого ограниченного управления.
Выведены
уравнения движения в орбитальных элементах, учитывающие как сжатие Земли, так и
создаваемое управление. Проведено усреднение уравнений в предположении малости
возмущений. Непосредственно указаны аналитические выражения для управления,
устраняющего вековые уходы в зависимости от начальных условий. Показано, что
существует область значений параметров, в которой величина управления сравнима
с величиной возмущающего ускорения от сжатия Земли.
Для некоторых
типовых примеров проведено численное моделирование относительного движения с
использованием исходных уравнений движения. Показана состоятельность метода
получения управления для устранения вековых уходов из-за гравитационного
возмущения.
Получено
значение характеристической скорости, необходимой для устранения влияния сжатия
Земли. Оценено время жизни спутника.
Предложенный
способ управления может быть использован для устранения влияния малых вековых
возмущений различной природы, например, сопротивления атмосферы.
8.
Благодарности
Работа
поддержана РФФИ (Грант N 06-01-00389, N
07-01-92001) и Федеральным агентством по науке и инновациям (Контракт N
02.514.11.4068).
СПИСОК ЛИТЕРАТУРЫ
1. В.В.Белецкий, Очерки о движении
космических тел, М.: Наука, 1972, 360с.
2. D.A.Vallado with
contribution by Wayne D.MacClain, Fundamentals of Astrodynamics and
Applications (Second Edition), Space Technology Library, Microcosm Press, 2006,
958p.
3. E. Wnuk
and J. Golebiewska, The relative motion of Earth orbiting
satellites, Celestial Mechanics and
Dynamical Astronomy, Vol. 91, N 3-4, 2005, pp.
373-389.
4. C. Xu,
R. Tsoi, N. Sneeuw, Analysis of J2-Perturbed
Relative Orbits for Satellite Formation Flying,
GGSM2004, Jekeli, C., Bastos, L. & Fernandes, J.(Ed.) IAG Proceedings, Springer, Vol. 129, 2005, pp. 36-41.
5. D.
Izzo. Formation Flying Linear Modelling. In 5th International Conference On
Dynamics and Control of Systems and Structures in Space, Cambridge, UK,
July 2002, pp. 283–289,
https://dspace.lib.cranfield.ac.uk/handle/1826/882.
6. H. Schaub,
S.R. Vadali, J.L. Junkins, K.T.
Alfriend, Spacecraft Formation Flying Control Using Mean
Orbit Elements, Journal of the Astronautical Sciences, Vol. 48, N 1, Jan.–March, 2000, pp.69–87.
7. K. T.
Alfriend, S. R. Vadali, H. Schaub, Formation Flying Satellites:
Control by an Astrodynamicist, Celestial Mechanics and Dynamical Astronomy,
Vol. 81, N 1–2, 2001, pp.57–62.
8. K.D.
Kumara,
H.C. Bangb, M.J. Tahkb, Satellite Formation Flying
Using Along-track Thrust, Acta Astronautica Vol. 61, N 7-8, 2007, pp.553-564.
9. И.Е. Зараменских, Множество
достижимых траекторий относительного движения двух спутников при управлении
вдоль вектора магнитного поля, Сборник трудов V
Научно-практической конференции "Микротехнологии в авиации и
космонавтике", Москва, 17-19 сентября, 2007, 10 с.
10. G.V.Smirnov,
M. Ovchinnikov, A.Guerman, Use of Solar Radiation Pressure to Maintain a
Spatial Satellite Formation, Acta Astronautica, 2007, Vol. 61, N 6-7,
Academy Transactions Note, pp.724 – 728.
11. Ю.М.Урличич, А.С.Селиванов,
Ю.М.Тучин, О.Е.Хромов, И.В.Никушкин, Технологический наноспутник минимальной
комплектации ТНС-0. Аннотации докладов на III Конференции
«Микротехнологии в авиации и космонавтике», Санкт-Петербург, 8-9 июня, 2004 г.
12. Н.В.Куприянова, М.Ю.Овчинников, В.И.Пеньков,
А.С.Селиванов, Пассивная магнитная система ориентации первого российского наноспутника
ТНС-0,
Препринт ИПМ № 46, Москва, 2005
г.
13.
D.Burleson, Space Programs
Outside the United States: All Exploration and Research Efforts, Country by
Country, McFarland, 2005, 325 p.
14.
http://epizodsspace.testpilot.ru/bibl/nk/1995/21/21-1995-2.html
15.
H. Schaub, Relative Orbit
Geometry Through Classical Orbit Element Differences, Journal of Guidance,
Navigation and Control, Vol.27, N 5, Sept.-Oct., 2004, pp.839 – 848.
16. М.Ф.Решетнев, А.А.Лебедев,
В.А.Бартенев, М.Н.Красильщиков, В.А.Малышев, В.В.Малышев, Управление и
навигация искусственных спутников Земли на околокруговых орбитах, М.:
Машиностроение, 1988, 336с.
17. Н.Н.Моисеев, Асимптотические
методы нелинейной механики, М.: Наука, 1981, 400с.
18. Д.Е.Охоцимский,
Ю.Г.Сихарулидзе, Основы механики космического полета, М.: Наука, 1990, 448с.
19. А.Н.Колмогоров, С.В.Фомин,
Элементы теории функций и функционального анализа, Учебник для вузов, 6-е изд.,
испр. М.: Наука, 1989, 624с.
20. И.Лисов, Малютке SNAP-1 не
хватило силенок…, Новости космонавтики, 2001, №8 (223).
21.
Snap – 1: Propulsion System,
Surrey Satellite Technology LTD, SSTL-9017-02. 17-09-2003,
http://centaur.sstl.co.uk/datasheets/SNAP-1%20Propulsion.pdf
22.
http://directory.eoportal.org/presentations/887/8334.html
|
![]() . На рис.6 показана относительная траектория при наличии
управления, на рис.7 построен график зависимости управления от времени. Видим,
что управление значительно уменьшило вековой уход с 25 м на 5-ти витках до 25
см. Характеристическая скорость, необходимая для управления на пяти витках,
рассчитывается как интеграл от модуля функции управления и равна в нашем случае
0.0998 м/сек.
. На рис.6 показана относительная траектория при наличии
управления, на рис.7 построен график зависимости управления от времени. Видим,
что управление значительно уменьшило вековой уход с 25 м на 5-ти витках до 25
см. Характеристическая скорость, необходимая для управления на пяти витках,
рассчитывается как интеграл от модуля функции управления и равна в нашем случае
0.0998 м/сек.![]() , направление на перигей составляет 90o с линией узлов. На рис.8
показано относительное движение при отсутствии управления. Видим, что в
относительном движении есть незначительный уход. На рис.9 показан результат
применения управления к такой формации. Видим, что вековой уход исчез. Величина
управления построена на рис.10. Все траектории также построены на пяти витках.
Характеристическая скорость на пяти витках рассчитывается как интеграл от
модуля функции управления и равна в этом случае 0.0810 м/сек.
, направление на перигей составляет 90o с линией узлов. На рис.8
показано относительное движение при отсутствии управления. Видим, что в
относительном движении есть незначительный уход. На рис.9 показан результат
применения управления к такой формации. Видим, что вековой уход исчез. Величина
управления построена на рис.10. Все траектории также построены на пяти витках.
Характеристическая скорость на пяти витках рассчитывается как интеграл от
модуля функции управления и равна в этом случае 0.0810 м/сек.


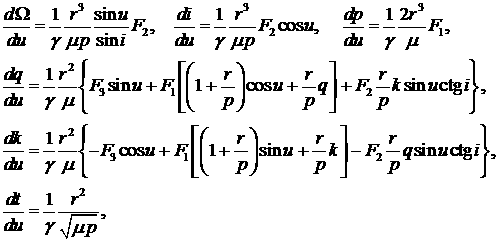
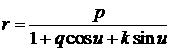 ,
,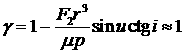 , при
, при 
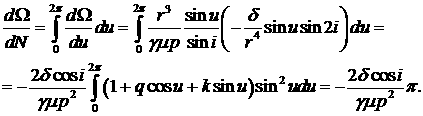
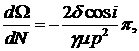
 ,
, 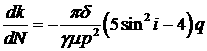 .
.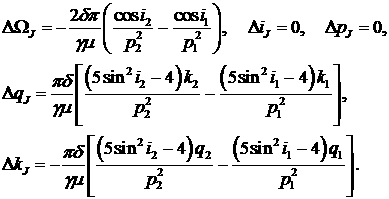
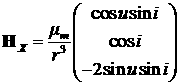 .
.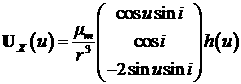 .
.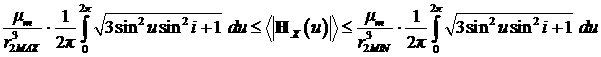 ,
,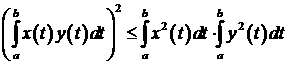
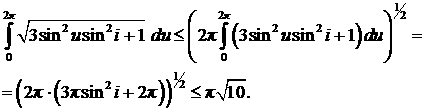
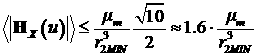 ,
,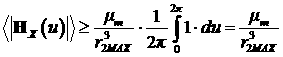 .
.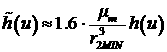
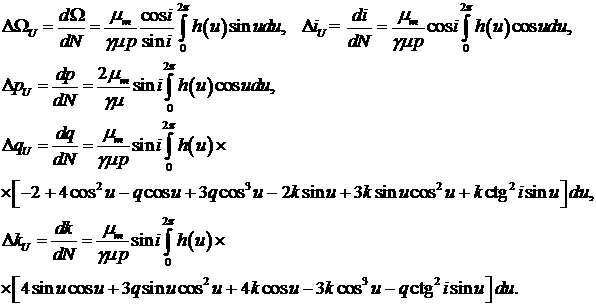
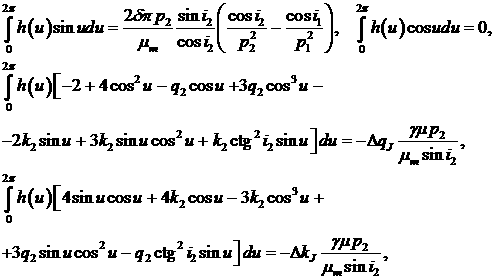
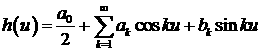 ,
,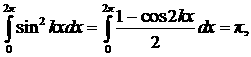
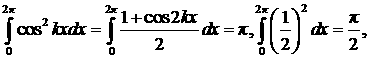
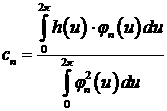 ,
, 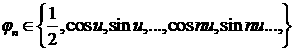
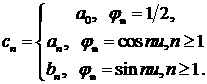
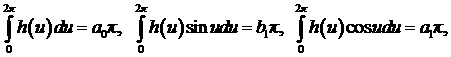
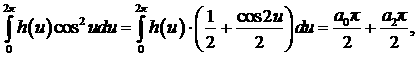
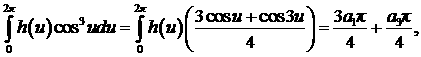
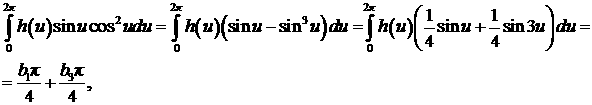
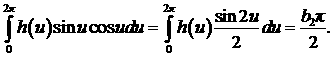
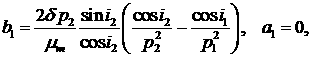
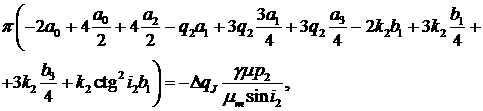
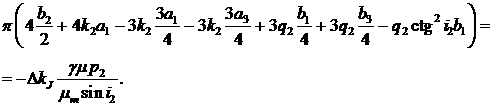
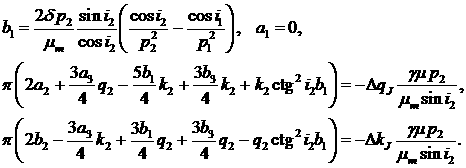
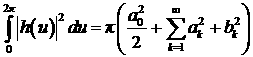 .
.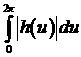 , но в выбранном классе функций квадрат функции представим
более простым выражением с использованием коэффициентов разложения в ряд Фурье,
чем модуль той же функции. Поэтому для обоснования использования квадрата от
функции вместо модуля обратимся к неравенству (6). Если
, но в выбранном классе функций квадрат функции представим
более простым выражением с использованием коэффициентов разложения в ряд Фурье,
чем модуль той же функции. Поэтому для обоснования использования квадрата от
функции вместо модуля обратимся к неравенству (6). Если 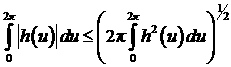 .
.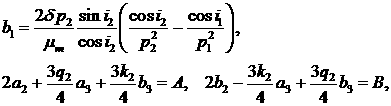
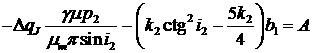 ,
,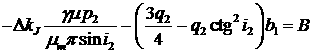 .
.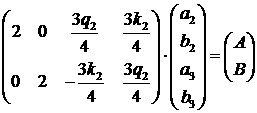 .
.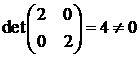 .
.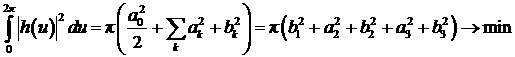 .
.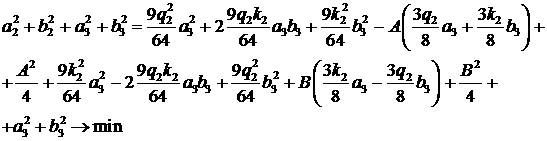
 .
.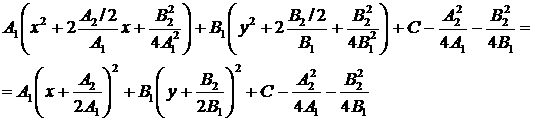 .
.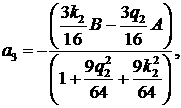
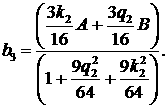
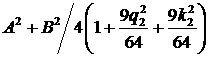 .
.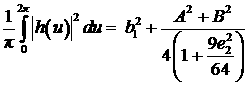
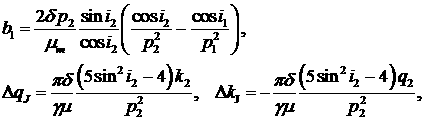
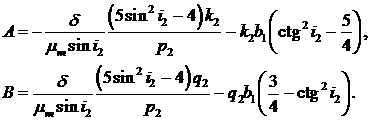
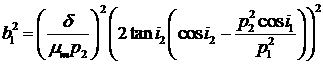
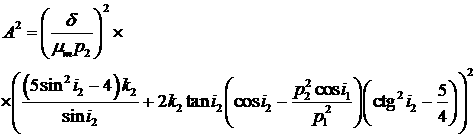
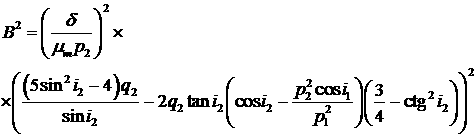
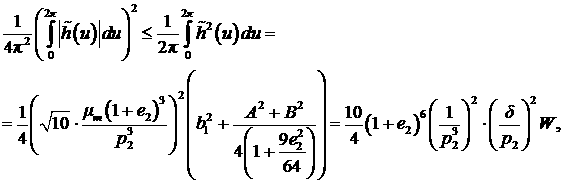
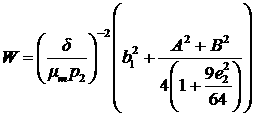 .
.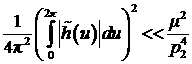 ,
,