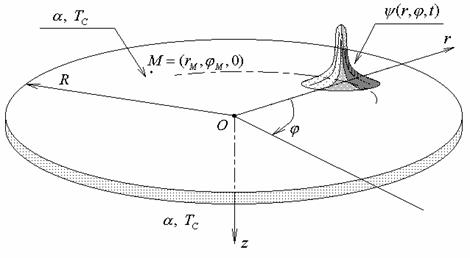
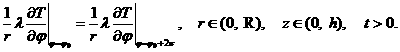Численное моделирование динамики температурных полей на плоских мишенях при нестационарном интенсивном лазерном воздействии
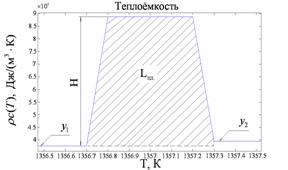
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Рис. 2. Фрагмент графика
зависимости коэффициента теплопроводности |
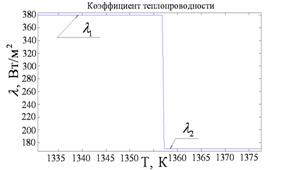
Рис. 3. Фрагмент графика
зависимости объёмной теплоёмкости |
Зависимость объёмной теплоёмкости
в окрестности температуры плавления представим в виде кусочно-линейной функции,
которая представляет собой на отрезке ![]() трапецию, площадь под
которой равна величине удельной теплоты плавления
трапецию, площадь под
которой равна величине удельной теплоты плавления ![]() (рис. 3). Обозначим
значение объёмной теплоёмкости до плавления через
(рис. 3). Обозначим
значение объёмной теплоёмкости до плавления через ![]() , удельную теплоёмкость жидкого расплава металла -
, удельную теплоёмкость жидкого расплава металла - ![]() . Также введём следующие величины: коэффициент
. Также введём следующие величины: коэффициент ![]() , равный отношению длины верхнего основания трапеции к длине нижнего;
, равный отношению длины верхнего основания трапеции к длине нижнего;
![]() ;
;
![]()
при ![]()
при ![]()
С использованием введённых обозначений
объёмную теплоёмкость на ![]() можно представить в
виде
можно представить в
виде
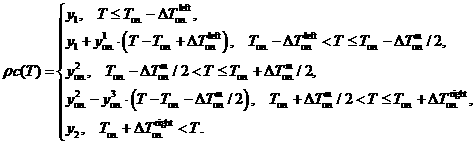
Интегрирование функции ![]() на рассматриваемом
отрезке даёт нам функцию плотности внутренней энергии:
на рассматриваемом
отрезке даёт нам функцию плотности внутренней энергии:
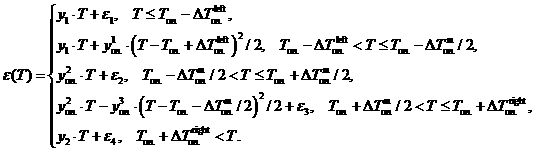
Здесь ![]() ,
, ![]() ,
, ![]() ,
, ![]()
3. Численная реализация математической модели
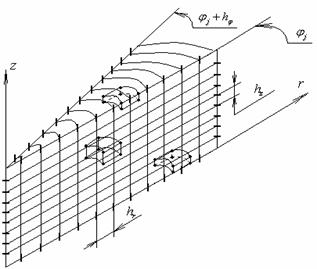
Для численного решения задачи (1) – (8) воспользуемся
интегро-интерполяционным методом [16, 17] для построения консервативной разностной
схемы. Введём в области ![]() равномерную
пространственную сетку с шагами
равномерную
пространственную сетку с шагами ![]() ,
, ![]() и
и ![]() , где
, где ![]() ,
,![]() ,
,![]() – число точек разбиения по осям
– число точек разбиения по осям ![]() ,
, ![]() и
и ![]() соответственно (рис. 4).
Заметим, что по угловой координате сетка имеет следующий вид:
соответственно (рис. 4).
Заметим, что по угловой координате сетка имеет следующий вид:
![]()
Центры граней рассматриваемой
сетки разбивают пластину на множество элементарных объёмов, часть которых
примыкает к верхней, нижней и боковой поверхностям пластины. Такие элементы
будем называть внешними. Если же элементы разбиения не примыкают к поверхности
пластины, то будем называть их внутренними. Для построения консервативной
разностной схемы необходимо проинтегрировать обе части дифференциального
уравнения теплопроводности (1) по этим элементарным объёмам, учитывая граничные
условия (3) – (8).
|
|
|
|
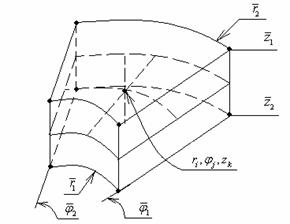
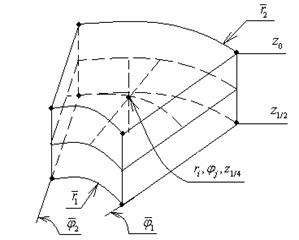
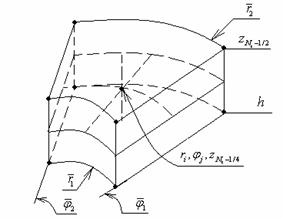
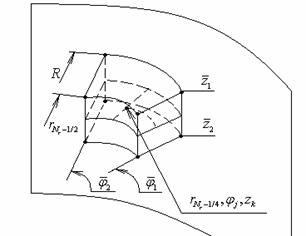
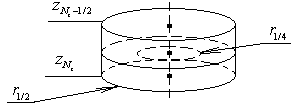
Рис. 4. Разбиение сектора
пластины |
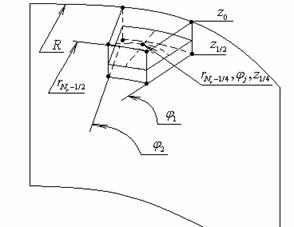
Рис. 5. Внутренний элемент
разбиения пластины |
На временном интервале введём
равномерную сетку с шагом ![]() . Сначала проведём интегрирование по внутренним элементам
разбиения (рис. 5). Будем использовать следующие обозначения:
. Сначала проведём интегрирование по внутренним элементам
разбиения (рис. 5). Будем использовать следующие обозначения: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Тогда объём внутренних элементов
. Тогда объём внутренних элементов
![]() .
.
Удельную теплоёмкость ![]() в узле с координатами
в узле с координатами ![]() в момент времени
в момент времени ![]() (на s-м временном слое) будем обозначать
(на s-м временном слое) будем обозначать ![]() . Аналогичную величину на предыдущем временном слое
. Аналогичную величину на предыдущем временном слое ![]() будем обозначать
будем обозначать ![]() . Такие же обозначения используем и для других величин.
. Такие же обозначения используем и для других величин.
1. Рассмотрим множество ![]() всех внутренних точек
пластины для момента времени
всех внутренних точек
пластины для момента времени ![]() . Интегрируем обе части уравнения (1) по внутренним элементам
. Интегрируем обе части уравнения (1) по внутренним элементам
![]() ,
, ![]() ,
, ![]() ,
, ![]() . Получим
. Получим
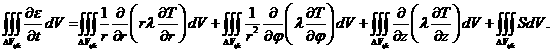 (9)
(9)
Интегралы по объему ячейки в правой части (9) преобразуются
в поверхностные. После подстановки пределов интегрирования, замены неизвестной
функции ![]() сеточной
сеточной ![]() , замены обычных производных разностными и деления обеих
частей полученного равенства на
, замены обычных производных разностными и деления обеих
частей полученного равенства на ![]() получим разностные
уравнения
получим разностные
уравнения
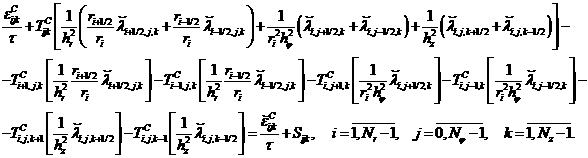 (10)
(10)
Уравнения дополнительно преобразованы,
приведены подобные члены. Эти преобразования возможны благодаря накладываемым
на функцию температуры и её производную условий непрерывности и ограниченности
на множестве ![]() [15]. Учитывая зависимость
для плотности внутренней энергии
[15]. Учитывая зависимость
для плотности внутренней энергии ![]() , получаем:
, получаем:
![]() (11)
(11)
Совершенно аналогичные (11) равенства справедливы и для остальных точек сетки. Поэтому далее они не выписываются.
Заметим, что в силу условия (7) верны соотношения:
![]()
2. Рассмотрим элементы разбиения ![]() , которые примыкают к поверхности
, которые примыкают к поверхности ![]() пластины, не имеющие
общие точки с её боковой поверхностью (рис. 6). Объём этого элемента
пластины, не имеющие
общие точки с её боковой поверхностью (рис. 6). Объём этого элемента
![]()
|
|
|
|
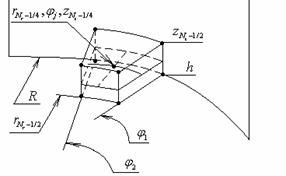
Рис. 6. Внешний элемент
разбиения |
Рис. 7. Внешний элемент
разбиения |
Проинтегрировав обе части
уравнения (1) по элементам ![]() и выполнив изложенные выше
действия, получаем следующие разностные уравнения:
и выполнив изложенные выше
действия, получаем следующие разностные уравнения:
 (12)
(12)
При вычислении потока тепла через границу учтено условие (4).
3. Рассмотрим элементы разбиения ![]() , которые примыкают к поверхности
, которые примыкают к поверхности ![]() пластины и не имеют
общих точек с её боковой поверхностью (рис. 7). Объём этих элементов
пластины и не имеют
общих точек с её боковой поверхностью (рис. 7). Объём этих элементов
![]() .
.
При интегрировании уравнения (1)
по элементам ![]() учтём граничное условие
(3). В результате получим следующие разностные уравнения:
учтём граничное условие
(3). В результате получим следующие разностные уравнения:
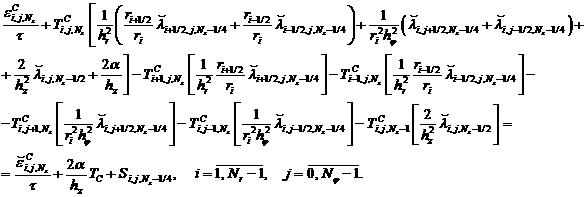 (13)
(13)
4. Рассмотрим элементы разбиения ![]() , которые примыкают к боковой поверхности
, которые примыкают к боковой поверхности ![]() , не имеющие общие точки с поверхностями
, не имеющие общие точки с поверхностями ![]() и
и ![]() пластины (рис. 8).
Объём таких элементов
пластины (рис. 8).
Объём таких элементов
![]() .
.
Выполнив те же, что и ранее, действия с учетом граничного условия (5), получим следующие разностные уравнения:
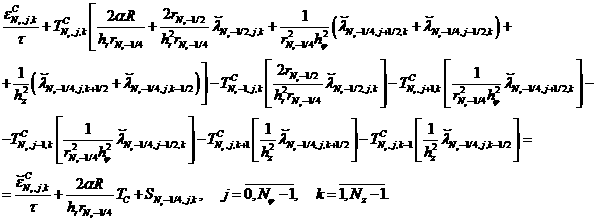 (14)
(14)
5. Рассмотрим элементы разбиения ![]() , которые примыкают одновременно к боковой поверхности
, которые примыкают одновременно к боковой поверхности ![]() и к поверхности
и к поверхности ![]() пластины (рис. 9).
Объём таких элементов
пластины (рис. 9).
Объём таких элементов
![]() .
.
Интегрирование уравнения (1) с учетом граничных условий (5), (4) приводит к следующим разностным уравнениям:
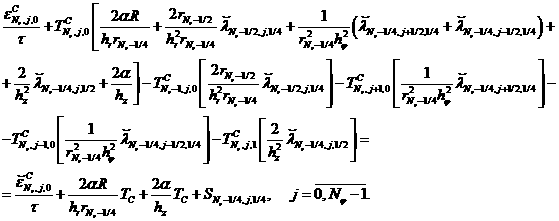 (15)
(15)
|
|
|
|
Рис. 8. Внешний элемент
разбиения пластины |
Рис. 9. Внешний элемент разбиения
пластины |
|
|
|
|
Рис. 10. Внешний элемент
разбиения пластины |
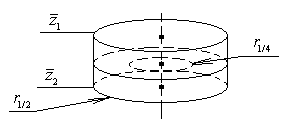
Рис. 11. Внутренний
элемент разбиения |
6. Рассмотрим элементы разбиения ![]() , которые примыкают одновременно к боковой поверхности
, которые примыкают одновременно к боковой поверхности ![]() и к поверхности
и к поверхности ![]() пластины (рис. 10).
Объём таких элементов
пластины (рис. 10).
Объём таких элементов
![]() .
.
Интегрирование уравнения (1) по
элементам ![]() с учетом граничных условий
(5) и (3) приводит к разностным уравнениям:
с учетом граничных условий
(5) и (3) приводит к разностным уравнениям:
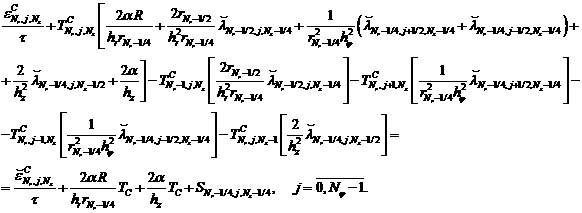 (16)
(16)
7. Рассмотрим внутренние элементы разбиения ![]() , ось симметрии которых совпадает с осью пластины (рис. 11).
Объём таких элементов
, ось симметрии которых совпадает с осью пластины (рис. 11).
Объём таких элементов
![]() .
.
При этом узлы сетки на оси ![]() тождественны для всех
значений аргумента
тождественны для всех
значений аргумента ![]() :
:
![]() .
.
Интегрирование уравнения (1) с учетом граничного условия (6) и условия (8) приводит к следующим разностным уравнениям:
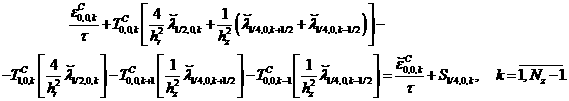 (17)
(17)
8. Рассмотрим внешний элемент разбиения ![]() , примыкающий к поверхности
, примыкающий к поверхности ![]() ,
ось симметрии которого совпадает с осью пластины (рис. 12). Объём этого
элемента
,
ось симметрии которого совпадает с осью пластины (рис. 12). Объём этого
элемента
![]() .
.
Интегрирование обеих частей
уравнения (1) по элементу ![]() с учетом граничных условий
(4, 6) и условия (8) приводит к следующему разностному уравнению:
с учетом граничных условий
(4, 6) и условия (8) приводит к следующему разностному уравнению:
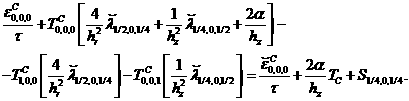 (18)
(18)
9. Рассмотрим внешний элемент разбиения ![]() , примыкающий к поверхности
, примыкающий к поверхности ![]() ,
ось симметрии которого совпадает с осью пластины (рис. 13). Объём этого
элемента
,
ось симметрии которого совпадает с осью пластины (рис. 13). Объём этого
элемента
![]() .
.
|
|
|
|
Рис. 12. Внешний элемент
разбиения |
Рис. 13. Внешний элемент
разбиения |
Интегрирование уравнения (1) с учетом граничных условий (3, 6) и условия (8) приводит к следующему разностному уравнению:
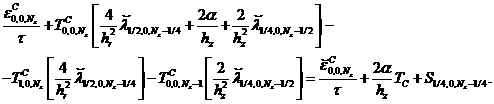 (19)
(19)
Разностные соотношения (10) – (19) представляют собой систему
![]() (20)
(20)
Система (20) состоит из ![]() уравнений с
уравнений с ![]() неизвестными. Число
неизвестными. Число ![]() определяется формулой
определяется формулой
![]() (21)
(21)
Вектор неизвестных ![]() представляет собой
вектор значений сеточных функций
представляет собой
вектор значений сеточных функций ![]() и
и ![]() в узлах сетки.
Соответствие между некоторым узлом сетки с координатами
в узлах сетки.
Соответствие между некоторым узлом сетки с координатами ![]() и индексом
и индексом ![]() элемента
элемента ![]() вектора
вектора ![]() , соответствующего значению функции температуры и функции
плотности внутренней энергии в данном узле, определяются соответственно по
формулам:
, соответствующего значению функции температуры и функции
плотности внутренней энергии в данном узле, определяются соответственно по
формулам:
![]()
где 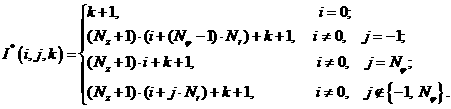
При такой нумерации узлы сетки на оси симметрии пластины (![]() ), тождественны для всех значений переменной
), тождественны для всех значений переменной ![]() .
.
Вследствие того, что в разностные соотношения входит
нелинейная функция плотности внутренней энергии ![]() , система уравнений (20) является нелинейной. Для численного
решения систем нелинейных уравнений можно использовать метод Ньютона. Для того,
чтобы им воспользоваться, требуется составить матрицу Якоби для системы (20) –
матрицу частных производных по всем переменным. Матрица Якоби имеет размерность
, система уравнений (20) является нелинейной. Для численного
решения систем нелинейных уравнений можно использовать метод Ньютона. Для того,
чтобы им воспользоваться, требуется составить матрицу Якоби для системы (20) –
матрицу частных производных по всем переменным. Матрица Якоби имеет размерность
![]() , где
, где ![]() определяется по формуле
(21), и является сильно разреженной, что позволяет применять специально
разработанные численные алгоритмы для решения подобных систем уравнений. Одним
из применяемых методов численного решения СЛАУ является метод LU-разложения матрицы системы. На основе
представленной математической модели в дальнейших публикациях планируется
представить результаты численного исследования для конкретного материала
пластины.
определяется по формуле
(21), и является сильно разреженной, что позволяет применять специально
разработанные численные алгоритмы для решения подобных систем уравнений. Одним
из применяемых методов численного решения СЛАУ является метод LU-разложения матрицы системы. На основе
представленной математической модели в дальнейших публикациях планируется
представить результаты численного исследования для конкретного материала
пластины.
4. К сравнительному анализу
пространственно-неоднородных и нестационарных температурных полей, получаемых
при численном моделировании
4.1. О некоторых результатах численного и лабораторного моделирования оптико-теплофизических
задач
В литературе известны описания множества моделей лазерной абляции для различных спектрально-энергетических режимов лазерного воздействия: УФ-ИК область спектра, плотности мощности излучения 104 – 1013 Вт/см2, длительности импульса от нескольких фемто- до сотен микросекунд, различных давлений и химических составов среды, окружающей зону воздействия; материалов мишени: металлы, керамики, полимеры, жидкости, биологические ткани. Большая часть моделей базируется на тепловых процессах: нагрев с последующим плавлением и испарением. Они описывают взаимодействия излучения с веществом на макроуровне, т.е. через уравнение теплопроводности. Такой подход наиболее адекватен при рассмотрении взаимодействия наносекундных (и длиннее) импульсов с металлами, когда вся энергия излучения мгновенно преобразуется в тепло.
При длительности импульса, сопоставимой или меньше времени релаксации (для металлов порядка 10-13 с), необходимо учитывать неравновесные процессы, что приводит к значительному усложнению модели, в том числе к двухтемпературности – отдельному рассмотрению электронной и атомной температур. Если же рассматриваемым веществом является, например, полимер, то, кроме особенностей поведения вещества при нагреве, в коротковолновой области спектра значительную роль начинают играть фотохимические процессы, что также значительно затрудняет моделирование.
Рассмотрение процессов только в теле мишени при длительностях воздействия более 10-9 с имеет тот существенный недостаток, что не рассматривается формирование облака испаренного вещества, которое не только может поглотить часть энергии поступающего импульса, но и оказывает обратное влияние на мишень (рис. 14).
Среди всего многообразия численных моделей чаще всего внимание уделяется моделированию процессов в паро-плазменном образовании, появляющемся в результате воздействия на мишень лазерного излучения, при этом распределение температур в мишени, если и моделируется, то или одномерно (вглубь), или точечно (центральная точка на поверхности мишени, где температура максимальна). То же относится и к эксперименту. Для рассмотрения процессов в облаке испаренного вещества существует множество моделей, в то время как процессы в теле мишени в подавляющем большинстве случаев описываются упомянутым выше уравнением теплопроводности.
|
|
|
|
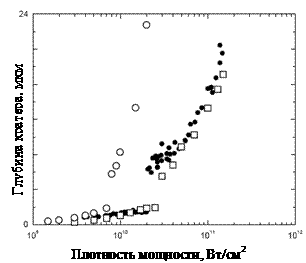
Рис. 14. Зависимость
глубины кратера от плотности мощности излучения рассчитанная без учета
экранировки излучения (окружности) и с учетом экранировки (квадраты); точки –
экспериментальные данные, полученные в результате облучения кристаллического
кремния 3 нс импульсом с длиной волны 266 нм [1] |
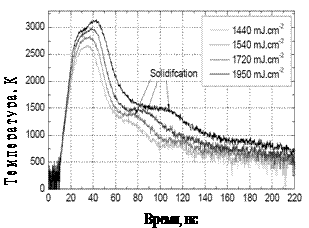
Рис. 15. Изменение
температуры на поверхности никелевой мишени во времени для различных
плотностей энергии излучения с длиной волны 248 нм при длительности импульса
25 нс [2] |
|
|
|
|
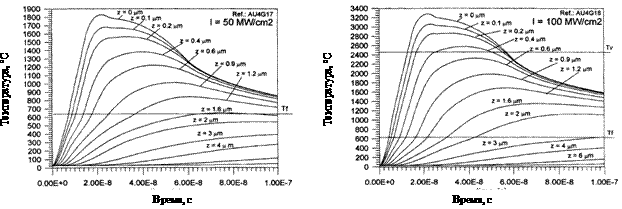
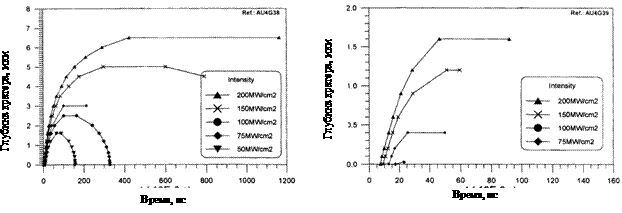
Рис. 16. Расчетное
распределение температур по глубине мишени (AU4G) в
результате облучения 20 нс импульсом с длиной волны 248 нм (слева – 20 МВт/см2,
справа – 100 МВт/см2) [3] |
|
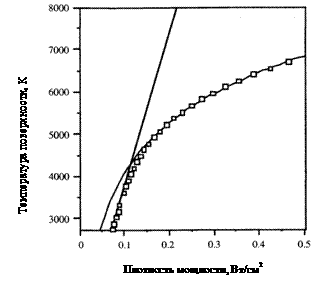
В рассматриваемой задаче определяющим параметром является температура. Точнее, её распределение на поверхности и в глубине мишени (рис. 15, 16) и зависимость этого распределения от параметров воздействия. На рис. 15 представлены результаты эксперимента, на рис. 17 – численного моделирования.
Однако экспериментально определить температуру как на поверхности, так и в глубине мишени довольно сложно, а определить динамику температурных полей с хорошим пространственным и временным разрешением практически невозможно. Поэтому кроме возможности определения зависимостей интересующих параметров без проведения сложных и дорогостоящих экспериментов, численное моделирование может служить источником данных, получение которых при наблюдении процесса затруднено или невозможно (рис. 18 – 19).
|
|
|
|
Рис. 17. Зависимость
максимальной температуры поверхности медной мишени от плотности мощности
поступающего излучения с длиной волны 248 нм и энергией в импульсе 0,1 Дж,
при изменении длительности импульса от 10 до 50 нс [4] |
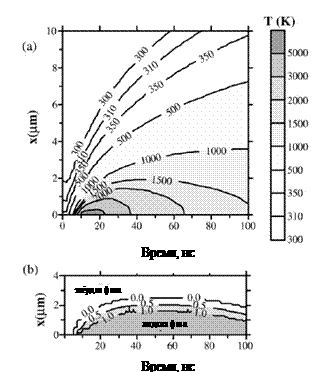
Рис. 18. Распределение
температур и фаз по глубине медной мишени в результате воздействия 10 нс
лазерного импульса [5] |
Чаще всего при рассмотрении взаимодействия излучения с поверхностью мишени определяют глубину, реже форму, кратера (рис. 20), в том числе ее изменение во времени (рис. 21) и в зависимости от параметров воздействия (рис. 22 – 24). Таким образом, этот параметр является наиболее простым для сравнения экспериментальных и расчетных данных по модификации поверхности в результате ее облучения (рис. 25 – 28).
|
|
|
|
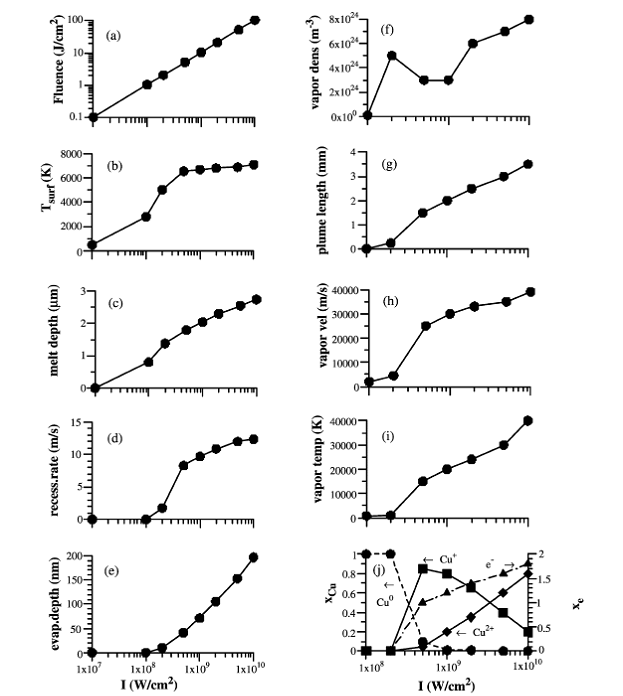
Рис. 19. Зависимости
различных параметров на поверхности мишени и в облаке испаренного вещества от
плотности мощности падающего излучения, полученные в результате численного
моделирования [5] |
|
|
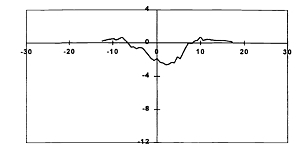
Рис. 20. Измеренная
контактным профилометром форма кратера в среднем сечении на поверхности
медной мишени в результате воздействия импульса 60 мкДж (пятно воздействия 8 мкм)
[6] |
|
|
|
|
|
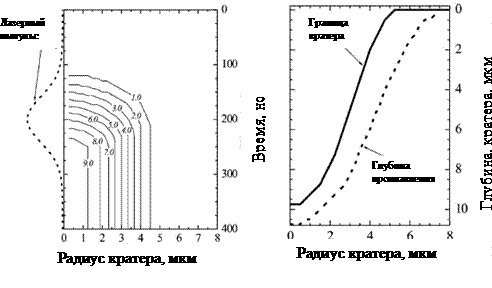
Рис. 21. Расчетная
динамика кратера и зоны проплавления при облучении стали AISI M3 127
Дж/см2 импульсом длительностью 100 нс с длиной волны излучения 1064 нм [7] |
|
|
|
|
|
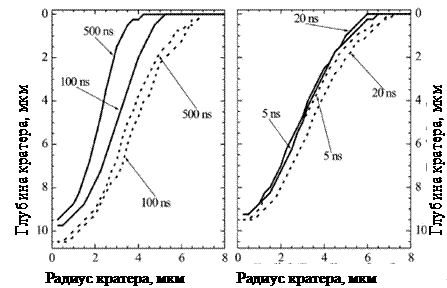
Рис. 22. Зависимость
конечных границ кратера и зоны проплавления при облучении мишени 125 Дж/см2
импульсами различной длительности [7] |
|
|
|
|
|
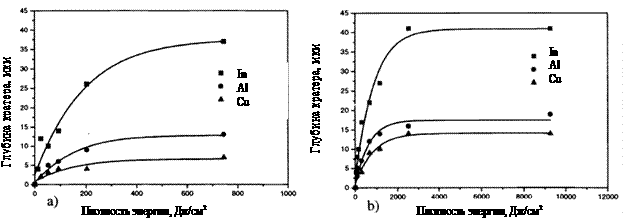
Рис. 23. Изменение глубины
кратера на поверхности легкоплавких металлов в зависимости от плотности
энергии падающего излучения с длиной волны 578 нм при длительности импульса
40 нс [8] |
|
|
|
|
|
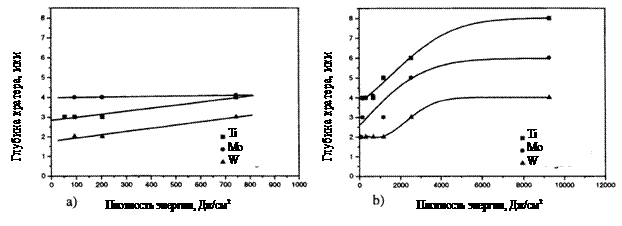
Рис. 24. Изменение глубины
кратера на поверхности тугоплавких металлов в зависимости от плотности
энергии падающего излучения с длиной волны 578 нм при длительности импульса
40 нс [8] |
|
|
|
|
|
Рис. 25. Предполагаемая
динамика границы области проплавления (слева) и испарения (справа) в
результате облучения мишени (AU4G) 20 нс импульсом с длиной волны 248 нм [3] |
|
|
|
|
|
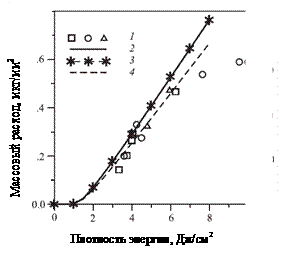
Рис. 26. Массовый расход с
поверхности графитовой мишени: сравнение данных эксперимента (1) с различными
расчетными моделями [9] |
|
Создание модели, описывающей взаимосвязь всех факторов, влияющих на результат взаимодействия излучения с веществом, представляется мало реальным. Простые модели, позволяющие быстро получать результаты, хотя бы и с невысокой точностью, в широком диапазоне параметров и условий воздействия, могут оказаться более востребованными, чем высокозатратные и высокоточные, но узкоспециализированные пакеты. Такие близкие к качественным расчётные данные могли бы позволить при сопоставлении с результатами экспериментов получать представление о ходе процессов по недоступным для диагностической техники параметрам значительно быстрее, чем длительные вычисления при подробном моделировании.
|
|
|
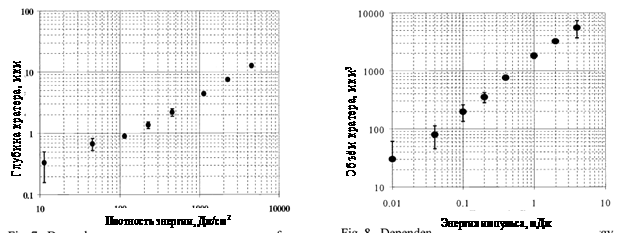
Рис. 27. Изменение глубины
(слева) и объема (справа) кратера на поверхности мишени в зависимости от
плотности энергии и энергии импульса излучения с длиной волны 532 нм при
длительности импульса 6 нс [10] |
|
|
|
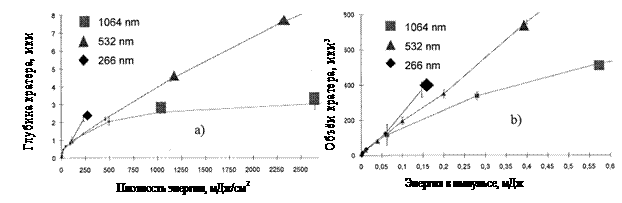
Рис. 28. Изменение глубины
(слева) и объема (справа) кратера на поверхности мишени в зависимости от
плотности энергии и энергии импульса излучения (при диаметре пятна 10 мкм) с
различными длинами волн при длительности импульса 6 нс [10] |
4.2. О параметризации процесса лазерной абляции
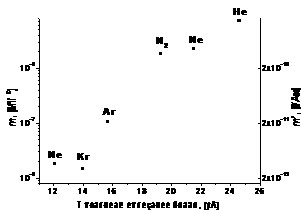
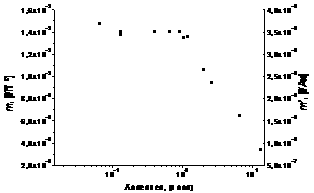
Динамика температурных полей на поверхности и в теле мишени определяется множеством параметров, наиболее значимые из которых: длительность импульса воздействия (табл. 1); длина волны излучения, определяющая характер воздействия, оказываемого излучением на мишень; количество поглощенной энергии; теплопроводность материала мишени; состояние мишени к моменту начала воздействия; условия окружающей среды. Далее рассмотрим эти параметры подробнее.
Табл.
1. Удельный объем кратера на поверхности мишени (108 мкм3/Дж),
определенный для ряда веществ при различных условиях воздействия импульсов с
энергией 60 мкДж [6].
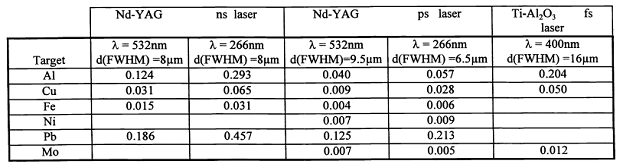
Длительность импульса воздействия определяет механизм нагрева мишени. При длительностях импульса, превышающих время релаксации, можно считать, что поглощенная энергия излучения мгновенно преобразуется в тепло, если же длительность импульса меньше времени релаксации или близка к нему, необходимо рассматривать более сложные неравновесные процессы. Кроме того, при длительностях импульса свыше 10-9 с часть излучения может быть экранирована пароплазменным образованием у поверхности мишени. При больших энергиях и длительностях воздействия необходимо также рассматривать вклад излучения этого образования в нагрев мишени.
Под характером воздействия подразумевается, приводит ли облучение мишени только к ее нагреву, инициируются ли вдобавок к нагреву фотохимические реакции или фотохимические процессы преобладают над тепловыми.
Количество поглощенной энергии определяется:
- коэффициентом поглощения сред на пути от источника воздействия до поверхности мишени;
- коэффициентом отражения поверхности мишени, зависящим от угла падения и длины волны излучения, шероховатости и температуры поверхности мишени;
- линейным коэффициентом поглощения, зависящим от угла падения и длины волны излучения, температуры мишени, наличия включений.
Под состоянием мишени к моменту начала воздействия подразумевается распределение температуры, модификация (упрочнение, наличие сажи, глубоких кратеров) поверхности, наличие неоднородностей (включений, пузырьков, трещин) в теле мишени. Эти факторы, точнее их изменение, становятся особенно актуальны при многократном воздействии.
Условия окружающей среды – ее химический состав и давление – оказывают значительное влияние как на процесс испарения с поверхности облучаемой мишени, так и на формирование экранирующего мишень паро-плазменного образования (рис. 29).
|
|
|
Рис. 29. Примеры изменения
масс-расходных параметров в зависимости от химического состава (сверху – Cu, 1064 нм, 5 кДж/см2, [10]) и давления (снизу – Al, 10600 нм, 4 кДж/см2, [11]) среды воздействия |
5. О методиках физического моделирования и
параметрах сравнительного анализа экспериментальных и расчетно-теоретических
результатов
5.1. Нестационарные Т-поля
Для диагностики нестационарных температурных полей используются как контактные, так и бесконтактные методы. Преимуществом контактных методов является возможность измерения температуры не только на поверхности, но и в глубине мишени. Недостаток же их в инертности и неудобстве монтажа в большом количестве в мишень.
Бесконтактные методы измерения температурных полей основаны на законах Планка и Вина, когда анализируется спектр, переизлучаемый поверхностью конденсированной мишени; на использовании зондирующего излучения с последующим анализом рассеянного излучения или спектрального коэффициента отражения (рис. 30), если известна его температурная зависимость [2]. Недостатками бесконтактных методов является их аппаратурная сложность, возможность получения распределения температуры только на поверхности мишени. К преимуществам относятся высокое временное и пространственное разрешение, возможность получения динамики фазовых превращений при использовании зондирующего излучения.
Так, в [2] температура поверхности измерялась при помощи (HgCdTe)-детекторов ИК-излучения. Для определения температуры в малых областях использовалась система металлических фокусирующих зеркал. Для интерпретации сигнала, полученного в ходе эксперимента, предварительно проводилась калибровка сигнала от фотодетектора путем нагревания каждого образца до фиксированных температур. Кроме температуры на поверхности, при помощи данного метода измерялась теплопроводность, определялись порог плавления и длительность процесса плавления.
5.2. Динамика формы кратера на поверхности конденсированной мишени и
массового расхода
Для определения глубины и формы
кратера используются контактные и оптические профилометры, последние, как и
интерферометрия поверхности, позволяют регистрировать и динамику кратера in-situ. Разрешающая способность
доступных контактных профилометров меньше 10-
Наиболее удобным способом измерения глубины кратера является просвечивание тонких мишеней потоком высокоэнергетичных квантов (в области мягкого рентгена) [12]. Вынос вещества мишени уменьшает оптическую толщину в зоне воздействия, и детектор, расположенный за мишенью, регистрирует более интенсивный сигнал, чем вне зоны воздействия (рис. 31). В этом случае возможна регистрация как глубины, так и характерного диаметра кратера с высоким временным разрешением.
Измерение формы кратера методами поверхностной интерферометрии основано на анализе изменений в распределении фаз и амплитуд, возникающих в отраженном от поверхности потоке в результате ее модификации лазерным излучением. Точность таких методов по пространству сопоставима с длиной волны зондирующего излучения, а по времени – определяется используемой для регистрации камерой.
При определении массового расхода с поверхности конденсированной мишени прямыми измерениями обычно удается получить только интегральную величину изменения массы путем взвешивания мишени или пластины-ловушки до и после воздействия; иногда применяют кварцевые кристаллические детекторы, используемые для контроля толщины напыляемых пленок. Однако такой подход не учитывает обратного потока частиц и тяжелых капель, масса которых может достигать 25% испаренного вещества [9]. В зависимости от параметров воздействия и облучаемого вещества массовый расход сильно изменяется, но для большинства случаев лазерного воздействия в умеренном диапазоне (10-100 мДж, 1-100 нс) не превосходит 10 мкг/импульс, а чаще всего меньше 1 мкг/импульс [13]. Измерение столь малых величин может привести к значительным погрешностям или вынудит усреднять расход, полученный для нескольких импульсов, пренебрегая возникающими эффектами, выражающимися в уменьшении массового расхода с ростом числа импульсов [11, 14], вызванном механической и оптической модификацией поверхности, газодинамическом запирании канала кратера, или появлении эффектов накопления при высокой частоте следования импульсов лазерного излучения, наиболее выраженным из которых является экранировка поверхности мишени плазменным образованием.
Временная динамика массового расхода может быть определена косвенными измерениями – глубины кратера, плотности паров у поверхности, энергии ударной волны [4], массового и эмиссионного спектра.
Измерения массового расхода с поверхности мишени по косвенным данным – энергии ударной волны и масс-спектральным интенсивностям – основываются на том, что эти показатели пропорциональны количеству испаренного вещества. При таком подходе сначала проводят тарировку на основании прямых изменений массового расхода, а затем используют полученные данные для экстраполяции, основываясь на измерении только энергии ударной волны или масс-спектра. Такие методы хоть и не очень точны, но удобны для экспресс-анализа.
Отдельная группа методов определения массового расхода с поверхности мишени основана на оптической диагностике облака испаренного вещества и заключается в определении концентрации нейтральных частиц, ионов и электронов с использованием фотографии: теневые, шлиреновские, абсорбционные и интерференционные снимки (рис. 32 – 33). Общим для этих методик является анализ оптической плотности среды облака испаренного с поверхности мишени материала в разных его участках с последующей интерпретацией полученных данных для получения распределения концентрации частиц.
И, наконец, концентрация электронов и электронная температура в облаке могут быть определены в результате анализа эмиссионных спектров. Электронная температура пропорциональна ширине спектральной линии, определенной по полувысоте, а концентрация электронов – площади под кривой контура линии с учетом центральной длины волны.
|
|
|
|
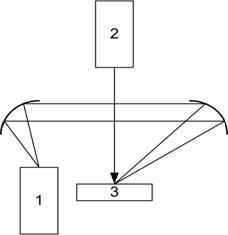
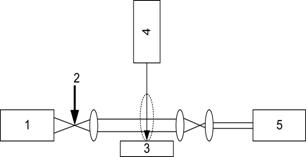
Рис. 30. Схема регистрации
повременного распределения температур на поверхности мишени с использованием
методов ИК-радиометрии [2]. 1 – ИК-фотодетектор; 2 – лазер воздействия; 3 –
мишень |
Рис. 31. Схема определения
глубины кратера на поверхности мишени при помощи ЭУВ или МР излучения. 1 –
ПЗС-камера; 2 – мишень; 3 – лазер воздействия; 4 – источник высокоэнергетичных
квантов |
|
|
|
|
Рис. 32. Схема регистрации
шлирен-грамм. 1 – ПЗС-камера; 2 – нож Фуко; 3 – мишень; 4 – лазер
воздействия; 5 – лазер подсветки |
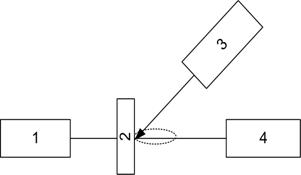
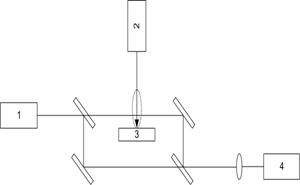
Рис. 33. Схема регистрации
интерферограмм на основе четырехзеркального интерферометра. 1 – лазер
подсветки; 2 – лазер воздействия; 3 – мишень; 4 – ПЗС-камера |
5.3.
Об экспериментальном определении спектрально-энергетических порогов фазовых
переходов и динамики волн испарения и ионизации
В качестве параметров, определяющих характеристики и динамику взаимодействия излучения с веществом на разных режимах воздействия, рассматриваются различные пороговые значения плотности мощности (плотности энергии) излучения. Это могут быть пороги плавления, испарения, ионизации, фотодекомпозиции. При превышении пороговых значений режим взаимодействия излучения с веществом изменяется. С одной стороны, пороговые значения удобны для экспериментального определения и сравнения с полученными в результате численного моделирования данными по признаку наличия или отсутствия явления, с другой – конкретные значения очень сильно зависят от условий воздействия, причем не только от спектрально-энергетических характеристик излучения. В связи с этим уместно говорить не о спектрально-энергетических порогах для вещества вообще, а о порогах конкретно при данных условиях воздействия. В работах множества авторов исследовался порог абляции; их результаты продемонстрировали, что пороговые значения зависят и от таких второстепенных параметров как размер пятна фокусировки, модовой структуры лазерного пучка, поляризации излучения и др., а также отличаются для одноименных материалов разных производителей.
Волны испарения и ионизации существенно влияют на поглощение лазерного излучения до мишени. Инструментом для определения их динамики служат соответственно теневая и интерференционная фотография с разрешением по времени. Кроме того, исследование распространения волн ионизации возможно при помощи электрических (лэнгмюровских) зондов, что значительно проще, чем интерференционная фотография, и при проведении эксперимента, и при последующей обработке данных. Для получения данных о концентрации электронов на основе интерференционных снимков анализируется частота чередования светлых и темных полос; с помощью зонда получают значения электронного или ионного токов.
6. Литература
1. Lu Q. et al. Thermal model of phase explosion for high-power
laser ablation. In High-Power Laser Ablation IV. 2002. Taos, NM, USA: SPIE.
2. Semmar N. et al. Coupled
photo-thermal and time resolved reflectivity methods to original investigation
of laser/material nanosecond interaction. In High-Power Laser Ablation VI.
2006. Taos, NM, USA: SPIE.
3. Ocana J.L. et al. Ablation
processes induced by UV lasers in metals and ceramics. In High-Power Laser
Ablation. 1998. Santa Fe, NM, USA: SPIE.
4. Stauter C., Gerard P., and
Fontaine J. Shock wave generated during laser ablation. In High-Power Laser
Ablation. 1998. Santa Fe, NM, USA: SPIE.
5. Bogaerts A. et al. Laser ablation
for analytical sampling: what can we learn from modeling? Spectrochimica Acta
Part B: Atomic Spectroscopy, 2003. 58:
p. 1867-1893.
6. Semerok A.F. et al. Laser
ablation efficiency of pure metals with femtosecond, picosecond, and nanosecond
pulses. In High-Power Laser Ablation. 1998. Santa Fe, NM, USA: SPIE.
7. Dumitru G., Romano V. and Weber
H.P. Model and computer simulation of nanosecond laser material ablation.
Applied Physics A: Materials Science & Processing, 2004. 79(4): p. 1225-1228.
8. Fishburn J.M. et al. Exploring
the explosive ablation regime of metals in nanosecond micromachining. In
High-Power Laser Ablation II. 2000. Osaka, Japan: SPIE.
9. Morozov A.A. Thermal model of
pulsed laser ablation: back flux contribution. Applied Physics A: Materials
Science & Processing, 2004. 79(4):
p. 997-999.
10. Semerok A. et al. Microablation of
pure metals: laser plasma and crater investigations. In Nonresonant
Laser-Matter Interaction (NILMI-10). 2001: SPIE.
11. Pakhomov A.V., Lin J. and Herren
K.A. Effect of air pressure on propulsion with TEA CO[sub 2] laser. In
High-Power Laser Ablation V. 2004. Taos, NM, USA: SPIE.
12. Tallents G.J. et al. X-ray
lasers as probes to measure plasma ablation rates. In Soft X-Ray Lasers and
Applications VII. 2007. San Diego, CA, USA: SPIE.
13. Torrisi L. et al. Plasma-laser
characterization by electrostatic mass quadrupole analyzer. Nuclear Instruments
and Methods in Physics Research Section B: Beam Interactions with Materials and
Atoms, 2008. 266(2): p. 308-315.
14. Kononenko T.V. et al. Processing
of diamond and ceramics by picosecond/nanosecond laser pulses in IR-UV spectral
range. In High-Power Laser Ablation. 1998. Santa Fe, NM, USA: SPIE.
15. Волков И.К., Канатников А.Н. Интегральные преобразования и операционное исчисление. – М.: Изд-во МГТУ им. Н. Э. Баумана, 1996. – 228 с.
16. Самарский
А.А. Теория разностных схем. М.: Наука, Физматлит., 1989. – 616 с.
17. Самарский А.А., Моисеенко Б.Д. Экономичная схема сквозного счета для многомерной задачи Стефана // ЖВМ и МФ. 1965. Т. 5. № 5. С. 816 – 827.