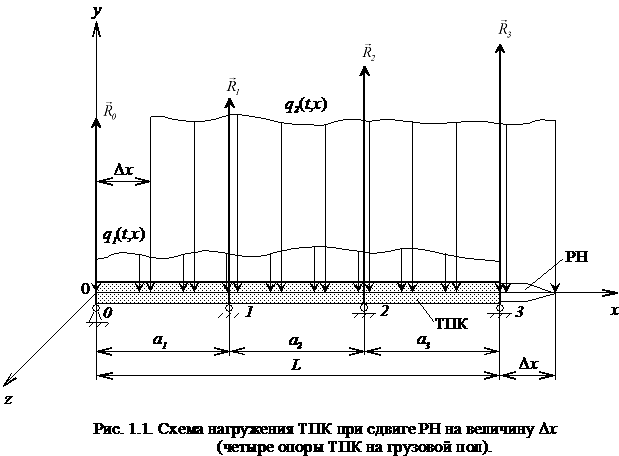
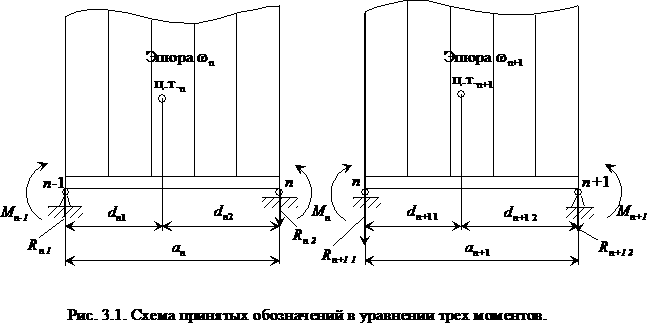Динамические нагрузки на самолет-носитель при реализации воздушного старта ракеты-носителя (четырехопорная схема)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Примечание |
|
0£ |
70 |
196 |
3,73 |
1,12 |
|
|
2,8< |
3290 |
4606 |
3,94 |
1,18 |
Бак
«Г1» |
|
4,2< |
9450 |
17010 |
3,94 |
1,18 |
Бак
«Г1» |
|
6,0< |
550 |
825 |
3,89 |
1,15 |
|
|
7,5< |
12830 |
52605 |
3,73 |
1,12 |
Бак
«О1» |
|
11,6< |
410 |
1804 |
0,85 |
0,24 |
|
|
16,0< |
8770 |
8770 |
2,20 |
0,45 |
Бак
«О2» |
|
17,0< |
820 |
1640 |
1,20 |
0,20 |
|
|
19,0< |
6710 |
2684 |
1,80 |
0,35 |
Бак
«Г2» |
|
19,4< |
250 |
475 |
1,80 |
0,35 |
|
|
21,3< |
1650 |
10560 |
0,44 |
0,08 |
КРБ+ПН |
|
27,7< |
250 |
825 |
0,20 |
0,09 |
|
|
|
|
S=102000 |
|
|
|
*) от хвостовой
части РН.
Здесь Е–
модуль упругости, ![]() – осевой момент инерции поперечного сечения РН,
– осевой момент инерции поперечного сечения РН, ![]() – модуль сдвига (модуль упругости второго рода),
– модуль сдвига (модуль упругости второго рода), ![]() – площадь поперечного сечения РН.
– площадь поперечного сечения РН.
Средняя погонная масса РН составляет
![]() . (2.2)
. (2.2)
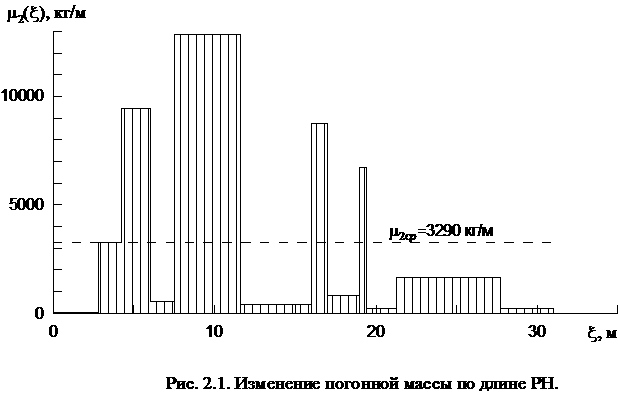
На рис. 2.1 показано изменение
погонной массы РН по длине. Видно, что в местах расположения баков погонная
масса на порядок больше, чем в местах расположения межбаковых и хвостовых
отсеков.
3.
Методика расчета четырехопорной схемы
Основную систему для расчета статически
неопределимой балки получают путем ее разрезания в сечениях над опорами.
Неизвестными являются изгибающие (опорные) моменты, возникающие в сечениях над
опорами. Неизвестные моменты считаются положительными, когда они вызывают
сжатие верхних волокон балки.
Методика расчета статически
неопределимой балки включает следующие шаги [2]:
1.
Построение расчетной схемы статически неопределимой
балки.
2.
Нумерация слева направо опор и пролетов балки.
3.
Построение эпюры изгибающих моментов от заданной внешней
нагрузки для каждого пролета балки (как для простой балки на двух опорах).
4.
Составление уравнения трех моментов для каждой
промежуточной опоры балки.
5.
Решение системы уравнений трех моментов для определения
значений неизвестных опорных моментов в сечениях над промежуточными опорами.
6.
Построение эпюр поперечной силы и изгибающего момента для
каждого пролета балки, как для однопролетной простой балки, под действием
заданной нагрузки и опорных моментов.
7.
Определение опорных реакций в исходной балке.
3.1. Уравнения трех моментов
Уравнение трех моментов для некоторой опоры ![]() в общем случае имеет
следующий вид:
в общем случае имеет
следующий вид:
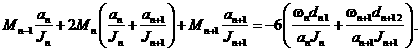 (3.1)
(3.1)
В это уравнение входят три неизвестных момента: ![]() Физически условие
(3.1) показывает, что взаимный угол поворота двух смежных поперечных сечений
над опорой
Физически условие
(3.1) показывает, что взаимный угол поворота двух смежных поперечных сечений
над опорой ![]() равен нулю. Здесь
равен нулю. Здесь ![]() - длины пролетов,
соответственно, между опорами
- длины пролетов,
соответственно, между опорами ![]() и
и ![]() ;
; ![]() - моменты инерции
пролетов
- моменты инерции
пролетов ![]() ;
; ![]() - площади эпюр
изгибающих моментов, возникающих от заданной внешней нагрузки в простых балках
с пролетами
- площади эпюр
изгибающих моментов, возникающих от заданной внешней нагрузки в простых балках
с пролетами ![]() ;
; ![]() - расстояние от центра тяжести площади эпюры
- расстояние от центра тяжести площади эпюры ![]() до левой опоры пролета
до левой опоры пролета
![]() ;
; ![]() - расстояние от центра тяжести площади эпюры
- расстояние от центра тяжести площади эпюры ![]() до правой опоры
пролета
до правой опоры
пролета ![]() . Принятые обозначения в уравнении трех моментов показаны на
рис. 3.1. При построении эпюр изгибающих моментов от внешних нагрузок не
учитывают действие опорных моментов
. Принятые обозначения в уравнении трех моментов показаны на
рис. 3.1. При построении эпюр изгибающих моментов от внешних нагрузок не
учитывают действие опорных моментов![]() ,
,![]() ,
,![]() , которые приложены в местах условных разрезов исходной балки
заданной системы. Каждый отдельный пролет, полученный в результате
«разрезания», считается простой балкой на двух опорах.
, которые приложены в местах условных разрезов исходной балки
заданной системы. Каждый отдельный пролет, полученный в результате
«разрезания», считается простой балкой на двух опорах.
В правую часть уравнения трех моментов (3.1) входят
произведения ![]() и
и ![]() , которые по существу являются статическими моментами площади
левой эпюры изгибающего момента относительно левой опоры и площади правой
эпюры изгибающего момента
относительно правой опоры.
, которые по существу являются статическими моментами площади
левой эпюры изгибающего момента относительно левой опоры и площади правой
эпюры изгибающего момента
относительно правой опоры.
Если известен статический
момент ![]() относительно левой
опоры пролета
относительно левой
опоры пролета ![]() , то статический момент относительно правой опоры можно
определить пересчетом по формуле
, то статический момент относительно правой опоры можно
определить пересчетом по формуле
![]() .
(3.2)
.
(3.2)
Используем уравнение трех моментов для раскрытия дважды
статически неопределимой системы, которой является ТПК на четырех опорах (рис.
1.1). В этой системе неизвестны опорные моменты ![]() , приложенные в местах «разреза» ТПК над внутренними опорами 1
и 2. Левый конец ТПК предполагается шарнирно опертым, поэтому
, приложенные в местах «разреза» ТПК над внутренними опорами 1
и 2. Левый конец ТПК предполагается шарнирно опертым, поэтому
![]() .
(3.3)
.
(3.3)
На правом конце
ТПК в общем случае прикладывается момент ![]() от вышедшей на
величину
от вышедшей на
величину ![]() части РН, т.е.
части РН, т.е.
![]() . (3.4)
. (3.4)
Знак «-» взят по
той причине, что в сечении над опорой 3 рассматривается момент от
внешних нагрузок, приложенных справа [2]. Сам момент ![]() положителен, так как
действует по часовой стрелке.
положителен, так как
действует по часовой стрелке.
Будем полагать, что ТПК имеет постоянное
сечение, поэтому момент инерции по длине будет постоянным, и система уравнений
для определения неизвестных опорных моментов ![]() с учетом условий (3.3)
и (3.4) имеет вид
с учетом условий (3.3)
и (3.4) имеет вид
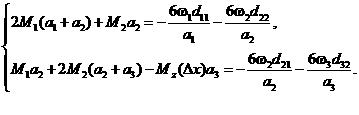 (3.5)
(3.5)
Здесь ![]() - расстояние от центра
тяжести эпюры изгибающего момента
- расстояние от центра
тяжести эпюры изгибающего момента ![]() -го пролета (i=1,2, 3) до левой опоры, если j = 1, и до правой
опоры, если j = 2.
-го пролета (i=1,2, 3) до левой опоры, если j = 1, и до правой
опоры, если j = 2.
Исключим из уравнений (3.5) неизвестный
момент ![]() и вычислим
и вычислим ![]() :
:
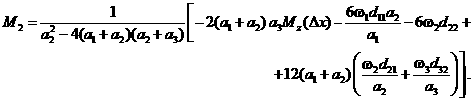 (3.6)
(3.6)
С использованием соотношений типа (3.2) выразим в (3.6)
статические моменты относительно правых опор ![]() через статические
моменты относительно левых опор
через статические
моменты относительно левых опор ![]() , соответственно для пролетов
, соответственно для пролетов ![]() . Тогда уравнение (3.6) можно привести к виду
. Тогда уравнение (3.6) можно привести к виду
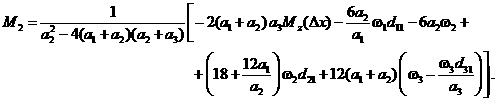 (3.7)
(3.7)
После вычисления ![]() посредством (3.7), можно из первого уравнения (3.5)
определить
посредством (3.7), можно из первого уравнения (3.5)
определить ![]() , выразив статический момент относительно правой опоры
, выразив статический момент относительно правой опоры ![]() через статический
момент относительно левой опоры
через статический
момент относительно левой опоры ![]() :
:
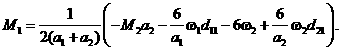 (3.8)
(3.8)
Соотношения (3.7) и (3.8) позволяют
вычислять опорные моменты при различных длинах пролетов ![]() и произвольном
распределении нагрузок по длине ТПК. Для вычисления
и произвольном
распределении нагрузок по длине ТПК. Для вычисления ![]() необходимо задать
следующие величины:
необходимо задать
следующие величины:
![]() - момент от вышедшей
на
- момент от вышедшей
на ![]() части РН;
части РН;
![]() - площади эпюр
изгибающих моментов для пролетов
- площади эпюр
изгибающих моментов для пролетов ![]() ;
;
![]() - статические моменты площадей эпюр изгибающих моментов
относительно левых опор для пролетов
- статические моменты площадей эпюр изгибающих моментов
относительно левых опор для пролетов ![]() .
.
Получим уравнения для расчета
необходимых величин. Принято, что к ТПК приложена суммарная погонная нагрузка
(1.3), включающая погонную силу ![]() от распределенной
массы ТПК (1.4) и погонную силу
от распределенной
массы ТПК (1.4) и погонную силу ![]() от распределенной
массы РН (1.5). В соответствии с принятыми обозначениями, при
от распределенной
массы РН (1.5). В соответствии с принятыми обозначениями, при ![]() погонные силы
направлены вниз, т.е. отрицательны. На правом конце ТПК при выходе РН на величину
погонные силы
направлены вниз, т.е. отрицательны. На правом конце ТПК при выходе РН на величину![]() возникает перерезывающая сила (1.6) и изгибающий момент
(1.7).
возникает перерезывающая сила (1.6) и изгибающий момент
(1.7).
3.2. Определение реакций в опорах
Предварительно введем условные
обозначения![]() для реакций в опорах
от заданной внешней нагрузки, рассматривая каждый пролет ТПК как простую
балку на двух опорах. Здесь первый индекс
для реакций в опорах
от заданной внешней нагрузки, рассматривая каждый пролет ТПК как простую
балку на двух опорах. Здесь первый индекс ![]() указывает на номер
пролета, а второй индекс
указывает на номер
пролета, а второй индекс ![]() указывает на номер
опоры: 1 – левая опора, 2 – правая опора.
указывает на номер
опоры: 1 – левая опора, 2 – правая опора.
Для построения эпюры изгибающих моментов
от заданной внешней нагрузки в каждом пролете балки (как для простой балки на
двух опорах) необходимо определить реакции в опорах. Так, для первого пролета,
где ![]() , реакция в правой опоре (номер 1 на рис. 1.1)
определяется из условия равенства нулю всех моментов относительно левой опоры
(номер 0 на рис. 1.1):
, реакция в правой опоре (номер 1 на рис. 1.1)
определяется из условия равенства нулю всех моментов относительно левой опоры
(номер 0 на рис. 1.1):
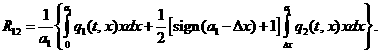 (3.9)
(3.9)
Реакция в левой опоре находится из условия равенства нулю
проекций всех сил на ось у:
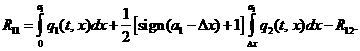 (3.10)
(3.10)
Аналогично можно определить
реакции для второго пролета ТПК, где ![]() :
:
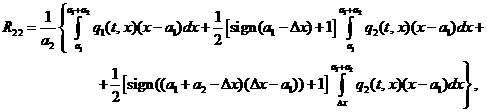 (3.11)
(3.11)
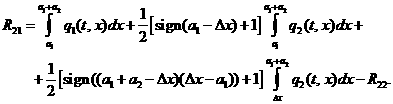 (3.12)
(3.12)
Таким же способом определяются
реакции для третьего пролета, где ![]() :
:
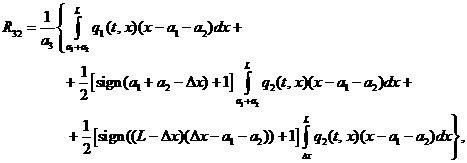 (3.13)
(3.13)
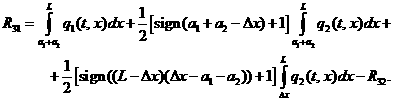 (3.14)
(3.14)
3.3. Изгибающие моменты и их интегралы
Зная внешние
нагрузки в каждом пролете как в простой балке на двух опорах и вычисленные выше
реакции от этих нагрузок, можно получить уравнения изгибающего момента для
каждого пролета, затем вычислить площади эпюр изгибающего момента и определить
статические моменты этих площадей относительно левых опор.
Для вычисления изгибающего момента в
произвольном сечении х первого пролета, где ![]() , воспользуемся соотношением (3.11) из [1], тогда
, воспользуемся соотношением (3.11) из [1], тогда
 (3.15)
(3.15)
Первые два слагаемых существуют при
любом ![]() сдвиге РН относительно
ТПК, а третье слагаемое существует только при
сдвиге РН относительно
ТПК, а третье слагаемое существует только при ![]() .
.
Площадь ![]() эпюры изгибающего
момента, возникающего в первом пролете от заданной внешней нагрузки,
определяется интегралом
эпюры изгибающего
момента, возникающего в первом пролете от заданной внешней нагрузки,
определяется интегралом
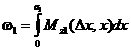 ,
,
или подробно с
учетом (3.15):
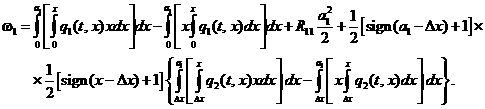 (3.16)
(3.16)
Статический момент относительно левой
опоры ![]() эпюры изгибающего момента на первом пролете
определяется интегралом
эпюры изгибающего момента на первом пролете
определяется интегралом
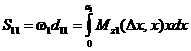 ,
,
или подробно с
учетом (3.15):
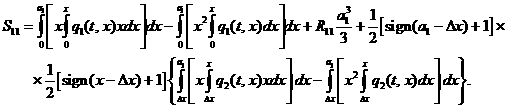 (3.17)
(3.17)
Изгибающий
момент в произвольном сечении х второго пролета, где ![]() , определяется соотношением, подобным (3.15):
, определяется соотношением, подобным (3.15):
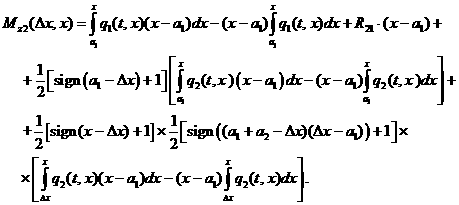 (3.18)
(3.18)
Площадь ![]() эпюры изгибающего
момента, возникающего во втором пролете от заданной внешней нагрузки,
определяется интегралом
эпюры изгибающего
момента, возникающего во втором пролете от заданной внешней нагрузки,
определяется интегралом
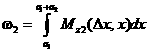 ,
,
или подробно с учетом (3.18):
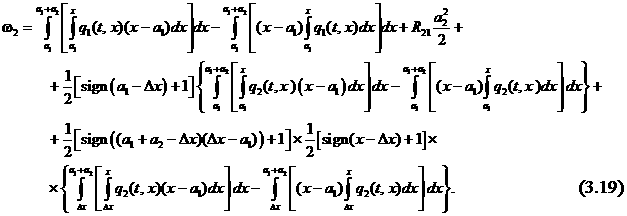
Статический
момент относительно левой опоры ![]() эпюры изгибающего момента на втором пролете определяется
интегралом
эпюры изгибающего момента на втором пролете определяется
интегралом
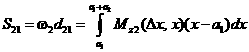 ,
,
или подробно с учетом (3.18):
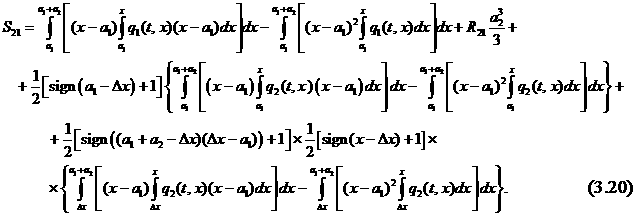
Изгибающий
момент в произвольном сечении х третьего пролета, где ![]() , определяется соотношением, подобным (3.15):
, определяется соотношением, подобным (3.15):
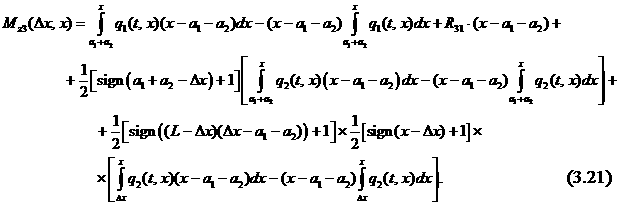
Площадь ![]() эпюры изгибающего
момента, возникающего в третьем пролете от заданной внешней нагрузки,
определяется интегралом
эпюры изгибающего
момента, возникающего в третьем пролете от заданной внешней нагрузки,
определяется интегралом
 ,
,
или подробно с
учетом (3.21):
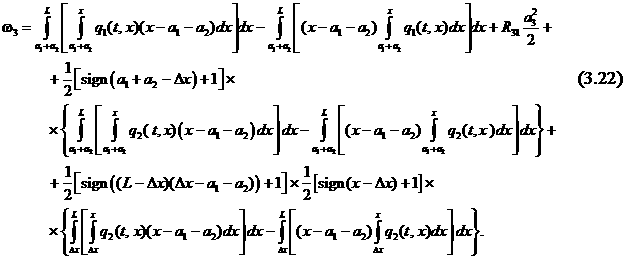
Статический момент относительно
левой опоры ![]() эпюры изгибающего момента на третьем пролете определяется интегралом
эпюры изгибающего момента на третьем пролете определяется интегралом
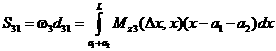 ,
,
или подробно с
учетом (3.21):
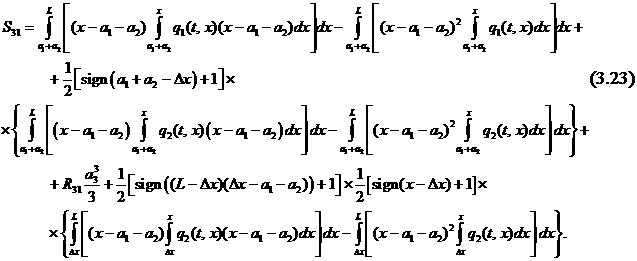
Полученные выше соотношения являются
наиболее общими и верны при любых длинах пролетов ![]() , любых видах погонных нагрузок от РН
, любых видах погонных нагрузок от РН ![]() и ТПК
и ТПК ![]() , а также при любом сдвиге
, а также при любом сдвиге ![]() РН относительно ТПК.
РН относительно ТПК.
3.4. Расчет нагрузок на ТПК и грузовой пол СН
Вычисленные в
общем виде площади эпюр изгибающих моментов на всех пролетах и их статические
моменты относительно левых опор пролетов позволяют решать задачу трех моментов
в общем случае. После вычисления опорных моментов ![]() и
и ![]() по формулам (3.7) и
(3.8), соответственно, можно определить нагрузки на ТПК и грузовой пол СН.
Эпюры поперечной силы и изгибающего момента строятся для каждого пролета ТПК
между опорами, как для однопролетной простой балки на двух опорах, под действием
заданной нагрузки и опорных моментов
по формулам (3.7) и
(3.8), соответственно, можно определить нагрузки на ТПК и грузовой пол СН.
Эпюры поперечной силы и изгибающего момента строятся для каждого пролета ТПК
между опорами, как для однопролетной простой балки на двух опорах, под действием
заданной нагрузки и опорных моментов ![]() и
и ![]() .
.
В общем случае, для n-го пролета
величины изгибающего момента и поперечных сил в сечении х определяются
следующими соотношениями [2]:
![]() (3.24)
(3.24)
![]() (3.25)
(3.25)
Здесь ![]() - изгибающий момент и
поперечная сила от заданной внешней нагрузки;
- изгибающий момент и
поперечная сила от заданной внешней нагрузки;
![]()
- изгибающий
момент от опорных моментов ![]() ;
;
![]()
- поперечная
сила от опорных моментов ![]() (равная левой опорной
реакции от действия указанных опорных моментов); координата х измеряется
от левой границы n-го пролета.
(равная левой опорной
реакции от действия указанных опорных моментов); координата х измеряется
от левой границы n-го пролета.
Опорные реакции для ТПК, как неразрезной
балки, равны разности поперечных сил, действующих в сечениях, расположенных
слева и справа от каждой опоры в непосредственной близости, и представляют
собой величины скачков в эпюре поперечных сил [2]:
![]() .
(3.26)
.
(3.26)
Направление вверх для опорных реакций
считается положительным.
Воспользуемся уравнениями (3.24) и
(3.25) для построения нагрузок на ТПК как неразрезной балки.
Для первого пролета (n=1), где ![]() , имеем
, имеем
![]() (3.27)
(3.27)
![]() (3.28)
(3.28)
Здесь ![]() определяется
уравнением (3.15),
определяется
уравнением (3.15), ![]() , перерезывающая сила от внешних нагрузок вычисляется как
, перерезывающая сила от внешних нагрузок вычисляется как
![]() , (3.29)
, (3.29)
![]() задается условием
(3.10).
задается условием
(3.10).
Для второго пролета (n=2) , где ![]() , имеем
, имеем
![]() (3.30)
(3.30)
![]() (3.31)
(3.31)
Здесь ![]() определяется
уравнением (3.18), а перерезывающая сила от внешних нагрузок вычисляется как
определяется
уравнением (3.18), а перерезывающая сила от внешних нагрузок вычисляется как
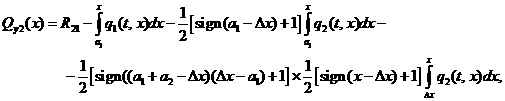 (3.32)
(3.32)
![]() задается условием
(3.12).
задается условием
(3.12).
Для третьего пролета (n=3), где ![]() , имеем
, имеем
![]() (3.33)
(3.33)
![]() (3.34)
(3.34)
Здесь ![]() определяется
уравнением (3.21),
определяется
уравнением (3.21), ![]() согласно (3.4),
перерезывающая сила от внешних нагрузок вычисляется как
согласно (3.4),
перерезывающая сила от внешних нагрузок вычисляется как
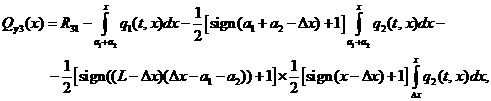 (3.35)
(3.35)
где ![]() задается условием (3.14).
задается условием (3.14).
4.
Определение нагрузок при четырехопорной схеме
При определении нагрузок для четырехопорной схемы
крепления ТПК к грузовому полу СН рассматривается тестовый набор следующих
режимов нагружения:
по
перегрузке
·
постоянная перегрузка;
·
линейно меняющаяся по длине РН и ТПК перегрузка;
по
изменению погонной массы РН
·
средняя погонная масса РН;
·
переменная по длине погонная масса РН (рис.2.1);
по
положению РН относительно ТПК
·
транспортировка заправленной РН в СН (![]() );
);
·
выход РН из ТПК в условиях квазиневесомости (![]() ).
).
4.1. Действие постоянной перегрузки
Рассматриваются два режима нагружения. Первый
режим связан с транспортировкой заправленной РН в СН, т.е. до начала выхода
РН из ТПК (![]() ). Расчетная нормальная перегрузка составляет
). Расчетная нормальная перегрузка составляет
![]() .
.
Второй режим связан с выходом
РН из ТПК в условиях квазиневесомости. Эксплуатационная нормальная перегрузка
составляет
![]() ,
,
и с учетом
коэффициента безопасности k=1,5 расчетная нормальная перегрузка
![]() .
.
В этом случае имеет место дополнительное
нагружение ТПК вследствие сдвига РН относительно ТПК на величину ![]() . В принятой модели взаимодействия РН с ТПК в процессе выхода
(РН – упругая цилиндрическая балка, ТПК – труба) РН не может поворачиваться
относительно ТПК вплоть до полного выхода. Вышедшая часть РН будет создавать на
срезе ТПК сосредоточенную силу
. В принятой модели взаимодействия РН с ТПК в процессе выхода
(РН – упругая цилиндрическая балка, ТПК – труба) РН не может поворачиваться
относительно ТПК вплоть до полного выхода. Вышедшая часть РН будет создавать на
срезе ТПК сосредоточенную силу ![]() и сосредоточенный момент
и сосредоточенный момент ![]() , величины которых однозначно определяются длиной
, величины которых однозначно определяются длиной ![]() вышедшей части РН из
ТПК. Максимальные величины
вышедшей части РН из
ТПК. Максимальные величины ![]() и
и ![]() будут достигаться непосредственно перед выходом РН из ТПК,
т.е. при
будут достигаться непосредственно перед выходом РН из ТПК,
т.е. при ![]() . На следующем этапе модель взаимодействия будет уточнена за
счет рассмотрения опорно-ведущих поясов РН. В этом случае РН будет вращаться
относительно ТПК (вокруг последнего опорно-ведущего пояса) после выхода
предпоследнего опорно-ведущего пояса из ТПК. Из-за вращения РН величины
. На следующем этапе модель взаимодействия будет уточнена за
счет рассмотрения опорно-ведущих поясов РН. В этом случае РН будет вращаться
относительно ТПК (вокруг последнего опорно-ведущего пояса) после выхода
предпоследнего опорно-ведущего пояса из ТПК. Из-за вращения РН величины ![]() и
и![]() будут меньше, чем в первой модели, но при этом возникает
опасность соударения РН с ТПК или СН.
будут меньше, чем в первой модели, но при этом возникает
опасность соударения РН с ТПК или СН.
Для получения предварительных количественных оценок
приняты следующие числовые данные:
-
погонная масса ТПК ![]() ;
;
-
средняя погонная масса РН ![]() ;
;
-
длина РН и ТПК ![]() =31 м;
=31 м;
-
расстояние между опорами a1=a2= a3=a=10,33 м.
Модель постоянной погонной массы РН (![]() ) и ТПК (
) и ТПК (![]() ) и постоянной перегрузки приводят к постоянной погонной
нагрузке, что является общепринятым в сопротивлении материалов [2]. В
исследуемой задаче эта модель рассматривается в качестве исходного эталона, с
которым сравниваются другие случаи нагружения при переменной погонной массе РН
и линейном изменении нормальной перегрузки по длине ТПК.
) и постоянной перегрузки приводят к постоянной погонной
нагрузке, что является общепринятым в сопротивлении материалов [2]. В
исследуемой задаче эта модель рассматривается в качестве исходного эталона, с
которым сравниваются другие случаи нагружения при переменной погонной массе РН
и линейном изменении нормальной перегрузки по длине ТПК.
Два рассматриваемых случая по положению РН относительно
ТПК (транспортировка РН к месту запуска со средней расчетной перегрузкой ![]() при
при ![]() и выход РН из ТПК в
процессе выполнения маневра «Горка» со средней расчетной перегрузкой
и выход РН из ТПК в
процессе выполнения маневра «Горка» со средней расчетной перегрузкой ![]() при
при ![]() ), безусловно, не исчерпывают всех расчетных случаев для
выбора элементов конструкции ТПК из условия прочности. Однако оба случая
являются достаточно «жесткими», так как в первом случае нормальная перегрузка
является максимальной, а во втором случае перемещение РН относительно ТПК
порождает дополнительные нагрузки.
), безусловно, не исчерпывают всех расчетных случаев для
выбора элементов конструкции ТПК из условия прочности. Однако оба случая
являются достаточно «жесткими», так как в первом случае нормальная перегрузка
является максимальной, а во втором случае перемещение РН относительно ТПК
порождает дополнительные нагрузки.
Ниже представлены результаты расчетов для рассмотренных
режимов нагружения: эпюры перерезывающей силы ![]() (рис. 4.1) и
изгибающего момента
(рис. 4.1) и
изгибающего момента ![]() (рис. 4.2) по длине
ТПК. Видно, что максимальная перерезывающая сила для режима транспортировки
возникает в сечениях над опорами 1 и 2, которые расположены ближе
к центру ТПК. Максимальная перерезывающая сила в режиме выхода РН из ТПК
возникает в сечениях над опорами 2 и 3, которые расположены ближе
к срезу ТПК. В режиме выхода РН из ТПК для значений
(рис. 4.2) по длине
ТПК. Видно, что максимальная перерезывающая сила для режима транспортировки
возникает в сечениях над опорами 1 и 2, которые расположены ближе
к центру ТПК. Максимальная перерезывающая сила в режиме выхода РН из ТПК
возникает в сечениях над опорами 2 и 3, которые расположены ближе
к срезу ТПК. В режиме выхода РН из ТПК для значений ![]() перерезывающая сила
оказывается больше, чем в режиме транспортировки.
перерезывающая сила
оказывается больше, чем в режиме транспортировки.
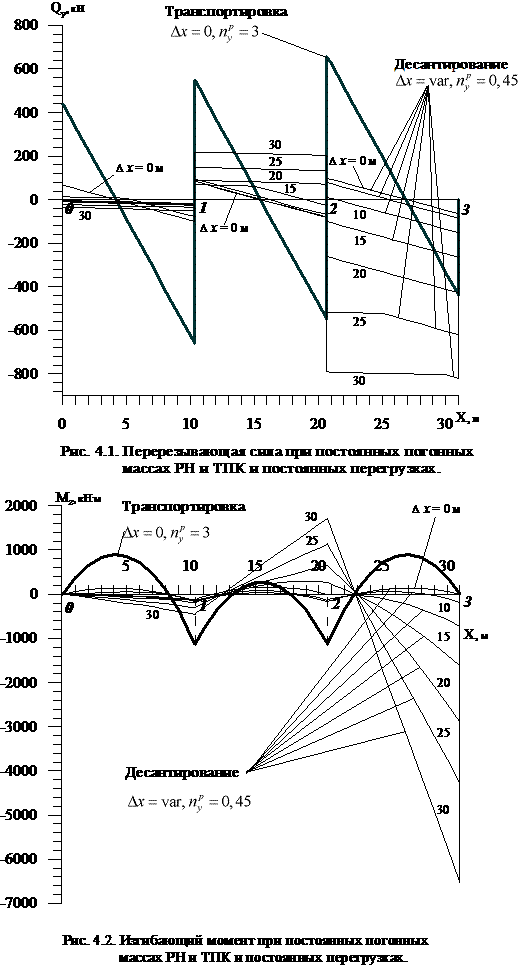
Максимальный изгибающий момент при транспортировке РН в
СН возникает в сечениях над опорами 1 и 2, которые расположены
ближе к центру ТПК, и в середине пролетов a1 и a3. Максимальный
изгибающий момент в режиме выхода РН из ТПК возникает в сечении над опорой 3,
которая расположена на срезе ТПК. При перемещении РН на величину ![]() в процессе
десантирования максимальный изгибающий момент оказывается больше, чем при
транспортировке РН.
в процессе
десантирования максимальный изгибающий момент оказывается больше, чем при
транспортировке РН.
Величина максимальной перерезывающей силы, которая
реализуется в режиме выхода РН из ТПК, составляет Qy max=821 кН, что примерно
на четверть превышает
величину максимальной перерезывающей силы,
достигаемой в
режиме транспортировки
Qy max=659 кН.
Величина максимального изгибающего момента, которая
реализуется в режиме выхода РН из ТПК, составляет Mz max=6528кН·м,
что
примерно в 6 раз превышает
максимальную величину изгибающего
момента, достигаемого в
режиме транспортировки,
Mz
max
=1134
кН·м.
При транспортировке, реакции в опорах ТПК составляют R0=R3=439 кН и R1=R2=1208 кН, т.е.
наиболее нагруженными оказываются опоры 1 и 2,
которые расположены ближе к центру ТПК. При десантировании и выходе РН почти на
полную длину реакции в опорах ТПК имеют разные знаки: R0=-36 кН (направлена
вниз), R1=269 кН (направлена
вверх), R2=-995 кН (направлена
вниз), R3=821 кН (направлена
вверх).
Видно, что при расчете ТПК на прочность в рассматриваемой
постановке (т.е. при постоянных погонных нагрузках) следует анализировать оба
режима нагружения: для опор 0 и 1 более критичен режим
транспортировки, для опор 2 и 3 – режим выхода РН из ТПК.
Реальное распределение погонной массы по
длине РН (табл. 2.1, рис. 2.1) существенно
отличается от равномерного. Поэтому происходит качественное и количественное
перераспределение перерезывающих сил и изгибающих моментов по длине РН.
На рис. 4.3 показана перерезывающая сила,
а на рис. 4.4 показан
изгибающий момент по длине ТПК при переменной погонной массе РН и постоянных
перегрузках. В этом случае распределенная погонная сила, действующая на ТПК,
пропорциональна погонной массе РН.
Видно, что максимальная перерезывающая
сила имеет место в режиме транспортировки и возникает в сечении над опорой 1.
Это объясняется расположением над этой опорой бака окислителя «О1».
С учетом реального распределения массы
по длине РН максимальный изгибающий момент при транспортировке также возникает
в сечении над опорой 1. Максимальный изгибающий момент при выходе РН из
ТПК имеет место в сечении над опорой 3, которая расположена на срезе
ТПК.
Сравнение двух режимов нагружения
(транспортировка и выход РН) с учетом реального распределения массы РН по ее
длине позволяет выявить максимальные величины перерезывающей силы и изгибающего
момента.
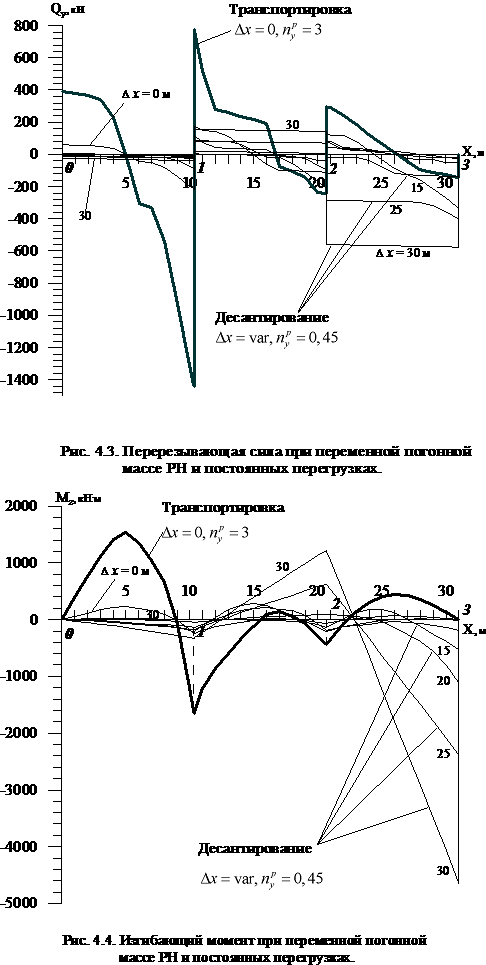
Максимальное значение перерезывающей
силы достигается при транспортировке и составляет Qy max=1441 кН,
что примерно в 2,5 раза больше величины перерезывающей силы при выходе РН из
ТПК (Qy max=576 кН).
Максимальное значение изгибающего
момента достигается при выходе РН из ТПК на наибольшую длину. Это максимальное
значение Mz max=4646 кН·м
примерно в 2,8 раза превышает максимальную величину изгибающего момента при
транспортировке (Mz max=1652 кН·м).
Видно, что переход от упрощенной модели
распределения погонной массы по длине РН (средняя погонная масса) к реальной
модели распределения при постоянной нормальной перегрузке приводит к изменению
картины нагрузок как для перерезывающей силы Qy, так и для
изгибающего момента Mz. При этом существенно изменяется величина максимальной
перерезывающей силы Qy (с 821 кН до 1441 кН, т.е. увеличивается в 1,75 раза) и величина
максимального изгибающего момента Mz (с 6528 кН·м до 4646 кН·м т.е.
уменьшается в 1,4 раза). В целом, при определении расчетных нагрузок на ТПК
четырехопорной схемы в случае постоянной нормальной перегрузки следует
учитывать изменение погонной массы РН по ее длине.
Учет реального
распределения массы РН по длине приводит к изменению реакций в опорах ТПК (по
сравнению с постоянными погонными нагрузками). При транспортировке они меняются
существенно: R0=392 кН, R1=2220 кН, R2=540 кН и R3=142 кН. При десантировании
и выходе РН почти на полную длину реакции составляют R0=-24 кН, R1=196 кН, R2=-703 кН и R3=575 кН, что тоже
существенно отличается от значений, полученных для модели постоянной массы РН.
4.2. Действие линейной перегрузки
Другая апробация вычислительных
алгоритмов и случаев нагружения проводилась в предположении линейного изменения
расчетной перегрузки по длине РН и ТПК. При построении линейной модели
перегрузки принято, что в центре ТПК величина перегрузки равна расчетной
перегрузке для случая транспортировки РН в СН (![]() ) и для случая выхода РН из ТПК (
) и для случая выхода РН из ТПК (![]() ), соответственно. На левом конце ТПК перегрузка на 1/3
меньше, а на правом конце на 1/3 больше. В результате получены следующие
линейные модели расчетных перегрузок для случая транспортировки РН в СН и для
случая выхода РН из ТПК:
), соответственно. На левом конце ТПК перегрузка на 1/3
меньше, а на правом конце на 1/3 больше. В результате получены следующие
линейные модели расчетных перегрузок для случая транспортировки РН в СН и для
случая выхода РН из ТПК:
![]() , (4.1)
, (4.1)
![]() , (4.2)
, (4.2)
Для случая транспортировки РН в СН
предполагается, что имеет место маневр в вертикальной плоскости с вращением СН
относительно центра масс. В результате этого маневра СН происходит
перераспределение перегрузки по линейному закону (4.1). Для случая выхода РН из
ТПК предполагается, что имеют место угловая скорость и угловое ускорение, что
также приводит к перераспределению перегрузки по линейному закону (4.2).
Расчеты проводились как для случая
средней погонной массы РН ![]() , так и для случая переменной по длине погонной массы РН
(табл .2.1, рис. 2.1).
, так и для случая переменной по длине погонной массы РН
(табл .2.1, рис. 2.1).
Ниже представлены результаты расчетов:
·
эпюры перерезывающей силы ![]() (рис. 4.5) и
изгибающего момента
(рис. 4.5) и
изгибающего момента ![]() (рис. 4.6) по длине
ТПК для случая средней погонной массы РН;
(рис. 4.6) по длине
ТПК для случая средней погонной массы РН;
·
эпюры перерезывающей силы ![]() (рис. 4.7) и
изгибающего момента
(рис. 4.7) и
изгибающего момента ![]() (рис. 4.8) по длине
ТПК для случая переменной по длине погонной массы РН.
(рис. 4.8) по длине
ТПК для случая переменной по длине погонной массы РН.
Сравнение условий нагружения четырехопорного ТПК под
действием постоянной и линейной нормальных перегрузок в модельных задачах с
постоянными погонными массами РН и ТПК и с переменной по длине погонной
массой РН показывает значительное различие в величинах перерезывающей силы и изгибающего момента.

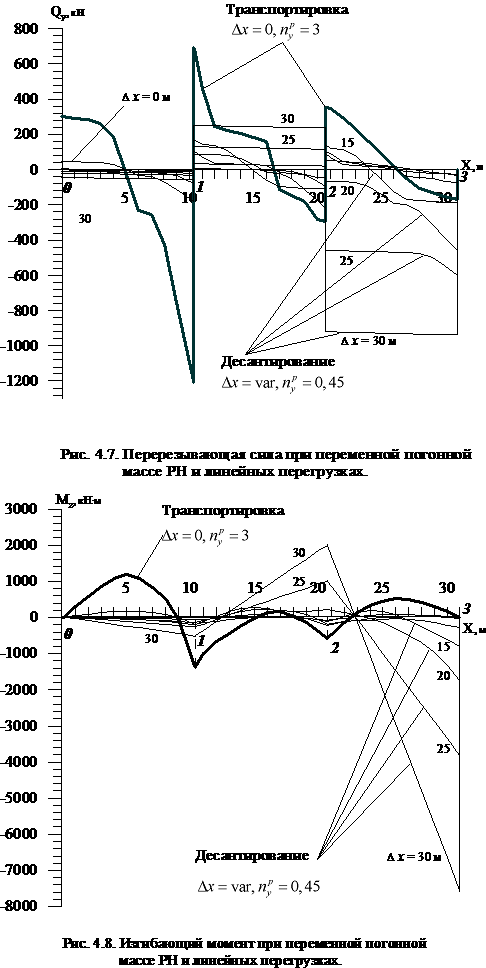
Линейная перегрузка, которая «в среднем» совпадает с
постоянной и увеличивается к срезу ТПК, порождает существенно большие нагрузки
на ТПК и грузовой пол СН, чем постоянная перегрузка, поэтому необходимо
учитывать фактор возможного изменения перегрузки по длине ТПК и РН.
Перерезывающая сила достигает экстремальных значений Qy max=1438 кН (для случая
постоянной погонной массы РН) при десантировании, когда РН почти полностью
выходит из ТПК, и Qy max=1206 кН (для случая переменной по длине погонной массы РН) при
транспортировке. Изгибающий момент достигает максимальных значений Mz max=11516 кН·м (для случая
постоянной погонной массы РН) и Mz max=7594 кН·м (для случая переменной по
длине погонной массы РН) при пуске, когда РН почти полностью выходит из
ТПК. Следовательно, при оценке условий нагружения, необходимо
рассматривать оба случая.
При постоянной и при линейной перегрузке перерезывающая
сила Qy достигает экстремальных
значений в сечениях ТПК над опорами 2 и 3, которые расположены
ближе к срезу ТПК. Это происходит при пуске, когда РН почти полностью выходит
из ТПК.
В режиме транспортировки наибольшее влияние на значение
экстремальной величины перерезывающей силы Qy оказывает закон
распределения погонной массы РН. При равномерном распределении погонной массы
наиболее нагруженными оказываются средние опоры 1 и 2. Для случая
переменной погонной массы наиболее нагруженной в режиме транспортировки
оказывается опора 1, на которую приходится наибольший вес бака
окислителя «О1».
Изгибающий момент Mz достигает
экстремальных значений в сечении над опорой 3, расположенной на срезе
ТПК. Это происходит при пуске, когда РН почти полностью выходит из ТПК.
Линейная перегрузка приводит к изменению величин реакций
в опорах ТПК по сравнению с постоянной перегрузкой. Это вызвано
перераспределе-нием погонных сил по длине РН и ТПК. В случае постоянной
погонной массы РН реакции в опорах ТПК при транспортировке составляют R0=317 кН, R1=1025 кН, R2=1391 кН и R3=561 кН, а при
десантировании (в конце выхода РН из ТПК) реакции составляют R0=-70 кН, R1=459 кН, R2=-1765 кН и R3=1438 кН. Учет
переменности погонной массы РН по длине существенно перераспределяет величины
реакций в опорах ТПК. Так, при транспортировке реакции составляют R0=301 кН, R1=1901 кН, R2=650 кН и R3=172 кН, а при выходе
РН из ТПК почти на полную длину в процессе десантирования реакции составляют R0=-45 кН, R1=308 кН, R2=-1157 кН и R3=939 кН.
В таблицах 4.1 и 4.2 представлены величины максимальной
перерезывающей силы и максимального изгибающего момента для всех рассмотренных
случаев нагружения (для двухопорной [1] и четырехопорной схем крепления ТПК к
полу СН).
Сравнение двухопорной и четырехопорной схем крепления ТПК
к грузовому полу СН показывает, что максимальная перерезывающая сила
уменьшается практически во всех рассмотренных случаях нагружения. Изгибающий
момент, который является определяющим для расчета потребной из условия
прочности массы ТПК, уменьшается почти в два раза. Отсюда следует, что
четырехопорный ТПК должен иметь массу почти в два раза меньше, чем двухопорный
ТПК.
В табл. 4.3 представлены реакции в опорах ТПК, т.е. силы,
приложенные к грузовому полу СН в точках опор, для всех рассмотренных случаев
нагружения (для двухопорной и для четырехопорной схем крепления ТПК к полу СН).
Сравнение с двухопорной схемой [1] позволяет сделать
заключение, что при четырехопорной схеме нагрузки на пол СН уменьшаются
примерно в 1,5-2 раза. Однако для
случая переменной массы
РН, за счет
большого веса бака «О1» и его расположения непосредственно над опорой 1, нагрузка на эту опору в
режиме транспортировки примерно в 1,4 раза превышает аналогичную нагрузку для
двухопорной схемы.
Таблица 4.1. Величина максимальной
перерезывающей силы
в ТПК при различных случаях нагружения
|
Модель нагружения |
Расчетный случай |
Точка приложения и величина
максимальной перерезывающей силы |
|||
|
Двухопорная схема |
Четырехопорная схема |
||||
|
опора |
Qy max,кН |
опора |
Qy max, кН |
||
|
Постоянная погонная масса РН, постоянная перегрузка |
Транспортировка, |
1275 |
1, 2 |
659 |
|
|
Десантирование, |
B |
855 |
3 |
821 |
|
|
Переменная погонная масса РН, постоянная перегрузка |
Транспортировка, |
А |
1350 |
1 |
1441 |
|
Десантирование, |
720 |
3 |
576 |
||
|
Постоянная погонная масса РН, линейная перегрузка |
Транспортировка, |
B |
1536 |
2 |
781 |
|
Десантирование, |
B |
1453 |
3 |
1438 |
|
|
Переменная погонная масса РН, линейная перегрузка |
Транспортировка, |
А |
1082 |
1 |
1206 |
|
Десантирование, |
B |
1143 |
3 |
939 |
|
Таблица 4.2. Величина максимального
изгибающего момента
в ТПК при различных случаях нагружения
|
Модель нагружения |
Расчетный случай |
Точка приложения и величина
максимального изгибающего момента |
|||
|
Двухопорная схема |
Четырехопорная схема |
||||
|
опора |
Mz maх, кН·м |
опора |
Mz maх, кН·м |
||
|
Постоянная погонная масса РН, постоянная перегрузка |
Транспортировка, |
B |
7700 |
1, 2 |
1134 |
|
Десантирование, |
B |
12050 |
3 |
6528 |
|
|
Переменная погонная масса РН, постоянная перегрузка |
Транспортировка, |
B А-В* |
2691 3765 |
1 |
1652 |
|
Десантирование, |
B |
10165 |
3 |
4646 |
|
|
Постоянная погонная масса РН, линейная перегрузка |
Транспортировка, |
B |
9592 |
2 |
1345 |
|
Десантирование, |
B |
20556 |
3 |
11516 |
|
|
Переменная погонная масса РН, линейная перегрузка |
Транспортировка, |
B А-В* |
3295 3015 |
1 |
1196 |
|
Десантирование, |
B |
16147 |
3 |
7594 |
|
(*) А-В – изгибающий
момент достигает максимального значения между опорами А и В.
Таблица 4.3.
Реакции в опорах ТПК при различных случаях нагружения
|
Модель нагружения |
Расчетный случай |
Двухопорная схема |
Четырехопорная схема |
||||
|
Реакции в опорах, кН |
Реакции в опорах, кН (при a1=a2= a3=10,33 м) |
||||||
|
RА |
RВ |
R0 |
R1 |
R2 |
R3 |
||
|
Постоянная погонная масса РН, постоянная перегрузка |
Транспортировка, |
802 |
2492 |
439 |
1208 |
1208 |
439 |
|
Десантирование, |
-828 |
1322 |
-36 |
269 |
-995 |
821 |
|
|
Переменная погонная масса РН, постоянная перегрузка |
Транспортировка, |
1684 |
1610 |
392 |
2220 |
540 |
142 |
|
Десантирование, |
-696 |
1190 |
-24 |
196 |
-703 |
575 |
|
|
Постоянная погонная масса РН, линейная перегрузка |
Транспортировка, |
404 |
2890 |
317 |
1025 |
1391 |
561 |
|
Десантирование, |
-1429 |
2214 |
-70 |
459 |
-1765 |
1438 |
|
|
Переменная погонная масса РН, линейная
перегрузка |
Транспортировка, |
1330 |
1693 |
301 |
1901 |
650 |
172 |
|
Десантирование, |
-1120 |
1864 |
-45 |
308 |
-1157 |
939 |
|
Приведенные выше результаты
моделирования условий нагружения ТПК и грузового пола СН соответствуют
одинаковому расстоянию между опорами 0-1, 1-2, 2-3.
Были проведены также расчеты для смещенных влево и вправо на 1-2 м средних опор 1
и 2. Установлено, что такое смещение указанных опор не приводит к существенному
изменению нагрузок на ТПК и грузовой пол СН.
В целом, даже на уровне рассмотренных
модельных задач нагружения, видны преимущества четырехопроной схемы ТПК по
сравнению с двухопорной.
Выводы
Основные результаты выполненной работы
состоят в следующем:
1.
Разработан вычислительный алгоритм и создано программное
обеспечение, позволяющие определять нагрузки на ТПК и грузовой пол СН для
четырехопорной схемы при любом смещении РН относительно ТПК и при любой
погонной нагрузке (из-за переменной погонной массы РН по ее длине или из-за
переменной нормальной перегрузки по длине ТПК и РН).
2.
Показано, что учет изменения погонной массы по длине РН
значительно изменяет распределение нагрузок на ТПК и реакции опор грузового
пола, особенно в случае переменной по длине ТПК и РН перегрузки.
3.
Показана необходимость учета изменения перегрузки по
длине ТПК и РН, так как при этом происходит существенное перераспределение
нагрузок по сравнению со случаем постоянной перегрузки.
4.
На модельных задачах нагружения конструкции ТПК и СН
показано, что увеличение числа опор с двух до четырех должно позволить
существенно уменьшить массу ТПК.
5.
Рассмотренная четырехопорная схема крепления ТПК к полу
СН является промежуточным этапом при переходе к многоопорным схемам, которые, как предполагается, позволят уменьшить нагрузки
на ТПК и грузовой пол СН.
Литература
1.
Сихарулидзе Ю.Г. Жуков Б.И. Динамические нагрузки на
самолет-носитель при реализации воздушного старта ракеты-носителя (двухопорная
схема). Препринт № 9 ИПМ РАН за 2008.
2.
Дарков А.В. Шпиро Г.С. Сопротивление материалов. «Высшая
школа», М. 1975.