Содержание........................................................................................................................................ 4

1. ВВЕДЕНИЕ.................................................................................................................................... 5

1.1. Биологический нейрон .............................................................................................................. 7

1.2. Формальный нейрон................................................................................................................... 9

1.3. Моделирование нетривиального (интеллектуального) адаптивного поведения.............. 11

1.4. Бионический нейрон ............................................................................................................... 14

2.РАЗРАБОТКА ПРОСТЫХ БИОНИЧЕСКИХ НЕЙРОННЫХ СЕТЕЙ................................. 19

2.1.Логические элементы................................................................................................................ 19

2.2. Логический элемент or............................................................................................................. 20

2.3. Логический элемент and ......................................................................................................... 20

2.4.Логический элемент XOR........................................................................................................ 21

2.5. Логический элемент not........................................................................................................... 23

2.6. Преобразователь сигналов из параллельных в последовательные..................................... 23

2.7.Десятичный счетчик.................................................................................................................. 24

2.8 Сеть, считывающая состояние нейрона.................................................................................. 24

2.9.Анализатор состояния нейрона................................................................................................ 25

3.РАЗРАБОТКА МОДЕЛИ АДАПТИВНОГО ПОВЕДЕНИЯ В ЛАБИРИНТЕ..................... 26

3.1 Модель окружающей среды (лабиринт).................................................................................. 26

3.4. Модель нейронной сети........................................................................................................... 27

ЗАКЛЮЧЕНИЕ................................................................................................................................ 28

СПИСОК ЛИТЕРАТУРЫ............................................................................................................... 29

             1. ВВЕДЕНИЕ

 

В настоящее время становится очевидным, что дальнейшее развитие различных аспектов проблем автоматического управления сложными системами не возможно без объединения усилий технических и биологических наук. Общими задачами для этих наук являются: управления динамическими объектами и базами данных, а так же оптимизация управления. Для осуществления управления сложными системами и объектами применяются нейронные сети.

Современный подход к созданию нейросистем эволюционирует в направлении отдаления их функционирования от реальных биологических аналогов. Для моделирования современных нейросистем используется сильно упрощенная модель базового элемента (нейрона). Для перехода к более приближённой биологическому аналогу модели нейрона, необходимо изменить подход и обратиться к исследованиям базовых элементов (нейронов) коры головного мозга человека, а эта область на данный момент исследована недостаточно полно. Любые исследования здесь очень важны для использования в современных технологиях.

  В обзорной статье А. В. Савельева "На пути к общей теории нейросетей. К вопросу о сложности" (грант РФФИ 04-06-80460. Журнал Нейрокомпьютеры: разработка, применение №4-5, 2006 г., с. 4) приведены результаты исследования нейросетей принципиально неадекватных их биологическим аналогам. На основе открытой гиперсложности биологических нейронов, превышающей сложность сетей и не сводимой к ней, автором статьи показана возможность обобщения теории нейросетей, которая может иметь следствием совершенно иной принцип организации архитектуры нейрокомпьютеров. Однако мы считаем, что при построении практических моделей нет необходимости учитывать всю системную гиперсложность нейрона. Генетика, питание, дыхание, биохимия нейрона имеют второстепенное значение для нейроинформатики. Необходимо получить принципиально новые модели биологических нейронов и нейросетей на их основе за счет использования последних достижений нейробиологии и нейрофизиологии.

Традиционная нейроинформатика подходит к созданию нейросетей основываясь на принципе, который говорит о том, что чем сложнее задача, тем более крупные нейронные сети или их конгломераты нужно использовать. Однако это не всегда верно. Использование в качестве базового элемента современных искусственных нейросетей формального нейрона приводит к тому, что за счёт полной абстракции от сложного биологического нейрона возникают технические ограничения на возможности таких нейросетей. Но и использование бионического нейрона, сделанного максимально близко к биологическому, так же не представляется возможным ввиду его многоструктурной сложности. Таким образом, возникает необходимость поиска универсальной нейробионической парадигмы, направленной на анализ механизмов, закономерностей и принципов, предназначенных для создания и работы новой базовой основы нейрокомпьютеров, сочетающей в себе простоту проектирования классических нейросетей и базовую сложность и многофункциональность бионических нейронов. Мы считаем, что для решения этой задачи необходима разработка комплекса математических моделей бионических нейронов одновременно отвечающих потребностям нейрофизиологии и нейроинформатики. При этом наши усилия будут сконцентрированы в следующих направлениях:

·        анализ динамики пространственно–временного распределения и взаимодействия работающих и не работающих функциональных блоков;

·        влияние соотношения силовых и временных параметров, информационных и управляющих, поступающих на нейрон;

·        влияние нейрона на реализацию разных функций и взаимодействие функционально различных нейронов за счет дифференцированного распределения информационных и управляющих сигналов, поступающих по разным ветвям выходного аксона одного нейрона;

·        специфика основных типов нейронов ассоциативной коры больших полушарий головного мозга.

Для разработки подобной модели предполагается, что будут использованы методы системного анализа при обобщении экспериментальных данных и классификации биологических нейронов. Так как задача поиска оптимального решения в ряде случаев является невычислимой по причине эмпирического характера данных или методов работы с ними, экспоненциальной сложности решения задачи путем перебора и т.д., то необходимость воспользоваться бионическими методами построения технических систем становится более очевидной.

Для решения поставленных целей необходимо решение следующих частных задач.

1. Обобщение экспериментальных данных по биологическим нейронам, в том числе человека.

2. Классификация биологических нейронов по функциям и свойствам.

3. Определение основных механизмов работы биологического нейрона:

- пороговые принципы ограничения потенциала нейрона,

- принципы торможения и возбуждения и их временные зависимости,

- механизмы генерации последовательностей импульсов и их ограничения по потенциалу и порогу,

- влияние входов нейрона на его потенциал,

- механизмы памяти и динамика изменения коэффициента обученности в процессе работы нейрона в составе сети (обучение, переобучение и разобучение нейрона),

-  механизм задержки поступления импульсаций между нейронами и его зависимость от веса и усталости синапса,

- основные состояния бионического нейрона для каждого класса нейронов и механизмы переходов между ними;

- определить основные типы входов и выходов нейрона, их принципиальные функциональные отличия, а также их значимость для работы нейрона в целом и влияние на принципы построение искусственных нейросетей на таких бионических нейронах;

-  выделить основные свойства и функции элементов биологических нейронов: дендритов, аксонов, синапсов, сомы.

4. Математическое моделирование свойств и функций биологических нейронов.

5. Математическое моделирование каждого отдельного класса нейронов.

6. Разработка инструментария для работы с бионическими нейронами.

7. Построение нейросетей на данных моделях и проверка их работоспособности для различных классов задач.

На данный момент проведено предварительное обобщение биологических экспериментальных данных по нейронам головного мозга человека. Осуществлена теоретическая проработка возможных математических моделей выделенных классов нейронов.

Исследования, которые ведутся в данном проекте, основаны на использовании моделей функционирования базовых элементов коры головного мозга человека – бионических нейронов, с этой целью созданы нейронные сети всех логических элементов, счётчик, анализатор состояния нейрона, фильтр доминанты и система ориентирования робота в лабиринте. Это позволит в дальнейшем создать базу для внедрения нейротехнологий в робототехнику.

 

             1.1. Биологический нейрон

Основным структурным элементом нервной системы является нервная клетка, или нейрон [1]. Через нейроны осуществляется передача информации от одного участка нервной системы к другому, обмен информацией между нервной системой и различными участками тела. В нейронах происходят сложнейшие процессы обработки информации. С их помощью формируются ответные реакции организма (рефлексы) на внешние и внутренние раздражения.

Нейрон может обладать разными размерами и формой, но схематически его всегда легко представить как клетку с отростками (рисунок 1). Он состоит из тела клетки (сома), содержащего ядро, и отростков, которые подразделяются на дендриты, по которым к нейронам поступает нервный импульс, и аксон, по которому нервный импульс распространяется от нейрона к другим клеткам.

Дендриты - это отростки нейрона, проводящие импульсы к телу нейрона. Они, как правило, короткие, относительно широкие, сильно ветвящиеся, образуют множество синапсов с другими нервными клетками.

 Каждый аксон оканчивается на теле или дендритах других нейронов контактом, названном синапсом. Синапс - это специализированная структура, которая обеспечивает передачу возбуждения с одной возбудимой структуры на другую. Термин "синапс" введен Ч. Шеррингтоном и означает "сведение", "соединение", "застежка".

              Рисунок 1 - Структура нейрона

 

Все раздражения, поступающие в нервную систему, передаются на нейрон через определенные участки его мембраны, находящиеся в области синаптических контактов. В большинстве нервных клеток эта передача осуществляется химическим путем с помощью медиаторов. Ответом нейронов на внешнее раздражение является изменение величины, мембранного потенциала.

Чем больше синапсов на нервной клетке, тем больше воспринимается различных раздражений и, следовательно, шире сфера влияний на ее деятельность и возможность участия нервной клетки в разнообразных реакциях организма.

Эффекты, возникающие при активации синапса, могут быть возбуждающими или тормозящими.

При одновременной активации нескольких возбуждающих синапсов, общий возбуждающий импульс нейрона представляет собой сумму отдельных местных возбуждающих импульсов каждого синапса. При одновременном возникновении двух различных синаптических влияний — возбуждающего и тормозящего — происходит взаимное вычитание их эффектов. В конечном итоге реакция нервной клетки определяется суммой всех синаптических влияний.

 С появлением потенциала действия (ПД), который в отличие от местных изменений мембранного потенциала является распространяющимся процессом, нервный импульс начинает проводиться от тела нервной клетки вдоль по аксону к другой нервной клетке или рабочему органу, то есть осуществляется эффекторная функция нейрона.

Величина мембранного потенциала является основным параметром, который определяет значения важнейших показателей функционального состояния нейрона — его возбудимость.

Возбудимость нейрона — это его способность отвечать на синаптическое воздействие потенциалом действия. Она зависит от соотношения двух параметров - мембранного потенциала и критического уровня деполяризации (порога). В нормальных условиях деятельности критический уровень деполяризации нейрона относительно постоянный, поэтому возбудимость нейрона определяется в основном величиной мембранного потенциала.

Величина деполяризации нервных клеток находится в линейной зависимости от частоты, раздражающих импульсов. Высшие отделы мозга, посылая импульсы различной частоты к нейронам нижележащих отделов, регулируют их возбудимость, осуществляя контроль за ответными реакциями организма.

             1.2. Формальный нейрон

Нейрон является составной частью нейронной сети. На рисунке 2 показана его структура [2].

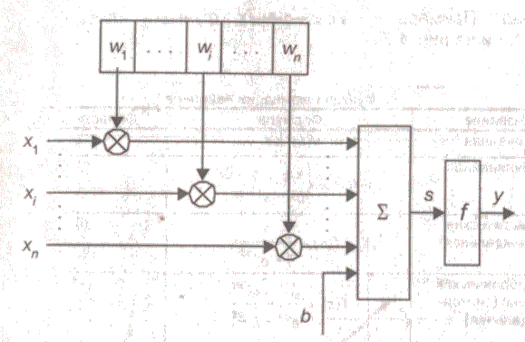
Рисунок 2 – Структура формального нейрона

Он состоит из элементов трех типов: умножителей (синапсов) - w, сумматора –Σ и нелинейного преобразователя - f. Синапсы осуществляют связь между нейронами, умно­жают входной сигнал на число, характеризующее силу связи, (вес синапса). Сумматор выполняет сложение сигналов, поступающих по синаптическим связям от других нейронов, и внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента - выхода сумматора. Эта функция на­зывается функцией активации или передаточной функцией нейрона. Нейрон в целом реализует скалярную функцию векторного аргумента. Математическая модель нейрона:

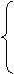
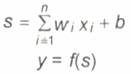,                                                                          (1)

где

Wi - вес (weight) синапса, i = 1...n;

 b - значение смещения (bias);

 s - результат суммирования (sum);

 Xi - компонент входного вектора (входной сигнал), i = 1...n;

 у - выходной сигнал нейрона;

 n - число входов нейрона;

f - нелинейное преобразование (функ­ция активации).

В общем случае входной сигнал, весовые коэффициенты и смещение могут принимать действительные значения, а во многих практических задачах - лишь некоторые фиксированные значения. Выход определяется видом функции активации и может быть как действительным, так и целым.

Синаптические связи с положительными весами называют возбуждающими, с отрицательными весами – тормозящими [3].

Описанный вычислительный элемент можно считать упро­щенной математической моделью биологических нейронов. Чтобы подчеркнуть различие нейронов биологических и искусственных, вторые иногда называют нейроподобными элементами или формальными нейронами.

На входной сигнал нелинейный преобразователь отвеча­ет выходным сигналом, который представляет собой выход у нейрона. Одной из наиболее распространенных функций активации нелинейного преобразователя является нелинейная функция активации с насыщением, так называемая логистическая функция или сигмоид (функция S-образного вида):

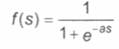                                                                             (2)

где

s – аргумент функции

а – коэффициент

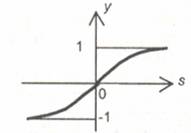
Рисунок 3 - Сигмоид (гиперболический тангенс)

Из выражения (2) очевидно, что выходное значение нейрона лежит в диапазоне (0, 1).

Сигмоидальная функция дифферен­цируема на всей оси абсцисс, что используется в некоторых алго­ритмах обучения. Кроме того, она обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыще­ние от больших сигналов, так как они соответствуют областям ар­гументов, где сигмоид имеет пологий наклон.

 Нейронная сеть представляет собой совокупность нейроподобных элементов, определенным образом соединенных друг с другом и с внешней средой с помощью связей, определяемых ве­совыми коэффициентами. В зависимости от функций, выполняемых нейронами в сети, можно выделить три их типа:

- входные нейроны, на которые подается вектор, кодирую­щий входное воздействие или образ внешней среды; в них обычно не осуществляется вычислительных процедур, а информация пе­редается с входа на выход путем изменения их активации;

- выходные нейроны, выходные значения которых пред­ставляют выходы нейронной сети; преобразования в них осущест­вляются по выражениям (1);

- промежуточные нейроны, составляющие основу нейрон­ных сетей, преобразования в которых выполняются также по вы­ражениям (1).

В большинстве нейронных моделей тип нейрона связан с его расположением в сети. Если нейрон имеет только выходные связи, то это входной нейрон, если наоборот - выходной нейрон. Однако возможен случай, когда выход топологически внутреннего нейрона рассматривается как часть выхода сети. В процессе функциониро­вания сети осуществляется преобразование входного вектора в выходной, некоторая переработка информации. Конкретный вид выполняемого сетью преобразования данных обусловливается не только характеристиками нейроподобных элементов, но и особен­ностями ее архитектуры, а именно топологией межнейронных связей, выбором определенных подмножеств нейроподобных элемен­тов для ввода и вывода информации, способами обучения сети, наличием или отсутствием конкуренции между нейронами, на­правлением и способами управления и синхронизации передачи информации между нейронами.

Выбор структуры нейронной сети осуществляется в соответ­ствии с особенностями и сложностью задачи [4]. Для решения от­дельных типов задач уже существуют оптимальные конфигурации. Если же задача не может быть сведена ни к одному из известных типов, приходится решать сложную про­блему синтеза новой конфигурации.

 

             1.3. Моделирование нетривиального (интеллектуального) адаптивного поведения

 Целенаправленность. Одна из отличительных черт поведения животных – целенаправленность, стремление достичь определенной цели. Цели поведения животных связаны с необходимостью удовлетворения потребностей. Основная потребность организма – потребность выживания. В качестве ведущих потребностей (подчиненных основной потребности) можно выделить потребность энергии (потребность питания), потребность безопасности и потребность размножения, а также – как отмечается в работах А.А. Жданова [5] – потребность накопления знаний.

         Стремление к удовлетворению потребностей можно характеризовать мотивациями, причем характеризовать количественно. Например, если у животного есть потребность питания, то мотивацию к удовлетворению этой потребности можно ввести таким образом: чем больше у животного чувство голода, тем больше данная мотивация; когда животное находит пищу, ест ее и удовлетворяет потребность питания, эта мотивация уменьшается; когда животное насытится, данная мотивация обращается в нуль (предполагаем, что мотивация неотрицательна).

         Попытки моделирования мотиваций и их роли в адаптивном поведении в нескольких различных аспектах были осуществлены рядом авторов.  Л.Е.Цитоловский исследовал простую стохастическую схему оптимизации (минимизации мотиваций), приводящую к удовлетворению потребностей, а также анализировал роль мотиваций в функционировании отдельного нейрона [6].   М.С. Бурцев и др. предложили и проанализировали модель эволюционного возникновения целенаправленного адаптивного поведения с особым акцентом на роль мотиваций в адаптивном поведении [7].  Х.Балкениус сделал краткий аналитический обзор схем и моделей когнитивных систем, учитывающих мотивационную составляющую [8].  

Целостное адаптивное поведение. При моделировании поведения животных естественно рассматривать целостное адаптивное поведение, при котором учитываются общая иерархическая структура потребностей и целей: частные потребности и цели организма подчинены основной потребности – потребности выживания. Целостное адаптивное поведение анализируется в теории функциональных систем П.К. Анохина [9,10]. Схема моделирования целостного адаптивного поведения предложена в проекте "Животное" М.М. Бонгарда с сотр. [11-12]. В проекте "Животное" [11] моделирование целостного адаптивного поведения рассматривается как задача близкая к моделированию мышления. В работе [13] предлагается схема моделирования мышления, включающая в себя элементы адаптивного поведения (в контексте целостного адаптивного поведения).

         Внутренняя модель. Еще одно понятие, которое естественно использовать при моделировании интеллектуального адаптивного поведения, – "внутренняя модель". Действительно, если животное может строить свою внутреннюю модель внешней среды и своего взаимодействия с внешней средой, то на основе такой модели оно может предсказывать будущие события во внешней среде и результаты своих действий и адекватно использовать эти прогнозы в своем адаптивном поведении. Более того, при прогнозах животное может делать определенные "логические выводы" на базе своей модели.

         Человек, естественно, тоже имеет свои модели ситуаций и модели, характеризующие его общие представления о внешнем мире. Более того, общая научная картина мира – создаваемая всем международным научным сообществом – также может рассматриваться как совокупность моделей. Т.е. отталкиваясь от понятия "внутренняя модель", мы можем попытаться перейти от исследований "интеллекта" животных к анализу наиболее интересных форм мышления – мышления ученого, мышления, используемого в научном познании Природы. Отметим, что понятие внутренней модели подчеркивалось рядом авторов.   В.Ф. Турчин рассматривает моделирование, формирование животными и человеком моделей окружающей среды, на основе которых происходит предвидение, как важную компоненту познавательного процесса [14]. Э. Янч отмечает, что возникновение способности строить модели внешнего мира было одним из этапов самоорганизации биосферы [15]. Ф.Хейлигхен и К. Джослин специально вводят понятие эндо-модель – внутренняя модель, т.е. модель, которую формирует анализируемый объект (животное, человек, робот, или какая-либо иная кибернетическая система), и отличают это понятие от понятия экзо-модель – модель самого объекта, которую строит исследователь, анализирующий поведение рассматриваемого объекта [16].  Р. Саттон и Э. Берто [17], предложили и проанализировали простую нейросетевую модель "внутренней модели". Для конкретизации рассмотрения кратко изложим основные идеи этой работы. В [18] моделируется следующий эксперимент с крысами. Есть Т-образный лабиринт, с двумя камерами, присоединяемыми к плечам лабиринта (рис. 1). Красная камера присоединена к правому плечу лабиринта, зеленая к левому плечу.  Эксперимент состоит из трех стадий. На первой исследовательской стадии животное помещают на вход лабиринта и разрешают ему перемещаться по лабиринту и изучить его, без какого-либо подкрепления или наказания. На второй ассоциативной стадии обе камеры отделяют от лабиринта, переносят в другую комнату и там поощряют либо наказывают: в красной камере животное получает пищу, а зеленой – удар током. На третьей стадии тестирования камеры возвращаются обратно и прикрепляются к лабиринту, а животное помещают на вход лабиринта и наблюдают, – куда оно пойдет. Эксперимент демонстрирует, что при тестировании животные преимущественно перемещаются направо.  Согласно этому эксперименту животное должно построить модель внешней среды и скомбинировать два независимых фактора: 1) поворот направо/налево ведет в красную/зеленую камеру, 2) в красной/зеленой камере можно получить поощрение/наказание. Т.е., животное делает "логический вывод" примерно такого вида:

 

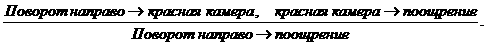
 Этот вывод аналогичен одной из основных формул логического вывода [17,18]: 

(Если из А следует В , и из В следует С, то из А следует С).

 В [17] построена нейросетевая модель, объясняющая поведение животных в описанном эксперименте. Схема этой нейросети показана на рис. 4

Эта нейронная сеть содержит 5 нейронов и состоит из двух модулей. В предсказывающий модуль входят нейроны 1-3, в модуль выбора действия – нейроны 4,5. Из внешней среды на вход нейронной сети поступают сигналы о цвете камеры и подкреплении ("Зеленый", "Красный", "Подкрепление"). На выходе сети формируются команды действий ("Направо" или "Налево"). Предсказывающий модуль строит упрощенную модель внешней среды и предсказывает состояние входов от внешней среды в предстоящие моменты времени. Модуль выбора действия формирует команды действий.

         В схему входили специальные модельные нейроны, разработанные на основе концепции А.Г. Клопфа "Целеустремленный нейрон" [19]. Эти нейроны подобны обычным нейронам с модифицируемыми синапсами Хебба, но дополнительно обладают определенной формой кратковременной памяти. Подробнее об этой модели нейронов см. [20].

 

Рис. 4 Схема нейронной сети, осуществляющей прогноз [17]. Нейроны показаны квадратами с цифрами 1-5 внутри, синапсы – кружками, выходы нейронов – жирными стрелками, направления передачи сигналов между нейронами – тонкими стрелками, воздействие внешней среды – штриховыми стрелками.

 

         При моделировании эксперимента на исследовательской стадии в предсказывающем модуле формировалась ассоциативная память (за счет модификации синапсов связи между нейронами 4, 5 и 1,2), в которой запоминалось, что при движении налево/направо животное попадает в зеленую/красную камеру. На ассоциативной стадии в предсказывающем модуле формировались рекурентные связи между нейронами 1 и 2 и нейроном 3 (предсказывающие, что в зеленой/красной камере можно получить отрицательное/положительное подкрепление), а также модифицировались синапсы на входах нейронов 4, 5, что обеспечивало преимущественный выбор движения вправо. На стадии тестирования подтверждалось, что данная модель действительно качественно соответствует описанному выше эксперименту.

         Конечно, модель Саттона [17] – это только пример подхода к моделированию внутренних моделей, на основе которых животные делают прогнозы будущих событий во внешней среде и адекватно используют эти прогнозы. Тем не менее, интуитивно чувствуется, что "внутренние модели" могут характеризовать весьма нетривиальные знания животного о внешнем мире и обеспечивать познавательные способности животных. И, как отмечено выше, на пути анализа таких моделей мы могли бы попытаться нащупать связи познавательных способностей животных с познанием  человеком внешнего мира, в том числе с научным познанием Природы.

             1.4. Бионический нейрон

Реализуемая в проекте модель бионического нейрона разработана д.б.н. профессором В.Б.Вальцевым.

Нейрон – элемент нейронной сети. Каждый нейрон имеет входы и выходы. Входы бывают нескольких типов: возбуждение, регуляция, память, торможение, запрет. Текущее состояние нейрона определяется текущим потенциалом и текущим порогом. Нейрон способен принимать и испускать импульсы.

Текущее состояние нейрона меняется со временем. Если подача на входы импульсов отсутствует, то значение текущего потенциала стремится к нулю по экспоненциальному закону:

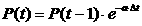,                                                                       (3)

где

P(t) – текущее значение потенциала

P(t-1) – значение потенциала в момент времени t-1

 α – коэффициент затухания потенциала

 Δt – время, прошедшее с момента, когда потенциал был равен P(t-1)

При этом значение текущего порога со временем стремится к некоторому постоянному значению, называемому порогом покоя. Порог покоя – величина, большая нуля:

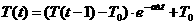,                                                             (4)

где

T(t) – текущее значение порога;

T(t-1) - значение порога в момент времени t-1

T₀ - порог покоя

 α – коэффициент затухания порога

 Δt – время, прошедшее с момента, когда потенциал был равен T(t-1)

Потенциал нейрона ограничен величинами Pmin и Pmax  соответственно снизу и сверху (Pmin ≤ 0; Pmax > 0). Порог ограничен сверху величиной Tmax, снизу – величиной Tmin (причём, 0 ≥Tmin > 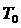> maxT). Ограничения потенциала и порога учитываются при расчёте эффекта от поступившей импульсации.

Принимать сигналы (импульсы) нейрон может с помощью входов. Каждый вход нейрона характеризуется весовым коэффициентом W (вес входа). Импульсы, поступая на вход нейрона, изменяют его текущее состояние. Эффект от импульса определяется типом входа, на который он поступил, весом этого входа а также текущим состоянием нейрона. На рисунке 5 представлена модель бионического нейрона.

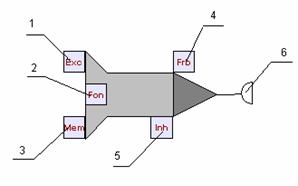
Рисунок 5 - Модель бионического нейрона

1 - вход возбуждения

2 - вход регуляции

3 - вход памяти

4 - вход запрета

5 - вход торможения

6 - выход (синапс) нейрона

Одиночный импульс, пришедший на вход нейрона типа возбуждение, повышает величину потенциала нейрона на некоторое значение:

P = P’ + H,                                                                                             (5)   

где

P – текущее значение потенциала

P’ – прежнее значение потенциала;

H – величина изменения потенциала зависит от потенциала и меняется по закону:

H = W·f(P’),                                                                                  (6)

где

W – вес синапса, по которому пришёл импульс

 f(P) – функция, лежит в области значений от нуля до единицы, и:

f(P≤0)=1,

 f(P) стремится к нулю при P стремящемся к Рmax. На сегменте где Р больше нуля, функция f(P) может быть определена как:

 f(P) = 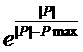  ,                                                                      (7)

Таким образом: если нейрон не возбуждён (потенциал равен нулю), то импульс увеличивает значение потенциала на величину, равную весу входа. Продолжительная периодическая импульсация поднимает  потенциал «ступеньками», высота которых убывает с возрастанием самого потенциала. Высота ступенек становится равной нулю, когда потенциал достигает предельного максимального значения (Рmax). При данном задании функции, потенциал может превышать максимальное значение на величину, пренебрежимо малую.

 Если на вход возбуждения нейрона последовательно подавать импульсы так, что бы либо их частота или вес входа компенсировали коэффициент затухания потенциала, то потенциал будет ступенчато возрастать, как показано на рисунке 6. Вертикальными пунктирными линиями показана выходная импульсация нейрона.

 

Рисунок 6 - Возбуждение нейрона

Сходным образом ведёт себя вход Торможения. Однако его роль заключается в  уменьшении потенциала на величину H, которая рассчитывается аналогично:

P = P’ - H,                                                                                    (8)

где

P’ – прежнее значение потенциала,

H – величина, которая меняется по закону:

H = W·f(-P’),                                                                                (9)

где

W – вес синапса, по которому пришёл импульс

В данном случае аргумент взят со знаком минус, при этом в роли ограничителя выступает Рmin:

f(P)= 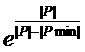,                                                                          (10)

 

Если на вход торможения нейрона последовательно подавать импульсы так, что бы либо их частота или вес входа компенсировали коэффициент затухания потенциала (с обратным знаком), то потенциал будет ступенчато убывать, как показано на рисунке 7. На рисунке 7 выходная импульсация не изображена, так как её нет, из за того, что потенциал нейрона ниже порога. 

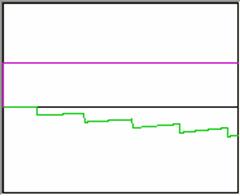
Рисунок 7 - Торможение нейрона

 

Изменение значений порога осуществляется импульсацией на входы регуляции и запрета. Импульс, поступивший на вход регуляции, уменьшает значение порога на величину H, которая рассчитывается аналогично по формулам (8-10).

Соответственно запрет увеличивает значение порога на величину H и вычисляется аналогично по формулам (5-7).

Особенным образом работает вход памяти. Аналогично возбуждению он увеличивает потенциал, но приращение потенциала теперь зависит не только от веса входа, но также от текущего состояния коэффициента обученности. Коэффициент обученности в отличие от веса меняет своё значение динамически в процессе работы нейронной сети. Он может принимать значения в диапазоне от 0 до 1. Приращение потенциала рассчитывается по формуле:

H = µ·W·f(|P’|),                                                                            (11)

где

µ -  коэффициент обученности

W – вес синапса, по которому пришёл импульс

f(P) – функция, вычисляемая по формуле (7)

Если µ = 0, то вход считается необученным – в этом случае импульсация на этот вход не оказывает никакого влияния на состояние нейрона. Максимально обученный вход (µ = 1) работает аналогично входу возбуждения с весом W, пока значение µ снова не изменится (уменьшится).

Обучение, переобучение, разобучение – механизмы, регулирующие значение µ и, как следствие, работу входов памяти нейрона.

Обучение входа – увеличение µ на некоторую постоянную величину ∆µ₊ (очевидно меньшую единицы), так называемую, способность к обучению. Эта величина неизменна и  зафиксирована в значении ∆µ₊ = 0,2. Обучение происходит при одновременном выполнении условий:

1)  на данный вход поступил сигнал

2) сигнал на вход памяти был подкреплён сигналом с входа возбуждения (сигнал на возбуждение должен прийти не позже чем через время ∆T)

3) значение порога в этот момент было меньше, чем 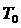 – порог покоя (что возможно только при наличии регулирующей импульсации).

Переобучение – уменьшение µ, происходит в тех случаях, когда сигнал, поступивший на вход памяти, не был подкреплён последующим сигналом на вход возбуждения, или не сопровождался регулирующей импульсацией (при этом  T ≥ 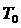). В этой ситуации значение µ уменьшится на ∆µ_-.

Таким образом, вход памяти отличается от входа возбуждения умением менять  значимость своего вклада в общий потенциал в зависимости от характера импульсации.

Помимо общей для всех типов входов весовой характеристики W и частных характеристик входов типа Память (µ, ∆µ₊, ∆µ_-) каждый вход также характеризуется величиной Delay.

Delay определяет задержку поступления импульсации с одного нейрона на другой.

В модели это реализуется следующим образом: каждый вход запоминает импульс, поступивший на него, но эффект от него рассчитывает лишь спустя время Delay. Для большинства функций и процессов сети, параметр Delay может не понадобиться, поэтому значение этого параметра по умолчанию выставляется в ноль.

Генерация импульсов происходит, если величина ∆Ω положительна:

∆Ω = P – T ,

То есть потенциал превысил порог. Частота генерации импульсов зависит от ∆Ω линейно:

w = w’ + k∆Ω,                                                                             (12)

где

w – частота импульсации

w’ – минимальная частота

k – коэффициент пропорциональности

Ограничения на частоту импульсации вытекают из верхнего ограничения на потенциал и нижнего ограничения на порог (Pmax, Tmin).

Математическая модель составлялась на основе знаний о работе реального биологического нейрона, с некоторыми принятыми упрощениями.

Так как топология сетей для бионической модели не определена то, несмотря на потери времени на разработку структуры, есть возможность построить более оптимальную и гибкую систему, с возможностью добавления новых модулей, расширяющих возможность  сети.

Так же, в связи с высоким уровнем формализации бионического нейрона, имеется возможность исследовать алгоритм функционирования сети и гарантировать реакцию системы на любые воздействия,  что в формальных НС не всегда возможно.

Существенное отличие бионического нейрона от формальных моделей, даёт основания полагать, что дальнейшее исследование данной модели и построение на её основе нейронных сетей приведёт к расширению применения нейротехнологии в различных областях человеческой деятельности.

 

 

             2.РАЗРАБОТКА ПРОСТЫХ БИОНИЧЕСКИХ НЕЙРОННЫХ СЕТЕЙ

             2.1.Логические элементы

Для полноценного проектирования нейронных сетей любого типа необходимы готовые базисные блоки. В частности такими блоками являются простые логические функции, различные счетчики, анализаторы, простые функции. Этот раздел посвящён проектированию именно таких базисных блоков, которые в будущем станут основой сложных сетей. Одновременно мы проверяем возможности бионического нейрона и сетей на его основе.

             2.2. Логический элемент or

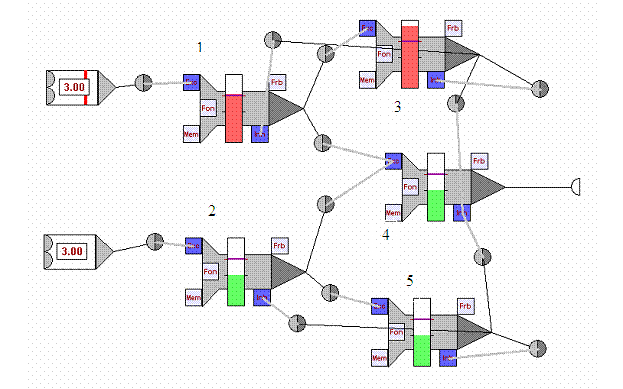
Рисунок 8 Логический элемент or

 

Нейроны 1 и 2 являются входными. Нейроны 3 и 5 нужны для возвращения сети в исходное состояние после прохождения импульса. Нейрон 4 выполняет функцию ИЛИ, а так же является выходным нейроном.

 

Логический элемент ИЛИ даёт сигнал на выходе в тех случаях, когда на входы поступил хотя бы один сигнал. Если генераторы возбуждают нейроны 1, или 2, или сразу оба, то возбуждается нейрон 4. Он подаёт сигнал на выход, после чего нейроны 3 и 5 возвращают сеть в исходное состояние.

 

             2.3. Логический элемент and

Логический элемент &. Нейрон, генерирующий выходящие импульсы, возбудится только в том случае, если входящие сигналы придут на него одновременно.

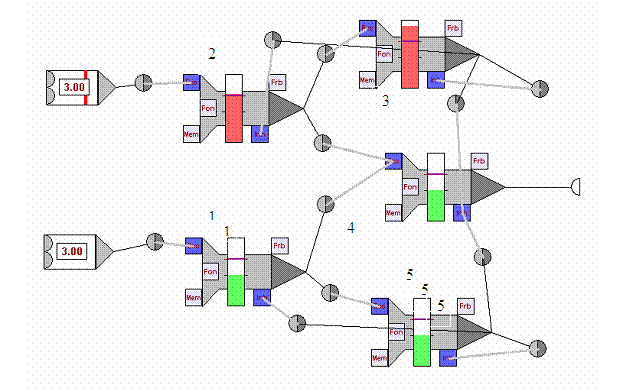
Рисунок 9 Логический элемент and

 

Элемент И внешне является точной копией элемента ИЛИ, однако синапсы от нейронов 1 и 2 к нейрону 4 настроены так, что нейрон 4 возбудится только при поступлении обоих сигналов одновременно.

 

             2.4.Логический элемент XOR

Логический элемент XOR генерирует импульс только в случае если получает импульс только с одного из входов. Достигнуто исключением из элемента ИЛИ элемента И. Оба эти элемента подключены параллельно, но если сработал И, то сигнал не проходит. Если сработал ИЛИ, а И не сработал, то сигнал проходит.

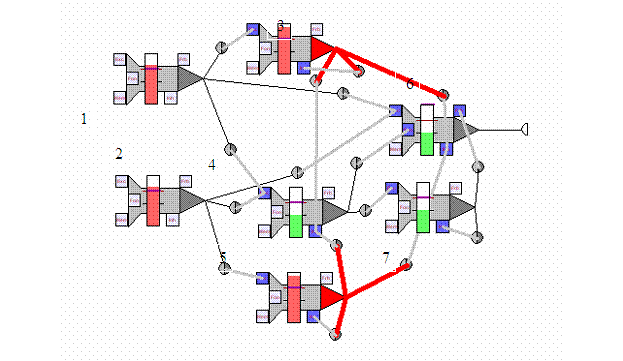
Рисунок 10 Логический элемент xоr

 

1-ый и 2-ой нейроны выполняют функции генераторов входного сигнала. 3-ий как и 5-й являются входными нейронами. 5-ый нейрон является элементом И. 7-й вставочный нейрон запирающий 6-й – выходной, если сигналы пришли одновременно с обоих генераторов.

 

Существует три варианта развития событий.

1. Нейроны 1 и 2 не генерируют сигналов. В таком случае сеть не активна и на выходном нейроне сигнала не будет.

2. Оба нейрона как 1 так и 2 генерируют сигналы и подают их в сеть. В результате этого возбудятся нейроны 3 и 5, которые будут возбуждать выходной нейрон. Вместе генераторы 1 и 2 смогут возбудить нейрон 4, выполняющий функцию И. И тогда нейрон 7 под воздействием нейрона 4 подаст запрет на выходной нейрон 6. Таким образом, сигнала на выходе не будет. Все остальные синапсы нужны для возвращения нейронов сети в исходное состояние после прохождения сигнала.

3. Сигнал приходит только с одного нейрона, например с нейрона 1. После попадания в сеть сигнал возбудит нейрон 3. Но синапсы настроены таким образом, чтобы в одиночку нейрон 3 не мог возбудить нейрон 4, поэтому запирания выходного нейрона 6 не произойдёт, и нейрон 3 передаст свой сигнал на выход сети.

 

Такое построение является не единственно верным. Задача может быть решена многими способами. Например, возвращение сети в исходное состояние может быть достигнуто за счёт экспоненциального спада возбуждённости нейронов, а не за счёт введения дополнительных синапсов

             2.5. Логический элемент not

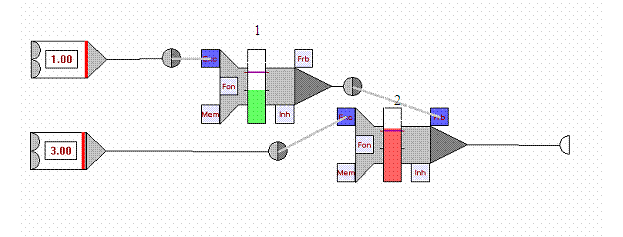
 Рисунок 11 Логический элемент not

 

Нейрон 1 является входным нейроном. Нейрон 2 всегда возбуждён и непрерывно подаёт на выход сигнал. В случае возбуждения нейрона 1 происходит запирание нейрона 2 и сигнал на выходе пропадает.

             2.6. Преобразователь сигналов из параллельных в последовательные

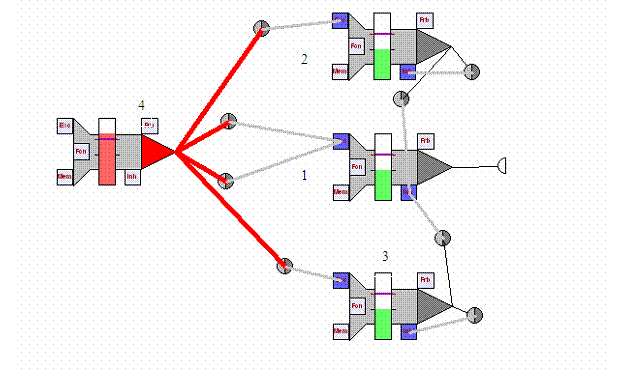
Рисунок 12 Логический элемент, превращающий несколько одновременных входных сигналов во временную их последовательность

 

Нейрон 1 является выходным нейроном. Нейроны 2 и 3 приводят сеть в исходное состояние после прохождения сигналов. Нейрон 4 генерирует два одновременных сигнала. Благодаря различной задержке на синапсах происходит их разделение во времени, после чего они генерируют последовательные сигналы на выходном нейроне.

             2.7.Десятичный счетчик

Этот счётчик в состоянии сосчитать пришедшие на него сигналы от 0 до 999.

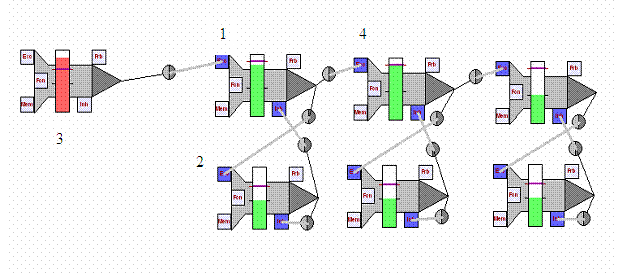
Рисунок 13 Десятичный счетчик из 6 нейронов, по два нейрона на каждый разряд.

 

Сеть состоит из нейрона 3 выполняющего функцию генератора и блоков по два нейрона последовательно соединённых между собой. Каждый такой блок добавляет один порядок числу максимальному для счётчика. Нейрон 1 принимает импульсы от нейрона 3 и по получении 10-го импульса возбуждается. Далее нейрон 2 тормозит Нерон 1 до начального состояния, а на нейрон 4 передаётся один импульс.

             2.8 Сеть, считывающая состояние нейрона

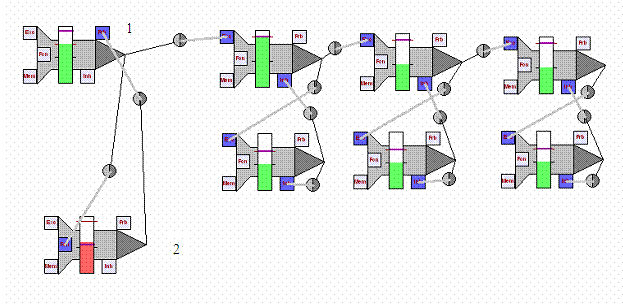
Рисунок 14 Сеть, считывающая состояние нейрона.

 

Сеть устроена по принципу счётчика. Нейрон 1 дискретно уменьшает порог исследуемого нейрона и одновременно подаёт по одному импульсу на счётчик. Таким образом, к моменту, когда порог нейрона 2 станет ниже уровня его возбужденности, на счётчике будет записано сколько раз уменьшался порог. После возбуждения нейрон 2 тормозит нейрон 1 и сеть останавливается.

 

               2.9.Анализатор состояния нейрона

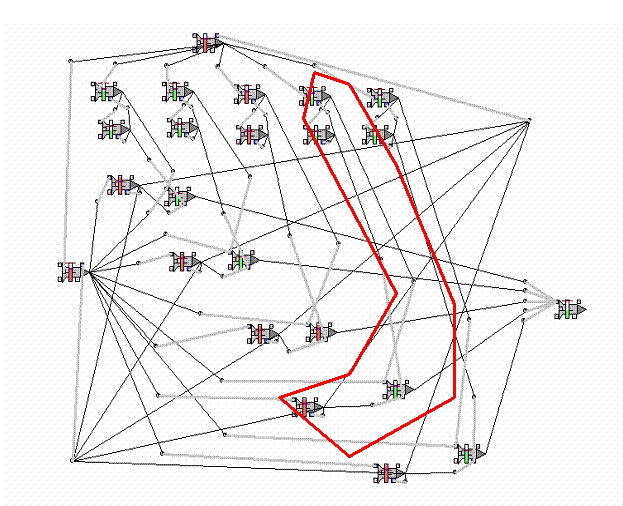
Рисунок 15  Сеть, определяющая к какому из заданных пяти диапазонов можно отнести исследуемый нейрон по уровню возбуждённости.

 

По сути сеть состоит из пяти элементов И (один из них выделен красным контуром), каждый из которых состоит из 4 нейронов. На одном входе каждого элемента стоит исследуемый нейрон, на ольно сложная сеть определяющая к какому дипозону  останавливается.на счётчике будет записано сколько раз уменьшался порог. рирвтором эталонный. Изначально пороги, исследуемого нейрона и всех эталонных нейронов, имеют максимальное значение. С помощью специального нейрона-генератора мы начинаем медленно снижать пороги этих нейронов. В определённый момент происходит возбуждение исследуемого нейрона. В таком случае импульс пройдёт через тот элемент И эталонный нейрон которого так же возбуждён. Таким образом настроив по разному выходные синапсы с каждого элемента И можно узнать, к какому из заданных нами пяти диапазонов относится исследуемый нами нейрон.

 

             3.РАЗРАБОТКА МОДЕЛИ АДАПТИВНОГО ПОВЕДЕНИЯ В ЛАБИРИНТЕ

         Поведение животных при выполнении различных задач в лабиринтах является прекрасным  материалом для изучения работы центральной нервной системы при ориентации  и процессов адаптации к изменению условий эксперимента. Соответственно моделирование поведения интеллектуальных систем при решении аналогичных задач даёт богатую пищу для размышлений над адекватностью наших моделей реальной работе биологических нейронных сетей. В связи  с чем кажется вполне естественным попытаться решить задачу ориентации в лабиринте при поиске «пищи» (модель потребности) с учетом анализа пройденных  участков лабиринта. С этой целью была разработана и программно реализована модель лабиринта, модель потребности, бионическая нейронная сеть и проведено исследование работы нейронной сети для решения поставленной задачи.

 

             3.1 Модель окружающей среды (лабиринт)

         Модельный объект под названием «жук» имеет следующие функции:

1.Способность перемещаться в четырёх направлениях по лабиринту. За один цикл работы управляющей нейронной сети «жук» перемещается на один шаг – одно звено лабиринта.

2. Потребность в «пище». Для этого он перемещается в том направлении, которое не запрещено (тупик) и приближает его к пище. Если два направления равноценны (одинаковое расстояние), то разыгрывается случайный процесс выбора одного из направлений.

3. Лабиринт представляет из себя прямоугольную решётку, некоторые элементы которой удалены случайным образом.  Таким образом, движение по участкам решётки возможно не всюду, что эквивалентно простому прямоугольному лабиринту с числом звеньев (участков) (рисунок 16) равным 2*N*(N-1)-k, где N –число перекрётсков  по одной из осей, k- число удалённых случайным образом звеньев.  

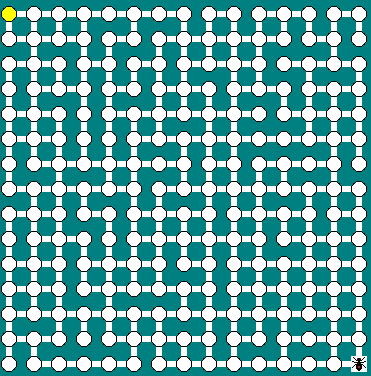
Рисунок 16 Лабиринт 15 на 15. Жёлтым обозначена пища

 

             3.4. Модель нейронной сети

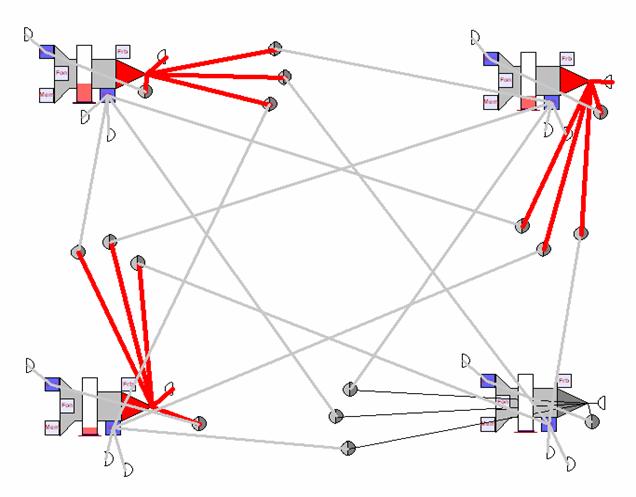
Рисунок 17 Нейронная сеть “жука”

Данная сеть была максимально уменьшена и оптимизирована для решения модельной задачи. Сеть состоит из четырёх тормозных нейронов. Каждый из нейронов отвечает за выбор направления движения внутри лабиринта: Вверх, влево, вниз, или вправо. Каждый нейрон имеет вход возбуждения, куда подаются импульсы в количестве соответствующем величине потребности (близости пищи) с данной стороны. Так же каждый нейрон имеет два входа торможения. Один вход сильный для запрета, если с этой стороны нет прохода. Второй вход слабый, куда подаются импульсы только в случае, если с этой стороны виден след “жука”, то есть если “жук” там уже был. Количество подаваемых импульсов на вход торможения связанный со следом “жука” связано обратно пропорционально с давностью этого следа. Каждый нейрон имеет синапс, замкнутый на самого себя, это необходимо для самовозбуждения нейрона, когда происходит считывание его уровня возбуждённости. Каждый нейрон тормозит все остальные, таким образом, самый сильно возбужденный останется единственным активным в результате работы сети и определит направление движения “жука”.

 

             ЗАКЛЮЧЕНИЕ

В рамках  первого года проекта была разработаны модели: простых логических элементов, десятичного счётчика, анализатора состояния нейрона, система управления ориентацией во внешней среде с использованием бионических нейронов.

В процессе моделирования установлено:

а) данная бионическая модель нейрона пригодна для построения неоднородных нейронных сетей.

б) возможности данной модели нейрона не исчерпываются созданными нейронными сетями.

в) данный проект является базовым для перехода к следующей, более сложной модели бионического нейрона.

Разработанную реализацию процесса ориентации планируется использовать для дальнейшего исследования и оснащения данного процесса новыми функциями, что, возможно, позволит обеспечить развитие этого направления.

      СПИСОК ЛИТЕРАТУРЫ

1. Николлс Дж., Мартин Р., Валлас Б., Фукс П. От нейрона к мозгу – М.: Издательство Эдиториал УРСС, 2003.

2.  Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика – М.: Издательство Горячая линия-Телеком, 2002.

3.   Беркинблит М.Б. Нейронные сети – М.: Издательство МИРОС, 1993.

4.  Мак-Каллок У., Питтс В. Логическое исчисление идей, относящихся к нервной активности // Нейрокомпьютер. –1992. - №3/4. – Р.40-50

5.    Жданов А. А. Метод автономного адаптивного управления // Известия Академии Наук. Теория и системы управления. 1999. № 5. С. 127-134.

6.    Tsitolovsky L.E. (1997) A model of motivation with chaotic neuronal dynamics // Journ. of Biological Systems, 1997. V. 5. N.2, pp. 301-323. Описание модели минимизации мотивации, предложенной в данной работе, есть на сайте: http://dserv.keldysh.ru/pages/BioCyber/Lectures/Lecture13/Lecture13.html

7.    Бурцев М.С.,  Гусарев Р.В., Редько В.Г. Модель эволюционного возникновения целенаправленного адаптивного поведения 1. Случай двух потребностей. // Препринт ИПМ РАН, 2000, N 43. см. также: http://www.keldysh.ru/pages/BioCyber/PrPrint/PrPrint.htm

8.    Balkenius C. The roots of motivations. // In J.-A. Mayer, H. L. Roitblat and S. W. Wilson (eds.), From Animals to Animats II, MA: MIT Press., 1993. http://www.lucs.lu.se/People/Christian.Balkenius/Abstracts/ROM.html

9.    Анохин П.К.  Системные механизмы высшей  нервной  деятельности. // М.: Наука, 1979, 453 с. Анохин П.К. Очерки по физиологии функциональных систем. – М.: Медицина, 1975. Анохин П.К. Принципиальные вопросы общей теории функциональных систем // Принципы системной организации функций. – М.: Наука, 1973. См. также: http://www.keldysh.ru/pages/BioCyber/RT/Functional.pdf

10.    Швырков В.Б. Теория функциональной системы как методологическая основа нейрофизиологии поведения // Успехи физиологических наук. 1978. Т. 9. №1.

11.    Бонгард М.М., Лосев И.С., Смирнов М.С. Проект модели организации поведения – Животное // Моделирование обучения и поведения. – М.: Наука, 1975. см. также:
http://www.keldysh.ru/pages/mrbur-web/misc/bongard.htm
http://mbur.narod.ru/misc/bongard.htm

12.    М. М. Бонгард, И. С. Лосев, В. В. Максимов М. С. Смирнов. Формальный язык описания ситуаций, использующий понятие связи. // Моделирование обучения и поведения. – М.: Наука, 1975.

13. Вайнцвайг М.Н., Полякова М.П. О моделировании мышления. Статья на КС-2002: http://www.keldysh.ru/pages/BioCyber/RT/Vaintsvaig.htm

14. Турчин В.Ф. Феномен науки. Кибернетический подход к эволюции. М.: Наука, 1993. 295с. (1-е изд). М.: ЭТС, 2000. 368с (2-е изд). См. также:   http://www.refal.net/turchin/phenomenon/ http://www.refal.org/turchin/phenomenon/

15. Jantsch E. The self-organising universe. Pergamon Press: Oxford etc, 1980. 340 p.

16. Heylighen F. & Joslyn C. (2001): "Cybernetics and Second Order Cybernetics", in: R.A. Meyers (ed.), Encyclopedia of Physical Science & Technology , Vol. 4 (3rd ed.), (Academic Press, New York), p. 155-170.

17. Sutton, R.S., & Barto, A.G. (1981). An adaptive network that constructs and uses an internal model of its world, Cognition and Brain Theory 4:217-246.

18.  Клини С. Математическая логика. М.: Мир, 1973. 480 с.

19. Klopf A.H.  The hedonistic neuron: a theory of memory, learning, and intelligence. Hemisphere publishing corporation, Washington etc, 1982. 140 p.

20. Sutton, R.S., & Barto, A.G. (1981). Toward a modern theory of adaptive networks: Expectation and prediction, Psychological Review 88:135-140.

21.  Вальцев В.Б., Григорьев И.Р., Лавров В.В., Черкашин Е.А. Неоднородные сети и проблемы моделирования высших функций мозга. Нейроинформатика Сб. тр. М. 2000,

с.52-56.

22. И. С. Лосев, В. В. Максимов. О задаче обобщения начальных ситуаций. // Моделирование обучения и поведения. – М.: Наука, 1975.