Аннотация
С использованием техники малых возмущений рассматривается эволюция возмущений, возникающих на стадии разгона тонких
плоских оболочек под действием газового поршня при работе мишеней в инерциальном термоядерном синтезе.
При этом рассматриваются возмущения всей системы газ-оболочка.
В результате аналитического исследования линейной стадии развития возмущений оболочки установлено,
что наличие конечной плотности у газового поршня стабилизирует (т.е. уменьшает инкременты роста) неустойчивые моды
возмущений по сравнению со случаем нулевой плотности.
Показано, что задача описания возмущений в газе сводится к решению задачи Дирихле 2-го рода для уравнения Лапласа (задача Неймана).
Результаты анализируются на примере типичных цилиндрических мишеней, применяемых при расчетах ионного термоядерного синтеза.
Abstract
Small perturbation technique is used to consider linear stability of a thin shell that is accelerated by
gaseous piston while working of heavy-ion fusion target.
The analytical investigation established that the finite density of gas of piston stabilizes
(i.e. decreases the increments of perturbation growth) the unstable modes of perturbations as compared with the case of zero density.
The investigation proves that the problem of calculation of perturbation in gaseous piston can be
reduced to the well-known Laplace’s equation with the Neumann boundary conditions.
The results are applied to the examples of typical cylindrical targets used for computer modeling of heavy ion fusion.
Введение.
Предметом настоящего исследования
является развитие возмущений при разгоне оболочек в мишенях инерциального
термоядерного синтеза. Общим элементом
при таком разгоне является то, что плотность вещества горячего поршня,
разгоняющего оболочку, меньше, чем плотность вещества самой оболочки. Хорошо
известно, что на контактной границе поршня с оболочкой в этом случае
развивается неустойчивость Рэлея-Тейлора (РТ) с экспоненциальным ростом малых
возмущений во времени. Причем в процессе движения оболочки условия для роста
возмущений на ее поверхности возникают дважды: на стадии разгона и на стадии
торможения. При этом в последнем случае растут возмущения на внутренней
поверхности оболочки – на ее границе с термоядерным горючим, D-T газом, и
препятствуют достижению высоких степеней сжатия газа.
Именно на стадии торможения возникают
наиболее серьезные трудности по сохранению сферической (или аксиальной)
симметрии сжатия, которая разрушается РТ неустойчивостью. Влияние же
“разгонной” РТ неустойчивости на конечный результат работы мишеней (возможность
достижения зажигания) носит опосредованный характер. Эта неустойчивость в
основном проявляется в том, что она способствует созданию начальных возмущений
на внутренней поверхности оболочки мишени, которые на стадии торможения
нелинейным образом развиваются.
Тем не менее, в настоящей работе мы
рассматриваем возмущения, возникающие на разгонной стадии. С одной стороны,
именно для таких возмущений может быть эффективно применен аппарат теории малых
возмущений, а с другой стороны, понимание механизма действия РТ неустойчивости
в этом процессе представляется важным в силу того, что указанная неустойчивость
создает главные физические ограничения, которые необходимо учитывать при
конструировании мишеней. Причем задачу разгона оболочки необходимо решать как в
сферических мишенях - при разгоне сферической оболочки посредством абляции /1/,
так и в цилиндрических - при разгоне цилиндрических оболочек газом, нагретым
ионным пучком /2/.
Развитие возмущений в оболочках рассматривалось
ранее как аналитически, так и численно /3,4,5/. Как правило, при таком
рассмотрении возмущения оболочки рассматривались отдельно от возмущений,
возникающих в газовом поршне.
В частности, в гл. 2 в /5/ детально
рассмотрена задача развития возмущений при разгоне оболочки и получены
количественные характеристики роста амплитуды возмущений в зависимости от
главных параметров задачи: аспектного отношения 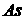 (отношения радиуса оболочки к толщине), номера
сферической гармоники (отношения радиуса оболочки к толщине), номера
сферической гармоники 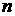 . При этом, однако, поршень
предполагался состоящим из невесомого идеального газа, т.е. эволюция возмущений
в поршне не рассматривалась. . При этом, однако, поршень
предполагался состоящим из невесомого идеального газа, т.е. эволюция возмущений
в поршне не рассматривалась.
В настоящей работе мы предлагаем
расширение развитых ранее аналитических подходов к расчету линейной стадии
развития возмущений, рассматривая задачу расчета развития малых возмущений в
системе газ – оболочка, состоящей из произвольных материалов. Другими словами,
мы распространяем задачу на случаи, в которых плотность газа, участвующего в
развитии возмущений, оказывается сравнимой с плотностью вещества оболочки.
Кроме того, как и раньше, масса газового поршня также считается сравнимой с
соответствующей массой, заключенной в оболочке.
Для получения замкнутого аналитического
результата мы по возможности упрощаем задачу, сводя ее к локальной. В выше
введенных обозначениях мы рассматриваем случай  . .
В этом случае допустимо пренебречь как
кривизной оболочки, так и ее толщиной. По этой причине ниже мы, как правило,
сначала рассматриваем систему: газовый поршень-оболочка, в которой оболочка
считается тонкой и плоской. Впоследствии мы обобщаем результат на случаи
сферической и цилиндрической симметрии системы. Ниже будет показано, что такой
подход позволяет получить дисперсионное отношение в рассматриваемой системе и,
кроме того, имеет ряд дополнительных преимуществ, связанных с отсутствием
зависимости от уравнений состояния материала оболочки и газа. Показано также,
что в указанных предположениях кривизной оболочки и уравнениями состояния
элементов системы действительно можно пренебречь. Для этого прямым расчетом
вычислено дисперсионное соотношение для сферической и цилиндрической систем
поршень-оболочка.
Выше отмечалось, что для работы мишеней
термоядерного синтеза наиболее существенна амплитуда возмущений на внутренней
поверхности оболочек, в то время как условия РТ неустойчивости реализуются на
внешней поверхности. С учетом этого выбор номера гармоники такого, чтобы
удовлетворялось двойное неравенство  , имеет еще одно обоснование:
поскольку коротковолновые возмущения являются наиболее быстро растущими, то
неравенство , имеет еще одно обоснование:
поскольку коротковолновые возмущения являются наиболее быстро растущими, то
неравенство 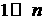 обеспечивает быстрый рост амплитуды гармоники,
а поскольку в тонкой оболочке возмущения внешней и внутренней поверхностей
оболочки совпадают, то условие тонкой оболочки обеспечивает быстрый рост амплитуды гармоники,
а поскольку в тонкой оболочке возмущения внешней и внутренней поверхностей
оболочки совпадают, то условие тонкой оболочки 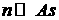 обеспечивает, что амплитуда внутренней поверхности
также быстро растет. обеспечивает, что амплитуда внутренней поверхности
также быстро растет.
Ниже приведем пример конкретной системы с
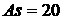 , к которой могут быть
приложены полученные результаты. , к которой могут быть
приложены полученные результаты.
Основные результаты работы.
Ниже рассмотрены малые возмущения тонкой
оболочки (плоской, цилиндрической или сферической), разгоняемой газовым
поршнем. При этом предполагается, что длины волн возмущений много больше
толщины оболочки и много меньше размеров газа.
В указанных предположениях:
1) Рассчитано дисперсионное соотношение
для системы газ–оболочка в случае конечной плотности газа. Показано, что
наличие плотного газового поршня оказывает стабилизирующее действие на
оболочку, заметно уменьшая инкремент роста возмущений по сравнению со случаем
нулевой плотности газа.
2) Показано, что развитие возмущений не
зависит от уравнений состояния элементов системы.
1. Параметры
рассматриваемых систем.
Типичный пример слоистой цилиндрической мишени,
которые разработаны, исходя из возможностей реальных сильноточных ускорителей
тяжелых ионов, описан в /2/ и представлен на рис.1. Энерговложение
осуществляется в область, заполненную свинцом, облучением с открытых торцов
мишени пучками ионов в направлении оси симметрии на всю ее длину. В /2/ указаны
и параметры энерговложения - они таковы, что за время порядка 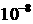 c обеспечивается плотность
поглощенной энергии c обеспечивается плотность
поглощенной энергии 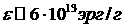 , испаряющей свинец и
превращающей его в газ. , испаряющей свинец и
превращающей его в газ.
По грубым оценкам, считая, что за это время газ не
успевает сильно разлететься, возникающее давление в неподвижном газе составит  . Введя удобную для расчетов
мишеней систему единиц: . Введя удобную для расчетов
мишеней систему единиц: 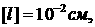 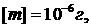 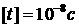 , получим: плотность энергии , получим: плотность энергии 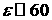 и давление и давление 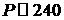 . Это давление не постоянно по
толщине слоя газа. Для оценки величины ускорения примем, что система плоская,
что правая граница свинца неподвижна, давление в неподвижной точке равно . Это давление не постоянно по
толщине слоя газа. Для оценки величины ускорения примем, что система плоская,
что правая граница свинца неподвижна, давление в неподвижной точке равно 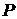 и скорость разлета в газе зависит от координаты
(лагранжевой) линейно. Тогда легко получить, что при скорости оболочки и скорость разлета в газе зависит от координаты
(лагранжевой) линейно. Тогда легко получить, что при скорости оболочки 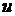 , массе (единицы площади)
оболочки , массе (единицы площади)
оболочки 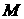 и массе газа и массе газа 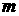 кинетическая энергия системы газ-оболочка равна кинетическая энергия системы газ-оболочка равна
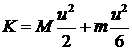 , (1.1) , (1.1)
что
приводит к уравнению для ускорения 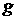 : :
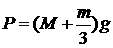 . (1.2) . (1.2)
Подставляя данные из рис. 1, получим, что ускорение
оболочки составит 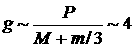 , а время полета к центру , а время полета к центру 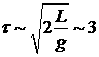 . .
Сравнение приведенных оценок с данными детальных
численных расчетов, приведенными в /2/, показывает их хорошее согласие между
собой.
DT
Au Pb Au
|------------------|-----------------|/////////////////////|-----------------|---
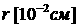 0 20 21 39 44.4 0 20 21 39 44.4
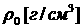 0.05 20 6 20 0.05 20 6 20
Рис
1. Радиальная геометрия слоистой цилиндрической мишени с указанием начальных
параметров мишени.
2. Задача о
неустойчивости Рэлея-Тейлора на границе жидкости.
2.1. Нулевая
плотность поршня.
Решим в рассматриваемой нами геометрии (тонкая
оболочка, бесконечный газ) известную задачу Тейлора. Пусть в поле тяжести с
ускорением g находится несжимаемая жидкость в
виде слоя 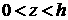 c плотностью c плотностью 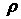 . С обеих сторон жидкость
через свободные поверхности граничит с газом нулевой плотности. Поле тяжести
уравновешивается постоянной разностью давлений. . С обеих сторон жидкость
через свободные поверхности граничит с газом нулевой плотности. Поле тяжести
уравновешивается постоянной разностью давлений.
Тогда, согласно известному анализу, приведенному в
/6/, расчет малых возмущений в жидкости сводится к введению потенциала
скоростей j и решению уравнения
Лапласа
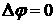 (2.1) (2.1)
с
граничным условием (равенство нулю производной давления по времени)
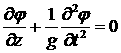 , (2.2) , (2.2)
выполняющемся
на обеих поверхностях 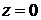 и и 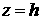 . .
Если искать решение этих уравнений в виде плоской
волны 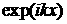 , то легко получаем, что дисперсионное соотношение имеет вид , то легко получаем, что дисперсионное соотношение имеет вид 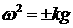 . Решение имеет вид . Решение имеет вид  , где для , где для 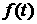 возможны 4 моды: возможны 4 моды:
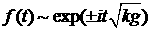 , либо , либо 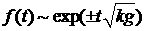 . .
Очевидно, что из них наиболее существенно растущее
решение:
 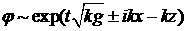 . (2.3) . (2.3)
Решение имеет вид (2.3) при всех 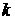 , в том числе и для тонкой оболочки, для которой , в том числе и для тонкой оболочки, для которой 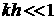 . .
2.2
Ненулевая плотность поршня.
Существенно, что в случае, когда область 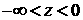 заполнена не газом, а
несжимаемой жидкостью малой плотности заполнена не газом, а
несжимаемой жидкостью малой плотности 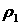 , граничное условие при , граничное условие при 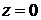 изменяется: вместо
(2.2) на границе требуется выполнение непрерывности вертикальной скорости и
производной давления по времени, что приводит к требованию непрерывности при изменяется: вместо
(2.2) на границе требуется выполнение непрерывности вертикальной скорости и
производной давления по времени, что приводит к требованию непрерывности при 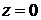 двух величин: двух величин:
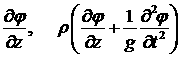 . (2.4) . (2.4)
В этом случае ищем для плоской волны решение в виде:
 для для 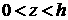 , (2.5.1) , (2.5.1)
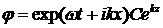 для для 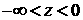 .
( 2.5.2) .
( 2.5.2)
Из граничных условий имеем три уравнения для 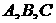 – два уравнения (2.4)
при – два уравнения (2.4)
при 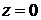 и одно уравнения (2.2)
при и одно уравнения (2.2)
при 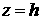 . .
Тогда условие существования ненулевых решений дает два
возможных дисперсионных соотношения:
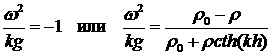 (2.6) (2.6)
Первое соотношение описывает
гравитационные волны, возникающие на свободной верхней поверхности 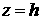 . Оно не зависит от плотности
поршня. Второе описывает РТ неустойчивость на поверхности . Оно не зависит от плотности
поршня. Второе описывает РТ неустойчивость на поверхности 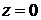 . Вводя поверхностную
плотность оболочки . Вводя поверхностную
плотность оболочки 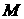 такую, что такую, что 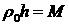 , перепишем дисперсию для
растущих решений в (2.6) в виде: , перепишем дисперсию для
растущих решений в (2.6) в виде:
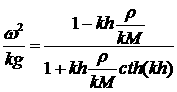 (2.7) (2.7)
Переход в (2.6) к пределу 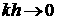 , соответствующему тонкой оболочке, должен сохранять , соответствующему тонкой оболочке, должен сохранять 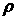 и и 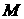 . В результате получаем из
(2.7) при . В результате получаем из
(2.7) при 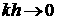 : :
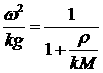 (2.8) (2.8)
Заметим, что в полученном результате
(2.8) на величину отношения 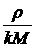 не накладывается
никаких ограничений. не накладывается
никаких ограничений.
Из выражения (2.8) следует, что наличие плотного
газового поршня оказывает стабилизирующее действие на оболочку, заметно
уменьшая инкремент роста возмущений. Если формально приложить этот результат к
параметрам мишени, рассмотренной в разделе 1, то величина стабилизирующего
эффекта окажется следующей: из приведенных выше оценок для k, g и полного
времени разгона t следует, что 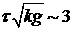 , что приводит к росту за время t амплитуды возмущения изолированной оболочки в , что приводит к росту за время t амплитуды возмущения изолированной оболочки в 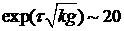 раз. При наличии газа имеем из оценок: раз. При наличии газа имеем из оценок: 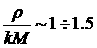 и, соответственно, рост амплитуды в и, соответственно, рост амплитуды в 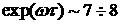 раз. Таким образом,
получаем уменьшение амплитуды возмущений в 2.5 раза. раз. Таким образом,
получаем уменьшение амплитуды возмущений в 2.5 раза.
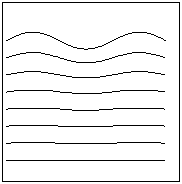 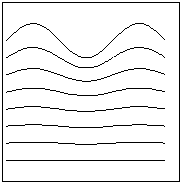 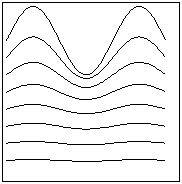
Рис 2. На
рисунке изображена величина возмущения (потенциал j), заданного в виде плоской волны, для трех
моментов времени: 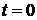 , , 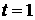 , , 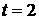 . Верхняя кривая соответствует оболочке. Ниже показаны
возмущения в газовом поршне на различных расстояниях от оболочки. . Верхняя кривая соответствует оболочке. Ниже показаны
возмущения в газовом поршне на различных расстояниях от оболочки.
Возмущения экспоненциально растут со временем. Так, рисунки
соответствуют таким значениям 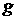 и и 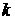 , что удвоение амплитуды происходит за каждую единицу
времени, а возмущения в газе имеют вид волны, движущейся вниз с фазовой
скоростью , что удвоение амплитуды происходит за каждую единицу
времени, а возмущения в газе имеют вид волны, движущейся вниз с фазовой
скоростью 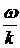 . .
2.3
Цилиндрический и сферический случаи.
2.3.1
Цилиндрический случай.
В тех случаях, когда система поршень-плюс-оболочка
имеет цилиндрическую симметрию, рассмотрение возмущений может быть проведено
вполне аналогично плоскому случаю. Пусть оболочка с плотностью 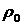 граничит с поршнем с плотностью граничит с поршнем с плотностью 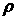 на радиусе на радиусе 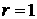 , а при , а при 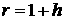 имеет свободную поверхность. Тогда условие (2.2)
выполняется на свободной поверхности имеет свободную поверхность. Тогда условие (2.2)
выполняется на свободной поверхности 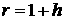 , а условия (2.4) выполняются
на границе , а условия (2.4) выполняются
на границе 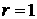 . .
Рассмотрим возмущения в виде простой угловой гармоники
с номером 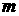 . В этом случае ищем решение в
виде: . В этом случае ищем решение в
виде:
для 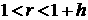 : : 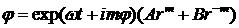 , ,
для 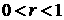 : : 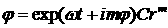 . .
Как и выше, из граничных условий имеем три уравнения
для 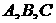 – два уравнения (2.4) при – два уравнения (2.4) при 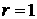 и одно уравнения (2.2) при и одно уравнения (2.2) при 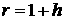 . .
На границе 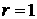 : :
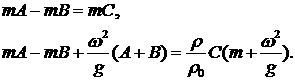
На границе 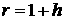 : :
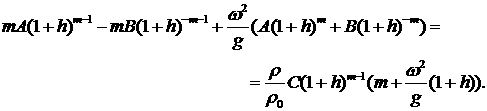
Переходя в уравнениях к пределу 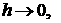 с учетом с учетом 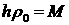 , получим, что для членов
нулевого порядка эта система уравнений выполняется тождественно, а учет членов
первого порядка , получим, что для членов
нулевого порядка эта система уравнений выполняется тождественно, а учет членов
первого порядка 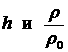 показывает, что
условием существования ненулевых решений является выполнение уравнений (здесь
введены обозначения показывает, что
условием существования ненулевых решений является выполнение уравнений (здесь
введены обозначения 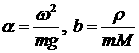 , где , где 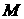 – масса единицы площади оболочки): – масса единицы площади оболочки):
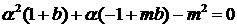 .
(2.9) .
(2.9)
Решая это уравнение в приближении  , получим дисперсионные
соотношения: , получим дисперсионные
соотношения:
1) для гравитационных волн: 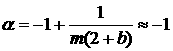 , (2.10.1) , (2.10.1)
2) для растущих решений: 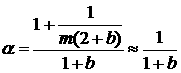 . (2.10.2) . (2.10.2)
В случае, когда поршень находится дальше от оси, чем
оболочка, аналогичный анализ дает близкий результат (ответ отличается только
знаком при малом поправочном члене), и полный ответ имеет вид:
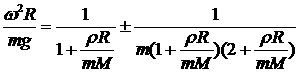 , (2.11) , (2.11)
где
верхний знак относится к внутреннему, а нижний – к внешнему положению поршня по
отношению к оболочке, находящейся на расстоянии 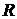 от оси. Очевидно, что формула (2.11) находится
в полном согласии с соответствующей формулой (2.8), описывающей плоский случай. от оси. Очевидно, что формула (2.11) находится
в полном согласии с соответствующей формулой (2.8), описывающей плоский случай.
2.3.2
Сферический случай.
В тех случаях, когда система поршень-оболочка имеет
сферическую симметрию, рассмотрение возмущений также может быть проведено
вполне аналогично плоскому случаю. Пусть оболочка с плотностью 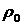 граничит с поршнем с плотностью граничит с поршнем с плотностью 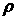 на радиусе на радиусе 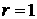 , а при , а при 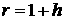 имеет свободную поверхность. Тогда условие (2.2)
выполняется на свободной поверхности имеет свободную поверхность. Тогда условие (2.2)
выполняется на свободной поверхности 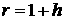 , а условия (2.4) выполняются
на границе , а условия (2.4) выполняются
на границе 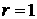 . .
Рассмотрим возмущения в виде сферической гармоники с
номером 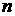 . В этом случае ищем решение в
виде: . В этом случае ищем решение в
виде:
для 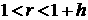 : : 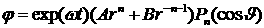 , ,
для 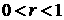 : : 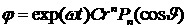 . .
Как и выше, из граничных условий имеем три уравнения
для 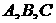 – два уравнения (2.4) при – два уравнения (2.4) при 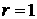 и одно уравнения (2.2) при и одно уравнения (2.2) при 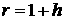 . Записав их и перейдя в них к
пределу . Записав их и перейдя в них к
пределу 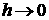 , получим, что условием существования ненулевых решений
является выполнение уравнения (здесь введены такие обозначения: , получим, что условием существования ненулевых решений
является выполнение уравнения (здесь введены такие обозначения: 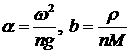 ): ):
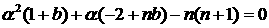 (2.12) (2.12)
Решая это уравнение в приближении 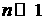 , получим дисперсионные
соотношения, аналогичные (2.10) , получим дисперсионные
соотношения, аналогичные (2.10) (2.11). Решив аналогичную
задачу для внешнего положения поршня, получим следующие выражения для растущих
решений: (2.11). Решив аналогичную
задачу для внешнего положения поршня, получим следующие выражения для растущих
решений:
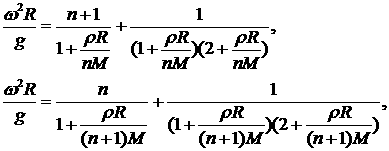 (2.13) (2.13)
где верхняя формула относится к внутреннему, а нижняя
– к внешнему положению поршня по отношению к оболочке, находящейся на
расстоянии 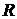 от оси. от оси.
Очевидно, что формула (2.13) находятся в полном
согласии с соответствующими формулами, описывающими плоский и цилиндрический
случаи.
3.
Возмущения тонкой оболочки из произвольного материала.
Формальному применению результатов (2.8), (2.11) и (2.13) к расчетам
термоядерных мишеней мешает то, что они получены в приближении, когда все
вещества – несжимаемые жидкости. В реальных мишенях, рассмотренных выше,
давление в разгоняющем поршне достигает величины 240 Мбар. Это более чем на
полтора порядка превосходит модуль объемной сжимаемости золота, из которого
состоит оболочка. Соответственно, модель несжимаемой жидкости к оболочке не
должна применяться. Тем более она не может применяться и по отношению к горячему
поршню.
Ниже мы приводим доказательство
того, что полученные дисперсионные соотношение (2.8), (2.11) и (2.13) тем не
менее, оказываются справедливыми при произвольных уравнениях состояния
материалов, из которых состоит система: поршень-оболочка. Для этого достаточно
выполнения двух неравенств, о которых говорилось выше: длина волны возмущений
должна быть много больше толщины оболочки и много меньше размеров
неоднородностей в поршне.
3.1 Вывод
системы уравнений для возмущений тонкой оболочки.
Рассмотрим движение в тонкой плоской оболочке,
движущейся с ускорением. При этом предполагается, что оболочка является
настолько тонкой, что скорость точек оболочки можно считать постоянной по всей
ее толщине. Предположим, что в начальный момент оболочка расположена в
плоскости 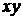 , а ускорение g направлено в
положительном направлении оси , а ускорение g направлено в
положительном направлении оси 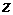 и обусловлено
разностью давлений и обусловлено
разностью давлений 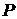 . .
Мы
запишем уравнения гидродинамики в лагранжевом виде.
Ниже
используются следующие обозначения:
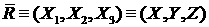 - Эйлеровы
координаты, - Эйлеровы
координаты,
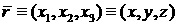 - Лагранжевы координаты (в этом качестве
выбраны координаты частиц до начала движения). - Лагранжевы координаты (в этом качестве
выбраны координаты частиц до начала движения).
Тогда трехмерные уравнения движения оболочки, согласно
/4/, могут быть выведены при помощи следующего рассуждения: выделим на
поверхности оболочки вблизи точки с координатой  площадку со сторонами площадку со сторонами 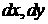 . В процессе движения через произвольный промежуток времени
площадка оказывается вблизи точки . В процессе движения через произвольный промежуток времени
площадка оказывается вблизи точки 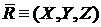 , и стороны ее оказываются равны , и стороны ее оказываются равны 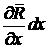 и и 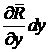 . Сила, действующая на площадку, пропорциональна ее площади и
равна . Сила, действующая на площадку, пропорциональна ее площади и
равна
 . (3.1) . (3.1)
Учитывая, что масса площадки 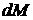 не изменилась и что не изменилась и что 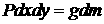 , получаем, что , получаем, что  или окончательно
(здесь производная по времени понимается в лагранжевом смысле - как производная
вдоль траектории частицы - и обозначается точкой): или окончательно
(здесь производная по времени понимается в лагранжевом смысле - как производная
вдоль траектории частицы - и обозначается точкой):
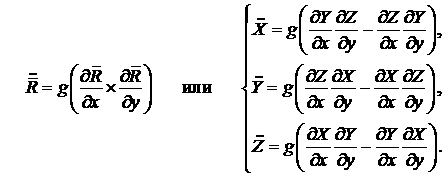 (3.2) (3.2)
Уравнения движения в виде (3.2), полученные впервые в /3/, имеют довольно
общий характер в силу того, что величина ускорения может зависеть и от
координат, и от времени. В частности, они могут быть использованы и для расчета
развития малых возмущений оболочки. В
рассматриваемой нами системе газ-оболочка, в данное уравнение необходимо
добавить член, связанный с наличием возмущения давления на поверхности оболочки.
В отсутствии возмущений система (3.2) имеет вид:
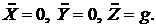
Интегрирование этих уравнений с очевидными начальными
условиями:
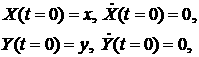
приводит к решению:
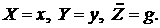 (3.3) (3.3)
Линеаризуя систему (3.2) вблизи этого решения, т.е.
представляя переменные в виде суммы основного решения и малых возмущений:
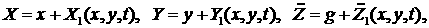 (3.4) (3.4)
получим
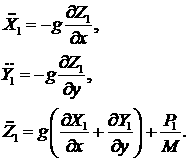 (3.5) (3.5)
При этом в последнем уравнении мы заменили возмущение
ускорения 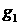 эквивалентным ему выражением эквивалентным ему выражением 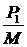 , где , где 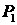 – возмущение давления
на границе между поршнем и оболочкой, – возмущение давления
на границе между поршнем и оболочкой, 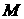 – масса единицы
площади оболочки. – масса единицы
площади оболочки.
Предположим, что в течении отсутствуют вихри,
вращающиеся вокруг оси 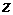 . Тогда течение в плоскости . Тогда течение в плоскости 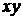 имеет потенциальный
вид. Введем величину имеет потенциальный
вид. Введем величину 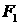 (потенциал смещений)
так, что (потенциал смещений)
так, что
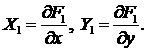 (3.6) (3.6)
Обозначим D лапласиан в плоскости 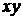 за за 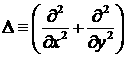 . (3.7) . (3.7)
Тогда окончательно получаем для 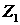 , , 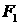 систему уравнений: систему уравнений:
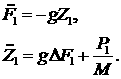 (3.8) (3.8)
При этом для перехода от (3.5)–(3.6) к (3.8)
потребовалось интегрирование по 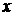 и по и по 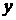 . Потенциал определяется с точностью до произвольной функции
от времени, поэтому значение констант интегрирования не имеет значения. Мы
положили константы интегрирования равными нулю. . Потенциал определяется с точностью до произвольной функции
от времени, поэтому значение констант интегрирования не имеет значения. Мы
положили константы интегрирования равными нулю.
Отметим, что характеристики вещества, из которого
состоит оболочка, никак не влияют на коэффициенты уравнения (3.8). Это тем
более существенно, что для реальных мишеней, которые описаны выше, при
рассматриваемых давлениях материал оболочек (золото) ведет себя сложным образом
и не может быть описан простыми моделями. Для того, чтобы описываемая
инвариантность по отношению к уравнению состояния материала оболочки имела
место, достаточно, чтобы оболочка была тонкой, т.е. толщина оболочки должна
быть много меньше характерного размера пространственной неоднородности
возмущения 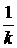 , где , где 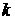 – волновой вектор. – волновой вектор.
3.2
Особенности решения, описывающего возмущения в оболочке.
Для дальнейших оценок построим решение для свободных
колебаний оболочки – когда плотность поршня равна нулю. Будем искать решение
уравнений (3.8) в факторизованном виде - как произведение временной и
пространственной части. В этом случае находим частные решения, пространственная
часть которых удовлетворяет очевидному граничному условию – ограниченности на
бесконечности:
1) Плоские волны:
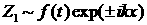 , где для , где для 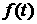 возможны 4 моды: возможны 4 моды:
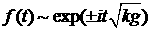 , либо , либо 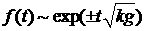 . .
Очевидно, что из них наиболее существенно растущее
решение:
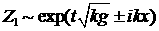 . (3.9) . (3.9)
2) Центрально-симметричное решение (локальное),
зависящее от радиуса как функция Бесселя нулевого порядка и затухающее на
бесконечности, для которого также из 4 мод выбираем:
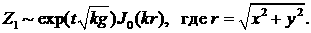 (3.10) (3.10)
Очевидно, что при этом получено полное формальное
совпадение с результатами раздела 2.1. Тем самым получено обобщение последних
на произвольное уравнение состояния оболочки, а совпадение результатов подходов
Отта и Тейлора является взаимным подтверждением справедливости полученных формул.
Отметим также замечательную особенность
решения Отта с плоскими волнами: такое решение не зависит от координаты 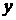 . Если исключить эту
координату из исходной системы уравнений (3.2), то эта система становится
линейной (впервые на это указано в /3/). Она приобретает вид: . Если исключить эту
координату из исходной системы уравнений (3.2), то эта система становится
линейной (впервые на это указано в /3/). Она приобретает вид:
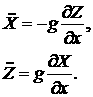 (3.11) (3.11)
В отличие от (3.5) здесь 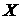 и и 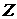 не являются малыми величинами. Это означает,
что удовлетворяющее этой системе решение (3.9) может описывать (при
соответствующей амплитуде) и несинусоидальную стадию развития возмущений. не являются малыми величинами. Это означает,
что удовлетворяющее этой системе решение (3.9) может описывать (при
соответствующей амплитуде) и несинусоидальную стадию развития возмущений.
Действительно, в /4/ приведено такое
решение, имеющее вид (3.9) и одновременно описывающее нелинейные эффекты:
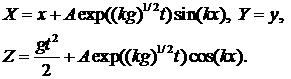 (3.12) (3.12)
В соответствующий момент времени (когда 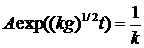 ) уравнение поверхности ) уравнение поверхности 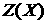 представляет собой параметрическую форму
уравнения циклоиды с остриями, направленными вниз (моделирующими образование
струй) и “пузырями” между ними. К сожалению, дальше этого момента времени
решение (3.12) не может быть продолжено – оно становится неоднозначным, точнее,
в оболочке появляются самопересечения. представляет собой параметрическую форму
уравнения циклоиды с остриями, направленными вниз (моделирующими образование
струй) и “пузырями” между ними. К сожалению, дальше этого момента времени
решение (3.12) не может быть продолжено – оно становится неоднозначным, точнее,
в оболочке появляются самопересечения.
3.3. Вывод
системы уравнений для возмущений оболочки из законов сохранения.
Система уравнений для возмущений (3.8) может быть
получена сразу из законов сохранения. Действительно, если массу единицы площади
оболочки обозначить 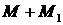 , где , где 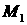 – возмущение, скорость
перетекания массы обозначить за – возмущение, скорость
перетекания массы обозначить за 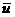 и предположить, что с
одной стороны приложена разность давлений и предположить, что с
одной стороны приложена разность давлений 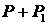 , где , где 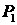 – возмущение, то
уравнения сохранения массы и двух компонент импульса будут иметь вид: – возмущение, то
уравнения сохранения массы и двух компонент импульса будут иметь вид:
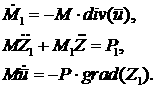 (3.13) (3.13)
Отсюда, вводя потенциал смещений 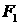 так, что так, что 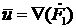 и учитывая, что и учитывая, что 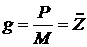 , получаем систему уравнений (3.8). , получаем систему уравнений (3.8).
3.3.1 Вывод системы уравнений для возмущений оболочки
в криволинейных координатах.
В случае сферической или цилиндрической
оболочки соответствующую систему уравнений можно построить на основе
уравнений (3.13), добавив, где это
необходимо, соответствующие степени радиуса оболочки 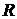 , который заменяет теперь в
уравнениях координату , который заменяет теперь в
уравнениях координату 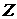 . Так, например, в сферическом
случае уравнение сохранения радиальной компоненты импульса имеет вид (здесь за . Так, например, в сферическом
случае уравнение сохранения радиальной компоненты импульса имеет вид (здесь за 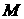 обозначена масса единицы телесного угла): обозначена масса единицы телесного угла):
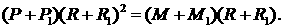 (3.14) (3.14)
Вместо перпендикулярной компоненты
импульса записывается уравнение момента импульса, которое имеет вид:
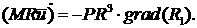 (3.15) (3.15)
Учитывая, что уравнение сохранения массы
имеет тот же вид, что и в “плоской” системе (3.13), получаем окончательно
систему уравнений для возмущений, аналогичную (3.8):
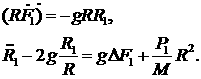 (3.16) (3.16)
Аналогично выводится система уравнений
для цилиндрической оболочки, которая имеет вид (здесь за 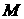 обозначена масса площадки: единица линейного
угла ´ единица длины
цилиндра): обозначена масса площадки: единица линейного
угла ´ единица длины
цилиндра):
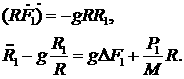 (3.17) (3.17)
4. Вывод
системы уравнений для возмущений в поршне.
Рассмотрим движение в газовой области, поставив задачу
построения системы уравнений для возмущений. Как и выше, мы запишем трехмерные
уравнения гидродинамики в лагранжевом виде, выбирая форму уравнений из /7/.
Обозначим r0  начальная плотность, r начальная плотность, r  плотность, плотность,
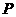  давление, давление, 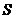  энтропия. энтропия.
По определению, начальная плотность есть функция от
лагранжевых координат 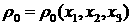 . Далее введем якобиан перехода от лагранжевых к эйлеровым
координатам: . Далее введем якобиан перехода от лагранжевых к эйлеровым
координатам: 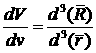 , понимаемый как отношение объемов, натянутых на базисные
векторы, - в декартовых координатах, которые используются ниже, якобиан имеет
вид: , понимаемый как отношение объемов, натянутых на базисные
векторы, - в декартовых координатах, которые используются ниже, якобиан имеет
вид:
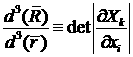 . (4.1) . (4.1)
Тогда в обозначениях параграфа 1 уравнения
адиабатичности, непрерывности и уравнение движения имеют вид:
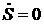  уравнение адиабатичности, (4.2) уравнение адиабатичности, (4.2)
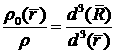  уравнение неразрывности, (4.3) уравнение неразрывности, (4.3)
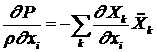  уравнение движения. (4.4) уравнение движения. (4.4)
Пусть невозмущенное движение газа является плоским,
направленным вдоль оси z. Тогда для
невозмущенного движения система уравнений (4.2)  (4.4) выглядит следующим
образом (дифференцирование по z обозначаем
штрихом, а по времени (4.4) выглядит следующим
образом (дифференцирование по z обозначаем
штрихом, а по времени  точкой): точкой):
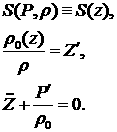 (4.5) (4.5)
Понятно, что переменные 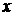 , , 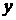 в эту систему
уравнений не входят. в эту систему
уравнений не входят.
4.1.
Линеаризация уравнений.
В систему уравнений (3.2) (3.4) мы подставляем гидродинамические
величины (эйлерова координата, давление, плотность, энтропия), соответствующие
возмущенному течению, представленные в виде суммы невозмущенных (плоских)
величин, описываемых формулами (3.5), и малых возмущений: (3.4) мы подставляем гидродинамические
величины (эйлерова координата, давление, плотность, энтропия), соответствующие
возмущенному течению, представленные в виде суммы невозмущенных (плоских)
величин, описываемых формулами (3.5), и малых возмущений: 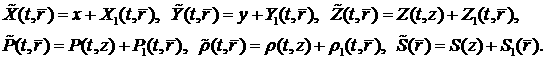 (4.6) (4.6)
Как и выше, при рассмотрении возмущений оболочки в
уравнениях (3.6), мы предположим, что в течении отсутствуют вихри, вращающиеся
вокруг оси  , и введем величину , и введем величину  (потенциал смещений)
так, что (потенциал смещений)
так, что
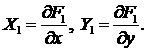 (4.7) (4.7)
Снова обозначим D лапласиан в плоскости 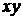 : : 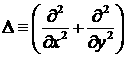 . Тогда подстановка представления (3.6) в якобиан (3.1)
сделает его равным следующему выражению: . Тогда подстановка представления (3.6) в якобиан (3.1)
сделает его равным следующему выражению:
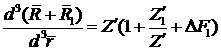 . (4.8) . (4.8)
Далее мы подставляем разложение (4.6) в систему
уравнений (4.2) (4.4) и после окончания
процедуры линеаризации получаем следующие уравнения для возмущений (ниже мы
по-прежнему обозначаем точкой лагранжеву частную производную по времени, а
штрихом – производную по лагранжевой координате (4.4) и после окончания
процедуры линеаризации получаем следующие уравнения для возмущений (ниже мы
по-прежнему обозначаем точкой лагранжеву частную производную по времени, а
штрихом – производную по лагранжевой координате 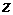 ): ):
уравнение адиабатичности:
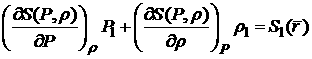 , (4.9) , (4.9)
уравнение неразрывности:
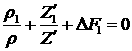 , (4.10) , (4.10)
радиальная (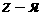 ) компонента уравнения
движения: ) компонента уравнения
движения:
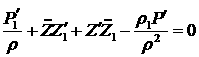 , (4.11) , (4.11)
перпендикулярная к 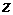 компонента уравнения движения: компонента уравнения движения:
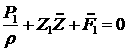 . (4.12) . (4.12)
Возмущения плотности можно исключить из уравнений.
Выполнив это, получаем окончательно (за 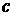 обозначена скорость звука): обозначена скорость звука):
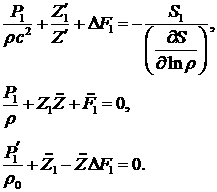 (4.13) (4.13)
Полученная система уравнений является довольно общей.
Она описывает развитие возмущений в произвольном плоском одномерном движении, причем для сферического и
цилиндрического случаев вывод соответствующей системы уравнений производится
совершенно аналогично.
Заметим, что при выводе системы уравнений для
возмущений (4.13) мы не предполагали
определенного уравнения состояния среды, в которой развиваются возмущения. Если
в дальнейшем рассматривать только адиабатические возмущения (обычно так и
бывает), то правая часть в первом уравнении в (4.13) становится равной нулю, и
вся информация об уравнении состояния среды заключается только в выражении для
скорости звука.
4.2 Вывод системы уравнений для возмущений в поршне в
криволинейных координатах
Так же, как для оболочки, соответствующую
систему уравнений в газовой области в сферических или цилиндрических
координатах можно построить на основе уравнений (4.13), добавив, где это
необходимо, соответствующие степени радиуса оболочки 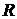 , который заменяет теперь в
уравнениях координату , который заменяет теперь в
уравнениях координату 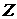 . .
Так, например, в сферическом случае
выражение для якобиана (4.8) приобретает вид:
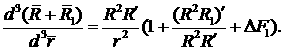 (4.14) (4.14)
В результате 1-е и 3-е уравнения системы
(4.13) изменяются. Кроме того, следует учесть, что теперь лапласиан D содержит дифференцирование только по угловым
переменным. Размерность его изменилась по сравнению с плоским случаем - он
становится безразмерным. Изменилась и размерность углового потенциала 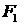 – он также становится безразмерным. Это, в
свою очередь, приводит к изменению 2-го уравнения системы (4.13). В результате
она приобретает вид: – он также становится безразмерным. Это, в
свою очередь, приводит к изменению 2-го уравнения системы (4.13). В результате
она приобретает вид:
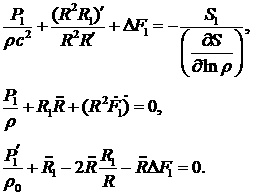 (4.15) (4.15)
Аналогичная система уравнений для
цилиндрической системы имеет вид:
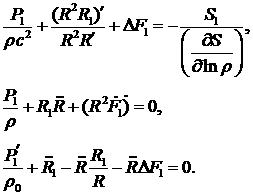 (4.16) (4.16)
5.
Постановка задачи о развитии возмущений в системе газ – оболочка.
5.1.
Преобразование уравнений к виду, пригодному для расчета возмущений в мишени.
Выше мы получили, что оболочка должна быть тонкой. Это
означает, что длина волны возмущения должна быть много больше толщины оболочки.
Можно записать неравенство для волнового вектора 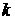 , обеспечивающее справедливость уравнений (3.8): , обеспечивающее справедливость уравнений (3.8):
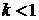 (5.1) (5.1)
Предположим,
что одновременно длины волн возмущений достаточно малы, чтобы быть много меньше
размеров газовой области. Такое возможно при выполнении двойного неравенства
(см. рис.1, где указана длина поршня,
равная
18), по смыслу совпадающего с неравенством  , приведенным выше: , приведенным выше:
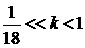 . (5.2) . (5.2)
Такие возмущения (коротковолновые) наиболее интересны
с физической точки зрения как растущие наиболее быстро. Рассматривая такие
возмущения, можно считать коэффициенты в (4.13) постоянными. Кроме того, легко
видеть, что коэффициенты системы (4.13) в этом случае оказываются различных
порядков малости. Большой величиной, по степеням которой ведется сравнение,
является волновой вектор 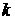 . Пространственное дифференцирование имеет порядок . Пространственное дифференцирование имеет порядок 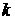 , дифференцирование по времени, согласно дисперсионному
соотношению из (3.9): , дифференцирование по времени, согласно дисперсионному
соотношению из (3.9): 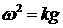 , - имеет порядок , - имеет порядок 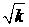 . С учетом этого матрица коэффициентов в (4.13) при
переменных . С учетом этого матрица коэффициентов в (4.13) при
переменных 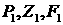 выглядит следующим
образом: выглядит следующим
образом:
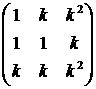 (5.3) (5.3)
Очевидно, что левый коэффициент в первой строке имеет
пониженный порядок – его можно положить равным нулю. Опуская этот член и считая
возмущения энтропии равными нулю, получим из уравнений (4.13):
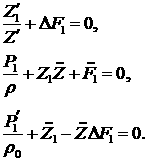 (5.4) (5.4)
Такая система без труда преобразуется к виду:
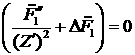 . (5.5) . (5.5)
Это уравнение интегрируется и приобретает вид
“полного” лапласиана в эйлеровых координатах:
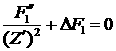 , (5.6) , (5.6)
а
первое уравнение из (4.4) приобретает вид:
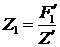 (5.7) (5.7)
и
становится граничным условием для 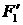 , заданным на оболочке (при , заданным на оболочке (при 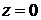 ). ).
Поясним, что переход в эйлеровы координаты в уравнении
(5.6) должен производиться по схеме:
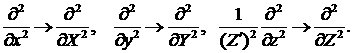 (5.8) (5.8)
В результате уравнение (4.6) приводится к виду
трехмерного уравнения Лапласа в эйлеровых координатах:
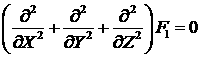 (5.9) (5.9)
с
граничным условием на оболочке:
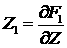 . (5.10) . (5.10)
Попутно отметим, что благодаря использованию
коротковолнового приближения, нам в системе уравнений (4.13) удалось
освободиться от единственного члена, коэффициенты которого зависят от уравнения
состояния газа, из которого состоит поршень. Таким образом, получаем, что при
выполнении двойного неравенства (5.2) уравнения, описывающие развитие
возмущений и в оболочке, и в газовом поршне, оказываются не зависящими от
уравнений состояния всех элементов системы.
5.2.
Постановка задачи.
Таким образом, мы приходим к следующей формулировке
задачи о развитии возмущений, возникающих при разгоне оболочек газовым поршнем
в мишенях инерциального термоядерного синтеза:
Найти растущие решения для линейных коротковолновых
возмущений, возникающих на контактной границе между оболочкой и газом и
описываемых системами уравнений (3.8) (в оболочке – при 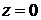 ) и (4.4) (в газе – при ) и (4.4) (в газе – при 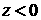 ): ):
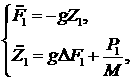 (5.11) (5.11)
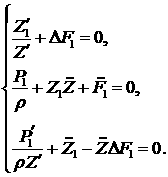 (5.12) (5.12)
Граничным
условием для систем этих уравнений является совпадение 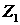 и и 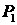
при 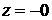 . .
Поверхность оболочки является неустойчивой. По смыслу
задачи эта поверхность является и источником возмущений в газовой области 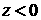 . По этой причине полное граничное условие для возмущений в
газовой области включает в себя условие при . По этой причине полное граничное условие для возмущений в
газовой области включает в себя условие при 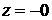 и условие затухания
возмущений вдали от оболочки при и условие затухания
возмущений вдали от оболочки при 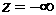 : :
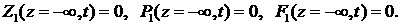 (5.13) (5.13)
6. Решение
системы уравнений для возмущений в системе газ – оболочка.
6.1
Дисперсионное соотношение.
Ищем экспоненциально растущее решение уравнений
(5.11)–(5.12) для возмущения, заданного в виде плоской волны.
Решение
в газе: 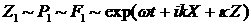 , (6.1) , (6.1)
решение
в оболочке:  . (6.2) . (6.2)
Подстановка (5.1) в систему уравнений (4.12) приводит
к равенствам:
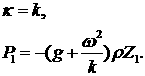  (6.3) (6.3)
Подстановка (5.2) в систему уравнений (4.11) приводит
к равенству:
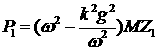 (6.4)
(6.4)
Из (5.3)–(5.4) получаем окончательно:
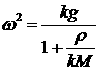 (6.5) (6.5)
Дисперсионное соотношение (6.5) является основным
результатом нашего анализа.
В разделе 2 это же дисперсионное соотношение было
получено более простым образом для частного случая, когда оболочка и поршень
состоят из несжимаемых жидкостей. Целью всего последующего рассмотрения было
достижения более высокой степени общности (для произвольных уравнений
состояния) для формулы (6.5).
Как и раньше, из выражения (6.5) следует, что наличие
плотного газового поршня оказывает стабилизирующее действие на оболочку,
заметно уменьшая инкремент роста возмущений.
6.2 Задача
Неймана для возмущений в газе.
Существенно, что возмущения давления на поверхности оболочки,
хоть они и не равны нулю, не являются источником для возмущений в газе.
Источником же являются граничные условия для смещения (искривления оболочки) 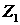 . .
Таким образом, граничные условия для возмущений в газе
в эйлеровых координатах имеют вид (см. (4.9) и (4.10)) граничных условий
Неймана:
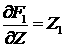 (6.6) (6.6)
для
уравнения Лапласа
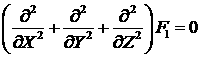 . (6.7) . (6.7)
При этом решение для возмущений оболочки имеет тот же
вид, что и в случае нулевой плотности газа, но с другим дисперсионным
соотношением. Это решение (функция 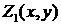 ) является граничным
условием для уравнения Лапласа (6.7), описывающего возмущения в газе. Решение
краевой задачи в общем случае произвольной функции ) является граничным
условием для уравнения Лапласа (6.7), описывающего возмущения в газе. Решение
краевой задачи в общем случае произвольной функции 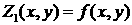 хорошо известно из
электростатики. Аналогия с электростатикой становится полной, если учесть
второе граничное условие в рассматриваемой задаче – обращение в нуль скалярного
потенциала на бесконечности. Оно записывается в виде потенциала простого слоя
(далее под хорошо известно из
электростатики. Аналогия с электростатикой становится полной, если учесть
второе граничное условие в рассматриваемой задаче – обращение в нуль скалярного
потенциала на бесконечности. Оно записывается в виде потенциала простого слоя
(далее под 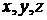 всюду подразумеваются эйлеровы координаты): всюду подразумеваются эйлеровы координаты):
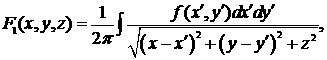 (6.8) (6.8)
где
интегрирование проводится по поверхности оболочки.
Решение (5.8) не предполагает какого-то определенного
распределения величины возмущения по поверхности оболочки – функция 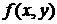 может быть в
значительной степени произвольной. Ограничения на ее вид – поведение на
бесконечности - накладывает только требование сходимости интеграла (6.8). может быть в
значительной степени произвольной. Ограничения на ее вид – поведение на
бесконечности - накладывает только требование сходимости интеграла (6.8).
Ниже мы детально рассмотрим частный случай такого
распределения свойств забивки и окружающей среды. Мы рассмотрим случай, когда
функция 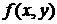 имеет центральную
симметрию: имеет центральную
симметрию: 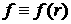 . .
Тогда, вводя полные эллиптические интегралы 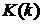 , , 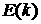 : :
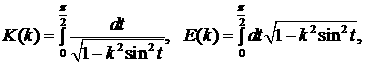 (6.9) (6.9)
запишем интеграл (5.8) в виде:
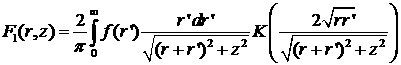 (6.10) (6.10)
Выберем функцию
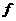 в виде функции Бесселя в виде функции Бесселя
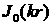 . .
Тогда, согласно (5.7) и (6.5), возмущение на
поверхности оболочки будет иметь вид:
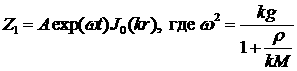 (6.11) (6.11)
Внутри газа при удалении от оболочки величина
возмущений будет определяться выражением:
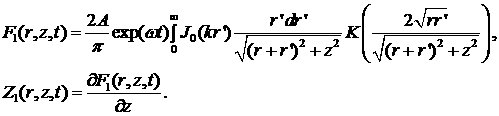 (6.12) (6.12)
При 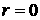 интегрирование в
(6.12) удается провести до конца. интегрирование в
(6.12) удается провести до конца.
Используем табличное значение интеграла
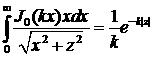 (6.13) (6.13)
и
получаем окончательно:
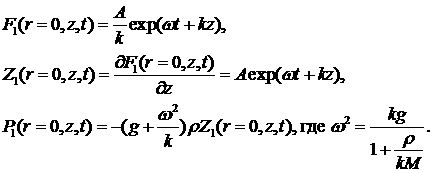 (6.14) (6.14)
Заметим, что рассматриваемое возмущение имеет отличия,
делающие его удобным для проверки правильности численного счета – оно зависит
экспоненциально как от времени, так и от пространственных координат.
7. Возмущения в системе газ–оболочка в криволинейных
координатах.
Поскольку выше была доказана
независимость результатов расчета эволюции возмущений от уравнений состояния
материалов поршня и оболочки, результаты, полученные нами для частного случая,
а именно - для случая, когда и оболочка, и поршень состоят из несжимаемой
жидкости, - мы вправе распространить и на общий случай произвольного состава
элементов системы. Таким образом, полученные выше выражения для дисперсионных
соотношений (2.11), (2.13) являются решениями для сферических и цилиндрических
систем поршень-оболочка в общем случае.
Заключение.
Рассмотрены малые возмущения тонкой плоской оболочки,
разгоняемой газовым поршнем. При этом предполагалось, что длины волн возмущений
много больше толщины оболочки и много меньше размеров газа.
Рассчитано дисперсионное соотношение для системы газ –
оболочка в случае конечной плотности газа. Показано, что наличие плотного
газового поршня оказывает стабилизирующее действие на оболочку, заметно
уменьшая инкремент роста возмущений по сравнению со случаем нулевой плотности
газа.
Показано, что задача описания возмущений в газе
сводится к решению задачи Дирихле 2-го рода для уравнения Лапласа.
Показано, что развитие коротковолновых возмущений,
длина волны которых много больше толщины оболочки и много меньше размеров газа,
не зависит от уравнений состояния веществ, входящих в состав поршня и оболочки.
Результаты анализируются на примере типичных
цилиндрических мишеней, применяемых при расчетах ионного термоядерного синтеза.
Полученные решения, описывающие экспоненциальный рост
малых возмущений в системе газ-оболочка, могут быть использованы для сравнения
с результатами численных расчетов разгона оболочек в мишенях ИТС с
использованием программ 2D и 3D гидродинамики.
Литература.
1. Nuckolls et al. Laser
Compression of Matter to Super-High Densities: Thermonuclear (CTR) Applications,
Nature Vol.
239, p. 129, 1972.
2. Баско М.М., Гуськов С.Ю., Недосеев С.Л., Чуразов
М.Д., Мишени ИТС. В сб. “Ядерный синтез с инерционным удержанием” под ред. Б.Ю. Шаркова, стр. 53-56, раздел 3.3. М., Физматлит, 2005.
3. E.Ott. Nonlinear Evolution of the
Rayleigh-Taylor Instability of a Thin Layer, Phys.Rev. Lett. 29,
1429-1432, 1972.
4. W.Manheimer,
D.Colombant and E.Ott. Three-dimensional, nonlinear evolution of the
Rayleigh-Taylor Instability of a thin layer, Phys.Fluids 27,
p. 2164, 1984.
5.
И.С.Лебо, В.Ф.Тишкин. М. Исследование гидродинамической
неустойчивости в задачах лазерного термоядерного синтеза, М., Физматлит, 2006.
6.
Ландау Л.Д., Лифшиц Е.М., Курс теоретической физики. Том 6 “Гидродинамика”. М., Наука, 1986.
7. Станюкович К.П.
Неустановившиеся движения сплошной среды. М., Наука, 1971.
|