Аннотация
Работа посвящена сравнительному анализу особенностей, проявляющихся на различных уровнях вейвлет разложений полей
газодинамических величин, найденных методом сквозного счета. Сравнение проведено также для расчетов,
полученных на сетках с шагами дискретизации h и h/2. Численные эксперименты показали, что использование
нескольких шагов кратно-масштабного анализа позволяет получить дополнительную информацию о структуре разрывов в течении.
Кроме того, оказалось, что построенный детектор позволяет локализовать артефакты течения,
возникающие из-за локальных неточностей в дискретизации.
Abstract
Singularities found at different levels of the wavelet decomposition of gas-dynamic fields calculated by
shock-capturing methods on various grids are compared. Numerical experiments demonstrate that several
steps of the multi-scale decomposition of the field enable to get essential information on the shock waves.
Moreover, detector suggested in the paper singles out artifacts due to the local inaccuracies of the discretisation.
Введение.
Известно, что использование алгоритмов сквозного счета
при численном моделировании газодинамических задач приводит к размазыванию и
зашумлению разрывов. Однако для широкого круга задач (адаптивное построение расчетных
сеток) необходима информация о расположении сингулярностей. Таким образом,
задача автоматического выделения и классификации особенностей расчета
становится особенно важной.
Кроме того, при решении этой задачи следует учитывать,
что в одном и том же расчете могут присутствовать эффекты соответствующие
разным масштабам, такие как разрывы разных интенсивностей, шумы разных частот и
амплитуд, структуры обусловленные типом разностной схемы и численных методов.
Поэтому перед решением задачи о выделении и классификации особенностей
необходимо решить задачу о разложении исходных данных по уровням, так что на
каждом уровне разложения остаются только структуры соответствующего масштаба.
После разложения можно либо исключить из обработки
структуры соответствующие мелким масштабам, как несущественные, либо проводить
полный анализ с учетом того, что мелкомасштабные структуры могут относиться, например,
погрешностям вычислений.
Предыдущие исследования [4] были посвящены построению
детектора сингулярностей на основе вейвлет анализа. В качестве исходных данных
детектор использует результаты расчета газодинамических полей полученных на прямоугольной
сетке. В результате алгоритм присваивает каждому узлу сетки число, которое
характеризует тип течения в окрестности этого узла. Особенностью алгоритма
является то, что он не требует обязательного задания порогов чувствительности,
хотя такая возможность apriori имеется.
Это расширяет область использования детектора для автоматического выделения
разрывов, но приводит к появлению артефактов, которые могли бы быть исключены
при дополнительной, тонкой настройке.
Еще одной особенностью детектора является то, что
значения функции в узлах сетки отождествляются с коэффициентами ее вейвлет
разложения. И хотя, в силу компактности носителя материнского вейвлета, это
соотношение выполняется с достаточно высокой точностью, и такой подход,
некоторые называют его “wavelet
crime”, используется во многих приложениях, он не является
математически строгим и может приводить к появлению артефактов.
Вейвлет анализ предлагает естественный метод
многомасштабного разложения исходного сигнала. На каждом шаге разложения сигнал
разлагается на две компоненты: сглаженную низкочастотную и зашумленную высокочастотную.
На каждом последующем шаге происходит разложение низкочастотной компоненты
разложения. При этом каждый последующий уровень разложения соответствует более
грубой сетке.
Данная работа посвящена сравнительному анализу
сингулярностей и артефактов, проявляющихся на различных уровнях вейвлет разложения
исходного поля, выполненного при помощи различных вещественных и комплексных
вейвлетов.
При анализе для определения интенсивности особенностей
в детекторе вводились различные пороги чувствительности. Целью данной работы
являлось определить: особенности какого типа и интенсивности выделяются детектором
наиболее надежно.
Также большой интерес представляет сравнительный
анализ одного и того же расчета, произведенного на различных сетках, таких, что
при разложении расчета проведенного на более мелкой сетке переходим на сетку
соответствующую расчету, проведенному на грубой сетке. При этом можно определить:
насколько точно локализованы разрывы на грубой сетке, какие тонкие структуры не
удается на ней обнаружить, и в каких областях чаще проявляются счетные артефакты.
Данному вопросу посвящена заключительная часть этой работы.
Работа в целом посвящена описанию широкого круга
экспериментов, проведенных в рамках решения задачи о построении наиболее
качественного алгоритма автоматического выделения сингулярностей в газодинамических
полях полученных методами сквозного счета.
Численное
моделирование.
В качестве модельной была выбрана задача об эволюции и
взаимодействии разрывов в канале под действием импульсного вложения энергии.
Постановка задачи представлена на рис. 1. В начальный
момент времени плоская ударная волна с числом Маха 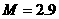 располагается в
сечении располагается в
сечении 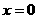 . В эксперименте в объемную часть разряда . В эксперименте в объемную часть разряда 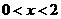 , , 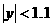 | (область 2 на рис. 1) вкладывалось 0.83 Дж, в листы
около стенок | (область 2 на рис. 1) вкладывалось 0.83 Дж, в листы
около стенок 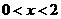 , ,  (области 3 на
рис. 3.1) – по 0.11 Дж. На основании ранее проведенных
исследований [6] предполагалось, что в поступательные степени свободы мгновенно
переходит 50% вложенной энергии. (области 3 на
рис. 3.1) – по 0.11 Дж. На основании ранее проведенных
исследований [6] предполагалось, что в поступательные степени свободы мгновенно
переходит 50% вложенной энергии.
Таким образом, в начальный момент времени существует 5
областей с постоянными значениями газодинамических величин.
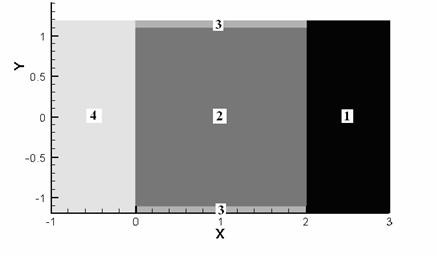
Рис.
1. Начальное распределение давления
для 2D расчета.
Моделирование проводилось в рамках математической
модели нестационарных 2D уравнений
Эйлера. Расчет производился «сквозным» образом на неподвижной сетке с
размазыванием разрывов. С учетом симметрии задачи, расчет проводился только для
области 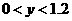 . .
В работах [3, 4] был проведен подробный анализ этого
течения для расчета, выполненного по разностной схеме первого порядка
аппроксимации на сетке, содержащей 2048*256 узлов. Также в работах представлено
решение одномерного варианта этой задачи (при исключении энерговложения в
областях 3). Это решение позволяет проследить эволюцию вертикальных разрывов в
начальные моменты времени и позволяет теоретически обосновать полученные результаты.
Для данной работы были выполнены еще 2 варианта
расчета этой же задачи. Оба расчета выполнены по схеме второго порядка аппроксимации.
Расчет 1 выполнен на сетке 2048*256 узлов, а расчет 2 на сетке содержащей
4096*512 точек.
Поскольку все расчеты проводились для верхней половины
симметричного течения, дальнейшие результаты обработки также представлены
только для области  . .
Многомасштабный
вейвлет анализ.
Основными соотношениями вейвлет анализа являются
соотношения рескейлинга:
 (1) (1)
Эти соотношения устанавливают связь между сдвигами и
растяжениями вейвлета  и масштабирующей
функции и масштабирующей
функции 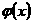 . Здесь . Здесь 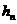 и и 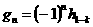 - соответствующие,
вообще говоря, комплексные низкочастотный и высокочастотный зеркальные фильтры. - соответствующие,
вообще говоря, комплексные низкочастотный и высокочастотный зеркальные фильтры.
Из соотношения 1 следует, что проекцию 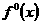 разложения
произвольной функции разложения
произвольной функции 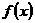 на базис сдвигов
масштабирующей функции на базис сдвигов
масштабирующей функции 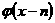 можно разложить на две
компоненты: можно разложить на две
компоненты:
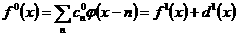 , где (2) , где (2)
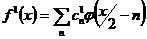 , , 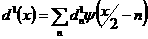 , а , а
 , , 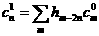 , , 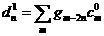 . .
Соотношение 2 можно интерпретировать как разложение
исходного сигнала 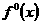 на сглаженную на сглаженную  и высокочастотную и высокочастотную  компоненты. Аналогичным
образом сглаженную компоненту компоненты. Аналогичным
образом сглаженную компоненту  можно разложить на можно разложить на 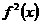 и и  . Эту цепочку можно продолжать и дальше, слой, за слоем
удаляя шумы из исходного сигнала. . Эту цепочку можно продолжать и дальше, слой, за слоем
удаляя шумы из исходного сигнала.
Обычно в приложениях при работе с дискретным исходным
сигналом 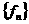 на первом шаге
дискретизацию функции отождествляют с коэффициентами её вейвлет разложения на первом шаге
дискретизацию функции отождествляют с коэффициентами её вейвлет разложения 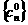 . В [4] показано, что, для задачи выделения особенностей
газодинамических течений, это допущение с высокой точностью соответствует
истине. . В [4] показано, что, для задачи выделения особенностей
газодинамических течений, это допущение с высокой точностью соответствует
истине.
Особо следует остановиться на случае использования
комплексных вейвлетов. Поскольку в приложениях исходный сигнал обычно
соответствует некоторой физической величине, то получаемая в результате разложения
комплекснозначная функция нефизична. На практике в этом случае анализируют
вещественную часть разложения.
Само использование комплексных вейвлетов обусловлено
тем, что вещественные вейвлеты с компактным носителем сильно несимметричны. В
исследуемой задаче использование таких вейвлетов может привести к смещению разрывов.
Можно ожидать, что при переходе да следующий уровень
вейвлет разложения будут исключаться наименее значимые для данного уровня
разрывы. Кроме того, за счет удаления шумов, могут проявиться тонкие структуры,
которые ранее не удавалось выделить.
Сравним результаты обработки первого уровня вейвлет
разложения поля плотности для расчета выполненного на сетке 4096*512.
а)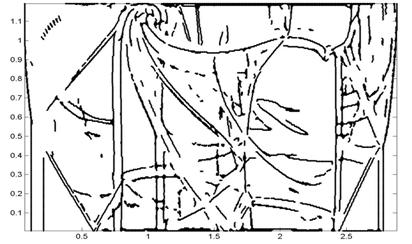
б)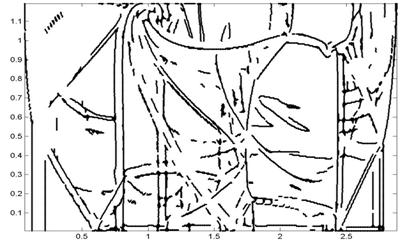
в)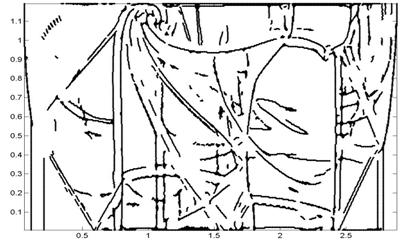
Рис. 2. Обработка первого уровня вейвлет разложения поля плотностей.
Разложение выполнялось с помощью вейвлетов а) dcoms6, б) dau20, в) dcoms22.
При разложении использовались три различных вейвлета
Добеши:
1) комплексный симметричный, содержащий 6 ненулевых
коэффициентов - dcoms6,
2) вещественный, содержащий 20 ненулевых коэффициентов - dau20
3) комплексный симметричный, содержащий 22 ненулевых
коэффициентов - dcoms22.
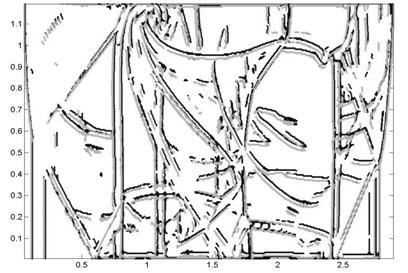
Рис. 3. Обработка первого уровня вейвлет разложения поля
плотностей. Разложение выполнялось с помощью вейвлетов: черный - dau20, серый - dcoms22.
При работе с комплексными вейвлетами анализировалась
только вещественная компонента разложения.
На рисунках 2, 3 представлен результат, полученный
после применения только основного детектора, без корректора [4]. Линии
представленные на рисунках должны соответствовать сильным разрывам поля
плотностей, то есть ударным волнам и контактным разрывам.
Из рисунков 2, 3 видно, что все основные разрывы
выделяются на всех вариантах разложения, однако для вещественного
несимметричного вейвлета разрывы внутри возмущенной области смещены
относительно разрывов, выделяемых симметричными вейвлетами. При этом разрывы на
границе возмущенной области практически совпадают.
Комплексные
симметричные вейвлеты дают практически эквивалентный результат, однако в
целом использование вейвлета dcoms22 приводит
к небольшому сокращению количества артефактов, линии разрывов, выделенные с
помощью этого вейвлета, получаются более гладкими.
а)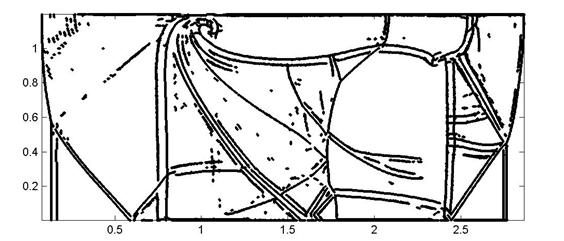
б)
в)
Рис. 4. Обработка нулевого (а), первого (б) и второго (в)
уровней вейвлет разложения поля плотностей.
а)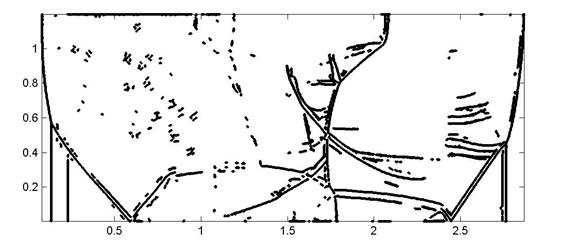
б)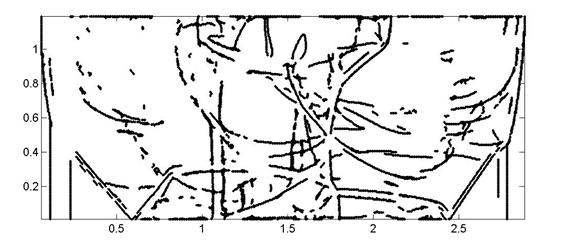
Рис. 5. Обработка нулевого (а) и первого (б) уровней вейвлет
разложения поля давления.
Теперь сравним результаты обработки нулевого, первого
и второго уровней вейвлет разложения поля плотности. Разложение выполнялось с
помощью вейвлета dcoms22. Напомним, что каждый
следующий уровень разложения соответствует вдвое более грубой сетке, чем
предыдущий. Таким образом, нулевому уровню 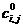 соответствует сетка
4096*512 (0< i <4097, 0< j <513, соответствует сетка
4096*512 (0< i <4097, 0< j <513,  ), первому уровню ), первому уровню 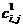 2048*256 (0< i <2049,
0< j <257, 2048*256 (0< i <2049,
0< j <257,  ), второму уровню ), второму уровню 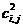 1024*128 (0< i <1025,
0< j <129, 1024*128 (0< i <1025,
0< j <129,  ). ).
Сразу можно отметить, что на втором уровне разложения
(рис. 4(в)) отражается только часть существенных разрывов, причем достаточно
грубо и обрывочно. Это может быть вызвано уже достаточно грубой сеткой, тем,
что при вейвлет - разложении отбрасывается мнимая часть коэффициентов, и
сильной размазанностью разрывов.
Гораздо больше результатов дает сравнение нулевого
(рис. 4(а)) и первого (рис. 4(б)) уровня разложения. Заметно сокращение числа
артефактов (область [0, 0.5]*[1, 1.2]). Часть двойных линий стали одинарными
[1, 2]*[0.8, 1] и наоборот [1, 1.7]*[0.5, 0.8]. Пропали некоторые разрывы [0,
0.2]*[0.4, 0.6], но появились и новые структуры [1.7, 2.2]*[0.5, 0.7].
Большинство новых структур появляется в областях,
которые раньше были сильно зашумлены. Хотя и возникает сомнение в физичности
этих структур, тот факт, что структура в области [1.7, 2.2]*[0.5, 0.7]
проявляется и при анализе поля давления (рис. 5) указывает на то, что она не
является ошибочной для детектора.
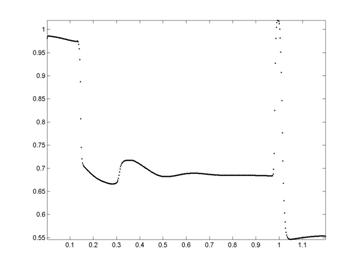
Рис. 6. Распределение плотности в сечении X = 2.
Тем не менее, из рисунка 6 видно, что этой структуре
не соответствуют ни какие разрывы, а лишь перегибы плотности. Это недостаток
детектора может быть устранен только анализом интенсивности разрывов и
введением порогов. Для этих целей был разработан корректор, который
используется для проверки разрывов выделенных основным детектором.
Граничные
условия.
Особого внимания заслуживают разрывы, выделенные на
границе расчетной области. Поскольку ось Y = 0 является осью симметрии течения, а также тому,
что, при обработке поля вейвлет фильтрами, на границе поле продолжается из соображений
симметрии, на этой оси не должно возникать разрывов. Более тщательный анализ показал,
что поле плотностей имеет излом в окрестности оси симметрии рис 7.
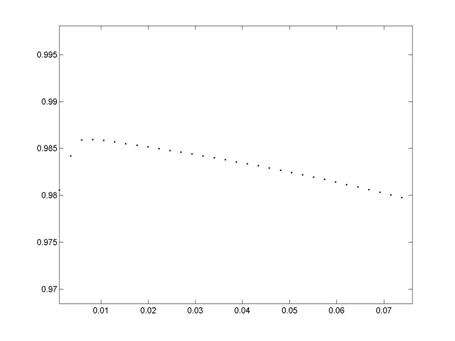
Рис. 7. Распределение плотности в сечении X = 2.
Этот эффект объясняется граничными условиями на оси
симметрии, которые не включают в себя равенства нулю вертикальной компоненты
скорости, поскольку в расчете нет узлов лежащих непосредственно на оси
симметрии.
Аналогичные эффекты имеют место и на
границу Y = 1.2.
Таким образом детектор может быть
использован для проверки корректности постановки граничных условий при
моделировании течений.
Анализ
интенсивности разрывов.
Теперь обратимся к анализу результатов корректора см.
[4]. Хотя корректор и выдает больше артефактов, он также позволяет вводить
порог чувствительности, который эти артефакты отсеивает. Результаты обработки
расчета, проведенного на сетке 4096*512, приведены на рисунке 8.
а)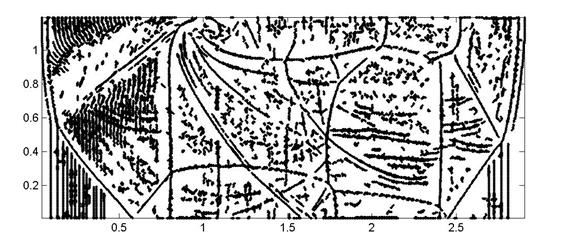
б)
в) 
г)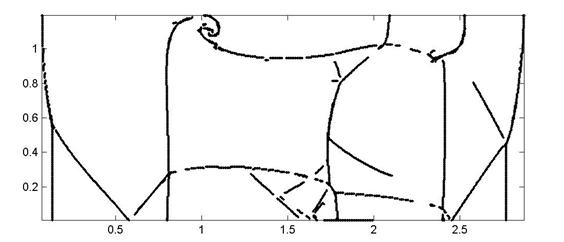
Рис. 8. Обработка с помощью корректора первого уровня вейвлет
разложения поля плотностей для расчета выполненного на сетке 4096*512. Разложение
выполнялось с помощью вейвлета dcoms22. Порог
чувствительности равен а) 0, б) 0.00002, в) 0.00005, г) 0.0005.
Корректор выделяет точку n с порогом чувствительности 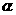 , если: , если:
 , ,
где {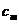 } – исследуемое поле, { } – исследуемое поле, { } – вещественная часть низкочастотного фильтра симметричного
комплексного вейвлета Добеши (dcoms6), { } – вещественная часть низкочастотного фильтра симметричного
комплексного вейвлета Добеши (dcoms6), {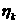 } – высокочастотный фильтр вещественного вейвлета Добеши (dau6). } – высокочастотный фильтр вещественного вейвлета Добеши (dau6).
Результат обработки с нулевым (рис. 8(а)) порогом
чувствительности сильно зашумлен, особенно в области между ударной волной и
контактным разрывом 0 < x < 0.7.
Однако все существенные разрывы отделены от зашумленных областей. Кроме того,
следует помнить, что обычно мы используем корректор только для отбраковки части
разрывов основного детектора, а, следовательно, артефакты корректора не входят
в окончательный результат. После введения порога (рис. 8(б)) видно, что
наибольшей интенсивностью обладают те артефакты и “ложные” структуры, которые
выделяются и на основном детекторе (рис. 8(б)) области [0, 0.5]*[1, 1.2], [1.7,
2.2]*[0.5, 0.7].
Эти артефакты удаляются при дальнейшем увеличении
порога (рис. 8(в)), хотя по-прежнему сохраняется ряд двойных и сомнительных
линий.
Однако последующее увеличение порога (рис. 8(г))
приводит к исключению части наклонных разрывов, в то время как все
горизонтальные и вертикальные разрывы выделяются почти идеально.
Сравнение
расчетов выполненных на разных сетках.
Перейдем к сравнительному анализу результатов
обработки расчетов выполненных на различных сетках.
а)
б)
Рис. 9. Обработка нулевого (а) и первого (б) уровней вейвлет
разложения поля плотностей для расчета выполненного на сетке 2048*256.
Разложение выполнялось с помощью вейвлета dcoms22.
а)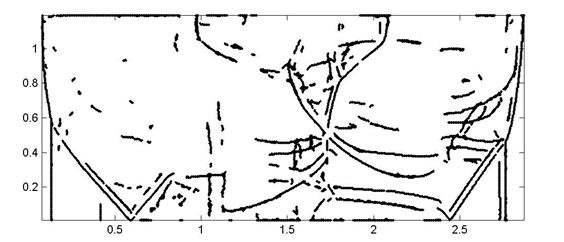
б)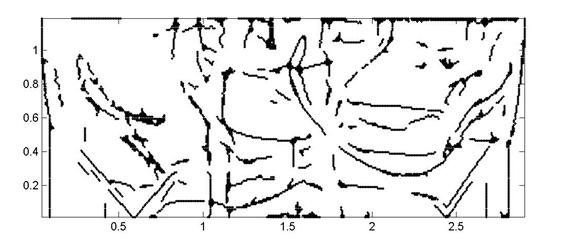
Рис. 10. Обработка нулевого (а) и первого (б) уровней вейвлет
разложения поля давления для расчета выполненного на сетке 2048*256. Разложение
выполнялось с помощью вейвлета dcoms22.
Наибольший интерес представляет сравнение пар
рисунков:
4(б) – первый уровень разложения поля плотностей
расчета выполненного на сетке 4096*512,
9(а) – нулевой уровень разложения поля плотностей
расчета выполненного на сетке 2048*256;
и
5(б) – первый уровень разложения поля давления расчета
выполненного на сетке 4096*512,
10(а) – нулевой уровень разложения поля давления
расчета выполненного на сетке 2048*256.
Эти рисунки соответствуют одной и той же сетке
2048*256.
Однако сначала отметим, что сравнение рисунков 4(в),
9(а), 10(а) показывает, что одной из причин достаточно плохого результата на
рисунке 4(в) действительно является довольно грубая сетка. Тем не менее
структура разрывов на рисунке 9(а) все же более четкая чем на рисунке 4(в),
откуда следует, что переход на следующий уровень разложения сглаживает данные
сильнее, чем переход на более грубую сетку при расчете.
В целом при сравнении рисунков 4(б) и 9(а) видно, что
выделяются практически одни и те же структуры, но на рисунке 4(б) они более
четкие. Но, с точки зрения представления разрывов (сдвоенные или одинарные линии),
рисунок 9(а) ближе к рисунку 4(а).
Заключение.
Эксперименты показали, что использование
многомасштабного анализа позволяет получить дополнительную информацию о
структуре разрывов в течении. Однако это возможно только в том случае, если
расчет выполнен на достаточно мелкой сетке.
Для многомасштабного разложения целесообразно
использовать симметричные и достаточно гладкие вейвлеты. Использование же
несимметричных вейвлетов приводит к смещению разрывов.
Переход от анализа исходного поля к анализу его
вейвлет разложения позволяет исключить часть шумовых эффектов, но приводит к
проявлению слабых структур соответствующих перегибам. Эти структуры могут быть
удалены совместным анализом исходного поля и вейвлет разложения, либо использованием
корректора.
Кроме того, опыты показали, что детектор может быть
использован для исследования корректности граничных условий.
Хотя структура разрывов вейвлет разложения для расчета
выполненного на мелкой сетке в целом соответствует структуре разрывов грубого
расчета, анализ грубого расчета дает больше артефактов и свидетельствует о
более сильном размазывании части разрывов (в основном горизонтальных).
Приложение.
Низкочастотные фильтры, использованных в работе
вейвлетов:
dcoms6 =
{-0.066291 – i * 0.085582; 0.11049 – i *0.085582;
0.66291 + i * 0.17116; 0.66291 + i * 0.17116;
0.11049 – i *0.085582; -0.066291 – i * 0.085582}.
dau6 =
{0.33267; 0.806891; 0.459877; -0.135011, -0.085441; 0.035226}.
dcoms22 =
{-2.843587e-4 – i *
5.619067e-5; 3.943661e-5 – i *
1.995730e-4;
3.503067e-3 - i * 6.987157e-6; 2.610443e-4 + i * 1.162351e-3;
-1.826877e-2 + i * 3.762785e-3; -2.986205e-3
+ i * 5.055616e-3;
5.069295e-2 - i * 1.130173e-2; -1.211437e-2
- i * 5.680614e-2;
-1.204103e-1 - i * 7.712723e-2; 1.474823e-1
+ i * 6.042637e-3;
6.59192e-1 + i * 1.294744e-1; 6.59192e-1
+ i * 1.294744e-1;
1.474823e-1 + i * 6.042637e-3; -1.204103e-1
- i * 7.712723e-2;
-1.211437e-2 - i
* 5.680614e-2; 5.069295e-2 - i *
1.130173e-2;
-2.986205e-3 + i * 5.055616e-3; -1.826877e-2
+ i * 3.762785e-3;
2.610443e-4 + i * 1.162351e-3; 3.503067e-3
- i * 6.987157e-6;
3.943661e-5 - i * 1.99573e-4; -2.843587e-4
- i * 5.619067e-5}.
daus20 =
{0.026670057901;
0.188176800078;
0.527201188932;
0.688459039454;
0.281172343661;
-0.249846424327;
-0.195946274377;
0.127369340336;
0.093057364604;
-0.071394147166;
-0.029457536822;
0.033212674059;
0.003606553567;
-0.010733175483;
0.001395351747;
0.001992405295;
-0.000685856695;
-0.000116466855;
0.000093588670;
-0.000013264203}
.
Список литературы.
1.
А.Л. Афендиков, В.В. Горбунова, Л.И. Левкович-Маслюк, А.В. Плёнкин, Локализация
сингулярностей газодинамических полей при помощи комплексных и вещественных
вейвлетов, Препринт Института прикладной
математики им. М.В. Келдыша РАН №98, 2005г.
2.
А.Л. Афендиков, Л.И. Левкович-Маслюк. Локализация особенностей газодинамических
полей при помощи комплексных ортогональных вейвлет - разложений. Препринт
№101, 2003г.
3. A. Afendikov, L. Levkovich-Masliuk,
Localization of Singularities of Gas-Dynamic fields by using complex orthogonal
wavelet expansion, Russian Journal of
Math. Phis. VII, № 3, pp 250-258, 2004.
4. А.Л. Афендиков, Л.И. Левкович-Маслюк, А.Е. Луцкий, А.В. Плёнкин. Локализация разрывов в полях газодинамических функций
с помощью вейвлет анализа, Математическое Моделирование 2008, том 20, №7,
страницы 65-84.
5.
И.А Знаменская, А.Е. Луцкий, Исследование эволюции и взаимодействия разрывов
течения в канале под действием импульсного вложения энергии, Препринт Института прикладной математики им.
М.В. Келдыша РАН №88, 2005г.
6.
Знаменская И.А., Луцкий А.Е., Мурсенкова И.В. Исследование поверхностного
энерговклада в газ при инициировании импульсного разряда типа «плазменный
лист» // Письма в ЖТФ, Т.30, вып. 24 С.
38-42.
|