Идея использования слабого шума для управления подавлением сильного шума
в экранируемой подобласти в реальном времени
В.С. Рябенький
Рассматривается линейная разностная
задача в реальном времени в области, состоящей из двух подобластей, в одной из
которых сосредоточены источники, возбуждающие процесс. Отклонение решения от
нуля в другой подобласти интерпретируется как нежелательный шум. Построены
дополнительные источники, которые в заданное 
число раз ослабляют
шум. Идея сохранения слабого шума в экранируемой подобласти позволяет построить
ослабляющее шум активное управление в реальном времени, используя только ту
информацию об управляемом процессе, которая содержится к текущему моменту
времени вблизи границы раздела подобластей.
Пусть
на плоскости 
введена сетка
точек 
с шагами 
и 
по пространству и
времени. Зададим 
, 
и рассмотрим область 
, причем будем считать, что 
и 
целые числа.
Рассмотрим разностное уравнение вида
(1)
Здесь 
множество точек сетки, лежащих внутри
области 
, где 
и 
- целые числа ; 
и 
- заданные коэффициенты
и правые части, шаблон 
состоит из пяти
точек
Будем считать, что
если 
, если 
Решения 
уравнения (1)
определены на множестве 
. Дополним уравнение
(1) начальными и граничными условиями
,
где 
и 
- заданные числа.
Функции 
, 
, удовлетворяющие этим начальным и граничным условиям,
образуют линейное пространство, которое обозначим 
. Тогда начальные и граничные условия, которым должны
удовлетворять решения уравнения (1), можно записать как включение
(2)
Разобьем множество на два
непересекающиеся подмножества 
и 
точек , отнеся к и те точки 
, для которых 
и 
соответственно.
Обозначим 
, 
; 
, 
; 
. Граница между подобластями 
и 
состоит,
очевидно, из точек 
и 
, 
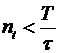. Относительно , 
, будем предполагать, что
, если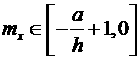 
или если 
.
Определение 1. Функцию
, где 
вещественный параметр,
будем называть - экранирующим
подобласть активным управлением, если решение задачи
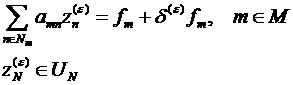(3)
задается формулой
(4)
Теорема 1.
Активное - экранирующее
управление существует, единственно и задается следующими формулами (5)-(7):
если 
и 
(5)
если 
и 
(6)
если 
(7)
Определение
2. Задачу построения управления будем называть
задачей в реальном времени, если к моменту 
еще не
выработались (неизвестны) значения и при 
.
Пример 1. Пусть в момент становятся известны , , 
. По этой информации в силу (1), (2) к моменту могут быть сосчитаны для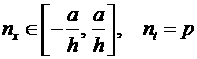 
, а затем по формулам
(5)-(7) сосчитано управление 
при 
.
Определение 3. Зададим число 
, 
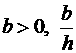целое. Назовем 
= приграничной
информацией об управляемом процессе (3), (4) в момент числа , при 
, 
, а также значения
(8)
решения задачи (3), (4).
Пример
2. Построим управление 
, в реальном времени на основе использования = приграничной
информации последовательно для 
, 
.
Функции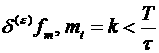 
, будем строить с помощью индукции по номеру 
. Введем таблицу
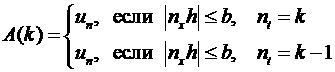(9)
Очевидно, что 
в силу (1), (2)
состоит из нулей. Функция 
, от аргумента в силу формул (5)-(7)
есть тождественный нуль, 
.
Допустим, что таблица 
уже построена при . Тогда в момент известны значения , 
и 
, 
, используя которые получаем 
, по формулам (5)-(7).
Опишем алгоритм получения таблицы 
, которая позволяет вычислить , при 
.
Первую строчку таблицы при 
вычисляем в силу явного
разностного уравнения (1) по формуле
,
где 
есть множество точек,
полученное из выбрасыванием точки 
, а при 
по формулам
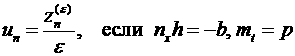(10)
(11)
Формулы (10) и (11) имеют место в силу равенства (4).
Вторая строчка
таблицы получается из первой
строчки таблицы .
Заметим, что описанный в
примере алгоритм получения в экранируемой подобласти слабого (при малом ) шума 
за счет активного
управления не проходит при 
. Это не случайно, так как имеет силу теорема 3:
Теорема
3. Пусть 
, фиксировано, а 
достаточно велико.
Тогда =приграничные входные данные при не содержат
информации, определяющей при достаточно больших
, 
.
Таким образом алгоритм из примера 2
показывает, что слабый (при малом по модулю ) шум 
, формируясь под влиянием всей информации о задаче (1), (2),
существующей к моменту , несет в себе всю ту информацию о коэффициентах 
, о правых частях , 
, и о числах 
, которая оказывает влияние на формирование управления при . Это позволяет вместо коэффициентов 
; правых частей 
, а также чисел , использовать для построения 
, приграничное условие (8).
Заметим, что условие (8) может
оказаться принципиально доступнее информации об 
при 
, а также о числах 
, если разностные задачи (1), (2) и (3), (4) являются
математическими моделями реальных процессов, так что величины 
, 
, имеют физический смысл. В этом случае условие (8) может быть получено прямым измерением
физических величин , 
, в текущий момент времени .
Задачами управления звуком занимались многие авторы [1].
Предлагаемая работа об ослаблении
или подавлении шума в экранируемой одномерной подобласти в реальном времени
примыкает к серии работ [2-8]. В этих работах рассматривается подавление
стационарных помех, одночастотного шума и нестационарного шума в условном
времени, когда для построения используется не только
информация о задаче, появляющаяся в текущий момент времени в однократно
протекающем управляемом процессе, но также предварительно полученная информация
о ходе процесса (1), (2), протекающего
без воздействия управления
Литература.
1.
P.A. Nelson and S.J.
Elliott, Active Control of Sound, Academic Press, San Diego, 1999.
2. Рябенький В.С. Разностная задача экранирования, Функциональный анализ и его приложения. 1995, т.29, № 1, с.70-71
3. Рябенький В.С. Нелинейная задача экранирования. Успехи мат. наук. 1995. т.50, № 4, с.146
4. Вейцман Р.И., Рябенький, В.С. Разностные задачи экранирования и имитации. //Докл. РАН.- 1997.- T.354. № 2. С. 151-154
5. Рябенький В.С. Метод разностных потенциалов и его приложения. //Физматлит, 2002, 494 c.
6. V.S. Ryaben'kii,
S.V. Utyuznikov, A.
Turan. On the application of difference
potential theory to active noise control, Advances in applied mathematics, (40)
No.2, 2008
7. H.Lim, S.V. Utyuznikov, Y.Lam,
A.Turan, M.R. Avis, V.S. Ryaben'kii , S.V.Tsynkov. An experimental validation
of the active noise control method based on difference potential, AIAA. т.47, № 4, с. 874-887, 2009.
8. В.С. Рябенький, С.В. Утюжников, С.В. Цынков. Разностная задача подавления шума и другие задачи активного управления одночастотным звуком в составной области. //Доклады Академии наук. 2009. т. 425. №4. с. 456-458