УДК 629.198

Траектории экспедиций космических аппаратов с двигателем малой тяги по доставке образцов грунта с астероидов Главного пояса и Фобоса.
Р.З. Ахметшин, Г.Б. Ефимов, Т.М. Энеев. – Космические исследования. 2009. т. 47, № 1. С. 38-47.

Аннотация

Исследованы траектории экспедиций космических аппаратов с электроракетными двигателями малой тяги по доставке образцов вещества с малых тел Солнечной системы – астероидов Веста, Фортуна и спутника Марса Фобоса. Для экспедиции к Фобосу проведен анализ траекторий полета, определены пределы оптимизации доставляемой к нему полезной массы КА, дана оценка потерь в полезной массе при использовании двигателя малой тяги с постоянной скоростью истечения. Показано удобство использования модели двигателя идеально регулируемой малой тяги для расчета и анализа траекторий перелета КА с малой тягой.

Ключевые слова: межпланетный полет, малая тяга, Фобос, астероид, проба грунта.

Trajectories of spacecraft missions with low thrust for delivering ground samples from Main Belt asteroids and Phobos. R.Z.Akhmetshin, G.B.Efimov, T.M.Eneev. Preprint of Keldysh Institute of Applied Mathematics, RAS, Moscow.

Abstract

Trajectories of spacecraft with electro-rocket engine for missions to the Main Belt asteroids Vesta, Fortuna and Mars’ satellite Phobos are investigated. The goal of missions – delivering of ground samples to the Earth. For Phobos mission analysis of trajectories is done for a big range of start/finish dates. The payload mass delivered to Phobos is estimated. The difference in payload mass for two models of low thrust: with variable (i.e. “ideal”) and constant jet velocity is considered. The usage of ideal model for calculation and analysis of trajectories is proved.

Key words: interplanetary flight, low thrust, Phobos, asteroid, ground sample.

УДК 629.198

Траектории экспедиций космических аппаратов с двигателем малой тяги по доставке образцов грунта с астероидов Главного пояса и Фобоса.
Р.З. Ахметшин, Г.Б. Ефимов, Т.М. Энеев.

Введение.

Научная важность исследования малых тел, в первую очередь астероидов Главного пояса, комет группы Юпитера и спутников больших планет основана на связи с фундаментальной научной проблемой – о происхождении и эволюции Солнечной системы и связанной с нею проблемы формирования и состава Земли, которая имеет важное прикладное значение [1]. Модель происхождения Солнечной системы, полученная путем численного моделирования в ИПМ им. М.В. Келдыша РАН в 1970-х годах Т.М. Энеевым и Н.Н. Козловым [2] предлагает некоторые подходы, имеющие соответствия в данных современной космохимии. Различные области Солнечной системы – кольцевые зоны формирования планет из общего протопланетного диска – согласно этой модели на первоначальной стадии имели слабое перемешивание и могли бы заметно отличаться по своему химическому составу, входящим в этот состав изотопам, а также по образовавшимся в них минералам. Для оценки химического состава Протоземли важно было бы получить образцы вещества из нескольких различных поясов Солнечной системы, чтобы по ним составить представление о веществе Земли.

При этом следует иметь в виду два обстоятельства. Во-первых, желательно, чтобы эти образцы относились к «реликтовому» веществу, сохранившему минеральный, химический и изотопный состав со времен формирования Солнечной системы в возможно неизмененном виде. Вещество больших планет этому условию не удовлетворяет, так как оно прошло через многочисленные геологические процессы. Считается, что в неизмененном виде может сохраниться вещество небесных тел размерами около 100-200 км в диаметре. Во-вторых, необходимо знать, из какой области Солнечной системы происходят полученные образцы вещества. Доставленные с Луны образцы грунта показали, в основном, близость с веществом Земли, притом, лунное вещество прошло через изменения и не может считаться реликтовым. Кроме земного вещества, в нашем распоряжении имеются многочисленные образцы вещества метеоритов. Однако, представляется весьма вероятным, что метеориты, как и порождающие их астероиды, сближающиеся с Землей (АСЗ), образующие группы Амура, Аполлона и Атона, являются мигрантами из отдаленных областей Солнечной системы [3]. Образцы реликтового вещества можно получить, причем с привязкой к известной области, с некоторых спутников планет и из Главного пояса астероидов. Чтобы содержать реликтовое вещество из данной зоны протопланетного диска, спутники должны быть относительно небольшими и близко расположенными к планете. Удовлетворяют этим требованиям спутники Марса Фобос и Деймос.

Необходимость детального изучения минерального и изотопного состава малых тел ставит задачу десанта на их поверхность и доставки образцов их вещества на Землю. С 1980-х годов в Институте прикладной математики им. М.В. Келдыша РАН проводились расчеты оптимальных траекторий полетов КА с электроракетными двигателями малой тяги (МТ) к малым телам Солнечной системы (см., например, [4-12]). Проекты Российско-германской исследовательской группы "Фортуна" [8] и российский "Фобос-Грунт" [14] ставят целью доставку с малых тел образцов "реликтового" вещества (сохранившегося в слабо измененном виде со времени формирования Солнечной системы) с использованием двигателей малой тяги. В работе излагаются результаты исследования траекторий экспедиций к астероидам Главного пояса и к спутнику Марса Фобосу с помощью двигателей МТ. Для полетов к астероидам (на примере астероидов Веста и Фортуна) предполагалось использование ракеты носителя Протон и ядерной энергоустановки типа "ТОПАЗ" [8], при полете к Фобосу, – ракеты носителя Союз и солнечных батарей [14]. Даты экспедиций приводятся в том виде, как они были получены, имея в виду, что окна старта к Весте и Фортуне повторяются через ~ 1.4 года, а к Фобосу – через 2 года. При этом основные качественные (и в значительной степени количественные) результаты исследования остаются справедливыми и для последующих дат экспедиций.

При межпланетных полетах КА с МТ принимается следующая схема полета: разгон с помощью двигательной установки (ДУ) большой тяги (БТ – химического двигателя) с орбиты низкого ИСЗ до гиперболического избытка скорости "на бесконечности" V_¥ в сфере действия Земли, межпланетный полет с ДУ МТ до цели, – например, малого тела. В наших расчетах траекторий полетов КА с МТ к малым телам, как правило, использовалась модель ДУ "идеально регулируемой" МТ – без ограничений на величину и направление вектора реактивной тяги и на величину скорости истечения реактивной струи. Технически более реалистична модель ДУ МТ с постоянной скоростью истечения реактивной струи V_с = const, однако, оптимизация траекторий перелета по этой модели МТ и их анализ усложнены по сравнению с моделью идеально регулируемой МТ. Притом, основные характеристики перелетов по обеим моделям МТ во многих случаях достаточно близки, – что позволяет использовать модель идеально регулируемой МТ на первом этапе расчета перелетов, для их анализа и в качестве начального приближения для расчетов по модели МТ с V_С = const. Расчет траектории по модели идеально регулируемой МТ указывает также предельные возможности для МТ с V_С = const по величине М_К массы КА у данной цели.

На заре исследования полетов КА с малой тягой было показано (см. [5, 13]), что для идеально регулируемого двигателя МТ при постоянной мощности N_ЭЛ его энергоустановки имеет место разделение задачи оптимизации на массовую и траекторную. Трудоемкое и сложное построение оптимальной по величине М_К траектории перелета может проводиться независимо от выбора параметров КА и ДУ; оно приводится к задаче минимизации критерия J затрат на перелет:

t_К

J ≡ ò f² (t) dt ® min , (1)

t_Н

где f – ускорение реактивной струи, t_Н, t_К – начальный и конечный моменты перелета. Затем, по величине J и характеристикам КА и ДУ, – M₀, начальной массы КА и N_С, мощности "в струе" (N_С = kN_ЭЛ, k – к.п.д. преобразования, N_ЭЛ электрическая мощность), массовые характеристики КА получаются простым досчетом

М_К = M₀ / (1+ ν ), ν º М_РТ / М_К = J M₀ / 2N_С. (2)

Здесь М_К, М_РТ – конечная масса КА и масса затрат рабочего тела,. Пусть М_ЭДУ , М_КА – масса энергетической установки вместе с ДУ и "сухая" масса КА (включая служебные системы), а масса баков М_Б пропорциональна массе рабочего тела М_Б = α М_РТ (например, α = 0.2), тогда из формул

M₀ = М_К + M_РТ , M₀ = (1+α) М_РТ + М_ЭДУ + М_КА + М_П ,

получается полезная масса М_П КА у цели

М_П = (1- α ν)M₀ /(1+ ν) – М_ЭДУ – М_КА . (3)

Величина ν характеризует экономичность полета, – долю М_РТ в общей массе КА. Заметим, что зависимость полезной массы М_П , как функции параметров траектории и КА, в случае близости к оптимуму является в большинстве случаев пологой. Поэтому небольшие отклонения значений параметров от оптимальных слабо влияют на величину М_П , что позволяет при анализе и прикидочных расчетах в ряде случаев ограничиться приближенными их значениями.

Экспедиции по доставке образцов вещества с астероидов Главного пояса

Задача доставки на Землю образца грунта с астероида Главного пояса представляет большой научный интерес. Тонкие анализы изотопного состава грунта, определение изотопного дефицита по отношению к веществу Солнца и т.п. имеют принципиальное значение для изучения Солнечной системы. Подобные анализы, возможные лишь в земных условиях, могли бы стать эталоном для калибровки более грубых анализов при автоматическом исследовании малых тел. В настоящее время для полетов к астероидам, кометам и доставки вещества с них используются и проектируются КА с ДУ МТ и с традиционными химическими двигателями БТ. Нами были рассмотрены траектории полетов КА с двигателями МТ к астероидам Главного пояса [6-11].

При исследовании полетов КА с МТ к астероидам предполагалось использование ядерной энергетической установки и разгон у Земли ракетой носителем Протон [8]. Принималось, что начальная масса КА на этапе межпланетного перелета М₀ = 5.8 т при V_¥ = 3 км/с (М₀ = 6.1 т при V_¥ = 2 км/с); масса баков М_Б = 0.2·М_РТ, ядерная энергоустановка типа "ТОПАЗ" имеет мощность N_ЭЛ = 20, 30 кВт и массу (вместе с ЭРД и служебными системами) М_ЭДУ = 3 т, мощность "в струе" N_С = 10, 14 кВт (к.п.д. преобразования k = 0.5), сухая масса КА М_КА = 1 т. После достижения астероида с помощью МТ с выравниванием скоростей его и КА, предполагалась посадка на него КА или посадочного модуля, забор грунта и доставка его к Земле с помощью БТ или МТ.

В случае возвращения образца вещества с помощью специальной ракеты БТ на астероид может садиться только посадочный модуль, который затем стартует к Земле. В случае доставки вещества на Землю с помощью МТ необходима либо стыковка посадочного модуля с КА на орбите спутника астероида, либо дистанционный забор грунта, либо посадка и подъем с астероида всего КА с МТ, что достаточно сложно. Однако такой возврат всего КА с МТ к Земле также рассматривался – для оценки энергозатрат на доставку вещества с астероида с помощью МТ. При возвращении необязательно выравнивать скорости КА или возвращаемого модуля и Земли, так как торможение в атмосфере позволяет гасить вторую космическую скорость и некоторый гиперболический ее избыток. Заметим, что окна старта для полетов к астероидам Главного пояса повторяются через определенный период (для ближней части пояса он равен DT ~ 1.4 года) и часто энергетически близки, так что представленные варианты экспедиций дают представление об экспедициях к целому ряду астероидов с близкими характеристиками орбитам (большой полуоси, эксцентриситета и наклонения) и об экспедициях к тем же астероидам с другими окнами старта.

Примером экспедиции КА с МТ по доставке образца вещества с астероида Главного пояса служат полеты к астероиду 4 Веста (спектральный класс U, диаметр ~576 км) [6-11]. Характеристики траекторий полетов КА с МТ от Земли к астероиду Веста (варианты I-IV) и обратно к Земле (варианты V-VI) приведены в табл.1. В ней даны даты t_Н старта и t_К финиша полета, его длительность Т, затраты J, величина V_¥ и полезная масса М_П в конце полета. Варианты полетов от Земли к Весте отличаются длительностью и величиной V_¥ (соответственно, величиной М₀). Окна для даты t_К подлета КА к Весте и t_Н старта для возврата от нее к Земле достаточно узкие, и должны быть согласованы. Совмещение пар траекторий Земля-Веста и Веста-Земля позволяет получить оценки возможности доставки вещества с Весты – общее время перелета Т_S, суммарные затраты J_S и величина полезной массы М_П, доставляемую к Земле, – которые приведены в конце табл.1 с обозначением сочетания вариантов полета к Весте и возврата от нее, например, – II+V.

Таблица 1.

________________________________________________________________________________________________________________ _

Вариант t_Н t_К. T,г V_¥,км/с J,м²/с³ M_П,т (N_С=10/14 кВт)

___________________________________________________________________________________________________________________

I 19.VII.1998 9.VIII.2000 2.05 2 1.32 0.00 / 0.55

II 03.IХ.1998 9.VIII.2000 1.92 3 1.09 0.13 / 0.59

III 23.ХII.1997 3.ХII.2000 2.95 2 0.93 0.48 / 0.87

IV 07.II.1998 23.V.2001 3.25 3 0.67 0.67 / 0.95

_____________________________________________________________________________________________________________________

V 10.VII.2000 V.2002 1.85 0.75

VI 18.IХ.2001 VII.2003 1.85 0.45

_____________________________________________________________________________________________________________________

II+V IХ.1998 V.2002 3.8 1.84 0.00 / 0.11

III+VI ХII.1997 VII.2003 5.6 1.38 0.00 / 0.41

IV+VI IХ.1998 VII.2003 5.5 1.12 0.09 / 0.49

_____________________________________________________________________________________________________________________

Из таблицы видно, что вариант V возврата к Земле стыкуется (если незначительно изменить времена отлета прилета к Весте и отлета от нее) с вариантами I и II перелета к Весте за Т ~ 2 года. С вариантами III и IV перелета к Весте за Т ~3 года стыкуется вариант возврата к Земле VI. Для каждого варианта полета приведены два значения величины М_П при N_С = 10 и 14 кВт. Начальная масса М₀ при возврате от астероида к Земле полагалась равной конечной массе М_К у астероида при перелете от Земли к Весте согласно (3). Из вариантов (II+V, III+VI, IV+VI) по затратам J_S оказываются лучшими два последних, с длительным полетом к Весте, и полезная масса, доставляемая к Земле, имеет приемлемую величину лишь в этих вариантах экспедиции, при N_С = 14 кВт.

Другая возможная схема экспедиции – спуск на астероид посадочного блока для забора пробы грунта и доставка его на Землю с помощью химического двигателя БТ. Такой вариант возвращения был рассмотрен для случая экспедиций к астероиду 19 Фортуна (класс С, 220 км) в проекте "Фортуна" Российско-германской исследовательской группы [8-11]. Характеристики траекторий полетов от Земли к Фортуне и обратно приведены в табл.2. В начале ее приведены даты t_Н и t_К полета от Земли к Фортуне (варианты I-IV, М₀ = 6.1 т при V_¥ = 2 км/с,), его длительность Т и угловая дальность Ф, затраты J и полезная масса М_П в конце полета (при N_С = 10 и 14 кВт). Затем, для полетов с БТ от Фортуны к Земле (варианты V-VII), приведены: даты t_Н и t_К, Т и Ф полета, требуемая скорость V_ХАР разгона КА у Фортуны. Для вариантов всей экспедиции (сочетание полета к Фортуне и от нее, например, I+V), приводится суммарное время Т_S и конечная масса М_ЗК возвращаемого аппарата в предположении, что его начальная масса у Фортуны равна всей полезной массе М_П, доставляемой к ней с помощью МТ. Приближенно учтены затраты на взлет с Фортуны (считая затраты на взлет DV_ХАР » 300 м/с).

Траектории были рассчитаны для окон старта полета к Фортуне в 1999, 2001, 2002 годах и окон старта возврата к Земле в 2002, 2003 и 2004 годах. Для полетов к Фортуне в первом окне старта приводятся две траектории с Т ~ 2 и 2.5 года. Из табл.2 видно, что суммарное время экспедиции Т_S ~ 4-5 лет. По величине М_П, доставляемой к Фортуне, окна старта с длительными перелетами от Земли дают заметный выигрыш; то же относится и к М_ЗК у Земли (и особенно при продолжительном сопровождении астероида, сочетание II+VI). Окно старта от Земли в 2003 г. близко по своим возможностям с предыдущим окном 2001 г. (также и ряд следующих окон старта). Траектории перелетов КА с МТ к Фортуне и возврата к Земле с БТ (по две траектории, пунктир) представлены на рис.1.

Таблица 2.

___________________________________________________________________________________________________________________________________________

Перелеты от Земли к Фортуне

__________________________________________________________________________________________________________________________________________ _

Вариант t_Н t_К T,г Ф,град J,м²/с³ M_П (N_с=10/14 кВт), т

____________________________________________________________________________________________________________________________________________

I ХII.1999 ХI.2001 2.0 302 0.94 0.47 / 0.85

II ХI.1999 IV.2002 2.5 378 0.77 0.71 / 1.05

III V.2001 IV.2003 2.0 292 1.10 0.26 / 0.68

IV IХ.2002 ХII.2004 2.3 302 0.98 0.41 / 0.81

______________________________________________________________________________________________________________________________________________________

Перелеты от Фортуны к Земле с двигателем БТ и данные по всей экспедиции

_______________________________________________________________________________________________________________________________________________________

Вариант t_Н t_К T,г Ф,град V_ХАР,км/с Вар. Т_S,г M_ЗК (N_с=10/14), т

____________________________________________________________________________________________________________________________________________

V IV.2002 VII.2003 1.2 208 5.22 I+V 3.7 0.07/0.13

II+V 3.75 0.11/0.17

VI V.2003 Х.2004 1.5 198 3.71 III+VI 3.5 0.07/0.18

II+VI 4.9 0.18/0.27

VII III.2004 I.2006 1.8 185 5.01 III+VII 4.6 0.04/0.14

____________________________________________________________________________________________________________________________________________

Рис. 1. Траектории полета к Фортуне с МТ и возврата к Земле с БТ.

Расчет указанных экспедиций по доставке образцов вещества с астероидов Веста и Фортуна с помощью КА с МТ показал возможность их осуществления при использовании ракеты носителя Протон и ядерной энергоустановки типа "ТОПАЗ" [8, 10-11]. Доставка вещества к Земле проще реализуема при помощи возвратной ракеты БТ, однако и в случае использования КА с МТ, получаются приемлемые величины доставляемой к Земле массы М_П. Приведенные примеры характеризуют также экспедиции к астероидам Веста и Фортуна со следующими окнами старта и к целому классу астероидов с близкими параметрами орбит.

Анализ траекторий экспедиции по доставке образца вещества с Фобоса

Фобос, спутник Марса, принадлежит к числу малых тел, сохранивших, вероятно, реликтовое вещество, слабо измененное со времен образования Солнечной системы и несущее информацию о процессах этого образования. Доставка образца вещества с Фобоса на Землю, благодаря близости Марса, легче осуществима, чем с других малых тел – астероидов Главного пояса и комет. Экспедиция по доставке вещества с Фобоса имеет большой научный интерес и в настоящее время включена в российскую федеральную космическую программу; в связи с этим она привлекает внимание исследователей [12, 14-16]. Для достижения Фобоса, точнее сферы действия Марса, предполагалось использовать КА с электроракетными двигателями МТ и энергетикой от солнечных батарей (СБ). При первоначальных расчетах оптимальных траекторий полета к Фобосу возник ряд вопросов. При их анализе использование модели идеально регулируемой МТ (с учетом особенностей энергетики от СБ) оказалось весьма полезным, как демонстрируется ниже.

Рассматривалась следующая схема экспедиции к Фобосу для доставки пробы вещества: разгон КА с орбиты ИСЗ до гиперболической скорости V_¥ ракетой носителем БТ, полет с МТ до сферы действия Марса с выравниванием скоростей КА и Марса. Затем – маневры в сфере действия Марса и посадка на Фобос с использованием ДУ БТ, доставка образца вещества к Земле с помощью возвратного модуля – стартующей с Фобоса ракеты БТ, которая тормозится в атмосфере Земли. Транспортный модуль, осуществляющий полет от Земли к Марсу с МТ и включающий ДУ МТ и СБ, предполагается сбрасывать после достижения сферы действия Марса. При расчетах полетов к Фобосу было принято, что масса КА после его разгона ракетой носителем Союз М₀ = 2.27 т при V_¥ = 2 км/с (М₀ = 2.37 т при V_¥ = 1 км/с); массу М_СДУ систем ДУ МТ вместе с массой СБ принимаем равной М_СДУ = 0.04*N_ЭЛ, масса баков М_Б = 0.2·М_РТ, мощность СБ на орбите Земли N_ЭЛ = 7.5 кВт, мощность в струе N_С = 3.75 кВт (k = 0.5). Масса возвратного модуля М_ВМ ~ 350-370 кг (в зависимости от необходимой для старта к Земле величины V_ХАР). Величину полезной массы М_П (включающей сам КА, возвратный модуль, средства стыковки с малым телом, научную аппаратуру) получаем из конечной массы М_К КА у цели по формуле

М_П = М_К – М_СДУ – М_Б . (5)

Применение современных солнечных батарей существенно облегчает КА с МТ: если для бортового ядерного реактора имеем удельную массу энергоустановки ~ 100 кг/кВт, то для СБ она ~ 15 кг/кВт [12]. Это позволяет использовать для экспедиции к Фобосу ракету носитель типа Союз, а не Протон, как в проекте "Фортуна" [8, 11]. Однако, при межпланетных полетах КА с МТ к малым телам мощность N_С СБ не постоянна, поскольку она зависит от расстояния r(t) КА до Солнца и падает примерно как 1/r²(t) с удалением от него. У Марса мощность СБ будет меньше в 2.5 раза их мощности на орбите Земли, в поясе астероидов – меньше в 4-10 раз. Возможность разделения траекторной и массовой задач при полетах КА с идеально регулируемой МТ и СБ может быть сохранена, если ввести модифицированный критерий эффективности J* [9, 12] (при этом модифицированная мощность N* = N_ЭЛ r²(t) = const)

t_К

J* ≡ ò f² (t) (r(t)/r₀)² dt, (4)

t_Н

где r₀ – радиус орбиты Земли. В критерии J* под интегралом появляется как бы "штрафной множитель". Характерные величины критерия J* для полетов к малым телам оказываются существенно больше, чем характерные величины J: при полете к Марсу J* ~ 0.7-1 м²/с³ (J ~ 0.5 м²/с³), при полетах к астероидам Весте и Фортуне J* ~ 3.5-4 м²/с³ (J ~ 0.9-1.3 м²/с³).

Целью исследования было построение и анализ оптимальных траекторий полета КА с МТ от Земли к Фобосу, анализ зависимости величины М_П у Марса от параметров КА, ДУ БТ и МТ, сравнение траекторий полета при использовании моделей идеально регулируемой МТ и МТ с V_С = const. Пример траектории перелета КА с МТ между сферами действия Земли и Марса для идеальной модели МТ при старте в 2005 году приведен на рис. 2. При полетах с МТ величины М_К, М_П зависят от года (окна) старта меньше, чем при полетах с БТ. Поэтому приводимые данные во многих случаях можно перенести на следующие окна старта полета к Марсу.

Интервал между окнами старта от Земли к Марсу и обратно, как известно, составляет около двух лет. Поэтому длительность Т полета с МТ от Земли к Марсу может меняться в больших пределах – от года с небольшим до более чем двух лет. Встает задача расчета и анализа траекторий в этом диапазоне по Т, а также в диапазоне изменения других параметров КА, ДУ БТ и МТ. Расчеты траекторий полета КА с МТ в этом диапазоне Т по модели МТ с V_С = const (например, [7]) дают большое число вариантов при разнообразии параметров: дат старта и финиша, величин V_С и V_¥ , числа пауз в работе ДУ МТ и их границ. Совместная оптимизация по всем этим параметрам создает трудности при осмыслении всей массы расчетов и анализе влияния отдельных факторов. Использование модели идеально регулируемой МТ с разделением массовой и траекторной задач оказывается для такого анализа удобной и полезной.

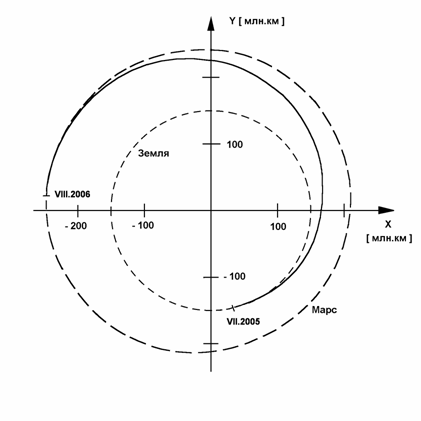
Рис.2. Траектория перелета КА с МТ от Земли к Марсу – сплошная линия. Пунктиром обозначены орбиты Земли и Марса.

При выбранном окне старта для перелетов КА с МТ к Марсу в 2005 году была построена картина изолиний М_К(t_Н, Т) = const при фиксированном значении V_¥ = 1 км/с в указанном диапазоне Т ≈ 300-850 суток, представленная на рис.3. Изолинии J*(t_Н, Т) = const для того же полета совпадают с этой картиной изолиний, но только максимуму М_К будет отвечать минимум J*, и наоборот.

Вторая картина изолиний, на рис.4, отличается выбором оптимального значения V_¥ в каждой точке. Картина изолиний J*(t_Н, Т) = const при этом уже не совпадают с картиной изолиний М_К(t_Н, Т) = const (как на рис.3), так как J* зависит от величины V_¥. Пунктиром на рис.4 приведены изолинии оптимальных значений V_¥ разгона у Земли с БТ. Для перелетов в основной, нижней части картины изолиний, как видно на рис.4, оптимальными оказываются значения V_¥ > 2 км/с; этим объясняется некоторое увеличение М_К на этом рисунке в сравнении с их значениями для тех же Т при V_¥ = 1 км/с на рис.3. Большие значения V_¥ указывают на напряженность полета с точки зрения использования МТ – оптимальное комбинирование БТ и МТ дает перераспределение в пользу повышения роли БТ. Когда время полета Т относительно невелико, в окне старта имеется один максимум М_К при дате старта t_Н, соответствующий "гребню холма" на картине изолиний ("дну оврага" на картине изолиний J*). Начиная с некоторого Т (@ 700 суток), появляется второй локальный максимум по t_Н, отличающийся значениями угловой дальности полета, оптимальной величины V_¥ и конечной массы М_К. Затем, с ростом Т, максимум сдвигается в область этого второго локального максимума.

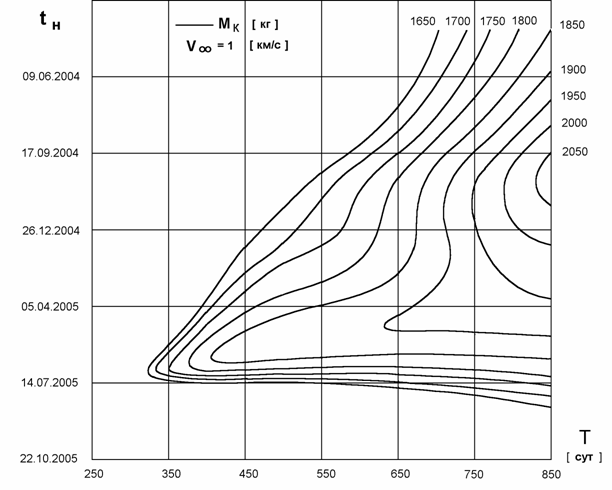
Рис. 3. Картина изолиний М_К (t_Н, Т) = const при V_¥ = 1 км/с.

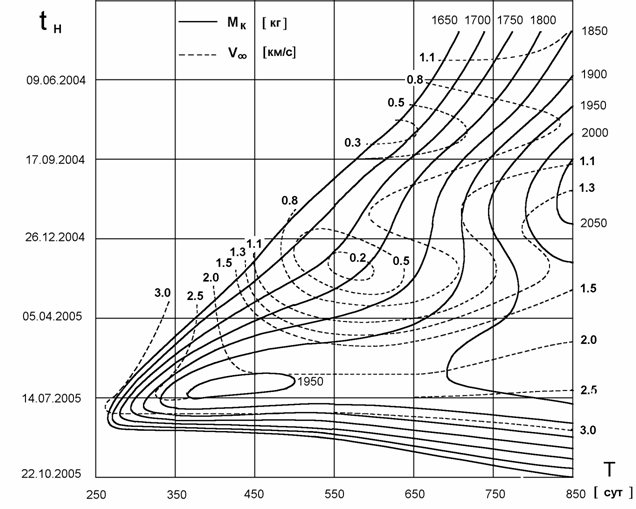
Рис. 4. Картина изолиний М_К(t_Н, Т) = const при оптимальной величине V_¥
в каждой точке. Пунктиром показаны изолинии V_¥ = const.

Особенностью картины изолиний в значительной части диапазона по Т (450-750 сут) является малое изменение М_К на "гребне холма", вдоль оси Т в нижней части рис.3. Прирост М_К за 300 суток составляет всего 100 кг, то есть ~ 6 %, а на рис.4 на том же интервале Т изменение М_К равно нулю, с небольшим уменьшением М_К в середине интервала. Модель идеальной МТ показывает предельные по М_К возможности для каждого полета, поэтому при переходе от нее к модели V_С = const происходят лишь небольшие потери в М_К, которые могут несколько различаться в разных областях диапазона по Т (и зависят также от выбора величины V_С). Малое изменение М_К наблюдается и при разрезе "поперек холма", вдоль оси t_Н. Так, при Т ~ 550 суток на рис.3 М_К почти постоянна в диапазоне t_Н = 5.IV-25.VI.2005 (около 3-х месяцев), а на рис.4 – в диапазоне 5.IV-25.VII.2005 (~ 4-х месяцев). Как видно из рис.4, в этом диапазоне существенно изменяется соотношение вклада БТ и МТ: при более ранних датах старта V_¥ = 1.1-1.5 км/с, при поздних – V_¥ = 2.5 км/с. Соответственно изменяются и затраты J*.

Графики изолиний М_К(Т), J*(Т) для перелетов с идеальной МТ показывают невозможность существенного увеличения М_К или уменьшения затрат J* у Марса с ростом Т. Проведенные расчеты по модели V_С = const еще сильнее "выровняли" значения М_К на рассмотренном диапазоне Т (450-800 сут.) – при отличии времени перелета почти вдвое разница М_К составляет всего единицы процентов (см. [15]). Здесь мы сталкиваемся с эффектом выхода на асимптоту Т ® ¥ гиперболы J*(T) [6-7, 12]. В случае V_С = const, качественно, с точки зрения энергетики, можно считать, что траектории с различными Т отличаются изменением длительности пауз в работе МТ и их перераспределением по траектории. Оптимальным комбинированием работы БТ (величины V_¥) и МТ можно объяснить и появление начальной паузы в работе ДУ МТ на межпланетном участке в некоторых вариантах полета (см. [11, 15]). При перелете КА с МТ к Марсу происходит падение мощности его СБ и, следовательно, тяги двигателя МТ. Попытки изменения траектории перелета так, чтобы парировать этот эффект за счет увеличения времени пребывания КА в областях, близких к Солнцу для увеличения энерговооруженности КА, как показывают примеры расчетов, не меняют ситуацию. На таких траекториях увеличиваются области с малым значением тяги, или, для МТ с V_С = const, увеличиваются паузы в работе ДУ МТ. Поскольку модель с идеально регулируемой МТ показывает предельные возможности перелета к цели при заданных условиях, видим, что в случае V_С = const также нет возможности для увеличения М_К на рассмотренном диапазоне по Т.

Построенная картина изолиний М_к(Т) отвечает на важный вопрос о резервах в величине М_К при достижении Марса за счет изменения длительности полета – она почти постоянна на большом диапазоне по Т. Это позволяет выбирать Т с учетом других требований к траектории – достаточности времени на маневры в сфере действия Марса, удобства проведения наблюдений траектории КА и ее коррекции и т.п.

Проведем оценки изменения полезной массы М_П у Марса с помощью производных М_П по ее аргументам (М₀, J*, N_С), которые можно получить из формул (3) [9]. При вычислении значений производных примем значения: М₀ = 2.27 т, J* @ 0.65 м²/c³, N_С = 3.75 кВт и ν = 0.195 (ν = М_РТ /М_К) – в области "гребня холма" функции М_к на рис.4. Производные М_п по аргументам будут равны: по М₀ = 0.64, по J* = - 0.55, по N_С = 0.02 (с учетом М_ЭДУ (N_С)). Как видим, производная М_П по N_С близка к нулю. Рост М_П может дать лишь увеличение начальной массы М₀ или уменьшение J*. Для получения, например, приращения DМ_П в 100 кг необходимо увеличить начальную массу М₀ на DМ₀ = 150 кг или уменьшить J* на DJ* = 0.18 м²/с³. Однако уменьшение J*, как показано выше, практически невозможно – имеет место выход функции J*(Т) на горизонтальную асимптоту. Таким образом, увеличение М_П возможно лишь при возрастании начальной массы М₀. Заметим, что при полетах к Фортуне и Весте аналогичные производные (по М₀ = 0.55 ± 0.1, в зависимости от варианта; по J* = - 1.2 ± 0.2; по N_С = 0.13-0.08, при N_с = 10 и 15 кВт) указывают на несколько иную зависимость М_П от аргументов: еще нет выхода на асимптоту по J, асимптота по N_С заметна только при N_С = 14 кВт. Величины DМ_П, вычисляемые для полетов к астероидам по производным и из табл. 1, 2 – близки. Оценки с помощью производных указывают на тенденции в изменении М_П с изменением аргументов, которые, как правило, сохраняются и при переходе к модели МТ с V_С = const.

Сравнение перелетов с моделью малой тяги идеально регулируемой
и с постоянной скоростью истечения струи

Представленные результаты для экспедиций к астероидам и Фобосу получены в предположении идеальной изменяемости вектора ускорения МТ. Учет реальных возможностей ДУ МТ, замена модели идеальной МТ на модель с V_С = const уменьшает величину М_П. Размеры проигрыша следует оценить.

Для модели идеальной МТ имеет место разделение задачи оптимизации на траекторную и весовую - при условии, что скорость V_¥ на границе точечной сферы действия Земли задана и фиксирована. Поэтому было предложено исследовать задачу для фиксированных значений V_¥ из дискретного набора значений (0, 1, ... 4 км/с) [4-5, 11]. При этом задача поиска оптимальной траектории, а также двухточечная краевая задача, к которой она может быть сведена с помощью принципа максимума, не зависят от конкретных параметров КА и ДУ МТ. Краевая задача в этом случае зависит от параметров начальной и конечной орбит, момента старта t_Н, продолжительности перелета Т и V_¥. Так как идеальная малая тяга не ограничена по величине, решение краевой задачи, в принципе, существует для любых значений t_Н, Т и V_¥. Проблема решения, в основном, упирается в наличие хорошего начального приближения, в качестве которого обычно используется какая-либо имеющаяся оптимальная траектория перелета к той же цели или к другой с близкими характеристиками орбиты. После того, как решение найдено, оно зависит (для выбранных начальной и конечной орбит и заданного V_¥) от двух параметров: t_Н и Т. От них зависят и функционал задачи J и соответствующая программа ускорения f(t). По параметру t_Н обычно имеется ярко выраженный минимум, который в плоскости параметров (t_Н, Т) соответствует "дну оврага" картины изолиний функционала J(t_Н, Т). С увеличением продолжительности перелета Т функционал J монотонно убывает, так как полет становится менее напряженным и требуются меньшие значения f(t).

Полученное значение J не дает полного представления о степени оптимальности полученной траектории; в большей степени об этом можно судить по виду функции f(t). На рис.5 представлен пример трех программ ускорения f(t) для перелета к одной и той же цели, различающихся параметрами V_¥ и Т. На кривой с Т = 2.7 года (штрих-пунктирной) величина f(t) сильно возрастает в конце траектории. Так как J есть интеграл от квадрата ускорения, последний участок дает немалый вклад в его величину. Как видно из графика, значения f(t) на конечном участке можно значительно уменьшить за счет небольшого (~10%) увеличения продолжительности перелета, и в результате уменьшить функционал J. Получающаяся программа f(t) (сплошная кривая) выглядит более сбалансированной – без явно проигрышных участков. Третья программа (штриховая кривая) имеет ярко выраженный "горб" в начале траектории. Этот "горб" можно уменьшить за счет увеличения V_¥, т.е. возрастания вклада большой тяги. Однако выигрыш в полезной массе М_П, можно оценить, лишь вычислив ее по формуле (3) при заданных параметрах КА и ДУ – N_С, М₀(V_¥) и a_Б, – и определить, достижимо ли необходимое значение М_П, и при каких V_¥, t_Н, Т.

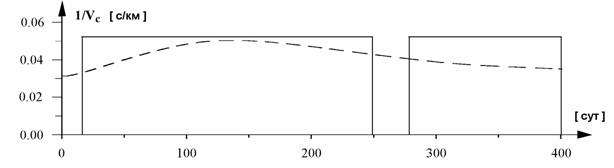
Получение приемлемых значений функционала J обычно отвечает на вопрос и о существовании траектории перелета к данному небесному телу не только с идеальной МТ, но и с V_С = const. Но так бывает не всегда. Возможны случаи, когда тяги КА не хватает для реализации перелета. Поэтому необходим дополнительный анализ. Тяга Р пропорциональна u^id(t)): P = 2N_с/V_с = 2N_с u. Для модели МТ с постоянной скоростью истечения величина u постоянна (или кусочно-постоянна) на активных участках. Мощность N_с, а следовательно и тяга P, есть переменная величина, т.к. 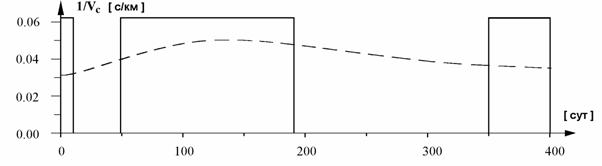зависит от расстояния КА до Солнца, поэтому ниже анализируется программа изменения u(t) = 1/V_с. На рис. 6, 7 для двух перелетов к Фобосу представлены (пунктиром) графики функции u^id(t) и графики u(t) для полета с МТ при значениях V_С = 16, 21 км/с (что соответствует ДУ МТ СПД-100 и СПД-160 [6-7]), полученные в результате решения задачи оптимизации. В отличие от идеальной тяги для них имеются паузы в работе, поэтому график имеет ступенчатый характер.

Рис. 5. Примеры программ ускорения f(t) при полете как функции V_¥ и Т.

График u^id(t) дает более точную информацию о траектории перелета, чем график ускорения f(t). Если на всей траектории график u^id(t) превышает значение u для МТ с V_С = const, значит ДУ имеет большую, чем у идеальной МТ, скорость истечения и развивает меньшую тягу. Решения краевой задачи за данное время не существует, и для осуществления перелета необходимо дополнительное время. Если значение u превышает u^id(t), то решение существует, но тяга ДУ с V_С = const избыточна в сравнении с идеальной МТ, что приводит к появлению пауз в работе ДУ, перерасходу рабочего тела и к проигрышу ∆М_К в конечной массе и в полезной массе.

На рис 6 изображены графики u(t) для V_с = const и u^id(t) для идеальной МТ при перелете к Фобосу с V_¥ = 2.3 км/с, M₀ = 2238 кг, N_С = 3.84 кВт, T = 400 суток и угловой дальностью Ф = 4.33 радиан. Для идеальной МТ конечная масса M_К^id = 1960 кг, масса рабочего тела М_РТ = 278 кг. Для ДУ МТ СПД-100, с V_С = 16 км/с (u(t) » 0.062, рис.6-а) программа u(t) на всем диапазоне превышает график u^id(t), что приводит к большим паузам и перерасходу М_РТ. Конечная масса равна M_К = 1845 кг, что меньше в сравнении с идеальной МТ на DM_К = 115 кг, или на 41% от массы М_РТ. Перелет с V_С = 21 км/с (рис.6-б) дает лучшее значение М_К = 1927 кг, а DM_К = 33 кг (12% от М_РТ, что в 3.5 раза меньше, чем при V_С = 16 км/с), поскольку для него u(t) ближе к графику для идеальной МТ. Заметно уменьшается и продолжительность пауз в работе ДУ.

(а)

(б)

Рис. 6 Сравнение функции u^id(t) = 1/V_С (t) для МТ с V_С = const и идеальной МТ (ступенчатые и штриховая кривые) при V_С = 16 (а) и 21 (в) км/с.

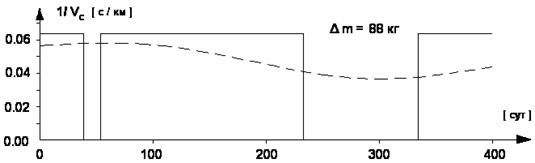
Таким образом, на основании графика u^id(t) и значения u для данного V_С = const можно оценить удачность выбранного значения скорости истечения, или судить об отсутствии решения при данном V_С. Например, в случае V_С = 50 км/с (ЭРД ES-XX [8]) график u^id(t) на рис. 6 на всем отрезке времени превышает значение 0.02, соответствующее этой скорости V_С. Значит, перелет с V_С = 50 км/с при данных краевых условиях невозможен. Иногда, как в случае, изображенном на рис.7 (перелет к Фобосу в те же сроки, но с V_¥ = 1.6 км/с, M₀ = 2326 кг; M_К^id = 1925 кг, M_РТ = 401 кг), только на основе графика u^id(t) трудно судить о существовании решения. В варианте, изображенном на рис.7а (как и в случаях рис. 6) график u^id(t) целиком лежит ниже значения u, что отвечает существованию решения. В случае рис. 7б график u^id(t) лежит частью выше, частью ниже значения u, поэтому не ясно, существует ли решение для V_С = 21 км/с. Аккуратные расчеты оптимальных траекторий показали, что при заданных V_С и краевых условиях перелет неосуществим.

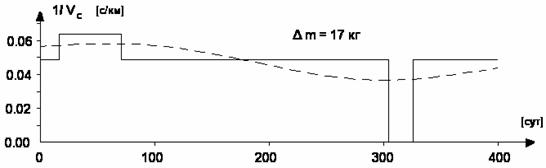
На рис.7(а, б) представлены два варианта полета с МТ при V_С = const. В первом случае используется одно значение V_С (16 км/с), во втором – два значения V_С (16 и 21 км/с), – с возможностью переключения с одного режима на другой, более экономный на текущем отрезке полета. В первом случае M_К = 1837 кг, DM_К = 88 кг (22% от M_РТ), во втором M_К = 1908 кг, DM_К = 17 кг (» 4% от M_РТ). Отметим, что использование двух значений V_С = const позволяет очень хорошо аппроксимировать график u^id(t) идеальной МТ и минимизировать перерасход рабочего тела.

Таким образом, график программы u^id(t) полета КА с моделью идеальной МТ может дать информацию об аналогичном полете с кусочно-постоянной МТ. Он позволяет увидеть, на каких участках траектории велики затраты М_РТ рабочего тела, и какие могут быть возможности их уменьшения (например, за счет некоторого изменения параметров t_Н, Т, V_¥). Также этот график позволяет оценить, насколько удачны параметры ДУ МТ (величина V_С) и на каких участках полета возможен перерасход М_РТ и проигрыш в величине М_К.

Аналогичное сравнение двух моделей МТ было проведено для перелетов от Земли к астероиду Фортуна [8-9, 11]. Были рассмотрены уровни тяги, соответствующие величинам V_С = 16, 21 и 35 км/с (первые два отвечают плазменному ДУ типа СПД-100 и СПД-140, третье – ионному RIT-35 [8]). При использовании ДУ с V_С = 21 км/с, значение u = 1/V_С на всем протяжении полета оказывается выше, чем кривая для идеальной МТ, т.е. тяга избыточна в сравнении с идеальной, что приводит к проигрышу DМ_К = 120 кг (~ 10 % от М_РТ). При V_С = 16 км/с перерасход М_РТ еще больше. При комбинировании работы двух ДУ МТ с V_С = 21 и 35 км/с потери DМ_К составляют ~ 50 кг. Таким образом, и в этом случае возможность использования двух типов ДУ МТ с V_С = const позволяет обеспечить минимальные потери в величине М_К.

(а)

(б)

Рис. 7. Сравнение функции u^id(t) = 1/V_с (t) для идеальной МТ и V_с = const (штриховая и ступенчатые кривые) при V_с = 16 км/с (а) и двух значениях – 16 и 21 км/с (в).

Заключение. Исследована возможность экспедиций по доставки образцов реликтового вещества с астероидов Главного пояса Веста и Фортуна (и близких к ним по параметрам орбит) и со спутника Марса Фобоса при использовании ЭРД с энергетикой от ядерной установки или солнечных батарей и ракет-носителей разного класса. Близость массовых характеристик перелетов КА с идеально регулируемой МТ и МТ с постоянной скоростью истечения обосновывает возможность использования модели идеально регулируемой МТ, более простой и удобной, в предварительных расчетах при исследовании перелетов КА с МТ к малым телам. С помощью этой модели МТ удается провести подробный анализ траекторий перелета и оценить его оптимальные характеристики, а также получить оценки параметров полета для ДУ МТ с постоянной скоростью истечения реактивной струи.

Работа поддержана грантом РФФИ N 04-01-00346 и научной школы НШ.1123.2008.1.

Литература

1. Энеев Т.М. Актуальные задачи исследования дальнего космоса // Космич. Исслед. 2005. Т. 43. № 6. С. 403-407.

2. Энеев Т.М., Козлов Н.Н. Модель аккумуляционного процесса формирования планетных систем. I. Численные эксперименты// Астрон. вестник. 1981. т.15. № 2. С. 80-94. - II. Вращение планет и связь с теорией гравитационной неустойчивости // Астрон. вестник. 1981. т.15. № 3. С. 131-141.

3. Энеев T.M., Ефимов Г.Б. Миграция малых тел в Солнечной системе // Земля и Вселенная. 2005. № 1. С. 80-89.

4. Р.З.Ахметшин, С.С.Белоглазов, Н.С.Белоусова, А.И.Глазков, В.В.Гущин, В.А. Егоров, Г.Б.Ефимов. Оптимизация перелетов к астероидам и кометам КА с комбинированием двигателей большой и малой тяги.- Препринт ИПМ им. М.В. Келдыша АН СССР N 144. М., 1985.

5. В.А.Егоров, Г.Б.Ефимов, Р.З.Ахметшин и др. О перелетах КА с малой тягой к кометам и астероидам. Исследование творчества основоположников космонавтики и ее современные проблемы. М. Наука, 1989, с. 134-143.

6. Eneev T.M., Efimov G.B., Smirnov V.V. On the simple return from the asteroid by low-thrust spacecraft// II German-Russian conference on Electric Propulsion Engines and their technical applications. Russia, Moscow. 1993. Summary of the Papers. Р.127.

7. Т.М.Энеев, В.А.Егоров, Г.Б.Ефимов, Р.З.Ахметшин, В.В.Смирнов. Траектории перелетов к астероидам и кометам КА с ЭРД. Препринт ИПМ им.М.В.Келдыша РАН, 1994, N 34. - Eneev T.M., Konstantinov M.S., Efimov G.B., Akhmetshin R.Z., Fedotov G.G., Petukhov V.G. Advenced interplanetary missions with solar-nuclear electric propulsion. Preprint Keldysh Inst.of Appl. Mathematics RAS, N 35,1996.

8. Loeb H.W., Popov G.A., Eneev T.M., Efimov G.B. et al. Advanced Interplanetary Missions Using Nuclear-Electric Propulsion. Study Report. Ed. by Joint Study Group, Bonn, Moscow and Paris. June, 1995. 217 pp.

9. Eneev T.M., Konstantinov M.S., Akhmetshin R.Z., Efimov G.B. et al. Mercury-to-Pluto rendezvous missions using solar-nuclear electric propulsion. Preprint № 111. М.: Keldysh Institute of Applied Mathematics RAS. 1996. - Eneev T.M., Konstantinov M.S., Efimov G.B. et al. Some methodical problems of low-thrust trajectory optimization. Preprint № 110. М.: Keldysh Institute of Applied Mathematics RAS. 1996.

10. В.А.Егоров, Т. М.Энеев, Р.З.Ахметшин, Г.Б.Ефимов и др. Траекторно-баллистический анализ полетов к астероидам и кометам космических аппаратов с малой тягой. - В кн.: Интеллектуальные системы автономных аппаратов для космоса и океана. Москва, 1997, с.40-72.

11. Eneev T.M., Akhmetshin R.Z., Efimov G.B., Yegorov V.A. Asteroid and Comet Rendezvous Missions Using Low-thrust Nuclear Electric Propulsion // Space Forum. 2000. V. 5. Р. 279–305.

12. Р.З.Ахметшин, Г.Б.Ефимов. О некоторых задачах в проекте "Фобос-Грунт" // Актуальные проблемы авиационных и аэрокосмических систем. 2007. v.12, N 1(23). P. 40-50.

13. В.В.Белецкий. Очерки по механике космического полета. М., Наука, 1964.

14. Авдуевский В.С., Аким Э.Л., Энеев Т.М. и др. Космический проект
«Фобос-Грунт»: основные характеристики и стратегия развития // Космонавтика и ракетостроение. 2000. Т. 19. С. 8–21.

15. Федотов Г.Г. Об использовании возможностей комбинации большой и малой тяги при полетах к Марсу// Космич. Исслед. 2001. Т.39. № 6. С. 613-621.

16. Zaslavsky G.S., Zharov V.G., Chernov A.V. Optimal transfer from Earth satellite orbit to Mars satellite orbit with using electric propulsion system at cruising phase // 17th International Symposium on Space Flight Dynamics. Proceedings. Moscow, 2003. V. 1. Р. 305-311.