1. Введение
Большое количество задач науки и техники, от моделирования активных зон ядерных реакторов до исследования процессов взаимодействия высокоэнергетичных потоков лазерного излучения с веществом, базируется на численном решении уравнения переноса незаряженных частиц или неполяризованного излучения. В одномерном нестационарном приближении это уравнение для одной группы частиц по энергии имеет вид:
Здесь введены следующие обозначения: – функция распределения, зависящая от фазовых переменных и времени, – косинус угла направления полета частицы, составляемого с направлением оси x, S(I) – член рассеяния, – внешний источник, – коэффициенты поглощения и рассеяния соответственно, – коэффициенты разложения индикатрисы рассеяния по полиномам Лежандра.
Для уравнения (1) ставится начально-краевая задача
В ряде задач ставятся более сложные краевые условия отражения.
Уравнение (1) является интегро-дифференциальным, и обычно по интегральным членам рассеяния (и деления) используется итерационный процесс. Для ряда задач такой итерационный процесс может быть медленно сходящимся.
2. HOLO алгоритмы
Эффективным методом ускорения итераций по членам рассеяния (и деления), а также для организации эффективной связи решения уравнения переноса с другими уравнениями, описывающими состояние среды, через которую проходит излучение или поток частиц, являются HOLO алгоритмы. Их основная идея заключается в совместном решении уравнений высокой размерности (HO – high order) и уравнений низкой размерности (LO – low order) [1–8].
В рассматриваемой задаче уравнением высокой размерности является уравнение переноса (1), а уравнением низкой размерности – система уравнений квазидиффузии. Для ее получения введем следующие величины: – плотность излучения, сопоставляемую с интегралом от функции распределения по угловой переменной : , и – поток, сопоставляемый с аналогичным интегралом с весовой функцией : . Проинтегрировав уравнение (1) по переменной с весом 1 и и использовав ортогональность многочленов Лежандра, получим систему уравнений квазидиффузии:
В уравнениях квазидиффузии введен коэффициент квазидиффузии
зависящий дробно-рациональным образом от искомого решения.
В рамках реализации HOLO алгоритма решения уравнения (1) и системы (3) оказываются тесно связанными. Из системы (3) рассчитываются плотность и поток излучения, их значения передаются в уравнение переноса (1) для вычисления главных трех первых членов интеграла рассеяния. Решение уравнения (1) для ряда угловых направлений, соответствующих выбору узлов квадратурной формулы по углам, позволяет рассчитать интегралы, входящие в коэффициент квазидиффузии (4) и в граничные условия для системы уравнений квазидиффузии. В данном простейшем одномерном случае использовались квадратуры Гаусса отдельно для положительных и отрицательных угловых направлений, т.к. на характеристике решение не только может быть недифференцируемым, оно может терпеть разрыв.
Для нахождения решения необходимо организовать итерационный процесс, включающий решение уравнений LO и HO и обмен данными между ними. Алгоритм повторяется до достижения необходимой точности на каждом шаге по времени.
3. Вывод бикомпактной схемы на примере уравнения переноса
Для решения начально-краевой задачи (1)–(2) в [9–15] были разработаны бикомпактные схемы, обладающие четвертым порядком аппроксимации по пространственным переменным и произвольным (в реализации третьим) по времени на минимальном двухточечном шаблоне по каждой из переменных. В качестве примера построения схемы для расчета, реализующей возможности достижения четвертого порядка аппроксимации по пространству и высокого порядка аппроксимации по времени, рассмотрим вывод схемы для уравнения переноса с изотропным рассеянием, которое в схеме HOLO итераций можно считать уравнением с известной правой частью:
Здесь величины – скорость рассматриваемой группы частиц и – косинус угла, составляемого направлением движения частицы с положительным направлением оси x, они не зависят от пространственной координаты и времени. Коэффициенты поглощения и рассеяния и их сумма могут зависеть от времени и пространственной координаты.
Для этого уравнения ставится начально-краевая задача (2).
Для начала введем сетку на отрезке и пространственный шаг . В дальнейшем индекс, указывающий на номер ячейки, будет опускаться, так как разностная схема строится в рамках одной ячейки.
Бикомпактная схема строится методом прямых с выводом полудискретной системы уравнений, при котором пространственные производные аппроксимируются конечными разностями, а производные по времени оставляются в дифференциальном виде. Вывод полудискретной формы бикомпактной схемы для уравнения переноса основан на смешанной FV (Finite Volume) – FD (Finite Difference) технике.
Стандартным образом на двухточечном шаблоне возможно достижение второго порядка аппроксимации, для увеличения порядка до четвертого используется расширение списка неизвестных и включение в него помимо узловых значений искомой функции интегральных средних от величины по ячейке. Введем для них следующее обозначение:
В рамках FV подхода уравнение (5) интегрируется по ячейке, в результате получается точное следствие исходного уравнения следующего вида:
,
.
В уравнение (7) входит среднее от произведения заданной и искомой функций . Замена доставляет лишь второй порядок аппроксимации по пространству. При заданном двойном наборе узловых и средних искомых величин для достижения четвертого порядка аппроксимации по пространству воспользуемся формулой Симпсона. Считая, что значение коэффициента доступно в любой пространственной точке, введем его значение в полуцелом узле. Записывая выражение для интегральных средних и с помощью формулы Симпсона и исключая неизвестной значение в полуцелом узле , имеем:
Таким образом, среднее от произведения примет вид:
Уравнения (7) с учетом (8) недостаточно для нахождения всех нужных величин. Вторым шагом (FD) для получения замкнутой системы уравнений к уравнению (7) добавляют проинтегрированное по ячейке первое дифференциальное следствие уравнения (5). Первое дифференциальное следствие представляет собой уравнение, правая и левая часть которого суть производные по x от соответствующей части исходного уравнения:
Тогда при интегрировании (10) по ячейке получим следующее выражение:
В него, помимо узловых значений , также входят пространственные производные функции распределения в узлах. Для исключения их вхождения в систему уравнений в [5] предложено использовать формулу Эйлера–Маклорена, обладающую четвертым порядком аппроксимации:
С учетом связи разности производных с узловыми значениями и интегральным средним (12) уравнение (11) оказывается возможным переписать следующим образом:
Система полудискретных уравнений (7), (13) замкнута относительно переменных , не содержит в себе производных по пространству и может быть проинтегрирована по времени любым удобным способом. Мы будем использовать L–устойчивый диагонально-неявный метод Рунге–Кутты третьего порядка аппроксимации с таблицей Бутчера
Как было показано в [16], каждая стадия данного метода может быть представлена как неявный метод Эйлера. Соответственно, данный метод определяет базовую схему реализации метода Рунге-Кутты по времени. Система уравнений для неявного метода Эйлера в применении к (7), (13) запишется следующим образом:
Система (15) вместе с соответствующим знаку граничным условием решается методом бегущего счета на каждом временном слое: для слева направо, для справа налево. Более подробно численная реализация схемы для уравнения переноса изложена, например, в [16].
4. Схема для системы уравнений квазидиффузии
Дифференциальная система уравнений низкой размерности (уравнений квазидиффузии) получается интегрированием уравнения переноса с весами 1 и по угловой переменной. Поэтому схему для LO системы уравнений можно строить двумя различными путями.
1. Строить схему для дифференциальной системы двух уравнений в частных производных. Принципы построения расчетной схемы для системы уравнений квазидиффузии мало отличаются от принципов, описанных выше для уравнения переноса.
2. Пусть у нас задана квадратурная формула для вычисления интегралов от функции распределения вида:
где – веса квадратурной формулы, – узлы квадратуры. Разностная схема может быть получена из разностной схемы для уравнения переноса суммированием с весами квадратурной формулы каждого из двух уравнений и их же, домноженных на .
Выпишем главные этапы вывода схемы первым из этих методов для системы следующего вида (изотропное рассеяние):
Система уравнений квазидиффузии (LO) (17) получена из уравнения (5) интегрированием по углам с весом 1 и . Начальные условия к ней также получаются интегрированием по углам начального условия (2).
В классическом варианте HOLO алгоритмов граничные условия для системы (17) получаются из решения уравнения переноса введением еще одного класса дробно-линейных функционалов:
Значения падающих плотности и потока излучения на границах области получаются из краевых условий (2):
В первую очередь для вывода схемы мы расширяем список неизвестных, добавляя средние по ячейке от обеих неизвестных. Введем обозначения:
Проинтегрировав по ячейке оба уравнения, получим первые два уравнения системы
Далее находим первые дифференциальные следствия от обоих уравнений и тоже интегрируем их по ячейке
Средние и раскроем с четвертым порядком аппроксимации, аналогично формулам (9). В эти формулы входит также среднее от .
Коэффициент не является независимым коэффициентом, а вводится как дробно-линейный функционал от интегрального среднего в ячейке при интегрировании по углам (4), (16):
Раскрытие средних по формуле, обладающей формально вторым порядком аппроксимации
из требования кинетической согласованности схем для уравнений квазидиффузии (HO) со схемой для уравнения переноса (LO) приводит к схеме четвертого порядка аппроксимации, т.к в этом случае при сходимости итераций выполняется точное равенство
Интегрирование по угловым переменным для LO уравнений приводит к тому, что на каждом шаге по времени возникает краевая задача по пространству. Для реализации базовой схемы при интегрировании по времени – неявного метода Эйлера, – в данном случае потребуется использовать метод потоковой прогонки. Подробности реализации схемы можно найти в [19]. Для интегрирования по углам используется метод Гаусса с пятью узлами на каждом из полуинтервалов от [–1,0] и [0,1].
5. Аналитический тест для HOLO алгоритма
Составим аналитическое решение для (5) на , в качестве функции распределения выберем
Коэффициенты рассеяния и поглощения зададим в виде:
Интегрированием по получатся следующие точные решения для плотности и потока излучения
В вычислениях потребуются величины F, Q0, Q1, , найдем F из (5):
Величины Q0, Q1 вычислим по (3).
Начально-краевая задача ставится в соответствии с (2). В [16] показано, что для достижения третьего порядка аппроксимации по времени для методов Рунге–Кутты краевые условия необходимо ставить, используя производные по времени
и интегрируя краевые условия (24) в общей схеме применения метода Рунге–Кутты. Это связано со структурой погрешности методов Рунге–Кутты [17–18].
Рассмотрим два варианта нахождения решения задачи (5), (2): решение только на основе уравнения переноса, т.е. классическим методом итераций источника (SIM), и в соответствии с HOLO алгоритмом. Результаты для порядков аппроксимации по времени и пространству представлены в таблицах I,II,III,IV,V,VI. Из таблицы III видно, что порядок аппроксимации по времени падает до второго при подключении к решению системы уравнений квазидиффузии. Это связано с тем, что краевые условия (18) мы не можем представить в виде типа условий (24) для производных по времени от искомых функций, которые необходимы для обеспечения третьего порядка сходимости по времени. В представленных ниже таблицах величина определяет точность сходимости итераций по членам рассеяния на каждой стадии используемого метода Рунге-Кутты. Исследовалось либо сгущение сеток при фиксированном гиперболическом числе Куранта, и тогда сходимость определяется членами наименьшего порядка аппроксимации, т.е. по времени, либо фиксировался малый временной шаг и измельчались сетки по пространству.
Таблица I
Погрешности численного решения и порядок сходимости по времени в методе итерации источника для теста.
| Порядок схемы | ||
|---|---|---|
| 25 | –6.20 | 2.95 |
| 50 | –7.09 | 2.97 |
| 100 | –7.99 | 2.97 |
| 200 | –8.91 | 2.89 |
| 400 | –9.79 | 2.36 |
| 800 | –10.54 | |
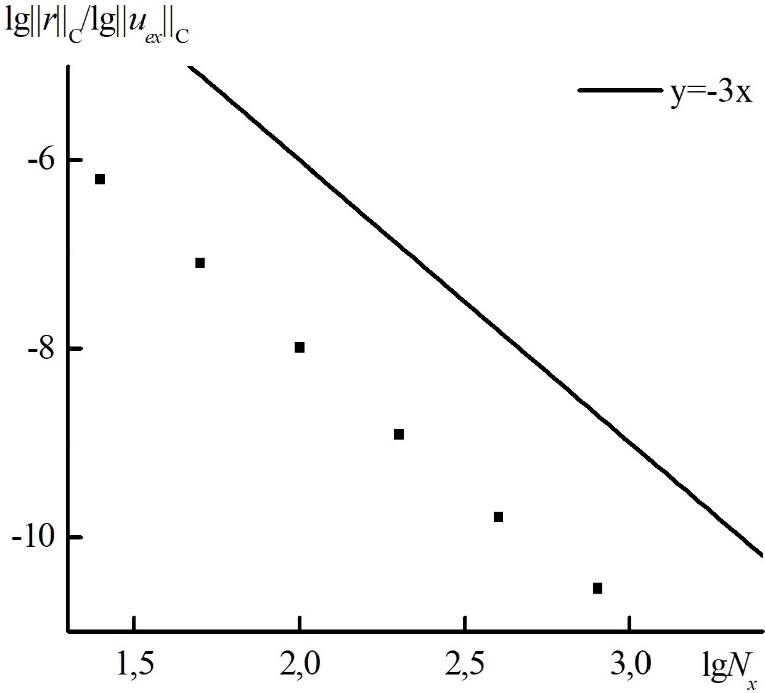
Рис. 1. Зависимость погрешности численного решения от числа узлов по пространству при фиксированном гиперболическом числе Куранта для аналитического теста (SIM). Для сравнения проведена прямая с наклоном –3 (порядка аппроксимации по времени).
Таблица II
Погрешности численного решения и порядок сходимости по пространству в методе итерации источника для теста
| Порядок схемы | ||
|---|---|---|
| 25 | –8.51 | 3.97 |
| 50 | –9.71 | 3.58 |
| 100 | –10.78 | |
Таблица III
Погрешности численного решения и порядок сходимости по времени при использовании HOLO алгоритма для теста с краевыми условиями (18)–(19)
| Порядок схемы | ||
|---|---|---|
| 25 | –4.74 | 1.96 |
| 50 | –5.33 | 1.93 |
| 100 | –5.93 | 1.96 |
| 200 | –6.53 | 1.98 |
| 400 | –7.13 | 1.99 |
| 800 | –7.73 | |
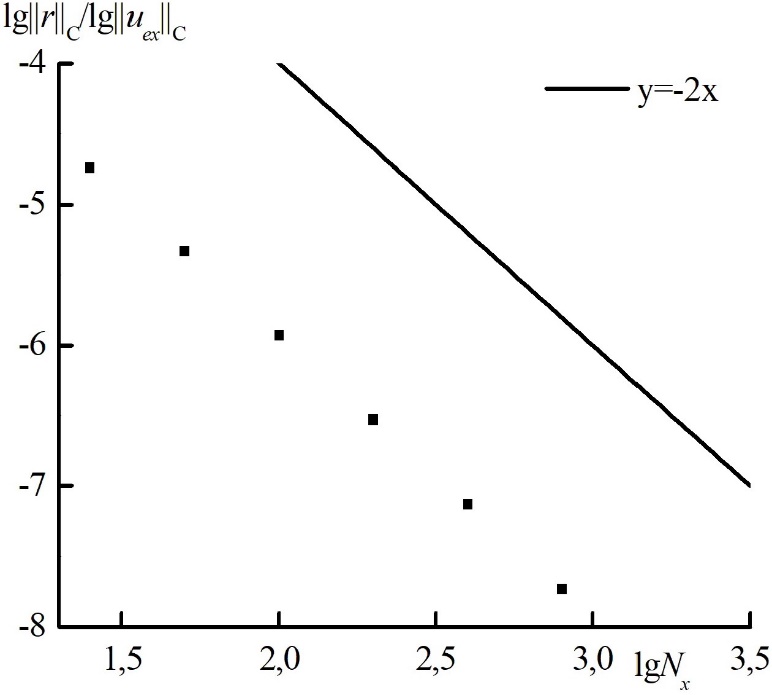
Рис. 2. Зависимость погрешности численного решения от числа узлов по пространству при фиксированном гиперболическом числе Куранта для теста c HOLO алгоритмом. Для сравнения проведена прямая с наклоном –2 (порядка аппроксимации по времени).
Таблица IV
Погрешности численного решения и порядок аппроксимации по пространству для HOLO алгоритма при использовании краевых условий (18)–(19) для теста
| Порядок схемы | ||
|---|---|---|
| 25 | –8.74 | 3.95 |
| 50 | –9.94 | 2.35 |
| 100 | –10.56 | |
Как видно из представленных данных, подключение системы LO уравнений (уравнений квазидиффузии) понижает порядок сходимости до второго по времени при использовании классической постановки краевых условий в виде (18), сохраняя четвертый порядок сходимости по пространству. Быстрое падение порядка сходимости в Табл. IV связано как с не слишком малым шагом по времени (и вторым порядком аппроксимации по этой переменной), так и с тем, что константа погрешности по пространству мала (1/1512).
Изучим вопрос о том, как добиться третьего порядка аппроксимации по времени при использовании HOLO алгоритма. Для этого рассмотрим еще один вариант постановки граничных условий. В этом случае мы отключим взаимодействие решения уравнения переноса и системы уравнений квазидиффузии через граничные условия (18), ожидая увеличения количества итераций, необходимого для достижения заданной точности по сравнению с HOLO алгоритмом без этой модификации.
Будем задавать граничные условия, используя значения плотности излучения, вычисленные на этапе решения уравнения переноса по квадратурным формулам.
Таблица V
Погрешности численного решения и порядок аппроксимации по времени для HOLO алгоритма при использовании краевых условий (25) для теста
| Порядок схемы | ||
|---|---|---|
| 25 | –5.85 | 3.00 |
| 50 | –6.75 | 3.00 |
| 100 | –7.66 | 3.00 |
| 200 | –8.56 | 2.99 |
| 400 | –9.46 | 2.93 |
| 800 | –10.34 | |
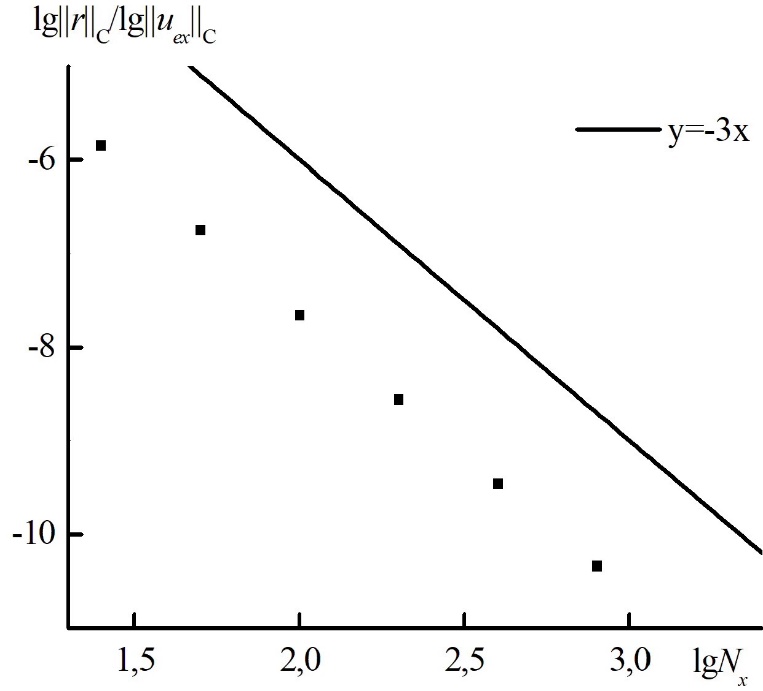
Рис. 3. Зависимость погрешности численного решения от числа узлов по пространству при фиксированном гиперболическом числе Куранта для теста. Для сравнения проведена прямая с наклоном –3 (порядка аппроксимации по времени).
Таблица VI
Погрешности численного решения и порядок аппроксимации по пространству для HOLO алгоритма при использовании граничных условий (25) для теста
| Порядок схемы | ||
|---|---|---|
| 25 | –8.74 | 3.99 |
| 50 | –9.95 | 4.03 |
| 100 | –11.16 | 2.50 |
| 200 | –11.92 | |
Сравним эффективность алгоритмов метода итераций источника (SIM – 1) и два варианта HOLO алгоритма: с использованием классических краевых условий метода квазидиффузии с введением дробно-линейных функционалов (18) (HOLOcl – 2) и с постановкой краевых условий непосредственно интегрированием функции распределения (HOLOmod – 2), сравнив число итераций по всем шагам и по всем стадиям, необходимых для достижения заданной точности. Результаты представлены на Рис. 4.
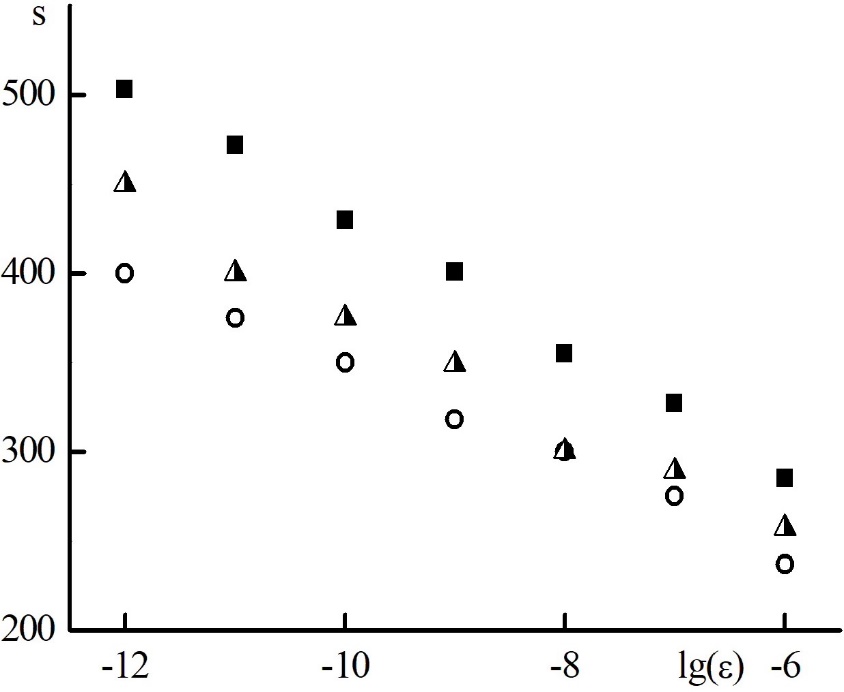
Рис. 4. Зависимость суммарного по всем стадиям и всем шагам по времени числа итераций, необходимых для достижения точности на каждой стадии каждого шага решения. . Закрашенные круги – метод итераций источника (SIM – 1), полузакрашенные треугольники – HOLOmod –2, полые круги – HOLOcl –2.
6. Задача Рида и ее результаты
Применим описанный метод для решения задачи Рида. Задача Рида является стационарной. Мы стационарное решение получим в пределе . В качестве начального условия возьмем . Справа поставим граничное условие , а слева – условие зеркального отражения .
Будем решать уравнение (5) совместно с системой (3). Начальные и граничные условия для нее ставятся следующим образом:
, ,
, .
Зададим также правые части и коэффициенты в соответствии с Таблицей VII.
Таблица VII
Коэффициенты и F в задаче Рида
| Слой | x | F | |||
|---|---|---|---|---|---|
| 1 | (0,2) | 50 | 0 | 50 | 25 |
| 2 | (2,3) | 5 | 0 | 5 | 0 |
| 3 | (3,5) | 0 | 0 | 0 | 0 |
| 4 | (5,6) | 1 | 0.9 | 0.1 | 0.5 |
| 5 | (6,8) | 1 | 0.9 | 0.1 | 0 |
Потребуем сходимость итерационного процесса на каждой из трех стадий используемого метода Рунге–Кутты.
Нами было получено стационарное решение (см. рис. 5 и таблица VIII), соответствующее решению этой задачи в [20].
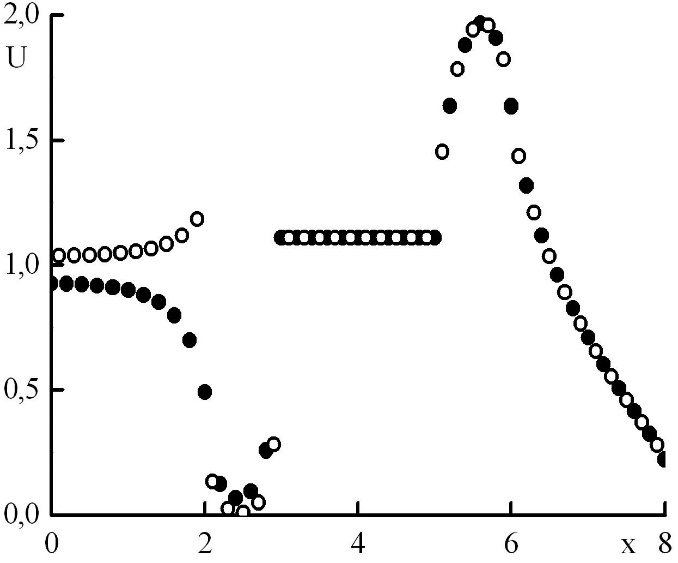
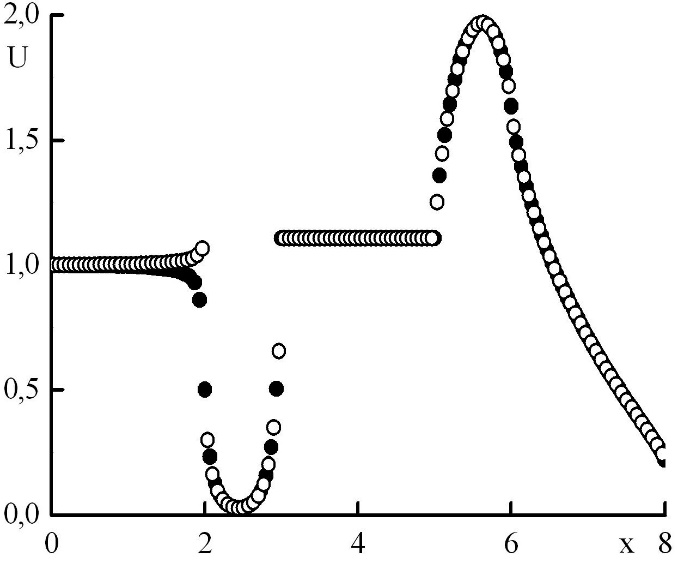
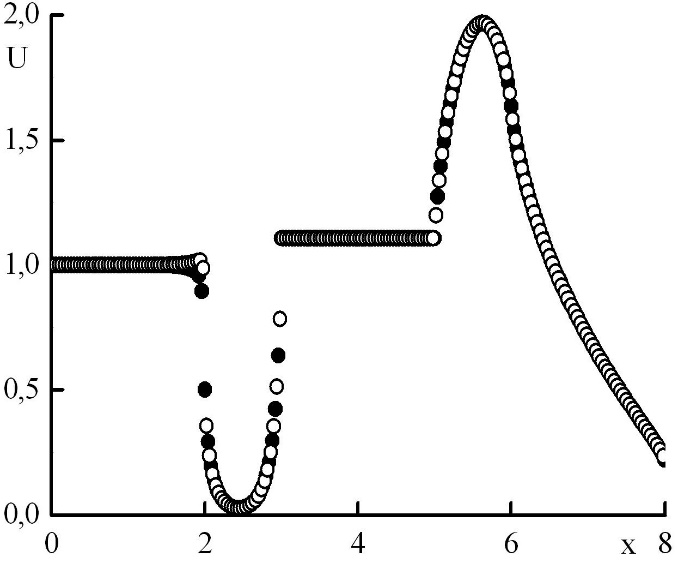
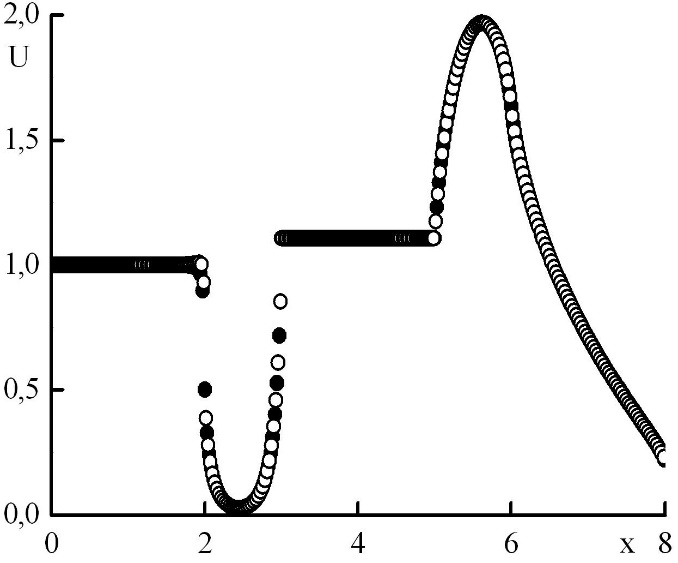
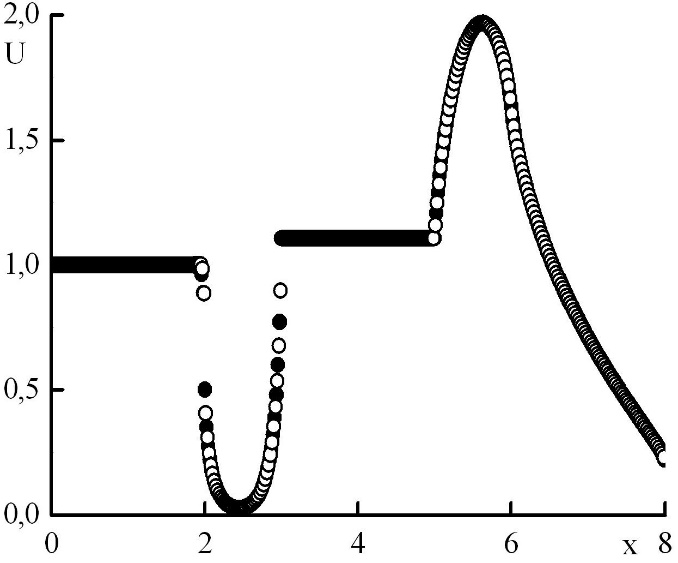
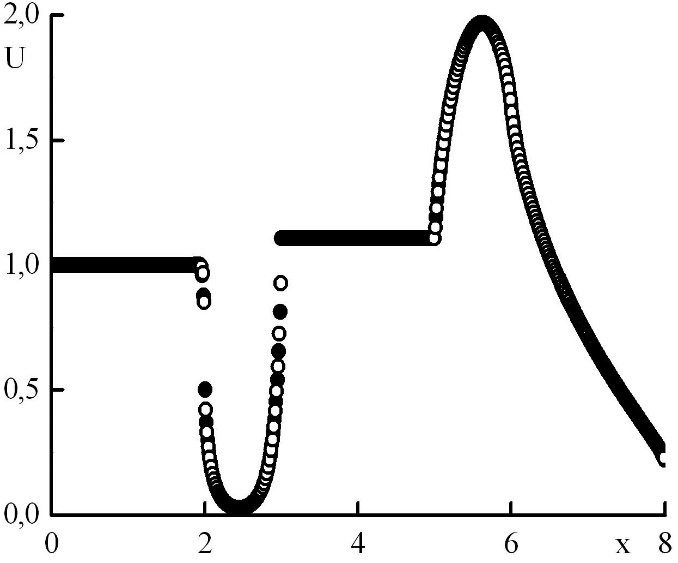
Была использована схема четвертого порядка по пространству, поэтому можно показать, что полученное решение может быть немонотонным. Проведем расчет на нескольких сетках, изобразим на одном графике решения в узловых точках и в полуцелых, посчитав их значения с четвертым порядком точности через узловые значения и средние по ячейкам при помощи формулы Симпсона. Исследуем, при каких параметрах сетки решение является немонотонным и при каких переходит в монотонное (рис. 5,6,7,8,9,10). Рис. 5 иллюстрирует, что момент перехода немонотонного решения в монотонное соответствует , и можно сформулировать следующий критерий: если максимальная оптическая толщина слоя, соответствующего одному шагу по пространству, превышает величину (27), то решение немонотонно, в противном случае – монотонно.
Таблица VIII
Экстремальные и промежуточные значения плотности излучения в стационарном решении задачи Рида. DD0 – взвешенная «алмазная» схема DD0 с коррекцией отрицательных потоков “fix-up” [22], LN – LN метод [23], МКЭ – метод конечных элементов [20], HOLOcl – реализуемый в данной работе варианта HOLO алгоритма с использованием классических краевых условий метода квазидиффузии с введением дробно-линейных функционалов при , , .
| DD0 | LN | МКЭ | HOLOcl | |
|---|---|---|---|---|
| Минимальное значение в слое 2 | 0.02135 | 0.03229 | 0.03035 | 0.02836 |
| Промежуточное значение в слое 3 | 1.10715 | 1.11248 | 1.10711 | 1.10649 |
| Максимальное значение в слое 4 | 1.95216 | 1.94328 | 1.95050 | 1.96628 |
Порядок аппроксимации в области монотонного решения демонстрирует таблица IX. Порядок аппроксимации по времени падает до первого, так как полученное решение не является гладким.
Таблица IX
Погрешности численного решения и порядок сходимости по времени при фиксированном отношении . За точное взято решение при
| Порядок схемы | ||
|---|---|---|
| 400 | 4.36·10–2 | 1.13 |
| 800 | 1.99·10–2 |
Эффективность алгоритма демонстрирует рис. 11. Из графика видно, что суммарное число итераций на всех стадиях и шагах по времени в случае, если использовать разработанный HOLO алгоритм, то есть подключать к решению нестационарного уравнения переноса излучения (5) систему уравнений квазидиффузии (3), примерно вдвое меньше, чем без его использования.
А)
Б)
В)
Г)
Д)
Е)
Рис. 5. Зависимость плотности излучения от координаты в стационарном решении задачи Рида. Закрашенные круги – решения в целых точках, полые круги – решения в полуцелых точках.
А)
Б)
В)
Г)
Д)
Е)
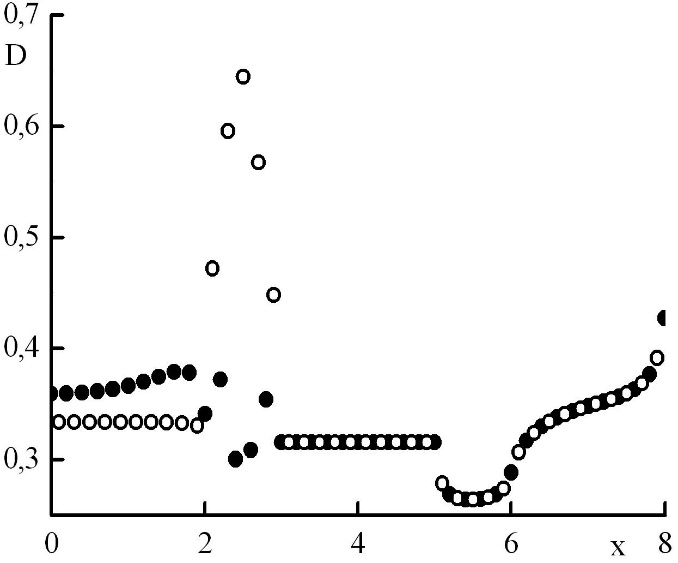
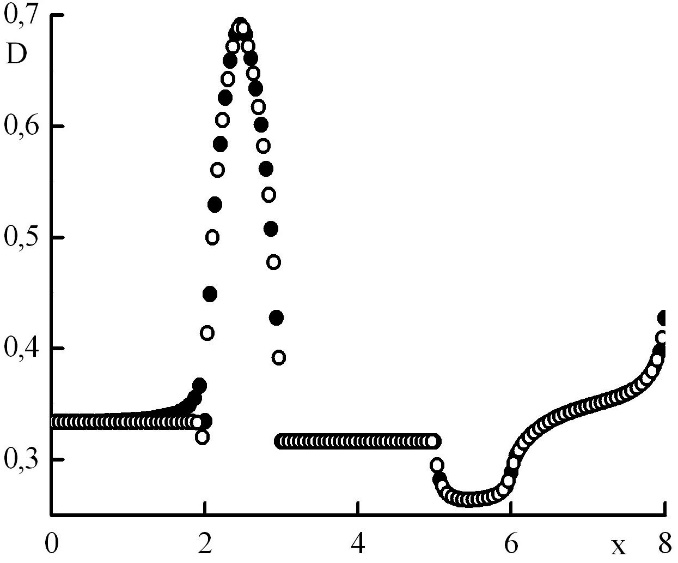
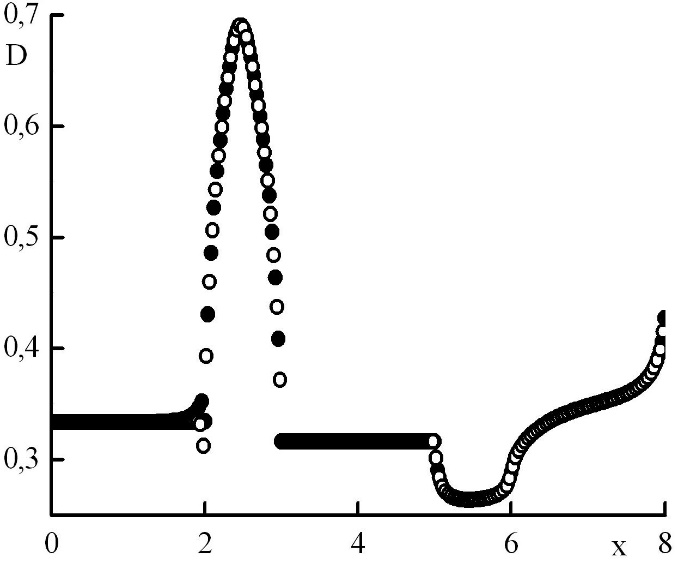
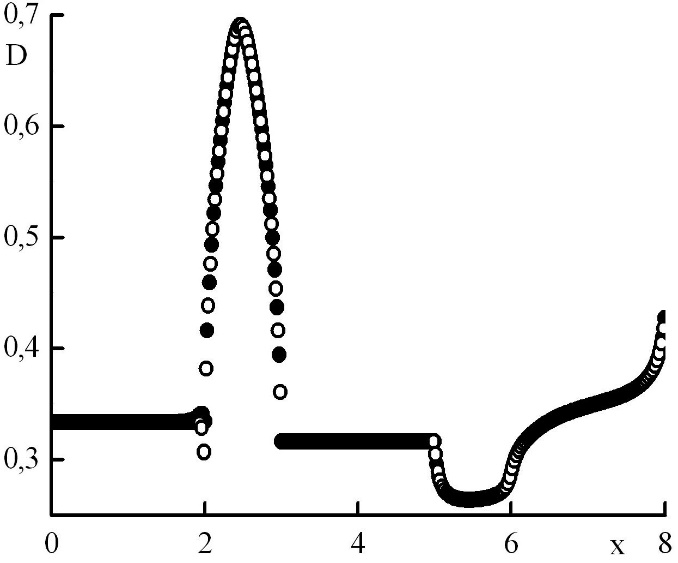
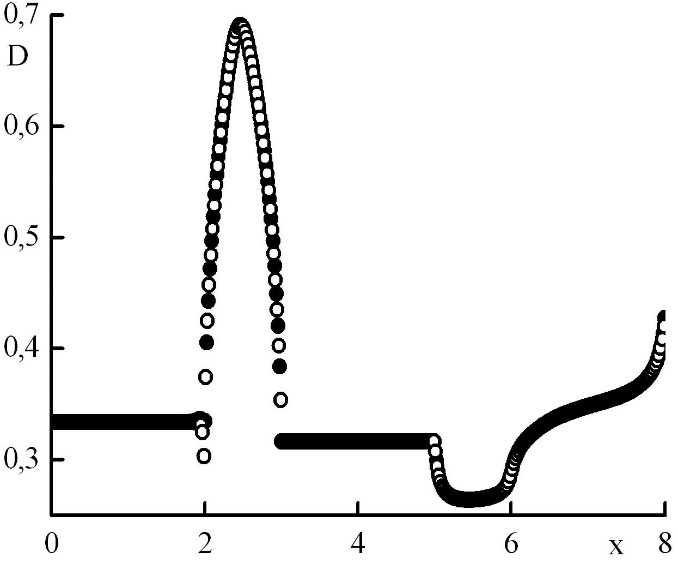
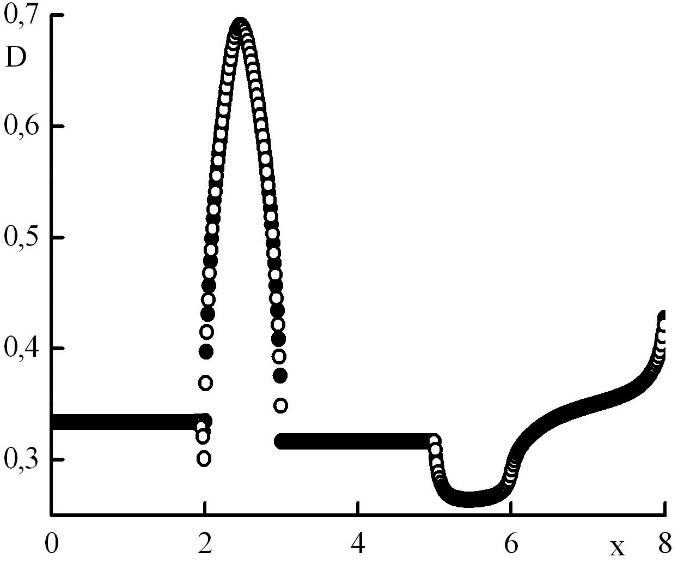
Рис. 6. Зависимость коэффициента квазидиффузии от координаты в стационарном решении задачи Рида. Закрашенные круги – решения в целых точках, полые круги – решения в полуцелых точках.
А)
Б)
В)
Г)
Д)
Е)
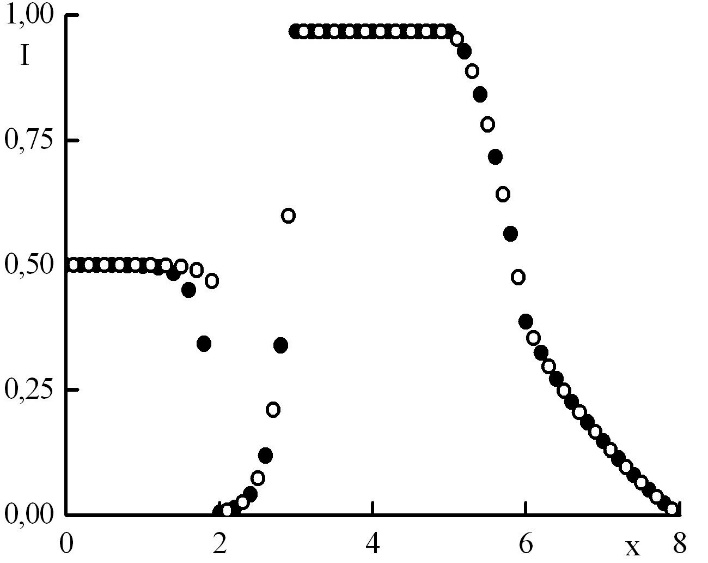
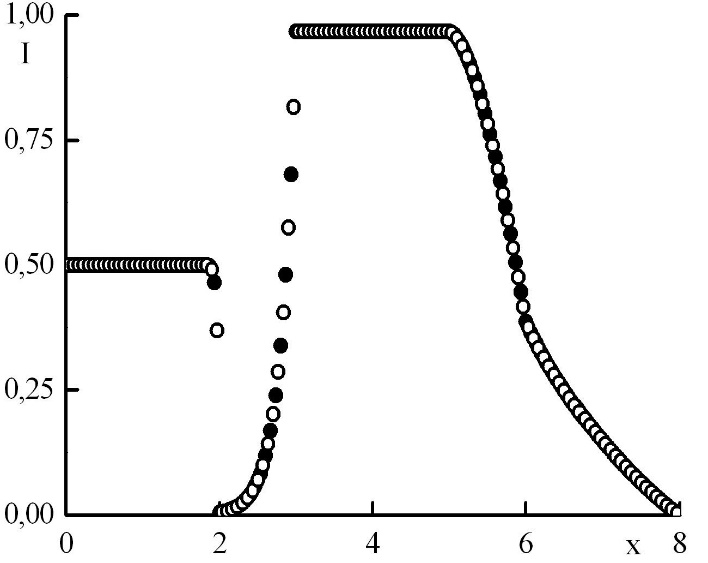
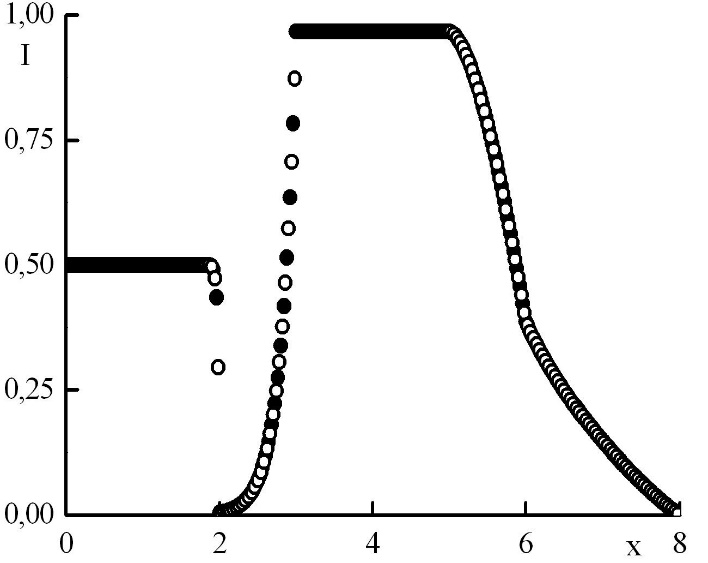
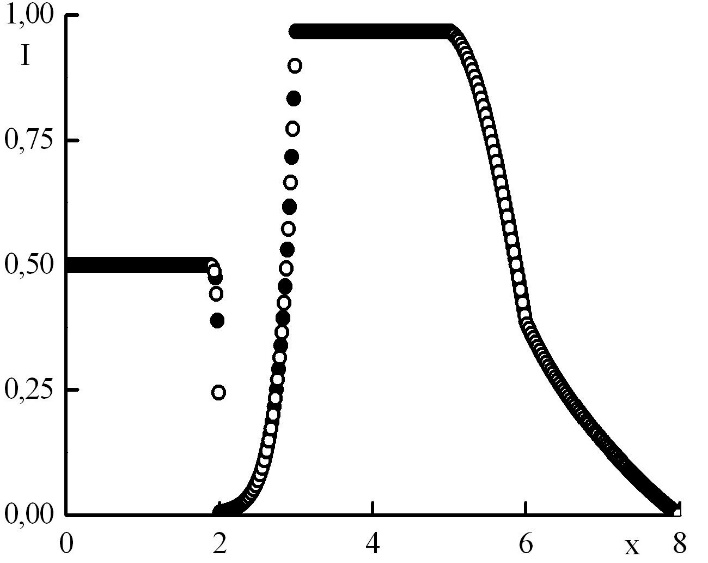
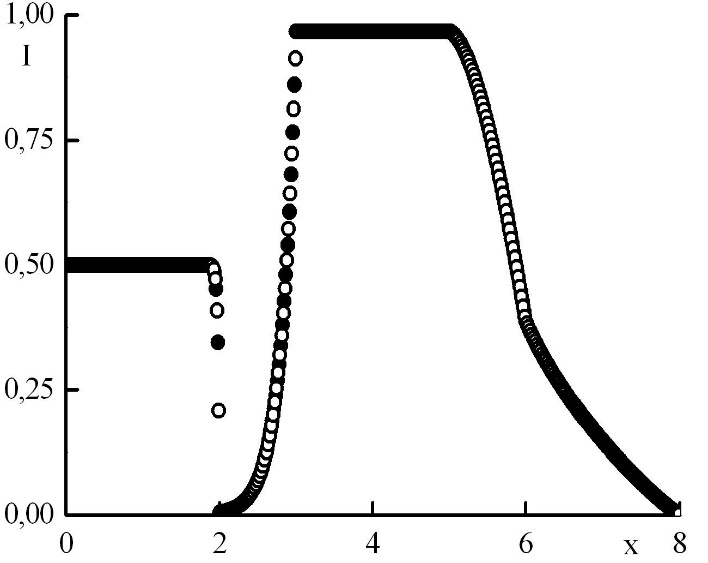
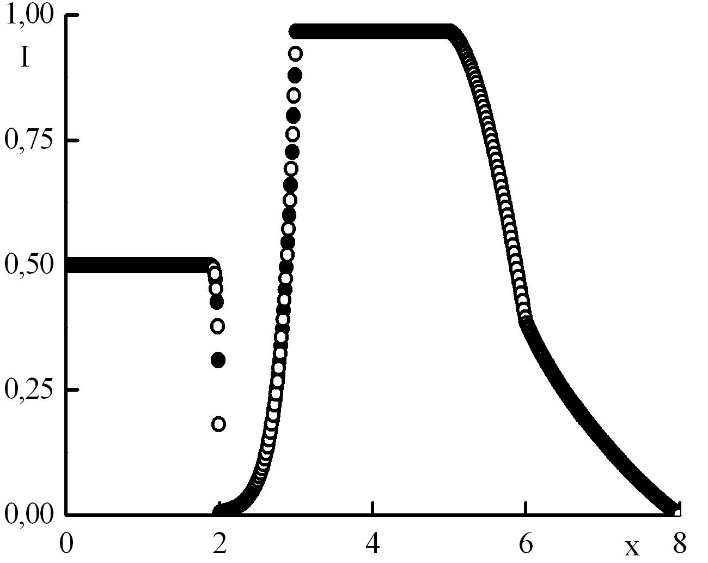
Рис. 7. Зависимость функции распределения от координаты в стационарном решении задачи Рида при минимальном отрицательном . Закрашенные круги – решения в целых точках, полые круги – решения в полуцелых точках.
А)
Б)
В)
Г)
Д)
Е)
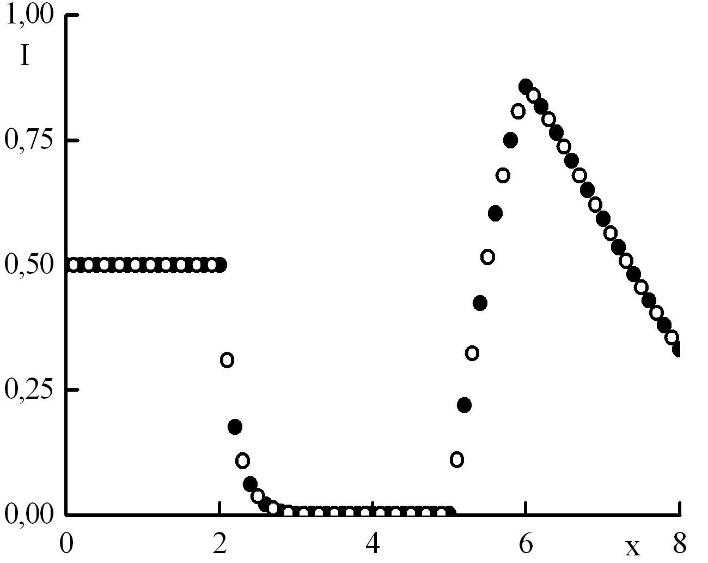
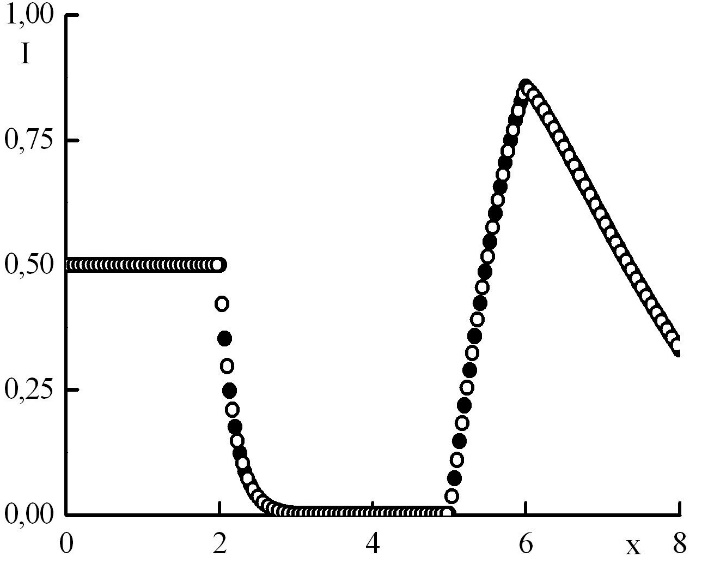
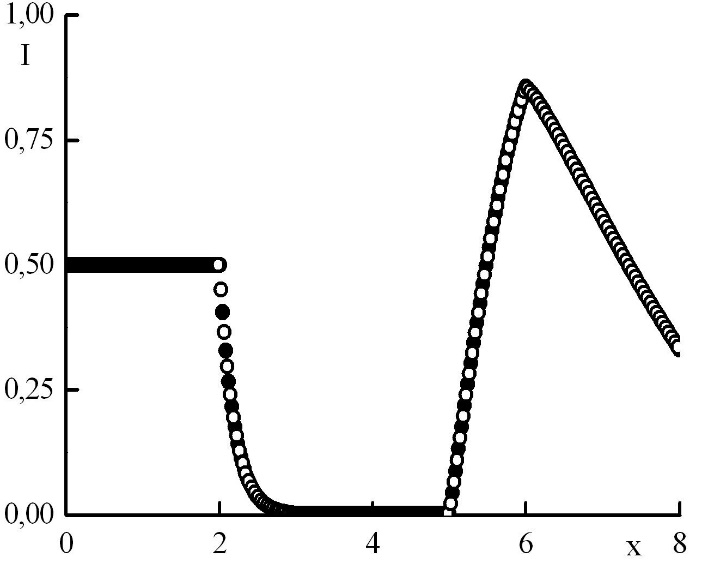
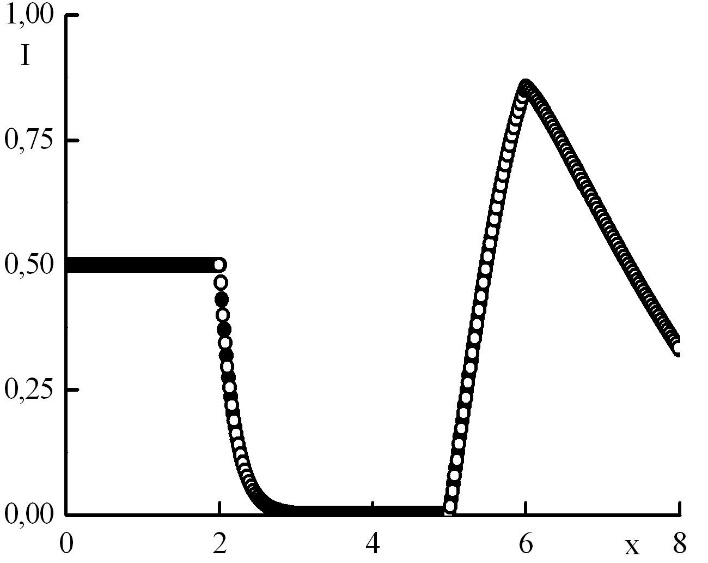
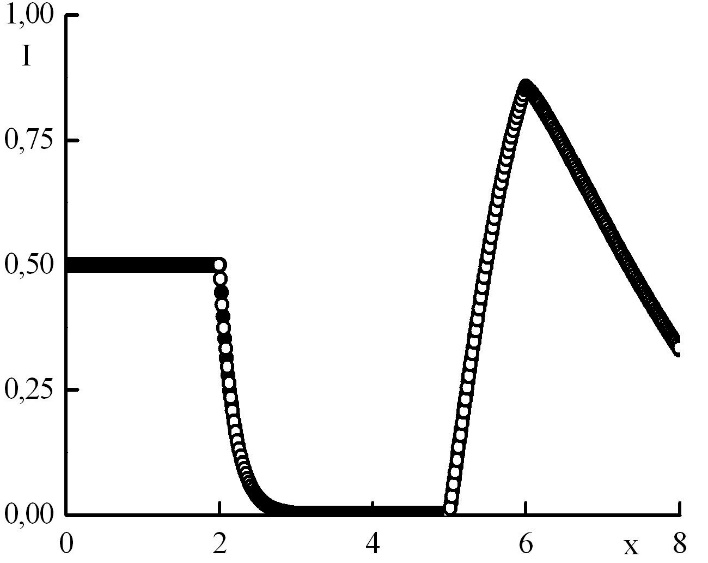
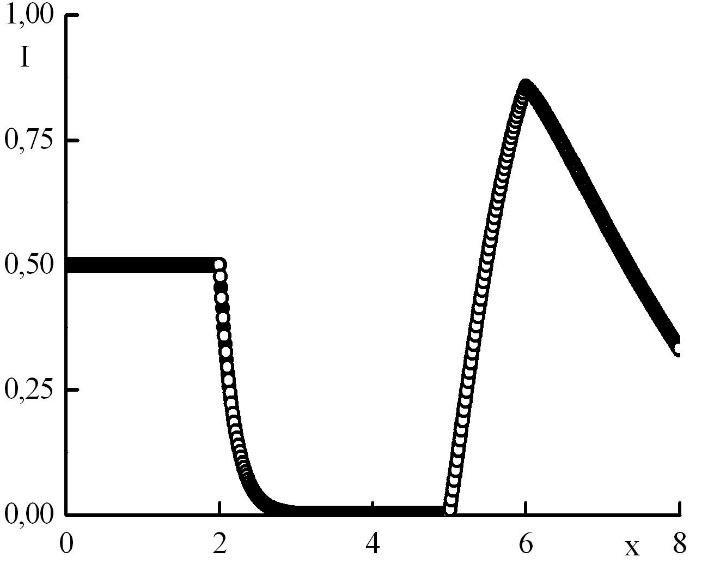
Рис. 8. Зависимость функции распределения от координаты в стационарном решении задачи Рида при максимальном положительном . Закрашенные круги – решения в целых точках, полые круги – решения в полуцелых точках.
А)
Б)
В)
Г)
Д)
Е)
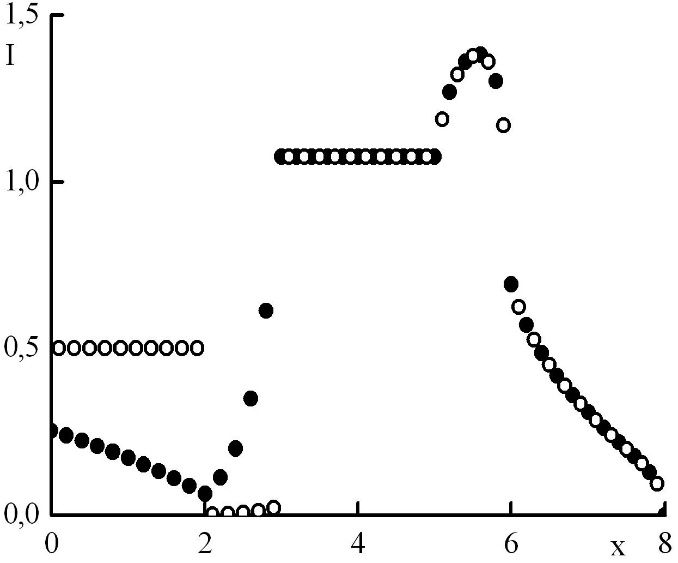
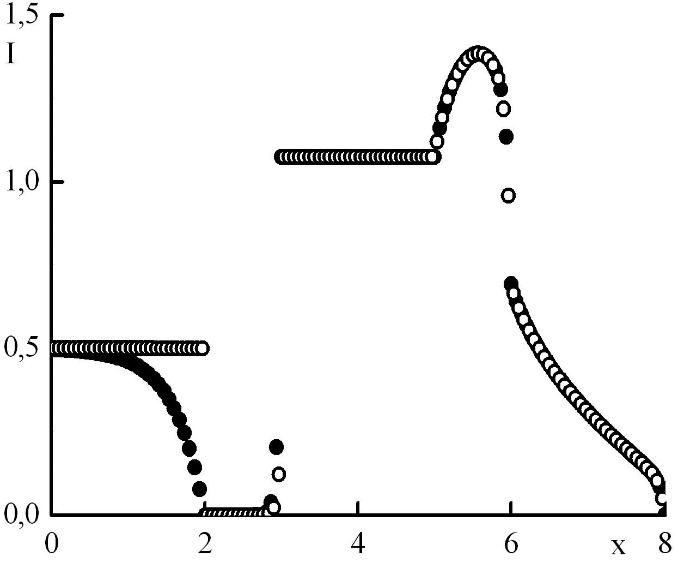
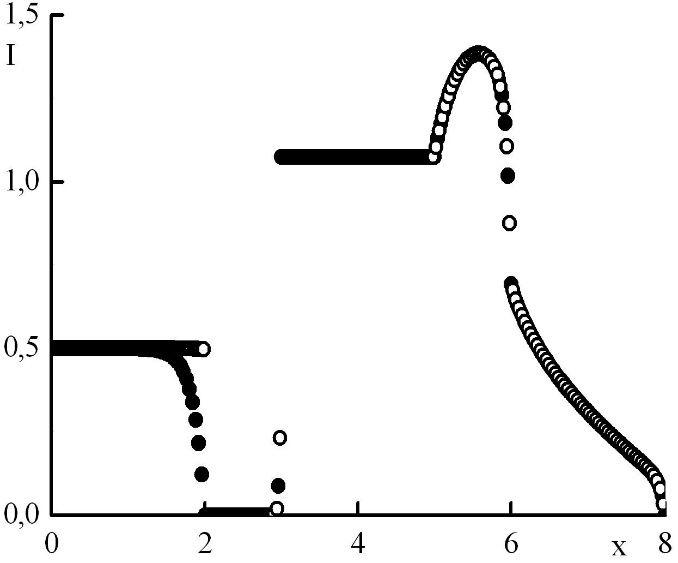
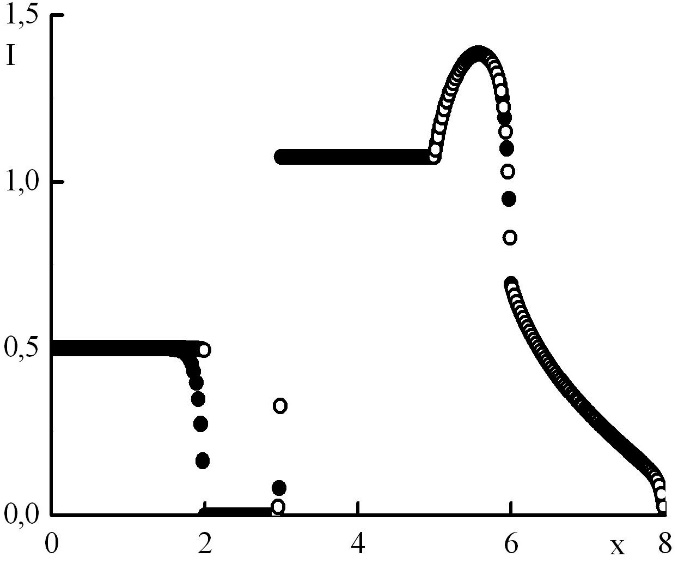
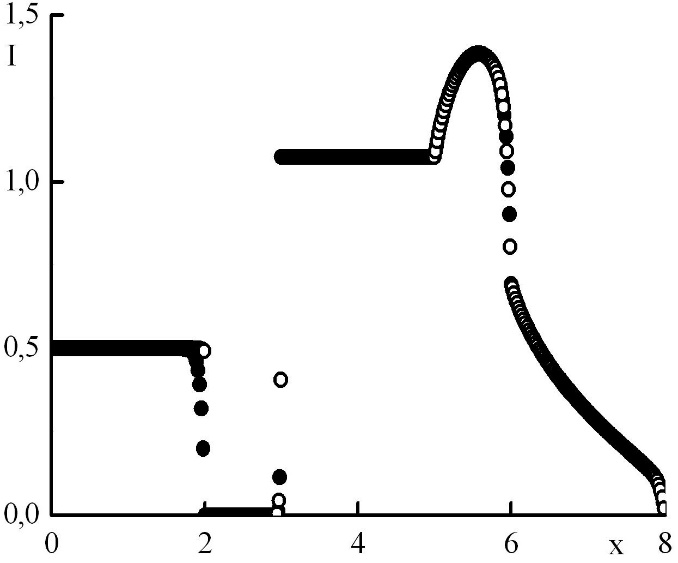
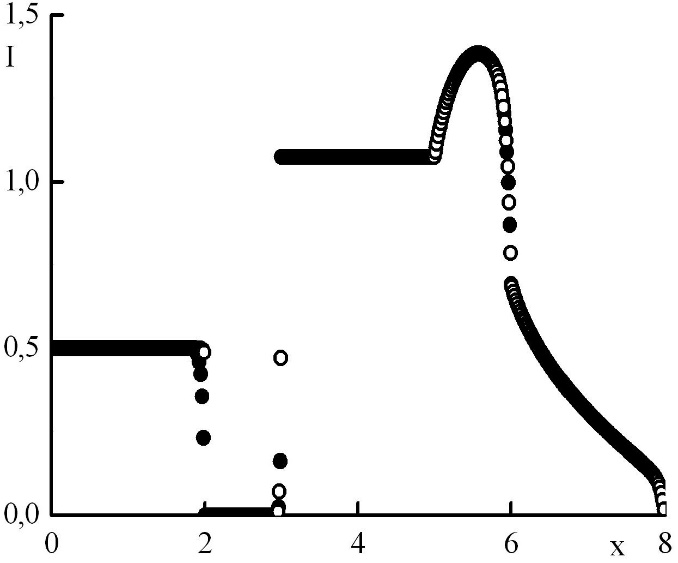
Рис. 9. Зависимость функции распределения от координаты в стационарном решении задачи Рида при максимальном отрицательном . Закрашенные круги – решения в целых точках, полые круги – решения в полуцелых точках.
А)
Б)
В)
Г)
Д)
Е)
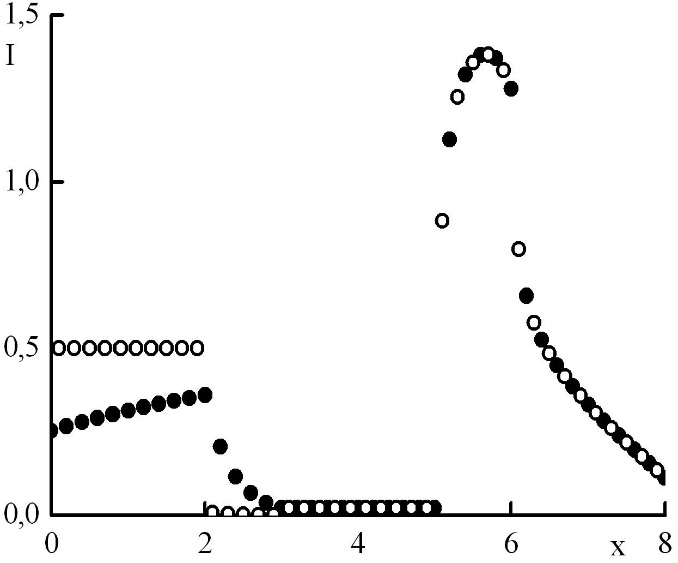
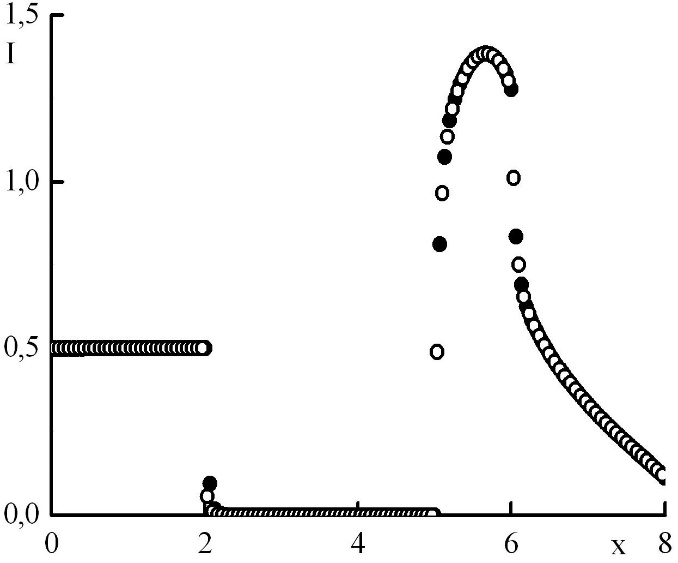
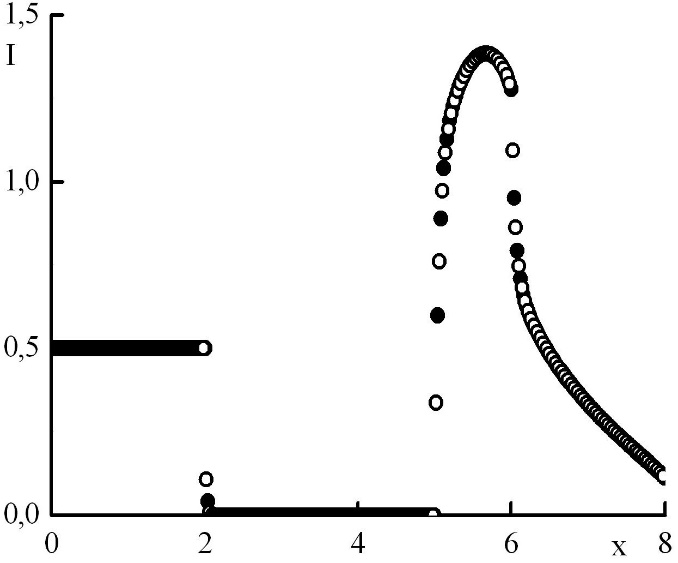
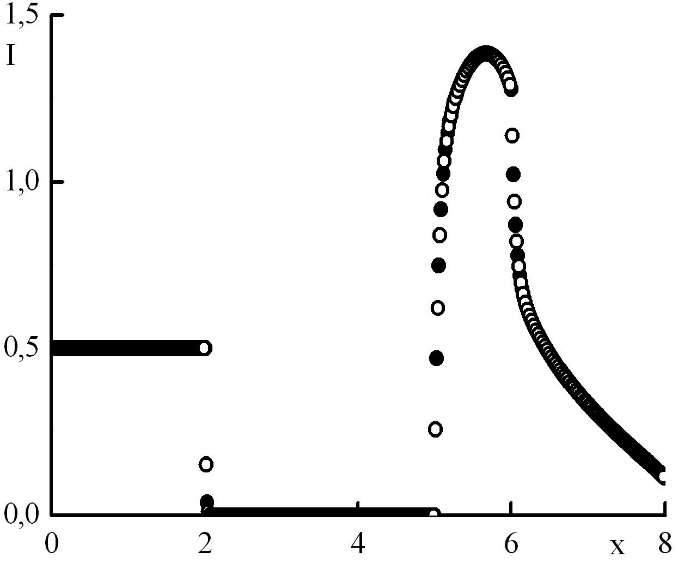
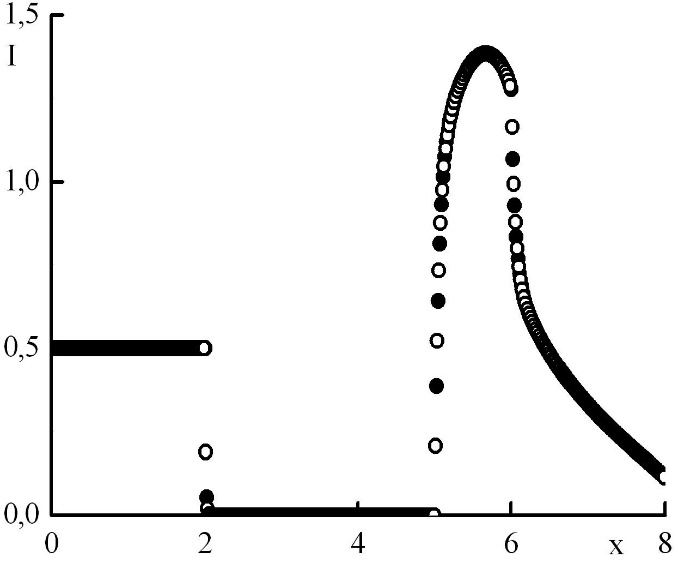
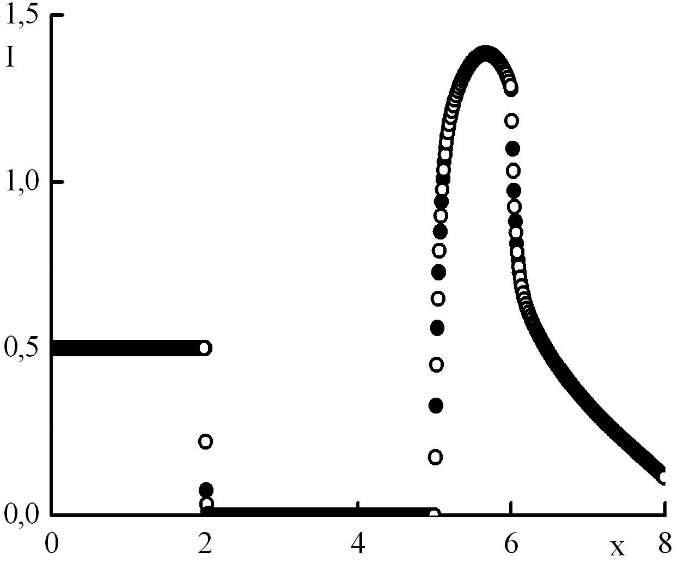
Рис. 10. Зависимость функции распределения от координаты в стационарном решении задачи Рида при минимальном положительном . Закрашенные круги – решения в целых точках, полые круги – решения в полуцелых точках.
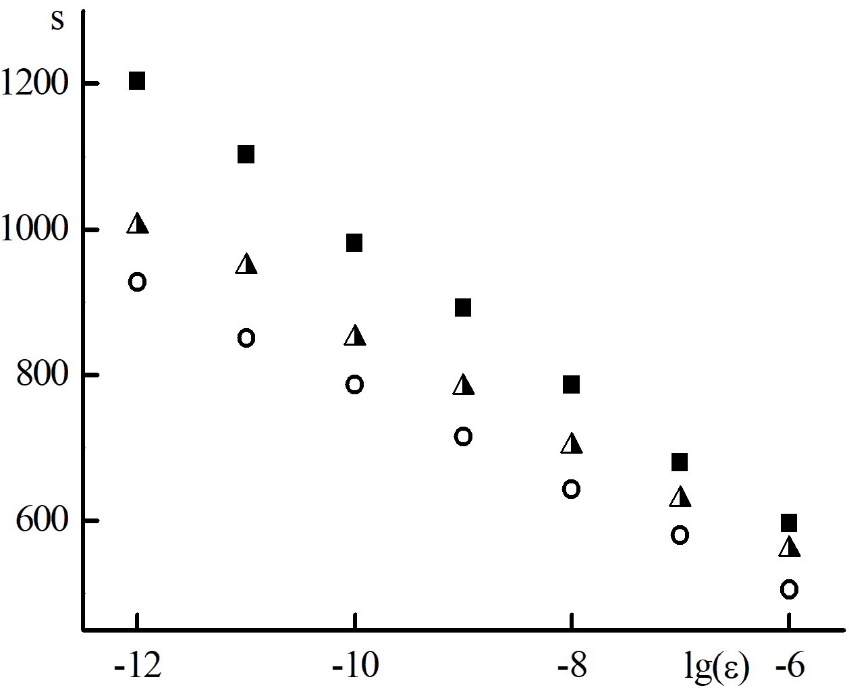
Рис. 11. Зависимость суммарного по всем стадиям и всем шагам по времени числа итераций, необходимых для достижения точности на каждой стадии каждого шага решения. . Закрашенные круги – метод итераций источника (SIM – 1), полузакрашенные треугольники – HOLOmod –2, полые круги – HOLOcl –2.
Отличия значений плотности и потока излучения, получаемых из системы уравнений (3) и как сумматорный интеграл из решения уравнения (5) в стационарном решении соответствуют порядку ошибок округления при вычислении с двойной точностью.
Заключение
Были построены и исследованы бикомпактные схемы для HOLO алгоритма решения нестационарного уравнения переноса в одномерной плоской геометрии (5). Схемы обладают третьим порядком аппроксимации по времени и четвертым по пространству. При реализации граничных условий для части LO (18) порядок аппроксимации по времени падает до второго. Порядок аппроксимации может быть вновь повышен для третьего, если в граничных условиях для системы уравнений квазидиффузии (3) использовать значения плотности излучения, рассчитанные из уравнения переноса (25), однако при этом увеличивается число итераций, которые необходимо совершить для достижения заданной точности, так что эффективность алгоритма падает.
