1. Введение
Изучение газовых гидратов в пористой среде представляет значительный интерес как в целях исследования потенциальных источников углеводородов, так и в связи с анализом и предотвращением возможных экологических и технологических катастроф, например, связанных с внезапными выбросами газа при освоении и разработке северных месторождений [1] или с взаимным влиянием климатических изменений и состояния газовых гидратов зоны вечной мерзлоты и шельфа арктических морей [2].
Процессы, связанные с разложением газовых гидратов в пористой среде, обычно происходят в регионах сложного геологического и литологического строения, для детального изучения которых требуется использование двух- и трехмерного моделирования. Один из подходов к моделированию процессов фильтрации флюидов в пористой среде в подобных регионах основан на применении метода опорных операторов [3]. Разрабатывается применение подобных подходов к задачам диссоциации газовых гидратов в пористой среде [4]. Но построение неодномерных моделей требует очень большой геологической и геофизической информации, получение которой, особенно в труднодоступных северных районах или на морском дне, является сложным, затратным, а порой – невозможным. Результаты расчетов не всегда легко обозримы, за деталями можно не увидеть основные, определяющие характеристики процесса. Проведение большого числа расчетов для сравнения результатов и получения итоговых выводов может потребовать значительного времени. Поэтому исследование одномерных задач, требующих значительно меньше исходной информации и значительно легче и быстрей решаемых, может оказаться полезным во многих случаях. Кроме того, понижение размерности модели возможно, если один из масштабов значительно больше других (например, случай тонкого пласта), а также если рассматриваемая область намного превышает размеры неоднородностей.
Одним из таких случаев является проблема взаимовлияния состояния природных газовых гидратов и изменений климата. Повышение температуры может приводить к разрушению газовых гидратов и выделению из них газа. В результате могут происходить локальные газовые выбросы, порой довольно крупного масштаба, постоянно наблюдаемые в различных областях Мирового океана, а также, возможно, и на суше (например, в ряде работ предполагают связь подобных процессов с образованием воронок выброса на Ямале [5]). Сосредоточение подобных событий в одной области может существенно влиять на ее экологическое состояние, а также создавать опасные ситуации при ее освоении в процессе человеческой деятельности. В ряде работ также обсуждается возможность влияния газов, выделяющихся при диссоциации гидратов, на климат вследствие вызываемого ими парникового эффекта [2]. Возможным фактором, уменьшающим эти опасности, может служить самоконсервация газовых гидратов при отрицательных температурах. Кроме того, в работе [6] на основании исследования математических моделей делается вывод о возможном формировании непроницаемого слоя при диссоциации газовых гидратов в пористой среде, что может значительно замедлить распад газовых гидратов и даже в некоторых случаях вызвать его прекращение.
Температурные изменения на поверхности Земли могут передаваться вглубь как путем теплопередачи, так и благодаря миграции подземных флюидов, переносящих тепло. Значительная доля этой миграции связана с разломами земной коры. Для детального изучения диссоциации газовых гидратов в результате климатических изменений необходимо решение трехмерной задачи. Но ее постановка требует детального знания геологических, литологических свойств региона, коллекторских свойств пород, степени и характера флюидонасыщенности, что труднодостижимо. Поэтому часто используются более простые модели, позволяющие рассчитать основные свойства процесса и выявить степень влияния на него различных факторов.
2. Физическая постановка задачи
При изучении влияния изменения температуры на гидрат можно рассмотреть два характерных случая, которые в первом приближении сводятся к одномерным задачам.
1. Изучается процесс в крупном масштабе – например, постепенное прогревание большой области суши или моря. Предполагается, что изменения температуры по площади не происходит, она меняется только по глубине. Локальными неоднородностями пренебрегаем. Интенсивность локальных выбросов газа усредняется по площади, а для ее оценки можно использовать решение рассматриваемой ниже одномерной задачи об истечении газа из разлома.
В этом случае получаем одномерную вертикальную задачу о диссоциации газового гидрата в пористой среде. Выделяющийся газ будет двигаться вверх и давить на вышележащие пласты. В зависимости от их свойств и возникающих давлений он может постепенно просачиваться по трещинам в атмосферу, может пробивать плохо проницаемые участки чисто гидродинамическим способом, аналогично тому, как это происходит при автоколебательных режимах образования месторождений углеводородов [7, 8], а также прорывать вышележащие толщи и вызывать катастрофические выбросы.
При использовании математического моделирования для вертикальных задач, учитывающих гравитацию, необходимо проверять выполнение условия гиперболичности, которое в задачах без гравитации (горизонтальных) выполняется всегда [9].
2. Рассмотрим однородный пласт большого простирания по плоскости, ограниченный с одной стороны вертикальным разломом, по которому может осуществляться миграция флюидов. С их потоком будет переноситься тепло, а газ, выделившийся при распаде гидрата, по этому разлому будет двигаться вверх. Поэтому задачу можно свести к одномерной горизонтальной, одна из границ которой будет соответствовать разлому. Задачи подобного рода могут соответствовать структуре наблюдающихся областей дегазации в ряде морей. Как показано в работе [10], значительные области выделения газа на морском дне, содержащие большое количество газовых факелов, соответствуют линеаментам – протяженным геотектоническим зонам различного масштаба, а также их сочленениям.
Еще один класс задач, где одномерное математическое моделирование может оказаться полезным – это задачи о скважинах, в том числе – о тепловом воздействии скважины на газовый гидрат [1]. При недостаточной теплоизоляции скважины вокруг нее может происходить диссоциация газовых гидратов, сопровождающаяся повышением давления, способным приводить к разрушению скважины и выбросам газа [1, 11]. Задачу о тепловом воздействии скважины на газовый гидрат в первом приближении также можно рассматривать как одномерную осесимметричную. Задачи подобного рода применяются также при исследовании возможности подземного хранения гидратов природного газа в зоне многолетней мерзлоты [12].
Путем сравнения решений задач 1 и 2 при типичных значениях параметров можно оценить, какой вклад в общую диссоциацию газовых гидратов вносит теплопередача через разлом, а какой – через толщу вышележащих пород. При этом следует учесть анизотропию проницаемости, связанную с жильным строением гидратосодержащих пластов, в которых гидратосодержащие и вообще высокопроницаемые пропластки и микропропластки имеют обычно одно направление, чаще всего горизонтальное, что делает горизонтальную проницаемость значительно выше.
Математическое моделирование одномерных задач о разложении газовых гидратов в пористой среде может также оказаться полезным для анализа результатов экспериментов. При этом следует учитывать, что применение моделей, основанных на предположении о равновесном характере процесса диссоциации газовых гидратов, возможно при временах, значительно превышающих характерное время разложения гидратов.
При математическом моделировании задач, связанных с газовыми гидратами, необходимо учитывать различие их свойств в зоне стабильности и в зоне метастабильного состояния, для исследования которой необходимо принимать во внимание эффект самоконсервации газовых гидратов и другие особенности их поведения в зоне метастабильности [13, 14]. Одна из таких особенностей – образование льда при диссоциации газового гидрата в области отрицательных температур, что происходит вследствие замерзания выделившейся воды. Подобные эффекты могут возникать и при положительных температурах, поэтому в более полных моделях необходимо учитывать возможность образования льда.
Для исследования некоторых одномерных задач, связанных с разложением газовых гидратов в пористой среде, в ряде работ используют автомодельные решения [15, 16]. Численное моделирование позволяет исследовать более широкий круг задач. Автомодельные решения при этом можно использовать для тестирования метода.
3. Математическая постановка задачи
Для математического описания диссоциации газовых гидратов в пористой среде использованы уравнения механики сплошной среды, выражающие законы сохранения массы, импульса и энергии в предположении выполнения закона Дарси. Область фильтрации естественным образом делится на две зоны: трехфазную, где присутствуют газ, вода и гидрат, и талую – с отсутствием газогидратов. Системы дифференциальных уравнений в частных производных, описывающих движение флюидов, в каждой зоне свои, и для единого описания всей области фильтрации необходимо произвести сшивку решений систем уравнений газогидратной флюидодинамики для всех областей плоскости P, T в рамках единой вычислительной схемы. Это достигается путем исследования методом характеристик аналитических условий согласованности систем уравнений.
Задача решается для области равновесного состояния газовых гидратов.
В трехфазной зоне система уравнений имеет вид [9]:
,
Здесь формулы (1), (2) – уравнения неразрывности; (3), (4) – закон Дарси; (5), (6) – уравнение энергии; (7) – соотношение фазового равновесия для гидратов (вместо (7) в ряде работ используют другие формулы, для которых разработанная методика также применима). Индексы относятся к газу, воде, гидрату, скелету пористой среды; – индекс, указывающий фазу; – давление; – водонасыщенность; – гидратонасыщенность; – растепленность; – плотности фаз; – массовая доля воды в гидрате; – радиус-вектор; – время; – вертикальный координатный орт; – ускорение свободного падения; – абсолютная проницаемость; – пористость; , – фазовые проницаемости; , – вязкости, , – плотности источников; – внутренние энергии фаз; – коэффициенты теплопроводности фаз, A и B – эмпирические константы, входящие в соотношение фазового равновесия для гидрата (7).
Внутреннюю энергию гидрата можно выразить через энергии создающих его газа и воды, используя следующее соотношение:
где – скрытая теплота фазового перехода единицы массы гидрата, – энтальпия.
В силу соотношения (7), в выражениях для всех параметров, где встречается зависимость от T, ее можно свести к зависимости от .
Исходная система уравнений преобразуется в двухблочную систему с расщеплением по физическим процессам [9], включающую в себя блок с системой гиперболических уравнений относительно водонасыщенности и растепленности на фоне фиксированных скоростей фильтрации, и блок, содержащий уравнение пьезопроводности для определения давления в пласте с газогидратными включениями.
В двухфазной зоне система уравнений принимает вид:
,
Здесь независимыми переменными являются давление, водонасыщенность и температура.
Система (9)–(12) также преобразуется к виду, содержащему гиперболическую и параболическую части [17].
4. Анализ результатов расчетов
Для численного решения задачи используется методика построения единого алгоритма расчета течения во всей области фильтрации, включающей двух- и трехфазную зоны, предложенная в работе [4]. Согласование уравнений на границе зон проводится при помощи метода двойной каркасности [4].
В качестве модельной задачи рассматривается задача о воздействии вертикального разлома на горизонтальный пласт. Предполагается, что первоначально поровое пространство пласта частично заполнено газовым гидратом, а остальная часть – газом и водой. В начальный момент времени , . Начальное давление МПа, что соответствует глубине 300 м, на которой в районах распространения криолитозоны возможно существование термодинамически равновесных газовых гидратов. На границе разлома предполагается, в пренебрежении весом столба газа, давление, равное атмосферному.
Рассматривается одномерная задача.
Для расчета были выбраны следующие значения параметров, характерные для Мессояхского газогидратного месторождения:
Длина модельного расчетного участка полагается равной l, , шаг по пространственной координате h, . Разлому соответствует правая граница участка, .
На рис. 1 приведены графики распределения растепленности в разные моменты времени до момента t=12000 c (дальше весь гидрат диссоциирует, растепленность становится равной единице и больше не меняется). Из них видно, как диссоциация гидрата, начинающаяся вблизи границы с пониженным давлением, постепенно распространяется на всю область, приводя к полному его исчезновению. На графиках выделяются два фронта. Основной, соответствующий Sν=0,97, обусловлен переходом от трехфазной зоны, содержащей гидрат, газ и воду, к двухфазной, содержащей только газ и воду. Второй связан с интервалом изменения Sν от 0,97 до 1, обусловлен методом расчета и на протекание процесса практически не влияет.
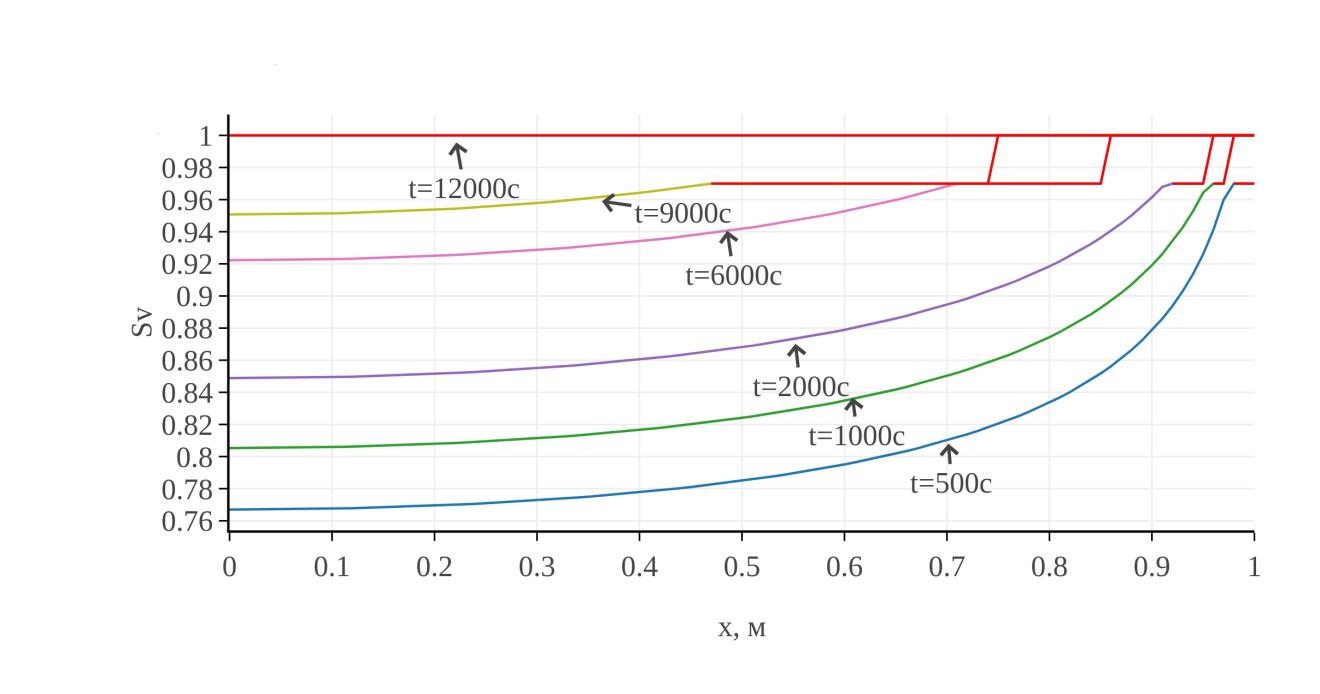
Рис. 1. Распределение растепленности для моментов времени 500, 1000, 2000, 6000, 9000, 12000 с.
На рис. 2, 3 представлено распределение давления в разные моменты времени.
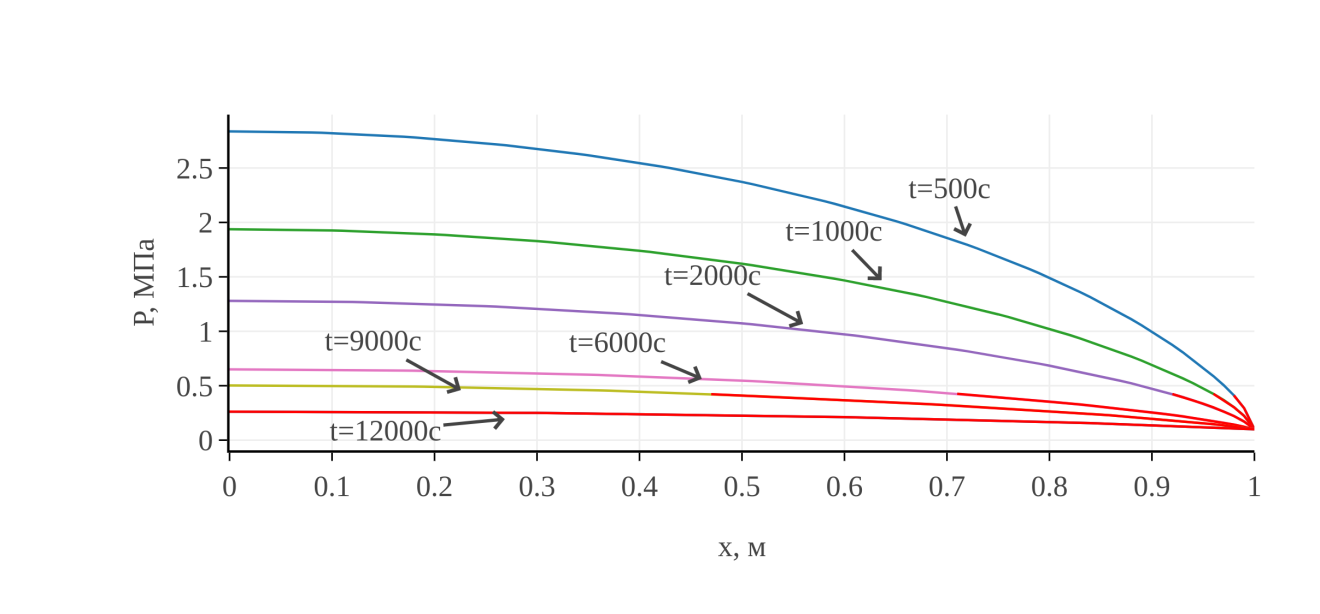
Рис. 2. Распределение давления для моментов времени 500, 1000, 2000,
6000, 9000, 12000 с.
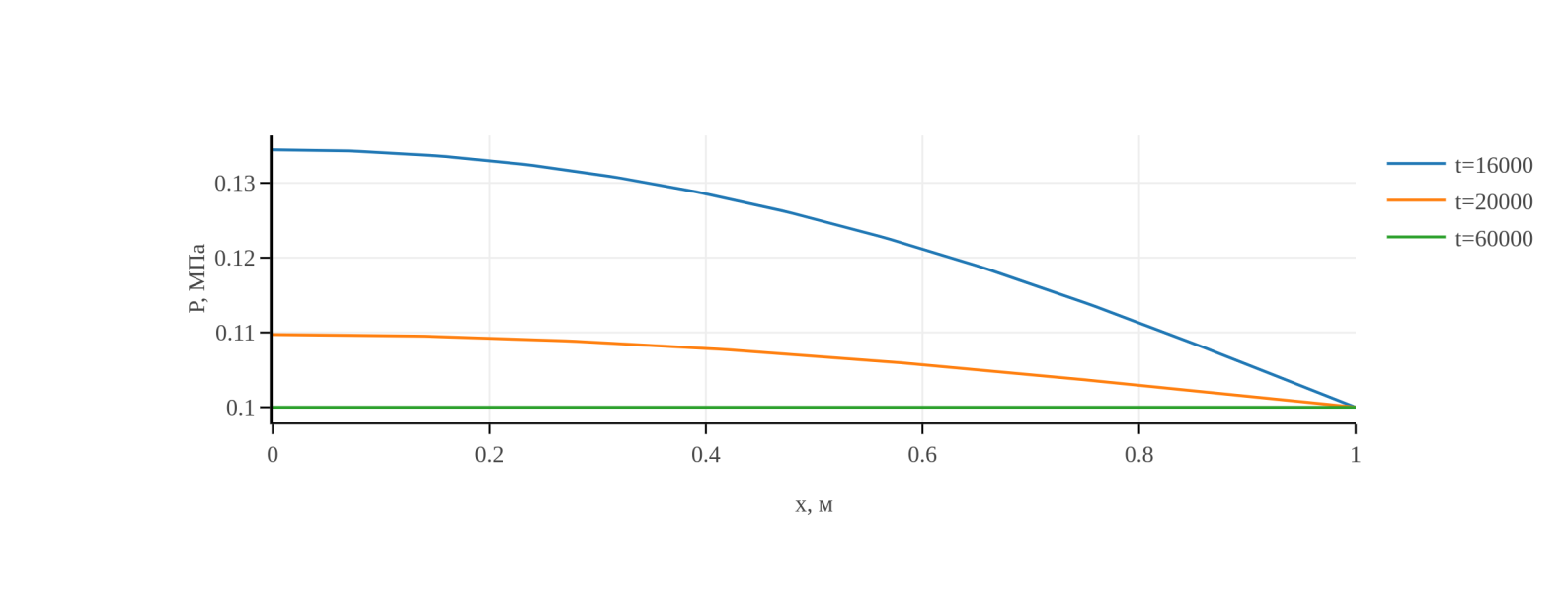
Рис. 3. Распределение давления для моментов времени 16000,
20000, 60000 с.
Из графиков видно, что на характер распределения давления наличие фронтов водонасыщенности и растепленности оказывает малое влияние, и давление изменяется почти как в однофазном случае, графики для которого (в задаче теплопроводности, аналогичной задаче однофазного упругого режима фильтрации) приведены в [18]. Давление стремится к постоянному, и, соответственно, скорости фильтрации газа и воды, пропорциональные градиенту давления, и зависящие от них члены уравнений стремятся к нулю. Таким образом, решение стабилизируется, растепленность во всей области становится равной единице, что соответствует полному разложению газового гидрата на газ и воду, а остаточные малые отклонения температуры от постоянной также медленно релаксируют к константе.
Сравнение графиков распределения температуры (рис. 4, 5) с графиками распределения растепленности показывает, что при переходе от трехфазной зоны к двухфазной на графиках наблюдается излом. Он связан с переходом от системы уравнений (1)–(7) с температурой, являющейся функцией давления, к системе (9)–(12), в которой температура является независимой переменной. Более детально это показано на рис. 6, где представлена зависимость температуры от давления в разные моменты времени. На этих графиках выделяются два участка, один из которых соответствует зависимости (7), а другой – случаю отсутствия этой функциональной зависимости.
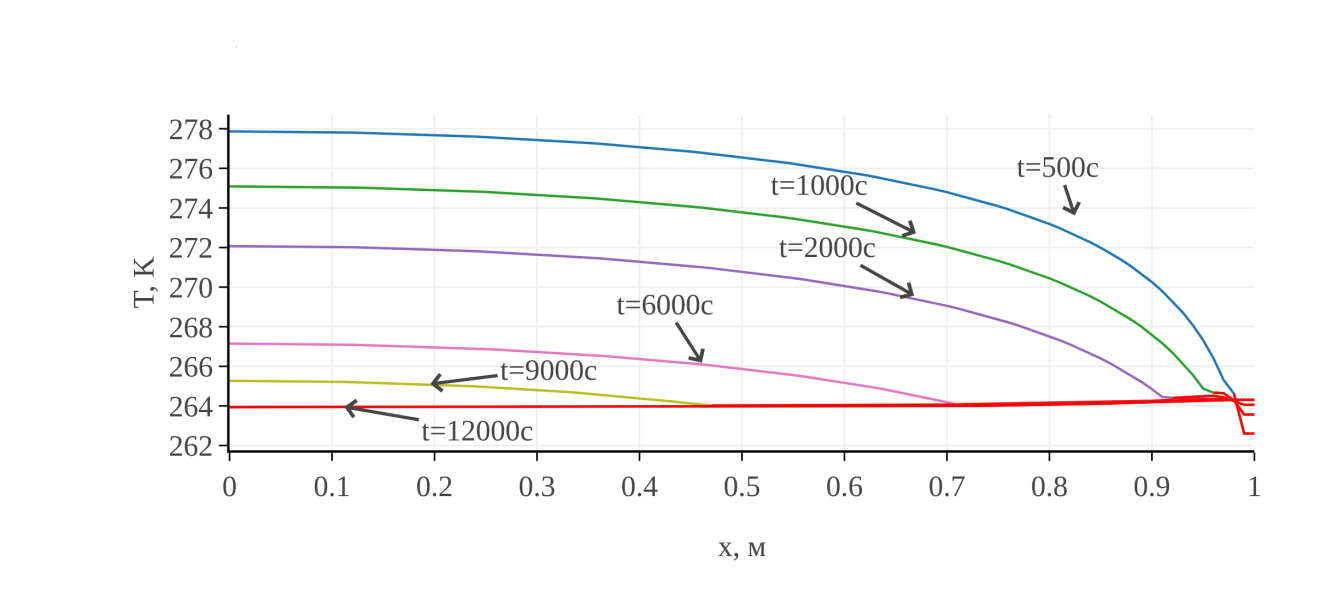
Рис. 4. Распределение температуры для моментов времени 500, 1000, 2000, 6000, 9000, 12000 с.
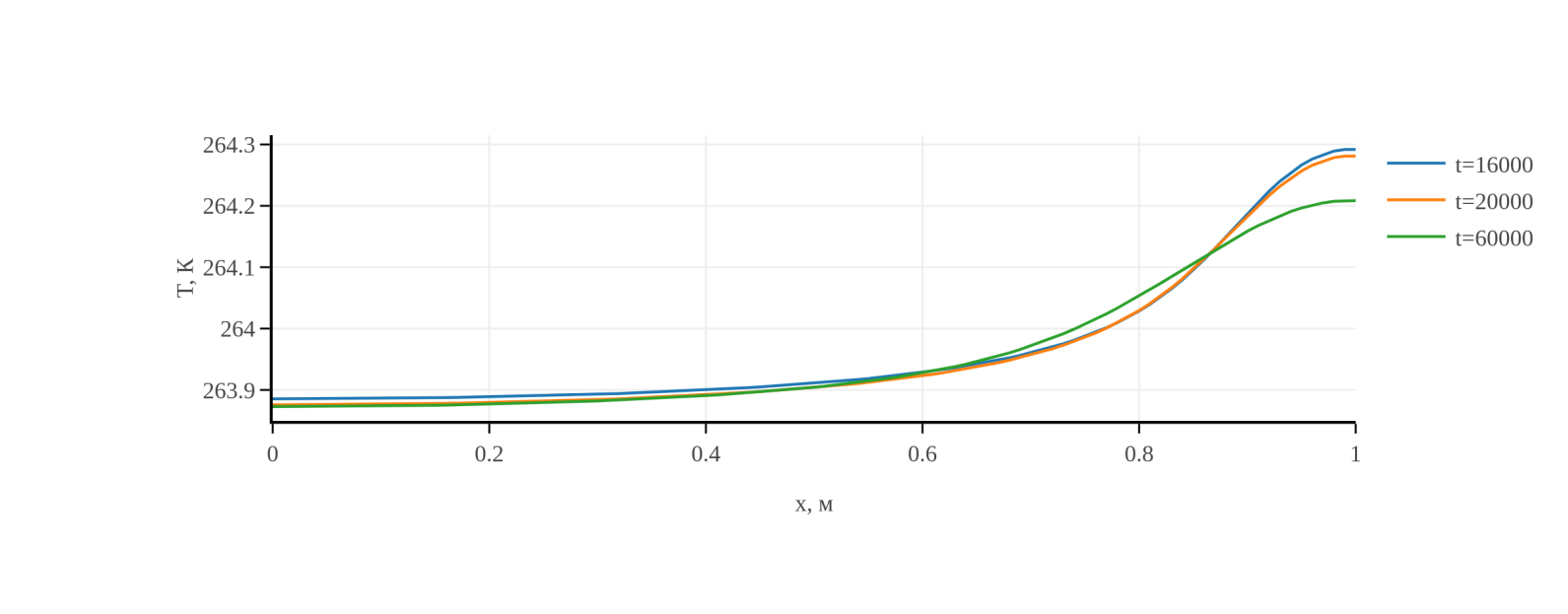
Рис. 5. Распределение температуры для моментов времени 16000,
20000, 60000 с.
Из графиков видно, что в процессе диссоциации гидрата и фильтрационного движения флюидов при заданных в расчетах условиях температура в некоторых частях области становится отрицательной. В этом случае модель должна усложняться изменением коэффициентов в формуле (7) для отрицательных температур, а также учетом эффекта самоконсервации газового гидрата [13,14]. Поскольку расчеты носят методический характер, здесь эти эффекты не учитывались.
При практическом отсутствии фильтрации на конечной стадии процесса остаточная динамика температуры (доли градуса) определяется теплопроводностью.
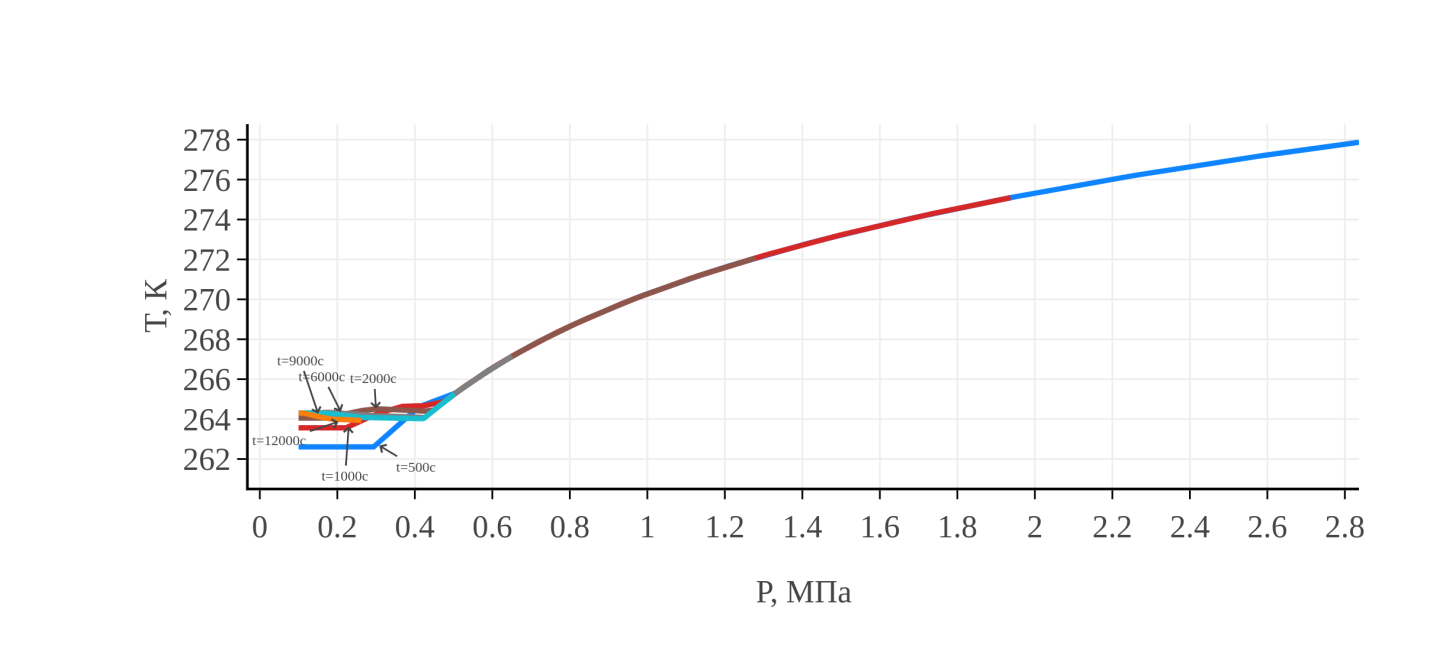
Рис. 6. Зависимость температуры от давления в разные моменты времени.
На рис. 7, 8 показано распределение водонасыщенности для различных моментов времени.
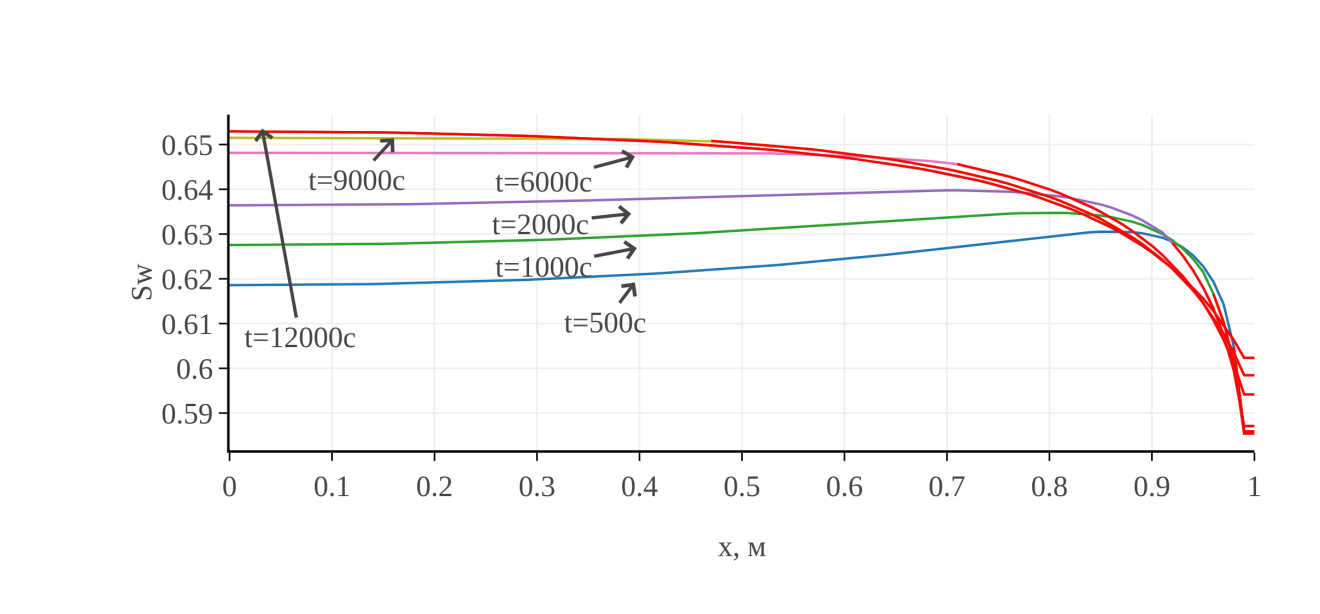
Рис. 7. Распределение водонасыщенности для моментов времени 500, 1000, 2000, 6000, 9000, 12000 с.
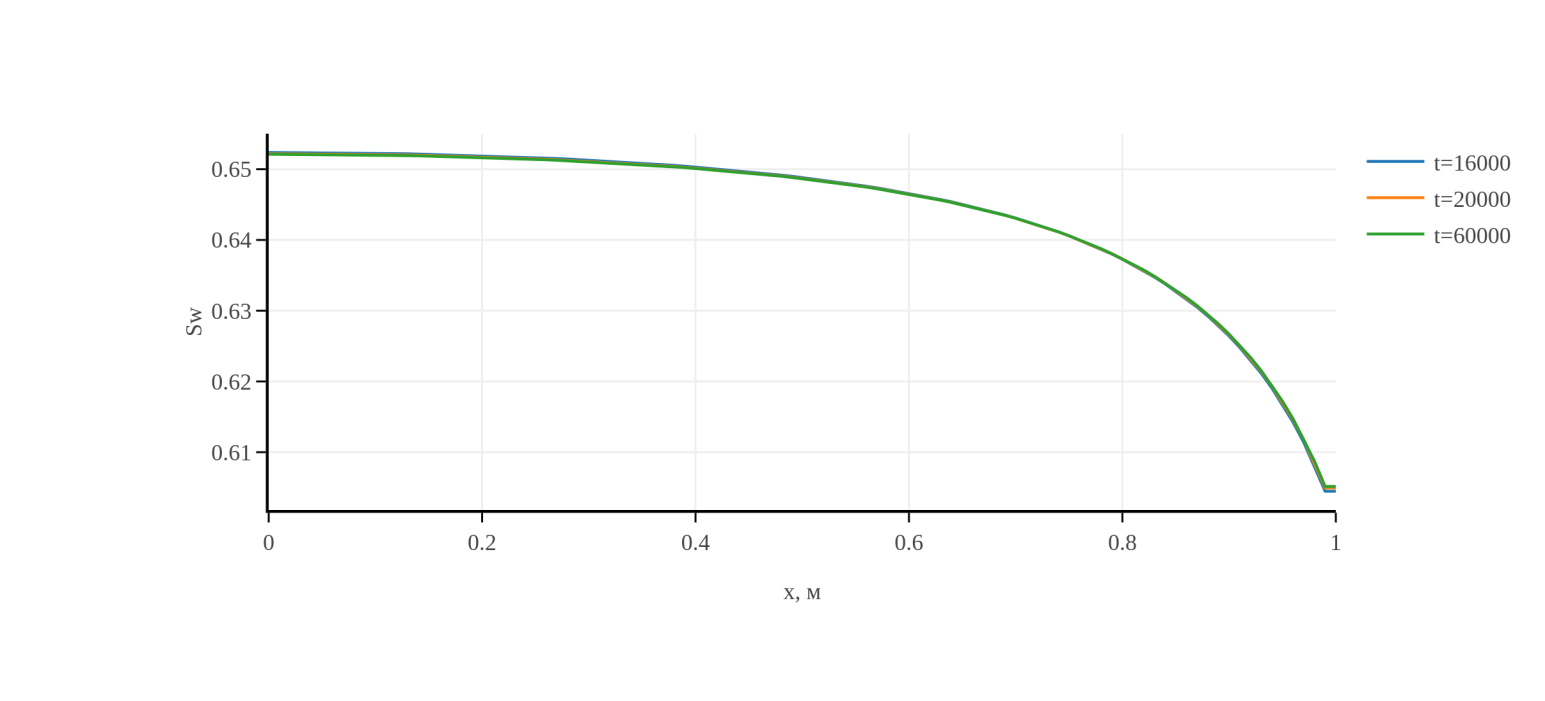
Рис. 8. Распределение водонасыщенности для моментов времени 16000,
20000, 60000 с.
Из графиков видно, что водонасыщенность на ранних и средних этапах процесса изменяется немонотонно, постепенно переходя к монотонному стационарному остаточному распределению.
5. Заключение
В работе показано, что при изучении ряда важных задач подземной флюидодинамики, связанных с разложением газовых гидратов в пористой среде, таких как исследование влияния изменений климата на состояние газовых гидратов, определение теплового влияния разломов и скважин на газовые гидраты, может быть в ряде случаев применено одномерное численное моделирование, для некоторых задач оказывающееся достаточно точным, а для других являющееся первым приближением. Проведенные расчеты показывают динамику взаимодействия трехфазной зоны, содержащей гидрат, газ и воду, и двухфазной, содержащей только газ и воду, демонстрируют возможность выхода на неоднородное стационарное решение. Полученные результаты соответствуют физике процесса и показывают возможность применения разработанных методов к реальным задачам, связанным с газовыми гидратами.
